1. Introduction
Pear is a very important fruit species and has a long tradition of cultivation in BiH. Pear belongs to the highest quality and profitable fruit species of temperate-continental climates. The genus Pyrus, known as pear, belongs to the subfamily Spiraeoideae and the family Rosaceae [
1,
2]. Pears are the most prized plants in the world, taking into account other fruits as well [
3]; they are available in the wild, but also in cultivated form as species, land races and varieties. Internationally, more than 50 countries produce pears, and contribute to their commercial market [
3].
Pear is of great economic importance. Fresh pears contain up to 20% dry matter, 9–15% total sugars, 0.30–0.60% organic acids, 0.80–1.50% cellulose, significant amounts of tannins, pectin, minerals, vitamins and other biologically important substances [
4]. In recent decades, the production of this fruit species has faced a number of problems related mainly to the sensitivity of varieties to pathogens that threaten their fertility, which makes their production more expensive and reduces the health safety of consumers [
5].
According to Maksimović et al. [
6] the area of Bosnia and Herzegovina has favorable natural and ecological conditions for intensive fruit production, which enables investment efficiency and a competitive market. Despite all that, today we have unorganized fruit production. Problems and limitations that occur in fruit production in Bosnia and Herzegovina are as follows: the inefficiency of agricultural production, inability to measure and monitor costs, lack of production documentation, the level of knowledge required in terms of production technology and basic management principles [
7]. In 2019, Bosnia and Herzegovina had pear production at the level of 30,345 tons on an area of over 11,000 ha. This represents only 0.12% of the structure of world production, which is extremely small considering the natural and climatic conditions in BiH. There are good conditions for growing pears in BiH because of the temperate continental climate. The world’s largest pear producer is China [
8], with 19,499,487 tons of production volume per year, while 24.003 tons of production volume per year is produced in BiH. In addition, it is necessary to strengthen the fruit processing capacities in BiH, in order to export not only fresh fruit but also fruit products. With the strengthening of production activity, agricultural activity is also strengthening because it is easier for fruit producers to market their products.
Raising a new orchard of fruit specie is a complex process for the producer. According to Lučić, et al. [
9], the choice of variety depends primarily on their purpose for consumers, and what can be produced from these varieties. In addition, when choosing a fruit variety, it is necessary to consider all aspects and make a decision in such a way as to choose the variety that best meets the set investment objectives [
10]. On that occasion, it is necessary to synthesize various collected data, as well as to consider all aspects of future investment. According to Rozman, et al. [
11] fruit growers often struggle with summarizing and accurately describing the success of a variety due to the large amount of data and many different assessment methods that are applied.
The aim of this paper is to make a decision concerning the selection of the pear variety that could give the best results to growers. The selection of pear varieties is carried out in order to raise a new orchard in the area of Semberija. Semberija is a lowland area in the northeast of BiH, located between the Sava and the Drina. These rivers represent the natural borders of BiH with the river Sava in the north, and the river Drina in the east. It is open in the north towards the Pannonian Basin, while in the west and south it is closed by the slopes of Majevica and other mountains.
The existence of several criteria in decision making, causes more complexity of decision making. Thus, it is necessary to use appropriate methods such as the method of multicriteria analysis (MCDA). These methods are used when we have multiple alternatives that are available, which are observed according to different criteria [
12]. This paper creates a model that would be based on a group of expert decision makers, where experts would actually, based on previous experience, evaluate pear varieties for the observed area in BiH. In order for the research goal to be realized, it is necessary to base the model of multicriteria decision making on fuzzy logic using fuzzy methods.
Imprecise statements are used in everyday speech, fast—slow, high—low, close—far, easy—difficult, etc. In order to be able to explain what it is fast, high, close, easy, etc. classical (binary) logic cannot be used. It is difficult to define what is small or large because there is no uniform definition of these terms. Fuzzy logic is then used to explain set affiliation. If it is said that, in classical logic, everything is black or white, then, for fuzzy logic, it can be said that everything is a shade of gray. According to Puška et al. [
13], the fuzzy approach is closer to human thinking because it is sometimes difficult to determine precise values.
The contribution of this paper is as follows:
- -
The methodology used allows the making of a simple decision in fruit growing using different fuzzy methods;
- -
A new model is formed for the evaluation of pear varieties when raising new fruit orchards in the area of Semberija;
- -
The proposed model and methodology provide a framework for decision making in fruit growing in a very flexible way using fuzzy methods.
2. Literature Review
The literature review will be performed in the following way: first the papers related to the research of pear varieties in fruit growing will be presented, followed by the review of papers on the application of fuzzy logic in fruit growing.
Different approaches were applied when selecting pear varieties. Mertoğluy and Evrenosoğlu [
14] investigated the high resistance of certain pear varieties to fire blight. In doing so, they used the summation of criterion values by individual varieties, and did not use MCDA methods. Li et al. [
15] investigated the quality attributes of pear varieties through testing soluble solids content. In this study, a multicultivar and individual cultivar model was developed using selection algorithms to optimize the model. Queiroz et al. [
16] performed a molecular characterization of 48 pear cultivars in Portugal and classified these cultivars into eight groups. Fang et al. [
17] identified bruises on the Korla pear variety and this was performed by combining three wavelength selections where the selection of variables and the concept of integration at the level of pear characteristics were carried out. This research shows which pears are less susceptible to damage during harvesting and transport or storage. This and similar research is focused on improving the quality of pear fruit.
Šebek [
18] followed the results of the phenological characteristics of 12 self-propelled pear varieties in Montenegro. Queiroz et al. [
19] determined the phenotypic variations of clones of the Rocha pear variety that dominates most pear production in Portugal, using the Bayesian decision model and cluster analysis. Minamikawa et al. [
20] applied genome level association and genomic selection studies to determine the marker of the pear population for reproduction. Wei and Gus [
21] processed data on the brown core of pears, which affects the taste and economic value of Chinese pears, by analyzing their main components.
From these and similar works, it could be seen that various selections were made for pear varieties. However, the previous works performed the selection of pear varieties based on their morphological characteristics. There are no works that selected the variety of pears for raising new orchards. Solving the problem of selecting pear varieties for raising fruit orchards is solved by applying multicriteria decision making. The application of decision making in agriculture is represented in modern production. The application of MCDA methods is based on the use of numerical and linguistic values. Linguistic values are used in this research because they adapt this problem to human thinking, since the experts, based on their knowledge, gave an assessment in the form of a linguistic value for a particular variety. Valuation through linguistic values is performed using the fuzzy approach. Based on that, in the second part of this selection, an overview of papers concerning the application of fuzzy logic in fruit growing will be performed.
There are numerous examples of how fuzzy numbers and fuzzy logic are used in agriculture. Maksimović et al. [
22] used fuzzy logic to select a viable supplier in integrated fruit production. They chose the fuzzy TOPSIS (technique for order of preference by similarity to ideal solution) and AHP (analytic hierarchy process) and entropy methods. Viais Neto et al. [
23] followed fuzzy logic to examine the effect of selected variables on tomato growth and productivity. Berk et al. [
24] decided to use a fuzzy logic algorithm to select methods of spraying plants in orchards, and proved that an intelligent automated system uses 4.8 times less spraying mixture compared to the conventional approach.
Nedeljković, et al. [
25] used the fuzzy PIPRECIA (pivot pairwise relative criteria importance assessment) MABAC (multiattributive border approximation area comparison) methods with the fuzzy Bonferroni operator to select a rapeseed variety. Putti et al. [
26] opted for a mathematical fuzzy model to estimate different doses of sewage sludge and irrigation with wastewater and drinking water. They argued that the use of sewage sludge could be a substitute for nitrogen based mineral fertilizers. Viais Neto et al. [
27] chose the fuzzy model to calculate the growth and yield of hybrid tomato varieties.
Paunović et al. [
28] used the FIS (fuzzy inference system) to select cherry varieties for raising orchards. Berk et al. [
29] focused on fuzzy logic to determine the doses of apple preservatives in orchards. Papageorgiou et al. [
30] selected an FIS and an adaptive neuro-fuzzy inference system (ANFIS) to determine the classification of apple quality. Prabakaran et al. [
31] used fuzzy logic to reduce fertilizer consumption and increase productivity in orchards. Kozlovskyi et al. [
32] applied fuzzy logic for the purpose of stimulating agricultural production in Ukraine. Badr et al. [
33] opted for fuzzy logic to precisely select the soil for planting vines. Petropoulos et al. [
34] applied the fuzzy AHP method to develop a simple and reliable tool for improving wine quality based on the selection of grape varieties. Medvediev et al. [
35] decided on the applied model on fuzzy logic to calculate the required vehicles for harvesting and transporting agricultural products. Maksimović et al. [
36] employed fuzzy logic when selecting plum varieties to raise new plum orchards. The fuzzy MARCOS method (measurement alternatives and ranking, according to the compromise solution) was used.
Krishnan et al. [
37] used global system for mobile communication (GSM) to reduce the energy invested in field irrigation. Osuch et al. [
38] opted for fuzzy logic to improve the quality of maintenance and servicing of agricultural machines. Salvacion [
39] benefited from using fuzzy logic when selecting land for banana and coconut production. Abbaspour-Gilandeh and Abbaspour-Gilandeh [
40] used a fuzzy and adaptive neuro-fuzzy inference system (ANFIS) to determine the mechanical characteristics of the soil and to determine what will be sown on specific agricultural land. Hoseini and Kamrani [
41] employed fuzzy logic to perform a qualitative assessment of soil suitability for the application of sprinkler irrigation. Salvacion [
42] performed observation of the suitability of planting corn in the Philippines in relation to spatiotemporal mapping under climatic constraints by observing rainy periods. Nedeljković et al. [
43] based their research on the CRITIC (criteria importance through intercriteria correlation) and fuzzy MARCOS methods to make a choice between three different apple pickers. From these and similar papers, it can be seen that the application of fuzzy logic is represented in all segments of fruit production.
3. Methodology
In order to select a pear variety to raise a new orchard, a fuzzy approach will be applied. The specificity of this approach is that experts will assess the importance of the criteria and characteristics of the variety on the basis of linguistic values. The use of linguistic values is adapted to the human way of thinking because attributive values are used and not numerical values. It is easier for human thinking to choose linguistic values than to work out a numerical value. The use of linguistic values is carried out using the fuzzy approach, where the ranking of the alternative is performed based on these values. In practice, there are a number of methods used to rank alternatives. The MABAC method is one of them. Since the method was formed in 2015, according to data from Google Scholar, this method is mentioned in 3690 papers, which makes it one of the most used new methods. Therefore, this paper uses fuzzy MABAC method. The MABAC method, unlike other MCDA methods, uses a geometric mean as a basis. If the values of the alternatives are greater than the geometric mean, the value for these alternatives will be positive, while the result for the alternatives will be negative if the values are less than the geometric mean. In this way, the result of the MABAC method ranges from −1 to 1, unlike other methods, where the result is in the range from 0 to 1. In addition, this method has fewer steps and is easier to use compared to other methods. The results obtained by this method also help to improve an alternative, because it can be seen whether this average alternative is below average or above average. On this basis, guidelines for improving alternatives can be provided.
Three phases were used in the research: initial phase, data collection and analysis and ranking of alternatives (
Figure 1).
In the first phase, the problem and the goal of the research are first defined. In the introductory part of this paper, the problem and goal of the research are defined. After that, a group of experts is formed. In this research, five experts working at the Institute of Fruit Growing in Čačak and Novi Sad were used. The experts were selected because they have great knowledge about raising new orchards and know different varieties of pears, and they are familiar with the territory of Semberija, where the raising of a new orchard was planned. After the experts were selected, the criteria by which the pear varieties would be observed were also selected. Economic–technical evaluation of pear cultivation was used, where all criteria were divided into two main criteria, namely, economic and technical criteria (
Table 1). These main criteria were then divided into three subcriteria for the economic criterion, and four subcriteria for the technical criterion. All these subcriteria were then divided into four subcriteria. Thus, the total number of subcriteria is 28.
The economic criterion is further divided into three subcriteria, namely: market, costs of raising varieties and costs of processing and transport of varieties. The market criterion examines the possibility of exporting certain varieties, their selling price and selling price of byproducts. The costs of raising the variety include the costs of preparing the orchards, the costs of raising the orchards, the costs of maintaining the orchards and the costs of harvesting. The costs of processing and transport of varieties include the costs of processing, packaging, transport and storage.
The technical criterion is further subdivided into four subcriteria: fruit, resistance, production characteristics and possibilities of processing and transport. The criterion of fruit variety examines yield, appearance, fruit size, quality and aroma. The resistance of the variety is observed in relation to spring frost, in relation to pests, diseases and other weather conditions. The criterion of production characteristics examines the service life of the variety, how suitable it is for planting, how much planting material is produced for that variety and what the pollination is. The criterion of processing and transport includes the possibility of processing, packaging, transport and storage of that variety.
After determining the criteria, the experts selected seven varieties of pears that are mostly produced in the areas of Semberija and took them into consideration. Varieties taken into consideration are:
A1—Viljamovka is a late summer variety, light yellow in color, very juicy, soluble in the mouth;
A2—Konferans, ripens in September, greenish–yellow in color, juicy and sweet and of fine texture;
A3—Junska ljepotica, ripens in June and is an early variety, the fruit is slightly smaller, yellowish–reddish in color, juicy and aromatic;
A4—Julska šarena, ripens in late July, the fruit is large and reddish–yellow, slightly acidic;
A5—Santa Marija, ripens in mid-August, the fruit itself is not too juicy, greenish–red in color;
A6—Etruska, ripens in July and August, the medium sized fruit is slightly elongated, greenish–yellow in color and is tasty and soluble;
A7—Šampionka, ripens in late September, is slightly acidic, the fruit is large and light green in color.
After the criteria and alternatives were defined, the research methodology was defined, which is realized through data collection and analysis of these data.
In the second phase, a questionnaire was formed based on criteria and alternatives. The questionnaire for the purpose of this research consists of two parts. The first part is intended to evaluate research alternatives where experts evaluated pear varieties with linguistic values ranging from very poor to exceptional. The level of agreement or disagreement with the seven statements was used (
Table 2). The second part of the questionnaire is related to the evaluation of criteria and subcriteria by an expert. In this part of the questionnaire, the linguistic values of agreement or disagreement with the seven statements were used (
Table 2). After the questionnaire was formed, it was sent to the experts for completion. The experts evaluated the alternatives by selecting the appropriate linguistic value by which, in their opinion, each variety should be evaluated. They evaluated only the values of the final subcriteria for each variety. In the same way, the experts evaluated the values of the criteria, but they had to choose how important, in their opinion, each criterion and subcriterion was, and, based on that, they gave the appropriate linguistic values. After the experts filled in the questionnaires, they returned them and the obtained values were transformed on the basis of belonging of a certain linguistic value to a certain fuzzy number. In this way, when determining the evaluation of criteria, the high value will be transformed into fuzzy numbers (7, 9, 10) so that operations with fuzzy numbers can be performed. In this way, all linguistic values are transformed. Based on that, the initial decision matrices for criteria and alternatives were formed.
After entering the collected survey questionnaires, the weights of the criteria were calculated and the alternatives were ranked using the MABAC method. The results were verified by sensitivity analysis. Sensitivity analysis has the task of examining how changes in weighting factors affect the final ranking of alternatives. In this way, it will be seen which criteria make certain alternatives worse or better.
4. Material and Methods
Fuzzy logic allows the introduction of a mean value defined between the traditional attitudes of yes/no, true/false, black/white, and so on [
44]. Fuzzy logic provides a broader framework than classical logic and focuses on the development of abilities that reflect human thinking in the real world [
45]. Fuzzy logic is a powerful mathematical tool for modeling fuzzy systems in economics, nature, and understanding people’s thinking. Its role is significant when applied to complex problems that cannot be easily described by traditional mathematical models.
Fuzzy logic is used in the application of imprecise information arising from human thinking [
25]. To make a decision in agriculture, it is necessary to include experts in decision making who can provide key information using their experience. When making decisions, the description does not have to be specified, but one can move in the opposite direction and allow the descriptions to be imprecise in accordance with human nature [
46].
The application of fuzzy logic has two approaches, a narrower approach, in which fuzzy logic is an extension of classical logic, and a broader approach, where fuzzy logic is used in sets that have no clear boundaries. Fuzzy logic allows the nuance of the degree of belonging of an element to a certain set, i.e., we assign a real number to each element as the degree of belonging of that element to the set [
47]. Fuzzy logic is closer to human thinking because, in the real world, there are situations that are not defined and for which it is difficult to determine the boundary of the set.
When using fuzzy logic, it is necessary to determine the membership function . This shows how much an individual element fulfills the condition of belonging to set A. By applying the classical theory, the membership function can receive only two values, one and zero. In fuzzy theory, the membership function can take any value in the range from zero to one. If the statement has “more truth”, it will to a greater extent meet the conditions of belonging to the set A, i.e., 0 ≤ ≤ 1 is valid for each element from set A. The process of applying fuzzy logic is called fuzzyfication.
The fuzzyfication of this method is made using triangular fuzzy numbers. A general form of triangular fuzzy number is given in the
Figure 2.
Triangular fuzzy numbers have the form T (m
1, m
2, m
3). Value m
1 represents the value of a fuzzy number ranging from 0 to 1, m
2 is where the fuzzy number membership function has the maximum value—equal to 1, and m
3 represents the value of a fuzzy number ranging from 1 to 0 [
48].
Operations that can be performed when we have two fuzzy sets
and
are [
49]:
Using these operations, the value of the alternatives is calculated using fuzzy numbers. It must be taken into account that it is possible, for example, to add only the first values of a fuzzy number when we have several sets, and the values of fuzzy numbers cannot be mixed. These are necessary to know in order to be able to apply fuzzy methods. The use of fuzzy logic in this research will be based on linguistic values, which represent values expressed in linguistic terms. Linguistic values need to be transformed into appropriate fuzzy numbers using the membership function. By applying linguistic values, qualitative values are obtained. Therefore, it is necessary to transform linguistic values into quantitative values. The application of fuzzy logic allows linguistic values to be transformed using fuzzy numbers into quantitative values on which it is possible to apply appropriate fuzzy methods.
Fuzzy MABAC Method
The MABAC method was developed by Pamučar and Ćirović in 2015 as a new MCDA method [
50], and this method is used in multiattribute decision-making problems. In agriculture, the MABAC method has been used in various studies, such as: selection of suppliers in agriculture [
51], evaluation of rapeseed variety [
25], evaluation of agricultural E-Commerce [
52], selection of byproducts in agriculture [
53], evaluation of jute fibers [
54], risk management in the supply chain in agriculture [
55] and in various other works. Based on its application, it is logical to take the MABAC method as the basis for the evaluation of pear varieties.
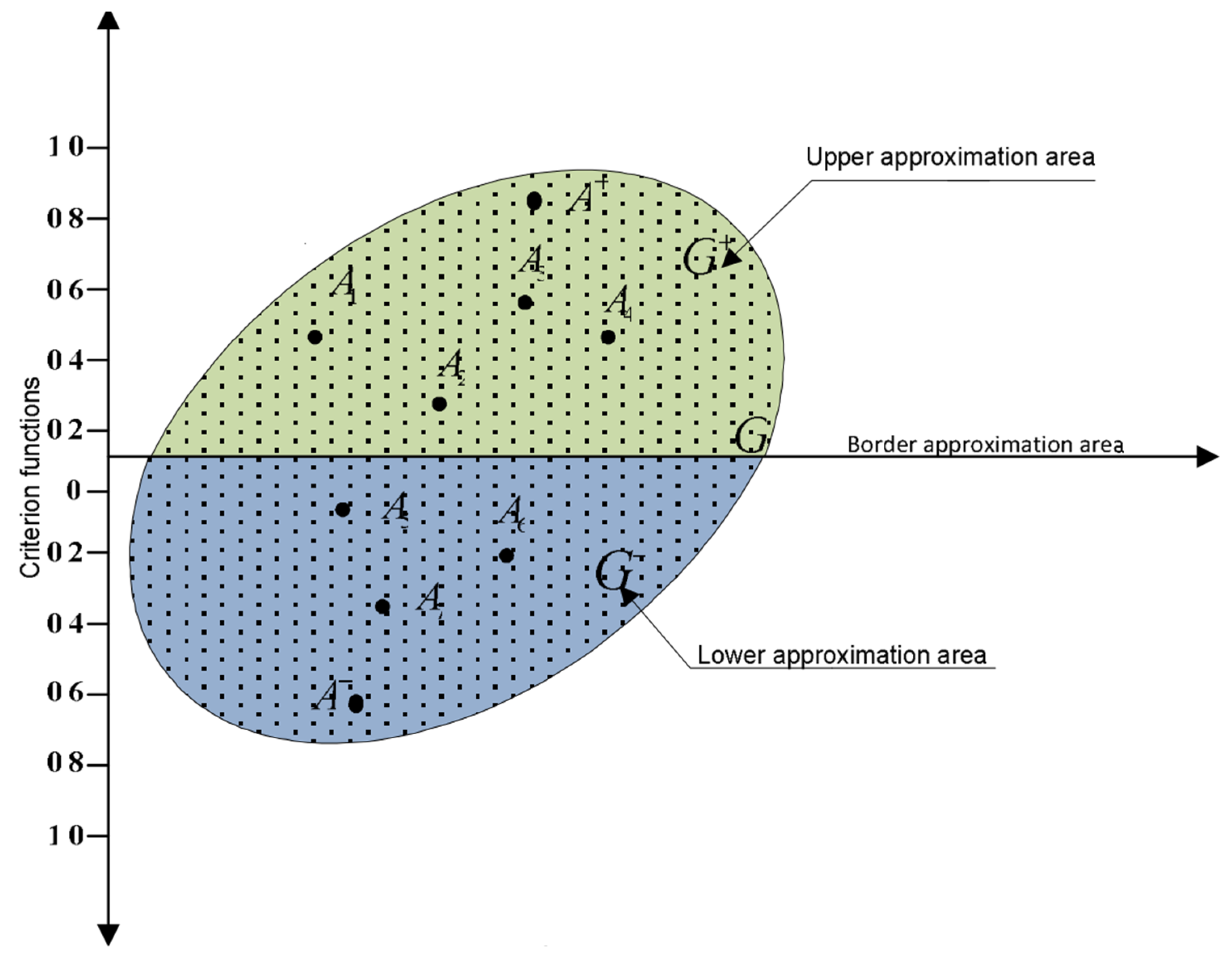
The assumption of the MABAC method is reflected in the definition of the distance of the alternative from the boundary approximate domain [
43]. The marginal approximate area represents the average value, taking into account all alternatives (
Figure 3). If the alternative is above the value of the boundary approximate domain, its value will be positive and vice versa.
The application of the fuzzy MABAC method is performed using 7 steps.
Step 1. Forming of the initial decision matrix. The formation of the decision matrix is performed in such a way that each alternative (i = 1, 2, 3,…, n) is assigned a certain value for a particular criterion (j = 1, 2, 3,…, m). Thus obtained is represented as xij. For fuzzy numbers, in this case, for triangular fuzzy numbers, we have three fuzzy numbers for each alternative according to each criterion (,,).
Step 2. Normalization of the initial matrix elements.
For benefit-type criteria:
For cost-type criteria:
where
l is the first
fuzzy number,
m the second
fuzzy number, and
u the third
fuzzy number, while
d is associated with the fuzzy number to be normalized.
These normalizations are used in relation to whether the value of the criteria should be higher or lower. If it is a question of some yield or income, it is logical that the value of the alternative will need to be higher in order for that alternative to have a better ranking. Normalization for benefit-type criteria is then used. If it is a criterion such as cost or pollution, it is logical that its value should be lower in order for that option to have a better ranking. Normalization for cost-type criteria is used.
Step 3. Calculation of the weighted matrix (V) elements. This is performed by first multiplying the normalized values by the appropriate weight and then adding that weight.
where
, represents the weighted coefficients of the criterion.
Step 4. Determination of the approximate border area matrix (
G) (
Figure 3). This represents the average geometric mean of the alternatives to the observed criterion.
where m represents total number of alternatives.
Step 5. Calculation of the matrix elements of alternative distance from the border approximate area.
where:
V—weighted matrix elements,
G—values of the border approximate areas.
Step 6. Ranking of alternatives. Ranking of the alternative is performed by summing up the matrix
elements per rows.
Step 7. Final ranking of alternatives. By defuzzyfication of the obtained values
, the final rank of alternatives is obtained.
where alternatives
t1,
t2 i t3 are values of alternatives by individual fuzzy number.
5. Results
Before evaluating the alternatives used in this study, it is necessary to determine the weight of the criteria used. The experts evaluated the criteria based on linguistic ratings from Very poor to Exceptional. The example of the main criteria will explain how the weights of the criteria were obtained, while for the other criteria the values of the experts and the final values of the weights will be given.
There are two main criteria in this research and they are economic and technical criteria. Five experts gave their assessments of the importance of these criteria (
Table 3). Experts assigned values ranging from Very low (VL) to Very High (VH) to the main criteria.
The first step in calculating criterion weights is to transform linguistic values into fuzzy numbers using the membership function (
Table 2). The weights are then added individually for each fuzzy number (
Table 4). Then, the individual value of the fuzzy number is divided by the cumulative value of the fuzzy numbers. This is performed by applying the rules for adding fuzzy numbers. In that way, the weight determined by one of the experts was obtained. In order to obtain values, it is necessary to calculate the average value of weights for each criterion. In this way, the same importance is given to all experts who participated in the research. If the average value is not used then one expert whould be given more credibility than another. Therefore, the same importance was given to all experts here and the average weight value was calculated.
Applying this procedure to the main criteria, the weight values for the auxiliary criteria are determined using linguistic values determined by individual experts (
Table 5).
The final values are obtained by multiplying the weights of the auxiliary criteria by the main criteria. When ranking alternatives using the MABAC method, the final values of the auxiliary criteria are used (
Table 6).
Once the final weight values have been determined, the value of the alternatives is calculated. First, the experts evaluated the alternatives using linguistic values, then these values are transformed into numerical values using the affiliation function. In order to assign the same importance to all experts, the average values of fuzzy numbers for each alternative were calculated for each subcriterion (
Table A1). After that, the steps from the fuzzy MABAC method are applied:
First, the data is normalized (
Table 7). Normalization is performed so that the data are uniform for calculation. Since the goal of all subcriteria was to make their value as high as possible, normalization for benefit-type criteria was applied.
Second, calculations weighted matrix (V) elements (
Table 8). This is achieved by multiplying the normalized values by the appropriate weight for those subcriteria. The meaning of weight is to give more importance to some subcriteria compared to other subcriteria. Due to that, the normalized values of the decision-making matrix are made more difficult.
Third, the approximate border area matrix is calculated and the deviation of alternatives from the approximate border area is calculated (
Table 9). The approximate border area matrix represents the average value of the difficult separation matrix. The higher the value of a certain value, the higher and more positive it will be, while if it is lower than the average, the value will be lower and negative.
Fourth, addition of alternative values is performed (
Table 10). This is carried out by adding the appropriate fuzzy numbers for the alternatives. The higher the value of these fuzzy numbers the better the alternative will be ranked and vice versa.
Fifth, fuzzy numbers go through defuzzyfication. Defuzzyfication is performed because the value for the corresponding member of the fuzzy number for alternatives is obtained in the transition step. In order to obtain the final value of the alternative it is necessary to execute defuzzyfication and get a crispy number. Once the final value of the alternative is obtained, they are ranked and the ranking order of the alternative is determined. The higher the value of the alternative, the better the ranking. Characteristic of the application of the MABAC method is that the values of the alternative can be negative. This happens in cases where the values of the alternative are less than the average values for all alternatives.
After all steps of the fuzzy MABAC method were performed, the ranking of alternatives was performed. Based on expert decision making and the application of the fuzzy MABAC method, alternative A7—Šampionka was evaluated as the best alternative for planting a pear plantation in the area of Semberija, followed by alternative A2—Konferans. These results were obtained by a compromise of the ratings for all applied pear varieties. Champion and Conference pear varieties did not have all the best grades in some subcriteria; some varieties had better grades for certain subcriteria. Experts mostly gave good ratings to these varieties and that is why they are the best ranked. Therefore, it can be said that this result is expected.
The worst rated pear variety for raising a pear plantation in the area of Semberija is the alternative A5—Santa Marija. Based on these results, fruit growers are recommended to use varieties A7—Šampionka and A2—Konferans when raising a pear plantation in the area of Semberija, because they showed the best characteristics based on the used criteria and subcriteria.
The validation and comparison of results will be performed using the methods WASPAS (weighted aggregated sum product assessment) fuzzy SAW (simple additive weighting), fuzzy MARCOS and fuzzy ARAS (additive ratio assessment). Each of these methods has its own specifics and therefore they will be used to confirm the results obtained by the FMABAC method. Unlike FMABAC, the FWASPAS method uses a compromise of two methods: the weighted sum model (WSM) and weighted product model (WPM). The FSAW method performs a simple collection of aggravated data. FMARCOS ranks alternatives based on ideal and anti-ideal points. The FARAS method ranks alternatives based on calculating the degree of utility for each alternative. Due to these differences in methods, it is necessary to examine which results these methods give and whether these results agree with the results obtained by applying the FMABAC method. The following will explain the fuzzy approach and the fuzzy MABAC method.
This analysis does not call into question the results obtained by the MABAC method but is confirmed by the results obtained by other methods. The following methods were used to test this: fuzzy WASPAS, fuzzy SAW, fuzzy MARCOS and fuzzy ARAS. The ranking results obtained by these methods (
Figure 4) are the same as in the fuzzy MABAC method, and based on that, the results were confirmed.
Next was the confirmation or refutation of these sensitivity analysis results. The purpose of this analysis is to determine how the ranking order would change in relation to changes in the weights of the subcriteria, without taking into account the weights determined by the experts, in order to reduce their impact in this analysis. In this way, it will be observed how the ranking of alternatives changes when weights are set differently. When conducting a sensitivity analysis, it is performed in such a way that one of the subcriteria is assigned a weight of 0.22 while the other subcriteria are assigned a weight of 0.03. In this way individual subcriteria are more important than other subcriteria by more than seven times (7.33). Applying a permanent approach gives a great advantage to one subcriterion over other subcriteria, and, when ranking alternatives, all subcriteria are taken into account in order to consider all the criteria at least partially. Applying the above, one subcriterion is assigned seven times more weight, since there are 28 subcriteria, 28 scenarios are formed, while in 29th scenario all criteria are assigned the same weight. Applying the above, a sensitivity analysis was performed.
The results of the sensitivity analysis (
Figure 5) show that alternative A7 took first place in 21 scenarios while in seven scenarios alternative A2 took first place. This showed that alternative A7 has worse scores of these seven subcriteria compared to alternative A2, and therefore alternative A2 is better in these scenarios compared to alternative A7. These results showed that alternatives A3 and A4 have equal grades, so they take 3rd or 4th place in the ranking of alternatives. Alternative A1 had better characteristics than alternatives A6 and A5, so it took 5th place in the ranking in 24 scenarios. In four scenarios, alternative A6 took 5th place.
The evaluation of the results showed that the confirmed results were obtained by the fuzzy MABAC method and that alternative A7 is the best of the observed alternatives.
6. Discussion
When selecting a pear for planting a new orchard for the area of Semberija within BiH, two main criteria were used, namely, the economic and technical criteria, which are further broken down into subcriteria. Thus, a total of 28 final subcriteria were used in this study. Expert evaluation was used in the evaluation of the used criteria. Experts gave linguistic values to individual criteria ranging from Very low (VL) to Very High (VH). Based on the assessments of experts, the most important, in their opinion, is subcriterion C113—Sales price of the variety, followed by C122—Costs of raising an orchard, while the least significant criterion is C233—Self-pollination. Based on that, it can be concluded that, based on expert opinion, economic criteria have a more significant role in raising pear orchards than technological criteria. However, in this research, all criteria were taken into account in order for the decision to be complete [
10], and all of them were given greater importance in certain scenarios in sensitivity analyses.
Based on the conducted research and the application of the fuzzy MABAC method, the results were obtained which showed that the variety A7—Šampionka has the best indicators for raising a new pear orchard, followed by the variety A2—Konferans. These two varieties showed the best results in the sensitivity analysis, and these two varieties are the best choice when raising pear orchards in the area of Semberija. The selection of these varieties is expected to increase the efficiency of the orchard and its production, since, according to experts, these varieties have the best economic and technical characteristics.
By applying the opinion of experts, those varieties that give better results would be produced more, so the production of pears in BiH would increase. In addition, these varieties of pears have shown to be more resistant to disease and more fertile than others. In that way, the costs of pear production would be reduced and the use of chemical protective agents would be reduced, which would increase the health safety of consumers [
5].
BiH, i.e., the area of Semberija, must use favorable natural and ecological conditions for more intensive production of all fruit species [
6] and, thus, pears. When raising new fruit plantations, it is necessary to consider all the factors that affect the production of that fruit. In addition, it is necessary to take care of uncertainty when raising an orchard. Here, uncertainty is understood as the influence of weather conditions on the fruit and on the production of the pear [
56]. It is necessary, in order to reduce uncertainty, to introduce the irrigation of orchards, installation of protective nets against the hail or the installation of antihail rockets if the orchard is large, and various other measures to reduce the impact of weather conditions on pear yield in this area.
It is especially necessary to work on branding certain varieties of pears that are indigenous to the area of BiH and Semberija. The model used, which was based on the use of the MABAC method, showed good results which were confirmed through the verification of the research results. This research has shown how to facilitate decision making even when there are a large number of criteria and subcriteria in the research. Using a larger number of criteria, all the specifics of raising an orchard are considered.
The results showed that there was no change in the ranking order of the alternatives using different fuzzy methods. This showed that the methodology used contributes to stability in decision making because using different methods does not lead to a change in ranking. However, a change in the ranking order occurred when different subcriteria were assigned different weights. This showed that the alternative A7—Šampionka is not the best in all criteria, but that in some of the observed criteria, the alternative A2—Konferans is better than it. Therefore, these two varieties of pears should be the first choices of fruit growers when raising new pear orchards.
7. Conclusions
The choice of pear variety is one of the most important steps in raising new pear orchards. Each variety has its pros and cons. In order to select the right variety for raising new plantations, multicriteria decision making is one of the options to be applied. As, if the wrong varieties are selected, the new pear orchard will not give the expected results and the investment will not be justified. Therefore, it is necessary to consider more criteria and make a decision. In order to solve this problem, a fuzzy approach and group decision making based on expert decision making were used in this research.
The MABAC method was used to determine the ranking of pear varieties. In order to use this method to rank pear varieties, it was necessary for experts to evaluate all varieties based on experience and knowledge. In doing so, they applied the assessment in the form of linguistic values. The research conducted in this way showed that the Šampionka variety is the first choice when raising new pear orchards. Apart from it, the variety Koferans, which is the second choice, also achieved good results. The results obtained by the MABAC method were confirmed using other fuzzy methods. In this way, the application of this method is justified, because the results obtained by this method do not deviate from the results of similar methods.
The model and methodology used showed high flexibility and good results in ranking pear varieties. It should be emphasized that this research was conducted on seven varieties that have been most used in this area, so this is one of the limitations of this paper. It is necessary to take more varieties in order to compare and obtain results for other varieties. However, these seven varieties were taken for the reason that they are mostly grown in this area. In future research, it is necessary to use other varieties, for example, indigenous varieties in certain areas and compare them with known varieties in order to obtain the most complete results on pear varieties. Another shortcoming of this research is the criteria used in the evaluation of pear varieties. The use of a larger number of criteria would only complicate the decision-making process for experts, as they would have to evaluate each criterion according to a larger number of criteria. Other criteria need to be included in future research in order to obtain complete results on pear varieties in BiH. However, the inclusion of additional criteria and additional varieties of pears would complicate the decision-making process itself. Applying the fuzzy approach is just one of the possible directions for evaluating pear varieties. In future research, it is necessary to use other forms used in decision making, such as: fuzzy 2-type, interval fuzzy logic, Pythagorean fuzzy set [
57], d-numbers and similar approaches that exist in practice, and develop new approaches in order to make the best possible decision in fruit growing and thus improve agricultural production. It should be emphasized that this model and the methodology used provided a good basis to improve decision making in agriculture.