Mathematical Model for the Electric Vehicle Routing Problem Considering the State of Charge of the Batteries
Abstract
:1. Introduction
2. Literature Review
- Capacity fading: When the capacity of a battery under reference conditions has been reduced to 80% compared to the nominal capacity.
- Energy fading: The maximum power delivered by the battery in the reference conditions is reduced to 80% compared to the nominal power.
3. Proposed Methodology
3.1. Electric Vehicle Routing Problem Considering the State of Charge of the Batteries
3.2. Proposed Mathematical Formulations
3.2.1. Model That Only Allows Batteries to Be Fully Recharged at Stations
| Customers | |
| Customers including the depot node , | |
| Real charging stations | |
| Fictitious charging stations, to visit other stations more than once | |
| Real and fictitious charging stations | |
| Customers including the charging stations | |
| Customers including the charging stations and the depot node , | |
| Customers including the charging stations and the depot node , | |
| Customers including the charging stations and the depots node and , |
| Euclidean distance from vertex to () | |
| Travel time from vertex to () | |
| Consumption energy from vertex to () | |
| Vehicle capacity | |
| Battery capacity | |
| Consumption energy rate of battery | |
| Charging rate of battery at the station | |
| Fleet size (number of electric vehicles) | |
| Average driver speed | |
| Demand of the node ( is 0 if | |
| Earliest time window of node () | |
| Latest time window of node i () | |
| Service time of node () |
| If node immediately precedes node () | |
| Otherwise | |
| Decision variable that indicates the arrival time at node () | |
| Decision variable that indicates the remaining capacity of the vehicle battery upon reaching the node (). | |
| Decision variable that indicates the status or remaining capacity of the battery in node (). |
3.2.2. Mathematical Model That Allows Partial Recharging of the Battery at Stations
3.2.3. Model That Allows Partial Recharging and Also Limits Battery Discharge
3.2.4. Model That Allows Partial Recharging, Defines a Maximum Charge Threshold, and Limits Battery Discharge
4. Computational Experiments
- Review the literature related to electric vehicles, their physical composition, the behavior of the battery, the types of charge, and their fundamental components. A review of the electric vehicle routing problem with time windows (E-VRPWT) was conducted.
- Define the considered problem.
- Formulate the optimization models mathematically and implement them in the Julia programming language.
- Generate structured instances used as input data for the models.
- Adapt instances of the literature according to the considered problem.
- Run experiments with the Gurobi commercial solver for each formulated instance.
- Compare the results obtained between the implemented models, considering the computing time according to the size of the instance, the objective function value, the number of used electric vehicles, the number of times the vehicle arrives at a charging station, and the quantity of energy supplied to recharge the battery.
- Carry out an analysis of the impact generated by allowing partial recharging and restricting the state of charge of the car batteries and how they influenced the results.
4.1. Discussion Results: Instance with 5 Customers—3 Recharging Stations
4.2. Discussion Results: Adapted Instance with 10 Customers—5 Recharging Stations
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Chunguang, Q.; Xiaojuan, C.; Kexi, W.; Pan, P. Research on Green Logistics and Sustainable Development. In Proceedings of the 2008 International Conference on Information Management, Innovation Management and Industrial Engineering, Taipei, Taiwan, 19–21 December 2008; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NY, USA, 2008; Volume 3, pp. 162–165. [Google Scholar]
- Pelletier, S.; Jabali, O.; Laporte, G.; Veneroni, M. Battery degradation and behaviour for electric vehicles: Review and numerical analyses of several models. Transp. Res. Part B Methodol. 2017, 103, 158–187. [Google Scholar] [CrossRef]
- Bektaş, T.; Demir, E.; Laporte, G. Green vehicle routing. In Green Transportation Logistics; Springer: Cham, Switzerland, 2016; pp. 243–265. [Google Scholar]
- Høyer, K.G. The history of alternative fuels in transportation: The case of electric and hybrid cars. Util. Policy 2008, 16, 63–71. [Google Scholar] [CrossRef]
- Kebriaei, M.; Niasar, A.H.; Asaei, B. Hybrid electric vehicles: An overview. In Proceedings of the 2015 International Conference on Connected Vehicles and Expo (ICCVE), Shenzhen, China, 19–23 October 2015; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NY, USA, 2015; pp. 299–305. [Google Scholar]
- Schmalfuß, F.; Mühl, K.; Krems, J.F. Direct experience with battery electric vehicles (BEVs) matters when evaluating vehicle attributes, attitude and purchase intention. Transp. Res. Part F Traffic Psychol. Behav. 2017, 46, 47–69. [Google Scholar] [CrossRef]
- Macioszek, E. Electric Vehicles—Problems and Issues. In Advances in Human Error, Reliability, Resilience, and Performance; Springer Science and Business Media LLC.: Berlin/Heidelberg, Germany, 2019; Volume 1091, pp. 169–183. [Google Scholar]
- Macioszek, E. E-mobility infrastructure in the Górnośląsko-Zagłębiowska Metropolis, Poland, and potential for development. In Proceedings of the 5th World Congress on New Technologies (NewTech’19), Lisbon, Portugal, 18–20 August 2019; Volume 108. [Google Scholar]
- Ling, Z.; Cherry, C.R.; Wen, Y. Determining the Factors That Influence Electric Vehicle Adoption: A Stated Preference Survey Study in Beijing, China. Sustainability 2021, 13, 11719. [Google Scholar] [CrossRef]
- Yong, J.Y.; Ramachandaramurthy, V.K.; Tan, K.M.; Mithulananthan, N. A review on the state-of-the-art technologies of electric vehicle, its impacts and prospects. Renew. Sustain. Energy Rev. 2015, 49, 365–385. [Google Scholar] [CrossRef]
- Gerssen-Gondelach, S.J.; Faaij, A.P. Performance of batteries for electric vehicles on short and longer term. J. Power Sources 2012, 212, 111–129. [Google Scholar] [CrossRef]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef] [Green Version]
- Millner, A. Modeling Lithium Ion battery degradation in electric vehicles. In Proceedings of the 2010 IEEE Conference on Innovative Technologies for an Efficient and Reliable Electricity Supply, Waltham, MA, USA, 27–29 September 2010; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NY, USA, 2010; pp. 349–356. [Google Scholar]
- Lam, L. A Practical Circuit-Based Model for State of Health Estimation of Lion Battery Cells in Electric Vehicles. Master’s Thesis, Delft University of Technology, The Netherlands, 2011. [Google Scholar]
- Battery University. Article BU-808: How to Prolong Lithium-Based Batteries. 2020. Available online: https://batteryuniversity.com/article/bu-808-how-to-prolong-lithium-based-batteries (accessed on 20 November 2021).
- Pelletier, S.; Jabali, O.; Laporte, G. 50th Anniversary Invited Article—Goods Distribution with Electric Vehicles: Review and Research Perspectives. Transp. Sci. 2016, 50, 3–22. [Google Scholar] [CrossRef]
- Myall, D.; Ivanov, D.; Larason, W.; Nixon, M.; Moller, H. Accelerated Reported Battery Capacity Loss in 30 kWh Variants of the Nissan Leaf. Technical Report. 2018. Available online: https://www.preprints.org/manuscript/201803.0122/v1 (accessed on 20 November 2021).
- Montoya, A.; Guéret, C.; Mendoza, J.; Villegas, J.G. The electric vehicle routing problem with nonlinear charging function. Transp. Res. Part B Methodol. 2017, 103, 87–110. [Google Scholar] [CrossRef] [Green Version]
- Hoimoja, H.; Rufer, A.; Dziechciaruk, G.; Vezzini, A. An ultrafast EV charging station demonstrator. In Proceedings of the International Symposium on Power Electronics Power Electronics, Electrical Drives, Automation and Motion, Sorrento, Italy, 20–22 June 2012; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NY, USA, 2012; pp. 1390–1395. [Google Scholar]
- Daza, J.M.; Montoya, J.R.; Narducci, F. Resolución del problema de enrutamiento de vehículos con limitaciones de capacidad utilizando un procedimiento metaheurístico de dos fases. Rev. EIA 2009, 6, 23–38. [Google Scholar]
- Schneider, M.; Stenger, A.; Goeke, D. The Electric Vehicle-Routing Problem with Time Windows and Recharging Stations. Transp. Sci. 2014, 48, 500–520. [Google Scholar] [CrossRef] [Green Version]
- Lin, B.; Ghaddar, B.; Nathwani, J. Deep Reinforcement Learning for the Electric Vehicle Routing Problem with Time Windows. IEEE Trans. Intell. Transp. Syst. 2021, 1–11. [Google Scholar] [CrossRef]
- Gonçalves, F.; Cardoso, S.R.; Relvas, S.; Barbosa-Póvoa, A.P.F.D. Optimization of a distribution network using electric vehicles: A VRP problem. In Proceedings of the IO2011-15 Congresso da Associação Portuguesa de Investigação Operacional, Coimbra, Portugal, 18–20 April 2011; pp. 18–20. [Google Scholar]
- Lebeau, P.; De Cauwer, C.; Van Mierlo, J.; Macharis, C.; Verbeke, W.; Coosemans, T. Conventional, Hybrid, or Electric Vehicles: Which Technology for an Urban Distribution Centre? Sci. World J. 2015, 2015, 302867. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van Duin, J.; Tavasszy, L.A.; Quak, H.J. Towards electric urban freight: First promising steps in the electric vehicle revolution. Eur. Transp. 2013, 54, 1–19. [Google Scholar]
- Hiermann, G.; Puchinger, J.; Ropke, S.; Hartl, R.F. The Electric Fleet Size and Mix Vehicle Routing Problem with Time Windows and Recharging Stations. Eur. J. Oper. Res. 2016, 252, 995–1018. [Google Scholar] [CrossRef] [Green Version]
- Conrad, R.G.; Figliozzi, M.A. The recharging vehicle routing problem. In Proceedings of the 2011 International Conference on Management Science and Industrial Engineering (MSIE 2011), Harbin, China, 8–11 January 2011. [Google Scholar]
- Erdoğan, S.; Miller-Hooks, E. A green vehicle routing problem. Transp. Res. Part E Logist. Transp. Rev. 2012, 4, 100–114. [Google Scholar] [CrossRef]
- Omidvar, A.; Tavakkoli-Moghaddam, R. Sustainable vehicle routing: Strategies for congestion management and refueling scheduling. In Proceedings of the 2012 IEEE International Energy Conference and Exhibition (ENERGYCON), Florence, Italy, 9–12 September 2012; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NY, USA, 2012; pp. 1089–1094. [Google Scholar]
- Desaulniers, G.; Errico, F.; Irnich, S.; Schneider, M. Exact Algorithms for Electric Vehicle-Routing Problems with Time Windows. Oper. Res. 2016, 64, 1388–1405. [Google Scholar] [CrossRef]
- Keskin, M.; Çatay, B. Partial recharge strategies for the electric vehicle routing problem with time windows. Transp. Res. Part C Emerg. Technol. 2016, 65, 111–127. [Google Scholar] [CrossRef]
- Felipe, Á.; Ortuño, M.T.; Righini, G.; Tirado, G. A heuristic approach for the green vehicle routing problem with multiple technologies and partial recharges. Transp. Res. Part E Logist. Transp. Rev. 2014, 71, 111–128. [Google Scholar] [CrossRef]
- Sassi, O.; Cherif, W.R.; Oulamara, A. Vehicle routing problem with mixed fleet of conventional and heterogenous electric vehicles and time dependent charging costs. Int. J. Math. Comput. Sci. 2014, 9. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Kiyama, N.; Aoshima, H.; Kashiyama, M. A route search method for electric vehicles in consideration of range and locations of charging stations. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NY, USA, 2011; pp. 920–925. [Google Scholar]
- Sassi, O.; Cherif-Khettaf, W.R.; Oulamara, A. Iterated Tabu Search for the Mix Fleet Vehicle Routing Problem with Heterogenous Electric Vehicles. In Advances in Human Error, Reliability, Resilience, and Performance; Springer Science and Business Media LLC.: Berlin/Heidelberg, Germany, 2015; Volume 359, pp. 57–68. [Google Scholar]
- Preis, H.; Frank, S.; Nachtigall, K. Energy-Optimized Routing of Electric Vehicles in Urban Delivery Systems. In Proceedings of the Operations Research; Springer Science and Business Media LLC.: Berlin/Heidelberg, Germany, 2014; pp. 583–588. [Google Scholar]
- Basso, R.; Kulcsar, B.; Egardt, B.; Lindroth, P.; Sanchez-Diaz, I. Energy consumption estimation integrated into the Electric Vehicle Routing Problem. Transp. Res. Part D Transp. Environ. 2019, 69, 141–167. [Google Scholar] [CrossRef]
- Alesiani, F.; Maslekar, N. Optimization of Charging Stops for Fleet of Electric Vehicles: A Genetic Approach. IEEE Intell. Transp. Syst. Mag. 2014, 6, 10–21. [Google Scholar] [CrossRef]
- Goeke, D.; Schneider, M. Routing a mixed fleet of electric and conventional vehicles. Eur. J. Oper. Res. 2015, 245, 81–99. [Google Scholar] [CrossRef]
- Sweda, T.M.; Klabjan, D. Finding minimum-cost paths for electric vehicles. In Proceedings of the 2012 IEEE International Electric Vehicle Conference, Greenville, SC, USA, 4–8 March 2012; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NY, USA, 2012; pp. 1–4. [Google Scholar]
- Sweda, T.M.; Dolinskaya, I.S.; Klabjan, D. Optimal Recharging Policies for Electric Vehicles. Transp. Sci. 2017, 51, 457–479. [Google Scholar] [CrossRef]
- Arslan, O.; Yıldız, B.; Karaşan, O.E. Minimum cost path problem for Plug-in Hybrid Electric Vehicles. Transp. Res. Part E Logist. Transp. Rev. 2015, 80, 123–141. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Sun, H. Battery swap station location-routing problem with capacitated electric vehicles. Comput. Oper. Res. 2015, 55, 217–232. [Google Scholar] [CrossRef]
- Verma, A. Electric vehicle routing problem with time windows, recharging stations and battery swapping stations. EURO J. Transp. Logist. 2018, 7, 415–451. [Google Scholar] [CrossRef]
- Hof, J.; Schneider, M.; Goeke, D. Solving the battery swap station location-routing problem with capacitated electric vehicles using an AVNS algorithm for vehicle-routing problems with intermediate stops. Transp. Res. Part B Methodol. 2017, 97, 102–112. [Google Scholar] [CrossRef]
- Raeesi, R.; Zografos, K.G. The electric vehicle routing problem with time windows and synchronised mobile battery swapping. Transp. Res. Part B Methodol. 2020, 140, 101–129. [Google Scholar] [CrossRef]
- Futalef, J.P.; Muñoz-Carpintero, D.; Rozas, H.; Orchard, M. Evolutionary Algorithm for the Electric Vehicle Routing Problem with Battery Degradation and Capacitated Charging Stations. In Proceedings of the Annual Conference of the PHM Society, Nashville, TN, USA, 9–13 November 2020; Volume 12, p. 9. [Google Scholar]
- Schiffer, M.; Klein, P.S.; Laporte, G.; Walther, G. Integrated planning for electric commercial vehicle fleets: A case study for retail mid-haul logistics networks. Eur. J. Oper. Res. 2021, 291, 944–960. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, S.; Qu, X. Optimal electric bus fleet scheduling considering battery degradation and non-linear charging profile. Transp. Res. Part E Logist. Transp. Rev. 2021, 154, 102445. [Google Scholar] [CrossRef]
- Xu, M.; Wu, T.; Tan, Z. Electric vehicle fleet size for carsharing services considering on-demand charging strategy and battery degradation. Transp. Res. Part C Emerg. Technol. 2021, 127, 103146. [Google Scholar] [CrossRef]
- Zang, Y.; Wang, M.; Qi, M. A column generation tailored to electric vehicle routing problem with nonlinear battery depreciation. Comput. Oper. Res. 2021, 137, 105527. [Google Scholar] [CrossRef]
- Reyes-Rubiano, L.; Ferone, D.; Juan, A.A.; Faulin, J. A simheuristic for routing electric vehicles with limited driving ranges and stochastic travel times. SORT 2019, 1, 3–24. [Google Scholar]
- Martins, L.D.C.; Tordecilla, R.D.; Castaneda, J.; Juan, A.A.; Faulin, J. Electric Vehicle Routing, Arc Routing, and Team Orienteering Problems in Sustainable Transportation. Energies 2021, 14, 5131. [Google Scholar] [CrossRef]
- Barco, J.; Guerra, A.; Muñoz, L.; Quijano, N. Optimal Routing and Scheduling of Charge for Electric Vehicles: A Case Study. Math. Probl. Eng. 2017, 2017, 8509783. [Google Scholar] [CrossRef] [Green Version]
- Linfati, R.; Escobar, J.W.; Cuevas, B. An algorithm based on granular tabu search for the problem of balancing public bikes by using multiple vehicles. DYNA 2014, 81, 284. [Google Scholar] [CrossRef]
- Bernal, J.; Escobar, J.W.; Linfati, R. A granular tabu search algorithm for a real case study of a vehicle routing problem with a heterogeneous fleet and time windows. J. Ind. Eng. Manag. 2017, 10, 646. [Google Scholar] [CrossRef]
- Bernal-Moyano, J.A.; Velasquez, J.W.E.; Marín-Moreno, C.; Linfati, R.; Gatica, G. A comparison of trajectory granular based algorithms for the location-routing problem with heterogeneous fleet (LRPH). DYNA 2017, 84, 193–201. [Google Scholar] [CrossRef]
- Bernal, J.; Escobar, J.W.; Paz, J.C.; Linfati, R.; Gatica, G. A probabilistic granular tabu search for the distance constrained capacitated vehicle routing problem. Int. J. Ind. Syst. Eng. 2018, 29, 453–477. [Google Scholar]
- Bernal, J.; Escobar, J.W.; Linfati, R. A simulated annealing-based approach for a real case study of vehicle routing problem with a heterogeneous fleet and time windows. Int. J. Shipp. Transp. Logist. 2021, 13, 185–204. [Google Scholar] [CrossRef]
- Escobar, J.W.; Duque, J.L.R.; García-Cáceres, R. A granular tabu search for the refrigerated vehicle routing problem with homogeneous fleet. Int. J. Ind. Eng. Comput. 2022, 13, 135–150. [Google Scholar] [CrossRef]
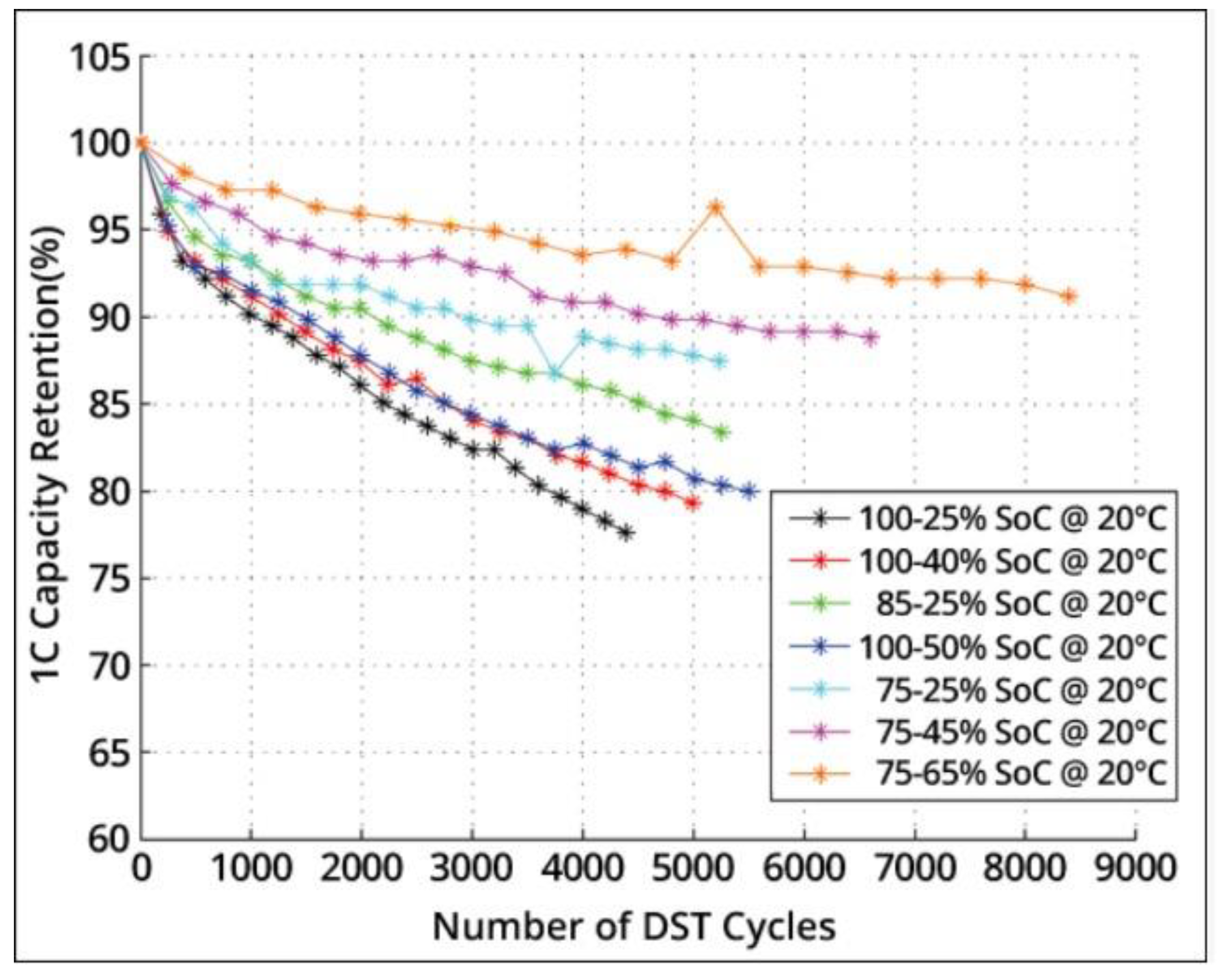



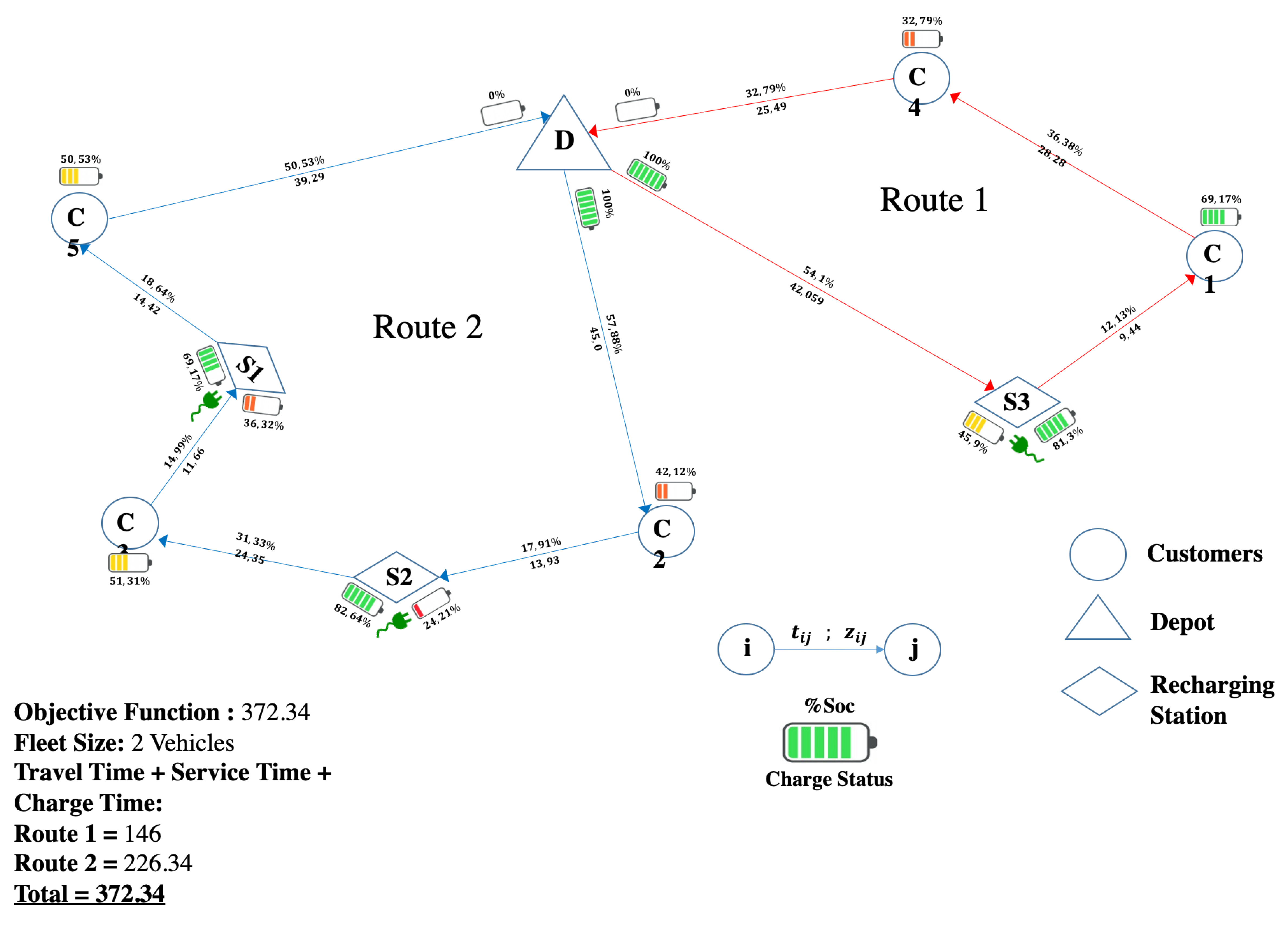

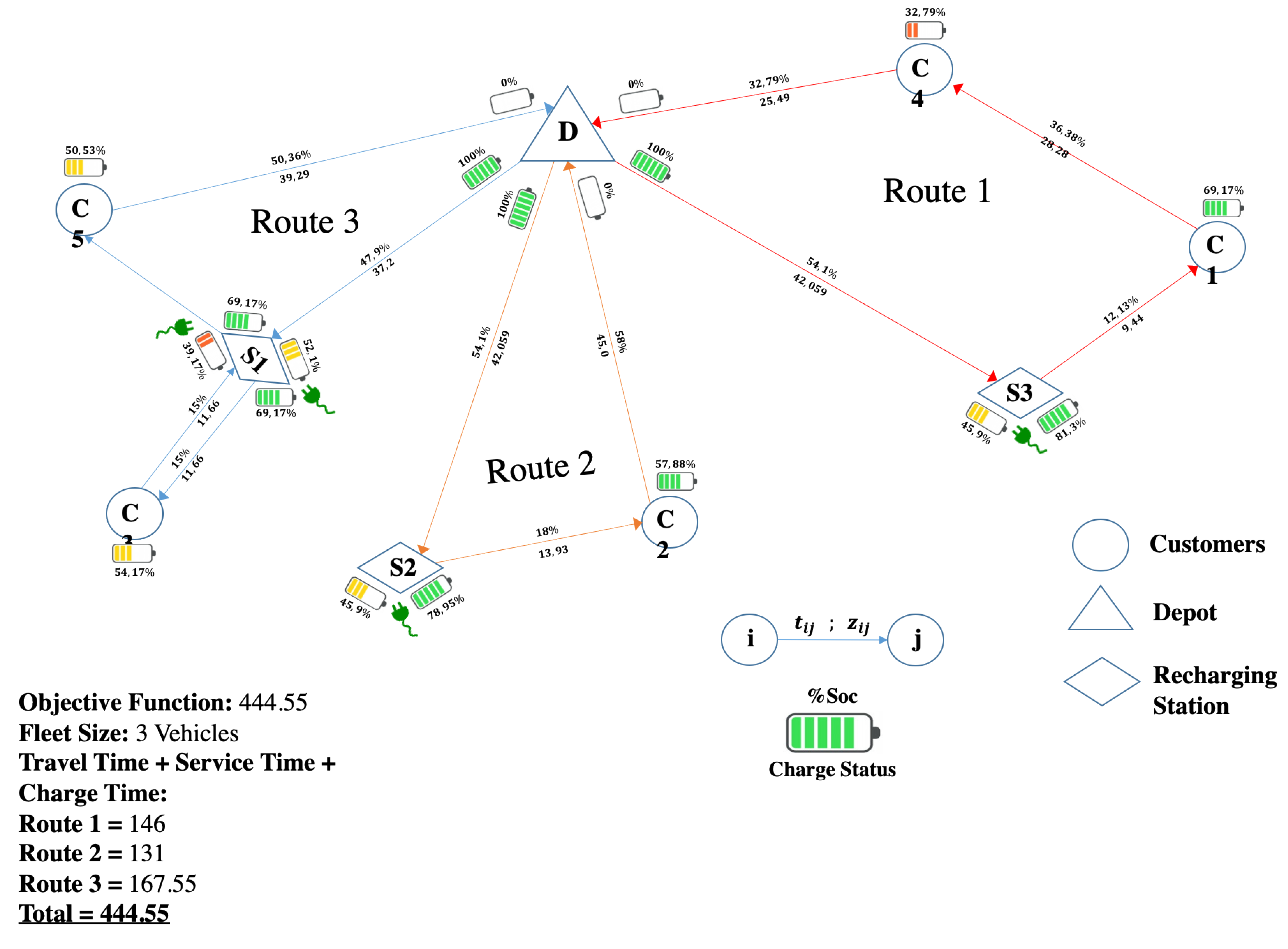
| Paper | Allows Partial Recharge | Considers Battery Charging Stations | Forces a Full Recharge | Time Window for Customers | Limits Complete Discharge | Penalizes Overcharging at Stations | Considers the Nonlinear Recharge Curve | Allows Exchange Batteries | Grants Multiple Recharge Options | Considers a Heterogeneous Fleet |
|---|---|---|---|---|---|---|---|---|---|---|
| Conrad and Figliozzi [27] | x | x | x | |||||||
| Sweda and Klabjan [40] | x | x | x | |||||||
| Barco et al. [54] | x | x | x | |||||||
| Schneider et al. [21] | x | x | x | |||||||
| Felipe et al. [32] | x | x | x | x | ||||||
| Goeke and Schneider [39] | x | x | x | |||||||
| Yang and Sun [43] | x | |||||||||
| Sweda et al. [41] | x | x | x | |||||||
| Hiermann et al. [26] | x | x | x | X | ||||||
| Desaulniers et al. [30] | x | x | x | x | ||||||
| Keskin and Çatay [31] | x | x | x | x | ||||||
| Hof et al. [45] | x | x | ||||||||
| Montoya et al. [18] | x | x | x | x | x | |||||
| Raeesi et al. [46] | x | |||||||||
| Futalef et al. [47] | x | x | x | |||||||
| Schiffer et al. [48] | x | x | x | x | ||||||
| Zhang et al. [49] | x | x | x | X | ||||||
| Xu et al. [50] | x | x | X | |||||||
| Zang et al. [51] | x | x | x | x | ||||||
| Our proposal | x | x | x | x | x | x |
| Instance | Coordinates | Time Windows | |||||
|---|---|---|---|---|---|---|---|
| ID | Type | X-Axis | Y-Axis | Earliest Time Windows | Latest Time Windows | Demand (Units) | Service Time (s) |
| D0 | Depot | 40 | 50 | 0 | 240 | 0 | 0 |
| S1 | Station | 10 | 28 | 0 | 240 | 0 | 10 |
| S2 | Station | 27 | 10 | 0 | 240 | 0 | 10 |
| S3 | Station | 77 | 30 | 0 | 240 | 0 | 10 |
| C1 | Customer | 85 | 35 | 68 | 182 | 30 | 10 |
| C2 | Customer | 40 | 5 | 55 | 185 | 10 | 10 |
| C3 | Customer | 4 | 18 | 58 | 131 | 35 | 10 |
| C4 | Customer | 65 | 55 | 26 | 111 | 14 | 10 |
| C5 | Customer | 2 | 40 | 96 | 190 | 20 | 10 |
| Description | Value |
|---|---|
| Battery Capacity (Q) | 77.75 kWh |
| Vehicle Capacity (C) | 200 Units |
| Energy Consumption Rate (h) | 1 kWh/m |
| Battery Charging Rate (g) | 0.39 s/kWh |
| Average driving speed | 1 m/s |
| Model | (a) | (b) | (c) | (d) |
|---|---|---|---|---|
| Fleet Size (vehicles) | 3 | 2 | 3 | 3 |
| Objective Function (s) | 452.07 | 372.34 | 429.93 | 444.55 |
| Computing Time (s) | <1 | <1 | <1 | <1 |
| Visits to charging stations | Route 1 = 1 | Route 1 = 1 | Route 1 = 1 | Route 1 = 1 |
| Route 2 = 1 | Route 2 = 2 | Route 2 = 1 | Route 2 = 1 | |
| Route 3 = 1 | Route 3 = 1 | Route 3 = 2 | ||
| Routing Time | Route 1 = 159.9 | Route 1 = 146.0 | Route 1 = 146.0 | Route 1 = 146.0 |
| (s) | Route 2 = 139.4 | Route 2 = 226.3 | Route 2 = 131.0 | Route 2 = 131.0 |
| Route 3 = 145.7 | Route 3 = 152.9 | Route 3 = 167.5 | ||
| Minimum Threshold | 0 | 0 | 77.75 kWh | 77.75 kWh |
| (SoC = 25%) | (SoC = 25%) | |||
| Maximum Threshold | 77.75 kWh | 77.75 kWh | 77.75 kWh | 66.08 kWh |
| (SoC = 100%) | (SoC = 100%) | (SoC = 100%) | (SoC = 85%) | |
| Minimum Value | 14.53 kWh | 18.82 kWh | 25.49 kWh | 25.49 kWh |
| (Customer or Station) | (SoC = 18.70%) | (SoC = 24.21%) | (SoC = 32.79%) | (SoC = 32.79%) |
| Maximum Value | 77.75 kWh | 64.25 kWh | 73.04 kWh | 63.20 kWh |
| (Customer or Station) | (SoC = 100.00%) | (SoC = 82.64%) | (SoC = 93.95%) | (SoC = 81.30%) |
| Charge Status (SoC) at the end of the route | Route 1 = 45% | Route 1 = 0% | Route 1 = 0% | Route 1 = 0% |
| Route 2 = 24% | Route 2 = 0% | Route 2 = 0% | Route 2 = 0% | |
| Route 3 = 6.2% | Route 3 = 0% | Route 3 = 0% | Route 3 = 0% |
| Instance | Number of Charging Stations | Number of Customers | Type of Customer |
|---|---|---|---|
| C101C5_S3 | 3 | 5 | C |
| R104C5_S3 | 3 | 5 | R |
| R105C5_S3 | 3 | 5 | R |
| RC204C5_S4 | 4 | 5 | R |
| C202C10_S5 | 5 | 10 | C |
| R102C10_S4 | 4 | 10 | R |
| R203C10_S5 | 5 | 10 | R |
| RC108C10_S4 | 4 | 10 | RC |
| C106C15_S3 | 3 | 15 | C |
| C208C15_S4 | 4 | 15 | C |
| Fleet Size (Number of Vehicles) | ||||
|---|---|---|---|---|
| Instance | (a) | (b) | (c) | (d) |
| C101C5S3 | 2 | 2 | 2 | 3 |
| R104C5S3 | 2 | 2 | 2 | 2 |
| R105C5S3 | 2 | 2 | 3 | 3 |
| RC204C5S4 | 1 | 1 | 1 | 2 |
| C202C10S5 | 1 | 1 | 2 | 2 |
| R102C10S4 | 4 | 4 | 4 | 4 |
| R203C10S5 | 1 | 1 | 1 | 3 |
| RC108C10S4 | 3 | 3 | 4 | 4 |
| C106C15S3 | 3 | 3 | 3 | 3 |
| C208C15S4 | 4 | 4 | 4 | 4 |
| Model | Number of Customers | 5 Customers | 10 Customers | 15 Customers | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Instances | C101C5S3 | R104C5S3 | R105C5S3 | RC204C5S4 | C202C10S5 | R102C10S4 | R203C10S5 | RC108C10S4 | C106C15S3 | C208C15S4 | |
| Item | |||||||||||
| (a) | Fleet Size | 3 | 2 | 2 | 2 | 2 | 4 | 2 | 4 | 3 | 4 |
| Objective Function (s) | 925.60 | 210.54 | 245.08 | 262.90 | 1571.70 | 416.96 | 424.21 | 572.86 | 2029.50 | 2134.50 | |
| Computing Time (s) | <1 | <1 | <1 | <1 | 51 | 3 | 6, 7 | 9, 5 | 1240 | . | |
| Visited Stations | 2 | 1 | 1 | 1 | 2 | 2 | 3 | 2 | 2 | 2 | |
| State of Charge (SoC) at Exiting Stations (%) | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | |
| (b) | Fleet Size | 3 | 2 | 2 | 2 | 2 | 4 | 2 | 4 | 3 | 4 |
| Objective Function (s) | 876, 2 | 206, 16 | 238, 29 | 258, 9 | 1.507, 4 | 415, 75 | 419, 39 | 557, 98 | 2.006, 9 | 2.033, 6 | |
| Computing Time (s) | <1 | <1 | <1 | <1 | 242 | 3, 2 | 11, 4 | 84, 2 | 3.727 | 770 | |
| Visited Stations | 2 | 1 | 1 | 1 | 2 | 2 | 3 | 3 | 2 | 3 | |
| State of Charge (SoC) at Exiting Stations (%) | 79; 87 | 85 | 77 | 58 | 85; 91 | 98; 92 | 98; 76; 76 | 72; 72; 79 | 96; 95 | 81; 67; 67 | |
| (c) | Fleet Size | 3 | 2 | 3 | 2 | 2 | 4 | 2 | 4 | 3 | 4 |
| Objective Function (s) | 876, 2 | 206, 16 | 255, 89 | 258, 9 | 1.556, 4 | 415, 75 | 443, 55 | 577, 71 | 2.016, 2 | 2.072, 5 | |
| Computing Time (s) | <1 | <1 | <1 | <1 | 273 | 3, 2 | 13, 2 | 22, 35 | 3.427 | 1.676 | |
| Visited Stations | 2 | 1 | 1 | 1 | 3 | 2 | 4 | 3 | 2 | 3 | |
| State of Charge (SoC) at Exiting Stations (%) | 79; 87 | 85 | 91 | 58 | 84; 77; 91 | 98; 92 | 96; 98; 90; 89 | 80; 89; 89 | 79; 95 | 80; 66; 82 | |
| (d) | Fleet Size | 3 | 2 | 3 | 2 | 2 | 4 | 3 | 4 | 4 | 4 |
| Objective Function (s) | 877, 45 | 225, 43 | 279, 10 | 272, 2 | 1.605, 2 | 450, 27 | 508, 17 | 605, 51 | 2.375, 6 | 2.072, 5 | |
| Computing Time (s) | <1 | <1 | <1 | <1 | 19 | 2, 7 | 12 | 3, 8 | 3.162 | 51, 54 | |
| Visited Stations | 2 | 2 | 2 | 2 | 4 | 4 | 5 | 4 | 5 | 3 | |
| State of Charge (SoC) at Exiting Stations (%) | 76; 73 | 66; 66 | 66; 77 | 65; 85 | 75; 73; 73; 85 | 53; 53; 81; 65 | 84; 76; 76; 76; 85 | 79; 79; 85; 85 | 82; 85; 82; 80; 80 | 80; 66; 82 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cataldo-Díaz, C.; Linfati, R.; Escobar, J.W. Mathematical Model for the Electric Vehicle Routing Problem Considering the State of Charge of the Batteries. Sustainability 2022, 14, 1645. https://doi.org/10.3390/su14031645
Cataldo-Díaz C, Linfati R, Escobar JW. Mathematical Model for the Electric Vehicle Routing Problem Considering the State of Charge of the Batteries. Sustainability. 2022; 14(3):1645. https://doi.org/10.3390/su14031645
Chicago/Turabian StyleCataldo-Díaz, Cristian, Rodrigo Linfati, and John Willmer Escobar. 2022. "Mathematical Model for the Electric Vehicle Routing Problem Considering the State of Charge of the Batteries" Sustainability 14, no. 3: 1645. https://doi.org/10.3390/su14031645






