Urban Densification Effect on Micrometeorology in Santiago, Chile: A Comparative Study Based on Chaos Theory
Abstract
:1. Introduction
1.1. Micrometeorology
1.2. Urban Densification
2. Theoretical Perspective
2.1. Dissipation and Complex Systems
2.2. Entropy and Entropy Flow
2.3. Kolmogorov’s Entropy and Its Relationship to the Loss of Information
3. Materials and Methods
3.1. Area of Study
3.2. The Data
3.3. Tools for Analysis in Nonlinear Time Series
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| PM10 | PM2.5 | CO | T | HR | WV | ||
|---|---|---|---|---|---|---|---|
| EML | 2010–2013 | ||||||
| H | 0.967 | 0.973 | 0.959 | 0.989 | 0.991 | 0.976 | |
| D | 1.033 | 1.027 | 1.041 | 1.011 | 1.009 | 1.024 | |
| 2017–2020 | |||||||
| H | 0.922 | 0.963 | 0.933 | 0.915 | 0.942 | 0.975 | |
| D | 1.078 | 1.037 | 1.067 | 1.085 | 1.058 | 1.025 | |
| EMM | 2010–2013 | ||||||
| H | 0.972 | 0.977 | 0.981 | 0.991 | 0.990 | 0.980 | |
| D | 1.028 | 1.023 | 1.019 | 1.009 | 1.010 | 1.02 | |
| 2017–2020 | |||||||
| H | 0.906 | 0.983 | 0.933 | 0.917 | 0.941 | 0.976 | |
| D | 1.094 | 1.017 | 1.067 | 1.083 | 1.059 | 1.024 | |
| EMN | 2010–2013 | ||||||
| H | 0.972 | 0.974 | 0.953 | 0.989 | 0.991 | 0.968 | |
| D | 1.028 | 1.026 | 1.047 | 1.011 | 1.009 | 1.032 | |
| 2017–2020 | |||||||
| H | 0.929 | 0.960 | 0.933 | 0.916 | 0.942 | 0.973 | |
| D | 1.071 | 1.04 | 1.067 | 1.084 | 1.058 | 1.027 | |
| EMO | 2010–2013 | ||||||
| H | 0.965 | 0.955 | 0.937 | 0.992 | 0.989 | 0.968 | |
| D | 1.035 | 1.045 | 1.063 | 1.008 | 1.011 | 1.032 | |
| 2017–2020 | |||||||
| H | 0.936 | 0.925 | 0.933 | 0.919 | 0.942 | 0.974 | |
| D | 1.064 | 1.075 | 1.067 | 1.081 | 1.058 | 1.026 | |
| EMS | 2010–2013 | ||||||
| H | 0.969 | 0.973 | 0.953 | 0.990 | 0.992 | 0.957 | |
| D | 1.031 | 1.027 | 1.047 | 1.010 | 1.008 | 1.043 | |
| 2017–2020 | |||||||
| H | 0.921 | 0.975 | 0.933 | 0.915 | 0.942 | 0.976 | |
| D | 1.079 | 1.025 | 1.067 | 1.085 | 1.058 | 1.024 | |
| EMV | 2010–2013 | ||||||
| H | 0.967 | 0.970 | 0.952 | 0.989 | 0.989 | 0.956 | |
| D | 1.033 | 1.03 | 1.048 | 1.011 | 1.011 | 1.044 | |
| 2017–2020 | |||||||
| H | 0.931 | 0.966 | 0.933 | 0.919 | 0.942 | 0.975 | |
| D | 1.069 | 1.034 | 1.067 | 1.081 | 1.058 | 1.025 | |
References
- Mauree, D.; Coccolo, S.; Deschamps, L.; Loesch, P.; Becquelin, P.; Scartezzini, J.L. Mobile Urban Micrometeorological Monitoring (MUMiM). J. Phys. Conf. Ser. 2019, 1343, 012014. [Google Scholar] [CrossRef] [Green Version]
- Foken, T. Micrometeorology; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Stull, R.B. Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands; London, UK, 1988; p. 666. [Google Scholar]
- Klausner, Z.; Ben-Efraim, M.; Arav, Y.; Tas, E.; Fattal, E. The Micrometeorology of the Haifa Bay area and Mount Carmel during the summer. Atmosphere 2021, 12, 354. [Google Scholar] [CrossRef]
- Fattal, E.; David-Saroussi, H.; Klausner, Z.; Buchman, O. An urban Lagrangian stochastic dispersion model for simulating traffic particulate-matter concentration fields. Atmosphere 2021, 12, 580. [Google Scholar] [CrossRef]
- Garratt, J.R.; Pearman, G.I. Retrospective analysis of micrometeorological observations above an australian wheat crop. Bound.-Layer Meteorol. 2020, 177, 613–641. [Google Scholar] [CrossRef]
- Landsberg, H.E. Micrometeorological temperature differentiation through urbanization. In Urban Climates, Technical Note; World Meteorologicai Organization: Geneva, Switzerland, 1970; pp. 129–136. [Google Scholar]
- Landsberg, H.E.; Maisel, T.N. Micrometeorological observations in an area of urban growth. Bound.-Layer Meteorol. 1972, 2, 365–370. [Google Scholar] [CrossRef]
- Saaroni, H.; Baruch Ziv, B. Estimating the urban heat island contribution to urban and rural air temperature differences over complex terrain: Application to an arid city. J. Appl. Meteorol. Climatol. 2010, 49, 2159–2166. [Google Scholar] [CrossRef]
- Tursilowati, L.; Sumantyo, J.T.S.; Kuze, H.; Adiningsih, E.S. The integrated wrf/urban modeling system and its application to monitoring urban heat island in Jakarta, Indonesia. J. Urban Environ. Eng. 2012, 6, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.H.; Kim, S.W.; Angevine, W.; Bianco, L.; McKeen, S.; Senff, C.; Trainer, M.; Tucker, S.; Zamora, R. Evaluation of urban surface parameterizations in the WRF model using measurements during the Texas air quality study 2006 field campaign. Atmos. Chem. Phys. 2011, 11, 2127–2143. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.-C.; Fröhlich, D.; Matzarakis, A.; Ping Lin, T. Urban roughness estimation based on digital building models for urban wind and thermal condition estimation—Application of the SkyHelios model. Atmosphere 2017, 8, 247. [Google Scholar] [CrossRef] [Green Version]
- MMA. Sistema de Información Nacional de Calidad del Aire. Ministerio del Medioambiente de Chile. 2020. Available online: https://sinca.mma.gob.cl/index.php (accessed on 9 September 2020).
- Sprott, J.C. Chaos and Time-Series Analysis; Oxford University Press: Oxford, UK, 2003; p. 528. [Google Scholar]
- Malyutinaa, E.I.; Shiryaevb, V.I. Time series forecasting using nonlinear dynamic methods and identification of deterministic chaos. Procedia Comput. Sci. 2014, 31, 1022–1031. [Google Scholar] [CrossRef] [Green Version]
- Salini, G.; Pérez, P. A study of the dynamic behavior of fine particulate matter in Santiago, Chile. Aerosol Air Qual. Res. 2015, 15, 154–165. [Google Scholar] [CrossRef] [Green Version]
- Pacheco, P.R.; Salini, G.A.; Mera, E.M. Entropía y neguentropía: Una aproximación al proceso de difusión de contaminantes y su sostenibilidad. Rev. Int. Contam. Ambient. 2021, 37, 167–185. [Google Scholar] [CrossRef]
- Salini, G.A.; Pacheco, P.R.; Mera, E.; Parodi, M.C. Probable relationship between COVID-19, pollutants and meteorology: A case study at Santiago, Chile. Aerosol Air Qual. Res. 2021, 21, 200434. [Google Scholar] [CrossRef]
- INE-Plataforma de datos Estadísticos. 2020. Available online: https://www.ine.cl/docs/default-source/encuesta-suplementaria-de-ingresos/publicaciones-y-anuarios/sntesis-de-resultados/2019/síntesis-nacional-esi-2019.pdf (accessed on 16 December 2020).
- MVU, Ministerio de Vivienda y Urbanismo y el Centro de Estudios de Ciudad y Territorio, (Housing and Urbanism Ministry and the Center for City and Territory Studies). 2020. Available online: https://www.observatoriourbano.cl (accessed on 1 December 2020).
- Salini, G.A.; Medina, E. Estudio sobre la dinámica temporal de material particulado PM10 emitido en Cochabamba, Bolivia. Rev. Int. Contam. Ambient. 2017, 33, 437–448. [Google Scholar] [CrossRef] [Green Version]
- Mexico Compacto-Senado de la Republica. 2021. Ciudad de México. Available online: https://www.senado.gob.mx/comisiones/vivienda/docs/mexico_compacto.pdf (accessed on 25 January 2021).
- Vergara, J.E. Verticalización. La edificación en altura en la región metropolitana de Santiago (1990–2014). Rev. INVI 2017, 32, 9–49. [Google Scholar] [CrossRef] [Green Version]
- PUBLICA. 2019. Available online: https://www.minvu.cl/wp-content/uploads/2019/06/CUENTA-PUBLICA-resumen-ejecutivo-2019-2.pdf (accessed on 6 April 2020).
- Stull, R.B. Meteorology for Scientists and Engineers; Brooks/Cole: Pacific Grove, CA, USA, 2000. [Google Scholar]
- Craig, S.; Grinham, J. Breathing walls: The design of porous materials for heat exchange and decentralized ventilation. Energy Build. 2017, 149, 246–259. [Google Scholar] [CrossRef]
- Travaglini, S.; Noble, J.; Ross, P.G.; Dharan, C.K.H. Mycology Matrix Composites. In American Society for Composites, Proceedings of the Twenty-Eighth Technical Conference, (Annual Technical Conference), State College, PA, USA, 9–11 September 2013; Curran Associates, Inc.: Red Hook, NY, USA; pp. 517–535. ISBN 9781629931432. (British Library Conference Proceedings).
- Prigogine, I. Introduction to Thermodynamics of Irreversible Processes; Interscience: New York, NY, USA, 1967; p. 147. [Google Scholar]
- Blunn, L.P.; Coceal, O.; Nazarian, N.; Barlow, J.F.; Plant, R.S.; Bohnenstengel, S.I.; Lean, H.W. Turbulence characteristics across a range of idealized urban canopy geometries. Bound.-Layer Meteorol. 2021, 182, 275–307. [Google Scholar] [CrossRef]
- Makedonas, A.; Carpentieri, M.; Placidi, M. Urban boundary layers over dense and tall canopies. Bound.-Layer Meteorol. 2021, 181, 73–93. [Google Scholar] [CrossRef]
- Shnapp, R.; Bohbot-Raviv, Y.; Liberzon, A.; Fattal, E. Turbulence-obstacle interactions in the Lagrangian framework: Applications for stochastic modeling in canopy flows. Phys. Rev. Fluids 2021, 5, 094601. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. The Local Structure of Turbulence in Incompressible Viscous Fluid for very Large Reynolds Numberst. Dokl. Akad. Nauk SSSR 1941, 30, 301–305. Available online: http://www.jstor.org/stable/51980 (accessed on 30 January 2021).
- Richardson, L.F. Weather Prediction by Numerical Processes; Cambridge University Press: Boston, MA, USA, 1922. [Google Scholar]
- Onsager, L. Statistical hydrodynamics. Nuovo Cim. 1949, 6, 279–287. [Google Scholar] [CrossRef]
- Weizsäcker, C.F. Das Spektrum der turbulenz bei großen Reynoldsschen Zahlen. Z. Phys. 1948, 124, 614–627. [Google Scholar] [CrossRef]
- Heisenberg, W. Zur statistischen theorie der turbulenz. Physik 1948, 124, 628–657. [Google Scholar] [CrossRef]
- Cardesa, J.I.; Vela-Martín, A.; Jiménez, J. The turbulent cascade in five dimensions. Science 2017, 357, 782–784. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thomson, D.J. Criteria for the selection of stochastic models of particle trajectories in turbulent flows. J. Fluid Mech. 1987, 180, 529–556. [Google Scholar] [CrossRef]
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Ruelle, D.P. Extending the definition of entropy to non-equilibrium steady states. Proc. Natl. Acad. Sci. USA 2003, 100, 3054–3058. [Google Scholar] [CrossRef] [Green Version]
- Cuesta, J.A. La entropía como creadora de orden. Rev. Esp. Física 2006, 20, 13–19. [Google Scholar]
- Liu, Y.; Liu, C.; Wang, D. Understanding atmospheric behaviour in terms of entropy: A review of applications of the second law of thermodynamics to meteorology. Entropy 2011, 13, 211–240. [Google Scholar] [CrossRef] [Green Version]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004; p. 387. [Google Scholar]
- Sivakumar, B.; Wallender, W.; Horwath, W.; Mitchell, J. Nonlinear deterministic analysis of air pollution dynamics in a rural and agricultural setting. Adv. Complex Syst. 2007, 10, 581–597. [Google Scholar] [CrossRef]
- Lorenz, E. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Kumar, U.; Prakash, A.; Jain, V.K. Characterization of chaos in air pollutants: A Volterra-Wiener-Korenberg series and numerical titration approach. Atmos. Environ. 2008, 42, 1537–1551. [Google Scholar] [CrossRef]
- Lee, C.K.; Lin, S.C. Chaos in air pollutant concentration (APC) time series. Aerosol Air Qual. Res. 2008, 8, 381–391. [Google Scholar] [CrossRef]
- Farmer, J.D. Chaotic attractors of an infinite dimensional dynamical system. Phys. D 1982, 4, 366–393. [Google Scholar] [CrossRef]
- Farmer, J.D.; Otto, E.; Yorke, J.A. The dimension of chaotic attractors. Phys. D 1983, 7, 153–180. [Google Scholar] [CrossRef] [Green Version]
- Kolmogorov, A.N. On Entropy per unit time as a metric invariant of automorphisms. Dokl. Akad. Nauk SSSR 1959, 124, 754–755. [Google Scholar]
- Martínez, J.A.; Vinagre, F.A. La Entropía de Kolmogorov; su Sentido Físico y su Aplicación al Estudio de Lechos Fluidizados 2D; Departamento de Química Analítica e Ingeniería Química, Universidad de Alcalá: Alcalá de Henares, Madrid, Spain, 2016; Available online: https://www.academia.edu/247937219/07/2019 (accessed on 20 September 2020).
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Brillouin, L. Science and Information Theory; Academic Press: New York, NY, USA, 1962; p. 304. [Google Scholar]
- Shaw, R. Strange attractors, chaotic behavior and information flow. Z. Nat. A 1981, 36, 80–112. [Google Scholar] [CrossRef]
- Cohen, A.; Procaccia, I. Computing the Kolmogorov entropy from time signals of dissipative and conservative dynamical systems. Phys. Rev. A Gen. Phys. 1985, 31, 1872–1882. [Google Scholar] [CrossRef]
- Rutland, J.; Garreaud, R. Meteorological air pollution for Santiago, Chile: Towards an objective episode forecasting. Environ. Monit. Assess. 1995, 34, 223–244. [Google Scholar] [CrossRef]
- Junninen, H.; Niska, H.; Tuppurainen, K.; Ruuskanen, J.; Kolehmainen, M. Methods for imputation of missing values in air quality data sets. Atmos. Environ. 2004, 38, 2895–2907. [Google Scholar] [CrossRef]
- Norazian, M.N.; Shruki, Y.A.; Azam, R.M.; Mustafa Al Bakri, A.M. Estimation of missing values in air pollution data using single imputation techniques. Sci. Asia 2008, 34, 341–345. [Google Scholar] [CrossRef]
- Emery, X. Simple and ordinary multigaussian Kriging for estimating recoverable reserves. Math. Geol. 2005, 37, 295–319. [Google Scholar] [CrossRef]
- Asa, E.; Saafi, M.; Membah, J.; Billa, A. Comparison of linear and nonlinear Kriging methods for characterization and interpolation of soil data. J. Comput. Civ. Eng. 2012, 26, 11–18. [Google Scholar] [CrossRef]
- Kyriakidis, P.; Journel, A. Geostatistical space-time models: A review. Math. Geol. 1999, 6, 651–684. [Google Scholar] [CrossRef]
- Ramos, Y.; St-Onge, B.; Blanchet, J.P.; Smargiassi, A. Spatio-temporal models to estimate daily concentrations of fine particulate matter in Montreal: Kriging with external drift and inverse distance-weighted approaches. J. Expo. Sci. Envion. Epidemiol. 2016, 26, 405–414. [Google Scholar] [CrossRef]
- Mera, E.; Cordero, B.; Condal, A.; Gutiérrez, L.; Ríos, C.; Da Silva, L. Filling of missing data in atmospheric series with linear krigeage. J. Phys. Conf. Ser. 2018, 1043, 012064. [Google Scholar] [CrossRef] [Green Version]
- Cressie, N.; Huang, H. Classes of no separable spatio temporal stationary covarianza function. J. Am. Stat. Assoc. 1999, 94, 1330–1340. [Google Scholar] [CrossRef]
- Sprott, J.C. Chaos Data Analyzer Software. 1995. Available online: http://sprott.physics.wisc.edu/cda.htm (accessed on 4 May 2021).
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick, 1980; Rand, D.Y., Young, L.S., Eds.; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef]
- Salini, G.; Pérez, P. Estudio de series temporales de contaminación ambiental mediante técnicas de redes neuronales artificiales. Ingeniare 2006, 14, 284–290. [Google Scholar] [CrossRef] [Green Version]
- Eckmann, J.P.; Oliffson, S.; Kamphorst, S.; Ruelle, D.; Ciliberto, C. Lyapunov exponents from time series. Phys. Rev. A 1986, 34, 4971–4979. [Google Scholar] [CrossRef] [PubMed]
- Grassberger, P.; Procaccia, L. Characterization of strange attractors. Phys. Rev. Lett. 1983, 50, 346–349. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D 1985, 16, 285–317. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.; Cao, Y.; Hu, J. Multiscale Analysis of Complex Time Series; Wiley and Sons Interscience: Hoboken, NJ, USA, 2007; p. 368. Available online: https://books.google.com/books?hl=zh-CN&lr=&id=rt_buhgaJEgC&oi=fnd&pg=PR1&dq=.+Multiscale+Analysis+of+Complex+Time+Series&ots=mUj4ukZpdH&sig=l3rfwzxZ_EDdEAzsXMo4H4-Kx1E#v=onepage&q=.%20Multiscale%20Analysis%20of%20Complex%20Time%20Series&f=false (accessed on 5 July 2021).
- Chelani, A.; Devotta, S. Nonlinear analysis and prediction of coarse particulate matter concentration in ambient air. J. Air Waste Manag. Assoc. 2006, 56, 78–84. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Horna, J.; Dionicio, J.; Martínez, R.; Zavaleta, A.; Brenis, Y. Dinámica simbólica y algunas aplicaciones. Sel. Mat. 2016, 3, 101–106. [Google Scholar] [CrossRef]
- Tong, N.Y.Y.; Leung, D.Y.C. Effects of building aspect ratio, diurnal heating scenario, and wind speed on reactive pollutant dispersion in urban street canyons. J. Environ. Sci. 2012, 24, 2091–2103. [Google Scholar] [CrossRef]
- Wales, D. Calculating the rate of loss of information from chaotic time series by forecasting. Nature 1991, 350, 485–488. [Google Scholar] [CrossRef]
- Köppen, W. Klassifikation der Klimate Nach Temperatur, Niederschlag und Jahresablauf. Petermanns Geogr. Mitt. 1918, 64, 193–203. Available online: http://koeppen-geiger.vu-wien.ac.at/pdf/Koppen_1918.pdf (accessed on 30 June 2021).
- Chao, Q.; Feng, A. Scientific basis of climate change and its response. Glob. Energy Interconnect. 2018, 1, 420–427. [Google Scholar] [CrossRef]
- Gramsch, E.; Morales, L.; Baeza, M.; Ayala, C.; Soto, C.; Neira, J.; Pérez, P.; Moreno, F. Citizens’ surveillance micro-network for the mapping of PM2.5 in the city of Concón, Chile. Aerosol Air Qual. Res. 2020, 20, 358–368. [Google Scholar] [CrossRef]
- Muñoz, A.A.; Klock-Barría, K.; Alvarez-Garreton, C.; Aguilera-Betti, I.; González-Reyes, Á.; Lastra, J.A.; Chávez, R.O.; Barría, P.; Christie, D.; Rojas-Badilla, M.; et al. Water Crisis in Petorca Basin, Chile: The combined effects of a mega-drought and water management. Water 2020, 12, 648. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Gao, P.; Song, C.; Cheng, C. Use of entropy in developing SDG-based indices for assessing regional sustainable development: A provincial case study of China. Entropy 2020, 22, 406. [Google Scholar] [CrossRef] [Green Version]
- Muñoz, R.C.; Corral, M.J. Surface indices of wind, stability, and turbulence at a highly polluted urban site in Santiago, Chile, and their relationship with nocturnal particulate matter concentrations. Aerosol Air Qual. Res. 2017, 17, 2780–2790. [Google Scholar] [CrossRef]
- Marsh, T.; Harvey, C.L. The Thames flood series: A lack of trend in flood magnitude and a decline in maximum levels. Hydrol. Res. 2012, 43, 203–214. [Google Scholar] [CrossRef] [Green Version]
- Tinker, L.; Cobb, D.; Bond, A.; Cashmore, M. Impact mitigation in environmental impact assessment: Paper promises or the basis of consent conditions? Impact Assess. Proj. Apprais. 2005, 23, 265–280. [Google Scholar] [CrossRef] [Green Version]
- Dorighello, T.D. Estudio del Comportamiento de la Humedad Relativa del Aire en Centros Urbanos. Boletín Asoc. Geógrafos. Españoles. 2002, 33, 159–170. Available online: https://www.bage.age-geografia.es/ojs/index.php/bage/article/view/420 (accessed on 5 July 2021).
- Ferrelli, F.; Lujan, M.; Piccolo, M.C. Modificaciones en la distribución espacial de la temperatura y la humedad relativa como resultado del crecimiento urbano: El caso de la ciudad de Bahía Blanca. Rev. Climatol. 2016, 16, 51–61. [Google Scholar]
- Wang, H.; Tang, L.; Qiu, Q.; Chen, H. Assessing the impacts of urban expansion on habitat quality by combining the concepts of land use, landscape, and habitat in two urban agglomerations in China. Sustainability 2020, 12, 4346. [Google Scholar] [CrossRef]
- Caldatto, F.C.; Bortoluzzi, S.C.; Pinheiro de Lima, E.; Gouvea da Cost, S.E. Urban sustainability performance measurement of a small Brazilian city. Sustainability 2021, 13, 9858. [Google Scholar] [CrossRef]
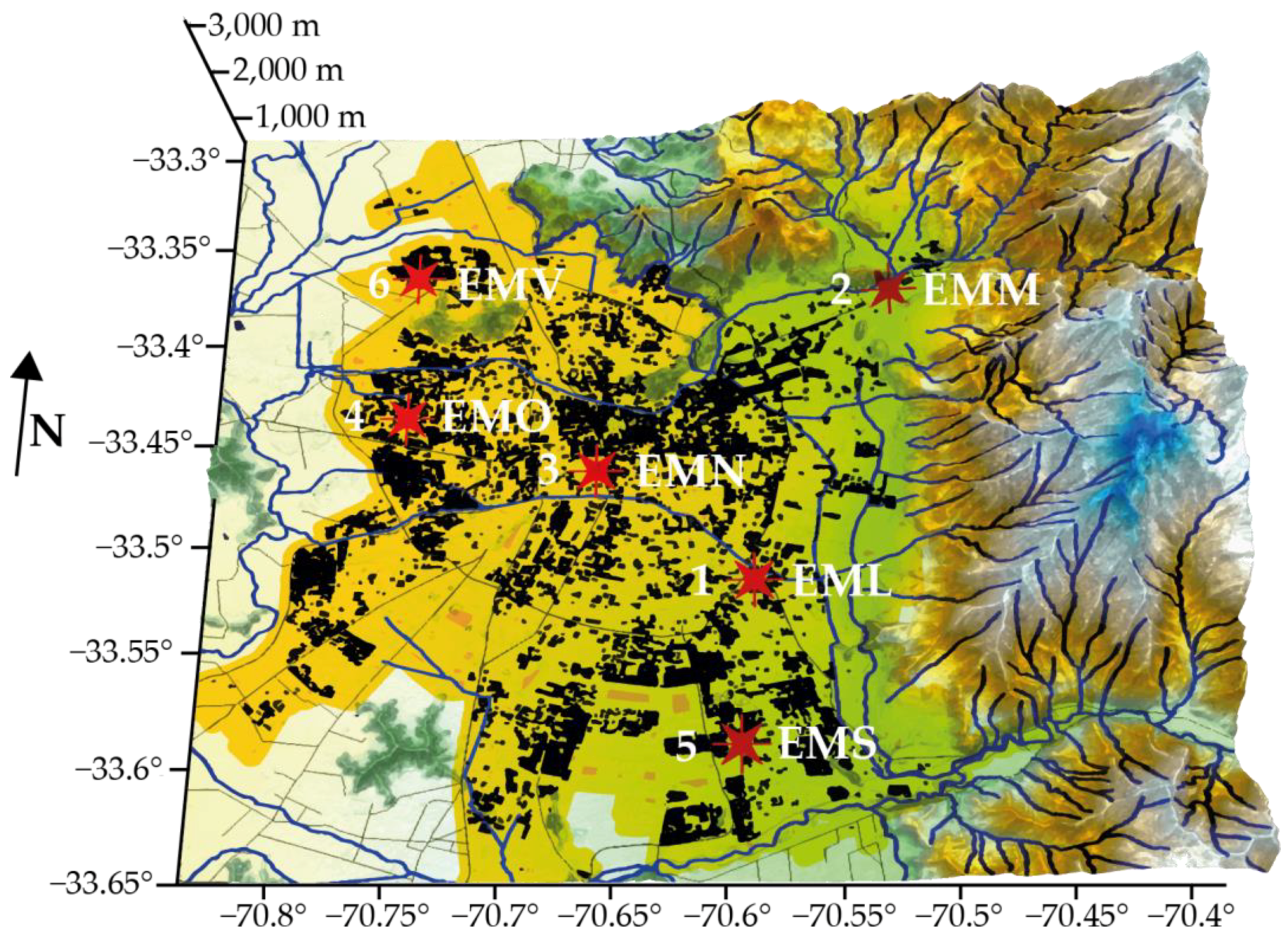

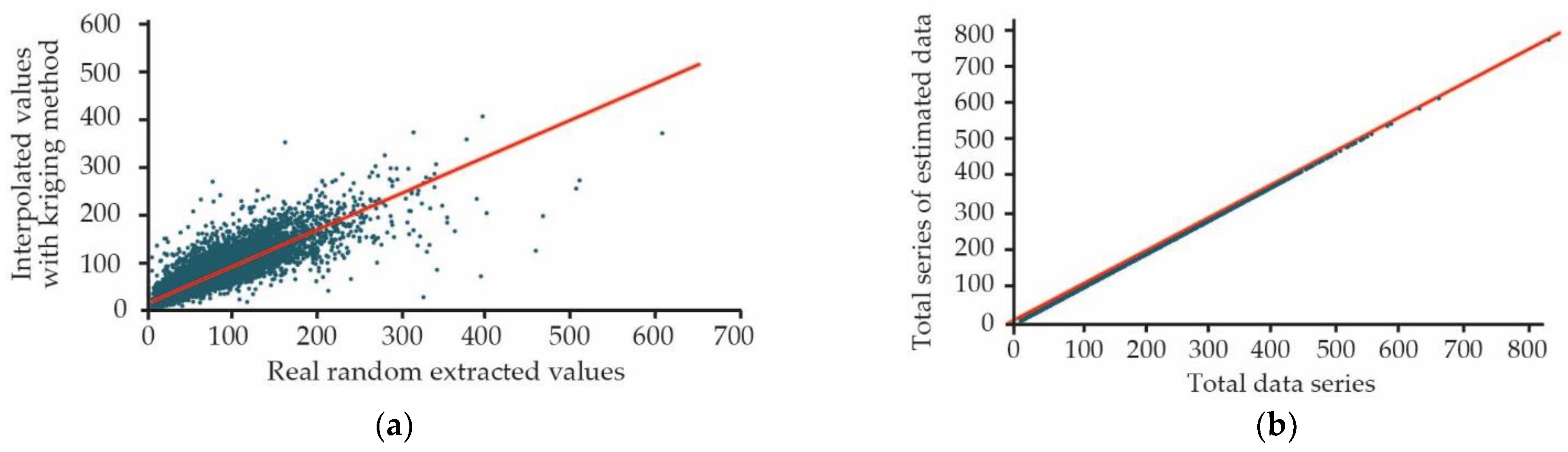






| Station Name | Location | PM10 | PM2.5 | CO | T | RH | WV | OWNER |
|---|---|---|---|---|---|---|---|---|
| 1.La Florida, EML, m.a.s.l.:784 [m] | 33°30′59.7″ S 70°35′17.4″ W | Attenuation Beta-Met One 1020 | Attenuation Beta-Met One 1020 | Gas Correlation Filter IR Photometry-Thermo 48i | VAISALA HMP35A | VAISALA HMP35A | Sensor-Met One 010C | SINCA |
| 2.Las Condes, EMM, m.a.s.l.:709 [m] | 33°22′35.8″ S 70°31′23.6″ W | Attenuation Beta-Met One 1020 | Attenuation Beta-Met One 1020 | Gas Correlation Filter IR Photometry-Thermo 48i | VAISALA HMP35A | VAISALA HMP35A | Sensor-Met One 010C | SINCA |
| 3.Santiago- Parque O’Higgins, EMN, m.a.s.l.: 570 [m] | 33°27′50.5″ S 70°39′38.5″ W | Attenuation Beta-Met One 1020 | Attenuation Beta-Met One 1020 | Gas Correlation Filter IR Photometry-Thermo 48i | VAISALA HMP35A | VAISALA HMP35A | Sensor-Met One 010C | SINCA |
| 4.Pudahuel, EMO, m.a.s.l.:469 [m] | 33°27′06.2″ S 70°40′07.8″ W | Attenuation Beta-Met One 1020 | Attenuation Beta-Met One 1020 | Gas Correlation Filter IR Photometry-Thermo 48i | VAISALA HMP35A | VAISALA HMP35A | Sensor-Met One 010C | SINCA |
| 5.Puente Alto, EMS, m.a.s.l.:698 [m] | 33°33′01.3″ S 70°34′51.4″ W | Attenuation Beta-Met One 1020 | Attenuation Beta-Met One 1020 | Gas Correlation Filter IR Photometry-Thermo 48i | VAISALA HMP35A | VAISALA HMP35A | Sensor-Met One 010C | SINCA |
| 6.Quilicura, EMV, m.a.s.l.:485 [m] | 33°21′51.6″ S 70°44′53.9″ W | Oscillating Element Microbalance TEOM-Thermo 1400AB | Attenuation Beta-Met One 1020 | Gas Correlation Filter IR Photometry-Thermo 48i | VAISALA HMP35A | VAISALA HMP35A | Sensor-Met One 010C | SINCA |
| Statistical Parameters | Periods | EMS | EML | EMN | EMO | EMV | EMM |
|---|---|---|---|---|---|---|---|
| Average | 2010–2013 2017–2020 | 62 (62) 65 (65) | 70 (70) 65 (65) | 69 (69) 69 (69) | 64 (65) 54 (54) | 79 (78) 66 (66) | 52 (52) 63 (63) |
| Min | 2010–2013 2017–2020 | 1 (1) 0 (0) | 1 (1) 0 (0) | 1 (1) 0 (0) | 1(1) 0 (0) | 0 (0) 0 (0) | 1 (1) 0 (0) |
| Max | 2010–2013 2017–2020 | 763 (763) 566 (566) | 686 (686) 609 (609) | 533 (533) 536 (536) | 592 (592) 807 (807) | 659 (659) 511 (511) | 770 (770) 460 (460) |
| Deviation | 2010–2013 2017–2020 | 42 (42) 40 (40) | 51 (50) 48 (47) | 47 (47) 46 (45) | 52 (52) 33 (33) | 57 (56) 44 (43) | 33 (33) 36 (36) |
| Median | 2010–2013 2017–2020 | 53 (53) 56 (56) | 59 (59) 53 (53) | 60 (59) 59 (59) | 51 (52) 47 (47) | 67 (66) 55 (55) | 46 (46) 57 (57) |
| Mode | 2010–2013 2017–2020 | 44 (42) 48 (48) | 55 (43) 42 (42) | 49 (37) 46 (46) | 40 (44) 34 (34) | 54 (49) 50 (50) | 33 (33) 48 (48) |
| Stations | |||||||
|---|---|---|---|---|---|---|---|
| Variable | Periods | EML (1) | EMM (2) | EMN (3) | EMO (4) | EMS (5) | EMV (6) |
| WV | 2010–2013 | 363 (1.3%) | 304 (1.1%) | 3065 (10.8%) | 441 (1.5%) | 2464 (8.7%) | 4799 (16.9%) |
| 2017–2020 | 1689 (5.8%) | 2001 (7%) | 503 (1.8%) | 1392 (4.9%) | 2569 (9%) | 463 (1.6%) | |
| T | 2010–2013 | 586 (2.1%) | 7123 (25%) | 648 (2.3%) | 902 (3.2%) | 736 (2.6%) | 1950 (6.9%) |
| 2017–2020 | 6879 (24.2%) | 2076 (7.3%) | 478 (1.7%) | 1561(5.5%) | 131(0.5%) | 2463 (8.7%) | |
| RH | 2010–2013 | 544 (1.9%) | 4245 (14.9%) | 597 (2.1%) | 3634 (12.8%) | 742 (2.6%) | 718 (2.5%) |
| 2017–2020 | 1736 (6.1%) | 2061 (7.2%) | 736 (2.6%) | 351 (1.2%) | 7588 (26.7%) | 843 (3%) | |
| CO | 2010–2013 | 369 (1.3%) | 118 (0.4%) | 525 (1.8%) | 842 (3%) | 205 (0.7%) | 525 (1.8%) |
| 2017–2020 | 1526 (5.4%) | 2249 (7.9%) | 2143 (7.5%) | 1706 (6%) | 0 (0%) | 1203 (4.2%) | |
| PM10 | 2010–2013 | 340 (1.2%) | 288 (1%) | 571 (2%) | 456 (1.6%) | 257 (0.9%) | 398 (1.4%) |
| 2017–2020 | 16 (0.1%) | 1439 (5.1%) | 664 (2.3%) | 505 (1.8%) | 600 (2.1%) | 598 (2.1%) | |
| PM2.5 | 2010–2013 | 2554 (9%) | 304 (1.1%) | 568 (2%) | 558 (2%) | 302 (1.1%) | 440 (1.5%) |
| 2017–2020 | 1711(6%) | 61 (0.2%) | 1040 (3.7%) | 1021 (3.6%) | 978 (3.4%) | 1641 (5.8%) | |
| Parameters Station | PM10 (µg/m3) | PM2.5 (µg/m3) | CO (ppm) | Temperature (°C) | HR (%) | WV(m/s) |
|---|---|---|---|---|---|---|
| EML | ||||||
| λ | 0.550 | 0.235 | 0.026 | 0.205 | 0.064 | 0.935 |
| Dc | 3.451 | 1.364 | 0.580 | 2.290 | 2.029 | 3.697 |
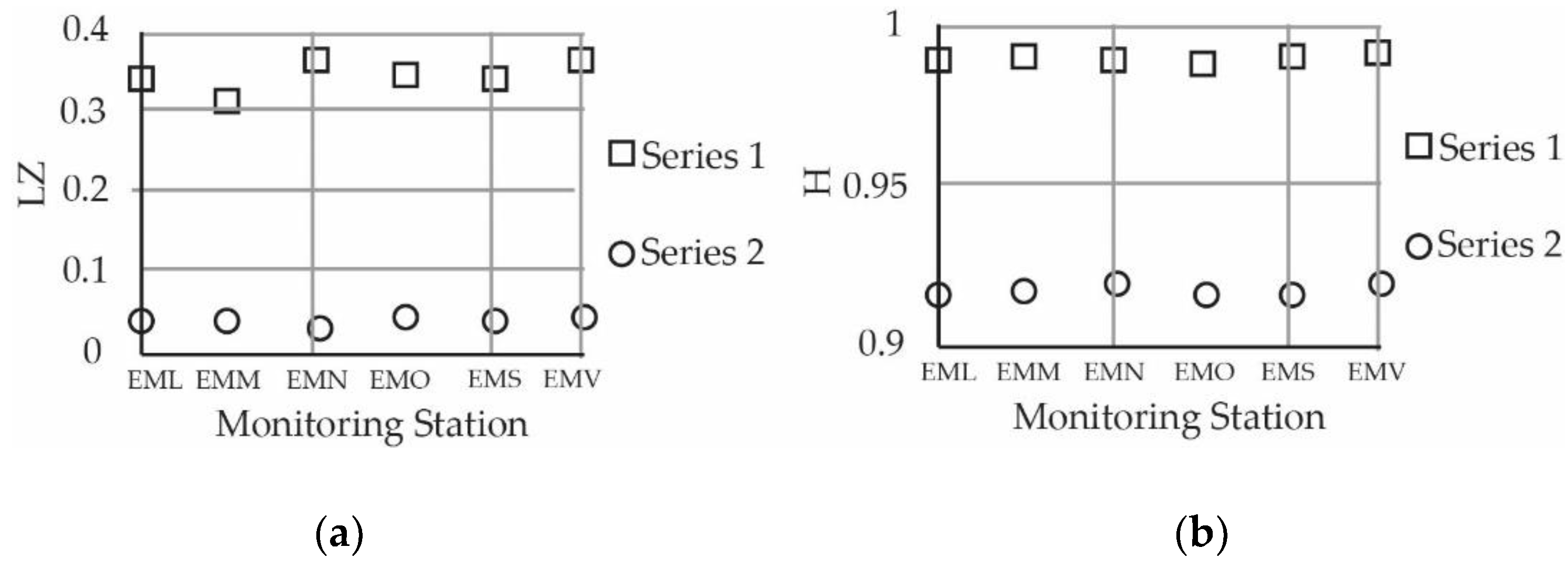
| H | 0.922 | 0.963 | 0.933 | 0.915 | 0.942 | 0.975 |
| SK (1/h) | 0.295 | 0.596 | 0.686 | 0.355 | 0.414 | 0.515 |
| LZ | 0.234 | 0.228 | 0.018 | 0.038 | 0.087 | 0.551 |
| EMM | ||||||
| λ | 0.383 | 0.614 | 0.013 | 0.184 | 0.067 | 0.937 |
| Dc | 2.530 | 1.215 | 1.254 | 2.102 | 2.203 | 3.729 |
| H | 0.906 | 0.983 | 0.933 | 0.917 | 0.941 | 0.976 |
| SK (1/h) | 0.514 | 0.400 | 0.492 | 0.377 | 0.309 | 0.519 |
| LZ | 0.196 | 0.255 | 0.011 | 0.037 | 0.089 | 0.557 |
| EMN | ||||||
| λ | 0.621 | 0.292 | 0.033 | 0.223 | 0.092 | 0.917 |
| Dc | 2.948 | 1.276 | 2.277 | 2.280 | 2.095 | 3.735 |
| H | 0.929 | 0.960 | 0.933 | 0.916 | 0.942 | 0.973 |
| SK (1/h) | 0.242 | 0.825 | 0.412 | 0.366 | 0.308 | 0.471 |
| LZ | 0.265 | 0.233 | 0.021 | 0.042 | 0.099 | 0.539 |
| EMO | ||||||
| λ | 0.550 | 0.332 | 0.046 | 0.189 | 0.081 | 0.928 |
| Dc | 2.659 | 1.284 | 2.334 | 1.611 | 2.010 | 2.755 |
| H | 0.936 | 0.925 | 0.933 | 0.919 | 0.942 | 0.974 |
| SK (1/h) | 0.819 | 0.424 | 0.387 | 0.184 | 0.330 | 0.479 |
| LZ | 0.220 | 0.265 | 0.022 | 0.040 | 0.106 | 0.537 |
| EMS | ||||||
| λ | 0.597 | 0.279 | 0.030 | 0.228 | 0.063 | 0.933 |
| Dc | 3.535 | 1.396 | 3.302 | 2.300 | 2.306 | 3.004 |
| H | 0.921 | 0.975 | 0.933 | 0.915 | 0.942 | 0.976 |
| SK (1/h) | 0.898 | 0.422 | 0.382 | 0.357 | 0.404 | 0.489 |
| LZ | 0.204 | 0.264 | 0.018 | 0.037 | 0.071 | 0.556 |
| EMV | ||||||
| λ | 0.516 | 0.304 | 0.031 | 0.170 | 0.065 | 0.915 |
| Dc | 1.148 | 1.419 | 2.149 | 1.577 | 1.947 | 2.355 |
| H | 0.931 | 0.966 | 0.933 | 0.919 | 0.942 | 0.975 |
| SK (1/h) | 0.267 | 0.463 | 0.490 | 0.171 | 0.428 | 0.395 |
| LZ | 0.231 | 0.296 | 0.019 | 0.029 | 0.085 | 0.544 |
| Stations | EML | EMM | EMN | EMO | EMS | EMV |
|---|---|---|---|---|---|---|
| Periods | <ΔI>P; <ΔI>MV | <ΔI>P; <ΔI>MV | <ΔI>P; <ΔI>MV | <ΔI>P; <ΔI>MV | <ΔI>P; <ΔI>MV | <ΔI>P; <ΔI>MV |
| 2010–2013 | −5.341; −6.079 | −5.039; −6.859 | −4.537; −6.357 | −3.271; −6.633 | −4.656; −6.955 | −3.825; −6.899 |
| 2017–2020 | −2.694; −4.000 | −3.355; −3.957 | −3.142; −4.092 | −3.083; −3.980 | −3.010; −4.066 | −2.827; −3.820 |
| Stations | EML | EMM | EMV | EMN | EMS | EMO |
|---|---|---|---|---|---|---|
| Periods | H; LZ | H; LZ | H; LZ | H; LZ | H; LZ | H; LZ |
| 2010–2013 | 0.976; 0.320 | 0.980; 0.558 | 0.956; 0.325 | 0.968; 0.286 | 0.957; 0.293 | 0.968; 0.538 |
| 2017–2020 | 0.975 (=); 0.551 (>) | 0.976 (=); 0.557 (=) | 0.975 (>); 0.544 (>) | 0.973 (>);0.539 (>) | 0.976 (>); 0.556 (>) | 0.974 (>); 0.537 (=) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pacheco, P.; Mera, E.; Salini, G. Urban Densification Effect on Micrometeorology in Santiago, Chile: A Comparative Study Based on Chaos Theory. Sustainability 2022, 14, 2845. https://doi.org/10.3390/su14052845
Pacheco P, Mera E, Salini G. Urban Densification Effect on Micrometeorology in Santiago, Chile: A Comparative Study Based on Chaos Theory. Sustainability. 2022; 14(5):2845. https://doi.org/10.3390/su14052845
Chicago/Turabian StylePacheco, Patricio, Eduardo Mera, and Giovanni Salini. 2022. "Urban Densification Effect on Micrometeorology in Santiago, Chile: A Comparative Study Based on Chaos Theory" Sustainability 14, no. 5: 2845. https://doi.org/10.3390/su14052845
APA StylePacheco, P., Mera, E., & Salini, G. (2022). Urban Densification Effect on Micrometeorology in Santiago, Chile: A Comparative Study Based on Chaos Theory. Sustainability, 14(5), 2845. https://doi.org/10.3390/su14052845








