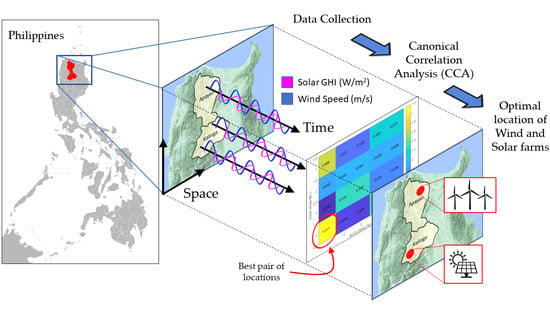
Spatio-Temporal Solar–Wind Complementarity Assessment in the Province of Kalinga-Apayao, Philippines Using Canonical Correlation Analysis †
Abstract
:1. Introduction
2. Materials and Methods
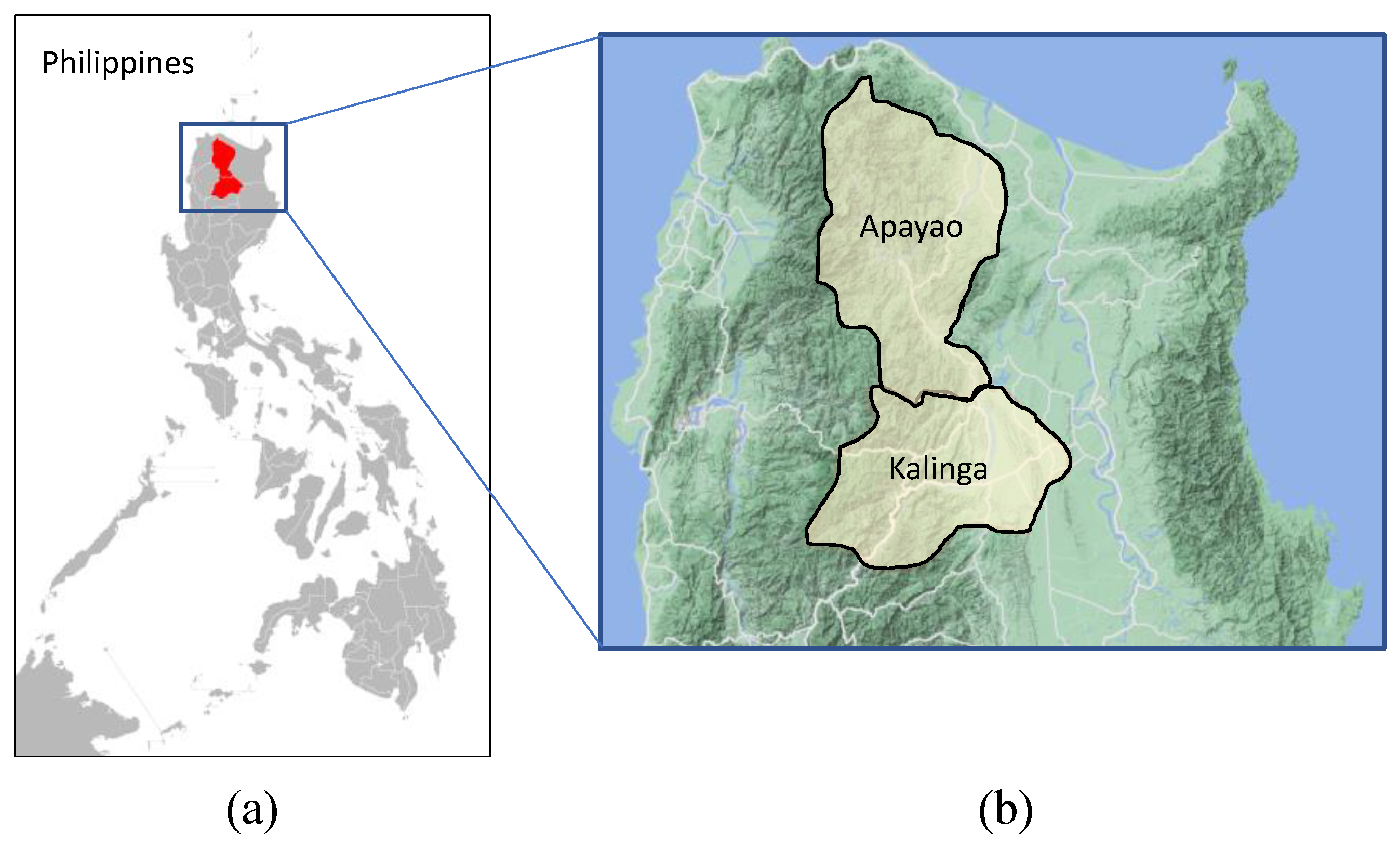
2.1. Data Collection and Pre-Processing
2.2. Canonical Correlation Analysis
3. Results and Discussion
3.1. Solar–Wind Complementarity Analysis
3.2. Comparison of CCA to Other Approaches
3.3. Consistency of Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jeong, J.; Ko, H. Bracing for Climate Impact: Renewables as a Climate Change Adaptation Strategy. Abu Dhabi, 2021. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2021/Aug/IRENA_Bracing_for_climate_impact_2021.pdf (accessed on 16 August 2021).
- International Energy Agency (IEA). Global Energy Review 2021. 2021. Available online: https://iea.blob.core.windows.net/assets/d0031107-401d-4a2f-a48b-9eed19457335/GlobalEnergyReview2021.pdf (accessed on 16 August 2021).
- IRENA. World Energy Transitions Outlook: 1.5 °C Pathway. Abu Dhabi, 2021. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2021/Jun/IRENA_World_Energy_Transitions_Outlook_2021.pdf (accessed on 16 August 2021).
- Bloomberg NEF. Energy Transition Investment Trends 2021. Technical Report. 2021. Available online: https://assets.bbhub.io/professional/sites/24/Energy-Transition-Investment-Trends_Free-Summary_Jan2021.pdf. (accessed on 16 August 2021).
- Katz, J.; Denholm, P. Using Wind and Solar to Reliably Meet Electricity Demand Greening the Grid Leveraging Renewable Energy to Achieve Long-Term Adequacy. National Renewable Energy Laboratory, 2015. Available online: https://www.nrel.gov/docs/fy15osti/63038.pdf (accessed on 16 August 2021).
- Solomon, A.A.; Child, M.; Caldera, U.; Breyer, C. Exploiting wind-solar resource complementarity to reduce energy storage need. AIMS Energy 2020, 8, 749–770. [Google Scholar] [CrossRef]
- Katz, J.; Cochran, J. Integrating Variable Renewable Energy into The Grid: Key Issues. National Renewable Energy Laboratory. 2015. Available online: https://www.nrel.gov/docs/fy15osti/63033.pdf (accessed on 16 August 2021).
- Sun, W.; Harrison, G.P. Wind-solar complementarity and effective use of distribution network capacity. Appl. Energy 2019, 247, 89–101. [Google Scholar] [CrossRef] [Green Version]
- Hoicka, C.; Rowlands, I.H. Solar and wind resource complementarity: Advancing options for renewable electricity integration in Ontario, Canada. Renew. Energy 2011, 36, 97–107. [Google Scholar] [CrossRef]
- Solomon, A.; Kammen, D.M.; Callaway, D. Investigating the impact of wind–solar complementarities on energy storage requirement and the corresponding supply reliability criteria. Appl. Energy 2016, 168, 130–145. [Google Scholar] [CrossRef] [Green Version]
- Santos-Alamillos, F.; Pozo-Vazquez, D.; Ruiz-Arias, J.A.; von Bremen, L.; Tovar-Pescador, J. Combining wind farms with concentrating solar plants to provide stable renewable power. Renew. Energy 2015, 76, 539–550. [Google Scholar] [CrossRef]
- Jurasz, J.; Canales, F.A.; Kies, A.; Guezgouz, M.; Beluco, A. A review on the complementarity of renewable energy sources: Concept, metrics, application and future research directions. Sol. Energy 2020, 195, 703–724. [Google Scholar] [CrossRef]
- Nikolakakis, T.; Fthenakis, V. The optimum mix of electricity from wind- and solar-sources in conventional power systems: Evaluating the case for New York State. Energy Policy 2011, 39, 6972–6980. [Google Scholar] [CrossRef]
- Pianezzola, G.; Krenzinger, A.; Canales, F.A. Complementarity Maps of Wind and Solar Energy Resources for Rio Grande do Sul, Brazil. Energy Power Eng. 2017, 09, 489–504. [Google Scholar] [CrossRef] [Green Version]
- Jerez, S.; Trigo, R.; Sarsa, A.; Plazas, R.L.; Pozo-Vazquez, D.; Montavez, J.P. Spatio-temporal Complementarity between Solar and Wind Power in the Iberian Peninsula. Energy Procedia 2013, 40, 48–57. [Google Scholar] [CrossRef] [Green Version]
- Monforti, F.; Huld, T.; Bódis, K.; Vitali, L.; D’Isidoro, M.; Arántegui, R.L. Assessing complementarity of wind and solar resources for energy production in Italy. A Monte Carlo approach. Renew. Energy 2014, 63, 576–586. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, Y.; Zhang, H.; Zhang, P. Complementarity assessment of wind-solar energy sources in Shandong province based on NASA. J. Eng. 2019, 2019, 4996–5000. [Google Scholar] [CrossRef]
- Neto, P.B.L.; Saavedra, O.R.; Oliveira, D.Q. The effect of complementarity between solar, wind and tidal energy in isolated hybrid microgrids. Renew. Energy 2020, 147, 339–355. [Google Scholar] [CrossRef]
- Rosa, C.D.O.C.S.; Christo, E.D.S.; Costa, K.A.; dos Santos, L. Assessing complementarity and optimising the combination of intermittent renewable energy sources using ground measurements. J. Clean. Prod. 2020, 258, 120946. [Google Scholar] [CrossRef]
- David, M.; Andriamasomanana, F.H.R.; Liandrat, O. Spatial and Temporal Variability of PV Output in an Insular Grid: Case of Reunion Island. Energy Procedia 2014, 57, 1275–1282. [Google Scholar] [CrossRef]
- Jurasz, J.; Beluco, A.; Canales, F.A. The impact of complementarity on power supply reliability of small scale hybrid energy systems. Energy 2018, 161, 737–743. [Google Scholar] [CrossRef]
- Berger, M.; Radu, D.; Fonteneau, R.; Henry, R.; Glavic, M.; Fettweis, X.; Le Du, M.; Panciatici, P.; Balea, L.; Ernst, D. Critical time windows for renewable resource complementarity assessment. Energy 2020, 198, 117308. [Google Scholar] [CrossRef] [Green Version]
- Lee, N.; Dyreson, A.; Hurlbut, D.; McCan, M.I.; Neri, E.V.; Reyes, N.C.R.; Capongcol, M.C.; Cubangbang, H.M.; Agustin, B.P.Q.; Bagsik, J.; et al. Ready for Renewables: Grid Planning and Competitive Renewable Energy Zones (CREZ) in the Philippines. 2020. Available online: https://www.nrel.gov/docs/fy20osti/76235.pdf (accessed on 16 August 2021).
- Li, W.; Stadler, S.; Ramakumar, R. Modeling and assessment of wind and insolation resources with a focus on their complementary nature: A case study of Oklahoma. Ann. Assoc. Am. Geogr. 2011, 101, 717–729. [Google Scholar] [CrossRef]
- Philippine Statistics Authority. Cordillera Administrative Region. 2020. Available online: http://rssocar.psa.gov.ph/kalinga (accessed on 16 August 2021).
- Stackhouse, P.W., Jr.; Macpherson, B.; Broddle, M.; McNeil, C.; Barnett, J.; Mikovitz, C.; Zhang, T. NASA Prediction of Worldwide Energy Resources (POWER) Project. 2021. Available online: https://power.larc.nasa.gov/ (accessed on 16 August 2021).
- Heide, D.; von Bremen, L.; Greiner, M.; Hoffmann, C.; Speckmann, M.; Bofinger, S. Seasonal optimal mix of wind and solar power in a future, highly renewable Europe. Renew. Energy 2010, 35, 2483–2489. [Google Scholar] [CrossRef]
- Hotelling, H. Relations between Two Sets of Variates. Biometrika 1936, 28, 321–377. [Google Scholar] [CrossRef]
- Pilario, K.E.S.; Cao, Y.; Shafiee, M. A Kernel Design Approach to Improve Kernel Subspace Identification. IEEE Trans. Ind. Electron. 2020, 68, 6171–6180. [Google Scholar] [CrossRef]

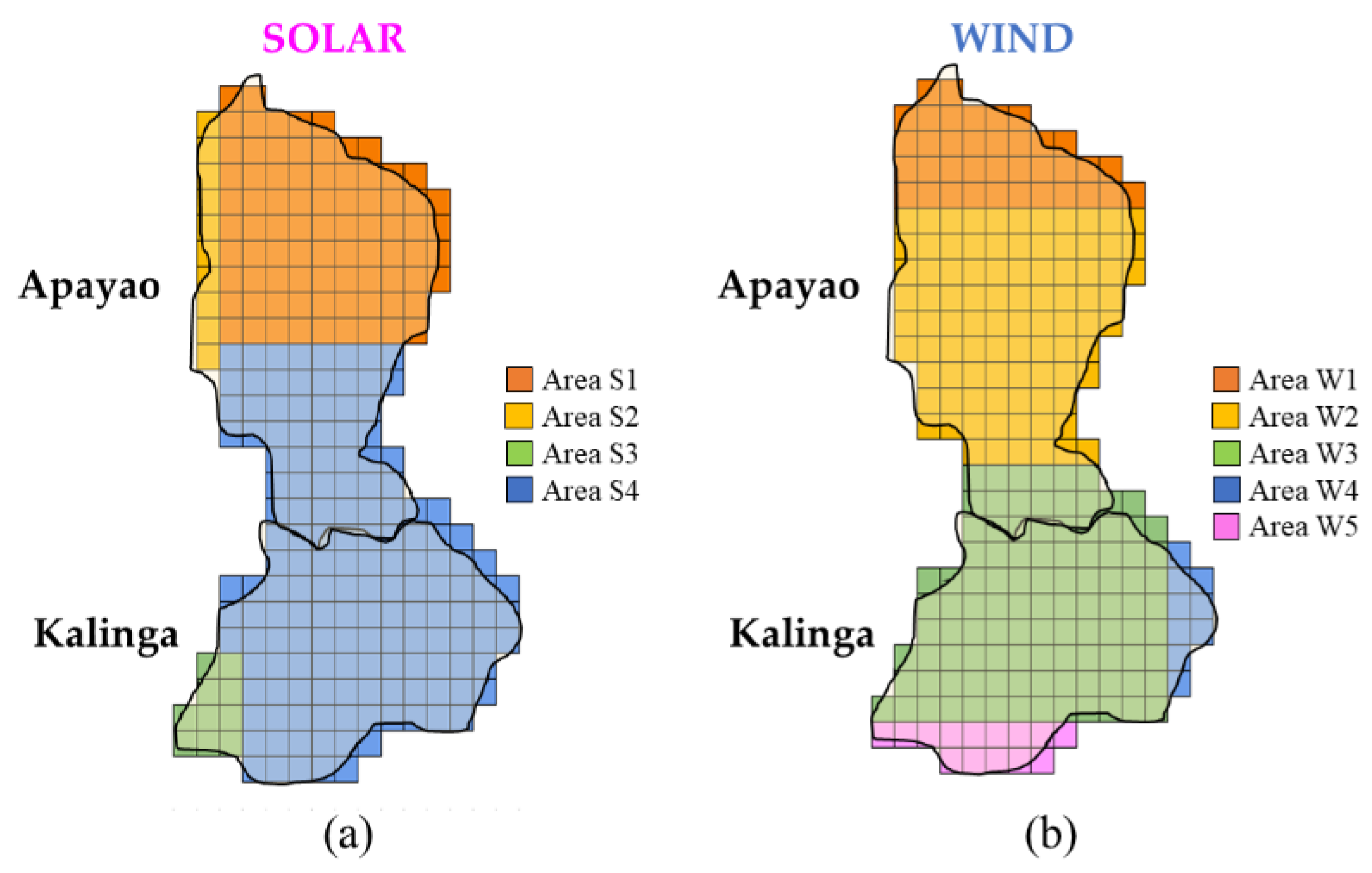






| Rank | Proposed CCA | Pearson Correlation | CIWS |
|---|---|---|---|
| 1 | S4-W1 * | S4-W1 | S4-W1 |
| 2 | S1-W1 | S1-W1 | S1-W1 |
| 3 | S4-W5 | S4-W2 | S4-W2 |
| 4 | S4-W4 | S4-W4 | S1-W2 |
| 5 | S3-W3 | S4-W3 | S4-W4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pilario, K.E.S.; Ibañez, J.A.; Penisa, X.N.; Obra, J.B.; Odulio, C.M.F.; Ocon, J.D. Spatio-Temporal Solar–Wind Complementarity Assessment in the Province of Kalinga-Apayao, Philippines Using Canonical Correlation Analysis. Sustainability 2022, 14, 3253. https://doi.org/10.3390/su14063253
Pilario KES, Ibañez JA, Penisa XN, Obra JB, Odulio CMF, Ocon JD. Spatio-Temporal Solar–Wind Complementarity Assessment in the Province of Kalinga-Apayao, Philippines Using Canonical Correlation Analysis. Sustainability. 2022; 14(6):3253. https://doi.org/10.3390/su14063253
Chicago/Turabian StylePilario, Karl Ezra S., Jessa A. Ibañez, Xaviery N. Penisa, Johndel B. Obra, Carl Michael F. Odulio, and Joey D. Ocon. 2022. "Spatio-Temporal Solar–Wind Complementarity Assessment in the Province of Kalinga-Apayao, Philippines Using Canonical Correlation Analysis" Sustainability 14, no. 6: 3253. https://doi.org/10.3390/su14063253
APA StylePilario, K. E. S., Ibañez, J. A., Penisa, X. N., Obra, J. B., Odulio, C. M. F., & Ocon, J. D. (2022). Spatio-Temporal Solar–Wind Complementarity Assessment in the Province of Kalinga-Apayao, Philippines Using Canonical Correlation Analysis. Sustainability, 14(6), 3253. https://doi.org/10.3390/su14063253