State Estimators in Soft Sensing and Sensor Fusion for Sustainable Manufacturing
Abstract
:1. Introduction
2. State Estimation Methods
2.1. State Observers
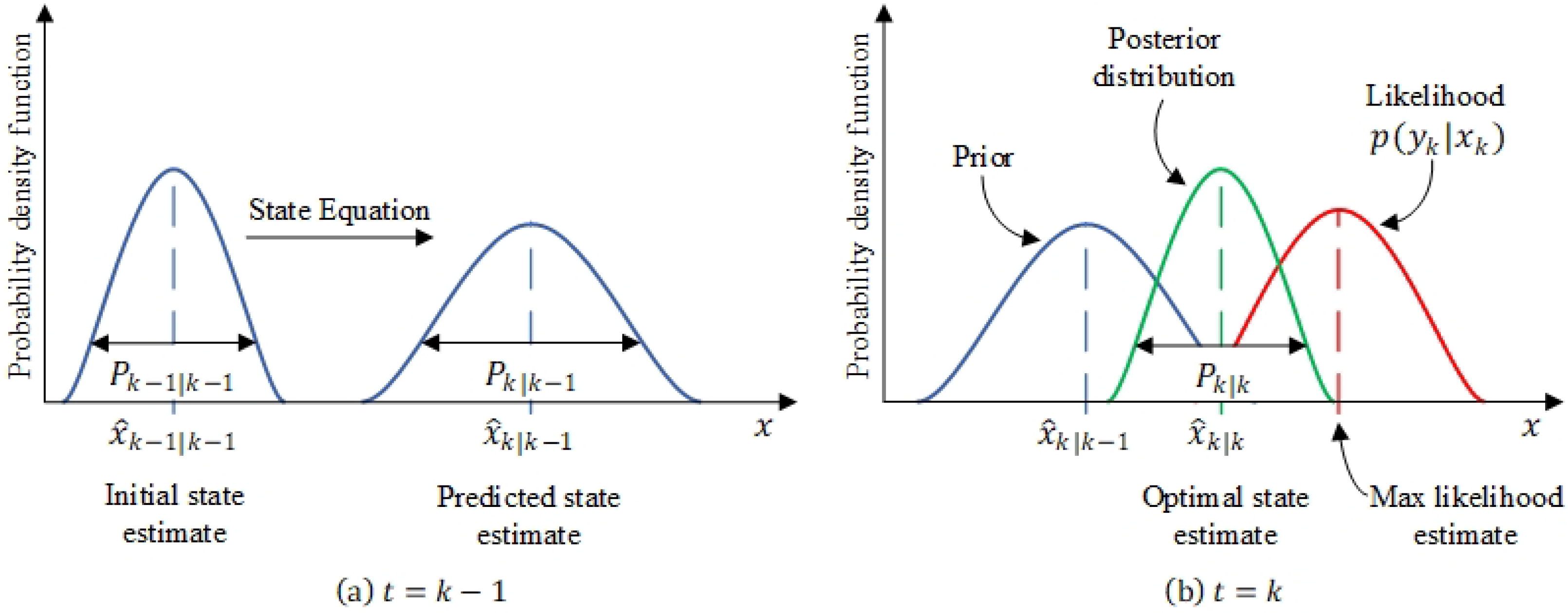
2.2. Kalman Filter and Extensions
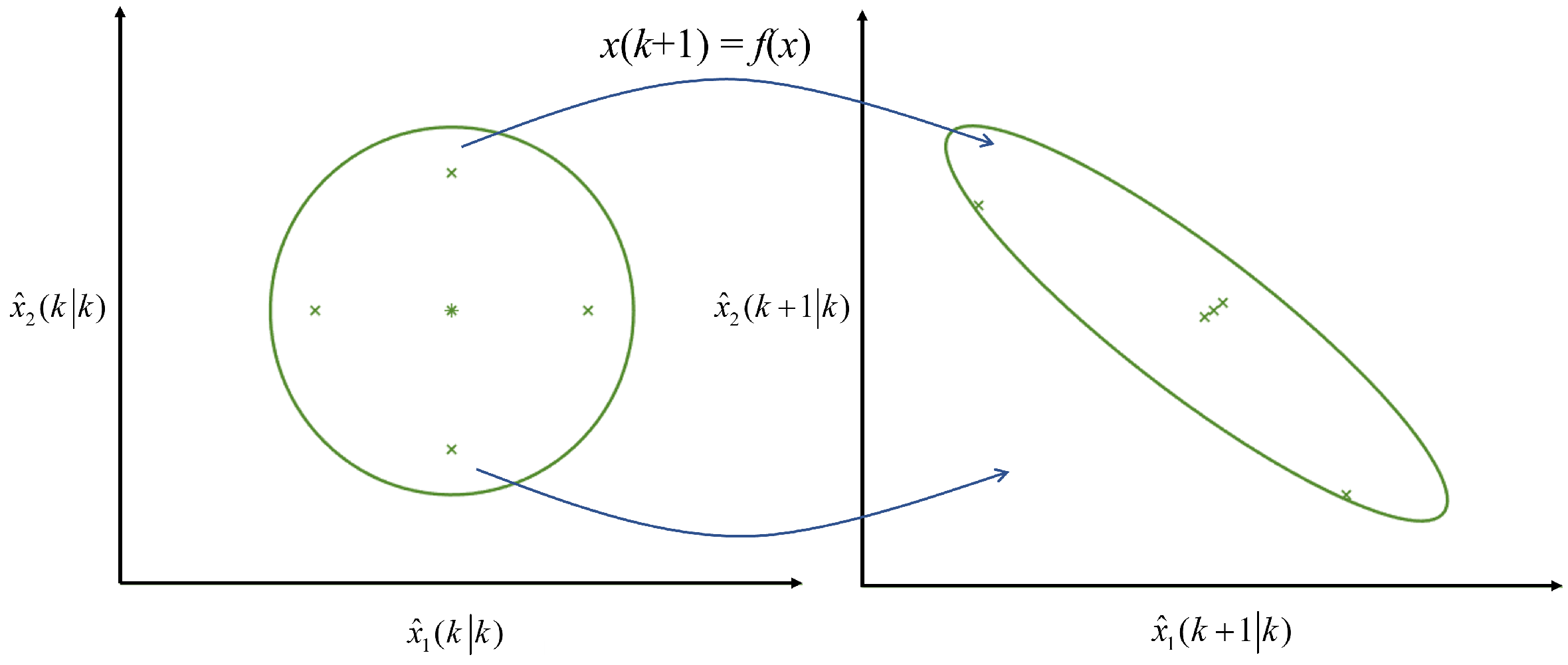
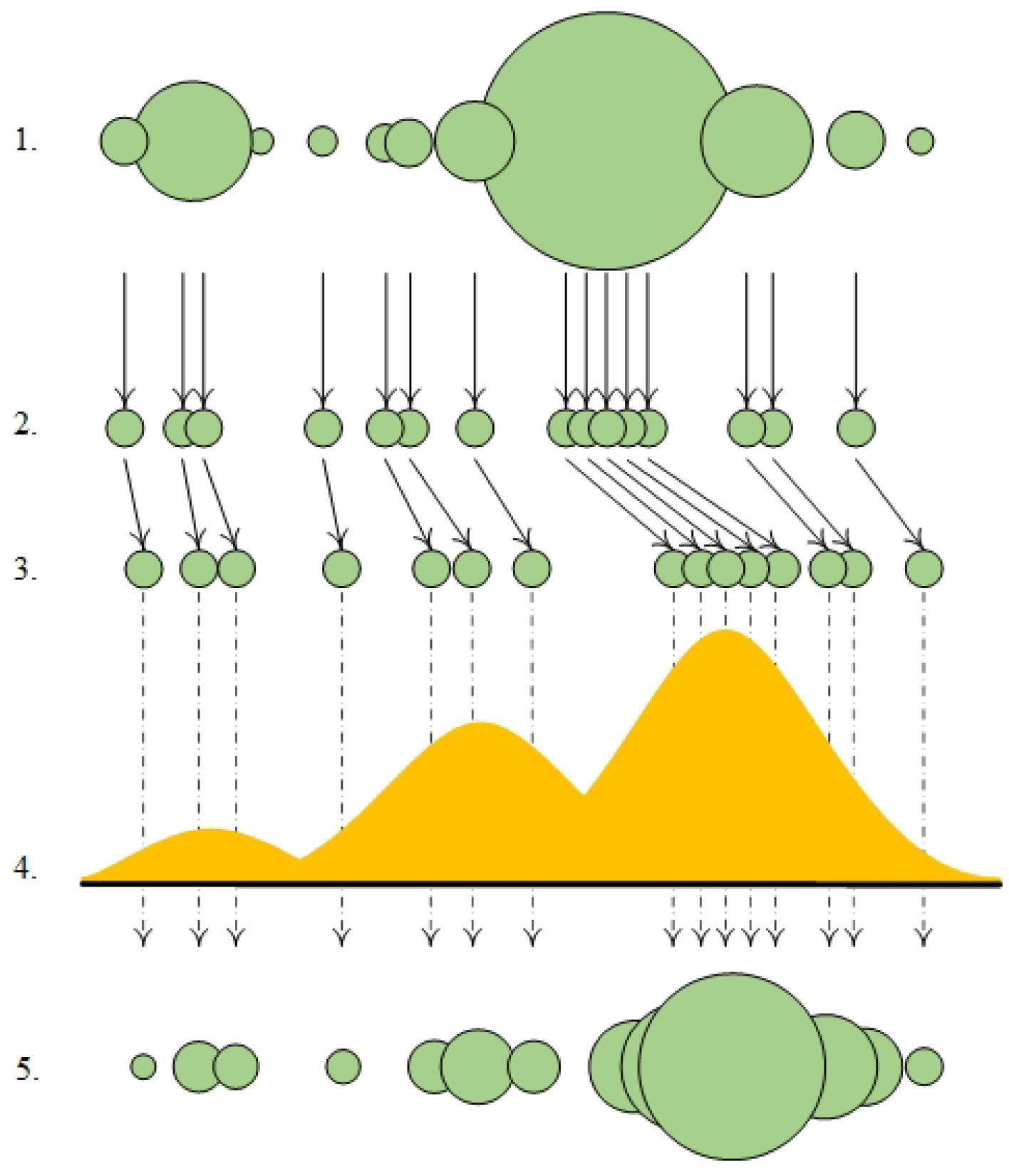
2.3. Particle Filter
- Weighted particles from last measurement update (usually sampled from a uniform distribution on initialization).
- Bootstrap resampling: Take N samples with replacement from the set, where the probability of selection is proportional to the weighting. All new samples have equal weighting so that the distribution is represented by particle density rather than weight.
- Each particle is propagated through the state equation adding noise generated by sampling from the distribution for the process noise to provide time updates (prediction at ).
- Measurement update: The predicted measurements given by the particles are compared to the true measurements to update the weights.
- The states are estimated by, e.g., a maximum a posteriori (MAP) estimate of the approximated posterior distribution.
3. Application of State Estimators in Improving Manufacturing Sustainability
3.1. Industrial Robotics
3.2. Chemical Process Industries
Polymerisation
3.3. Material Forming Processes
3.3.1. Injection Moulding
3.3.2. Other Forming Processes
3.4. Machining Processes
3.5. Semiconductor Manufacturing
3.6. Additive Manufacturing
4. Discussion
4.1. Limitations and Practical Issues
4.2. Spatio-Temporal Monitoring
4.3. Relationship between State Estimators and Machine Learning in Manufacturing
4.4. Systems-Level Approach
4.5. State Estimation and ‘Digital Twins’
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| [h] IoT | Internet of Things; |
| SMO | Sliding Mode Observer; |
| KF | Kalman Filter; |
| EKF | Extended Kalman Filter; |
| EnKF | Ensemble Kalman Filter; |
| UKF | Unscented Kalman Filter; |
| PF | Particle Filter; |
| SLAM | Simultaneous Localisation and Mapping; |
| AI | Artificial Intelligence; |
| ROS | Robot Operating System; |
| AMCL | Adaptive Monte Carlo Localisation; |
| Mw | Molecular Weight; |
| EMI | Excluding Mutual Information; |
| CI | Covariance Intersection; |
| MPC | Model Predictive Controller; |
| APF | Augmented Particle Filter; |
| AHH | Adaptive Hinging Hyperplane; |
| RHKF | Receding Horizon Kalman Filter; |
| PID | Proportional Integral Derivative; |
| LS-SVM | Least Square Support Vector Machine; |
| SSKF | Steady-State Kalman Filter; |
| SVR | Support Vector Regression; |
| GDP | Gross Domestic Product; |
| PCA | Principle Component Analysis; |
| K-PCA | Kernel Principle Component Analysis; |
| LSPF | Local Search Particle Filter; |
| R2R | Run to Run; |
| SPC | Statistical Process Control; |
| EWMA | Exponential Weighted Moving Average; |
| IMA | Integrated Moving Average; |
| IAR | Integrated auto-regressive; |
| PCC | Predictor Corrector Controller; |
| ESO | Extended State Observer; |
| AM | Additive Manufacturing; |
| CAD | Computer-aided Design; |
| PBF | Powder Bed Fusion; |
| DED | Directed Energy Deposition; |
| FDM | Fused Deposition Modelling; |
| FFF | Fused Filament Fabrication; |
| L-PBF | Laser beam Powder Bed Fusion; |
| E-PBF | Electron beam Powder Bed Fusion; |
| FEM | Finite Element Method; |
| MOR | Model Order Reduction; |
| ROM | Reduced Order Model; |
| POD | Proper Orthogonal Decomposition. |
References
- Giret, A.; Trentesaux, D.; Prabhu, V. Sustainability in manufacturing operations scheduling: A state of the art review. J. Manuf. Syst. 2015, 37, 126–140. [Google Scholar] [CrossRef]
- Henao-Hernández, I.; Solano-Charris, E.L.; Muñoz-Villamizar, A.; Santos, J.; Henríquez-Machado, R. Control and monitoring for sustainable manufacturing in the Industry 4.0: A literature review. IFAC-PapersOnLine 2019, 52, 195–200. [Google Scholar] [CrossRef]
- Zawadzki, P.; Żywicki, K. Smart product design and production control for effective mass customization in the Industry 4.0 concept. Manag. Prod. Eng. Rev. 2016, 7, 105–112. [Google Scholar] [CrossRef]
- Kagermann, H.; Helbig, J.; Hellinger, A.; Wahlster, W. Recommendations for Implementing the Strategic Initiative INDUSTRIE 4.0: Securing the Future of German Manufacturing Industry; Final Report of the Industrie 4.0 Working Group; Forschungsunion: Frankfurt am Main, Germany, 2013. [Google Scholar]
- Grewal, M.S.; Andrews, A.P. Applications of Kalman Filtering in Aerospace 1960 to the Present [Historical Perspectives]. IEEE Control Syst. Mag. 2010, 30, 69–78. [Google Scholar] [CrossRef]
- Jwo, D.J.; Cho, T.S. A practical note on evaluating Kalman filter performance optimality and degradation. Appl. Math. Comput. 2007, 193, 482–505. [Google Scholar] [CrossRef]
- Badue, C.; Guidolini, R.; Carneiro, R.V.; Azevedo, P.; Cardoso, V.B.; Forechi, A.; Jesus, L.; Berriel, R.; Paixao, T.M.; Mutz, F.; et al. Self-driving cars: A survey. Expert Syst. Appl. 2021, 165, 113816. [Google Scholar] [CrossRef]
- Luenberger, D.G. Observing the State of a Linear System. IEEE Trans. Mil. Electron. 1964, 8, 74–80. [Google Scholar] [CrossRef]
- Luenberger, D. Observers for multivariable systems. IEEE Trans. Autom. Control 1966, 11, 190–197. [Google Scholar] [CrossRef]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Control Engineering; Springer: New York, NY, USA, 2014; pp. 1–356. [Google Scholar] [CrossRef]
- Spurgeon, S.K. Sliding mode observers: A survey. Int. J. Syst. Sci. 2008, 39, 751–764. [Google Scholar] [CrossRef]
- Slotine, J.E.; Hedrick, J.K.; Misawa, E.A. On Sliding Observers for Nonlinear Systems. In Proceedings of the 1986 American Control Conference, Seattle, WA, USA, 18–20 June 1986; pp. 1794–1800. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Hedrick, J.K.; Misawa, E.A. On Sliding Observers for Nonlinear Systems. J. Dyn. Syst. Meas. Control 1987, 109, 245–252. [Google Scholar] [CrossRef]
- Pisano, A.; Usai, E. Globally convergent real-time differentiation via second order sliding modes. Int. J. Syst. Sci. 2007, 38, 833–844. [Google Scholar] [CrossRef]
- Bernard, P. Observer Design for Nonlinear Systems; Lecture Notes in Control and Information Sciences; Springer International Publishing: Cham, Switzerland, 2019; Volume 479. [Google Scholar] [CrossRef] [Green Version]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Gelb, A. Applied Optimal Estimation; MIT Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Stigter, J.; Beck, M. On the development and application of a continuous-discrete recursive prediction error algorithm. Math. Biosci. 2004, 191, 143–158. [Google Scholar] [CrossRef]
- Schmidt, S.F. Application of state-space methods to navigation problems. In Advances in Control Systems; Elsevier: Amsterdam, The Netherlands, 1966; Volume 3, pp. 293–340. [Google Scholar]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. Unscented filtering and nonlinear estimation. Proc. IEEE 2004, 92, 401–422. [Google Scholar] [CrossRef] [Green Version]
- Burgers, G.; Jan van Leeuwen, P.; Evensen, G. Analysis Scheme in the Ensemble Kalman Filter. Mon. Weather Rev. 1998, 126, 1719–1724. [Google Scholar] [CrossRef]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. Ocean. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Roth, M.; Hendeby, G.; Fritsche, C.; Gustafsson, F. The Ensemble Kalman filter: A signal processing perspective. EURASIP J. Adv. Signal Process. 2017, 2017, 56. [Google Scholar] [CrossRef] [Green Version]
- Gordon, N.J.; Salmond, D.J.; Smith, A.F. Novel approach to nonlinear/non-Gaussian Bayesian state estimation. IEE Proc. Radar Signal Process. 1993, 140, 107–113. [Google Scholar] [CrossRef] [Green Version]
- Isard, M.; Blake, A. Condensation—Conditional density propagation for visual tracking. Int. J. Comput. Vis. 1998, 29, 5–28. [Google Scholar] [CrossRef]
- Kitagawa, G. Monte Carlo filter and smoother for non-Gaussian nonlinear state space models. J. Comput. Graph. Stat. 1996, 5, 1–25. [Google Scholar]
- Gustafsson, F. Statistical Sensor Fusion, 3rd ed.; Studentlitteratur: Lund, Sweden, 2018. [Google Scholar]
- Gustafsson, F.; Gunnarsson, F.; Bergman, N.; Forssell, U.; Jansson, J.; Karlsson, R.; Nordlund, P.J. Particle filters for positioning, navigation, and tracking. IEEE Trans. Signal Process. 2002, 50, 425–437. [Google Scholar] [CrossRef] [Green Version]
- Gustafsson, F. Particle filter theory and practice with positioning applications. IEEE Aerosp. Electron. Syst. Mag. 2010, 25, 53–82. [Google Scholar] [CrossRef] [Green Version]
- Goel, R.; Gupta, P. Robotics and industry 4.0. In A Roadmap to Industry 4.0: Smart Production, Sharp Business and Sustainable Development; Springer: Berlin/Heidelberg, Germany, 2020; pp. 157–169. [Google Scholar]
- Li, M.; Milojević, A.; Handroos, H. Robotics in Manufacturing—The Past and the Present. In Technical, Economic and Societal Effects of Manufacturing 4.0; Palgrave Macmillan: Cham, Switzerland, 2020; pp. 85–95. [Google Scholar]
- Safeea, M.; Neto, P.; Bearee, R. On-line collision avoidance for collaborative robot manipulators by adjusting off-line generated paths: An industrial use case. Robot. Auton. Syst. 2019, 119, 278–288. [Google Scholar] [CrossRef] [Green Version]
- Naidoo, N.; Bright, G.; Stopforth, R. A Distributed Framework for Programming the Artificial Intelligence of Mobile Robots in Smart Manufacturing Systems. In Proceedings of the 2019 Southern African Universities Power Engineering Conference/Robotics and Mechatronics/Pattern Recognition Association of South Africa (SAUPEC/RobMech/PRASA), Bloemfontein, South Africa, 28–30 January 2019; pp. 34–41. [Google Scholar]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, present, and future of simultaneous localization and mapping: Toward the robust-perception age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef] [Green Version]
- Ding, X.; Guo, J.; Ren, Z.; Deng, P. State-of-the-art in perception technologies for collaborative robots. IEEE Sens. J. 2021. [Google Scholar] [CrossRef]
- Mahmud, M.A.; Aman, M.S.; Jiang, H.; Abdelgawad, A.; Yelamarthi, K. Kalman filter based indoor mobile robot navigation. In Proceedings of the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Eilat, Israel, 16–18 November 2016; pp. 1949–1953. [Google Scholar]
- Yuzhen, P.; Quande, Y.; Benfa, Z. The application of adaptive extended Kalman filter in mobile robot localization. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 5337–5342. [Google Scholar]
- Ruan, X.g.; Song, K.K. An adaptive extended Kalman filter for attitude estimation of Self-Balancing Two-Wheeled Robot. In Proceedings of the 2011 International Conference on Electric Information and Control Engineering, Wuhan, China, 15–17 April 2011; pp. 4760–4763. [Google Scholar]
- Luo, F.; Du, B.; Fan, Z. Mobile robot localization based on particle filter. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014; pp. 3089–3093. [Google Scholar]
- Kim, T.G.; Choi, H.T.; Ko, N.Y. Localization of a robot using particle filter with range and bearing information. In Proceedings of the 2013 10th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI), Jeju, Korea, 30 October–2 November 2013; pp. 368–370. [Google Scholar]
- Wang, Z.M.; Du, Z.J. Simultaneous localization and mapping for mobile robot based on an improved particle filter algorithm. In Proceedings of the 2009 International Conference on Mechatronics and Automation, Changchun, China, 9–12 August 2009; pp. 1106–1110. [Google Scholar]
- Silva, I.; Pendão, C.; Torres-Sospedra, J.; Moreira, A. TrackInFactory: A Tight Coupling Particle Filter for Industrial Vehicle Tracking in Indoor Environments. IEEE Trans. Syst. Man Cybern. Syst. 2021, 1–12. [Google Scholar] [CrossRef]
- Li, C.; Fahmy, A.; Sienz, J. An augmented reality based human-robot interaction interface using Kalman filter sensor fusion. Sensors 2019, 19, 4586. [Google Scholar] [CrossRef] [Green Version]
- Auger, F.; Hilairet, M.; Guerrero, J.M.; Monmasson, E.; Orlowska-Kowalska, T.; Katsura, S. Industrial applications of the Kalman filter: A review. IEEE Trans. Ind. Electron. 2013, 60, 5458–5471. [Google Scholar] [CrossRef] [Green Version]
- Khatibisepehr, S.; Huang, B.; Khare, S. Design of inferential sensors in the process industry: A review of Bayesian methods. J. Process Control 2013, 23, 1575–1596. [Google Scholar] [CrossRef]
- Mohd Ali, J.; Ha Hoang, N.; Hussain, M.; Dochain, D. Review and classification of recent observers applied in chemical process systems. Comput. Chem. Eng. 2015, 76, 27–41. [Google Scholar] [CrossRef] [Green Version]
- Alexander, R.; Campani, G.; Dinh, S.; Lima, F.V. Challenges and opportunities on nonlinear state estimation of chemical and biochemical processes. Processes 2020, 8, 1462. [Google Scholar] [CrossRef]
- Shekar, H.S.; Ramachandra, M. Green composites: A review. Mater. Today Proc. 2018, 5, 2518–2526. [Google Scholar] [CrossRef]
- Dünnebier, G.; van Hessem, D.; Kadam, J.V.; Klatt, K.U.; Schlegel, M. Optimization and control of polymerization processes. Chem. Eng. Technol. 2005, 28, 575–580. [Google Scholar] [CrossRef]
- Knox, S.T.; Warren, N.J. Enabling technologies in polymer synthesis: Accessing a new design space for advanced polymer materials. React. Chem. Eng. 2020, 5, 405–423. [Google Scholar] [CrossRef]
- Salas, S.; Ghadipasha, N.; Zhu, W.; Mcafee, T.; Zekoski, T.; Reed, W.; Romagnoli, J. Framework design for weight-average molecular weight control in semi-batch polymerization. Control Eng. Pract. 2018, 78, 12–23. [Google Scholar] [CrossRef]
- Crowley, T.J.; Choi, K.Y. Calculation of Molecular Weight Distribution from Molecular Weight Moments in Free Radical Polymerization. Ind. Eng. Chem. Res. 1997, 36, 1419–1423. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, R.; Wang, J.; Yu, T.; Su, A. Nonlinear state estimation with delayed measurements using data fusion technique and cubature Kalman filter for chemical processes. Chem. Eng. Res. Des. 2019, 141, 502–515. [Google Scholar] [CrossRef]
- Luo, X.L.; Xu, J.; Zhang, M.; Liu, J. Batch to batch optimal control based on multiinput multioutput adaptive hinging hyperplanes prediction and Kalman filter correction. Optim. Control Appl. Methods 2020, 41, 2048–2061. [Google Scholar] [CrossRef]
- Rangegowda, P.H.; Valluru, J.; Patwardhan, S.C.; Mukhopadhyay, S. Simultaneous and sequential state and parameter estimation using receding-horizon nonlinear Kalman filter. J. Process Control 2022, 109, 13–31. [Google Scholar] [CrossRef]
- Kariminejad, M.; Tormey, D.; Huq, S.; Morrison, J.; McAfee, M. Ultrasound sensors for process monitoring in injection moulding. Sensors 2021, 21, 5193. [Google Scholar] [CrossRef]
- Liu, H.; Hu, H.; Yung, K.L.; Xu, Y.; Zhang, X.W. Melt pressure signature tracking using an adaptive Kalman filter in microinjection molding. Adv. Mech. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Cao, Z.; Lu, J.; Zhang, R.; Gao, F. Iterative learning Kalman filter for repetitive processes. J. Process Control 2016, 46, 92–104. [Google Scholar] [CrossRef]
- Stemmler, S.; Ay, M.; Vukovic, M.; Abel, D.; Heinisch, J.; Hopmann, C. Cross-phase Model-based Predictive Cavity Pressure Control in Injection Molding. In Proceedings of the 2019 IEEE Conference on Control Technology and Applications (CCTA), Hong Kong, China, 19–21 August 2019; pp. 360–367. [Google Scholar] [CrossRef]
- Stemmler, S.; Vukovic, M.; Ay, M.; Heinisch, J.; Lockner, Y.; Abel, D.; Hopmann, C. Quality Control in Injection Molding based on Norm-optimal Iterative Learning Cavity Pressure Control. IFAC-PapersOnLine 2020, 53, 10380–10387. [Google Scholar] [CrossRef]
- Chen, B.; Wu, H.; Zhou, H.; Sun, D. EMP: Extended kalman filter based self-adaptive mold protection method on a toggle mechanism. Appl. Sci. 2020, 10, 940. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Li, K.; McAfee, M.; Nguyen, B.K.; McNally, G.M. Dynamic gray-box modeling for on-line monitoring of polymer extrusion viscosity. Polym. Eng. Sci. 2012, 52, 1332–1341. [Google Scholar] [CrossRef] [Green Version]
- El Amaoui, A.; Soulami, J.; Hattabi, M. Observer design for liquid composite molding process. Mater. Today Proc. 2020, 42, 1311–1316. [Google Scholar] [CrossRef]
- Ahn, S.; Beaman, J.J.; Williamson, R.L.; Melgaard, D.K. Model-Based Control of Electroslag Remelting Process Using Unscented Kalman Filter. J. Dyn. Syst. Meas. Control 2010, 132, 1–9. [Google Scholar] [CrossRef]
- Lopez, F.; Zhang, L.; Beaman, J.; Mok, A. Implementation of a particle filter on a GPU for nonlinear estimation in a manufacturing remelting process. In Proceedings of the 2014 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Besacon, France, 8–11 July 2014; pp. 340–345. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S. Plant-wide temperature drop monitoring in run-out table strip cooling process. In Proceedings of the 2011 International Symposium on Advanced Control of Industrial Processes (ADCONIP), Hangzhou, China, 23–26 May 2011; pp. 287–292. [Google Scholar]
- Speicher, K.; Steinboeck, A.; Kugi, A.; Wild, D.; Kiefer, T. Analysis and design of an Extended Kalman Filter for the plate temperature in heavy plate rolling. J. Process Control 2014, 24, 1371–1381. [Google Scholar] [CrossRef]
- Kloeser, D.; Martschin, J.; Meurer, T.; Tekkaya, E. Reduced order modelling for spatial-temporal temperature and property estimation in a multi-stage hot sheet metal forming process. Adv. Ind. Manuf. Eng. 2021, 3, 100055. [Google Scholar] [CrossRef]
- Havinga, J.; Mandal, P.K.; Mechanics, N.S.; Mathematics, A. Product-to-product State Estimation For Metal Forming Mass Production. In Proceedings of the Forming Technology Forum 2017, Enschede, The Netherlands, 12–13 October 2017; pp. 6–13. [Google Scholar]
- Yucel, E.; Gunay, M. An evaluation on machining processes for sustainable manufacturing. Gazi Univ. J. Sci. 2013, 26, 241–252. [Google Scholar]
- Ghosh, S.; Naskar, S.K.; Mandal, N.K. Estimation of residual life of a cutting tool used in a machining process. In Proceedings of the MATEC Web of Conferences, the 4th International Conference on Engineering, Applied Sciences and Technology (ICEAST 2018), Phuket, Thailand, 14 August 2018; EDP Sciences: Les Ulis, France, 2018; Volume 192, p. 01017. [Google Scholar]
- Moradnazhad, M.; Unver, H.O. Energy efficiency of machining operations: A review. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2017, 231, 1871–1889. [Google Scholar] [CrossRef]
- Peng, T.; Xu, X. Energy-efficient machining systems: A critical review. Int. J. Adv. Manuf. Technol. 2014, 72, 1389–1406. [Google Scholar] [CrossRef]
- Niaki, F.A.; Ulutan, D.; Mears, L. In-process tool flank wear estimation in machining gamma-prime strengthened alloys using kalman filter. Procedia Manuf. 2015, 1, 696–707. [Google Scholar] [CrossRef] [Green Version]
- Ulsoy, A.G. Monitoring and Control of Machining. In Condition Monitoring and Control for Intelligent Manufacturing; Wang, L., Gao, R.X., Eds.; Springer: London, UK, 2006; pp. 1–32. [Google Scholar] [CrossRef]
- Tiwari, K.; Shaik, A.; Arunachalam, N. Tool wear prediction in end milling of Ti-6Al-4V through Kalman filter based fusion of texture features and cutting forces. Procedia Manuf. 2018, 26, 1459–1470. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, C.; Zhang, J.; Zhou, L. Tool wear model based on least squares support vector machines and Kalman filter. Prod. Eng. 2014, 8, 101–109. [Google Scholar] [CrossRef]
- Sadhukhan, C.; Mitra, S.K.; Biswas, R.; Naskar, M.K. Tool condition monitoring: Unscented Kalman filter for tool flank wear estimation in turning of Inconel 718. Mach. Sci. Technol. 2021, 25, 331–348. [Google Scholar] [CrossRef]
- Wang, J.; Wang, P.; Gao, R.X. Tool Life Prediction for Sustainable Manufacturing. In Proceedings of the 11th Global Conference on Sustainable Manufacturing, Berlin, Germany, 23–25 September 2013; pp. 230–234. [Google Scholar] [CrossRef]
- Wang, J.; Wang, P.; Gao, R.X. Enhanced particle filter for tool wear prediction. J. Manuf. Syst. 2015, 36, 35–45. [Google Scholar] [CrossRef]
- Wang, J.; Zheng, Y.; Wang, P.; Gao, R.X. A virtual sensing based augmented particle filter for tool condition prognosis. J. Manuf. Process. 2017, 28, 472–478. [Google Scholar] [CrossRef]
- Wang, P.; Gao, R.X. Stochastic Tool Wear Prediction for Sustainable Manufacturing. Procedia CIRP 2016, 48, 236–241. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Gao, R.X. Adaptive resampling-based particle filtering for tool life prediction. J. Manuf. Syst. 2015, 37, 528–534. [Google Scholar] [CrossRef]
- Moliner-Heredia, R.; Abellán-Nebot, J.V.; Peñarrocha-Alós, I. Model-based observer proposal for surface roughness monitoring. Procedia Manuf. 2019, 41, 618–625. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, T.; Zhao, J. Surface generation modeling of micro milling process with stochastic tool wear. Precis. Eng. 2020, 61, 170–181. [Google Scholar] [CrossRef]
- Chandel, R.S.; Kumar, R.; Kapoor, J. Sustainability aspects of machining operations: A summary of concepts. Mater. Today Proc. 2021, 50, 716–727. [Google Scholar] [CrossRef]
- Lin, F.; Lin, S.W.; Lu, W.M. Sustainability assessment of Taiwan’s semiconductor industry: A new hybrid model using combined analytic hierarchy process and two-stage additive network data envelopment analysis. Sustainability 2018, 10, 4070. [Google Scholar] [CrossRef] [Green Version]
- Gupta, U.; Kim, Y.G.; Lee, S.; Tse, J.; Lee, H.H.S.; Wei, G.Y.; Brooks, D.; Wu, C.J. Chasing carbon: The elusive environmental footprint of computing. In Proceedings of the 2021 IEEE International Symposium on High-Performance Computer Architecture (HPCA), Seoul, Korea, 27 February–3 March 2021; pp. 854–867. [Google Scholar]
- Qin, S.J.; Cherry, G.; Good, R.; Wang, J.; Harrison, C.A. Semiconductor manufacturing process control and monitoring: A fab-wide framework. J. Process Control 2006, 16, 179–191. [Google Scholar] [CrossRef]
- Tan, F.; Pan, T.; Li, Z.; Chen, S. Survey on run-to-run control algorithms in high-mix semiconductor manufacturing processes. IEEE Trans. Ind. Inform. 2015, 11, 1435–1444. [Google Scholar] [CrossRef]
- Kim, H.; Park, J.H.; Lee, K.S. A Kalman filter-based R2R control system with parallel stochastic disturbance models for semiconductor manufacturing processes. J. Process Control 2014, 24, 119–124. [Google Scholar] [CrossRef]
- Chen, X.; Tomizuka, M. Overview and new results in disturbance observer based adaptive vibration rejection with application to advanced manufacturing. Int. J. Adapt. Control Signal Process. 2015, 29, 1459–1474. [Google Scholar] [CrossRef]
- Yang, J.; Hu, C.; Zhu, Y.; Wang, Z.; Zhang, M. Experimental investigation of shaping disturbance observer design for motion control of precision mechatronic stages with resonances. Mech. Syst. Signal Process. 2017, 92, 334–348. [Google Scholar] [CrossRef]
- Yang, R.; Wang, M.; Li, L.; Zenggu, Y.; Jiang, J. Integrated uncertainty/disturbance compensation with second-order sliding-mode observer for PMLSM-driven motion stage. IEEE Trans. Power Electron. 2018, 34, 2597–2607. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, N.; Wang, Y. Research on High Speed and High Precision Control Method Used in Semiconductor Packaging System. In Proceedings of the 2021 IEEE International Conference on Emergency Science and Information Technology (ICESIT), Chongqing, China, 22–24 November 2021; pp. 837–842. [Google Scholar] [CrossRef]
- Lee, A.C.; Pan, Y.R.; Hsieh, M.T. Output disturbance observer structure applied to run-to-run control for semiconductor manufacturing. IEEE Trans. Semicond. Manuf. 2010, 24, 27–43. [Google Scholar] [CrossRef]
- Lee, A.C.; Horng, J.H.; Kuo, T.W.; Chou, N.H. Robustness analysis of mixed product run-to-run control for semiconductor process based on ODOB control structure. IEEE Trans. Semicond. Manuf. 2014, 27, 212–222. [Google Scholar]
- Harirchi, F.; Vincent, T.; Subramanian, A.; Poolla, K.; Stirton, B. Characterizing and resolving unobservability in run-to-run control of high mix semiconductor manufacturing. In Proceedings of the 52nd IEEE Conference on Decision and Control, Firenze, Italy, 10–13 December 2013; pp. 7022–7027. [Google Scholar] [CrossRef]
- Wang, J.; He, Q.P.; Edgar, T.F. State estimation for integrated moving average processes in high-mix semiconductor manufacturing. Ind. Eng. Chem. Res. 2014, 53, 5194–5204. [Google Scholar] [CrossRef]
- Wang, H.Y.; Pan, T.H.; Wong, D.S.H.; Tan, F. An Extended State Observer-Based Run to Run Control for Semiconductor Manufacturing Processes. IEEE Trans. Semicond. Manuf. 2019, 32, 154–162. [Google Scholar] [CrossRef]
- Wang, H.; Pan, T.; Ding, S.; Chen, S. Design of a run-to-run controller based on discrete sliding-mode observer. Asian J. Control 2021, 23, 908–919. [Google Scholar] [CrossRef]
- Tsai, M.C.; Peng, C.C. Sliding Mode Observer Based Multi-Layer Metal Plates Core Temperature On-Line Estimation for Semiconductor Intelligence Manufacturing. IEEE Access 2020, 8, 194561–194574. [Google Scholar] [CrossRef]
- Wong, K.V.; Hernandez, A. A Review of Additive Manufacturing. ISRN Mech. Eng. 2012, 2012, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Peng, T.; Kellens, K.; Tang, R.; Chen, C.; Chen, G. Sustainability of additive manufacturing: An overview on its energy demand and environmental impact. Addit. Manuf. 2018, 21, 694–704. [Google Scholar] [CrossRef]
- Wood, N.; Hoelzle, D.J. On the feasibility of a temperature state observer for powder bed fusion additive manufacturing. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 321–328. [Google Scholar] [CrossRef]
- Razvi, S.S.; Feng, S.; Narayanan, A.; Lee, Y.T.T.; Witherell, P. A Review of Machine Learning Applications in Additive Manufacturing. In Volume 1: 39th Computers and Information in Engineering Conference; American Society of Mechanical Engineers: New York, NY, USA, 2019; Volume 59179, p. V001T02A040. [Google Scholar] [CrossRef]
- Goodridge, R.; Ziegelmeier, S. Powder bed fusion of polymers. In Laser Additive Manufacturing: Materials, Design, Technologies, and Applications; Brandt, M., Ed.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 181–204. [Google Scholar] [CrossRef]
- Palmero, E.M.; Bollero, A. 3D and 4D Printing of Functional and Smart Composite Materials. In Encyclopedia of Materials: Composites; Brabazon, D.B., Ed.; Elsevier: Oxford, UK, 2021; pp. 402–419. [Google Scholar] [CrossRef]
- Mwema, F.M.; Akinlabi, E.T. Basics of Fused Deposition Modelling (FDM). In Fused Deposition Modeling: Strategies for Quality Enhancement; Springer: Cham, Switzerland, 2020; pp. 1–15. [Google Scholar] [CrossRef]
- Kirka, M.M.; Unocic, K.A.; Raghavan, N.; Medina, F.; Dehoff, R.R.; Babu, S.S. Microstructure Development in Electron Beam-Melted Inconel 718 and Associated Tensile Properties. JOM 2016, 68, 1012–1020. [Google Scholar] [CrossRef]
- Peng, H.; Go, D.B.; Billo, R.; Gong, S.; Shankar, M.; Gatrell, B.A.; Budzinski, J.; Ostiguy, P.; Attardo, R.; Tomonto, C.; et al. Part-Scale Model for Fast Prediction of Thermal Distortion in DMLS Additive Manufacturing—Part 1: A Thermal Circuit Network Model. In Proceedings of the 27th Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 8–10 August 2016. [Google Scholar]
- Oakes, T.; Tang, L.; Landers, R.G.; Balakrishnan, S.N. Kalman Filtering for Manufacturing Processes; INTECHOpen: London, UK, 2009. [Google Scholar]
- Jiang, T.; Leng, M.; Chen, X. Control-oriented Mechatronic Design and Data Analytics for Quality-assured Laser Powder Bed Fusion Additive Manufacturing. In Proceedings of the 2021 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Delft, The Netherlands, 12–16 July 2021; pp. 1319–1324. [Google Scholar] [CrossRef]
- Lopez, F.; Witherell, P.; Lane, B. Identifying uncertainty in laser powder bed fusion additive manufacturing models. J. Mech. Des. 2016, 138, 114502. [Google Scholar] [CrossRef]
- Devesse, W.; De Baere, D.; Guillaume, P. The isotherm migration method in spherical coordinates with a moving heat source. Int. J. Heat Mass Transf. 2014, 75, 726–735. [Google Scholar] [CrossRef]
- Zheng, H.; Li, H.; Lang, L.; Gong, S.; Ge, Y. Effects of scan speed on vapor plume behavior and spatter generation in laser powder bed fusion additive manufacturing. J. Manuf. Process. 2018, 36, 60–67. [Google Scholar] [CrossRef]
- Zhang, Y.; Fuh, J.Y.H.; Ye, D.; Hong, G.S. In-situ monitoring of laser-based PBF via off-axis vision and image processing approaches. Addit. Manuf. 2019, 25, 263–274. [Google Scholar] [CrossRef]
- Wood, N.; Schwalbach, E.; Gillman, A.; Hoelzle, D.J. The Ensemble Kalman Filter as a tool for estimating temperatures in the powder bed fusion process. In Proceedings of the 2021 American Control Conference (ACC), New Orleans, LA, USA, 25–28 May 2021; pp. 4369–4375. [Google Scholar] [CrossRef]
- Kim, Y.; Alcantara, D.; Zohdi, T.I. Thermal state estimation of fused deposition modeling in additive manufacturing processes using Kalman filters. Int. J. Numer. Methods Eng. 2020, 1–13. [Google Scholar] [CrossRef]
- Garanger, K.; Khamvilai, T.; Feron, E. 3D Printing of a Leaf Spring: A Demonstration of Closed-Loop Control in Additive Manufacturing. In Proceedings of the 2018 IEEE Conference on Control Technology and Applications (CCTA), Copenhagen, Denmark, 21–24 August 2018; pp. 465–470. [Google Scholar] [CrossRef] [Green Version]
- Garanger, K.; Khamvilai, T.; Feron, E. Validating feedback control to meet stiffness requirements in additive manufacturing. IEEE Trans. Control Syst. Technol. 2020, 28, 2053–2060. [Google Scholar] [CrossRef]
- Stigter, J.; Vries, D.; Keesman, K. On adaptive optimal input design: A bioreactor case study. AIChE J. 2006, 52, 3290–3296. [Google Scholar] [CrossRef]
- Barz, T.; Körkel, S.; Wozny, G. Nonlinear ill-posed problem analysis in model-based parameter estimation and experimental design. Comput. Chem. Eng. 2015, 77, 24–42. [Google Scholar]
- Wang, H.; Sheen, D.A. Combustion kinetic model uncertainty quantification, propagation and minimization. Prog. Energy Combust. Sci. 2015, 47, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Daria, L.; Dmitry, Z.; Anastasiia, Y. Predicting cyber attacks on industrial systems using the Kalman filter. In Proceedings of the 2019 Third World Conference on Smart Trends in Systems Security and Sustainablity (WorldS4), London, UK, 30–31 July 2019; pp. 317–321. [Google Scholar] [CrossRef]
- Palleti, V.R.; Tan, Y.C.; Samavedham, L. A mechanistic fault detection and isolation approach using Kalman filter to improve the security of cyber physical systems. J. Process Control 2018, 68, 160–170. [Google Scholar] [CrossRef]
- Ahmed, C.M.; Adepu, S.; Mathur, A. Limitations of state estimation based cyber attack detection schemes in industrial control systems. In Proceedings of the 2016 Smart City Security and Privacy Workshop (SCSP-W), Vienna, Austria, 11 April 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Ding, D.; Han, Q.L.; Ge, X.; Wang, J. Secure State Estimation and Control of Cyber-Physical Systems: A Survey. IEEE Trans. Syst. Man, Cybern. Syst. 2021, 51, 176–190. [Google Scholar] [CrossRef]
- Wright, L.; Davidson, S. How to tell the difference between a model and a digital twin. Adv. Model. Simul. Eng. Sci. 2020, 7, 1–13. [Google Scholar] [CrossRef]
- Whitman, J.E.; Maske, H.; Kingravi, H.A.; Chowdhary, G. Evolving Gaussian Processes and Kernel Observers for Learning and Control in Spatiotemporally Varying Domains: With Applications in Agriculture, Weather Monitoring, and Fluid Dynamics. IEEE Control Syst. Mag. 2021, 41, 30–69. [Google Scholar] [CrossRef]
- Ghattas, O.; Willcox, K. Learning physics-based models from data: Perspectives from inverse problems and model reduction. Acta Numer. 2021, 30, 445–554. [Google Scholar] [CrossRef]
- Swischuk, R.; Kramer, B.; Huang, C.; Willcox, K. Learning physics-based reduced-order models for a single-injector combustion process. AIAA J. 2020, 58, 2658–2672. [Google Scholar] [CrossRef] [Green Version]
- Benner, P.; Schilders, W.; Grivet-Talocia, S.; Quarteroni, A.; Rozza, G.; Miguel Silveira, L. Model Order Reduction: Volume 2: Snapshot-Based Methods and Algorithms; De Gruyter: Berlin, Germany, 2020. [Google Scholar]
- Eftekhar Azam, S.; Mariani, S.; Attari, N. Online damage detection via a synergy of proper orthogonal decomposition and recursive Bayesian filters. Nonlinear Dyn. 2017, 89, 1489–1511. [Google Scholar] [CrossRef]
- Gunder, T.; Sehlinger, A.; Skoda, R.; Mönnigmann, M. Sensor placement for reduced-order model-based observers in hydraulic fluid machinery. IFAC-PapersOnLine 2018, 51, 414–419. [Google Scholar] [CrossRef]
- Narasingam, A.; Siddhamshetty, P.; Kwon, J.S.I. Handling spatial heterogeneity in reservoir parameters using proper orthogonal decomposition based ensemble Kalman filter for model-based feedback control of hydraulic fracturing. Ind. Eng. Chem. Res. 2018, 57, 3977–3989. [Google Scholar] [CrossRef]




| State Estimator | Advantages | Limitations |
|---|---|---|
| Luenberger observer | 1. Simple to design and implement 2. Suitable for well-defined linear systems | 1. Poor estimation in the presence of model uncertainties |
| Reduced-Order observer | 1. Better Performance 2. Lower computational cost | Complicated to design |
| Sliding Mode Observer | 1. Suitable for linear and nonlinear systems 2. High robustness 3. Fault detection capabilities | 1. Chattering of the estimator 2. Complexity of the design |
| Kalman Filter | 1. Suitable for noisy systems 2. Allows fusion of different measurement sources | 1. Suitable for linear system 2. Not Suitable for non-Gaussian noise 3. Not suitable for high order systems |
| Adaptive Kalman Filter | 1. Suitable for noisy systems 2. Allows fusion of different measurement sources 3. Suitable for unknown noise covariance | 1. Suitable for linear system 2. Not suitable for non-Gaussian noise 3. Not suitable for high order systems |
| Extended Kalman Filter | 1. Suitable for noisy systems 2. Allows fusion of different measurement sources 3. Suitable for nonlinear systems | 1. High computational time 2. Not suitable for high order systems |
| Unscented Kalman Filter | 1. Suitable for noisy systems 2. Allows fusion of different measurement sources 3. Suitable for nonlinear systems 4. Lower computational cost | Not suitable for high order systems |
| Ensemble Kalman Filter | 1. Suitable for noisy systems 2. Allows fusion of different measurement sources 3. Suitable for nonlinear systems 4. Low computational cost 5. Suitable for high order systems | Not suitable for non-Gaussian noise |
| Particle Filter | 1. Suitable for multimodal probability distributions 2. Suitable for nonlinear systems | High computational time and cost |
| Process Industry | Method | Desired Output | Sustainability Impact | Refs |
|---|---|---|---|---|
| Polymerisation | Cubature KF | Concentrations and molecular weight distribution (MWD) | Inline monitoring of the process and efficiency improvement | [54] |
| Polymerisation | PID and EKF | Molecular weight (Mw) | Better estimation of process, less waste and higher process quality | [52] |
| Polymerisation | KF | Number-average and weight-average chain length | Better estimation of process and efficiency improvement | [55] |
| Polymerisation | Receding-horizon KF | State of methyl methacrylate polymerisation | Less computational time and efficiency improvement | [56] |
| Micro-injection moulding | EKF | Pressure signature | Improvement in part quality and less material waste | [58] |
| Injection moulding | KF and iterative learning control | State estimation | Improvement in machine control and part quality and efficiency | [59] |
| Injection moulding | EKF and MPC | Pressure trajectory | Improvement in part quality and process | [60] |
| Injection moulding | EKF | Cavity pressure | Production of lighter parts and less raw material use | [61] |
| Injection moulding | EKF | Detected distance | Increase the tool life and efficiency improvement | [62] |
| Polymer Extrusion | Nonlinear State Observer | Melt viscosity | Part quality enhancement Ability to process recycled materials less waste and rework | [63] |
| Liquid composite molding | State observer | Pressure and permeability | Part quality and process efficiency enhancement by less waste and rework | [64] |
| Electroslag Remelting | Linear KF | Temperature distribution | Defect-free ingots and efficiency improvement | [65] |
| Vacuum Arc Remelting | PF | Solidification front | Production of defect-free ingots without heat treatment | [66] |
| Hot-rolled Strip Cooling | EKF | Transient Temperature distribution | Better control of microstructure resource efficiency and quality. | [67] |
| Heavy Plate Rolling | Full and reduced EKF | Plate temperature | Better control of microstructure. Reduction in material use and weight | [68] |
| Hot Sheet Metal Forming | EKF | Spatial-temporal Temperature distribution | Prediction of material properties and reduction in material use and weight | [69] |
| Metal Forming | PF | Physical properties (thickness, bend angle, etc.) | Improvement in production accuracy and efficiency | [70] |
| Machining Process | Method | Desired Output | Sustainability Impact | Refs |
|---|---|---|---|---|
| Milling | KF | Tool flank wear | Estimation of tool life and tool changes schedule | [75] |
| End-Milling | KF | Remaining tool life | Estimation of tool life, efficient tool changes and reduced waste | [77] |
| Milling | Least Square SVM and KF | Remaining tool life | Improve tool life prediction and process efficiency | [78] |
| Turning | Unscented KF | Remaining tool life | Tool life prediction, tool changes and process efficiency | [79] |
| Milling | PF | Wear width of the tool | Tool width estimation, tool change scheduling and process efficiency | [80] |
| Milling | PF | Remaining tool life | Tool life prediction, tool change scheduling and process efficiency | [81] |
| Milling | Augmented PF | Estimation of tool degradation | Tool life estimation and process efficiency | [82] |
| Milling | PF | Tool life estimation | Tool life monitoring, tool change scheduling and process efficiency | [83] |
| Milling | Local Search PF | Tool life estimation | Tool life monitoring, tool change scheduling and process efficiency | [84] |
| Milling | Model-based KF | Surface roughness | Improved part quality and efficiency improvement | [85] |
| Micro-Milling | PF | Surface roughness and Surface topology | Improved part quality and reduced waste | [86] |
| AM Process | Method | Desired Output | Sustainability Impact | Refs |
|---|---|---|---|---|
| DED | Two-step KF | Melt pool temperature | Better estimation of the process and efficiency improvement | [113] |
| PBF | PID and KF | Temperature of powder bed | Enhance the profits by reduction of computational cost | [114] |
| Laser PBF | KF | Melt pool width | Part quality and efficiency enhancement by less waste and rework | [115] |
| Laser PBF | Image processing and KF | Various features of melt pool, plume, and spatter | Part quality and efficiency enhancement by less waste and rework | [118] |
| Laser PBF | State-observer | Temperature estimation of underlying layers of the part | Higher precision part and less rework | [106] |
| E-PBF and L-PBF | Ensemble KF | Internal Temperature fields | Higher part quality and waste reduction | [119] |
| FDM | Linear KF | Printed part Temperature | Uncertainty estimation and process quality enhancement | [120] |
| Polymer AM | KF | Stiffness of the printed part | Part quality and efficiency enhancement by less waste and rework | [121] |
| Polymer AM | KF | Stiffness of a printed cantilever beam | Part quality and efficiency enhancement by less waste and rework | [122] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McAfee, M.; Kariminejad, M.; Weinert, A.; Huq, S.; Stigter, J.D.; Tormey, D. State Estimators in Soft Sensing and Sensor Fusion for Sustainable Manufacturing. Sustainability 2022, 14, 3635. https://doi.org/10.3390/su14063635
McAfee M, Kariminejad M, Weinert A, Huq S, Stigter JD, Tormey D. State Estimators in Soft Sensing and Sensor Fusion for Sustainable Manufacturing. Sustainability. 2022; 14(6):3635. https://doi.org/10.3390/su14063635
Chicago/Turabian StyleMcAfee, Marion, Mandana Kariminejad, Albert Weinert, Saif Huq, Johannes D. Stigter, and David Tormey. 2022. "State Estimators in Soft Sensing and Sensor Fusion for Sustainable Manufacturing" Sustainability 14, no. 6: 3635. https://doi.org/10.3390/su14063635
APA StyleMcAfee, M., Kariminejad, M., Weinert, A., Huq, S., Stigter, J. D., & Tormey, D. (2022). State Estimators in Soft Sensing and Sensor Fusion for Sustainable Manufacturing. Sustainability, 14(6), 3635. https://doi.org/10.3390/su14063635








