Control Strategy for Line Overload and Short Circuit Current of Networked Distribution Systems
Abstract
:1. Introduction
1.1. Motivation and Aims
1.2. Literature Survey
1.3. Contributions and Organization of the Paper
- The key contribution of this study is to present an operating strategy for preventing line overload and relieving the short circuit current to ensure system stability;
- This paper provides an assessment of the proposed method based on the standards of the Korea Electric Power Corporation (KEPCO) with practical indicators. A review from a practical point of view can facilitate the understanding of NDS operations;
- This study also contributes to the economic operation of NDSs by enhancing the line utilization rate and preventing line extension.
2. Proposed Method
2.1. Theoretical Background
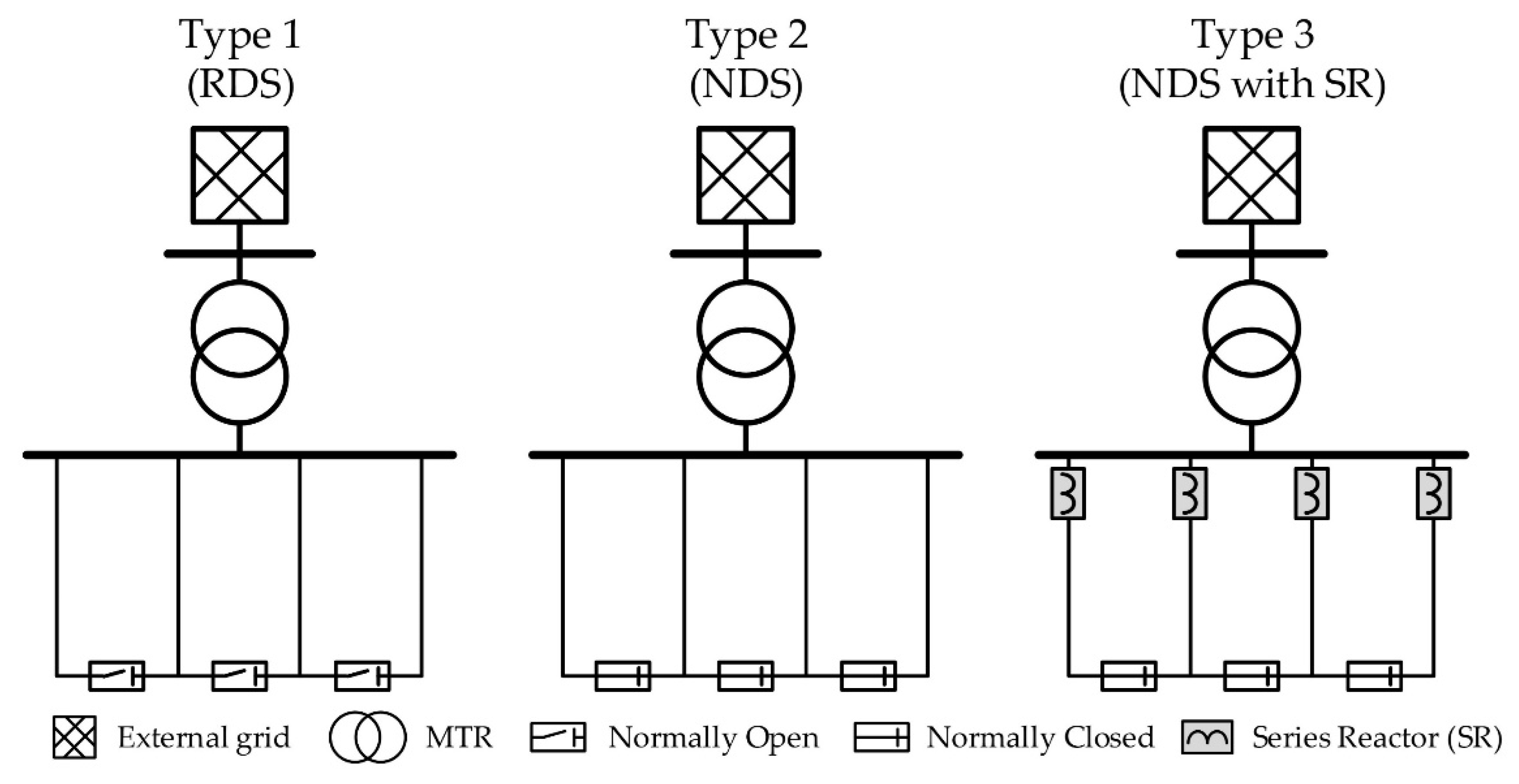
2.1.1. RDS
2.1.2. NDS
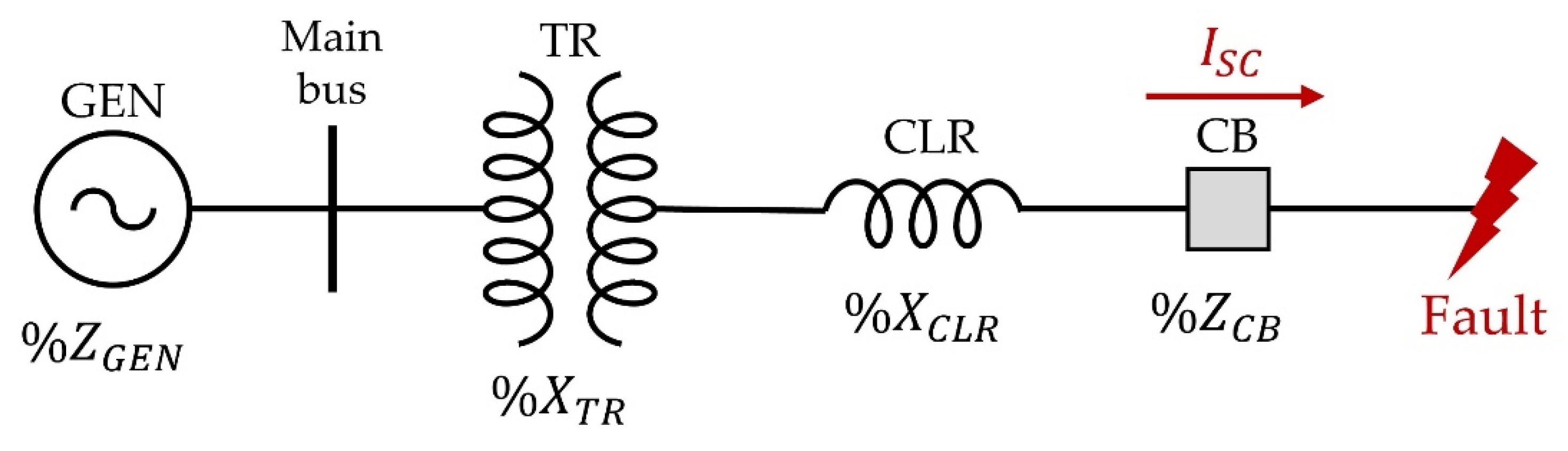
2.1.3. CLR
2.2. Indicator
2.2.1. Utilization Rate
2.2.2. Feeder Imbalance
2.2.3. Short Circuit Current
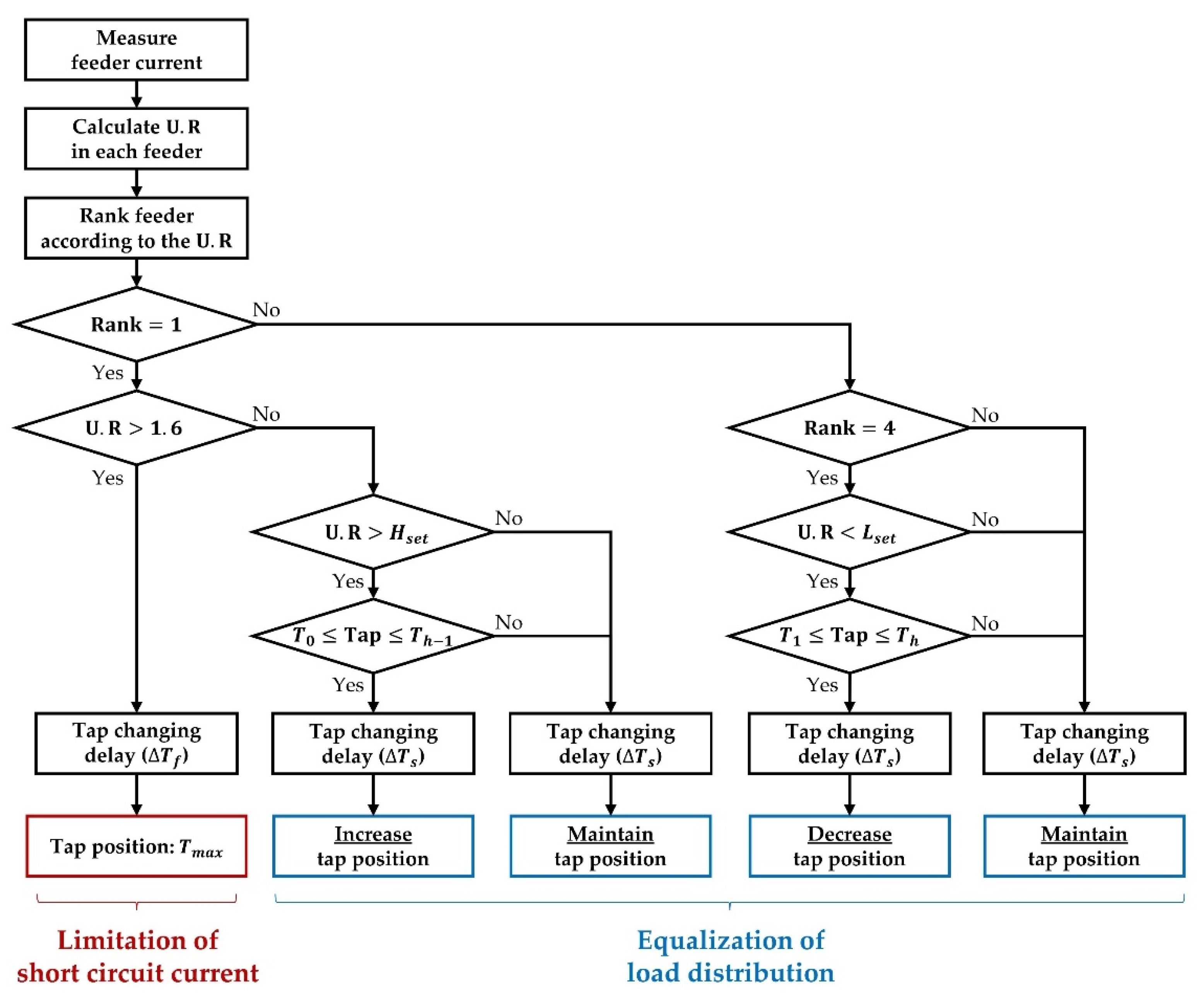
2.3. Proposed Method
2.3.1. Step 1: Line Equalization
2.3.2. Step 2: Tap Changing Control
3. Numerical Experiment Setup
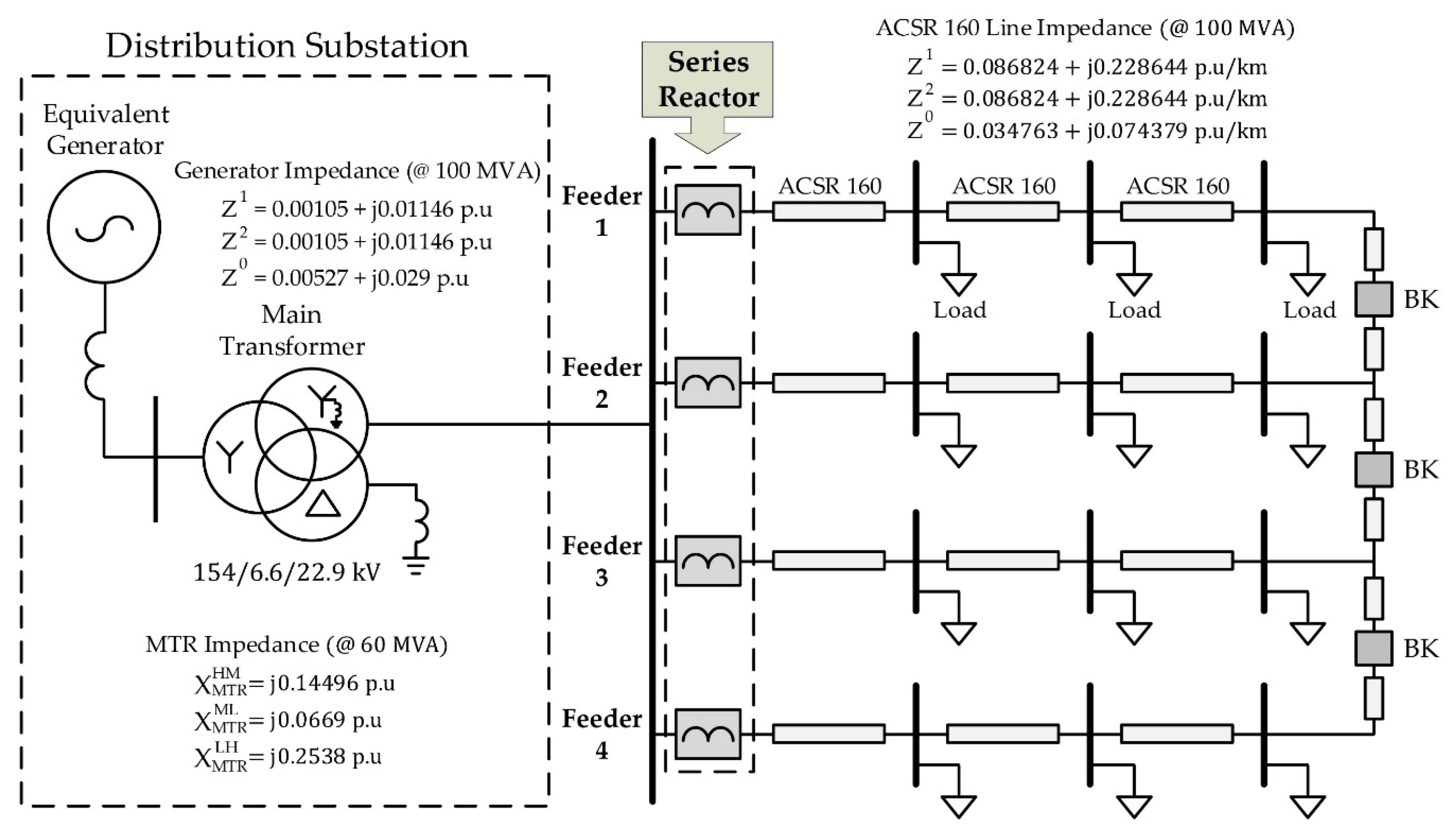
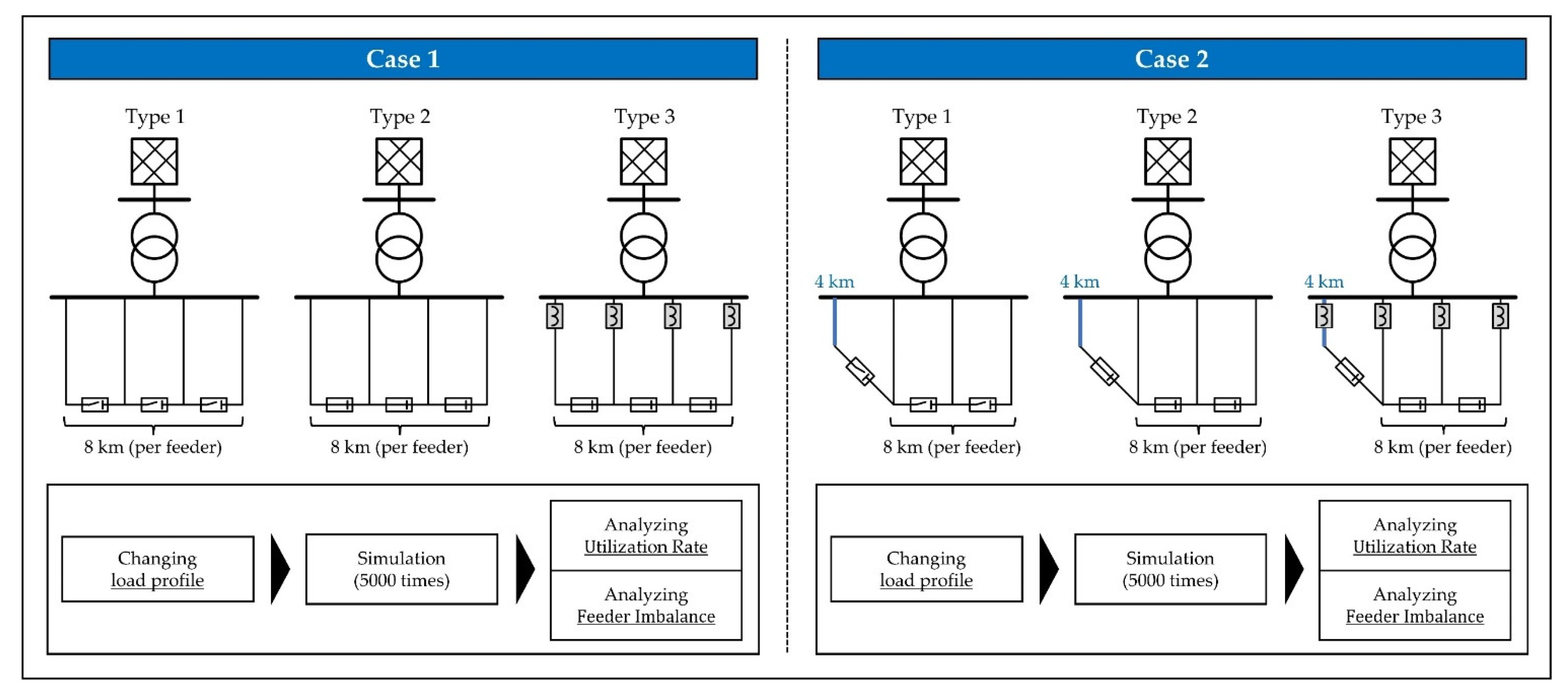
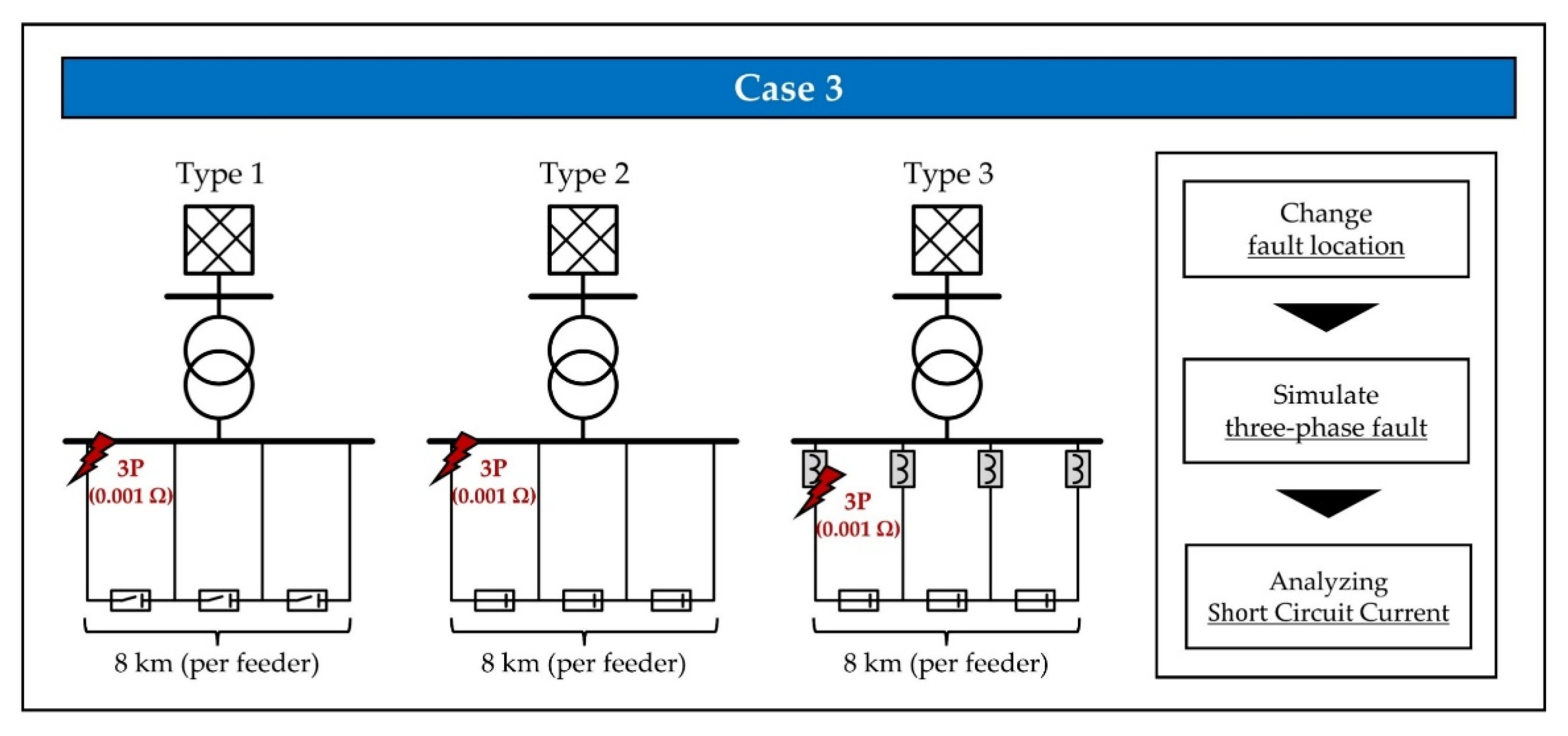
3.1. Test System
3.2. Simulation Setup
3.2.1. Steady-State Analysis
3.2.2. Short Circuit Analysis
4. Case Study
5. Discussions and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Sortomme, E.; Hindi, M.M.; MacPherson, S.D.J.; Venkata, S.S. Coordinated Charging of Plug-In Hybrid Electric Vehicles to Minimize Distribution System Losses. IEEE Trans. Smart Grid. 2011, 2, 198–205. [Google Scholar] [CrossRef]
- Zheng, Y.; Song, Y.; Hill, D.J.; Meng, K. Online Distributed MPC-Based Optimal Scheduling for EV Charging Stations in Distribution Systems. IEEE Trans. Ind. Inform. 2019, 15, 638–649. [Google Scholar] [CrossRef]
- Celli, G.; Pilo, F.; Pisano, G.; Allegranza, V.; Cicoria, R.; Iaria, A. Meshed vs. Radial MY Distribution Network in Presence of Large Amount of DG. In Proceedings of the IEEE PES Power Systems Conference and Exposition, New York, NY, USA, 10–13 October 2004; pp. 709–714. [Google Scholar]
- Meera, P.S.; Hemamalini, S. Integrated resource planning for a meshed distribution network under uncertainty. Electr. Power Syst. Res. 2021, 195, 107127. [Google Scholar] [CrossRef]
- Cruz, M.R.M.; Fitiwi, D.Z.; Santos, S.F.; Catalao, J.P.S. Meshed Operation of Distribution Network Systems: Enabling Increased Utilization of Variable RES Power. In Proceedings of the IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–6. [Google Scholar]
- Wang, B.; Zhang, C.; Dong, Z.Y.; Li, X. Improving Hosting Capacity of Unbalanced Distribution Networks via Robust Allocation of Battery Energy Storage System. IEEE Trans. Power Syst. 2020, 36, 2174–2185. [Google Scholar] [CrossRef]
- Nishant, B.; Niroj, G.; Heng, C.; Sri, R.K. Priority-based Management Algorithm in Distributed Energy Resource Management Systems. In Proceedings of the 2021 IEEE Green Technologies Conference (GreenTech), Denver, CO, USA, 7–9 April 2021; pp. 351–356. [Google Scholar]
- Ding, F.; Mather, B.; Gotseff, P. Technologies to Increase PV Hosting Capacity in Distribution Feeders. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Davoudi, M.; Cecchi, V.; Aguero, J.R. Investigating the Ability of Meshed Distribution Systems to Increase Penetration Levels of Distributed Generation. In Proceedings of the IEEE Southeastcon 2014, Lexington, KY, USA, 13–16 March 2014; pp. 1–5. [Google Scholar]
- Cruz, M.R.M.; Fitiwi, D.Z.; Santos, S.F.; Mariano, S.J.P.S.; Catalao, J.P.S. Prospects of a Meshed Electrical Distribution System Featuring Large-Scale Variable Renewable Power. Energies 2018, 11, 3399. [Google Scholar] [CrossRef] [Green Version]
- Alvarez-Herault, M.C.; N’Doye, N.; Gandioli, C.; Hadjsaid, N.; Tixador, P. Meshed distribution network vs reinforcement to increase the distributed generation connection. Sustain. Energy Grids Netw. 2015, 1, 20–27. [Google Scholar] [CrossRef]
- Wolter, D.; Zdrallek, M.; Stotzel, M.; Schacherer, C.; Mladenovic, I.; Biller, M. Impact of meshed grid topologies on distribution grid planning and operation. CIRED Open Access Proc. J. 2017, 2017, 2338–2341. [Google Scholar] [CrossRef]
- Capitanescu, F.; Ochoa, L.F.; Margossian, H.; Hatziargyriou, N.D. Assessing the Potential of Network Reconfiguration to Improve Distributed Generation Hosting Capacity in Active Distribution Systems. IEEE Trans. Power Syst. 2014, 30, 346–356. [Google Scholar] [CrossRef]
- Thapar, A.; Saha, T.K.; McDonald, J.D.F. An Investigation of Composite System Reliability in Meshed and Extended Networks. In Proceedings of the 2005 International Power Engineering Conference, Singapore, 29 November–2 December 2005; pp. 1099–1104. [Google Scholar]
- Ruben, B.; Cross, A.; Strickland, D.; Aten, M.; Ferris, R. Meshing Radial Networks at 11kV. In Proceedings of the 2011 2nd IEEE PES International Conference and Exhibition on Innovative Smart Grid Technologies, Manchester, UK, 5–7 December 2011; pp. 1–8. [Google Scholar]
- Cristian, N.; Ahmed, A.A.; Dakyo, B. Impact Analysis of Distributed Generation on Mesh and Radial Distribution Network. Overview and State of the art. In Proceedings of the PLUMEE Conference, Bucharest, Romania, 18–20 June 2013; pp. 1–10. [Google Scholar]
- Grzanic, M.; Antic, T.; Flammini, M.G.; Wilkening, H.; Prettico, G. Renewable energies integration in a DiNeMo model based on a German urban grid. In Proceedings of the CIRED 2020 Berlin Workshop (CIRED 2020), Oline Conference, 22–23 September 2020; pp. 596–598. [Google Scholar]
- Gandioli, C.; Alvarez-Herault, M.C.; Tixador, P.; Hadjsaid, N.; Medina, D.M.R. Innovative Distribution Networks Planning Integrating Superconducting Fault Current Limiters. IEEE Trans. Appl. Supercond. 2013, 23, 5603904. [Google Scholar] [CrossRef]
- Yu, P.; Venkatesh, B.; Yazdani, A.; Singh, B.N. Optimal Location and Sizing of Fault Current Limiters in Mesh Networks Using Iterative Mixed Integer Nonlinear Programming. IEEE Trans. Power Syst. 2016, 31, 4776–4783. [Google Scholar] [CrossRef]
- Penaloza, J.D.R.; Borghetti, A.; Napolitano, F.; Tossani, F.; Nucci, C.A. A New Transient-Based Earth Fault Protection System for Unearthed Meshed Distribution Networks. IEEE Trans. Power Deliv. 2021, 36, 2585–2594. [Google Scholar] [CrossRef]
- Yazdaninejadi, A.; Nazarpour, D.; Golshannavaz, S. Dual-setting directional over-current relays: An optimal coordination in multiple source meshed distribution networks. Int. J. Electr. Power Energy Syst. 2017, 86, 163–176. [Google Scholar] [CrossRef]
- Tsimtsios, A.M.; Nikolaidis, V.C. Toward Plug-and-Play Protection for Meshed Distribution Systems with DG. IEEE Trans. Smart Grid. 2020, 11, 1980–1995. [Google Scholar] [CrossRef] [Green Version]
- Hatata, A.Y.; Ebeid, A.S.; El-Saadawi, M.M. Optimal Restoration of Directional Overcurrent Protection Coordination for Meshed Distribution System Integrated with DGs based on FCLs and adaptive relays. Electr. Power Syst. Res. 2022, 205, 107738. [Google Scholar] [CrossRef]
- Muhammad, Y.; Amin, J.; Kashem, M.M.; Danny, S. An Adaptive Overcurrent Protection Scheme for Dual-Setting Directional Recloser and Fuse Coordination in Unbalanced Distribution Networks with Distributed Generation. IEEE Trans. Ind. Appl. 2022, 2, 1831–1842. [Google Scholar]
- Hoang, T.T.; Quoc, T.T.; Yvon, B. An Advanced Protection Scheme for Medium-voltage Distribution Networks Containing Low-voltage Microgrids with High Penetration of Photovoltaic Systems. Int. J. Electr. Power Energy Syst. 2022, 139, 107988. [Google Scholar] [CrossRef]
- Su, C.; Zhou, W.; Meng, L.; Yang, S.; Li, T.; Hu, X. Research on Loop-Closing Strategy of Two-Way Active Distribution Network Based on Power Flow Controller. In Proceedings of the 2021 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Chengdu, China, 2 December 2021; pp. 132–135. [Google Scholar]
- Chen, T.H.; Huang, W.T.; Gu, J.C.; Pu, G.C.; Hsu, Y.F.; Guo, T.Y. Feasibility Study of Upgrading Primary Feeders From Radial and Open-Loop to Normally Closed-Loop Arrangement. IEEE Trans. Power Syst. 2004, 19, 1308–1316. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.T.; Chen, T.H. Assessment of Upgrading Existing Primary Feeders from Radial to Normally Closed Loop Arrangement. In Proceedings of the IEEE/PES Transmission and Distribution Conference and Exhibition, Yokohama, Japan, 6–10 October 2002; pp. 2123–2128. [Google Scholar]
- Kerzel, M.; Garzon-Real, J.; Zdrallek, M.; Wolter, D.; Schacherer, C. Optimal Switch Configuration Algorithm for Dynamically Meshed Power Distribution Grids. In Proceedings of the 2020 International Conference on Smart Energy Systems and Technologies (SEST), Istanbul, Turkey, 7–9 September 2020; pp. 1–6. [Google Scholar]
- Loos, M.; Werben, S.; Maun, J.C. Circulating Currents in Closed Loop Structure, a New Problematic in Distribution Networks. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–7. [Google Scholar]
- Chen, L.; Xu, X.; Yao, L.; Xu, Q. Study of a Distribution Line Overload Control Strategy Considering the Demand Response. Electr. Power Compon. Syst. 2014, 42, 970–983. [Google Scholar] [CrossRef]
- Grond, M.O.W.; Morren, J.; Slootweg, J.G. Integrating Smart Grid Solutions into Distribution Network Planning. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013; pp. 1–6. [Google Scholar]
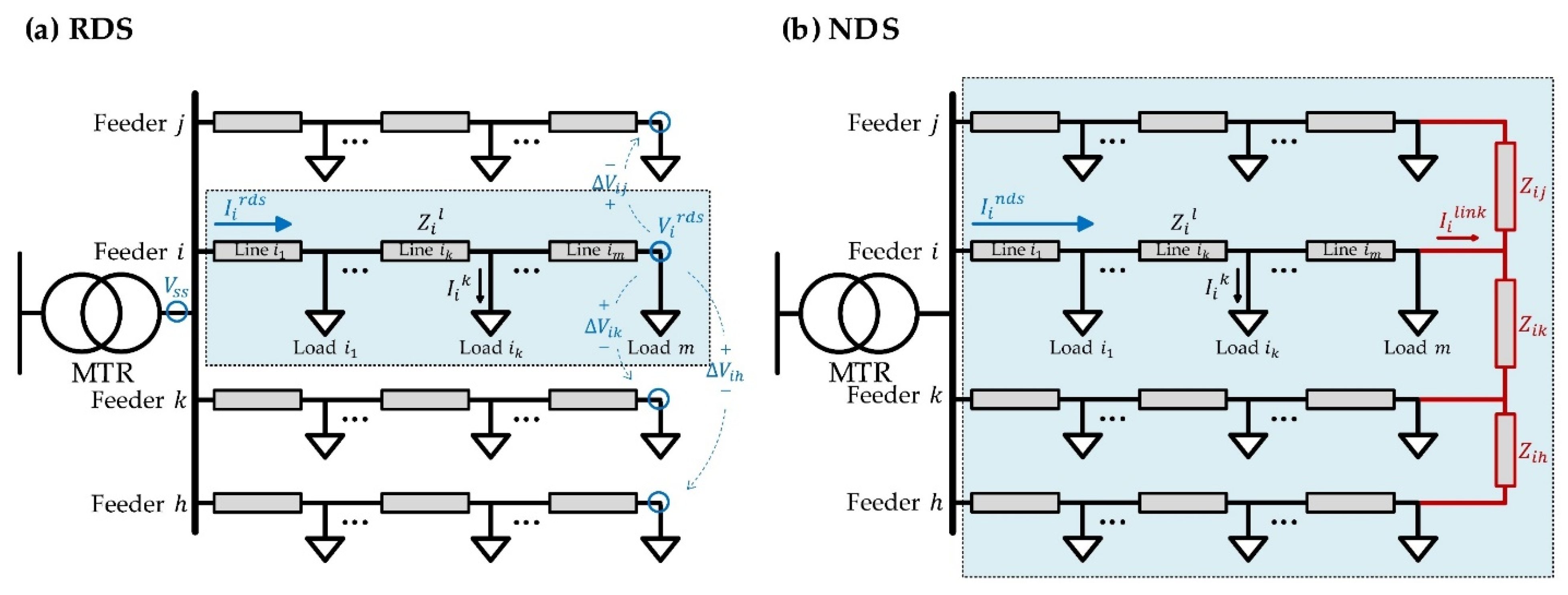









| Notation | Meaning |
|---|---|
| load current of feeder | |
| The number of loads in feeder | |
| line impedance of feeder | |
| The number of distribution lines in feeder | |
| Feeder current of feeder in (a) RDS | |
| Substation voltage in (a) RDS | |
| Terminal voltage of feeder in (a) RDS | |
| Voltage across the terminals of and feeder in (a) RDS | |
| Voltage across the terminals of and feeder in (a) RDS | |
| Voltage across the terminals of and feeder in (a) RDS | |
| Line impedance across the terminals of and feeder in (b) NDS | |
| Line impedance across the terminals of and feeder in (b) NDS | |
| Line impedance across the terminals of and feeder in (b) NDS | |
| Linkage line current flowing into/from feeder in (b) NDS | |
| Feeder current of feeder in (b) NDS |
| Notation | Meaning |
|---|---|
| Short circuit current | |
| Percent impedance of the generator | |
| Percent impedance of the transformer | |
| Percent impedance of the CLR | |
| Percent impedance of the circuit breaker | |
| Rated feeder current |
| Tap Position | Usage | |
|---|---|---|
| Equalization of load distribution | ||
| Limitation of short circuit current |
| Notation | Meaning |
|---|---|
| Minimum tap position | |
| Maximum tap position | |
| Initial inductance of feeder | |
| Common inductance among the four feeders | |
| k | Inductance gap of between tap positions |
| h | tap position |
| Notation | Meaning |
|---|---|
| High boundary setting | |
| Low boundary setting | |
| Tap changing delay time in fault state | |
| Tap changing delay time in steady state |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Chae, W.; Kim, W.; Choi, S. Control Strategy for Line Overload and Short Circuit Current of Networked Distribution Systems. Sustainability 2022, 14, 4208. https://doi.org/10.3390/su14074208
Lee J, Chae W, Kim W, Choi S. Control Strategy for Line Overload and Short Circuit Current of Networked Distribution Systems. Sustainability. 2022; 14(7):4208. https://doi.org/10.3390/su14074208
Chicago/Turabian StyleLee, Junwoo, Wookyu Chae, Woohyun Kim, and Sungyun Choi. 2022. "Control Strategy for Line Overload and Short Circuit Current of Networked Distribution Systems" Sustainability 14, no. 7: 4208. https://doi.org/10.3390/su14074208
APA StyleLee, J., Chae, W., Kim, W., & Choi, S. (2022). Control Strategy for Line Overload and Short Circuit Current of Networked Distribution Systems. Sustainability, 14(7), 4208. https://doi.org/10.3390/su14074208






