Impact of Climate Change on Productivity and Technical Efficiency in Canadian Crop Production
Abstract
:1. Introduction
2. Materials and Methods
2.1. Brief Overview of Canada’s Changing Climate
2.2. Theoretical Model Specification
2.3. Incorporating Climate/Weather in the General Stochastic Frontier Framework
2.4. Functional Form for the Production Function
2.5. Data Description
3. Results and Discussion
3.1. Final Model Specification
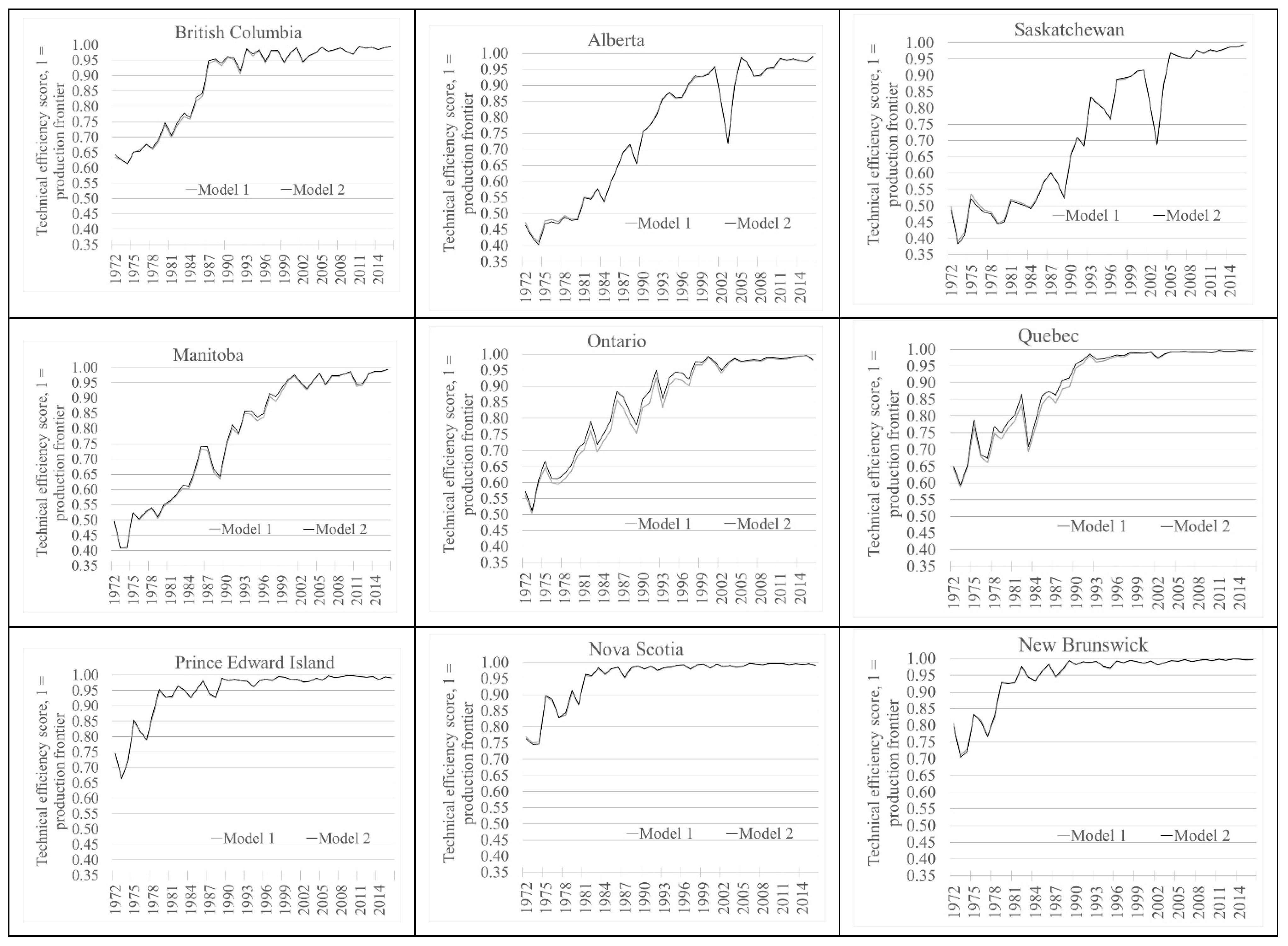
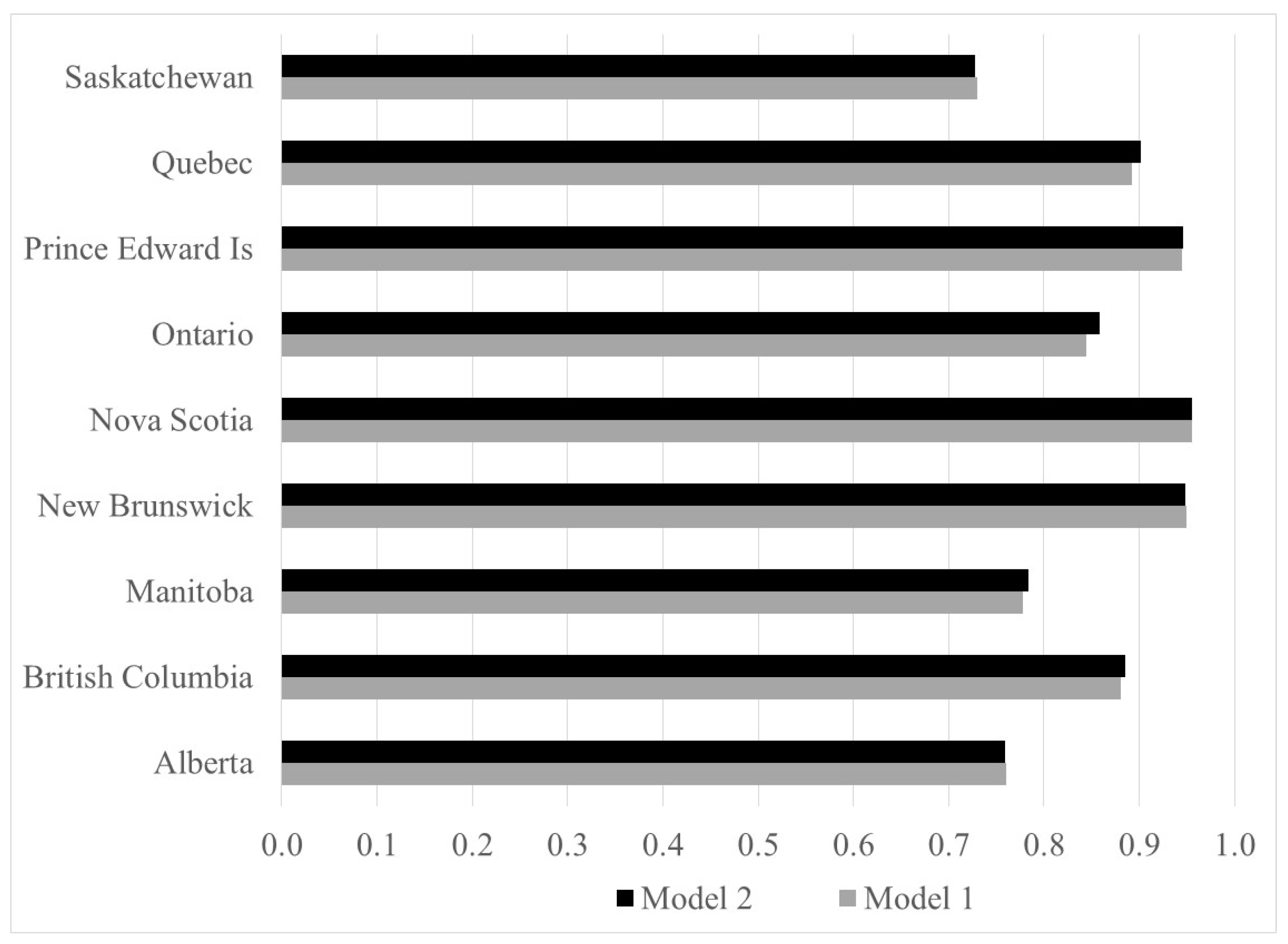
3.2. Estimation Results and Discussion
4. Conclusions and Policy Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Detailed Data Description
Appendix A.1. Climatic Data
Appendix A.2. Input and Output Data
| Variable | Source |
|---|---|
| Output | |
| Farm cash receipts from crop production (nominal value), thousand CAD | Statistics Canada, CANSIM 002-0001 (Table 32-10-0045-01) |
| Farm product price index, crop production, 2007 = 100 | Statistics Canada, CANSIM 002-0069 (Table 32-10-0099-01) |
| Inputs | |
| Farm input price index, crop production, 1986 = 100 | Statistics Canada, generated by Statistics Canada upon the authors’ request |
| Capital | |
| Machinery and Equipment (M&E), thousand CAD | Statistics Canada, CANSIM 002-0007 (Table 32-10-0050-01) |
| Depreciation on M&E, thousand CAD | Statistics Canada, CANSIM 002-0005 (Table 32-10-0049-01) |
| Machinery repairs, thousand CAD | Statistics Canada, CANSIM 002-0005 (Table 32-10-0049-01) |
| Land | |
| Value of land and buildings (L&B), thousand CAD | Statistics Canada, CANSIM 002-0007 (Table 32-10-0050-01) |
| Depreciation on buildings, thousand CAD | Statistics Canada, CANSIM 002-0005 (Table 32-10-0049-01) |
| Repairs to buildings and fences, thousand CAD | Statistics Canada, CANSIM 002-0005 (Table 32-10-0049-01) |
| Property taxes, thousand CAD | Statistics Canada, CANSIM 002-0005 (Table 32-10-0049-01) |
| Labour | |
| Paid labour: cash wages (family and non-family wages) and custom work, thousand CAD | Statistics Canada, CANSIM 002-0005 (Table 32-10-0049-01) |
| Operator labour and unpaid family labour, hours per year | Derived from Census of Agriculture, 1971–2016, using Cahill and Rich’s (2012) approach |
| Materials | |
| Electricity; fuel; fertilizer and lime; pesticide; commercial seed; telephone; twine, wire and containers; crop and hail insurance; business insurance; custom work; other operating expenses; irrigation. | Statistics Canada, CANSIM 002-0005 (Table 32-10-0049-01) |
References
- Marshall, E.; Aillery, M.; Malcolm, S.; Williams, R. Agricultural production under climate change: The potential impacts of shifting regional water balances in the United States. Am. J. Agric. Econ. 2015, 97, 568–588. [Google Scholar] [CrossRef] [Green Version]
- FAO. Climate Variability and Change: A Challenge for Sustainable Agricultural Production; Document for the Committee on Agriculture, COAG/01/05; Food and Agriculture Organization: Rome, Italy, 2001. [Google Scholar]
- Easterling, D.; Meehl, G.; Parmesan, C.; Changnon, S.; Karl, T.; Mearns, L. Climate extremes: Observations, modeling and impacts. Science 2000, 289, 2068–2074. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- IPCC. Third Assessment Report: Report of Working Group I; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- IPCC. Climate change 2001, impacts, adaptation and vulnerability. In Third Assessment Report: Report of Working Group II; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- US Environmental Protection Agency. Climate Change Indicators: Length of Growing Season. Available online: https://www.epa.gov/climate-indicators/climate-change-indicators-length-growing-season (accessed on 4 March 2022).
- Olesen, J.E.; Bindi, M. Consequences of climate change for European agricultural productivity, land use and policy. Eur. J. Agron. 2002, 16, 239–262. [Google Scholar] [CrossRef]
- Mora, C.; Caldwell, I.; Caldwell, J.; Fisher, M.; Running, S. Suitable days for plant growth disappear under projected climate change: Potential human and biotic vulnerability. PLoS Biol. 2015, 13, e1002167. [Google Scholar] [CrossRef] [Green Version]
- Luck, J.; Spackman, M.; Freeman, A.; Trebicki, P.; Griffiths, W.; Finlay, K.; Chakraborty, S. Climate change and diseases of food crop. Plant Pathol. 2011, 60, 113–121. [Google Scholar] [CrossRef]
- Cahill, S.A.; Rich, T. Measurement of Canadian agricultural productivity growth. In Productivity Growth in Agriculture: An International Perspective; Fuglie, K.O., Wang, S.L., Ball, V.E., Eds.; CAB International: Wallingford, UK; Cambridge, MA, USA, 2012. [Google Scholar]
- Darku, A.; Malla, S.; Tran, K. Sources of measurement of agricultural productivity and efficiency in Canadian provinces: Crops and livestock. Can. J. Agric. Econ. 2015, 64, 49–70. [Google Scholar] [CrossRef] [Green Version]
- Stewart, B.E.R. Measures and Causes of Productivity Growth in Prairie Agriculture: 1940–2004. Master’s Thesis, Department of Rural Economy, University of Alberta, Edmonton, AB, Canada, 2006. [Google Scholar]
- Sherlund, S.; Barrett, C.; Adesina, A. Smallholder technical efficiency controlling for environmental production conditions. J. Dev. Econ. 2022, 69, 85–101. [Google Scholar] [CrossRef]
- Key, N.; Sneeringer, S. Potential Effects of Climate Change on the Productivity of U.S. Dairies. Am. J. Agric. Econ. 2014, 96, 1136–1156. [Google Scholar] [CrossRef]
- Wang, S.; Ball, E.; Nehring, R.; Williams, R.; Chau, T. Impacts of Climate Change and Extreme Weather on U.S. Agricultural Productivity: Evidence and Projection; NBER Working Paper 23533; National Bureau of Economic Research: Cambridge, MA, USA, 2017. [Google Scholar]
- Vincent, L.; Zhang, X.; Mekis, E.; Wan, H.; Bush, E. Changes in Canada’s climate: Trends in indices based on daily temperature and precipitation data. Atmos. Ocean 2018, 56, 332–349. [Google Scholar] [CrossRef] [Green Version]
- Bush, E.; Lemmen, D.S. Canada’s Changing Climate Report; Government of Canada: Ottawa, ON, Canada, 2019; Available online: https://changingclimate.ca/CCCR2019/ (accessed on 3 January 2022).
- Lobell, D.; Field, C. Global scale climate-crop yield relationships and the impacts of recent warming. Environ. Res. Lett. 2007, 2, 014002. [Google Scholar] [CrossRef]
- Lobell, D.; Cahill, K.; Field, C. Historical effects of temperature and precipitation on California crop yields. Clim. Change 2007, 81, 187–203. [Google Scholar] [CrossRef]
- Lobell, D.; Schlenker, W.; Costa-Roberts, J. Climate trends and global crop production since 1980. Science 2011, 333, 616–620. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mendelsohn, R.; Nordhaus, W.D.; Shaw, D. The Impact of Global Warming on Agriculture: A Ricardian Analysis. Am. Econ. Rev. 1994, 84, 753. [Google Scholar]
- Aigner, D.; Lovell, C.; Schmidt, P. Formulation and Estimation of Stochastic Frontier Production Function Models. J. Econom. 1977, 6, 21–37. [Google Scholar] [CrossRef]
- Meeusen, W.; van den Broeck, J. Efficiency estimation from Cobb-Douglas production functions with composed error. Int. Econ. Rev. 1977, 18, 435–444. [Google Scholar] [CrossRef]
- Greene, W. The econometric approach to efficiency analysis. In The Measurement of Productive Efficiency and Productivity Change; Fried, H., Lovell, C.A.K., Schmidt, S., Eds.; Oxford University Press: New York, NY, USA, 2008. [Google Scholar]
- Jondrow, Y.; Lovell, C.; Materov, I.; Schmidt, P. On the estimation of technical efficiency in the stochastic production model. J. Econom. 1982, 19, 233–238. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, P.; Sickles, R. Production frontiers and panel data. J. Bus. Econ. Stat. 1984, 2, 367–374. [Google Scholar]
- Cornwell, C.; Schmidt, P.; Sickles, R. Production frontiers with cross-section and time series variation in efficiency levels. J. Econom. 1990, 46, 185–200. [Google Scholar] [CrossRef]
- Kumbhakar, S. Production frontiers, panel data and time varying technical efficiency. J. Econom. 1990, 46, 201–211. [Google Scholar] [CrossRef]
- Battese, G.; Coelli, T. Frontier production functions, technical efficiency and panel data: With application to paddy farmers in India. J. Product. Anal. 1992, 3, 153–169. [Google Scholar] [CrossRef]
- Battese, G.E.; Coelli, T.J. A model for technical inefficiency effects in a stochastic frontier production function for panel data. Empir. Econ. 1995, 20, 325–332. [Google Scholar] [CrossRef] [Green Version]
- Greene, W. Fixed and random effects in stochastic frontier models. J. Product. Anal. 2005, 23, 7–32. [Google Scholar] [CrossRef] [Green Version]
- Greene, W. Reconsidering heterogeneity in panel data estimators of the stochastic frontier model. J. Econom. 2005, 126, 269–303. [Google Scholar] [CrossRef]
- Beloti, F.; Daidone, S.; Ilardi, G. Stochastic frontier analysis using Stata. Stata J. 2013, 13, 719–758. [Google Scholar] [CrossRef] [Green Version]
- Kumbhakar, S.C.; Ghosh, S.; McGuckin, J.T. A generalized production frontier approach for estimating determinants of inefficiency in US dairy farms. J. Bus. Econ. Stat. 1991, 9, 279–286. [Google Scholar]
- Reifschneider, D.; Stevenson, R. Systematic departures from the frontier: A framework for the analysis of firm inefficiency. Int. Econ. Rev. 1991, 32, 715. [Google Scholar] [CrossRef]
- Wang, H.; Schmidt, P. One Step and Two Step Estimation of the Effects of Exogenous Variables on Technical Efficiency Levels. J. Product. Anal. 2002, 18, 129–144. [Google Scholar] [CrossRef]
- Oury, B. Allowing for weather in crop production model building. Am. J. Agric. Econ. 1965, 47, 270–283. [Google Scholar] [CrossRef]
- Paltasingh, K.R.; Goyari, P.; Mishra, R.K. Measuring weather impact on crop yield using aridity index: Evidence from Odisha. Agric. Econ. Res. Rev. 2012, 25, 205–216. [Google Scholar]
- Hatfield, J.; Prueger, J. Temperature extremes: Effect on plant growth and development. Weather Clim. Extrem. 2015, 10, 4–10. [Google Scholar] [CrossRef] [Green Version]
- Schlenker, W.; Roberts, M.J. Nonlinear Temperature Effects Indicate Severe Damages to US Crop Yields under Climate Change. Proc. Natl. Acad. Sci. USA 2009, 106, 15594–15598. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schlenker, W.; Roberts, M.J. Nonlinear Effects of Weather on Crop Yields: Implications for Climate Change. Rev. Agric. Econ. 2006, 28, 391–398. [Google Scholar] [CrossRef]
- Kopp, R.J.; Smith, K. Frontier production function estimates for steam electric generation: A comparative analysis. South. Econ. J. 1980, 47, 1049–1059. [Google Scholar] [CrossRef]
- Gong, B.H.; Sickles, R.C. Finite sample evidence on the performance of stochastic frontiers and data envelopment analysis using panel data. J. Econom. 1992, 51, 259–284. [Google Scholar] [CrossRef]
- Giannakas, K.; Tran, K.; Tzouvelekas, V. On the choice of functional form in stochastic frontier modeling. Empir. Econ. 2003, 28, 75–100. [Google Scholar] [CrossRef]
- Zellner, A.; Kmenta, J.; Dreze, J. Specification and estimation of Cobb-Douglas production function models. Econometrica 1966, 34, 784. [Google Scholar] [CrossRef]
- Griliches, Z. Estimates of the aggregate agricultural production function from cross-sectional data. J. Farm Econ. 1963, 45, 419. [Google Scholar] [CrossRef]
- Kelly, D.L.; Kolstad, C.D.; Mitchell, G.T. Adjustment costs from environmental change. J. Environ. Econ. Manag. 2005, 50, 468–495. [Google Scholar] [CrossRef]
- Zhang, T.; Zhu, J.; Wassman, R. Responses of rice yields to recent climate change in China: An empirical assessment based on long-term observations at different spatial scales (1981–2005). Agric. For. Meteorol. 2010, 150, 1128–1137. [Google Scholar] [CrossRef]
- Sarker, M.A.; Alam, K.; Gow, J. Exploring the relationship between climate change and rice yield in Bangladesh: An analysis of time series data. Agric. Syst. 2012, 112, 11–16. [Google Scholar] [CrossRef]
- Njuki, E.; Bravo-Ureta, B.; O’Donnell, C. A new look at the decomposition of agricultural productivity growth incorporating weather effects. PLoS ONE 2018, 13, e0192432. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schlenker, W.; Hanemann, W.M.; Fisher, A.C. The impact of global warming on US agriculture: An econometric analysis of optimal growing conditions. Rev. Econ. Stat. 2006, 88, 113–125. [Google Scholar] [CrossRef]
- Angstrom, A. A Coefficient of Humidity of General Applicability. Geogr. Ann. 1936, 18, 245–254. [Google Scholar]


| Model (1) | Model (2) | Model (3) | |
|---|---|---|---|
| Frontier Equation | |||
| Ln (Capital) a | −0.036 (0.098) | −0.011 (0.098) | −0.053 (0.103) |
| Ln (Land) | 0.387 *** (0.040) | 0.376 *** (0.040) | 0.390 *** (0.041) |
| Ln (Paid Labour) | 0.227 *** (0.057) | 0.247 *** (0.053) | 0.221 *** (0.058) |
| Ln (Unpaid Labour) | 0.113 * (0.065) | 0.058 (0.058) | 0.123 * (0.066) |
| Ln (Materials) | −0.028 (0.073) | 0.005 * (0.070) | −0.014 (0.073) |
| Ln (Standard Deviation of Precipitation) b | −0.133 *** (0.051) | −0.146 *** (0.053) | −0.118 ** (0.053) |
| Ln (Oury Index) | 0.111 ** (0.043) | 0.119 *** (0.045) | 0.081 * (0.045) |
| Ln (Farm Size) | 0.187 * (0.103) | - | 0.207 ** (0.105) |
| Trend dummy: 1981–1989 | −0.037 (0.034) | −0.038 (0.034) | −0.039 (0.035) |
| Trend dummy: 1990–1998 | −0.157 *** (0.048) | −0.151 *** (0.048) | −0.162 ** (0.048) |
| Trend dummy: 1999–2007 | −0.131 ** (0.054) | −0.125 ** (0.054) | −0.136 ** (0.055) |
| Trend dummy: 2008–2016 | −0.072 (0.056) | −0.048 (0.056) | −0.080 (0.057) |
| Inefficiency equation | |||
| OSI | 0.042 ** (0.017) | 0.043 ** (0.017) | - |
| Ln (Oury Index) | - | - | 0.080 (0.084) |
| Ln (Standard Deviation of Temperature) | 0.191 * (0.109) | 0.236 ** (0.104) | 0.181 * (0.110) |
| Ln (Standard Deviation of Precipitation) | −0.256 *** (0.095) | −0.249 *** (0.095) | −0.183 * (0.100) |
| Time trend | −0.031 *** (0.003) | −0.030 *** (0.003) | −0.031 *** (0.004) |
| Percentage of irrigated area | 0.006 (0.004) | 0.005 (0.004) | 0.007 * (0.004) |
| Percentage of output from grains/legumes in total crop output | 0.006 *** (0.001) | 0.006 *** (0.001) | 0.007 *** (0.001) |
| Ln (Degree Days) | 0.074 * (0.042) | 0.058 (0.040) | 0.018 (0.051) |
| Ln (Standard Deviation of Temperature) | 2.837 ** (1.478) | 3.348 ** (1.653) | 2.645 * (1.443) |
| Ln (Standard Deviation of Precipitation) | −1.112 (0.901) | −2.309 *** (0.868) | −0.908 (0.905) |
| Ln (Farm Size) | 0.667 ** (0.294) | - | 0.740 ** (0.296) |
| Constant | −11.609 *** (3.278) | −6.696 *** (2.53) | −11.999 *** (3.249) |
| Constant | −5.007 *** (0.125) | −4.925 *** (0.117) | −5.011 *** (0.133) |
| Observations | 405 | 405 | 405 |
| Wald chi2 (12) | 857.81 | 878.15 | 861.87 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galushko, V.; Gamtessa, S. Impact of Climate Change on Productivity and Technical Efficiency in Canadian Crop Production. Sustainability 2022, 14, 4241. https://doi.org/10.3390/su14074241
Galushko V, Gamtessa S. Impact of Climate Change on Productivity and Technical Efficiency in Canadian Crop Production. Sustainability. 2022; 14(7):4241. https://doi.org/10.3390/su14074241
Chicago/Turabian StyleGalushko, Viktoriya, and Samuel Gamtessa. 2022. "Impact of Climate Change on Productivity and Technical Efficiency in Canadian Crop Production" Sustainability 14, no. 7: 4241. https://doi.org/10.3390/su14074241
APA StyleGalushko, V., & Gamtessa, S. (2022). Impact of Climate Change on Productivity and Technical Efficiency in Canadian Crop Production. Sustainability, 14(7), 4241. https://doi.org/10.3390/su14074241







