Electrical and Mechanical Characteristics Assessment of Wind Turbine System Employing Acoustic Sensors and Matrix Converter
Abstract
:1. Introduction
1.1. Background
1.2. Need for Current Research
1.3. Existing Works Done
1.4. Objectives
- To measure the frequency of the vibration signal extracted from acoustic sensors using empirical wavelet transform.
- To assess the magnitude of the vibration of WECS for various wind speed profiles.
- To improve the efficiency of the converter employed for WECS.
- To reduce the THD of both voltage and current components to ensure the power quality of the generated power by WECS.
1.5. Organization of the Work
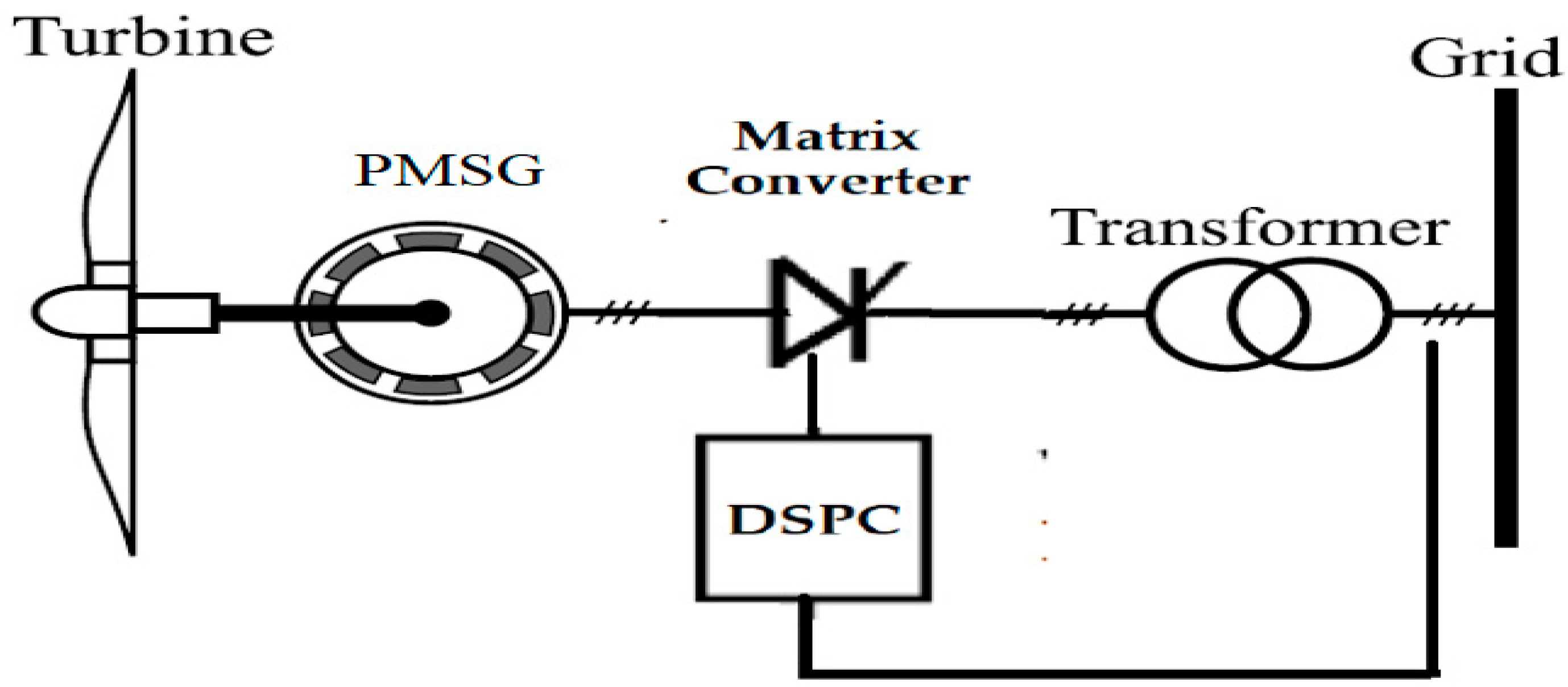
2. Modelling of WECS
2.1. Wind Turbine Configuration with PMSG
2.2. Wind Turbine Model
- A = π × R2 represents the turbine’s blade swept,
- V is the speed of the wind,
- (λ, β) signifies the power coefficient of the turbine,
- λ is the tip speed ratio,
- β terms the pitch angle,
- ω denotes the blades angular velocity,
- R defines the rotor radius.
2.3. PMSG Modeling
- is the q-axis current,
- is the d-axis voltage,
- is the q-axis voltage,
- is the angular frequency (electrical) of the generator,
- is the d-axis inductance of generator,
- is the q-axis inductance of generator,
- denotes the permanent flux,
- represents the stator resistance,
- P indicates the number of poles.
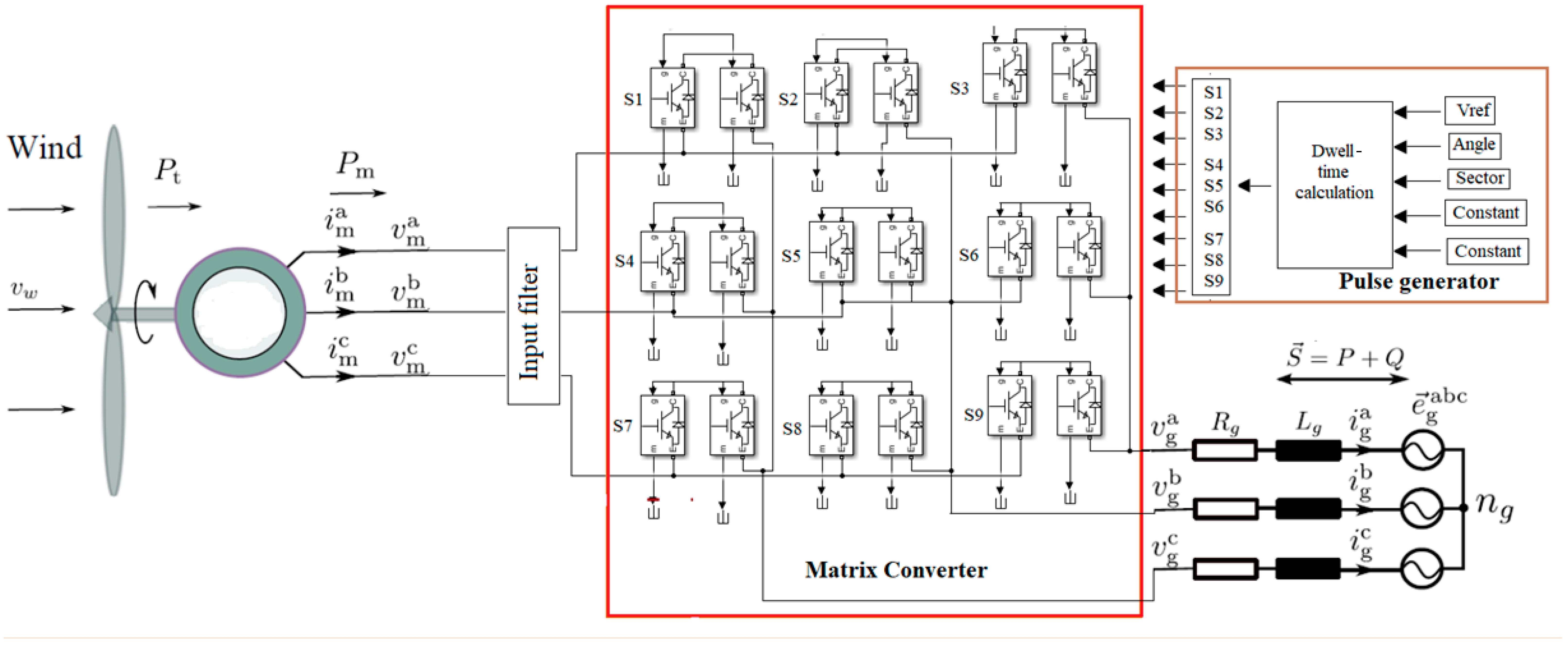
3. Proposed Methodology
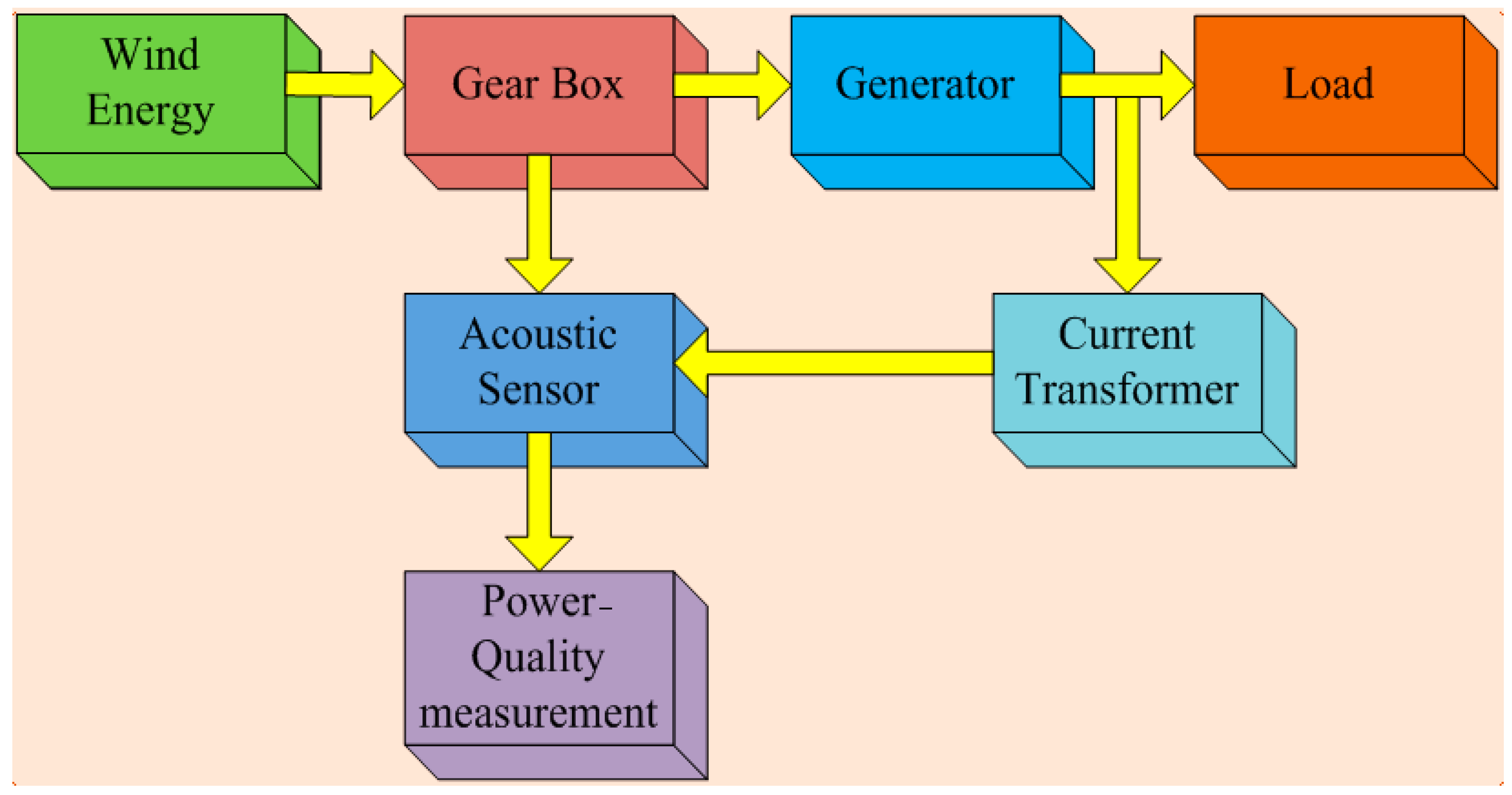
3.1. Vibration Analysis Model
3.1.1. Empirical Wavelet Transform
3.1.2. Acoustic Recording Modes
- ̶
- Records voltage and current samples recognized from sampling rate to the acoustic sensor.
- ̶
- The typical sampling level is 128 samples/cycle. This mode is generally utilized for the verification of transient signal analysis.
- ̶
- It can also trigger low-and high-speed disturbance with different operating settings.
- ̶
- Low-, medium-, and high-speed disturbance recording can be carried out on the complete system in this recording scheme.
- ̶
- The observed results are updated every quarter of a cycle or one cycle.
- ̶
- The user could sample the recorded disturbances through maximum, minimum, and average values.
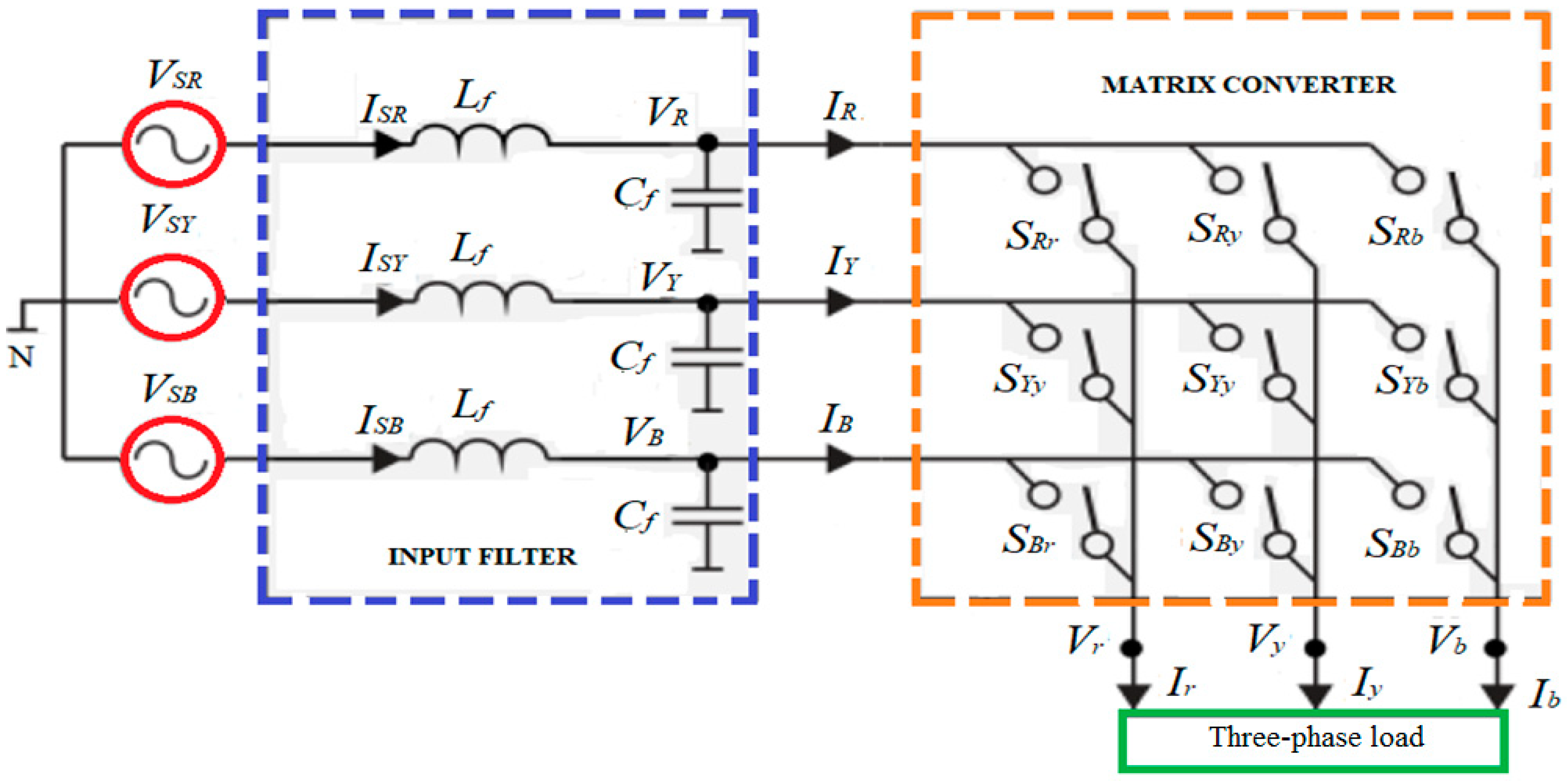
3.2. Proposed Matrix Converter
4. Results and Discussions
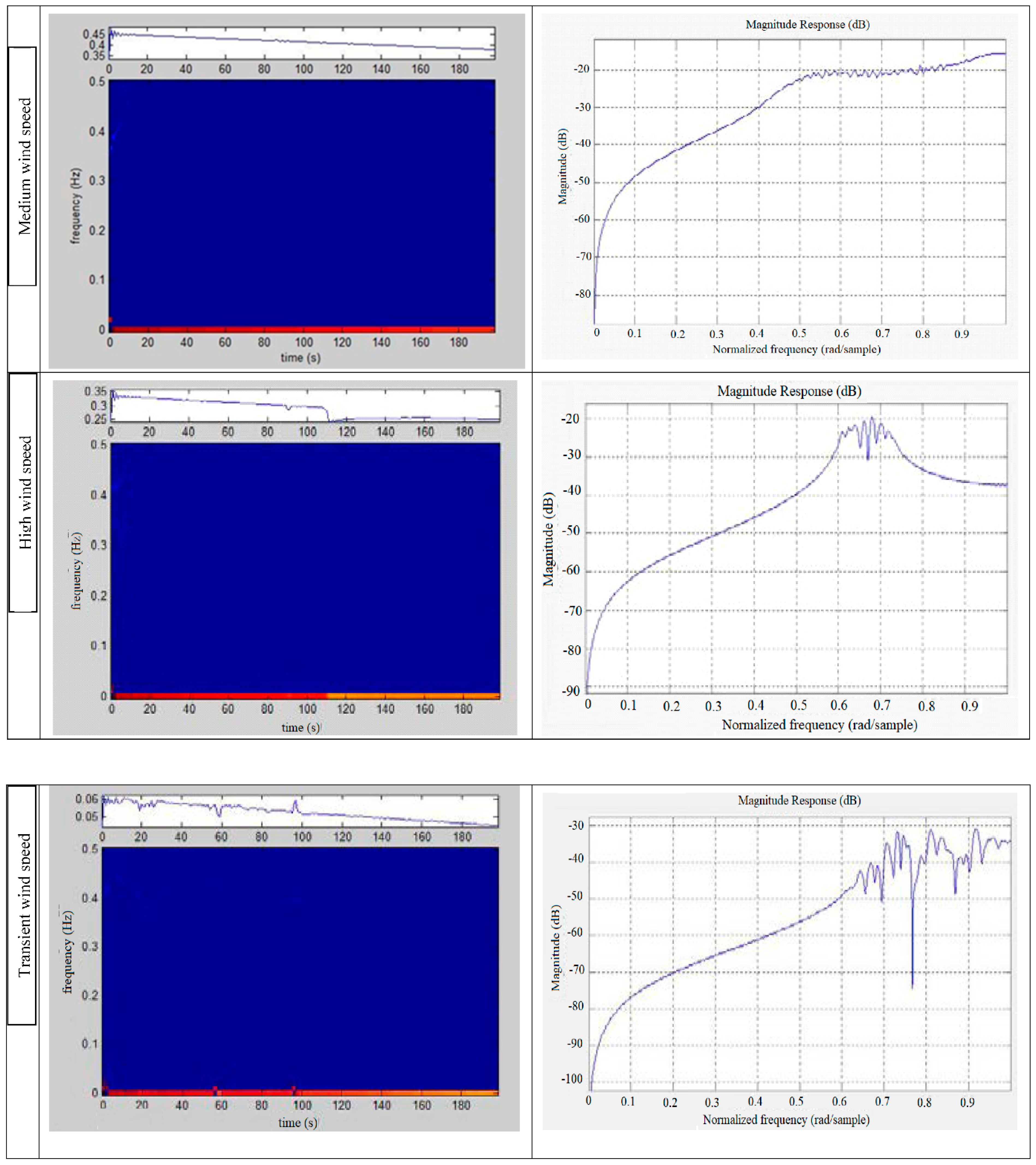
4.1. Vibration Assessment
- ̶
- Low-speed system,
- ̶
- Medium-speed system,
- ̶
- High-speed system,
- ̶
- Transient signal system.
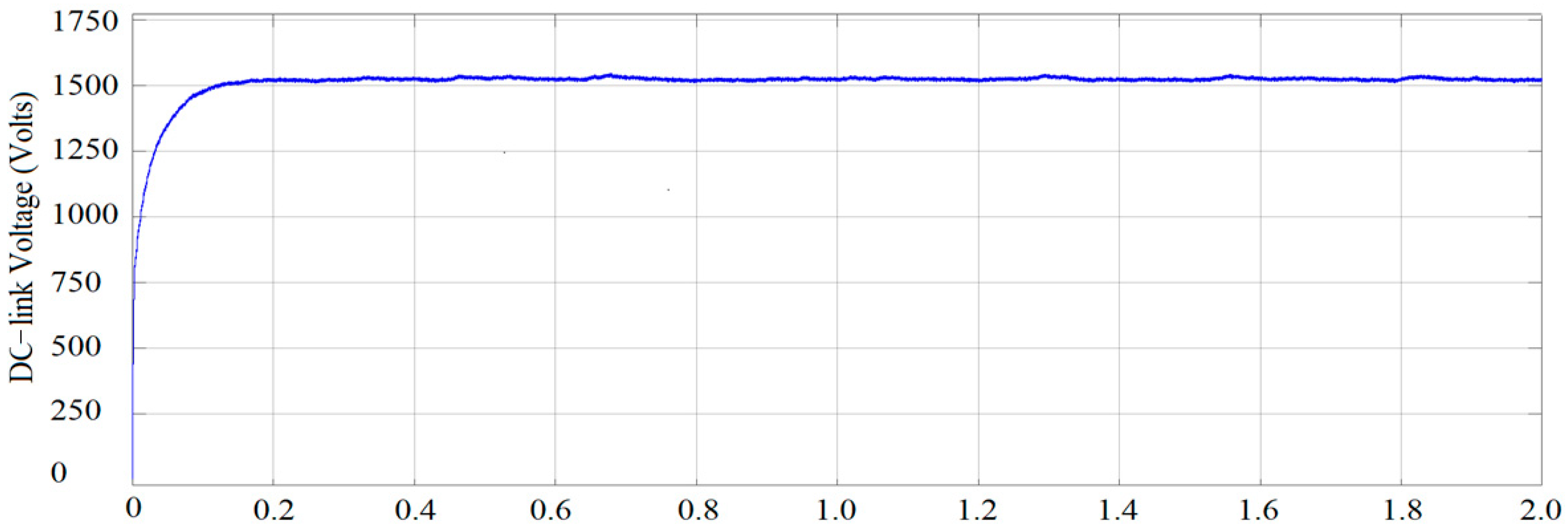
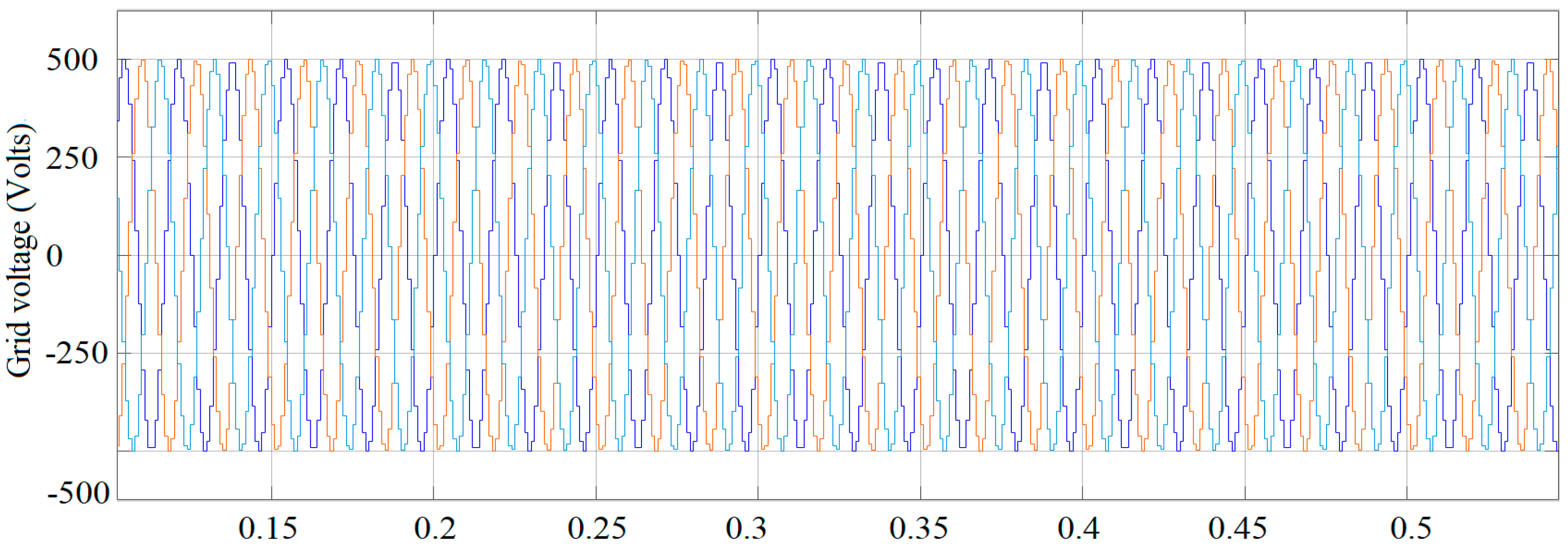
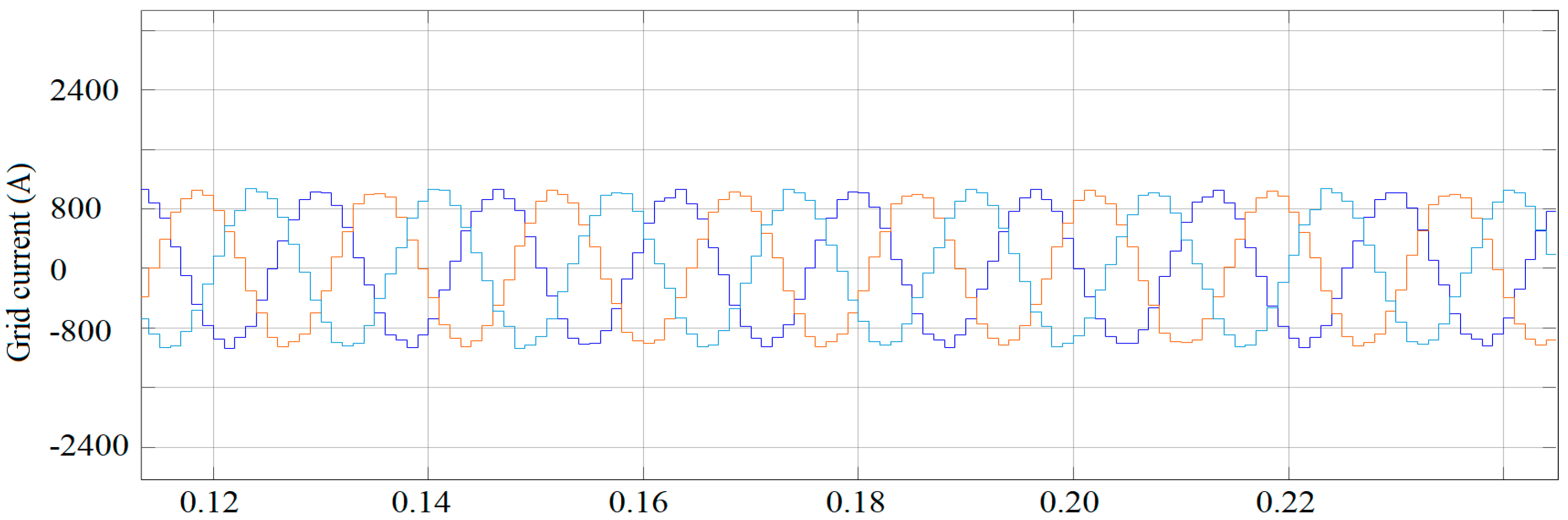
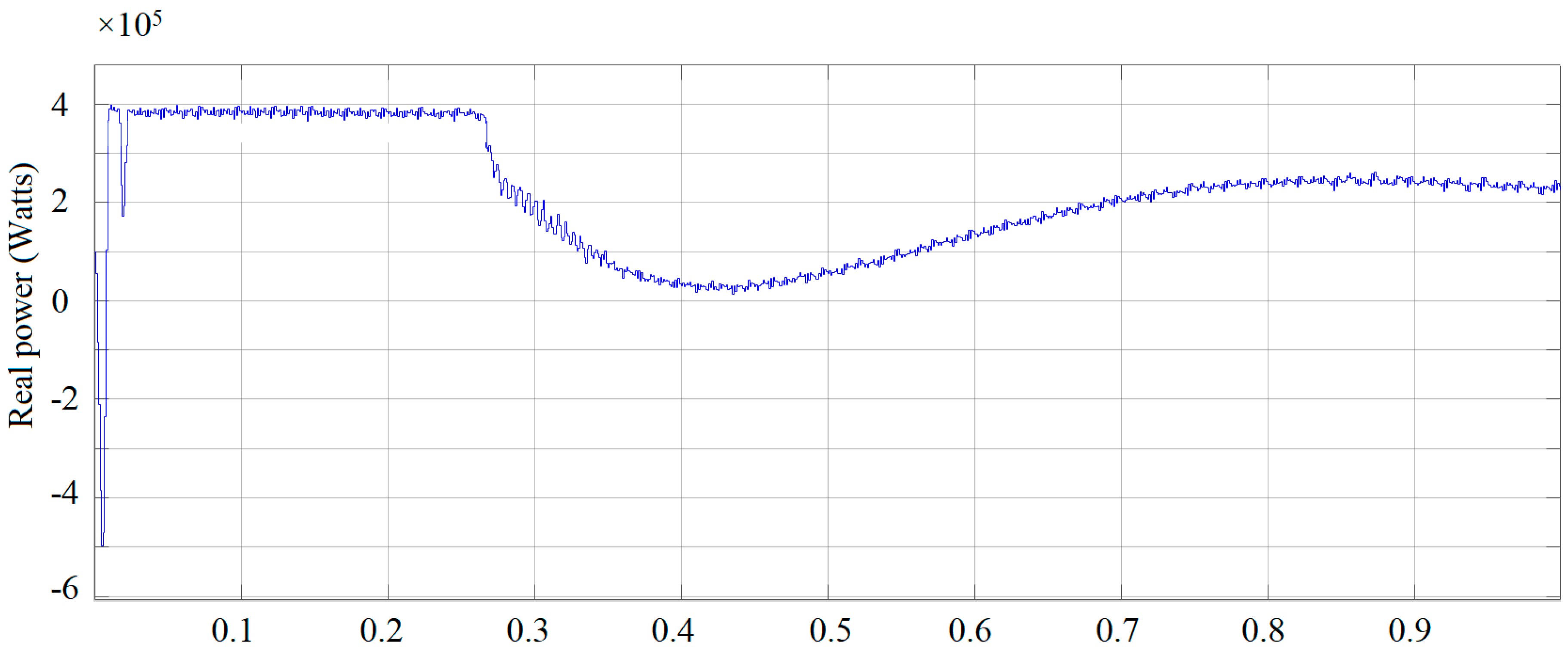
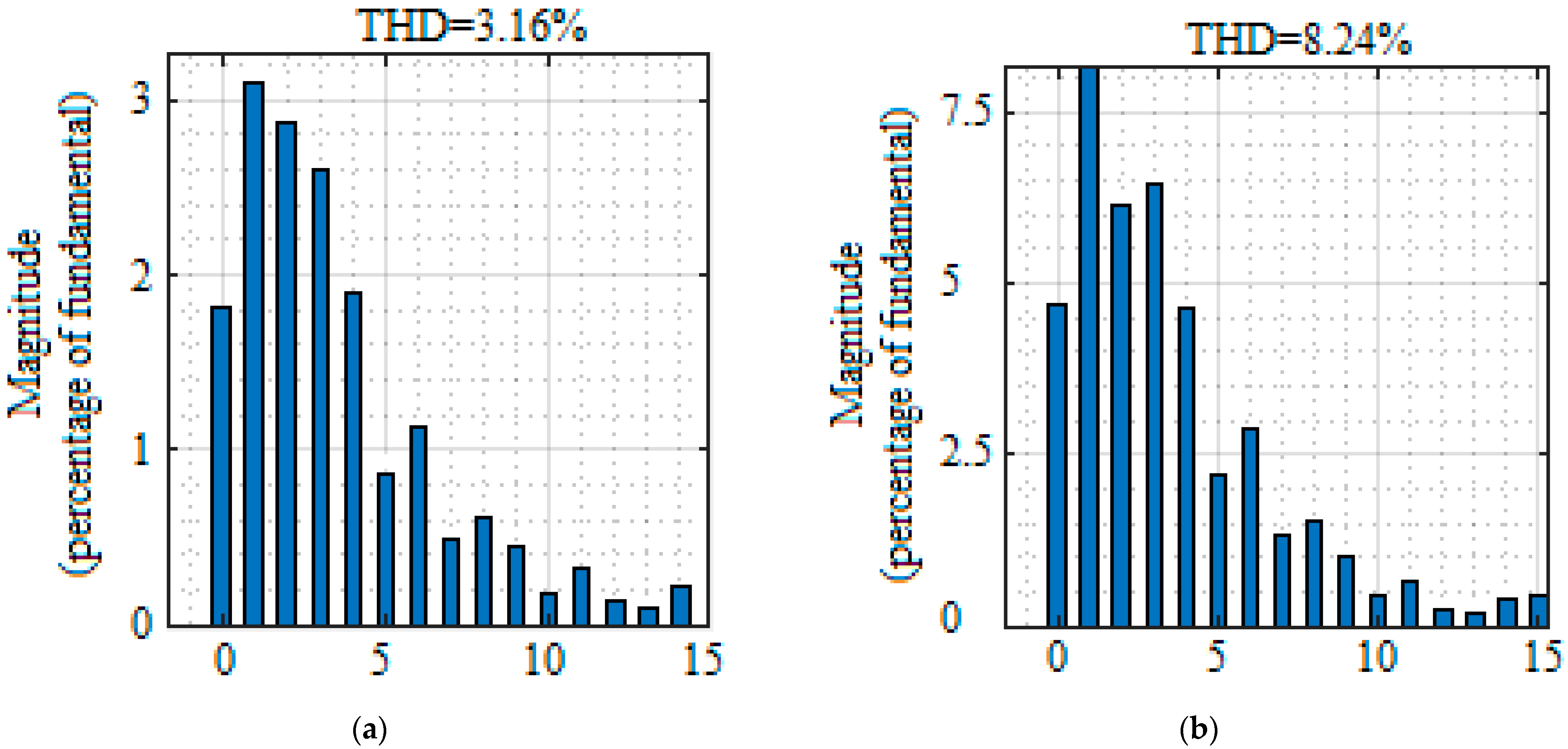
4.2. Performance of Proposed Converter with WECS
5. Conclusions
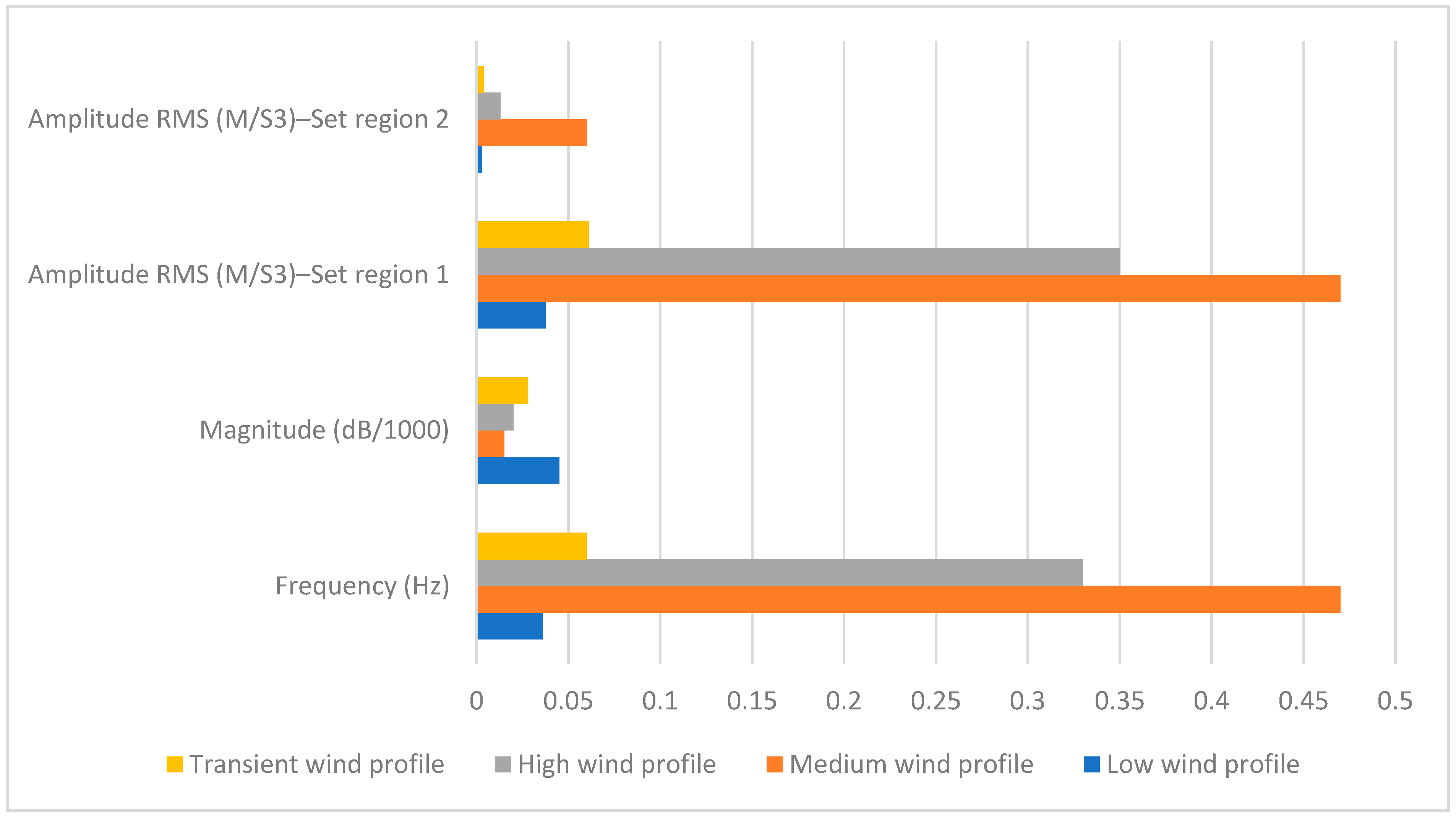
- The acoustic sensors employed with EWT identified the vibrational magnitude for low, medium, high, and transient wind speed profiles effectively.
- The frequency of the vibrational signal observed a lower scale for low wind profile and higher value for medium speed rather than high wind profile.
- The amplitude of the sampled vibrational signal was found to be low for low wind profile and higher amplitude for medium wind speed profile rather than high wind profile; there were similar trends for frequency characteristics.
- The matrix converter with input filter provided significant improvement in its efficiency and outperformed other existing schemes.
- THDs of voltage and current were also small, which warrant the better power quality of the WECS connected to the grid.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Balaguru, V.S.S.; Swaroopan, N.J.; Raju, K.; Alsharif, M.H.; Kim, M.-K. Techno-Economic Investigation of Wind Energy Potential in Selected Sites with Uncertainty Factors. Sustainability 2021, 13, 2182. [Google Scholar] [CrossRef]
- Venkatesan, C.; Kannadasan, R.; Alsharif, M.H.; Kim, M.-K.; Nebhen, J. Assessment and Integration of Renewable Energy Resources Installations with Reactive Power Compensator in Indian Utility Power System Network. Electronics 2021, 10, 912. [Google Scholar] [CrossRef]
- Raju, K.; Madurai Elavarasan, R.; Mihet-Popa, L. An Assessment of Onshore and Offshore Wind Energy Potential in India Using Moth Flame Optimization. Energies 2020, 13, 3063. [Google Scholar] [CrossRef]
- Subramanian, S.; Sankaralingam, C.; Elavarasan, R.M.; Vijayaraghavan, R.R.; Raju, K.; Mihet-Popa, L. An Evaluation on Wind Energy Potential Using Multi-Objective Optimization-Based Non-Dominated Sorting Genetic Algorithm III. Sustainability 2021, 13, 410. [Google Scholar] [CrossRef]
- Anthony, M.; Prasad, V.; Kannadasan, R.; Mekhilef, S.; Alsharif, M.H.; Kim, M.-K.; Jahid, A.; Aly, A.A. Autonomous Fuzzy Controller Design for the Utilization of Hybrid PV-Wind Energy Resources in Demand Side Management Environment. Electronics 2021, 10, 1618. [Google Scholar] [CrossRef]
- Alsharif, M.H.; Yahya, K.; Geem, Z.W. Strategic Market Growth and Policy Recommendations for Sustainable Solar Energy Deployment in South Korea. J. Electr. Eng. Technol. 2020, 15, 803–815. [Google Scholar] [CrossRef]
- Anthony, M.; Prasad, V.; Raju, K.; Alsharif, M.H.; Geem, Z.W.; Hong, J. Design of Rotor Blades for Vertical Axis Wind Turbine with Wind Flow Modifier for Low Wind Profile Areas. Sustainability 2020, 12, 8050. [Google Scholar] [CrossRef]
- Alsharif, M.H.; Kim, J. Hybrid Off-Grid SPV/WTG Power System for Remote Cellular Base Stations Towards Green and Sustainable Cellular Networks in South Korea. Energies 2017, 10, 9. [Google Scholar] [CrossRef] [Green Version]
- Holitinen, H.; Hirvonen, R. Power system requirement for wind power. In Wind Power in Power System; Ackermann, T., Ed.; Wiley: New York, NY, USA, 2005; pp. 143–157. [Google Scholar]
- Bansal, R.C.; Zobaa, A.F.; Saket, R.K. Some issue related to power generation using wind energy conversion system: An overview. Int. J. Emerg. Electr. Power Syst. 2005, 3, 1–14. [Google Scholar] [CrossRef]
- Smith, J.C.; Milligan, M.R.; DeMeo, E.A. Utility wind integration and operating impact state of the art. IEEE Trans. Energy Convers. 2007, 22, 900–907. [Google Scholar]
- Sadd-Saoud, Z.; Jenkins, N. Models for predicting flicker induced by large wind turbines. IEEE Trans. Energy Convers. 1999, 14, 743–751. [Google Scholar] [CrossRef]
- Hu, W.; Chen, Z.; Wang, Y.; Wang, Z. Flicker Mitigation by Active Power Control of Variable-Speed Wind Turbines with Full-Scale Back-to-Back Power Converters. IEEE Trans. Energy Convers. 2009, 24, 640–648. [Google Scholar]
- Zhou, F.; Joos, G.; Abhey, C. Voltage stability in weak connection wind farm. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 16 June 2005; Volume 2, pp. 1483–1488. [Google Scholar]
- Mohod, S.W.; Aware, M.V. Power quality issues & its mitigation technique in wind generation. In Proceedings of the 2008 13th International Conference on Harmonics and Quality of Power (ICHQP), Wollongong, Australia, 28 September–1 October 2008; pp. 1–6. [Google Scholar]
- Zhang, Z.; Li, Z.; Kazmierkowski, M.P.; Rodriguez, J.; Kennel, R. Robust Predictive Control of Three-Level NPC Back-to-Back Power Converter PMSG Wind Turbine Systems with Revised Predictions. IEEE Trans. Power Electron. 2018, 33, 9588–9598. [Google Scholar] [CrossRef]
- Djokic, S.Z.; Milanovic, J.V. Power quality and compatibility levels: A general approach. IEEE Trans. Power Deliv. 2007, 22, 1857–1862. [Google Scholar] [CrossRef]
- Villa, L.F.; Reñones, A.; Perán, J.R.; de Miguel, L.J. Angular Resampling for Vibration Analysis in Wind Turbines under Nonlinear Speed Fluctuation. Mech. Syst. Signal Process. 2011, 25, 2157–2168. [Google Scholar] [CrossRef]
- Uma Maheswari, R.; Umamaheswari, R. Trends in Non-Stationary Signal Processing Techniques Applied to Vibration Analysis of Wind Turbine Drive Train—A Contemporary Survey. Mech. Syst. Signal Process. 2017, 85, 296–311. [Google Scholar] [CrossRef]
- Kusiak, A.; Zhang, Z. Analysis of Wind Turbine Vibrations Based on SCADA Data. ASME J. Sol. Energy Eng. 2010, 132, 1–12. [Google Scholar] [CrossRef]
- Ghoshal, A.; Sundaresan, M.J.; Schulz, M.J.; Pai, P.F. Structural health monitoring techniques for wind turbine blades. J. Wind Eng. Ind. Aerodyn. 2000, 85, 309–324. [Google Scholar] [CrossRef]
- Yang, W.; Tavner, P.J.; Wilkinson, M.R. Condition monitoring and fault diagnosis of a wind turbine synchronous generator drive train. IET Renew. Power Gener. 2009, 3, 1–11. [Google Scholar] [CrossRef]
- Sheldon, J.S.; Watson, M.J.; Byington, C.S. Integrating oil health and vibration diagnostics for reliable wind turbine health predictions. In Proceedings of the ASME2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011; pp. 939–948. [Google Scholar]
- Rajalakshmi, M.; Chandramohan, S.; Kannadasan, R.; Alsharif, M.H.; Kim, M.-K.; Nebhen, J. Design and Validation of BAT Algorithm Based Photovoltaic System Using Simplified High Gain Quasi Boost Inverter. Energies 2021, 14, 1086. [Google Scholar] [CrossRef]
- Prakash, M.; Joo, Y.-H. Fuzzy Event-Triggered Control for Back to Back Converter Involved PMSG-Based Wind Turbine Systems. IEEE Trans. Fuzzy Syst. 2021. [Google Scholar] [CrossRef]
- Cui, Z.; Zhang, Z.; Yang, Q.; Kennel, R. Cascaded Model Predictive Control of Three-Level NPC Back-to-Back Power Converter PMSG Wind Turbine Systems. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018. [Google Scholar]
- Eedara, A.K.; Koritala, C.S.; Rayapudi, S.R. Modified Model Predictive Control of Back-to-Back T-Type NPC Converter Interfacing Wind Turbine-Driven PMSG and Electric Grid. Arab. J. Sci. Eng. 2019, 44, 7047–7065. [Google Scholar] [CrossRef]
- Benbouhenni, H.; Boudjema, Z.; Belaidi, A. Direct Vector Control of a DFIG Supplied by an Intelligent SVM Inverter for Wind Turbine System. Iran. J. Electr. Electron. Eng. 2019, 1, 45–55. [Google Scholar]
- Ni, K.; Hu, Y.; Lagos, D.T.; Chen, G.; Wang, Z.; Li, X. Highly Reliable Back-To-Back Power Converter without Redundant Bridge Arm for Doubly-Fed Induction Generator-Based Wind Turbine. IEEE Trans. Ind. Appl. 2019, 55, 3024–3036. [Google Scholar] [CrossRef]
- Bajestan, M.M.; Madadi, H.; Shamsinejad, M.A. Control of a New Stand-Alone Wind Turbine-Based Variable Speed Permanent Magnet Synchronous Generator Using Quasi-Z-Source Inverter. Electr. Power Syst. Res. 2019, 177, 106010. [Google Scholar] [CrossRef]
- Escaler, X.; Mebarki, T. Full-Scale Wind Turbine Vibration Signature Analysis. Machines 2018, 6, 63. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Zhang, L.; Carrasco, J. Vibration Analysis for Large-Scale Wind Turbine Blade Bearing Fault Detection with an Empirical Wavelet Thresholding Method. Renew. Energy 2020, 146, 99–110. [Google Scholar] [CrossRef]
- Naung, S.W.; Rahmati, M.; Farokhi, H. Nonlinear frequency domain solution method for aerodynamic and aeromechanical analysis of wind turbines. Renew. Energy 2021, 167, 66–81. [Google Scholar] [CrossRef]
- Inturi, V.; Sabareesh, G.R.; Supradeepan, K.; Penumakala, P.K. Integrated Condition Monitoring Scheme for Bearing Fault Diagnosis of a Wind Turbine Gearbox. J. Vib. Control 2019, 25, 1852–1865. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, L. Naturally Damaged Wind Turbine Blade Bearing Fault Detection Using Novel Iterative Nonlinear Filter and Morphological Analysis. IEEE Trans. Ind. Electron. 2020, 67, 8713–8722. [Google Scholar] [CrossRef]
- He, L.; Unnikrishnan, J.; Hao, L.; Matthews, B.; Qiao, W. Enhanced Wind Turbine Main Drivetrain Gearbox and Bearing Monitoring and Diagnostics via Information Fusion of Acoustic, Electrical, and Vibration Signatures. In Proceedings of the 2019 IEEE International Electric Machines & Drives Conference (IEMDC), San Diego, CA, USA, 12–15 May 2019. [Google Scholar]
- Mauricio, A.; Qi, J.; Gryllias, K. Vibration-Based Condition Monitoring of Wind Turbine Gearboxes Based on Cyclostationary Analysis. J. Eng. Gas Turbine Power 2019, 141, 031026. [Google Scholar] [CrossRef]
- Zhou, D.; Zhang, G.; Blaabjerg, F. Optimal Selection of Power Converter in DFIG Wind Turbine with Enhanced System-Level Reliability. IEEE Trans. Ind. Appl. 2018, 54, 3637–3644. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.-N.; Lin, W.-C.; Le, X.-K. Modelling of a PMSG Wind Turbine with Autonomous Control. Math. Probl. Eng. 2014, 2014, 856173. [Google Scholar] [CrossRef]
- Nguyen, M.-K.; Lim, Y.-C.; Park, S.-J. A comparison between single phase quasi-Z-source and quasi-switched boost inverters. IEEE Trans. Ind. Electron. 2015, 62, 6336–6344. [Google Scholar] [CrossRef]
- Caceres, R.O.; Barbi, I. A boost dc-ac converter: Analysis, design, and experimentation. IEEE Trans. Power Electron. 1999, 14, 134–141. [Google Scholar] [CrossRef]
- Kim, K.; Cha, H.; Kim, H.-G. A new single-phase switched-coupled inductor DC-AC inverter for photovoltaic systems. IEEE Trans. Power Electron. 2017, 32, 5016–5022. [Google Scholar] [CrossRef]
- Tang, Y.; Bai, Y.; Kan, J.; Xu, F. Improved dual boost inverter with half cycle modulation. IEEE Trans. Power Electron. 2017, 32, 7543–7552. [Google Scholar] [CrossRef]
- Khan, A.A.; Cha, H. Dual-buck-structured high-reliability and efficiency single-stage buck-boost inverters. IEEE Trans. Ind. Electron. 2018, 65, 3176–3187. [Google Scholar] [CrossRef]
- Abdelhakim, A.; Mattavelli, P.; Davari, P.; Blaabjerg, F. Performance Evaluation of the Single-Phase Split-Source Inverter Using an Alternative DC-AC Configuration. IEEE Trans. Ind. Electron. 2018, 65, 363–373. [Google Scholar] [CrossRef] [Green Version]
- Anderson, J.; Peng, F.Z. Four quasi-Z-source inverters. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 2743–2749. [Google Scholar]





| Ref. No. | Year | Methods/Techniques | Inferences | Limitations/Research Gaps |
|---|---|---|---|---|
| Converting techniques | ||||
| [9] | 2018 | NPC Back-to-Back Power Converter |
|
|
| [24] | 2021 | Simplified high-gain quasi-boost inverter (SHGqBI) |
|
|
| [25] | 2021 | Back-to-Back (BTB) Converter with Fuzzy Event-triggered Control (ETC) |
|
|
| [26] | 2018 | Cascaded Model Predictive Control with NPC Back-to-Back (BTB) Power Converter |
|
|
| [27] | 2018 | BTB controller with modified model predictive control (MMPC) |
|
|
| [28] | 2019 | Intelligent SVM Inverter with Direct Vector Control |
|
|
| [29] | 2019 | Back-To-Back Power Converter without Redundant Bridge Arm |
|
|
| [30] | 2019 | quasi-Z-source inverter (qZSI) |
|
|
| Vibration assessment | ||||
| [31] | 2018 | Digital signal processing with accelerometers |
|
|
| [20] | 2011 | Angular resampling |
|
|
| [32] | 2020 | Empirical wavelet thresh holding method |
|
|
| [33] | 2020 | Nonlinear Frequency-Domain Solution |
|
|
| [34] | 2019 | Discrete wavelet transform (DWT) |
|
|
| [35] | 2019 | Novel Iterative Nonlinear Filter (INF) |
|
|
| [36] | 2019 | Gaussian model-based fusion algorithm |
|
|
| [37] | 2018 | Cyclo-stationaryanalysis |
|
|
| System | Parameters | Unit | Range |
|---|---|---|---|
| Wind turbine | Power rating | kW | 2000 |
| Radius of blade | Meter | 35 | |
| Tip-speed ratio | 8 | ||
| Power coefficient | 0.4 | ||
| Air density | kg/m3 | 1.225 | |
| Wind cut-in speed | m3 | 3 | |
| Wind speed (rated) | m3 | 12 | |
| Wind cut-out speed | m3 | 25 | |
| Permanent magnet synchronous generator (PMSG) | Rated voltage | V | 5000 |
| Frequency | Hz | 50 | |
| Torque | N-m | 450 | |
| Stator resistance | Ohms | 0.01 | |
| Armature Inductance | H | 0.03 | |
| Lq | mH | 3.75 | |
| Ld | mH | 5.5 | |
| Poles | Nos. | 56 |
| On the States of Switches | ||||||
|---|---|---|---|---|---|---|
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 | - | 0 | - | |||
| 0 | - | 0 | - | |||
| 0 | - | 0 | - | |||
| Ref. No. | Configuration | Efficiency (%) |
|---|---|---|
| [40] | Quasi Z-source inverter | 90.20 |
| [41] | Differential boost inverter | 83.33 |
| [42] | Switched-coupled inductor inverter | 90.50 |
| [43] | Improved DBI | 92.60 |
| [44] | Buck-boost inverter | 96.10 |
| [45] | Split-inductor differential boost inverter type-I | 96.50 |
| [45] | Split-inductor differential boost inverter type-II | 97.00 |
| [46] | Split-source inverter | 95.50 |
| Proposed method | Matrix converter | 95.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rameshkumar, T.; Chandrasekar, P.; Kannadasan, R.; Thiyagarajan, V.; Alsharif, M.H.; Kim, J.H. Electrical and Mechanical Characteristics Assessment of Wind Turbine System Employing Acoustic Sensors and Matrix Converter. Sustainability 2022, 14, 4404. https://doi.org/10.3390/su14084404
Rameshkumar T, Chandrasekar P, Kannadasan R, Thiyagarajan V, Alsharif MH, Kim JH. Electrical and Mechanical Characteristics Assessment of Wind Turbine System Employing Acoustic Sensors and Matrix Converter. Sustainability. 2022; 14(8):4404. https://doi.org/10.3390/su14084404
Chicago/Turabian StyleRameshkumar, Thiyagarajan, Perumal Chandrasekar, Raju Kannadasan, Venkatraman Thiyagarajan, Mohammed H. Alsharif, and James Hyungkwan Kim. 2022. "Electrical and Mechanical Characteristics Assessment of Wind Turbine System Employing Acoustic Sensors and Matrix Converter" Sustainability 14, no. 8: 4404. https://doi.org/10.3390/su14084404







