Agricultural Ecological Efficiency under the Carbon Emissions Trading System in China: A Spatial Difference-in-Difference Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Description
Data Sources
2.2. Model Specification
2.2.1. The SBM of Non-Expected Output
2.2.2. Difference-in Difference (DID) Model
2.2.3. The Spatial Durbin Model (SDM)
3. Results and Discussion
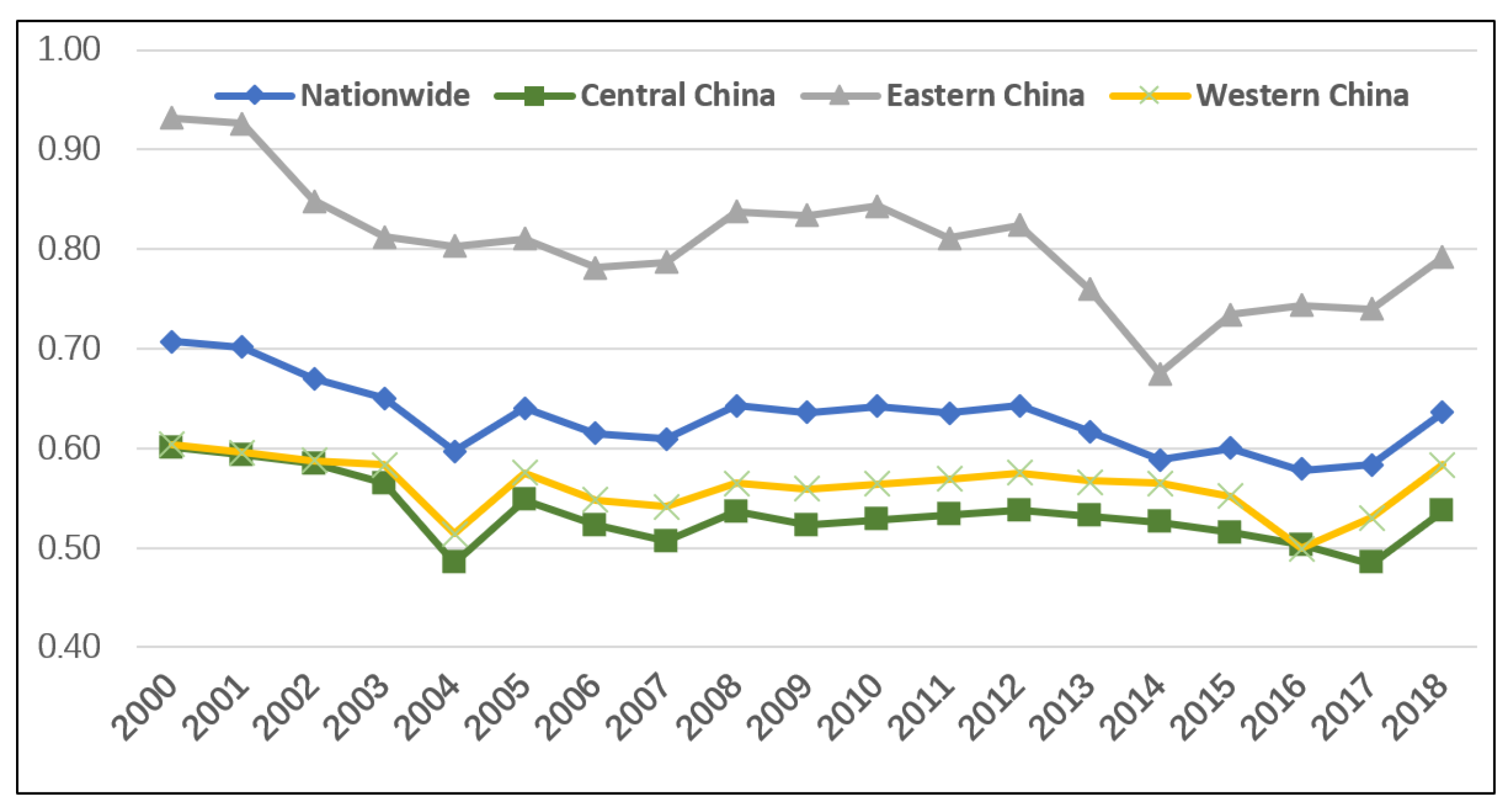
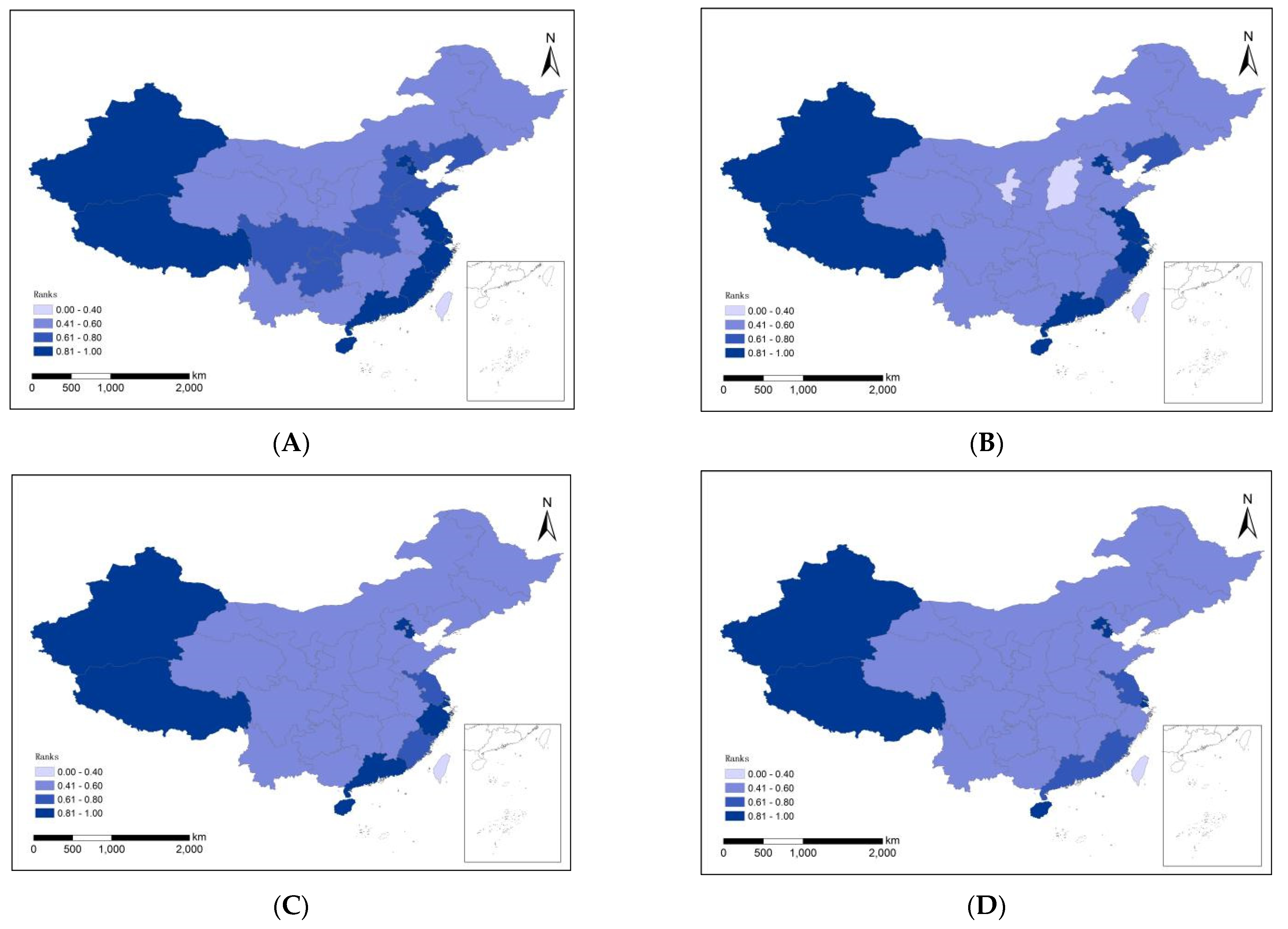
3.1. Spatial, Temporal Evolution and Agglomeration Characteristics of Regional AEE
Agglomeration Characteristics of AEE
3.2. Impact Assessment of CET Pilot Policy
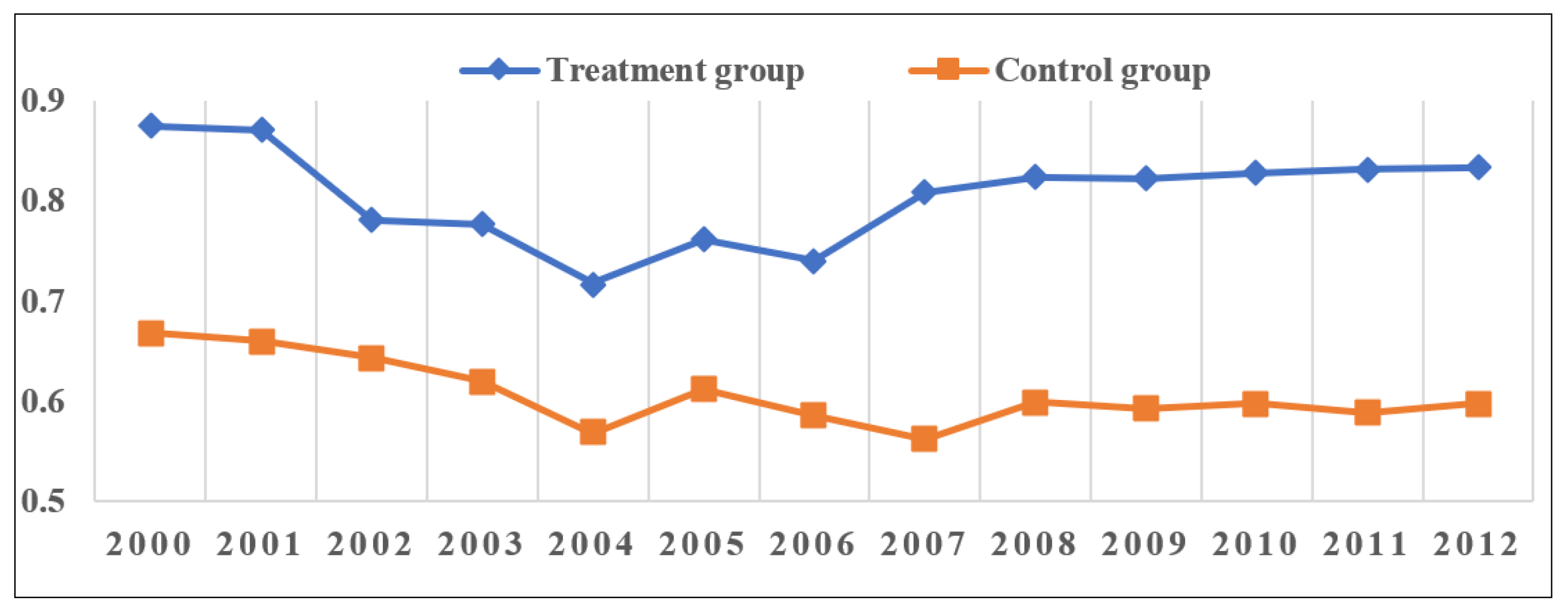
3.2.1. Applicability Analysis of DID
3.2.2. Analysis of Regression Results of DID Model
3.3. Spatial Spillover Effect (SSE) Analysis
4. Conclusions and Recommendation
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Baoyi, W.; Weiguo, Z. A Study on Spatial and Temporal Differences in Measurement of Agricultural Eco-efficiency in China. China Popul. Resour. Environ. 2016, 26, 11–19. [Google Scholar] [CrossRef]
- Feng, Y.; Qi, Q.; Han, J. Spatiotemporal evolution and driving factors of agricultural eco-efficiency in China. Bull. Soil Water Conserv. 2018, 6, 254–262. [Google Scholar] [CrossRef]
- Yin, K.; Wang, R.; Zhou, C.; Liang, J. Review of eco-efficiency accounting method and its applications. Acta Ecol. Sin. 2012, 32, 3595–3605. [Google Scholar] [CrossRef]
- Pingbo, H.; Yiping, Z. The mechanism of improving agricultural eco-efficiency by the integration of agriculture and tourism supported by the government: Taking the national leisure agriculture and rural tourism demonstration counties as an example. China Rural Econ. 2019, 12, 85–104. [Google Scholar]
- Shang, J.; Ji, X.; Chen, X. Study on the impact of China’s urbanization on agricultural ecological efficiency: Based on panel data of 13 major grain-producing regions in China from 2009 to 2018. Chin. J. Eco-Agric. 2020, 28, 1265–1276. [Google Scholar] [CrossRef]
- Nie, W.; Yu, F. Review of methodology and application of agricultural eco-. Chin. J. Eco-Agric. 2017, 9, 1371–1380. [Google Scholar] [CrossRef]
- Wu, X.Q.; Xu, Y.C.; Lu, G.F. The evaluation of agricultural eco-efficiency: A case of rice pot-experiment. Acta Ecol. Sin. 2009, 29, 2481–2488. [Google Scholar]
- Shui, W.; Chen, Y.P.; Su, Z.A.; Fan, S.S. Energy-based agricultural ecosystem analysis for specialized tea planting: A case study of Anxi County, Fujian Province. Chin. J. Eco-Agric. 2016, 24, 1703–1713. [Google Scholar] [CrossRef]
- Jiang, D.; Zhong, F.; Guo, A. Field corn production efficiency in oasis field: A case study of households in Zhangye district. J. Arid Land Resour. Environ. 2017, 10, 167–171. [Google Scholar] [CrossRef]
- Dan, P.; Ruiyao, Y. Agricultural eco-efficiency evaluation in China based on SBM model. Acta Ecol. Sin. 2013, 33, 3837–3845. [Google Scholar] [CrossRef] [Green Version]
- Cheng, C.Y.; Ren, J.M.; Wang, R.S. Spatial-temporal distribution of agricultural eco-efficiency in China. Acta Ecol. Sin. 2014, 34, 142–148. [Google Scholar] [CrossRef] [Green Version]
- Qu, Z.; Chen, G.; Liu, T. The measurement of agricultural ecological capital efficiency and analysis of its influencing factors. J. China Univ. Geosci. 2014, 14, 81–87. [Google Scholar]
- Hong, K.; Chen, C.; Feng, C.; Huang, J. The Spatial Temporal Differences of Agricultural Eco-Efficiency and Its Influential Factors. J. South China Agric. Univ. Soc. Sci. Ed. 2016, 2, 31–41. [Google Scholar]
- Wang, B.Y.; Zhang, W.G. Cross-provincial Differences in Determinants of Agricultural Eco-efficiency in China: An Analysis Based on Panel Data from 31 Provinces in 1996–2015. Chin. Rural Econ. 2018, 1, 46–62. [Google Scholar]
- Hou, M.; Yao, S. Spatial-temporal evolution and trend prediction of agricultural eco-efficiency in China: 1978–2016. Acta Geogr. Sin. 2018, 73, 2168–2183. [Google Scholar] [CrossRef]
- Hong, M.; Zheng, L. Regional differences and spatiotemporal and characteristics of agricultural eco-efficiency in China. Stat. Decis. 2020, 8, 56–61. [Google Scholar] [CrossRef]
- Wu, X.-Q.; Wang, Y.-P.; He, L.-M.; Lu, G.-F. Agricultural Eco-Efficiency Evaluation Based on AHP and DEA Model—A Case of Wuxi City. Resour. Environ. Yangtze Basin 2012, 21, 714–719. Available online: https://proxy.lib.umich.edu/login?url=https://search.proquest.com/docview/1093442720?accountid=14667&bdid=7723&_bd=rV54CWXzttVUiVcBTzpGUO3dUh8%3D (accessed on 2 January 2021).
- Ying, L.I.U.; Zhong, F.; Peng, L.I.; Yu, D. Performance and regional difference in Chinese ecological agriculture. Econ. Geogr. 2014, 3, 24–29. [Google Scholar] [CrossRef]
- Lin, J.; Liu, F.; Zheng, J. Evaluation and Improvement on Ecological Efficiency of Mountainous County in China—A Case of Datian County in Fujian. Sci. Technol. Manag. Res. 2015, 23, 59–63, 68. [Google Scholar]
- Zheng, J.; Yang, D. DEA-Malmquist analysis method of agricultural ecological efficiency measurement research—Taking the four provinces in the middle reaches of the Yangtze River as examples. Hubei Soc. Sci. 2016, 9, 65–71. [Google Scholar]
- Liu, F.; Zhong, P.; Zhang, W. Comprehensive Evaluation on Ecological Efficiency of Mountainous Counties in China—A Case Study of Wuping County in Fujian. J. Northwest AF Univ. Sci. Ed. 2015, 3, 94–99. [Google Scholar] [CrossRef]
- Hu, H.; Liu, G. Has Paid Use of Coal Resources Increased Efficiency and Reduced Emissions? Empirical Research Based on SBM-DID. Resour. Dev. Mark. 2020, 9, 942–950, 1020. [Google Scholar]
- Li, X.; Hu, Z.; Zhang, N.; Malin, S. Total factor productivity index of carbon emissons and Its various influencing factors during the 12th Five-Year. Nankai Econ. Stud. 2018, 5, 76–94. [Google Scholar] [CrossRef]
- Li, Z.; Yang, S. Can National High-Tech Zones Raise Urban Innovation Level ? South China J. Econ. 2019, 12, 49–67. [Google Scholar] [CrossRef]
- Tone, K. Dealing with Undesirable Outputs in DEA: A Slacks-Based Measure (SBM) Approach. GRIPS Res. Rep. Ser. 2003, 5, 44–45. Available online: https://220.130.147.155/UndesirableOutputs.pdf (accessed on 2 January 2021).
- Zheng, L.; Hong, M. Spatial and Temporal Characteristics and Driving Factors of Agricultural Ecological Efficiency in China. J. Jiangxi Univ. Financ. Econ. 2019, 5, 46–56. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W. Programming with linear fractional Functionals. Nav. Res. Logist. Q 1962, 9, 181–186. [Google Scholar] [CrossRef]
- Zhou, C.B.; Qin, Y. The impact of a carbon trading pilot policy on the low-carbon international competitiveness of industry in China: An empirical analysis based on a DDD model. Soft Sci. 2020, 10, 36–42, 55. [Google Scholar] [CrossRef]

| Indicators | Variables | Variable Description |
|---|---|---|
| Input | Labor | Number of employees in the primary industry (ten thousand people) |
| Machinery input | Total power of agricultural machinery (ten thousand kilowatts) | |
| Water input | Irrigation area (thousand hectares) | |
| Land input | The total sown area of crops (thousand hectares) | |
| Fertilizer input | Fertilizer application amount (ten thousand tons) | |
| Expected output | Agricultural economic growth | Total agricultural output value (price in 2000, 100 million yuan) |
| Non-expected output | Pollutant emission | COD (ten thousand tons) |
| TN (ten thousand tons) | ||
| TP (ten thousand tons) | ||
| Carbon emission | Carbon dioxide (CO2) emissions (ten thousand tons) |
| Region/Year | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 |
|---|---|---|---|---|---|---|---|---|---|---|
| Beijing | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Tianjin | 1.000 | 1.000 | 0.484 | 0.473 | 0.287 | 0.416 | 0.367 | 0.796 | 0.807 | 0.815 |
| Hebei | 0.622 | 0.599 | 0.576 | 0.563 | 0.516 | 0.561 | 0.545 | 0.530 | 0.548 | 0.543 |
| Shanxi | 0.521 | 0.510 | 0.508 | 0.502 | 0.398 | 0.466 | 0.451 | 0.431 | 0.446 | 0.451 |
| Inner Mongolia | 0.549 | 0.545 | 0.530 | 0.512 | 0.430 | 0.495 | 0.480 | 0.474 | 0.484 | 0.477 |
| Liaoning | 0.731 | 0.701 | 0.716 | 0.666 | 0.618 | 0.638 | 0.598 | 0.575 | 0.626 | 0.593 |
| Jilin | 0.569 | 0.563 | 0.581 | 0.577 | 0.456 | 0.539 | 0.523 | 0.503 | 0.548 | 0.521 |
| Heilongjiang | 0.555 | 0.559 | 0.544 | 0.532 | 0.455 | 0.535 | 0.500 | 0.490 | 0.503 | 0.500 |
| Shanghai | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Jiangsu | 1.000 | 1.000 | 1.000 | 0.786 | 0.857 | 0.866 | 0.826 | 0.650 | 0.671 | 0.657 |
| Zhejiang | 1.000 | 1.000 | 0.878 | 0.831 | 1.000 | 0.820 | 0.742 | 0.645 | 1.000 | 1.000 |
| Anhui | 0.565 | 0.555 | 0.541 | 0.510 | 0.429 | 0.493 | 0.474 | 0.465 | 0.486 | 0.486 |
| Fujian | 0.943 | 0.938 | 0.908 | 0.877 | 0.767 | 0.839 | 0.774 | 0.706 | 0.765 | 0.763 |
| Jiangxi | 0.566 | 0.567 | 0.549 | 0.538 | 0.444 | 0.523 | 0.497 | 0.486 | 0.514 | 0.501 |
| Shandong | 0.745 | 0.722 | 0.648 | 0.594 | 0.598 | 0.598 | 0.571 | 0.546 | 0.583 | 0.564 |
| Henan | 0.669 | 0.656 | 0.629 | 0.564 | 0.537 | 0.575 | 0.555 | 0.540 | 0.576 | 0.563 |
| Hubei | 0.616 | 0.614 | 0.592 | 0.582 | 0.493 | 0.559 | 0.533 | 0.517 | 0.538 | 0.525 |
| Hunan | 0.583 | 0.579 | 0.559 | 0.556 | 0.480 | 0.546 | 0.525 | 0.514 | 0.540 | 0.532 |
| Guangdong | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Guangxi | 0.574 | 0.569 | 0.574 | 0.564 | 0.491 | 0.552 | 0.533 | 0.525 | 0.562 | 0.554 |
| Hainan | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Chongqing | 0.632 | 0.609 | 0.609 | 0.605 | 0.524 | 0.593 | 0.540 | 0.539 | 0.597 | 0.592 |
| Sichuan | 0.633 | 0.602 | 0.601 | 0.595 | 0.522 | 0.573 | 0.541 | 0.530 | 0.557 | 0.548 |
| Guizhou | 0.629 | 0.605 | 0.587 | 0.583 | 0.520 | 0.562 | 0.531 | 0.512 | 0.530 | 0.509 |
| Yunnan | 0.592 | 0.582 | 0.572 | 0.570 | 0.496 | 0.554 | 0.536 | 0.526 | 0.561 | 0.550 |
| Tibet | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Shaanxi | 0.562 | 0.557 | 0.548 | 0.554 | 0.469 | 0.557 | 0.536 | 0.518 | 0.575 | 0.563 |
| Gansu | 0.548 | 0.561 | 0.543 | 0.543 | 0.454 | 0.534 | 0.506 | 0.496 | 0.516 | 0.507 |
| Qinghai | 0.493 | 0.509 | 0.483 | 0.487 | 0.476 | 0.514 | 0.444 | 0.457 | 0.454 | 0.455 |
| Ningxia | 0.437 | 0.435 | 0.431 | 0.426 | 0.324 | 0.422 | 0.408 | 0.402 | 0.422 | 0.431 |
| Xinjiang | 0.599 | 0.582 | 0.566 | 0.557 | 0.457 | 0.541 | 0.524 | 0.511 | 0.517 | 0.526 |
| National level | 0.708 | 0.701 | 0.670 | 0.650 | 0.597 | 0.641 | 0.615 | 0.609 | 0.643 | 0.636 |
| Central China | 0.601 | 0.594 | 0.585 | 0.565 | 0.485 | 0.548 | 0.523 | 0.507 | 0.536 | 0.523 |
| Eastern China | 0.931 | 0.926 | 0.849 | 0.812 | 0.803 | 0.810 | 0.782 | 0.787 | 0.837 | 0.834 |
| Western China | 0.604 | 0.596 | 0.587 | 0.583 | 0.514 | 0.575 | 0.548 | 0.541 | 0.565 | 0.559 |
| Region/Year | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | Average |
|---|---|---|---|---|---|---|---|---|---|---|
| Beijing | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Tianjin | 0.828 | 0.843 | 0.848 | 0.848 | 0.062 | 0.855 | 1.000 | 1.000 | 1.000 | 0.722 |
| Hebei | 0.552 | 0.550 | 0.558 | 0.548 | 0.540 | 0.525 | 0.517 | 0.495 | 0.539 | 0.549 |
| Shanxi | 0.449 | 0.457 | 0.463 | 0.468 | 0.459 | 0.450 | 0.435 | 0.442 | 0.494 | 0.463 |
| Inner Mongolia | 0.478 | 0.487 | 0.491 | 0.500 | 0.490 | 0.490 | 0.479 | 0.459 | 0.495 | 0.492 |
| Liaoning | 0.598 | 0.606 | 0.615 | 0.599 | 0.592 | 0.580 | 0.549 | 0.517 | 0.600 | 0.617 |
| Jilin | 0.531 | 0.536 | 0.541 | 0.545 | 0.541 | 0.524 | 0.515 | 0.490 | 0.540 | 0.534 |
| Heilongjiang | 0.498 | 0.503 | 0.505 | 0.510 | 0.504 | 0.502 | 0.486 | 0.471 | 0.512 | 0.509 |
| Shanghai | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Jiangsu | 0.700 | 0.666 | 0.683 | 0.616 | 0.605 | 0.560 | 0.536 | 0.500 | 0.672 | 0.729 |
| Zhejiang | 1.000 | 0.742 | 0.811 | 0.608 | 0.598 | 0.550 | 0.514 | 0.442 | 0.636 | 0.780 |
| Anhui | 0.490 | 0.497 | 0.504 | 0.504 | 0.497 | 0.490 | 0.472 | 0.457 | 0.508 | 0.496 |
| Fujian | 0.777 | 0.748 | 0.763 | 0.707 | 0.702 | 0.667 | 0.660 | 0.751 | 0.796 | 0.782 |
| Jiangxi | 0.503 | 0.513 | 0.515 | 0.527 | 0.521 | 0.518 | 0.508 | 0.488 | 0.536 | 0.517 |
| Shandong | 0.571 | 0.564 | 0.575 | 0.552 | 0.549 | 0.533 | 0.526 | 0.500 | 0.561 | 0.584 |
| Henan | 0.570 | 0.566 | 0.576 | 0.549 | 0.546 | 0.529 | 0.523 | 0.496 | 0.564 | 0.568 |
| Hubei | 0.530 | 0.535 | 0.537 | 0.522 | 0.517 | 0.510 | 0.502 | 0.480 | 0.525 | 0.538 |
| Hunan | 0.540 | 0.545 | 0.549 | 0.529 | 0.525 | 0.517 | 0.506 | 0.484 | 0.523 | 0.533 |
| Guangdong | 1.000 | 1.000 | 1.000 | 0.710 | 0.694 | 0.660 | 0.673 | 0.706 | 0.716 | 0.903 |
| Guangxi | 0.557 | 0.560 | 0.570 | 0.539 | 0.540 | 0.521 | 0.513 | 0.489 | 0.561 | 0.545 |
| Hainan | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Chongqing | 0.604 | 0.608 | 0.616 | 0.584 | 0.590 | 0.562 | 0.560 | 0.535 | 0.612 | 0.585 |
| Sichuan | 0.556 | 0.558 | 0.563 | 0.545 | 0.542 | 0.526 | 0.523 | 0.501 | 0.553 | 0.556 |
| Guizhou | 0.505 | 0.496 | 0.512 | 0.524 | 0.523 | 0.510 | 0.507 | 0.487 | 0.550 | 0.536 |
| Yunnan | 0.551 | 0.551 | 0.557 | 0.537 | 0.536 | 0.521 | 0.512 | 0.492 | 0.559 | 0.545 |
| Tibet | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.446 | 1.000 | 1.000 | 0.971 |
| Shaanxi | 0.579 | 0.593 | 0.601 | 0.564 | 0.574 | 0.546 | 0.543 | 0.518 | 0.602 | 0.556 |
| Gansu | 0.519 | 0.528 | 0.538 | 0.531 | 0.528 | 0.519 | 0.514 | 0.495 | 0.544 | 0.522 |
| Qinghai | 0.457 | 0.472 | 0.472 | 0.488 | 0.488 | 0.473 | 0.477 | 0.463 | 0.495 | 0.477 |
| Ningxia | 0.429 | 0.438 | 0.444 | 0.449 | 0.446 | 0.441 | 0.424 | 0.433 | 0.488 | 0.428 |
| Xinjiang | 0.533 | 0.535 | 0.540 | 0.537 | 0.527 | 0.518 | 0.504 | 0.489 | 0.540 | 0.532 |
| National level | 0.642 | 0.635 | 0.643 | 0.617 | 0.588 | 0.600 | 0.578 | 0.583 | 0.636 | 0.631 |
| Central China | 0.528 | 0.533 | 0.538 | 0.531 | 0.526 | 0.516 | 0.503 | 0.484 | 0.537 | 0.535 |
| Eastern China | 0.843 | 0.811 | 0.824 | 0.759 | 0.675 | 0.735 | 0.743 | 0.739 | 0.792 | 0.805 |
| Western China | 0.564 | 0.569 | 0.575 | 0.567 | 0.565 | 0.552 | 0.500 | 0.530 | 0.583 | 0.562 |
| DID | lnpgdp | Urban | lnpeople | lnRD | |
|---|---|---|---|---|---|
| Pearson | 0.175 *** | 0.264 *** | 0.319 *** | −0.234 *** | 0.0215 *** |
| (1) | (2) | |
|---|---|---|
| DID | 0.1481 *** | 0.0696 ** |
| (6.8640) | (2.6719) | |
| lnpgdp | 0.0781 *** | |
| (3.0640) | ||
| urban | 0.5874 *** | |
| (7.1142) | ||
| lnpeople | 0.0343 *** | |
| (4.2961) | ||
| lnrd | −0.0704 *** | |
| (−13.9649) | ||
| _cons | 0.6231 *** | −0.3996 |
| (39.6588) | (−1.6236) | |
| Obs. | 589 | 589 |
| R-squared | 0.0355 | 0.2036 |
| Coefficients | The Adjacent Spatial Weight Matrix | The Geographical Distance Weight Matrix |
|---|---|---|
| Cons. | −2.989282 *** (−5.529862) | −5.444846 *** (−6.717390) |
| DID | 0.054313 ** (2.056898) | 0.065400 *** (2.551654) |
| lnpgdp | 0.248871 *** (8.735223) | 0.339614 *** (12.097246) |
| urban | −0.458767 *** (−4.247770) | −0.725269 *** (−6.654841) |
| lnpeople | −0.123263 *** (−6.413339) | −0.100042 *** (−5.129031) |
| lnRD | 0.035486 *** (2.624192) | 0.021388 * (1.594869) |
| W × DID | 0.125443 *** (2.808217) | −0.054466 (−1.034768) |
| W × lnpgdp | −0.045147 (−0.924757) | 0.012978 (0.180682) |
| W × urban | 0.909285 *** (5.301019) | 1.734884 *** (7.111946) |
| W × lnpeople | 0.347690 *** (10.210177) | 0.504328 *** (9.938163) |
| W × RD | −0.199200 *** (−7.946907) | −0.324300 *** (−7.749624) |
| rho | 0.435505 *** (10.206927) | 0.283881 *** (4.327892) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, G.; Xie, Y.; Li, H.; Riaz, N. Agricultural Ecological Efficiency under the Carbon Emissions Trading System in China: A Spatial Difference-in-Difference Approach. Sustainability 2022, 14, 4707. https://doi.org/10.3390/su14084707
Wu G, Xie Y, Li H, Riaz N. Agricultural Ecological Efficiency under the Carbon Emissions Trading System in China: A Spatial Difference-in-Difference Approach. Sustainability. 2022; 14(8):4707. https://doi.org/10.3390/su14084707
Chicago/Turabian StyleWu, Guoyong, Yu Xie, Haoxin Li, and Noman Riaz. 2022. "Agricultural Ecological Efficiency under the Carbon Emissions Trading System in China: A Spatial Difference-in-Difference Approach" Sustainability 14, no. 8: 4707. https://doi.org/10.3390/su14084707
APA StyleWu, G., Xie, Y., Li, H., & Riaz, N. (2022). Agricultural Ecological Efficiency under the Carbon Emissions Trading System in China: A Spatial Difference-in-Difference Approach. Sustainability, 14(8), 4707. https://doi.org/10.3390/su14084707






