A Dynamic Analysis for Mitigating Disaster Effects in Closed Loop Supply Chains
Abstract
:1. Introduction
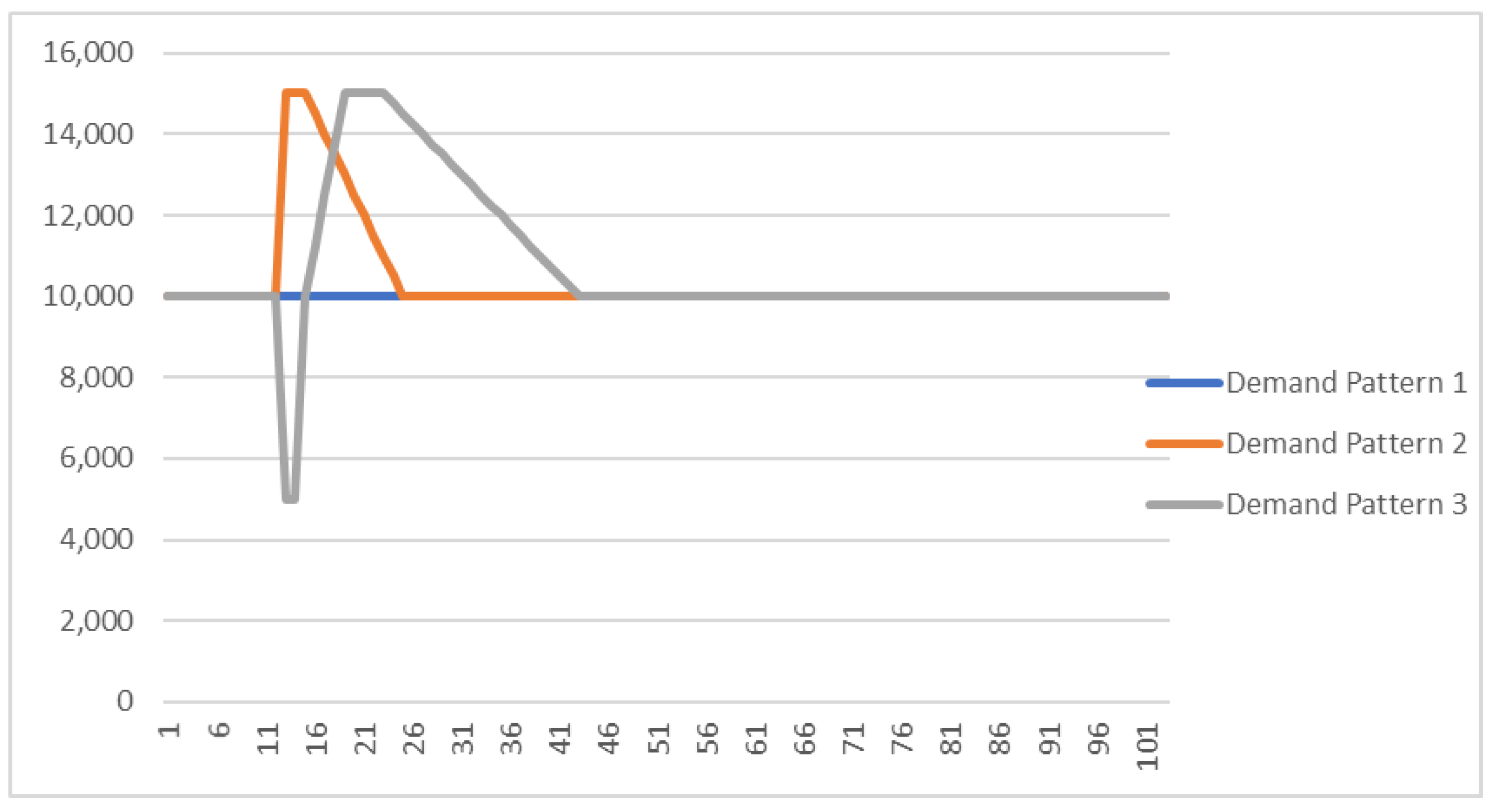
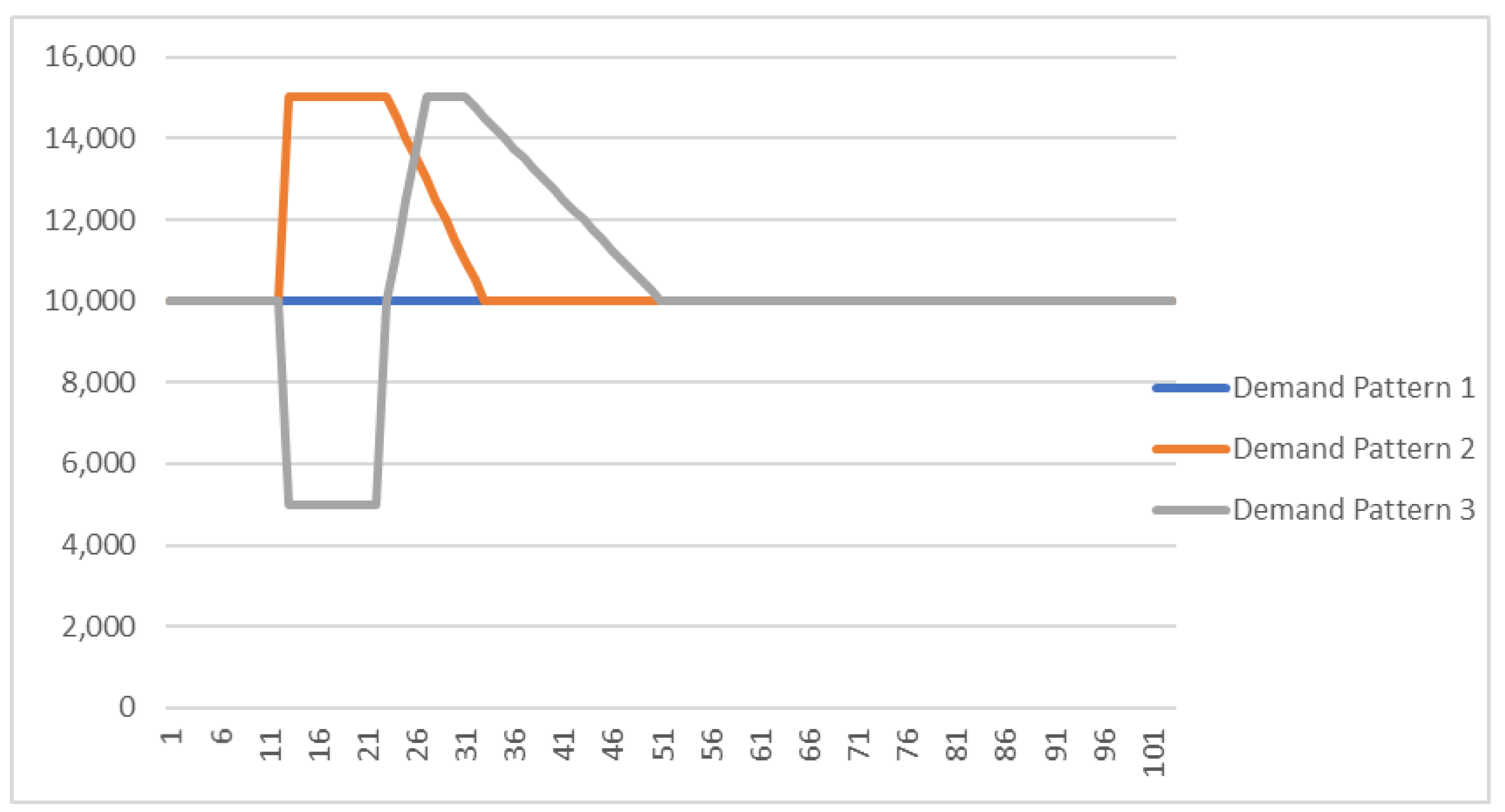
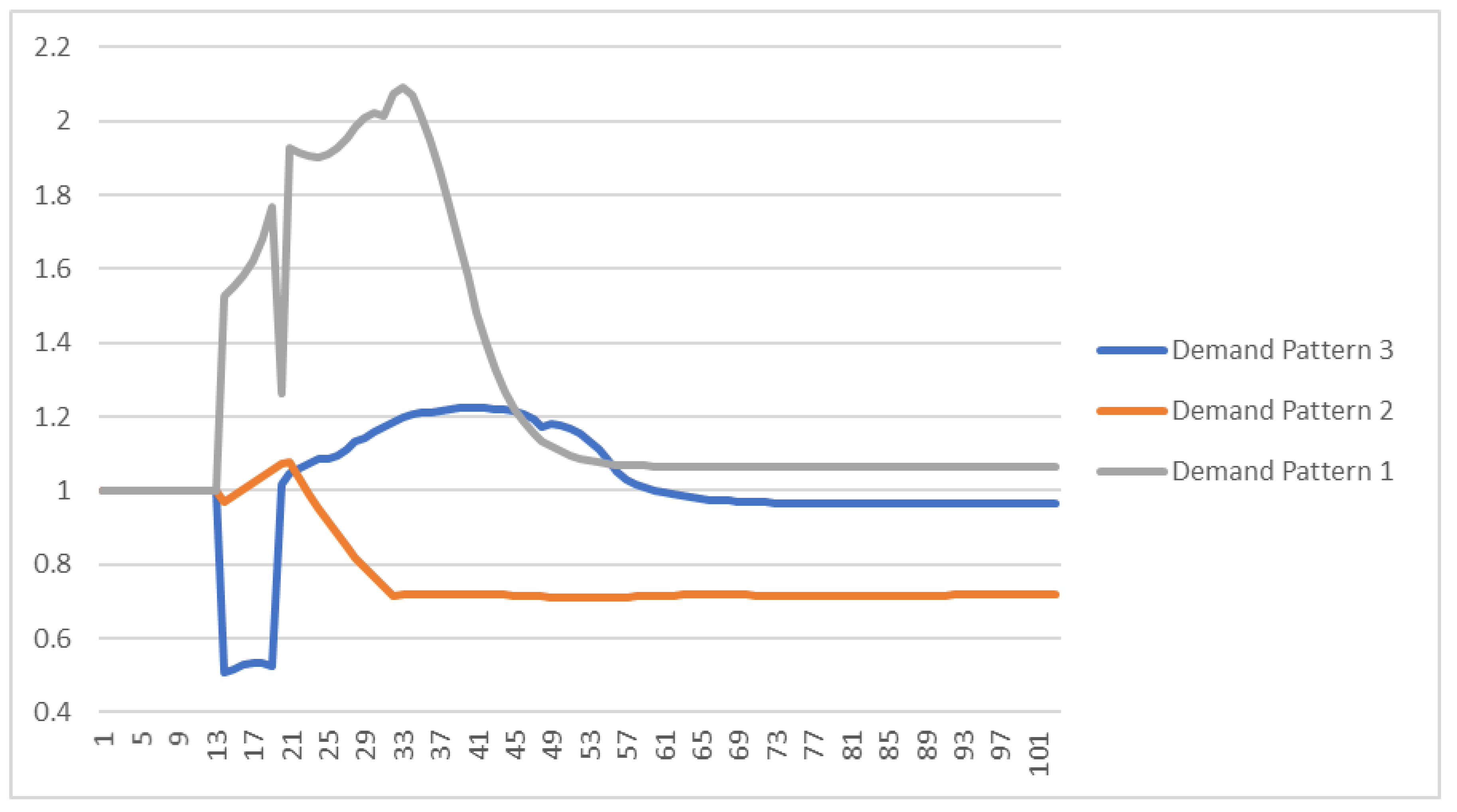
- Demand Pattern 1: Demand does not vary as a result of the phenomenon (for instance, food products during COVID-19 effect).
- Demand Pattern 2: Demand marks a sudden increase when disaster materializes. This increase is maintained for as long as the phenomenon last (disaster-period) and thereafter (post-disaster period) it returns to its pre-disaster level. An indicative example for this case is the sudden increase in demand for medical masks owing to the outbreak of COVID-19 [24].
- Demand Pattern 3: Demand marks a sudden decrease during the disaster period. During the post-disaster period, it increases to reach higher levels compared with pre-disaster conditions and after a certain amount of time, it returns to its pre-disaster level (for instance, the automotive industry during COVID-19 [24]).
2. Literature Review
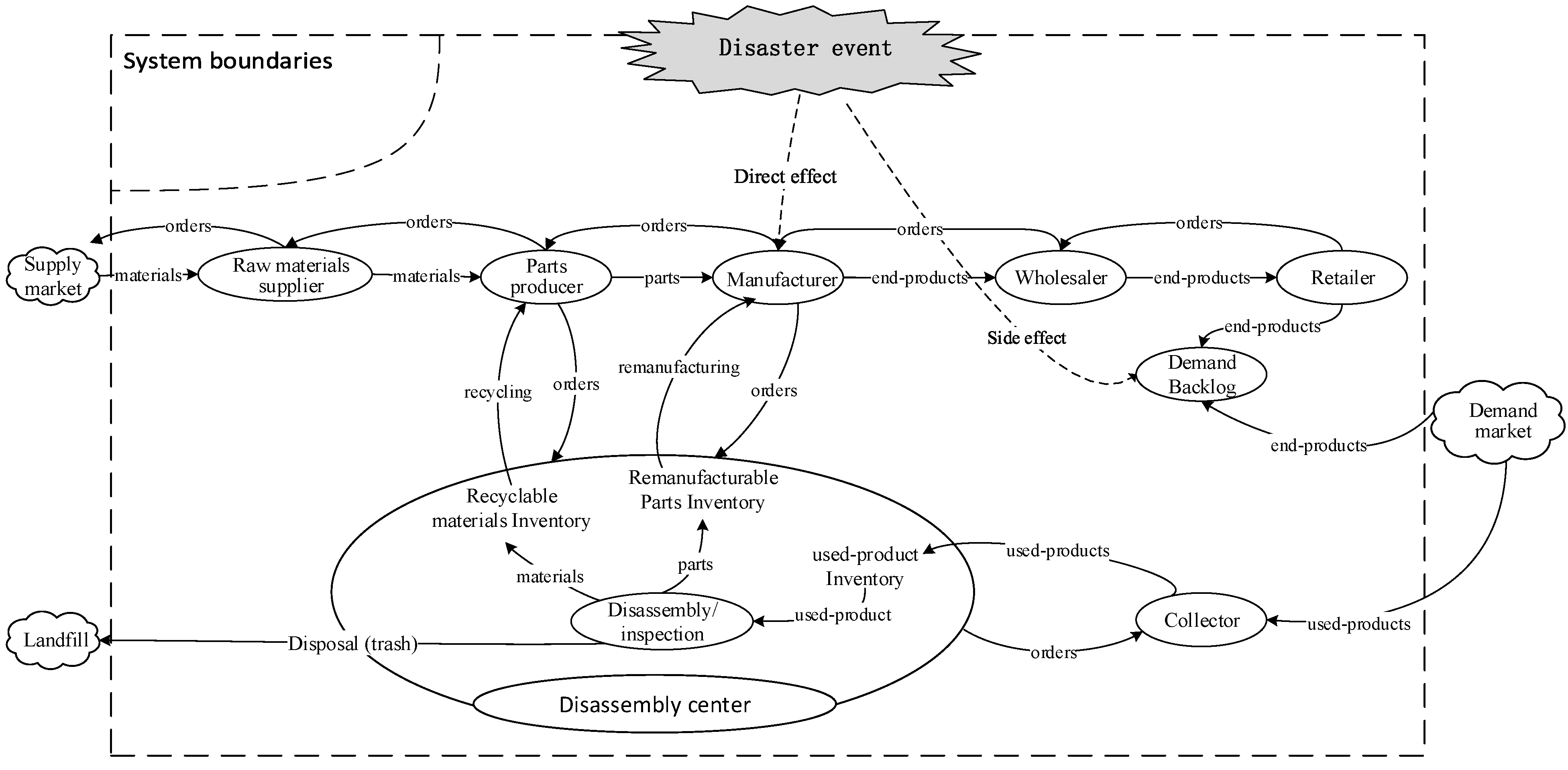
3. System and Problem Description
3.1. System Description
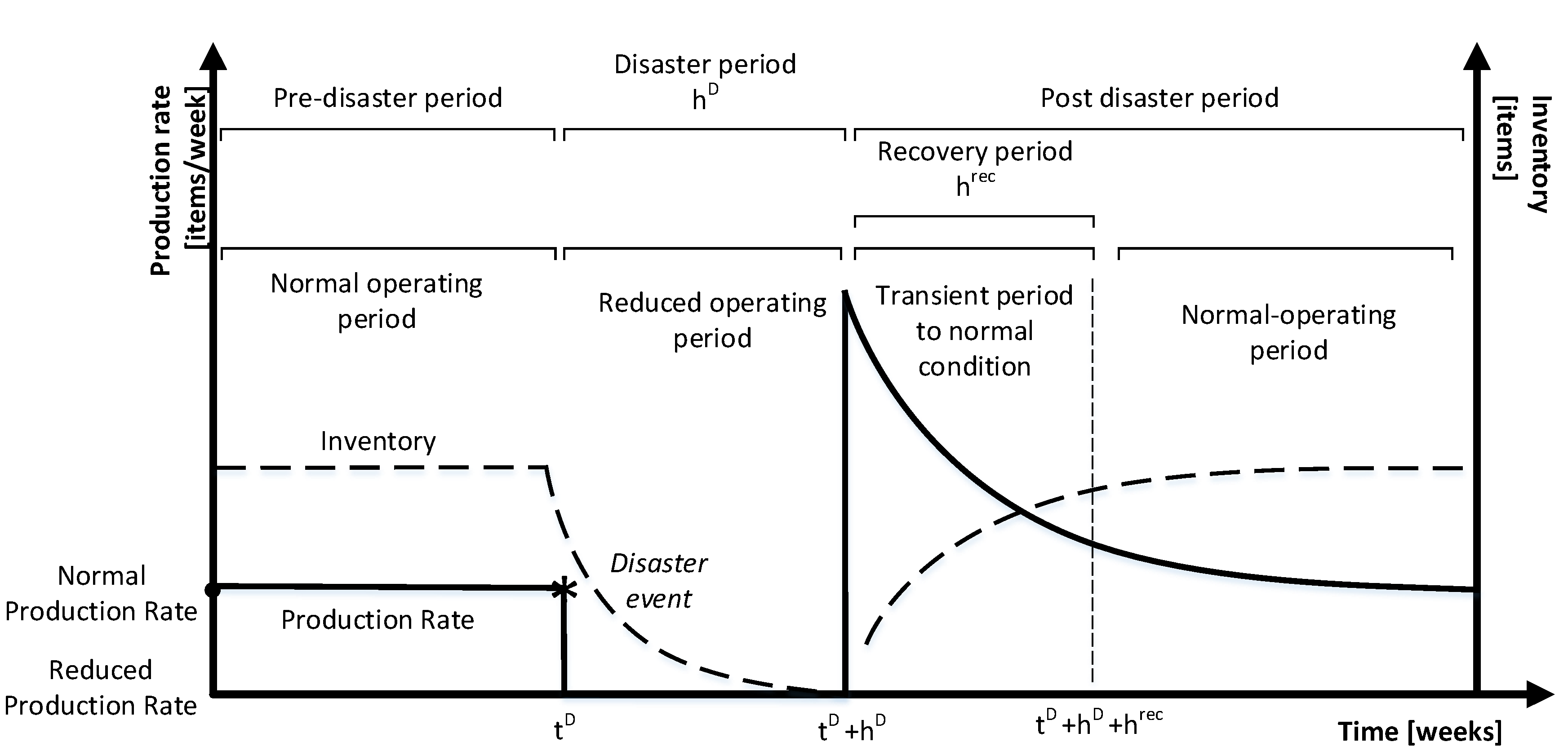
3.2. Problem Description
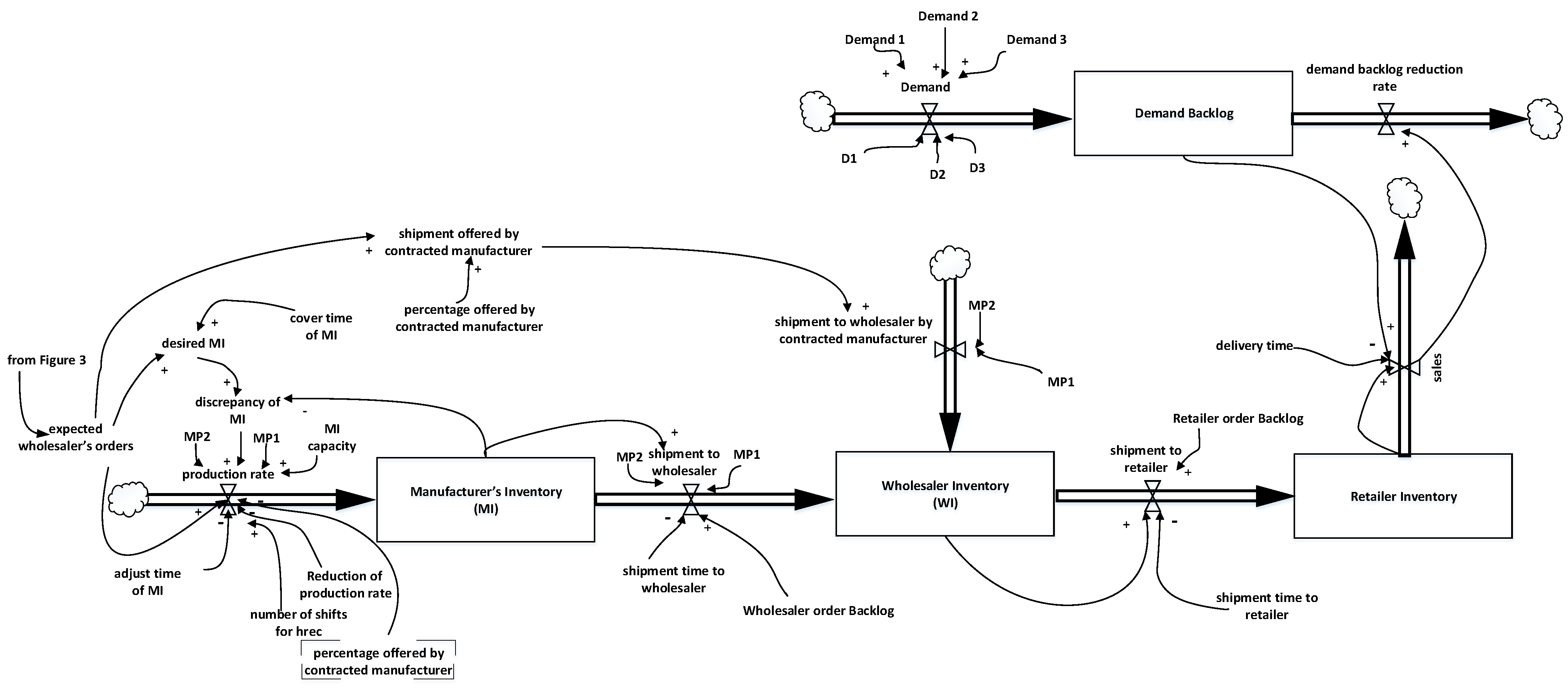
4. The SD Model
4.1. Generic Stock and Flow Structure
4.2. Mitigation Policies at the Manufacturer Level
- MP1: [MP1, cover time of MI, cover time of MI due to event, adjust time of MI, adjust time of MI due to event, hrec].
- MP2: [MP2, cover time of MI, cover time of MI due to event, adjust time of MI, adjust time of MI due to event percentage offered by contracted manufacturer, hrec].
4.3. Stock Equations
4.4. Flow Equation
4.5. Auxiliary Equations
4.6. Profit Equations
5. Numerical Experimentation and Discussion
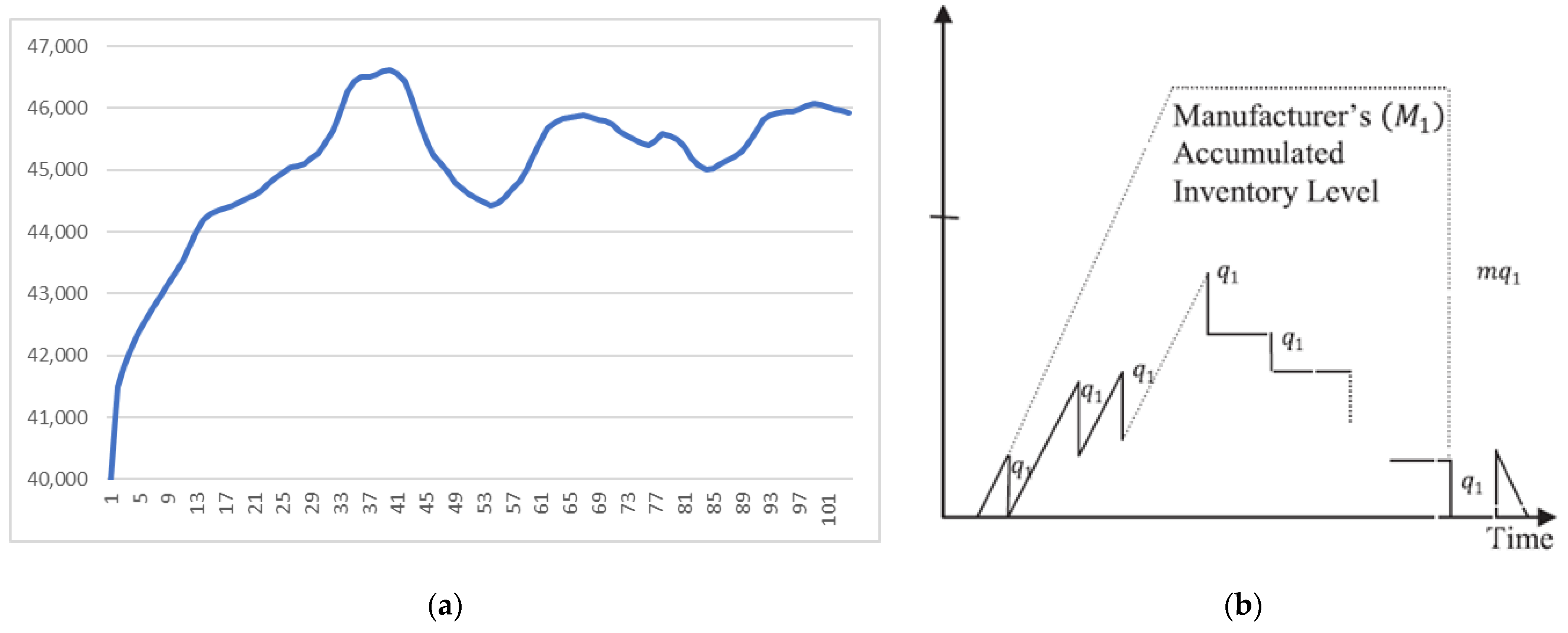
5.1. Validation of the SD Model
5.2. Settings
- MP1: [MP1, cover time of MI, cover time of MI due to event, adjust time of MI, adjust time of MI due to event, hrec].
- MP2: [MP2, cover time of MI, cover time of MI due to event, time of MI, adjust time of MI due to event, percentage offered by contracted manufacturer, hrec].
- BS: [Demand ~N(10,000 items/week, 1000 items/week, stock management: cover time of MI = 4 weeks; adjust time of MI = 6 weeks].
5.3. Recommendations for Mitigating Disaster Effects
5.3.1. Profitability of the CLSC System
5.3.2. Demand Backlog and Manufacturer Inventory
6. Summary, Limitations and Future Research
Author Contributions
Funding
Conflicts of Interest
References
- Liu, M.; Scheepbouwer, E.; Giovinazzi, S. Critical success factors for post-disaster infrastructure recovery: Learning from the Canterbury (NZ) earthquake recovery. Disaster Prev. Manag. Int. J. 2016, 25, 685–700. [Google Scholar] [CrossRef]
- Maureen, S.G.; Laura, H.J.; Linkov, I. Trends and applications of resilience analytics in supply chain modeling: Systematic literature review in the context of the COVID-19 pandemic. Environ. Syst. Decis. 2020, 40, 222–2430. [Google Scholar]
- Makridakis, S.; Hogarth, R.M.; Gaba, A. Why Forecasts Fail. What to Do Instead? MIT Sloan Manag. Rev. 2010, 51, 83–90. [Google Scholar]
- Simchi-Levi, D. Operations Rules: Delivering Customer Value through Flexible Operations; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Altay, N.; Green, W.G., III. OR/MS research in disaster operations management. Eur. J. Oper. Res. 2006, 175, 475–493. [Google Scholar] [CrossRef] [Green Version]
- Pawson, R.; Manzano, A.; Geoff, W. The Coronavirus Response: Known Knowns, Known Unknowns, Unknown Unknowns. In The Relevance of Realism in the Pandemic; The Rameses Projects: Oxford, UK, 2020. [Google Scholar]
- Lawrence, J.-M.; Hossain, N.; Rinaudo, C.; Buchanan, R.; Jaradat, R. An Approach to Improve Hurricane Disaster Logistics Using System Dynamics and Information Systems. In Proceedings of the 18th Annual Conference on Systems Engineering Research (CSER), Redondo Beach, CA, USA, 19–21 March 2020. [Google Scholar]
- Medel, K.; Kousar, R.; Masood, R. A collaboration–resilience framework for disaster management supply networks: A case study of the Philippines. J. Humanit. Logist. Supply Chain. Manag. 2020, 10, 509–553. [Google Scholar] [CrossRef]
- Peng, M.; Peng, Y.; Chen, H. Post-seismic supply chain risk management: A system dynamics Disruption analysis approach for inventory and logistics planning. Comput. Oper. Res. 2014, 42, 14–24. [Google Scholar] [CrossRef]
- Shareef, M.; Dwivedi, Y.; Mahmud, R.; Wright, A.; Rahman, M.; Kizgin, H.; Rana, N. Disaster management in Bangladesh: Developing an effective emergency supply chain network. Ann. Oper. Res. 2019, 283, 1463–1487. [Google Scholar] [CrossRef] [Green Version]
- Li, X.P.; Chen, Y.R. Impacts of supply disruptions and customer differentiation on a partial-backordering inventory system. Simul. Modeling Pract. Theory 2010, 18, 547–557. [Google Scholar] [CrossRef]
- Baz, J.E.; Ruel, S. Can supply chain risk management practices mitigate the disruption impacts on supply chains’ resilience and robustness? Evidence from an empirical survey in a COVID-19 outbreak era. Int. J. Prod. Econ. 2021, 233, 107972. [Google Scholar] [CrossRef]
- Rose, A. COVID-19 economic impacts in perspective: A comparison to recent U.S. disasters. Int. J. Disaster Risk Reduct. 2021, 60, 102317. [Google Scholar] [CrossRef]
- Zang, Y.; Wei, K.; Shen, Z.; Bai, X.; Lu, X.; Soares, C.G. Economic impact of typhoon-induced wind disasters on port operations: A case study of ports in China. Int. J. Disaster Risk Reduct. 2020, 50, 101719. [Google Scholar] [CrossRef]
- Natarajarathinam, M.; Capar, I.; Narayanan, A. Managing supply chains in times of crisis: A review of literature and insights. Int. J. Phys. Distrib. Logist. Manag. 2009, 39, 535–573. [Google Scholar] [CrossRef] [Green Version]
- Dixon, P.; Rimmer, M.; Giesecke, J.; King, C.; Waschik, R. The effects of COVID-19 on the U.S. Macro economy, industries, regions and national critical functions. In Report to the U.S. Department of Homeland Security Centre of Policy Studies, Victoria University, (Melbourne, Australia); Centre of Policy Studies (CoPS): Footscray, Australia, 2020. [Google Scholar]
- Eglin, R. Can suppliers bring down your firm? Sunday Times, 23 November 2003; 6. [Google Scholar]
- Latour, A. Trial by fire: A blaze in albuquerque sets off major crisis for cell phone giants. Wall Street Journal, 29 January 2001. [Google Scholar]
- Disasters 2018: Year in Review; Centre for Research on the Epidemiology of Disasters: Brussels, Belgium, 2019.
- Song, J.M.; Chen, W.; Lei, L. Supply chain flexibility and operations optimization under demand uncertainty: A case in disaster relief. Int. J. Prod. Res. 2018, 56, 3699–3713. [Google Scholar] [CrossRef]
- Ivanov, D.; Dolgui, A. Viability of Intertwined Supply Networks: Extending the Supply Chain Resilience Angles towards Survivability. A Position Paper Motivated by COVID-19 Outbreak. Int. J. Prod. Res. 2020, 58, 2904–2915. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, D. Predicting the Impact of Epidemic Outbreaks on the Global Supply Chains: A Simulation-Based Analysis on the Example of Coronavirus (COVID-19/SARS-CoV-2) Case. Transp. Res.–Part E 2020, 136, 101922. [Google Scholar] [CrossRef] [PubMed]
- Umar, M.; Wison, M. Supply Chain Resilience: Unleashing the Power of Collaboration in Disaster Management. Sustainability 2021, 19, 10573. [Google Scholar] [CrossRef]
- Ivanov, D. Viable supply chain model: Integrating agility, resilience and sustainability perspectives—lessons from and thinking beyond the COVID-19 pandemic. Ann. Oper. Res. 2020, 1–21. [Google Scholar] [CrossRef]
- Wen-Hui, X.; Dian-Yan, J.; Yu-Yuing, H. The remanufacturing reverse logistics management based on closed-loop supply chain management processes. Procedia Environ. Sci. 2011, 11, 351–354. [Google Scholar] [CrossRef]
- Hosseini-Motlagh, S.; Nami, N.; Farshadfar, Z. Collection disruption management and channel coordination in a socially concerned closed-loop supply chain: A game theory approach. J. Clean. Prod. 2020, 276, 124173. [Google Scholar] [CrossRef]
- Ullah, M.; Asghar, I.; Zahid, M.; Omair, M.; Al Arjani, A.; Sarkar, B. Ramification of remanufacturing in a sustainable three-echelon closed-loop supply chain management for returnable products. J. Clean. Prod. 2021, 290, 125609. [Google Scholar] [CrossRef]
- Garai, A.; Chowdhury, S.; Sarkar, B.; Kumar Roy, T. Cost-effective subsidy policy for growers and biofuels-plants in closed-loop supply chain of herbs and herbal medicines: An interactive bi-objective optimization in T-environment. Appl. Soft Comput. J. 2021, 100, 106949. [Google Scholar] [CrossRef]
- Garai, A.; Sarkar, B. Economically independent reverse logistics of customer-centric closed-loop supply chain for herbal medicines and biofuel. J. Clean. Prod. 2022, 334, 129977. [Google Scholar] [CrossRef]
- Ma, C. Impacts of demand disruption and government subsidy on closed-loop supply chain management: A model-based approach. Environ. Technol. Innov. 2022, 27, 102425. [Google Scholar] [CrossRef]
- Sarkar, B.; Debnath, A.; Chiu, A.; Ahmed, W. Circular economy-driven two-stage supply chain management for nullifying waste. J. Clean. Prod. 2022, 339, 130513. [Google Scholar] [CrossRef]
- Galindo, G.; Batta, R. Review of recent developments in OR/MS research in disaster operations anagement. Eur. J. Oper. Res. 2013, 23, 201–211. [Google Scholar] [CrossRef]
- Farahani, R.Z.; Lotfi, M.M.; Baghaian, A.; Ruiz, R.; Rezapour, S. Mass casualty management in disaster scene: A systematic review of OR&MS research in humanitarian operations. Eur. J. Oper. Res. 2020, 287, 787–819. [Google Scholar]
- Borja, P.; Mohamed, M.N.; Syntetos, A.A. The effect of returns volume uncertainty on the dynamic performance of closed-loop supply chains. J. Remanufacturing 2019, 10, 1–14. [Google Scholar]
- Surana, A.; Kumara, S.; Greaves, M.; Raghavan, U.N. Supply-chain networks: A complex adaptive systems perspective. Int. J. Prod. Res. 2005, 43, 4235–4265. [Google Scholar] [CrossRef]
- Li, G.; Hongjiao, Y.; Sun, L.; Ji, P.; Feng, L. The evolutionary complexity of complex adaptive supply networks: A simulation and case study. Int. J. Prod. Econ. 2010, 124, 310–330. [Google Scholar] [CrossRef]
- Braz, A.C.; De Melo, A.M. Circular economy supply network management: A complex adaptive system. Int. J. Prod. Econ. 2022, 243, 108317. [Google Scholar] [CrossRef]
- Hwarng, H.B.; Yuan, X. Interpreting supply chain dynamics: A quasi-chaos perspective. Eur. J. Oper. Res. 2014, 233, 566–579. [Google Scholar] [CrossRef]
- Gong, Y.; Chen, M.; Wang, Z.; Zhan, J. With or without deposit-refund system for a network platform-led electronic closed-loop supply chain. J. Clean. Prod. 2021, 281, 125356. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, D.Z. Demand fluctuation and chaotic behaviour by interaction between customers and suppliers. Int. J. Prod. Econ. 2007, 107, 250–259. [Google Scholar] [CrossRef]
- Helbing, D.; Ammoser, H.; Äuhnert, C.K. Disasters as Extreme Events and the Importance of Networks for Disaster Response Management. In Extreme Events in Nature and Society; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Peterson, M. The Limits of Catastrophe Aversion. Risk Anal. 2002, 22, 527–538. [Google Scholar] [CrossRef] [PubMed]
- Kwesi-Buor, J.; Menachof, D.A.; Talas, R.; Ivanov, D.; Sokolov, B. Scenario analysis and disaster preparedness for port and maritime logistics risk management. Accident Anal. Prev. 2019, 123, 433–447. [Google Scholar] [CrossRef]
- Mosekilde, E.; Laugesen, J.L. Nonlinear dynamic phenomena in the beer model. Syst. Dyn. Rev. 2008, 23, 229–252. [Google Scholar] [CrossRef]
- Chang, M.-S.; Tseng, Y.-L.; Chen, J.-W. A scenario planning approach for the flood emergency logistics preparation problem under uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2007, 43, 737–754. [Google Scholar] [CrossRef]
- Sterman, J.D. Business Dynamics: Systems Thinking and Modeling for a Complex World; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Tang, O.; Musa, S.N. Identifying risk issues and research advancements in supply chain risk management. Int. J. Prod. Econ. 2011, 133, 25–34. [Google Scholar] [CrossRef] [Green Version]
- Forrester, J.W. Industrial Dynamics; MIT Press: Cambridge, MA, USA, 1961. [Google Scholar]
- Größler, A.; Thun, J.H.; Milling, P.M. System dynamics as a structural theory in operations management. Prod. Oper. Manag. 2008, 17, 373–384. [Google Scholar] [CrossRef]
- Aydin, N. Designing reverse logistics network of end-of-life-buildings as preparedness to disasters under uncertainty. J. Clean. Prod. 2020, 256, 120341. [Google Scholar] [CrossRef]
- Georgiadis, P.; Michaloudis, C. Real-time production planning and control system for job-shop manufacturing: A system dynamics analysis. Eur. J. Oper. Res. 2012, 216, 94–104. [Google Scholar] [CrossRef]
- Yang, J.; Mu, D.; Li, X. A system dynamics analysis about the recycling and reuse of new energy vehicle power batteries: An insight of closed-loop supply chain. IOP Conf. Ser. Earth Environ. Sci. 2020, 508, 012058. [Google Scholar] [CrossRef]
- Ivanov, D.; Sokolov, B. Simultaneous structural–operational control of supply chain dynamics and resilience. Ann. Oper. Res. 2020, 283, 1191–1210. [Google Scholar] [CrossRef]
- Ozbayrak, M.; Papadopoulou, T.C.; Akgun, M. Systems dynamics modeling of a manufacturing supply chain system. Simul. Modeling Pract. Theory 2007, 15, 1338–1355. [Google Scholar] [CrossRef]
- Pierreval, H.; Bruniaux, R.; Caux, C. A continuous simulation approach for supply chain in the automotive industry. Simul. Modeling Pract. Theory 2007, 15, 185–198. [Google Scholar] [CrossRef]
- Keilhacker, M.; Minner, S. Supply chain risk management for critical commodities: A system dynamics model for the case of the rare earth elements. Resour. Conserv. Recycl. 2014, 125, 349–362. [Google Scholar] [CrossRef]
- Lai, C.L.; Lee, W.B.; Ip, W.H. A study of system dynamics in just-in-time logistics. J. Mater. Process. Technol. 2003, 138, 265–269. [Google Scholar] [CrossRef]
- Mikatia, N. Dependence of lead time on batch size studied by a system dynamics model. Int. J. Prod. Res. 2010, 48, 5523–5532. [Google Scholar] [CrossRef]
- Suryani, E.; Chou, S.; Hartono, R.; Chen, C.H. Demand scenario analysis and planned capacity expansion: A system dynamics framework. Simul. Modeling Pract. Theory 2010, 18, 732–751. [Google Scholar] [CrossRef]
- Wilson, M.C. The impact of transportation disruptions on supply chain performance. Transp. Res. Part E Logist. Transp. Rev. 2007, 43, 295–320. [Google Scholar] [CrossRef]
- Chen, J.X.; Li, G.H.; Shi, G.H. Supply Chain System Dynamics Simulation with Disruption Risks. Ind. Eng. Manag. 2011, 16, 35–41. [Google Scholar]
- Ankit, J. Impact of Supply Uncertainty in Supply Chain; LAP Lambert Academic Publishing AG & Co KG: Sunnyvale, CA, USA, 2010. [Google Scholar]
- Aguila-Olivares, J.; ElMaraghy, W.J. System dynamics modelling for supply chain disruptions. Int. J. Prod. Res. 2021, 59, 1757–1775. [Google Scholar] [CrossRef]
- Diaz, R.; Behr, J.; Longo, F.; Padovano, A. Supply Chain Modeling in the Aftermath of a Disaster: A System Dynamics Approach in Housing Recovery. IEEE Trans. Eng. Manag. 2020, 67, 531–544. [Google Scholar] [CrossRef]
- Bashiri, M.; Tjahjono, B.; Lazell, J.; Ferreira, J.; Tomy, P. The Dynamics of Sustainability Risks in the Global Coffee Supply Chain: A Case of Indonesia–UK. Sustainability 2021, 13, 589. [Google Scholar] [CrossRef]
- Zhang, Q.; Fan, W.; Lu, J.; Wu, S.; Wang, X. Research on Dynamic Analysis and Mitigation Strategies of Supply Chains under Different Disruption Risks. Sustainability 2021, 13, 2462. [Google Scholar] [CrossRef]
- Ivanov, D.; Dolgui, A. OR-methods for coping with the ripple effect in supply chains during COVID-19 pandemic: Managerial insights and research implications. Int. J. Prod. Econ. 2020, 232, 107921. [Google Scholar] [CrossRef]
- Georgiadis, P.; Vlachos, D.; Tagaras, G. The impact of product lifecycle on capacity planning of closed-loop supply chains with remanufacturing. Prod. Oper. Manag. 2006, 15, 514–527. [Google Scholar] [CrossRef]
- Georgiadis, P.; Athanasiou, E. Flexible long-term capacity planning in closed-loop supply chains with remanufacturing. Eur. J. Oper. Res. 2013, 225, 43–58. [Google Scholar] [CrossRef]
- Tombido, L.; Louw, L.; Van Eeden, J. The Bullwhip Effect in Closed-Loop Supply Chains: A Comparison of Series and Divergent Networks. J. Remanufacturing 2020, 3, 207–238. [Google Scholar] [CrossRef]
- Manoranjan, D.; Giri, B.C. Modeling a closed-loop supply chain with a heterogeneous fleet under carbon emission reduction policy. Transp. Res. Part E 2020, 133, 101813. [Google Scholar]
- Gu, Q.L.; Gao, T.G. Joint decisions for R/M integrated supply chain using system dynamics methodology. Int. J. Prod. Res. 2012, 50, 4444–4461. [Google Scholar] [CrossRef]
- Rebs, T.; Brandenburg, M.; Seuring, S. System dynamics modeling for sustainable supply chain management: A literature review and systems thinking approach. J. Clean. Prod. 2019, 208, 1265–1280. [Google Scholar] [CrossRef]
- Michel, B.; Chang, S.E.; Eguchi, R.T.; Lee, G.C.; O’Rourke, T.D.; Reinhorn, A.M.; Shinozuka, M.; Tierney, K.; Wallace, W.A.; von Winterfeldt, D. A framework to quantitatively assess and enhance the seismic resilience of communities. Earthq. Spectra 2003, 19, 733–752. [Google Scholar]
- Zobel, C.W.; Khansa, L. Characterizing multi-event disaster resilience. Comput. Oper. Res. 2014, 42, 83–94. [Google Scholar] [CrossRef]
- Sterman, J.D. Modeling managerial behavior: Misperceptions of feedback in a dynamic decision making experiment. Manag. Sci. 1989, 35, 321–339. [Google Scholar] [CrossRef] [Green Version]
- Samara, E.; Andronikidis, A.; Komninos, N.; Bakouros, Y.; Katsoras, E. The Role of Digital Technologies for Regional Development: A System Dynamics Analysis. J. Knowl. Econ. 2022. [Google Scholar] [CrossRef]
- Barlas, Y. Formal aspects of model validity and validation in system dynamics. Syst. Dyn. Rev. 2000, 12, 183–210. [Google Scholar] [CrossRef]
- Forrester, J.W.; Senge, P.M. Tests for building confidence in system dynamics models. TIMS Stud. Manag. Sci. 1980, 14, 209–228. [Google Scholar]
- Yadav, D.; Kumari, R.; Kumar, N.; Sarkar, B. Reduction of waste and carbon emission through the selection of items with cross-price elasticity of demand to form a sustainable supply chain with preservation technology. J. Clean. Prod. 2021, 297, 126298. [Google Scholar] [CrossRef]
- Patra, D.P.; Jha, J.K. A two-period newsvendor model for prepositioning with a post-disaster replenishment using Bayesian demand update. Socio-Econ. Plan. Sci. 2021, 78, 101080. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Goli, A.; Ghasemi, P.; Goodarzian, F. Designing a sustainable closed-loop supply chain network of face masks during the COVID-19 pandemic: Pareto-based algorithms. J. Clean. Prod. 2021, 333, 130056. [Google Scholar] [CrossRef] [PubMed]


| Approaches | Reference |
|---|---|
| Complex Adaptive Systems Theory | [35,36,37] |
| Chaos Theory | [38,39,40] |
| Catastrophe Theory | [41] |
| Catastrophe-Risk Approaches | [42] |
| Disaster Preparedness | [43] |
| System Dynamics | - |
| Non-Linear Dynamic Approaches | [40,44,45] |
| hD (Weeks) | Reduction of Production Rate | Demand Pattern | Best/Worst Cases | MP * | hrec (Weeks) | Adjust Time due to Event (Weeks) | Cover Time due to Event (Weeks) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Lower | Upper | Equilibrium State | ||||||||
| 2 | 0% | 1 | Basic Scenario (BS) | 100 | 100 | 100 | ||||
| 20% | 1 | Best | MP2 | 12 | 1 | 2 | 100 | 106.58 | 100.88 | |
| Worst | MP2 | 12 | 2 | 8 | 80.41 | 99.93 | 95.90 | |||
| 20% | 2 | Best | MP2 | 12 | 4 | 2 | 99.81 | 142.83 | 105.60 | |
| Worst | MP2 | 12 | 2 | 8 | 95.67 | 119.84 | 103.60 | |||
| 20% | 3 | Best | MP2 | 12 | 2 | 2 | 82.59 | 160.12 | 137.00 | |
| Worst | ΜP1 | 12 | 4 | 8 | 73.29 | 154.10 | 134.00 | |||
| 50% | 1 | Best | MP1 | 12 | 2 | 2 | 100 | 109.66 | 100 | |
| Worst | MP2 | 12 | 4 | 8 | 85.73 | 99.30 | 96.60 | |||
| 50% | 2 | Best | MP1 | 12 | 4 | 2 | 99.87 | 145.95 | 106.80 | |
| Worst | MP1 | 12 | 3 | 6 | 96.61 | 130.04 | 105.45 | |||
| 50% | 3 | Best | MP1 | 12 | 3 | 2 | 85.49 | 162.30 | 137.40 | |
| Worst | MP1 | 8 | 6 | 8 | 76.92 | 148.91 | 123.90 | |||
| 6 | 20% | 1 | Best | MP2 | 12 | 2 | 2 | 98.93 | 108.97 | 99.00 |
| Worst | MP2 | 12 | 2 | 8 | 82.13 | 97.99 | 94.58 | |||
| 20% | 2 | Best | MP2 | 12 | 2 | 2 | 99.26 | 156.45 | 108.20 | |
| Worst | MP1 | 12 | 4 | 8 | 95.90 | 132.55 | 107.50 | |||
| 20% | 3 | Best | MP2 | 12 | 2 | 2 | 65.08 | 151.73 | 133.86 | |
| Worst | MP1 | 12 | 4 | 8 | 45.07 | 145.35 | 131.60 | |||
| 50% | 1 | Best | MP1 | 8 | 4 | 2 | 100.33 | 114.48 | 100.53 | |
| Worst | MP2 | 12 | 1 | 8 | 91.84 | 99.17 | 97.79 | |||
| 50% | 2 | Best | MP1 | 12 | 3 | 2 | 101.13 | 163.40 | 109.82 | |
| Worst | MP2 | 8 | 3 | 6 | 97.82 | 147.99 | 107.97 | |||
| 50% | 3 | Best | MP1 | 12 | 4 | 2 | 67.64 | 155.12 | 135.10 | |
| Worst | MP1 | 12 | 3 | 8 | 53.80 | 147.33 | 132.97 | |||
| 10 | 20% | 1 | Best | MP2 | 8 | 6 | 2 | 98.11 | 110.12 | 98.15 |
| Worst | MP2 | 8 | 3 | 8 | 83.04 | 98.43 | 95.35 | |||
| 20% | 2 | Best | MP2 | 12 | 1 | 2 | 100.13 | 166.10 | 111.00 | |
| Worst | MP1 | 12 | 4 | 8 | 96.17 | 143.76 | 110.90 | |||
| 20% | 3 | Best | MP1 | 12 | 3 | 2 | 50.33 | 144.16 | 131.52 | |
| Worst | MP2 | 12 | 2 | 8 | 30.72 | 135.70 | 125.90 | |||
| 50% | 1 | Best | MP1 | 12 | 4 | 2 | 99.94 | 119.43 | 100.90 | |
| Worst | MP1 | 4 | 6 | 8 | 93.41 | 102.90 | 99.13 | |||
| 50% | 2 | Best | MP1 | 8 | 2 | 2 | 100.88 | 178.86 | 113.40 | |
| Worst | MP1 | 8 | 4 | 8 | 97.66 | 158.60 | 112.70 | |||
| 50% | 3 | Best | MP1 | 12 | 4 | 2 | 58.92 | 148.35 | 133.80 | |
| Worst | MP1 | 12 | 2 | 8 | 42.75 | 137.77 | 127.70 | |||
| hD (Week) | Reduction of Production Rate | Demand Pattern | MP | hrec [Weeks] | Adjust Time Due to Event (Week) | Cover Time Due to Event (Week) | ||
|---|---|---|---|---|---|---|---|---|
| Max | Equilibrium State (Value/Time (Week) 1) | |||||||
| 2 | 0% | 1 | Basic Scenario (BS) | 1 | - | |||
| 20% | 1 | MP2 | 12 | All values | 6 or 8 | 1.01 | 0.91/7 | |
| 20% | 2 | MP2 | 8 or 12 | All values | 6 or 8 | 1.52 | 0.93/36 | |
| 20% | 3 | MP1 or MP2 | 4 | All values | 6 or 8 | 1.54 | 1.02/60 | |
| 50% | 1 | MP1 | 12 | All values | 6 or 8 | 1.35 | 0.84/20 | |
| 50% | 2 | MP1 or MP2 | All values | All values | 4 or 6 or 8 | 2.05 | 1.06/50 | |
| 50% | 3 | MP1 or MP2 | 4 | All values | 6 or 8 | 2.05 | 1.11/74 | |
| 6 | 20% | 1 | MP1 | 12 | All values | 8 | 1.07 | 0.72/20 |
| 20% | 2 | MP1 or MP2 | All values | All values | 4 or 6 or 8 | 2.09 | 1.06/45 | |
| 20% | 3 | MP1 or MP2 | 4 | 1 | 8 | 1.23 | 0.96/50 | |
| 50% | 1 | MP1 | 12 | All values | 6 or 8 | 2.80 | 1.09/45 | |
| 50% | 2 | MP1 or MP2 | All values | All values | 4 or 6 or 8 | 5.50 | 1.11/80 | |
| 50% | 3 | MP2 | 4 | All values | 6 or 8 | 2.40 | 1.11/70 | |
| 10 | 20% | 1 | MP1 | 12 | All values | 8 | 1.14 | 0.72/25 |
| 20% | 2 | MP1 or MP2 | All values | All values | 4 or 6 or 8 | 4.85 | 1.12/70 | |
| 20% | 3 | MP1 or MP2 | 4 | 1 | 8 | 1.48 | 1.06/80 | |
| 50% | 1 | MP1 or MP2 | All values | All values | 4 or 6 or 8 | 7.41 | 1.09/45 | |
| 50% | 2 | MP1 or MP2 | All values | All values | 4 or 6 or 8 | 11.09 | 1.14/75 | |
| 50% | 3 | MP1 or MP2 | 4 | 1 or 2 or 3 or 4 | 6 or 8 | 3.67 | 1.12/70 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katsoras, E.; Georgiadis, P. A Dynamic Analysis for Mitigating Disaster Effects in Closed Loop Supply Chains. Sustainability 2022, 14, 4948. https://doi.org/10.3390/su14094948
Katsoras E, Georgiadis P. A Dynamic Analysis for Mitigating Disaster Effects in Closed Loop Supply Chains. Sustainability. 2022; 14(9):4948. https://doi.org/10.3390/su14094948
Chicago/Turabian StyleKatsoras, Efthymios, and Patroklos Georgiadis. 2022. "A Dynamic Analysis for Mitigating Disaster Effects in Closed Loop Supply Chains" Sustainability 14, no. 9: 4948. https://doi.org/10.3390/su14094948
APA StyleKatsoras, E., & Georgiadis, P. (2022). A Dynamic Analysis for Mitigating Disaster Effects in Closed Loop Supply Chains. Sustainability, 14(9), 4948. https://doi.org/10.3390/su14094948






