Ultimate Limit State Reliability-Based Optimization of MSE Wall Considering External Stability
Abstract
:1. Introduction
2. Methodology
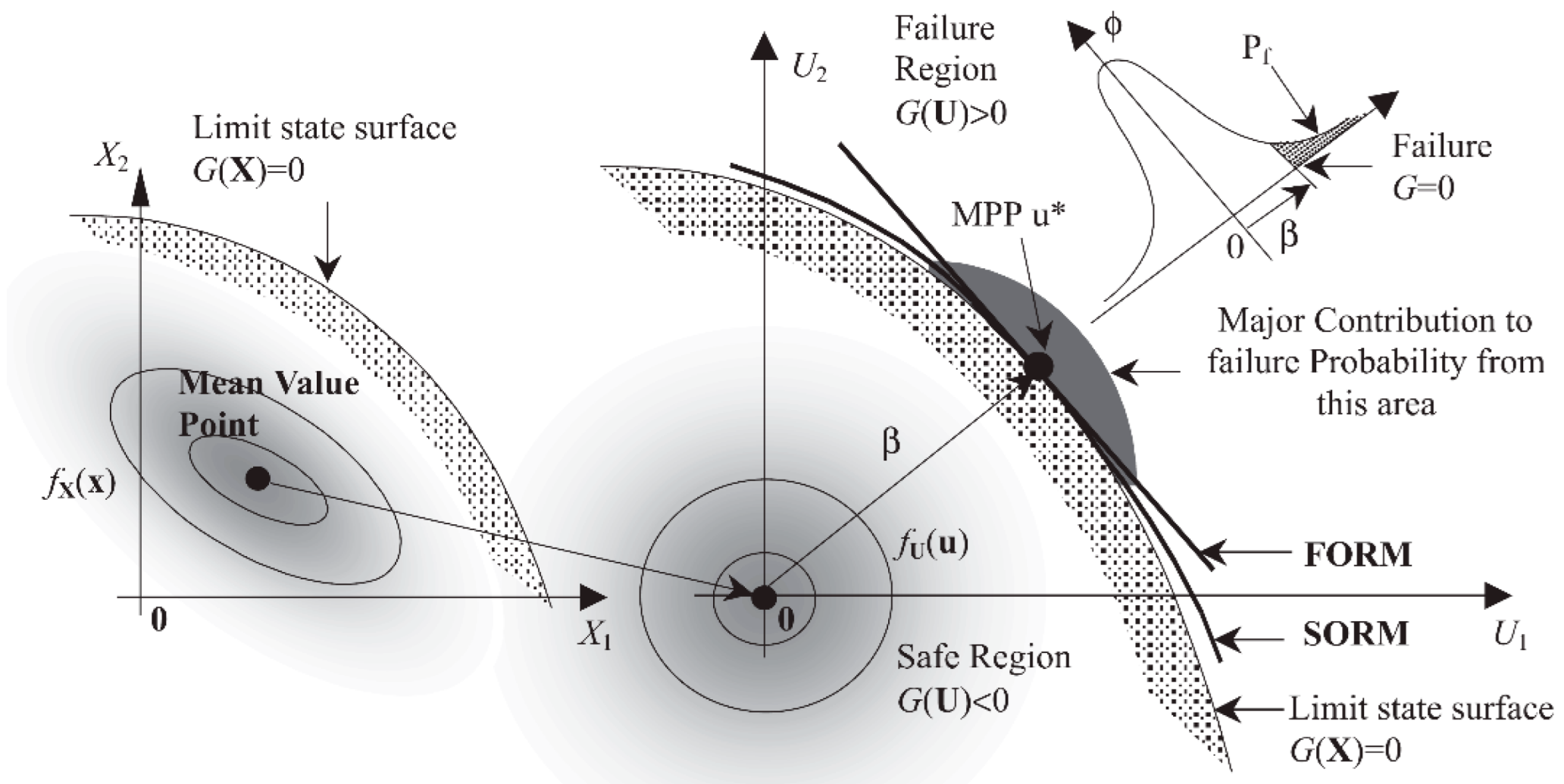
2.1. Reliability Index
2.2. Constrained Optimization with Linear Approximation (COBYLA)
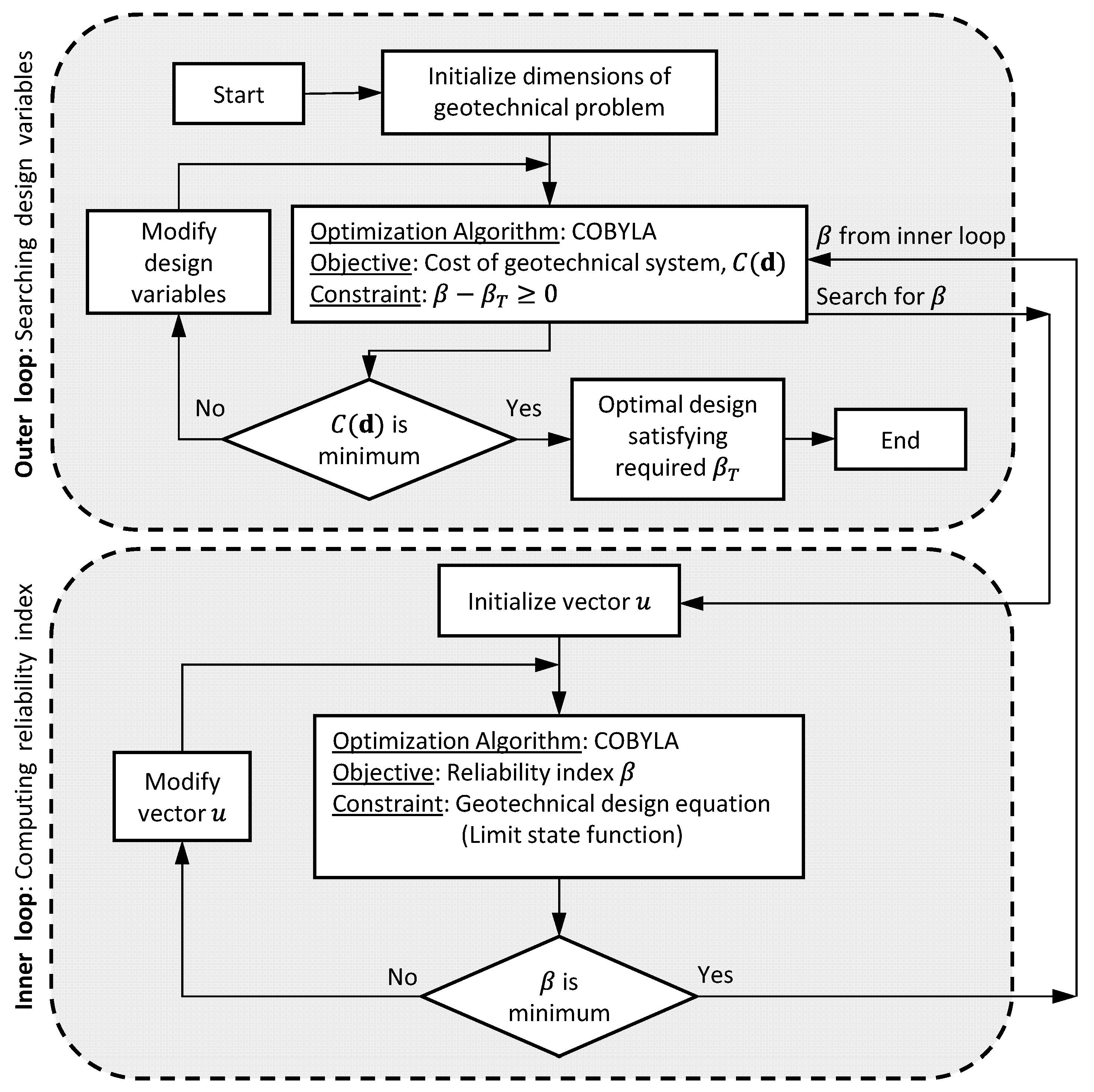
2.3. Process of Reliability-Based Optimization (RBO)
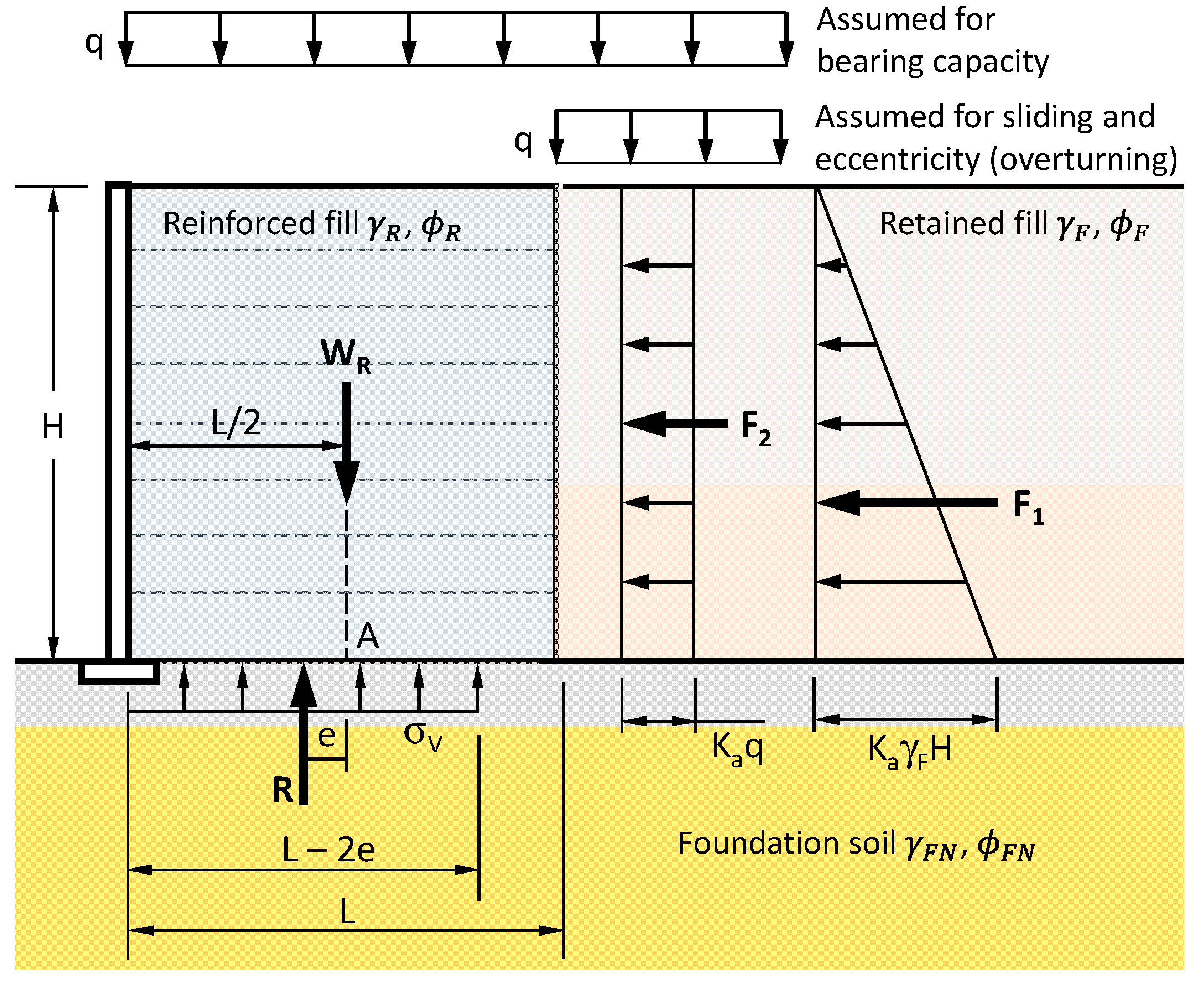
2.4. Reliability-Based Optimization of MSE Wall Considering External Stability
2.4.1. Limit State Equation for Sliding Failure
2.4.2. Limit State Equation for Eccentricity Failure
2.4.3. Limit State Equation for Bearing Capacity Failure
2.5. Assessment of Uncertainties
2.6. Process for Reliability-Based Optimization of MSE Wall
3. Results and Discussion
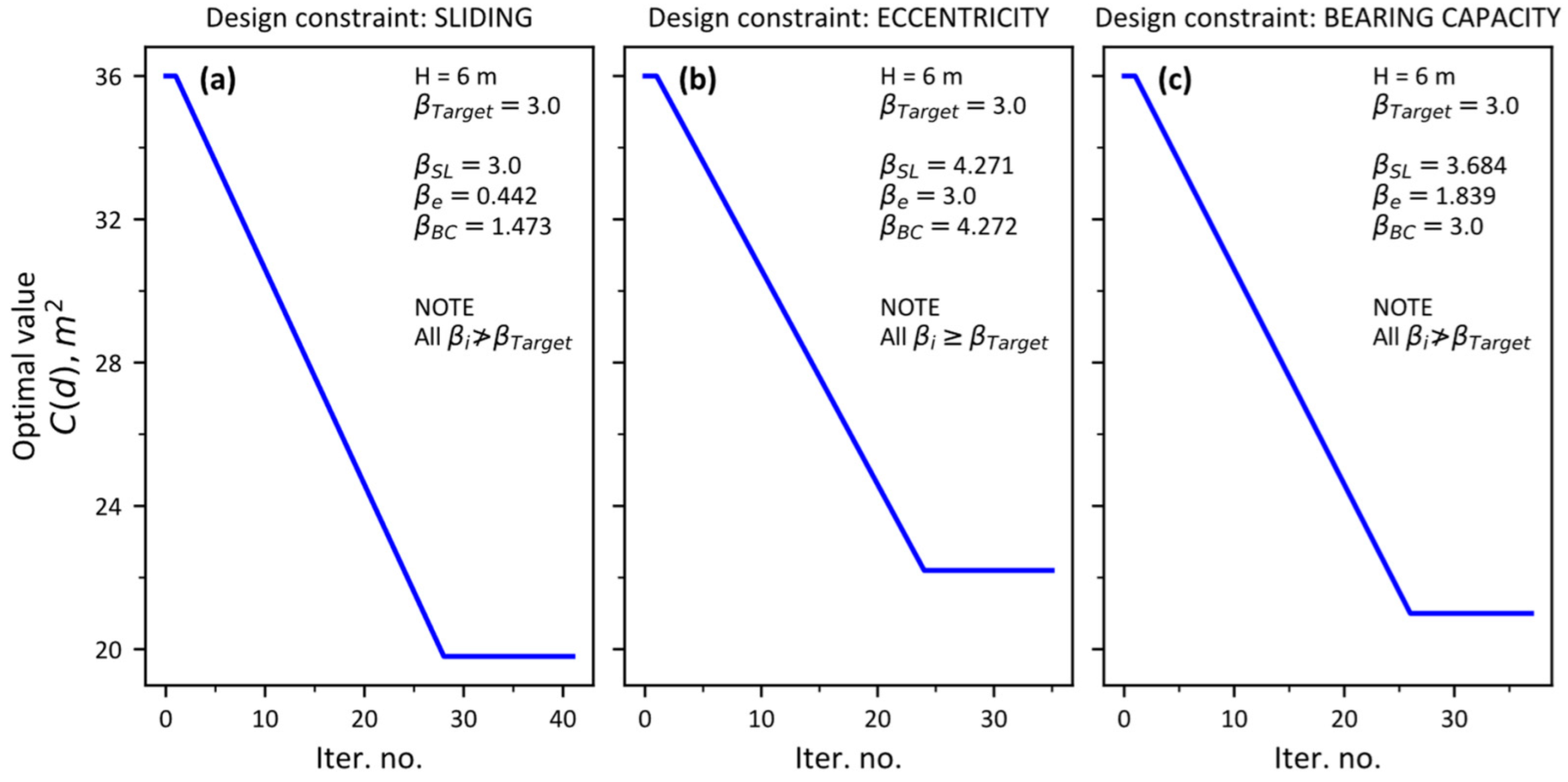
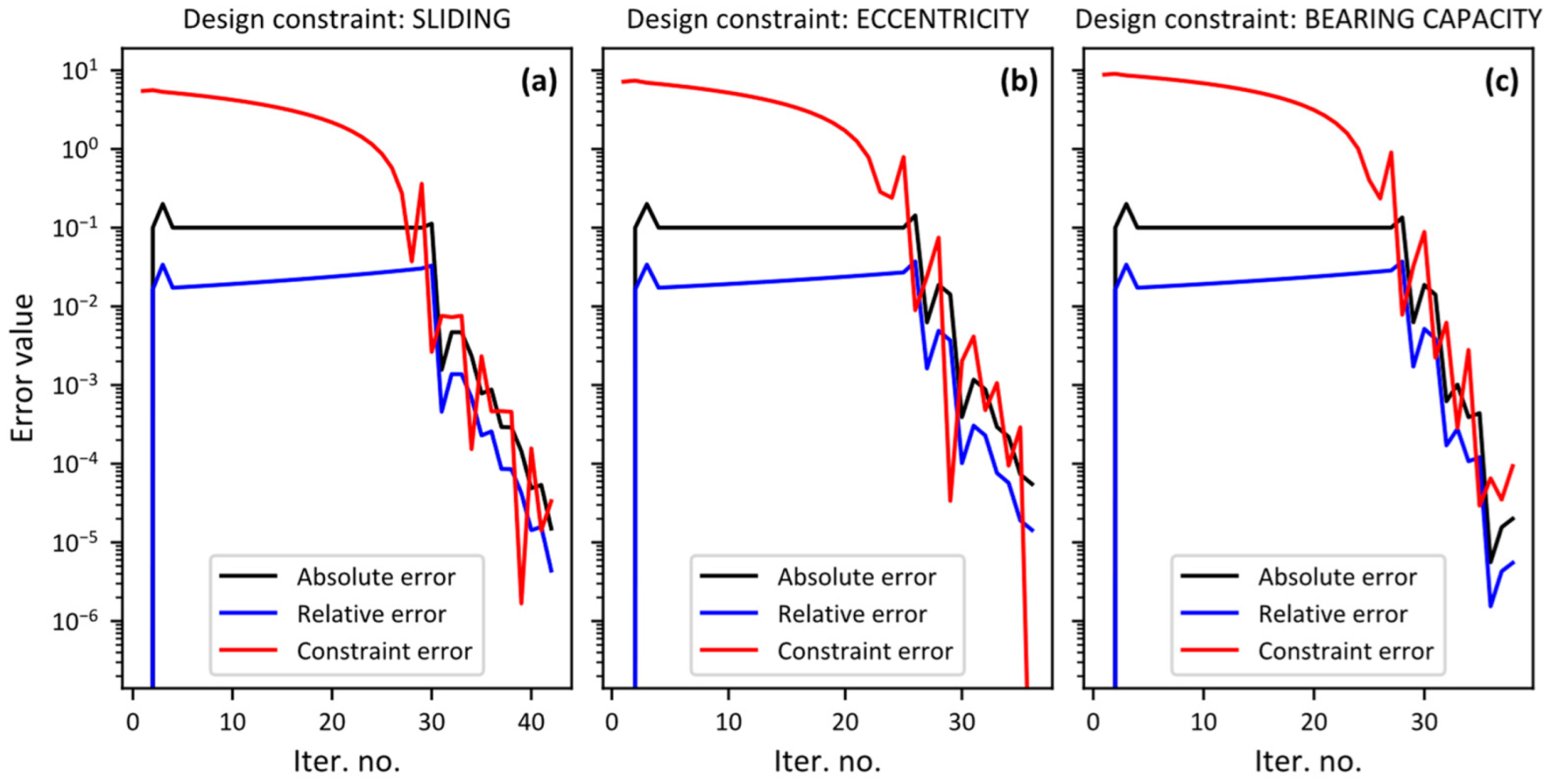
- Optimal 1 is the optimized solution for limit state of sliding (i.e., ). Figure 4a shows the convergence of cost function. From the optimal 1 solution, reliability indices , for other limit states (i.e., overturning and bearing capacity failures, respectively) are calculated. It is noted that both and are less than , therefore, this scenario does not satisfy all reliability constraints (i.e., all ) and thus design requirements.
- Optimal 2 is the optimized solution for limit state of eccentricity (i.e., ). Figure 4b shows the convergence of cost function. From optimal 2 solution, reliability indices , for other limit states are calculated. In this case, all reliability constraints (i.e., all ) and design requirements are satisfied.
- Optimal 3 is the optimized solution for limit state of bearing capacity (i.e., ). Figure 4c shows the convergence of the cost function. From this optimal solution, reliability indices , for other limit states are calculated. It is noted that is less than , therefore, this solution also does not satisfy all reliability constraints (i.e., all ) and thus design requirements.
| Optimal Scenario | Design Constraint | Reliability Index | Remarks | |||||
|---|---|---|---|---|---|---|---|---|
| L (m) | C(d) (m2) | |||||||
| Optimal 1 | Sliding | 3.412 | 20.470 | 0.569 | 3.000 | 0.442 | 1.473 | All |
| Optimal 2 | Eccentricity | 3.845 | 23.069 | 0.641 | 4.271 | 3.000 | 4.272 | All |
| Optimal 3 | Bearing Capacity | 3.636 | 21.816 | 0.606 | 3.684 | 1.839 | 3.000 | All |
4. Conclusions
- 1.
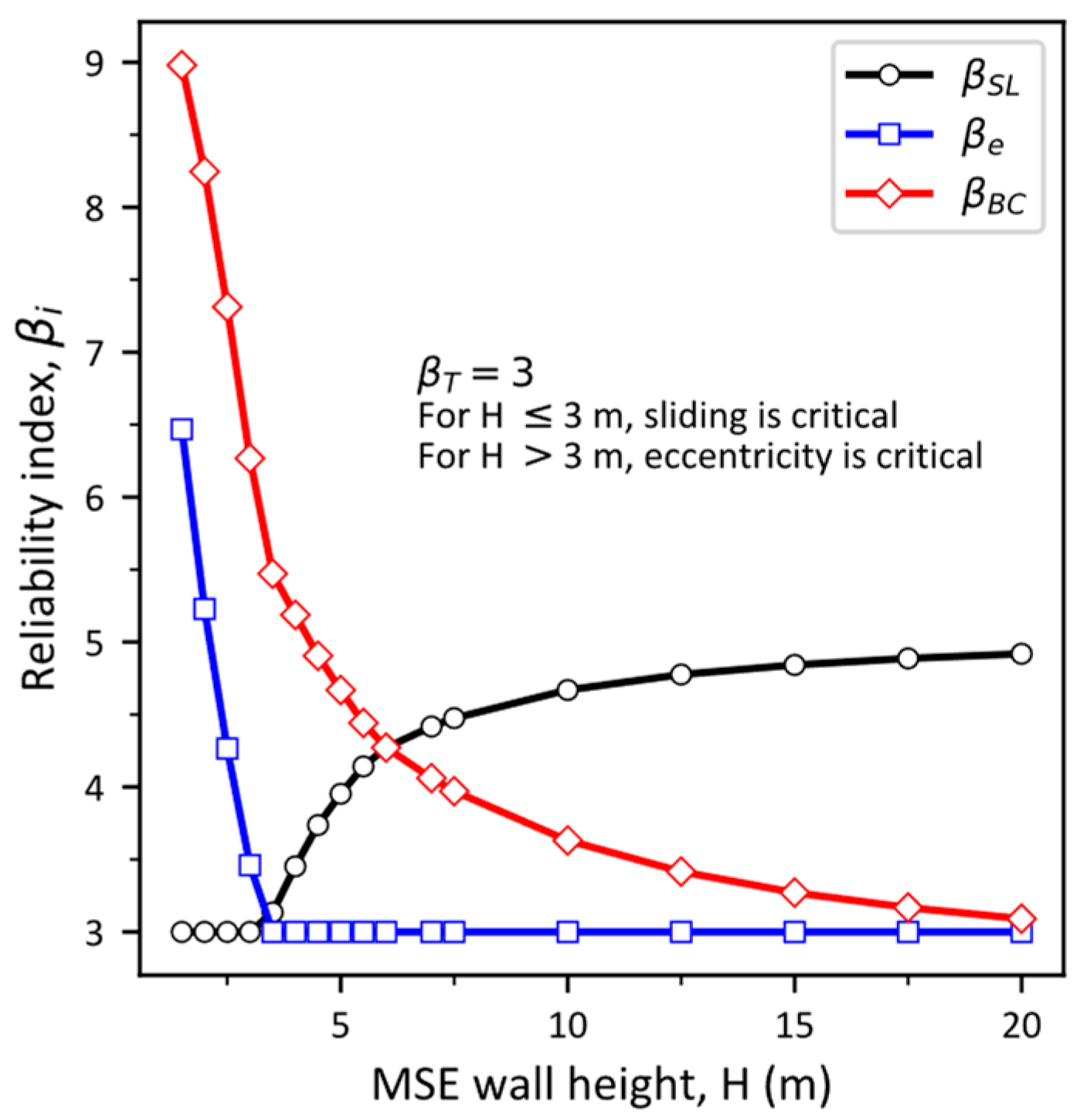
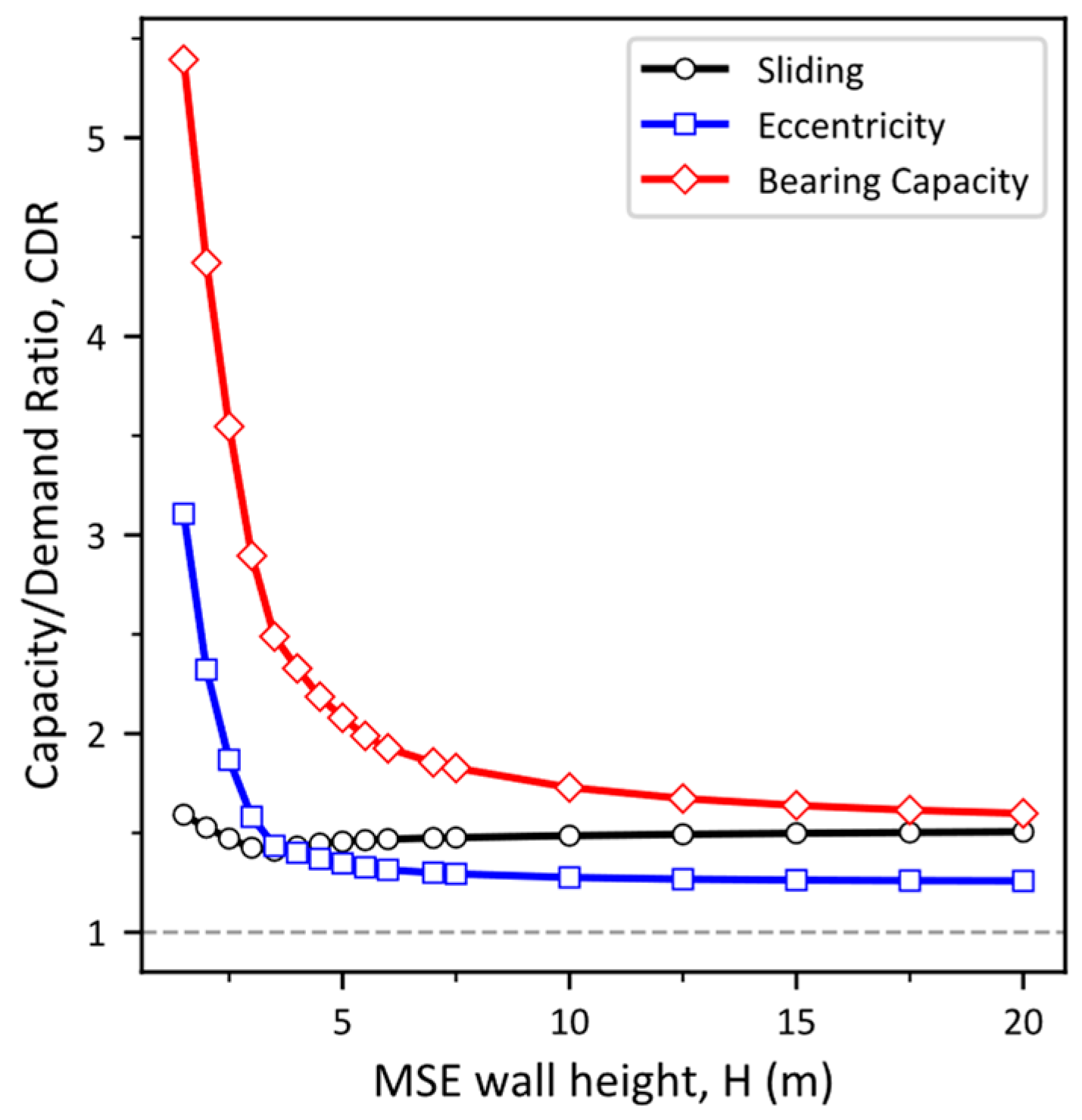
- At the low height of the MSE wall (i.e., m), the influence of live traffic surcharge, , is dominant (due to high values recommended by AASHTO), making sliding as the governing limit state. The influence of traffic surcharge decreases with the increase in the MSE wall height. For m, eccentricity is the governing limit state.
- 2.
- The influence of reinforced-fill unit weight, , increases with the increase in the MSE wall height and is prominent when the limit state of eccentricity governs the design.
- 3.
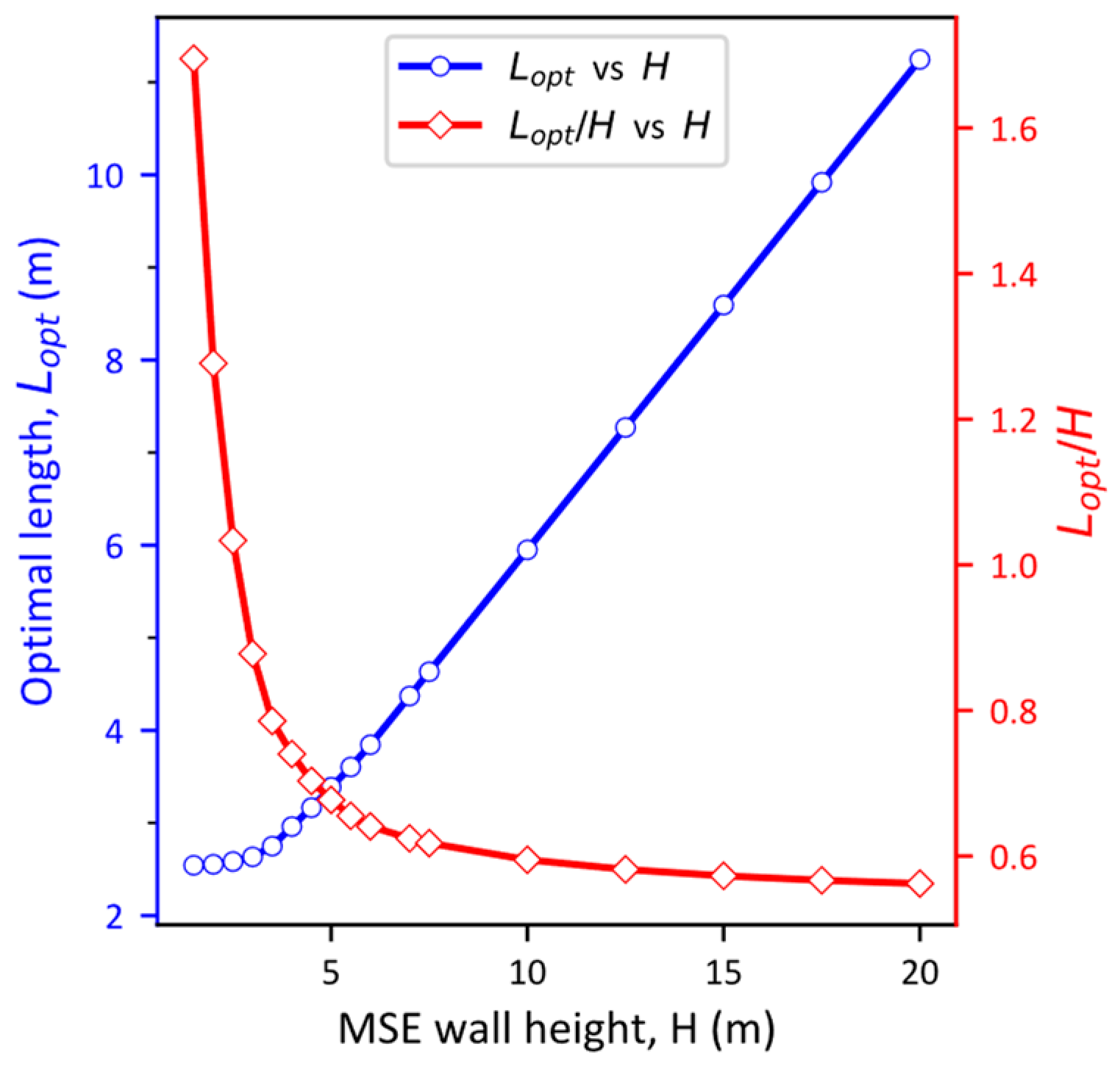
- For m, length to height ratio of the optimized solution, , is greater than 0.7 (minimum requirement of AASHTO), and then it decreases below the minimum required value of 0.7 for m.
- 4.
- If is kept as 0.7, as per AASHTO’s requirement, for m, the actual reliability index of the design will be well above the target reliability index of 3.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Casagrande, A. Role of the Calculated Risk in Earthwork and Foundation Engineering. J. Soil Mech. Found. Div. ASCE 1965, 91, 1–40. [Google Scholar] [CrossRef]
- Christian, J.T. Geotechnical Engineering Reliability: How Well Do We Know What We Are Doing? J. Geotech. Geoenviron. Eng. 2004, 130, 985–1003. [Google Scholar] [CrossRef]
- Phoon, K.K.; Kulhawy, F.H. Characterization of geotechnical variability. Can. Geotech. J. 1999, 36, 612–624. [Google Scholar] [CrossRef]
- Phoon, K.-K. Reliability-Based Design in Geotechnical Engineering: Computations and Applications; Taylor & Francis: London, UK; New York, NY, USA, 2008; ISBN 9780415396301 0415396301 9780203934241 (e-book) 0203934245 (e-book). [Google Scholar]
- Phoon, K.-K.; Ching, J. Risk and Reliability in Geotechnical Engineering; Phoon, K.-K., Ching, J., Eds.; CRC Press: Boca Raton, FL, USA, 2015; ISBN 9781482227215. [Google Scholar]
- Whitman, R. V Organizing and evaluating uncertainty in geotechnical engineering. J. Geotech. Geoenviron. Eng. ASCE 2000, 126, 583–593. [Google Scholar] [CrossRef]
- Phoon, K.-K.; Kulhawy, F.H. Evaluation of geotechnical property variability. Can. Geotech. J. 1999, 36, 625–639. [Google Scholar] [CrossRef]
- Baecher, G.B.; Christian, J.T. Reliability and Statistics in Geotechnical Engineering; John Wiley and Sons: Hoboken, NJ, USA, 2003; ISBN 9780471498339. [Google Scholar]
- Ang, A.H.-S.; Tang, W.H. Probability Concepts in Engineering: Emphasis on Applications in Civil Environmental Engineering, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2007; ISBN 9780471720645. [Google Scholar]
- Valdebenito, M.A.; Schuëller, G.I. A survey on approaches for reliability-based optimization. Struct. Multidiscip. Optim. 2010, 42, 645–663. [Google Scholar] [CrossRef]
- Sayed, S.; Dodagoudar, G.R.; Rajagopal, K. Reliability analysis of reinforced soil walls under static and seismic forces. Geosynth. Int. 2008, 15, 246–257. [Google Scholar] [CrossRef]
- Basha, B.M.; Babu, G.L.S. Target reliability based design optimization of anchored cantilever sheet pile walls. Can. Geotech. J. 2008, 45, 535–548. [Google Scholar] [CrossRef]
- Babu, G.L.S.; Basha, B.M. Optimum design of cantilever sheet pile walls in sandy soils using inverse reliability approach. Comput. Geotech. 2008, 35, 134–143. [Google Scholar] [CrossRef]
- Basha, B.M.; Babu, G.L.S. Optimum Design for External Seismic Stability of Geosynthetic Reinforced Soil Walls: Reliability Based Approach. J. Geotech. Geoenviron. Eng. 2010, 136, 797–812. [Google Scholar] [CrossRef]
- Chalermyanont, T.; Benson, C.H. Reliability-Based Design for External Stability of Mechanically Stabilized Earth Walls. Int. J. Geomech. 2005, 5, 196–205. [Google Scholar] [CrossRef]
- Yang, K.-H.; Ching, J.; Zornberg, J.G. Reliability-Based Design for External Stability of Narrow Mechanically Stabilized Earth Walls: Calibration from Centrifuge Tests. J. Geotech. Geoenviron. Eng. 2011, 137, 239–253. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, L.M.; Tang, W.H. Reliability-Based Optimization of Geotechnical Systems. J. Geotech. Geoenviron. Eng. 2011, 137, 1211–1221. [Google Scholar] [CrossRef]
- Zhao, H.; Zhao, M.; Zhu, C. Reliability-based optimization of geotechnical engineering using the artificial bee colony algorithm. KSCE J. Civ. Eng. 2016, 20, 1728–1736. [Google Scholar] [CrossRef]
- Santos, M.G.C.; Silva, J.L.; Beck, A.T. Reliability-based design optimization of geosynthetic-reinforced soil walls. Geosynth. Int. 2018, 25, 442–455. [Google Scholar] [CrossRef]
- Mahmood, Z. Reliability-based optimization of geotechnical design using a constrained optimization technique. SN Appl. Sci. 2020, 2, 168. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.C.; Liu, C.N.; Lin, B.H. Reliability based design for deformation targeted segment mechanically stabilized earth wall. J. Geoengin. 2020, 15, 1–11. [Google Scholar] [CrossRef]
- Anderson, P.L.; Brabant, K. Increased Use of MSE Abutments. In Proceedings of the 22nd Annual International Bridge Conference, Pittsburg, PA, USA, 13–15 June 2005; Engineers Society of Western Pennsylvania (ESWP): Pittsburgh, PA, USA; pp. 375–382. [Google Scholar]
- Kim, D.; Salgado, R. Load and Resistance Factors for External Stability Checks of Mechanically Stabilized Earth Walls. J. Geotech. Geoenviron. Eng. 2012, 138, 241–251. [Google Scholar] [CrossRef]
- AASTHO. LRFD Bridge Design Spesifications; TRID: Grapevine, TX, USA, 2014; ISBN 0003-4932. [Google Scholar]
- Baecher, G.B. Geotechnical Risk Analysis User’s Guide, FHWA-RD-87-011; ROSAP: McLean, VA, USA, 1987. [Google Scholar]
- Chalermyanont, T.; Benson, C.H. Reliability-Based Design for Internal Stability of Mechanically Stabilized Earth Walls. J. Geotech. Geoenviron. Eng. 2004, 130, 163–173. [Google Scholar] [CrossRef]
- Open TURNS Open Treatment of Uncertainties, Risk’s aNd Statistics, An Open Source Source Platform. Available online: https://www.researchgate.net/publication/29605221_OpenTURNS_an_Open_Source_initiative_to_Treat_Uncertainties_Risks′N_Statistics_in_a_structured_industrial_approach (accessed on 12 March 2022).
- Baudin, M.; Dutfoy, A.; Iooss, B.; Popelin, A.-L. OpenTURNS: An Industrial Software for Uncertainty Quantification in Simulation. In Handbook of Uncertainty Quantification; Ghanem, R., Higdon, D., Owhadi, H., Eds.; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-11259-6. [Google Scholar]
- Hasofer, A.M.; Lind, N.C. An exact and invariant second-moment code format. J. Eng. Mech. Div. 1974, 100, 111–121. [Google Scholar] [CrossRef]
- Liu, P.L.; Der Kiureghian, A. Multivariate distribution models with prescribed marginals and covariances. Probabilistic Eng. Mech. 1986, 1, 105–112. [Google Scholar] [CrossRef]
- Hohenbichler, M.; Rackwitz, R. NON-NORMAL DEPENDENT VECTORS IN STRUCTURAL SAFETY. ASCE J. Eng. Mech. Div. 1981, 107, 1227–1238. [Google Scholar] [CrossRef]
- Lu, Z.H.; Cai, C.-H.; Zhao, Y.-G. Structural Reliability Analysis Including Correlated Random Variables Based on Third-Moment Transformation. J. Struct. Eng. 2017, 143, 04017067. [Google Scholar] [CrossRef]
- Lu, Z.H.; Cai, C.H.; Zhao, Y.G.; Leng, Y.; Dong, Y. Normalization of correlated random variables in structural reliability analysis using fourth-moment transformation. Struct. Saf. 2020, 82, 101888. [Google Scholar] [CrossRef]
- Low, B.K.; Tang, W.H. Efficient Spreadsheet Algorithm for First-Order Reliability Method. J. Eng. Mech. 2007, 133, 1378–1387. [Google Scholar] [CrossRef]
- Youn, B.D.; Choi, K.K.; Du, L. Adaptive probability analysis using an enhanced hybrid mean value method. Struct. Multidiscip. Optim. 2005, 29, 134–148. [Google Scholar] [CrossRef]
- Powell, M.J.D. A Direct Search Optimization Method That Models the Objective and Constraint Functions by Linear Interpolation. In Advances in Optimization and Numerical Analysis; Gomez, S., Hennart, J., Eds.; Springer: Dordrecht, The Netherlands, 1994; pp. 51–67. [Google Scholar]
- Powell, M.J.D. Direct search algorithms for optimization calculations. Acta Numer. 1998, 7, 287–336. [Google Scholar] [CrossRef]
- Ingold, T.S. Reinforced Earth; Thomas Telford Limited: London, UK, 1982. [Google Scholar]
- Vesic, A.S. Analysis of ultimate loads of shallow foundations. ASCE J. Soil Mech. Found. Div. 1973, 99, 45–73. [Google Scholar] [CrossRef]
- Hummit, G.M. Statistical Analysis of Data from a Comparative Laboratory Test Program Sponsored by ACIL; No. AEWES-Misc Paper-4-785; U.S. Army Engineer Waterways Experiment Station Vicksburg Ms Geotechnical Lab: Vicksburg, MS, USA, 1966. [Google Scholar]
- Foye, K.C.; Salgado, R.; Scott, B. Assessment of Variable Uncertainties for Reliability-Based Design of Foundations. J. Geotech. Geoenviron. Eng. 2006, 132, 1197–1207. [Google Scholar] [CrossRef]
- Wolff, T.F. Evaluating the Reliability of Existing Levees, Technical Report; U.S. Army Engineer Waterways Experiment Station Geotechnical Laboratory: Vicksburg, MS, USA, 1994. [Google Scholar]
- Lacroix, Y.; Horn, H.M. Direct Determination and Indirect Evaluation of Relative Density and Its Use on Earthwork Construction Projects. In Evaluation of Relative Density and its Role in Geotechnical Projects Involving Cohesionless Soils; Selig, E.T., Ladd, R.S., Eds.; ASTM International: West Conshohocken, PA, USA, 1973; pp. 251–280. ISBN 978-0-8031-5534-3. [Google Scholar]
- Munwar Basha, B.; Sivakumar Babu, G.L. Reliability assessment of internal stability of reinforced soil structures: A pseudo-dynamic approach. Soil Dyn. Earthq. Eng. 2010, 30, 336–353. [Google Scholar] [CrossRef]
- Negussey, D.; Wijewickreme, W.K.D.; Vaid, Y.P. Constant-volume friction angle of granular materials. Can. Geotech. J. 1988, 25, 50–55. [Google Scholar] [CrossRef]
- Verdugo, R.; Ishihara, K. The Steady State of Sandy Soils. Soils Found. 1996, 36, 81–91. [Google Scholar] [CrossRef] [Green Version]
- Low, B.K. Reliability-based design applied to retaining walls. Geotechnique 2005, 55, 63–75. [Google Scholar] [CrossRef]


| Load Factor | Description | Value and Its Description | |
|---|---|---|---|
| Vertical pressure from dead load of earth fill | 1.00 1.35 | For sliding & eccentricity For bearing capacity | |
| Horizontal earth load | 1.50 1.50 | For sliding & eccentricity For bearing capacity | |
| Vertical pressure from live surcharge load | 1.75 | For bearing capacity | |
| Horizontal pressure from live surcharge load | 1.75 | For sliding, eccentricity & bearing capacity | |
| Resistance Factor | Description | Value |
|---|---|---|
| Sliding resistance | 1.0 | |
| Bearing resistance | 0.65 |
| MSE Wall Height H (m) | heq (m) | |
|---|---|---|
| 1.5 | 1.2 | 24 |
| 3.0 | 0.9 | 18 |
| ≥6.0 | 0.6 | 12 |
| MSE Wall Height H (m) | heq (m) | |
|---|---|---|
| Distance from Wall Backface to Edge of Traffic = 0 m | Distance from Wall Backface to the Edge of Traffic ≥ 0.3 m | |
| 1.5 | 1.5 | 0.6 |
| 3.0 | 1.05 | 0.6 |
| ≥6.0 | 0.6 | 0.6 |
| MSE Wall Height H (m) | heq (m) | q a (kN/m) |
|---|---|---|
| 1.5 | 1.20 | 24 |
| 2.0 | 1.09 | 21.8 |
| 2.5 | 0.99 | 19.8 |
| 3.0 | 0.90 | 18 |
| 3.5 | 0.82 | 16.4 |
| 4.0 | 0.76 | 15.2 |
| 4.5 | 0.70 | 14 |
| 5.0 | 0.66 | 13.2 |
| 5.5 | 0.62 | 12.4 |
| ≥6.0 | 0.60 | 12 |
| Variable | Distribution | Mean | COV | Std. Dev. |
|---|---|---|---|---|
| (o) | Lognormal | 36 | 0.025 | 0.9 |
| (kN/m3) | Normal | 20 | 0.050 | 1 |
| (o) | Lognormal | 30 | 0.025 | 0.75 |
| (kN/m3) | Normal | 18 | 0.050 | 0.9 |
| (o) | Lognormal | 33 | 0.025 | 0.825 |
| (kN/m3) | Normal | 18 | 0.050 | 0.9 |
| q (kN/m2) | Lognormal | varies | 0.2 | varies |
| State | Reliability Index | |||||
|---|---|---|---|---|---|---|
| L (m) | C(d) (m2) | |||||
| Initial | 6 | 36 | 1 | 8.458 | 10.167 | 11.812 |
| Optimized | 3.845 | 23.069 | 0.641 | 4.271 | 3.000 | 4.272 |
| Reliability Index | Critical Limit State | ||||
|---|---|---|---|---|---|
| 1.5 | 3 | 6.468 | 8.98 | SL | 1.695 |
| 2 | 3 | 5.228 | 8.246 | SL | 1.277 |
| 2.5 | 3 | 4.265 | 7.312 | SL | 1.033 |
| 3 | 3 | 3.461 | 6.268 | SL | 0.878 |
| 3.5 | 3.134 | 3 | 5.472 | e | 0.786 |
| 4 | 3.452 | 3 | 5.188 | e | 0.740 |
| 4.5 | 3.737 | 3 | 4.905 | e | 0.703 |
| 5 | 3.953 | 3 | 4.669 | e | 0.677 |
| 5.5 | 4.142 | 3 | 4.442 | e | 0.655 |
| 6 | 4.271 | 3 | 4.272 | e | 0.641 |
| 7 | 4.417 | 3 | 4.061 | e | 0.624 |
| 7.5 | 4.475 | 3 | 3.971 | e | 0.618 |
| 10 | 4.669 | 3 | 3.631 | e | 0.595 |
| 12.5 | 4.776 | 3 | 3.416 | e | 0.582 |
| 15 | 4.842 | 3 | 3.271 | e | 0.573 |
| 17.5 | 4.887 | 3 | 3.168 | e | 0.567 |
| 20 | 4.919 | 3 | 3.091 | e | 0.562 |
| H (m) | ||
|---|---|---|
| 1.5 | 1.695 | 3 |
| 2 | 1.277 | 3 |
| 2.5 | 1.033 | 3 |
| 3 | 0.878 | 3 |
| 3.5 | 0.786 | 3 |
| 4 | 0.740 | 3 |
| 4.5 | 0.703 | 3 |
| 5 | 0.7 | 3.595 |
| 5.5 | 0.7 | 4.230 |
| 6 | 0.7 | 4.701 |
| 7 | 0.7 | 5.292 |
| 7.5 | 0.7 | 5.549 |
| 10 | 0.7 | 6.470 |
| 12.5 | 0.7 | 6.858 |
| 15 | 0.7 | 7.105 |
| 17.5 | 0.7 | 7.274 |
| 20 | 0.7 | 7.397 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmood, Z.; Qureshi, M.U.; Memon, Z.A.; Imran Latif, Q.B.a. Ultimate Limit State Reliability-Based Optimization of MSE Wall Considering External Stability. Sustainability 2022, 14, 4968. https://doi.org/10.3390/su14094968
Mahmood Z, Qureshi MU, Memon ZA, Imran Latif QBa. Ultimate Limit State Reliability-Based Optimization of MSE Wall Considering External Stability. Sustainability. 2022; 14(9):4968. https://doi.org/10.3390/su14094968
Chicago/Turabian StyleMahmood, Zafar, Mohsin Usman Qureshi, Zubair Ahmed Memon, and Qadir Bux alias Imran Latif. 2022. "Ultimate Limit State Reliability-Based Optimization of MSE Wall Considering External Stability" Sustainability 14, no. 9: 4968. https://doi.org/10.3390/su14094968
APA StyleMahmood, Z., Qureshi, M. U., Memon, Z. A., & Imran Latif, Q. B. a. (2022). Ultimate Limit State Reliability-Based Optimization of MSE Wall Considering External Stability. Sustainability, 14(9), 4968. https://doi.org/10.3390/su14094968








