Damage Mechanism and Stress Distribution of Gypsum Rock Pillar Subjected to Blasting Disturbance

Abstract

The room-pillar mining technology of underground gypsum resources results in numerous gypsum rock pillars for controlling and supporting mined gobs, which forms a large area of roof hanging gobs. Owing to weathering and mining activities, gypsum rock pillar damage and failure will occur, thereby inducing a large area of gypsum mined-gob collapse accidents and disasters. Blasting is vital to the stability of gypsum rock pillars and is indispensable in mining engineering. Based on field blasting tests and using wave velocity as the basic parameter to characterise the integrity of gypsum rock, the damage mechanism of gypsum rock pillars subjected to blasting disturbance is investigated. With ten blasting tests, the maximum damage rate is 7.82% along the horizontal direction of pillar, and 3.52% along the vertical direction. The FLAC numerical simulation calculation software is used to analyse the stress distribution law of gypsum rock pillars with disturbances of different strengths from different distances. As the disturbance strength increased, the stress increased with no clear linear relationship; as the disturbance distance increased, the stress decreased gradually with a linear relationship. All stress after disturbance is greater than the original static stress, and lower than the ultimate compressive strength. However, the correlation between blasting tests results and numerical simulation results is poor and is discussed for many factors. The results can provide important guidance and reference for clarifying the damage mechanism of gypsum rock pillars subjected to blasting disturbance, as well as reveal the collapse mechanism of gypsum mined gobs.

1. Introduction

Gypsum is an indispensable mineral resource in the fields of civil and construction engineering; additionally, mining intensity continues to increase annually. Room-pillar and strip-mining technologies are the main methods for underground gypsum resource mining. These technologies involve numerous gypsum rock pillars for supporting and controlling the mined space, which forms a large area of roof hanging gobs. According to incomplete statistics, a gypsum mine gob in Shandong Province, China, measures as high as 2.5 million square meters and has become a serious issue in gypsum resource mining [1,2]. The stability of gypsum rock pillars directly determines the stability of large gypsum mined gobs. Blasting, as an indispensable process in mining engineering, mostly causes damage to gypsum rock pillars, thereby resulting in the failure of gypsum rock pillars and inducing gypsum mined gob collapse accidents [3].

Scholars have extensively investigated the effect of blasting disturbance damage on rock mass and obtained important results. Based on a dynamic finite element program, the rock damage mechanism of blasting excavation in deep buried tunnels and the corresponding control measures have been investigated and proposed, respectively [4,5]. By performing numerical simulation and similar simulation tests, the propagation law of blasting stress waves in the coal-rock structural zone was revealed [6]. A Hoek–Brown damage model considering cyclic blasts was established, and practical engineering applications were investigated to prove the practicability of the model in the field [7,8]. Based on numerical simulations, the cumulative damage effect of cyclic blasting to rocks was revealed [9,10]. Meanwhile, using advanced technologies, such as geological radar, an experiment was conducted to investigate the damage mechanism of blasting to surrounding rocks during tunnel excavation; subsequently, images of damage to the surrounding rocks were obtained [11,12]. Using the acoustic wave testing method, an experiment was conducted to investigate the cumulative damage mechanism of the slope and surrounding rock under multiple blasting disturbances [13]. A rock mass blasting cumulative damage model was established based on the decreasing sound velocity rate of rock, and it was then modified based on field tests [14]. Additionally, scholars have conducted extensive research regarding the damage to rock due to blasting disturbance using different research methods [15,16].

The physical and mechanical properties of gypsum rocks differ significantly to those of other rocks, e.g., their easy weathering and typical creep characteristics [17,18,19]. Currently, research pertaining to blasting and disturbance damage to gypsum rocks is limited. Based on previous research findings as well as blasting vibration testing technology, damage to gypsum rock pillars subjected to multiple blasting disturbances was investigated via field tests. A numerical calculation model of a gypsum mined gob with disturbances was constructed to analyse the stress distribution and evolution law of gypsum rock pillars based on different disturbance strengths at different distances.

Gypsum mine gob collapse accident caused by disturbance is a huge threat to gypsum mining. This paper will with a blasting test reveal the damage mechanism of gypsum pillar and analyse stress distribution via numerical simulation. Compared with current literature, the research content is innovation and uniqueness. The results can provide guidance and reference for clarifying the damage mechanism of gypsum rock pillars subjected to blasting disturbance, as well as reveal the mechanism of gypsum mined-gob collapse.

2. Gypsum Rock Damage with Blasting

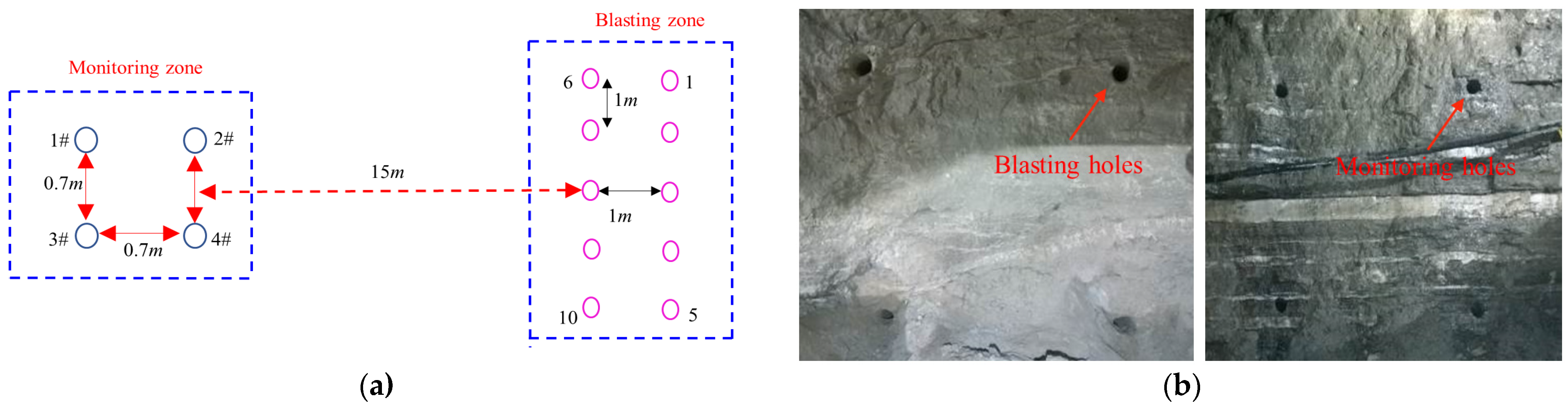
2.1. Test Design

The uniaxial compressive strength is the most effective and direct parameter for characterising rock damage and failure. However, it is difficult to characterise the degree of rock damage continuously based on multiple blasting disturbance tests. In a previous study [20], it was reported that the wave velocity can be used to characterise the integrity and damage degree of rock mass, while affording advantages of simplicity, high speed, and zero loss. Therefore, during the blasting tests, the wave velocity of the gypsum rock pillar was used to characterise the degree of damage.

The Luneng underground gypsum mine, which is located in Shandong Province, China, is mined using room-pillar mining technology. The mining technical parameters are as follow: room length, 4 m; pillar length, 4 m; mining height, 4 m; width of isolated gypsum pillar, 10–15 m. During testing using RMS acoustic wave analysis software, a blasting vibration recorder, an acoustic wave tester, and other equipment, the wave velocity of the gypsum rock pillar before and after each blasting test was obtained to analyse the damage mechanism of gypsum rock subjected to blasting disturbance.

2.2. Testing Parameter

The gypsum rock pillar (40 m (length) × 15 m (width) × height (4 m)) tested was a strip-shaped isolated pillar exhibiting continuity and integrity. The horizontal distance from the blasting zone to the wave velocity monitoring zone was 15 m. Ten blasting holes were established in two rows in the blasting zone. The diameter, depth, and interval distance of the blasting hole were 40 mm, 2.5 m, and 1 m, respectively. Rock emulsion explosive #2 (φ32 mm × 200 g) was used, and five cartridges were charged in a single blasting hole. To prevent blasting hole collapse, and the effects of multiple blasting tests, drilling, charging, and blasting were performed in the single-hole mode. The blasting sequence was from blasting holes #1 to #10. As shown in Figure 1, four monitoring holes (diameter of 40 mm) were arranged in the monitoring zone at a depth of 2.5 m; the diameter of wave velocity monitoring probe was 18 mm, and the interval distance of the monitoring holes was 0.7 m.

Before and after each blasting test, the wave velocity of any two monitoring holes at intervals of 0.5 m along the depth of the hole was measured. For example, between monitoring holes #1 and #3, the monitoring section was Sections 1–3. To compare the difference in wave velocity before and after the blasting test, the initial wave velocity of each section along the depth direction of the monitoring holes was measured before the blasting test, as shown in Figure 2.

3. Results

Wave velocity of the gypsum rock pillar in different depth was measured with the number of blasting tests increased. Thereby, wave velocity change and damage degree of the gypsum rock pillar were investigated.

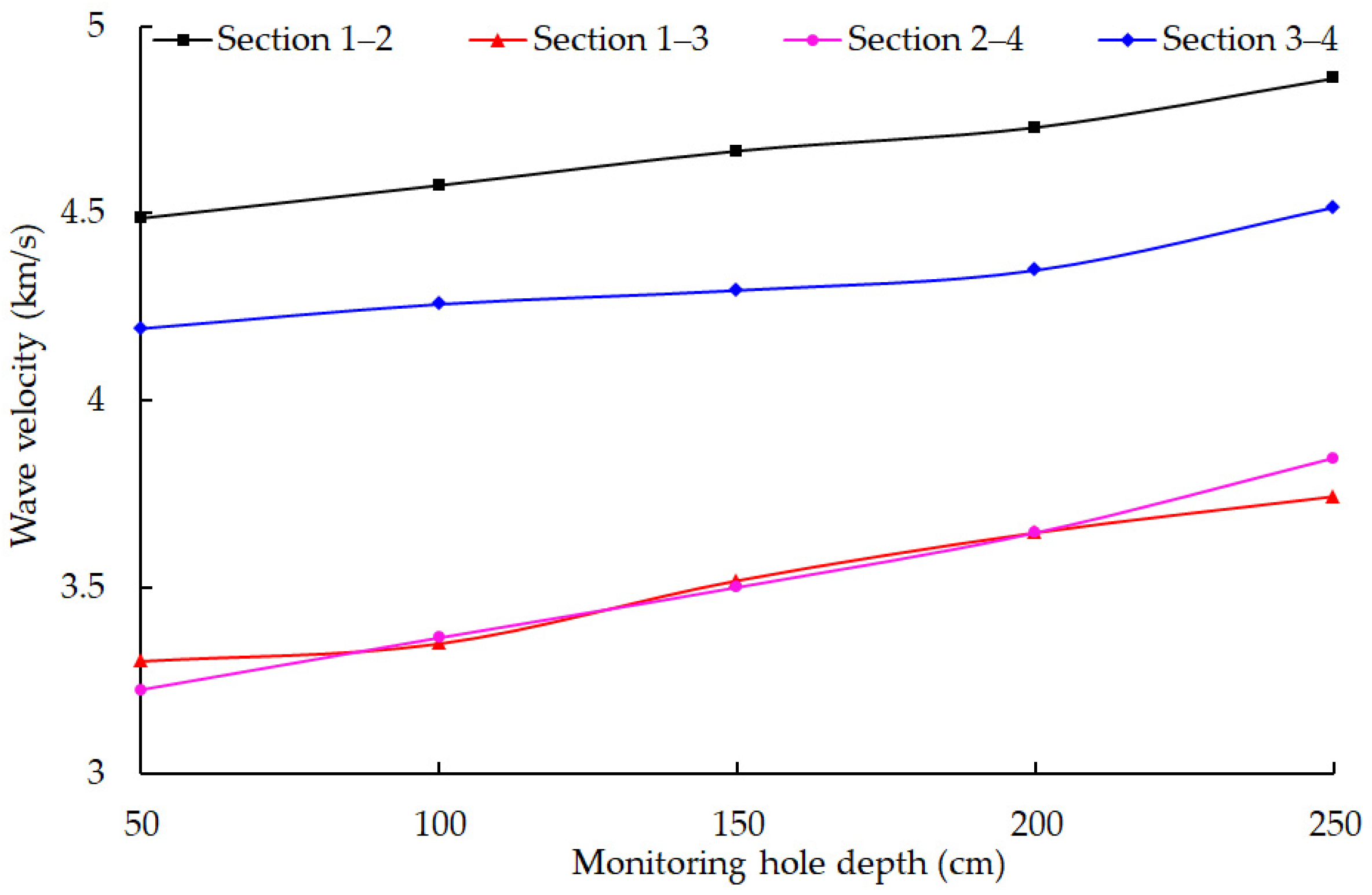
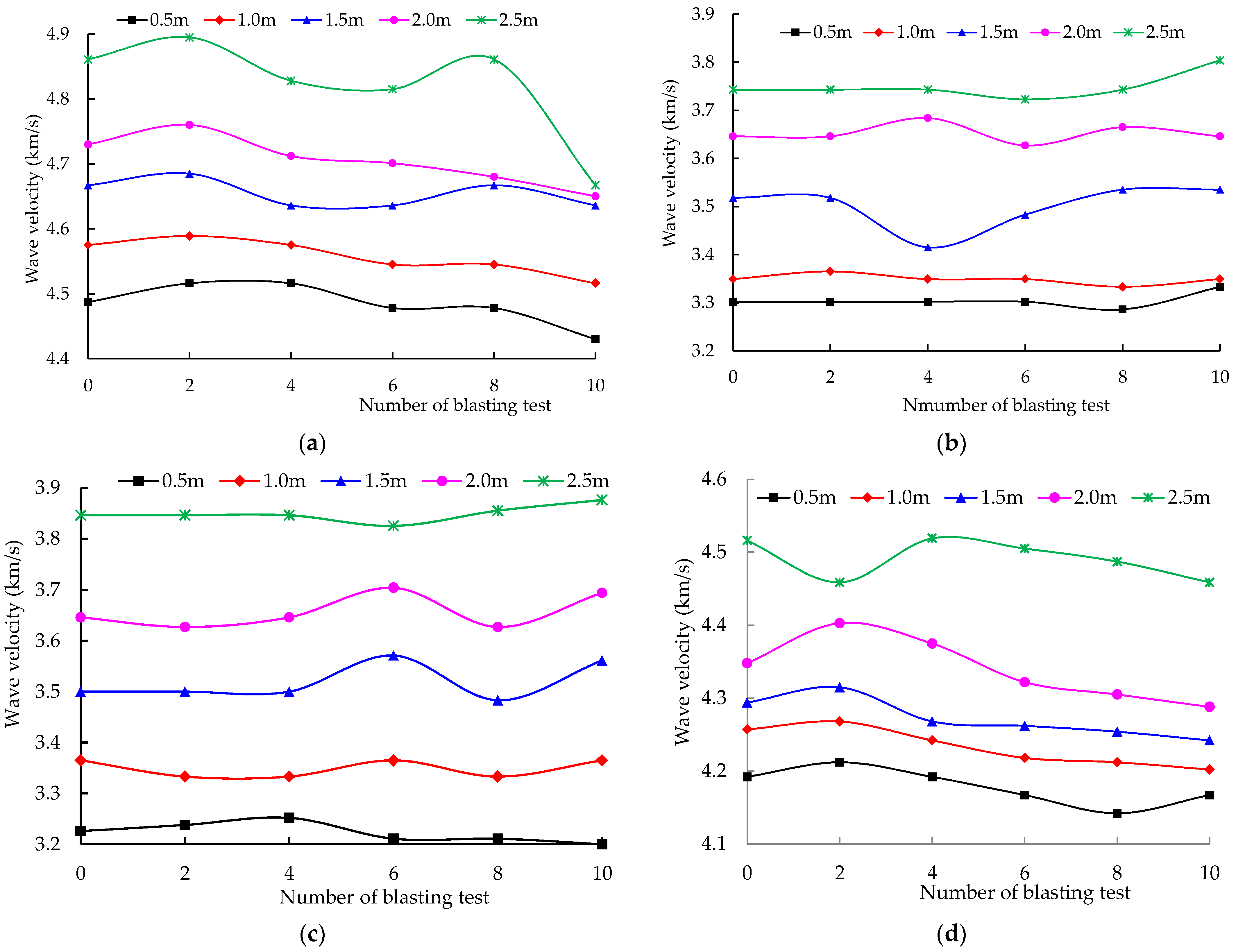
3.1. Wave Velocity Change

As the number of blasting tests increased, the change in the wave velocity for each monitoring section is as shown in Figure 3.

Owing to blasting, the wave velocity of each section indicated clear fluctuations. However, the change for different sections was different, as follows:

(1)

As the number of blasting tests increased, the wave velocity of Sections 1–4 in the horizontal direction decreased in general. The vertical wave velocity of Sections 1–4 fluctuated within a certain range in the early stage of the blasting stage; however, it increased slightly in the later stage of the blasting test. The increase or decrease in the wave velocity of each section indicated fluctuation, and the fluctuating range of the vertical section was greater than that of the horizontal section; however, the wave velocity change did not indicate a clear linear relationship as the number of blasting tests increased.

(2)

The wave velocity of the horizontal section increased, within several previous tests (3–4 times), which was primarily due to the closure and compaction of internal microstructures of gypsum rocks caused by blasting disturbance, and the integrity of gypsum rock improved. The vertical monitoring section did not indicate this feature.

(3)

As the depth of the monitoring holes increased, the wave velocity reduction range of the horizontal section increased in general, although fluctuations were observed as well. The wave velocity of the vertical section as the depth of the monitoring holes increased fluctuated significantly and did not exhibit regularity.

3.2. Damage Degree

The damage effect of blasting disturbance on gypsum rocks cannot be analysed intuitively based on only the wave velocity. Using the initial wave velocity before the blasting test of each monitoring section, the damage degree of gypsum rocks at different depths of each section with different blasting times can be analysed. According to previous results [21,22],

$$D=1-K=1-{(\frac{{\upsilon }_n}{{\upsilon }_0})}^2$$

(1)

where D is the damage degree of gypsum rocks caused by blasting disturbance, K is the integrity factor of gypsum rocks, ${\upsilon }_n$ is the wave velocity of each section after the nth blasting test (m/s), and ${\upsilon }_0$ is the initial wave velocity of each monitoring section (m/s).

As the number of blasting tests increased, the damage rate of gypsum rocks in each section at different depths is as shown in Figure 4.

The change in the damage degree of each section shows the same trend as the change in the overall wave velocity. In particular, the degree of damage in the horizontal direction of the gypsum rock pillar increased, with a maximum damage rate of 7.82%. However, the first three to four blasting tests showed a negative increase, with a maximum negative increase of 2.55%. As the depth increased, the damage degree increased in general, but with significant fluctuations. The degree of damage in the vertical direction of the gypsum rock pillar did not exhibit regularity. Finally, it indicated negative growth with a maximum value of 3.52%, which is significantly smaller than that in the horizontal direction, indicating that the degree of damage to the gypsum pillar in the horizontal direction was greater than that in the vertical direction due to blasting disturbance.

The blasting strength during the test, i.e., the amount of charge at one time, was significantly less than that during the entire field blasting, and the number of blasting tests was only 10, which is significantly less than the actual number of on-site blasts (thousands of times); meanwhile, the maximum damage rate of the gypsum rock pillar reached 7.82%. This proves that blasting significantly damaged the gypsum rock, which is an important factor that causes the failure of gypsum rock pillars and the collapse of gypsum mined gobs [23,24].

4. Stress Distribution and Evolution of Gypsum Rock Pillars Subjected to Disturbances

Owing to the different disturbance strengths and distances, the stress distribution and evolution of gypsum rock pillars are crucial for investigating the damage and failure mechanism of gypsum rock pillars, as well as for revealing the collapse mechanism of gypsum mined gobs. Considering the significant amount of effort required in field blasting tests, and because testing parameters cannot be continuously changed and controlled, based on the dynamic analysis and calculation function of the FLAC numerical simulation software, a numerical calculation model of a gypsum mined gob subjected to disturbance was established to analyse the stress distribution and evolution of gypsum rock pillars.

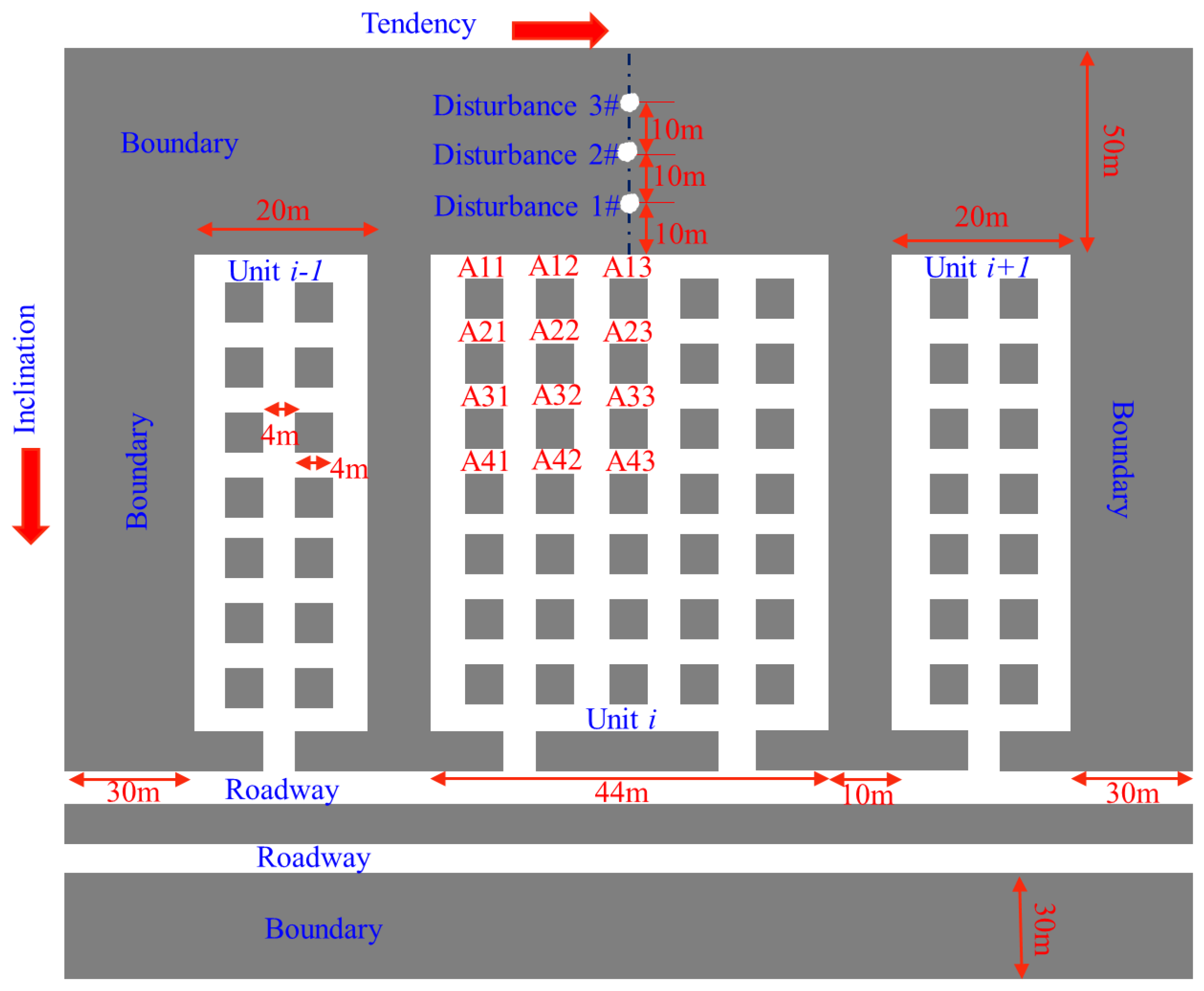
4.1. Numerical Simulation Calculation Model

(1) Simulation parameters

The parameters of the numerical calculation model of a gypsum mined gob subjected to disturbance used in this study were as follows: room and pillar measurements are 4 m × 4 m × 4 m; unit inclination length, 60 m; tendency length, 44 m. Five pillars were designed along the tendency, and seven pillars were designed along the inclination. Disturbance was applied to the gypsum layer at the boundary of the unit, and the width of the model boundary at the point of disturbance application was 50 m, whereas the width of the other boundary was set to 30 m to eliminate the boundary effect. After the model was constructed, a stable mined gob was formed after excavation, and the stress distribution of the gypsum rock pillars in the gob was recorded to compare and analyse the stress distribution after applying disturbance in the later period.

(2) Simulation scheme

The disturbance applying points were distributed along the centre line of the gob at 10, 20, and 30 m from the boundary, and the disturbance strengths applied were 4, 6, and 8 MPa to investigate the evolution law of stress distribution of gypsum rock pillars subjected to different disturbance strengths at different distances. During the calculation, the stress changes of the gypsum rock pillars were monitored. The gob unit was symmetrical along the tendency and inclination centrelines. The stress change of 12 gypsum rock pillars in the 1/4 mined gob area next to the disturbance boundary was selected as a representative of all gypsum rock pillars. The pillar codes were named matrix Aij. For example, A12 represents a pillar in the first row along the tendency and the second column along the inclination. The simulation scheme is illustrated in Figure 5. The simulation parameters are listed in

Table 1. Physical and mechanical parameters of overlying strata.

Rock Formation Name	Thickness (m)	Elastic Modulus (GPa)	Shear Modulus (GPa)	Cohesion (MPa)	Internal Friction (°)	Tensile Strength (MPa)
Gypsum-mudstone	4	5.22	3.31	5.87	41.0	1.10
Gypsum-marl	6	3.64	1.45	3.61	43.0	1.20
Mudstone	6	4.32	2.41	1.23	18.2	2.61
Silty-mudstone	4	6.25	2.76	1.64	37.5	1.37
Marl layer	12	4.68	2.57	1.51	23	1.92
Mudstone	2	4.32	2.41	1.23	18.2	2.61
Gypsum-mudstone	2	5.22	3.31	5.87	41.0	1.10
Gypsum-marl	2	3.64	1.45	3.61	43.0	1.20
II-1 layer	6	1.79	2.48	1.62	32.0	2.41
Gypsum-marl	4	3.64	1.45	3.61	43.0	1.20
II-2 layer	6	1.79	2.48	1.62	32.0	2.41
Marl layer	10	4.68	2.57	1.51	23.0	1.92

.

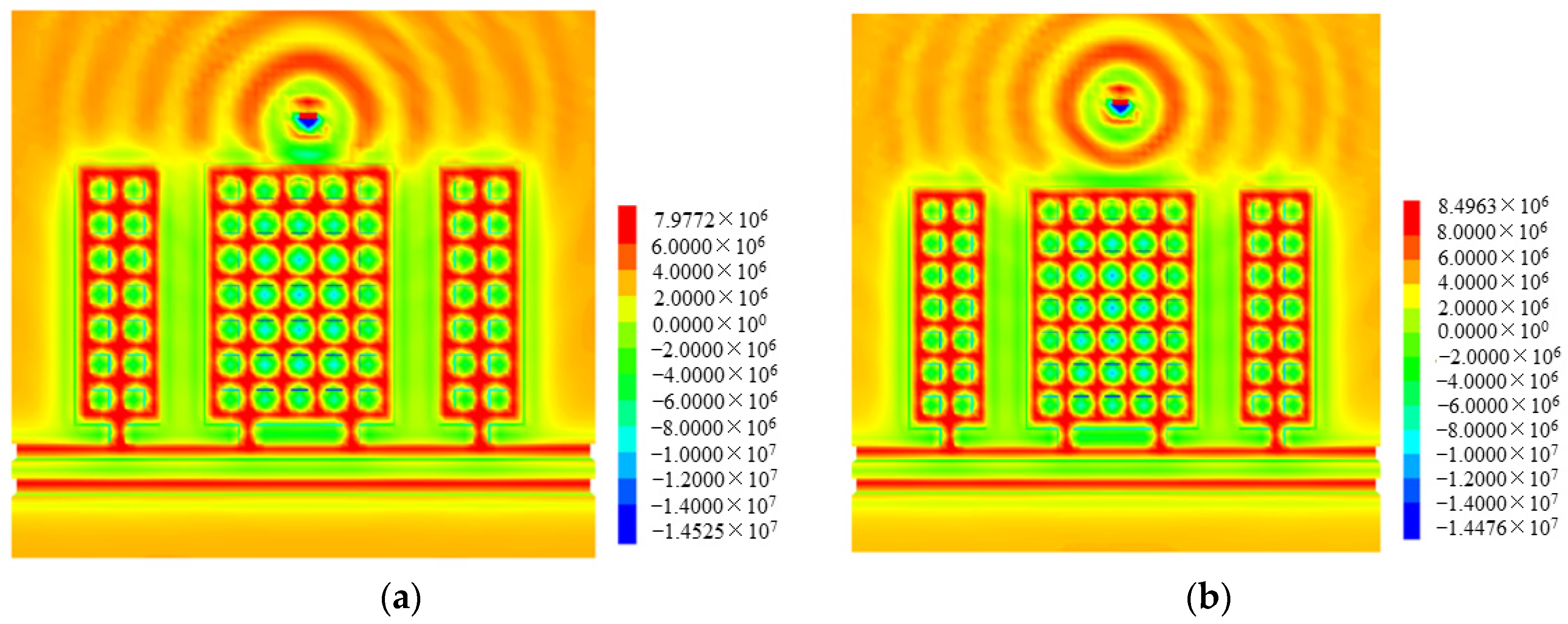
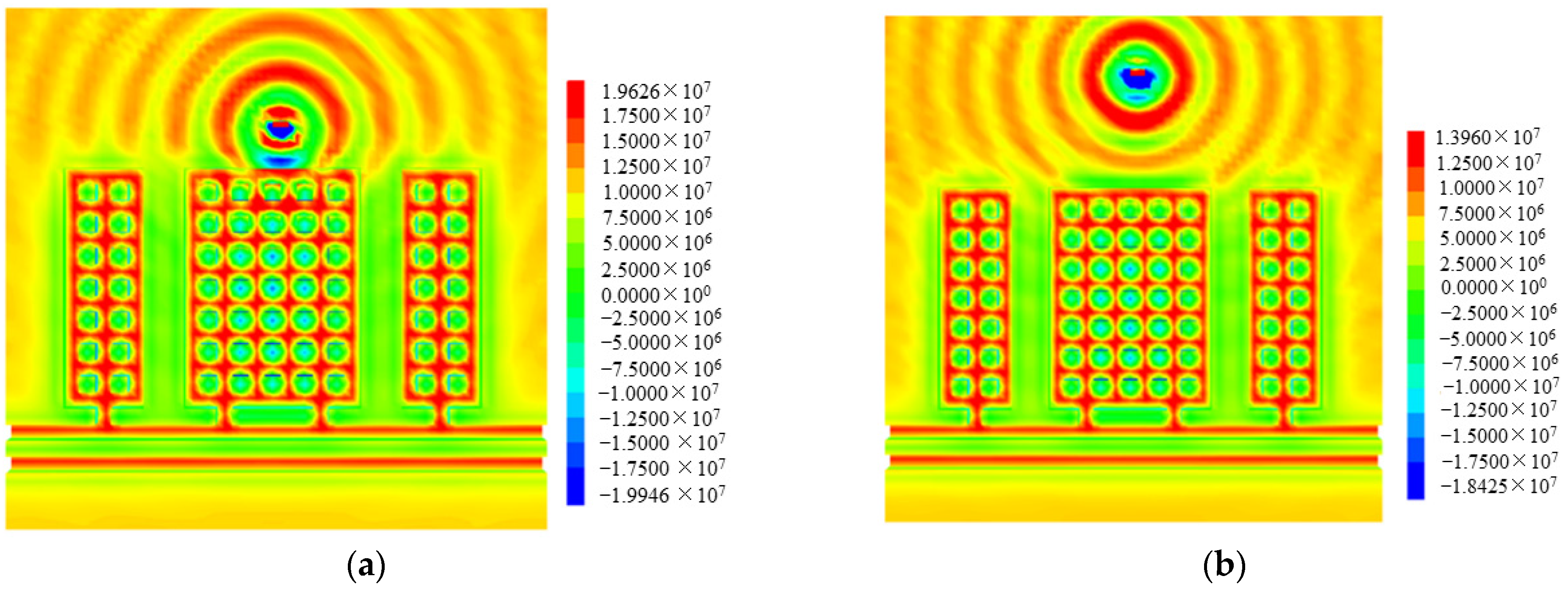
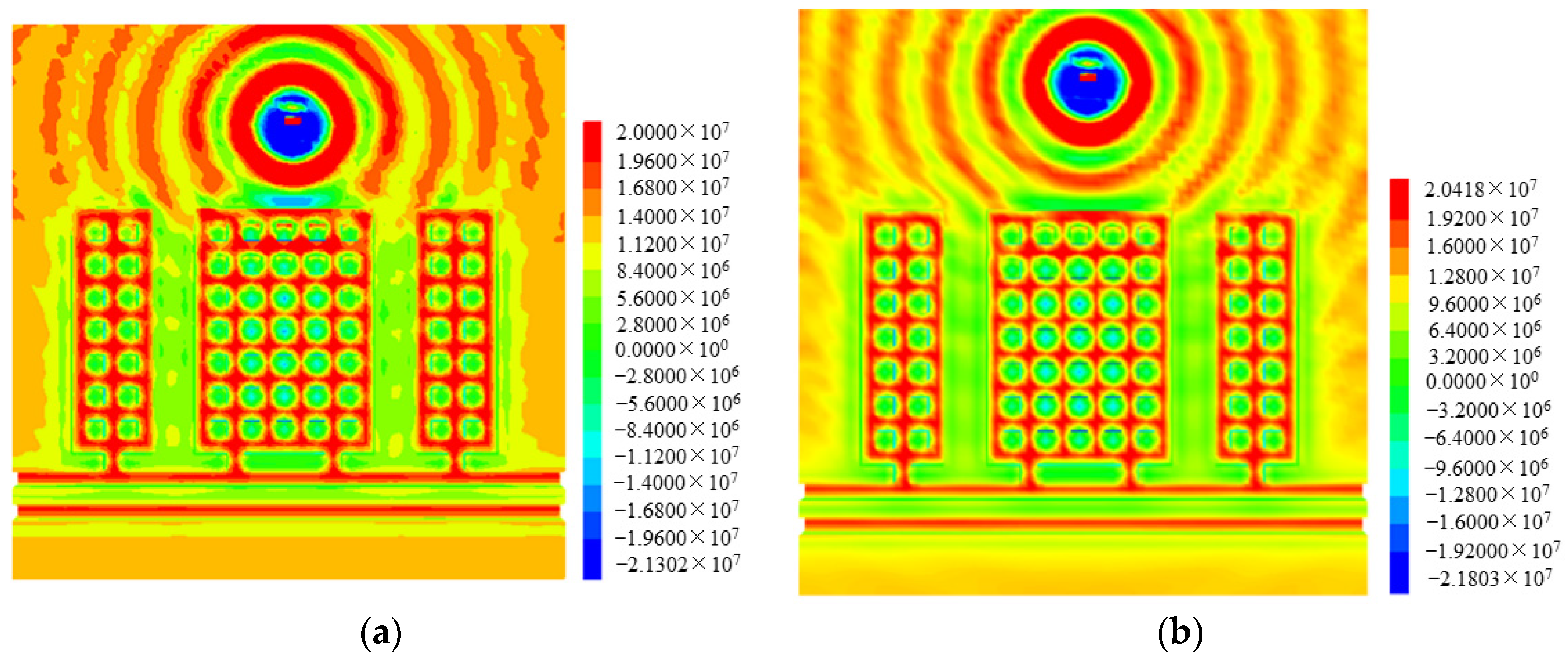
4.2. Stress Distribution

The stress distributions of gypsum rock pillars in gypsum mined gob subjected to disturbances of different strengths and distances are shown in Figure 6, Figure 7 and Figure 8.

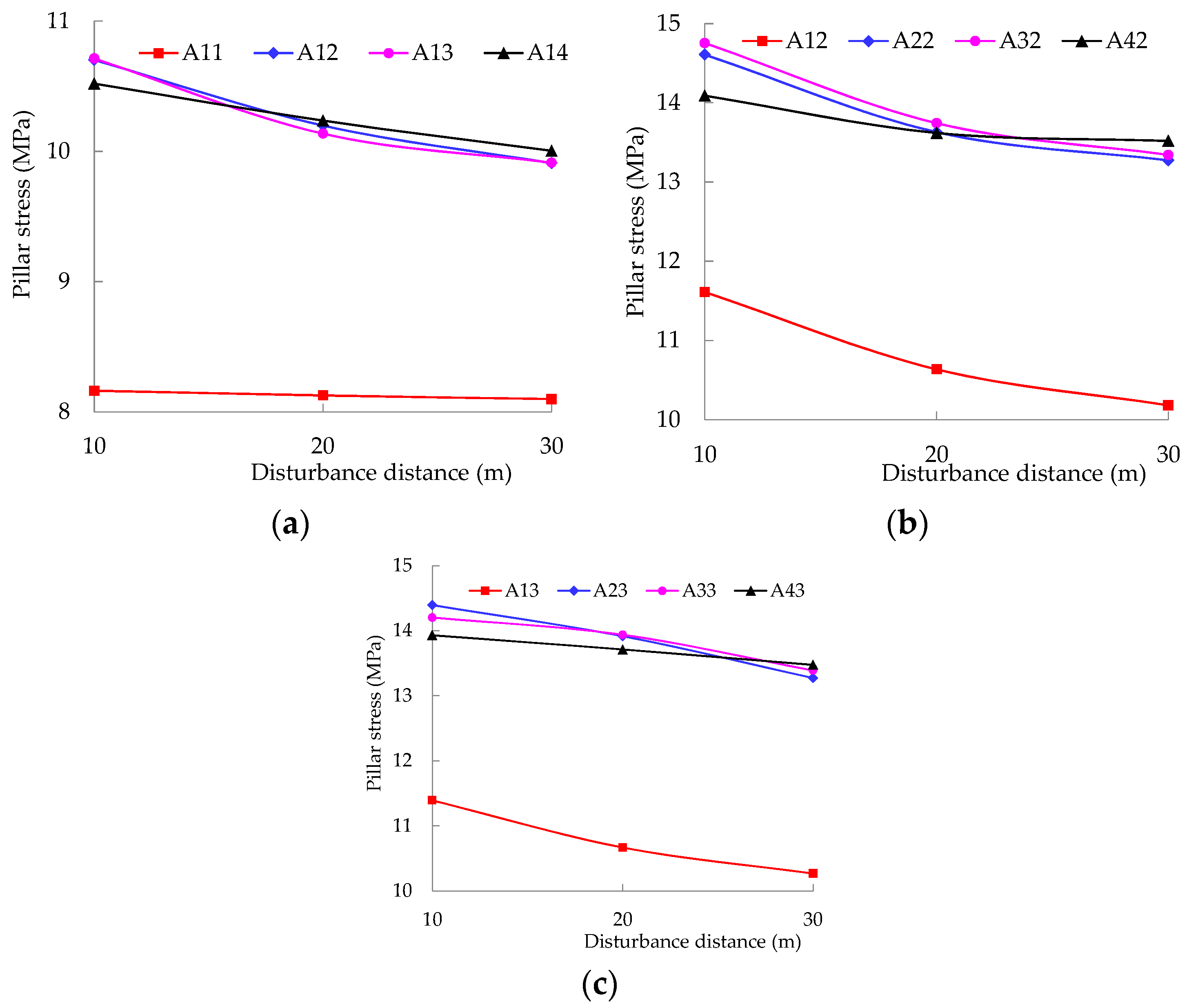
4.3. Stress Evolution

The disturbance distance was maintained constant (20 m as an example) to analyse the stress evolution of gypsum rock pillars subjected to different disturbance strengths, as shown in Figure 9. Meanwhile, the disturbance strength was maintained constant (6 MPa as an example) to analyse the stress evolution based on different disturbance distances, as shown in Figure 10.

Combining the stress distribution and evolution trends, the following findings were obtained:

(1)

As the disturbance strength increased, the stress of the gypsum rock pillars increased gradually. Meanwhile, as the disturbance distance increased, the stress of the gypsum rock pillars decreased gradually; however, the abovementioned stress was greater than the original static stress. The gypsum rock pillars next to the point where disturbance was applied not only indicated an increase in the vertical stress, but also a high tensile stress at the edge of the gypsum rock pillars. However, the tensile stress was much smaller than the vertical stress.

(2)

The first row of pillars A1j and the third column of pillars Ai3 were the most affected by disturbance. When the disturbance strength exceeded 6 MPa, the stress increased significantly. The greater the distance from the centreline of the disturbance application point, the less significant was the change in the gypsum rock stress, i.e., the stress change of the gypsum rock pillars indicated Aij < Aij + 1 and Ai + 1j < Aij.

(3)

As the disturbance distance increased, no abrupt significant changes were observed in terms of the pillar stress, and the overall relationship between them can be regarded as linear. However, the linear relationship between disturbance strength and stress was not evident. During the entire disturbance calculation process, all gypsum rock pillar stresses did not exceed its ultimate compressive strength of 24.12 MPa.

Based on the stress evolution of gypsum rock pillars subjected to disturbance, single and multiple disturbances did not cause the pillar stress to exceed its ultimate compressive strength; however, it should not be assumed that the disturbance did not affect the stability of the gypsum rock pillar and gypsum mined gob. According to the theory of rock mechanics, disturbance can be regarded as the short-term cyclic loading and unloading of gypsum rock pillars. Each type of disturbance caused internal fracture compaction and closure, which subsequently resulted in damage [25,26]. In particular, tensile stress appeared at the edge of the pillar, which further induced the weathering effect on the pillar. As the intensity of the disturbance increased, the gypsum rock pillars became damaged and eventually failed.

5. Discussion

With field blasting tests, the damage mechanism of the gypsum rock pillar was revealed, and stress distribution of the gypsum rock pillar was analysed via numerical simulation. Due to technological means and size of the gypsum rock pillar, the relationship between blasting test results and numerical simulation results was poor analysed and discussed. The specific reasons are as follows:

(1)

The size of the gypsum rock pillar in blasting test and numerical simulation is hard to design as the same. If the size of the pillar is too small in the blasting test, the pillar will fail with one or two blasts, and a multi-blasting test cannot be carried out. If the size of the pillar in numerical simulation is similar to the blasting test, it will be inconsistent with the actual mining situation.

(2)

Gypsum rock is different to other rocks with a significant feature of creep. It is a hard work to construct a suitable constitutive model for gypsum. Although the model of numerical simulation is extremely similar to gypsum rock, it is still different to gypsum mined gob. So, it is meaningless to analyse the relationship between blasting test results and numerical simulation results.

(3)

At present, it is difficult to represent rock damage degree with stress. The conditions of blasting test and numerical simulation are different, including boundary condition, blasting and disturbance strength. However, disturbance stress is the initial reason to induce gypsum damage and failure. So, we studied the issue in two parts.

6. Conclusions

The stability of gypsum rock pillars directly determines the stability of gypsum mined gobs. Based on field blasting tests and disturbance numerical simulation calculations, the damage mechanism of gypsum rock pillars subjected to blasting disturbance was analysed. The main conclusions obtained were as follows:

(1)

In the blasting test, as the number of blasting tests increased, the damage degree of the gypsum rock pillar along the horizontal direction increased, with a maximum damage rate of 7.82%. As the blasting-hole depth increased, the damage degree increased in general, but with significant fluctuations. The damage degree along the vertical direction eventually indicated a negative increase, with a maximum value of 3.52%. In the blasting test, the damage degree of the gypsum rock pillar in the horizontal direction test was greater than that in the vertical direction.

(2)

In disturbance numerical simulation calculations, as the disturbance strength increased, the stress of the gypsum rock pillars increased, although no clear linear relationship was observed between them. As the disturbance distance increased, the stress of the gypsum rock pillars decreased gradually, and a linear relationship was observed between them. However, the abovementioned stress was greater than the original static stress. Pillars next to the disturbance application point exhibited clear obvious tensile stress areas at the edges, although they were comparatively lower. During the disturbance calculation process, the stresses of all gypsum rock pillars did not exceed the ultimate compressive strength.

(3)

In the blasting test, the blasting strength was low, and the number of tests was small; however, the maximum damage of the gypsum rock pillar reached 7.82%. This proves that blasting and disturbance significantly damaged gypsum rocks, and that they were primary factors inducing gypsum rock pillar failure and gypsum mined-gob collapse.

(4)

The damage mechanism of gypsum rock pillars subjected to blasting disturbance was investigated, based on blasting tests and disturbance numerical simulation calculations, respectively. However, the correlation between blasting tests results and numerical simulation results was poor and the reason was discussed.