Analysis of Heat Dissipation Performance of Battery Liquid Cooling Plate Based on Bionic Structure

Abstract

To provide a favorable temperature for a power battery liquid cooling system, a bionic blood vessel structure of the power battery liquid cooling plate is designed based on the knowledge of bionics and the human blood vessel model. For three different discharge rates of 1C, 2C, and 3C, FLUENT is used to simulate and analyze the heat dissipation performance of the liquid cooling plate with a bionic vascular structure. The influence of the pipe distance (A1 and A2) at the coolant outlet, the thickness of the liquid cooling plate, the inner pipe turning radius R of the pipe in the channel, and the mass flow of coolant on the heat dissipation performance are studied. The results show that the pipe distance (A1 and A2), plate thickness, and inner pipe turning radius R have significant effects on the heat dissipation of the liquid cooling plate, especially under a 3C discharge. In addition, the channel area at the coolant outlet also has great influence on the heat dissipation performance of the liquid cooling plate, and the variable width optimization of the channel area at the outlet greatly improves the heat dissipation performance of the liquid cooling plate. Increasing the inlet mass flow rate can improve the heat dissipation capacity, but at the expense of a pressure drop. A verification experiment is designed for 3C discharge. The results show that the error between the experiment and simulation results is within 9.8%; therefore, the simulation is accurate, and the liquid cooling plate has a significant heat dissipation effect.

1. Introduction

In recent years, the rapid development of the global economy has also triggered a series of energy, environmental, and climate problems [1,2]. In order to solve these problems, the automotive industry is vigorously developing electric vehicles. The key to the development of electric vehicles depends on the power battery technology [3,4,5]. The thermal management of power batteries is one key battery technology [6,7,8]. The power battery generates a lot of heat during discharging operation [9,10,11,12], and the temperature of the battery directly affects the performance of the battery [13]. Therefore, the power battery has certain requirements on the temperature: the maximum temperature should be kept below 313.15 K (40 °C), and the temperature difference should be controlled within 5 °C [14,15]. Bionics is an interdiscipline between biology and engineering technology [16]. The purpose of bionics is to understand the principles of natural design and draw technical solutions [17,18]. Nature has existed for billions of years. After a long period of natural selection and survival of the fittest, nature has evolved many efficient systems [19]. For example, the fractal structure of the vascular network of the human body is a naturally optimized network flow channel for heat exchange or substance transfer. It has a uniform microchannel distribution and is conducive to the transfer of energy and substances. Compared with typical parallel channels, these microchannel structures improve the efficiency of heat exchange and reduce the energy loss in fluid flow. The shark skin structure is a good bionic structure for the reduction in fluid resistance, the leaf vein structure has some similarities with animal blood vessels in fluid movement, and spider web and honeycomb structures are mainly used in material structure strength and lightweight technology.

Tesla’s Model S has two-way cooling channels between the power batteries, which are wrapped by thermal conductive materials. This cooling structure greatly improves the heat capacity of the battery pack, increases the contact area of the battery and the pipeline, and makes the temperature distribution more uniform [20]. Brandner J. proposed and implemented an efficient microstructured heat exchanger. Research shows that the optimization of the structure or arrangement of the flow channels can improve heat dissipation performance [21]. Hermann designed a three-dimensional model of a biomimetic blood vessel using CAD software. A. Kremers studied a radiator with a biomimetic vessel structure using COMSOL software. The research shows that the structure with the straight inlet design had a better heat dissipation effect [22]. Hermanndesigned four kinds of micro-channels with the same heat exchange area, and the research shows that the heat dissipation effect of the fractal channel was better under the condition that the coolant inlet flow was the same [23]. Xia studied Effects of different geometric structures on fluid flow and heat transfer performance in microchannel heat sinks [24]. Hu and Yi improved the driving range of electric vehicles by considering the battery temperature, heat dissipation power, and power distribution of hybrid energy sources [25,26,27].Li Bo et al. designed a heat management device for battery packs. The device is provided with a heat transfer plate between the battery cells, and the heat transfer plate is also coated with a graphene layer. This structure increases the function of low-temperature heating. The heat dissipation effect and heating effect were effectively improved [28]. In this paper, a microchannel liquid cooling plate with a bionic vascular structure is designed, and the heat dissipation model of the liquid cooling plate is established and simulated by using Fluent software. The influence of the pipe distance (A1 and A2) at the coolant outlet, the plate thickness of the liquid cooling plate, the inner pipe turning radius R of the inner pipe of the channel, and the mass flow of the coolant on the heat dissipation performance are studied. It provides a theoretical and practical basis for the design and optimization of the bionic structure liquid cooling plate.

2. Structural Modeling and Calculation Settings

2.1. Modeling of Liquid Cooling Plate with Imitation Blood Vessel Structure

The human vascular system is optimized for efficient fluid delivery. During the entire blood delivery process, an efficient network delivery system can reduce the additional energy consumption generated by the blood flowing in the blood vessel; thus, the human blood vessel is an efficient microchannel network. Therefore, a liquid cooling plate suitable for power batteries can be designed according to this characteristic. Figure 1a shows a typical human blood vessel structure. Drawing on a similar distribution form and using a quasi-fractal design method, the bionic structure of the liquid cooling plate is shown in Figure 1b.

2.2. Verification of the Independence of Boundary Conditions and Grid

2.2.1. Boundary Conditions

The heat source of the battery is mainly from the reaction heat $Q_r$, the side reaction heat $Q_s$, the polarization heat $Q_p$, and the Joule heat $Q_j$ that generates inside the battery during its operation. The internal ohmic resistance of the lithium battery is mainly composed of the internal resistance of the electrode material and the separator. In the charging and discharging working state, the internal ohmic resistance produces Joule heat $Q_j$, which is the main reason for the increase in temperature in the battery. The formula for calculating the total calorific value of the battery is as follows [29,30]:

$$Q_{\mathrm{total}}=Q_r+Q_p+Q_j+Q_s\approx Q_j=I^2{R}_e$$

(1)

where $Q_{total}$ represents the total calorific value of the lithium ion battery; $I$ represents the battery charge and discharge current; $R_e$ represents the internal ohmic internal resistance of the battery.

In this study, the cold plate was assumed to be homogeneous and isotropic. The coolant was assumed to be steady and incompressible. The conservation equations for mass, momentum and energy are illustrated as follows:

$$\frac{\partial u_1}{\partial x}+\frac{\partial u_2}{\partial y}+\frac{\partial u_3}{\partial z}=0$$

(2)

$${\rho }_l\left(u_1\frac{\partial u_1}{\partial x}+u_2\frac{\partial u_1}{\partial y}+u_3\frac{\partial u_1}{\partial z}\right)=-\frac{\partial p}{\partial x}+\mu {\nabla }^2{u}_1$$

$${\rho }_l\left(u_1\frac{\partial u_2}{\partial x}+u_2\frac{\partial u_2}{\partial y}+u_3\frac{\partial u_2}{\partial z}\right)=-\frac{\partial p}{\partial y}+\mu {\nabla }^2{u}_2$$

(3)

$${\rho }_l\left(u_1\frac{\partial u_3}{\partial x}+u_2\frac{\partial u_3}{\partial y}+u_3\frac{\partial u_3}{\partial z}\right)=-\frac{\partial p}{\partial z}+\mu {\nabla }^2{u}_3.$$

$$\rho C_{pl}\left(u_1\frac{\partial T}{\partial x}+u_2\frac{\partial T}{\partial y}+u_3\frac{\partial T}{\partial z}\right)={\mathsf{\lambda }}_l{\nabla }^{2}T$$

(4)

where ${\rho }_l$ represents the density of water; ${\nabla }^2$ represents the Laplacian operator; $C_{pl}$ repressents the heat capacity of the fluid; ${\lambda }_f$ represents the thermal conductivity of the cooling water; P represents the pressure of the coolant; $u_1$, $u_2$, and $u_3$ represent the velocity components of the coolant in the x-, y-, and z-axes, respectively.

The properties of the fluid and the solid (aluminum) are presented in

Table 1. Properties of water and aluminum.

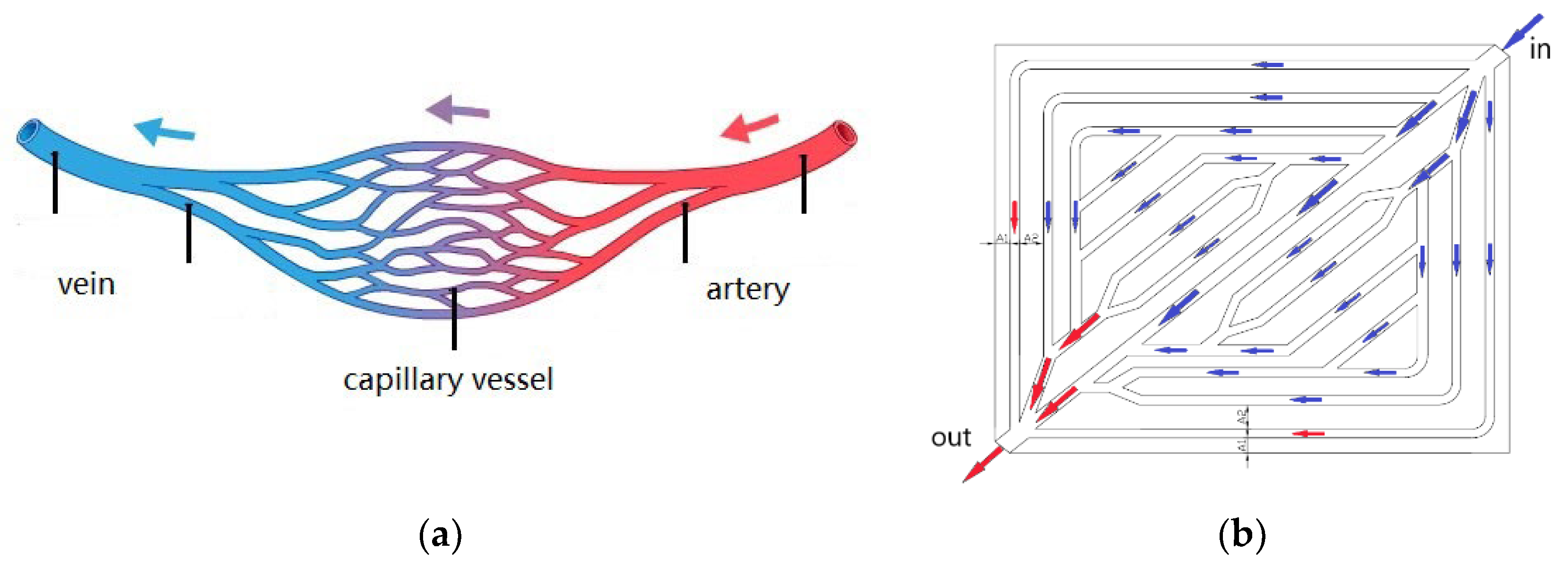
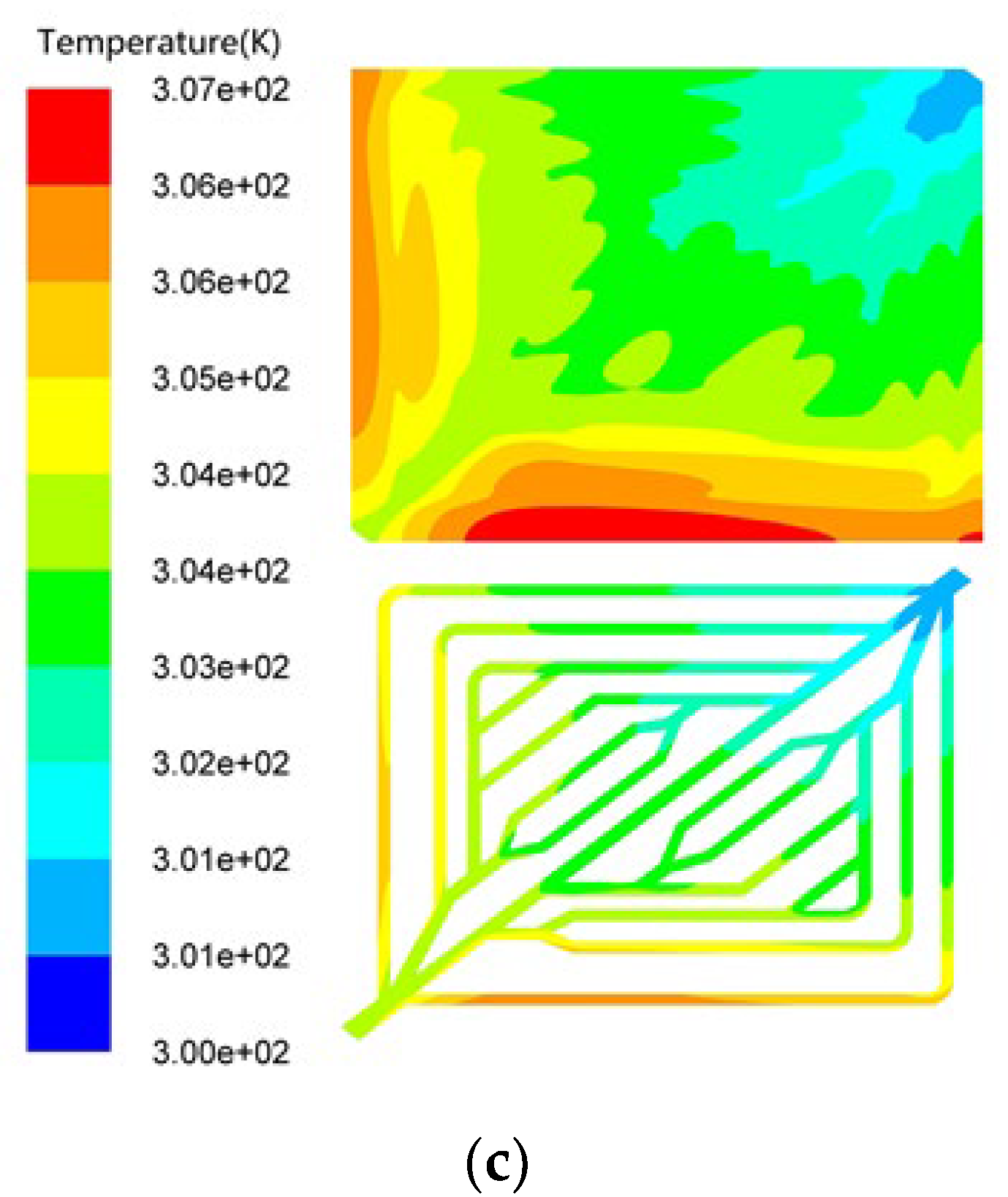
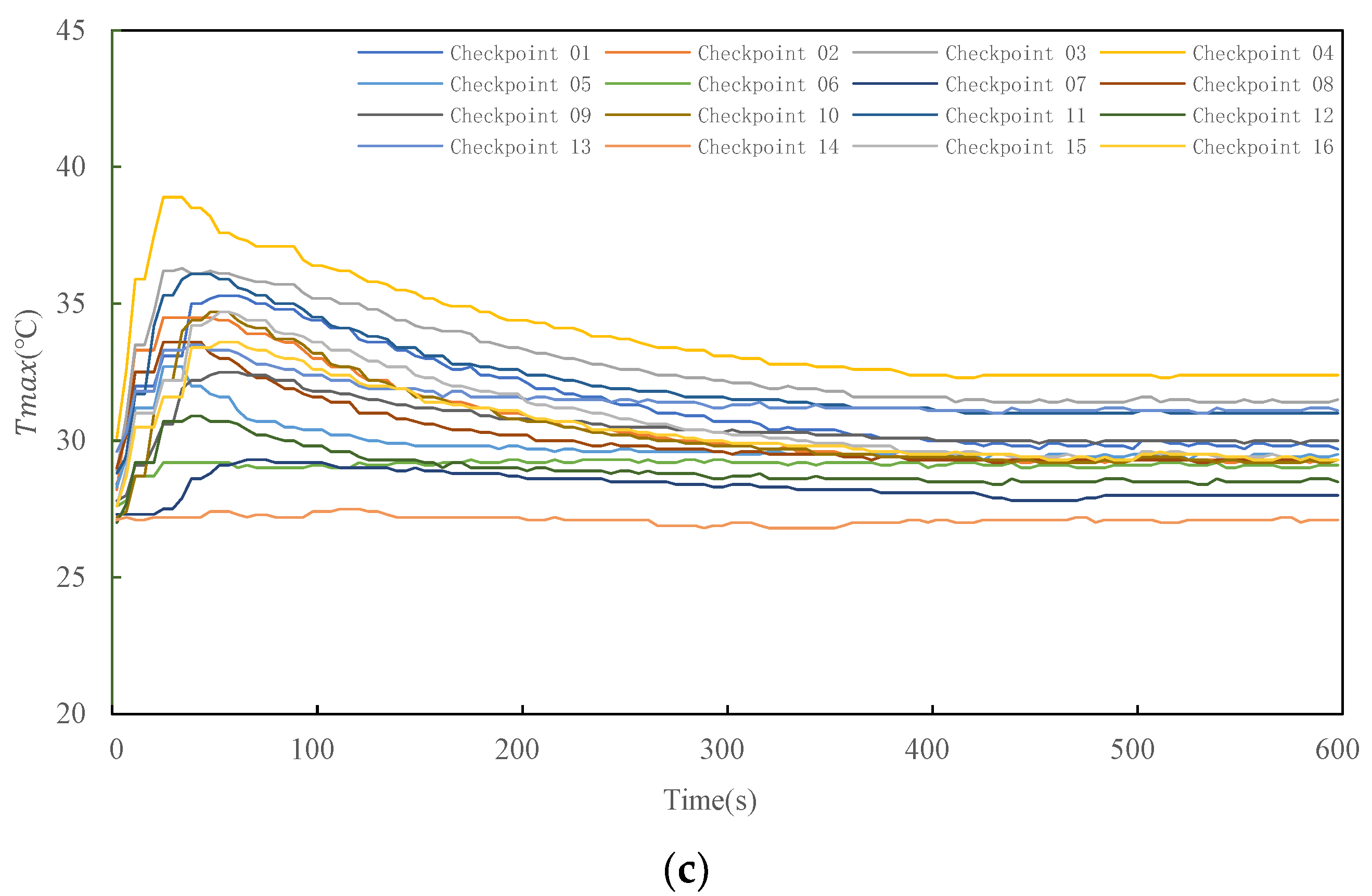
Parameter	${\mathit{C}}_{\mathit{P}} \mathbf{(}\mathbf{J}\mathbf{/}\mathbf{\left(}\mathbf{k}\mathbf{g}\mathbf{·}\mathbf{K}\mathbf{\right)}$	$\mathbf{\lambda } \mathbf{(}\mathbf{W}\mathbf{/}\mathbf{\left(}\mathbf{m}\mathbf{·}\mathbf{K}\mathbf{\right)}\mathbf{)}$	$\mathsf{\mu } \mathbf{\left(}{\mathbf{P}}_{\mathbf{a}}\mathbf{\right)}$	$\mathsf{\rho } \mathbf{\left(}\mathbf{k}\mathbf{g}\mathbf{/}{\mathbf{m}}^{\mathbf{3}}\mathbf{\right)}$
Aluminum	871	202.4	-	2719
Water	4182	0.6	1.003 × 10−4	998.2

, assuming that the upper and lower surfaces of the cold plate were subject to the same heat flux. We assumed a capacity of 20 Ah and a nominal voltage of 3.2 V for the batteries. When the battery was discharged at 1C, 2C, and 3C, the constant heat flux was calculated as 1400, 2800, and 4200 Wm⁻² (Φ = $P_h$/A′), assuming that the other surfaces were insulated.

The coolant inlet was set as a mass flow inlet; the outlet was a pressure outlet, and the outlet pressure was 0 Pa. The Reynolds number at the entrance was calculated according to Equation (5), and the corresponding boundary conditions are shown in

Table 2. Boundary conditions.

Boundary Conditions	Parameter Value
Inlet mass flow (kg/s)	0.02
Inlet temperature T0 (K)	300
Outlet pressure (Pa)	0

.

$$Re=\frac{\rho vd}{\mu }$$

(5)

where ρ represents the density; v represents the flow velocity; d represents the characteristic length; μ represents the dynamic viscosity.

The liquid cooling plate was attached between the two power batteries. The temperature difference between the liquid cooling plate and the battery surface was small, and radiation heat transfer could be ignored. The convection heat exchange between the wall surface of the liquid cooling plate and the coolant was the main cooling method, and the heat taken away by the coolant was:

$$Q_f=c_{p}m\mathsf{\Delta }T$$

(6)

where $Q_f$ represents the heat taken away by the coolant; $c_p$ represents the specific heat capacity of the coolant; $m$ represents the mass flow of the coolant; $\mathsf{\Delta }T$ represents the temperature rise of the coolant.

The mathematical model was realized and solved by Fluent software. The maximum temperature ($T_{max}$) of the liquid cooling plate could reflect the worst working state of the battery. The surface temperature difference ($\mathsf{\Delta }T$) of the liquid cooling plate indicated the temperature distribution of the battery. The smaller the temperature gradient of the battery, the more heat absorbed by the coolant, and the more uniform the temperature distribution. The inlet and outlet pressure drop ($\mathsf{\Delta }P$) of the coolant was equal to the sum of the pressure drop of all channels, which reflected the excellent heat dissipation performance from the perspective of energy consumption. The smaller the $\mathsf{\Delta }P$, the smaller the pump power required to drive the coolant through the channel.

2.2.2. Grid Independence Verification

In the simulation process, the mesh size of the fluid area was very important for the accuracy of the simulation results. Because the flow channel structure of this model was more complicated, the use of an unstructured mesh could reduce the workload. The model was divided into a solid area and a fluid area. Taking 3C discharge as an example, the grid size was selected to be 0.75 mm, 0.7 mm, 0.6 mm, and 0.5 mm under the working condition of ambient temperature of 300 K and a mass flow rate of 0.02 kg/s to verify the independence of the grids. The verification results are shown in

Table 3. Independent test of volume mesh number.

Grid Size/mm	Total Number of Grids	Maximum Temperature (K)	Temperature Difference (°C)
0.75	1,240,995	307.11	6.44
0.7	1,498,009	307.09	6.32
0.6	2,290,503	307.04	6.39
0.5	3,593,672	307.05	6.43

.

3. Simulation Analysis of Liquid Cooling Plate Heat Dissipation

3.1. The Influence of the Pipe Distance at the Coolant Outlet on the Heat Dissipation Performance

For the liquid cooling plate model in this study, the inlet mass flow rate was 0.02 kg/s to analyze the heat dissipation performance of the liquid cooling plate in an environment of 300 K at room temperature. The overall analysis flow chart was as Figure 2.

Figure 3 is the temperature diagram of the liquid cooling plate and the cooling liquid channel under 1C, 2C, and 3C discharge, respectively.

It can be concluded from Figure 4 that the temperature of the liquid cooling plate had the same changing trend under three different discharge rates. Along the inflow direction of the coolant, the lowest temperature zone was found; correspondingly, the highest temperature zone was found to be at the outlet. Especially under 3C discharge, the highest temperature ($T_{max}$) of the liquid cooling plate reached 307.09 K (33.94 °C), and the temperature difference (ΔT) was as high as 6.32 °C. At this time, the temperature uniformity of the liquid cooling plate was poor and the temperature difference exceeded the safe working requirements of the power battery.

Reason for analysis: When the coolant just flowed into the liquid cooling plate, the resistance was small and the temperature was low, and a minimum temperature area was formed at the entrance. As the coolant continued to flow, it was more and more affected by the thermal resistance; the more heat the coolant absorbed during the flow, the more the temperature rose, and a high temperature area formed at the outlet. The analysis of the temperature diagram of the flow channel showed that the two coolant pipes at the outlet had the highest temperature and a poor heat dissipation, resulting in a large temperature difference of the liquid cooling plate, thereby weakening the overall cooling performance of the liquid cooling plate.

In order to improve the heat dissipation performance of the liquid cooling plate, we focused on the analysis of the distance of the two cooling pipes at the outlet; the distance from the edge of the liquid cooling plate to the first pipe was set to A1, and the distance from the first pipe to the second pipe was set to A2, as shown in Figure 3. By analyzing the effect of the pipe distance at different coolant outlets on the heat dissipation performance, the best heat dissipation effect of the liquid cooling plate was achieved.

In this section, keeping other conditions unchanged, A1 was divided into 5 mm, 6 mm, 8 mm, and 10 mm, and A2 was divided into 5 mm, 6 mm, 8 mm, 10 mm, and 12 mm. In total, 20 kinds of structures (4 × 5) were generated through arrangement and combination. Figure 5a shows the relationship between the size of A1 and A2. With the maximum temperature ($T_{max}$), Figure 5b shows the relationship between the size of A1 and A2. With the temperature difference(ΔT), Figure 5c shows the relationship between the size of A1 and A2 with the pressure drop (ΔP).

Figure 5a,b shows that the change trends of the maximum temperature ($T_{max}$) and temperature difference (ΔT) of the liquid cooling plate were very similar. When A2 was fixed, $T_{max}$ and ΔT decreased as A1 decreased. In addition, the reduction in A1 could quickly weaken the influence of A2 on $T_{max}$ and ΔT.

From Figure 5a–c, it could be concluded that when A1 = 10 mm and A2 = 12 mm, the heat dissipation performance of the liquid cooling plate was the worst. Take 3C discharge as an example. At this time, the maximum temperature ($T_{max}$) reached 307.09 K (33.94 °C), the temperature difference (ΔT) was 6.32 °C, and the pressure drop (ΔP) was 4887.8 Pa. Under this structure, ΔT had exceeded the safe working range of the power battery. When A1 = A2 = 5 mm, the maximum temperature ($T_{max}$) of the liquid cooling plate dropped to 305.33 K (32.18 °C), and the drop was 1.76 °C. The temperature difference (ΔT) dropped to 4.54 °C with a drop of 28.2%. However, at this time, the pressure drop (ΔP) had risen to 5401.4 Pa. The premise of lowering the temperature of the liquid cooling plate was to bring about greater pressure loss.

Obviously, it was not advisable to blindly reduce A1 and A2 for heat dissipation performance. Reason for analysis: When A1 and A2 decreased, the coolant flow path was closer to the outlet, which improved the heat absorption capacity at the outlet of the liquid cooling plate, thereby improving the heat dissipation effect of the liquid cooling plate. However, the adverse effect was that the distance of coolant flows in the liquid cooling plate became longer; because the flow channel was a micro channel, the flow of the coolant needed to overcome a large resistance. The longer flow channel meant that the flow resistance became larger, and the pressure loss was inevitably increased, so the pressure difference at the inlet and outlet became larger, which increased the energy consumption of the cooling pump; thus, increasing the energy consumption of the power battery thermal management system.

Based on the above analysis, the pipe distances A1 and A2 had a significant effect on the heat dissipation effect of the liquid cooling plate, but the effect on the pressure difference had to still be considered while determining the values of A1 and A2. Therefore, the values of A1 and A2 should needed to be selected appropriately. It can be seen from Figure 4 that when A1 = 6 mm and A2 = 8 mm, the overall heat dissipation performance of the liquid cooling plate was the best. At this time, under 3C discharge, $T_{max}$ = 305.24 K (32.09 °C), ΔT = 4.48 °C, and ΔP = 4870.5 Pa greatly reduced the energy consumption of the thermal management system of the power battery when it met the requirements of the safe working temperature of the power battery. Therefore, in the following analysis, we set A1 to 6 mm and A2 to 8 mm.

3.2. The Influence of Liquid Cooling Plate Thickness on Heat Dissipation Performance

According to the model parameters analyzed in the previous section, in order to compare the effects of different liquid cooling plate thicknesses on heat dissipation performance, in this section, we designed five liquid cooling plate simulation analysis models with plate thicknesses of 3 mm, 4 mm, 5 mm, 6 mm, and 7 mm, respectively. Additionally, through a simulation calculation, the relationship between the maximum temperature ($T_{max}$) and the temperature difference (ΔT) of liquid cooling plates with different plate thicknesses under the same boundary conditions was obtained. Figure 5 shows the relationship between the plate thickness and heat dissipation performance in a room temperature environment of 300 K and an inlet mass flow rate of 0.02 kg/s.

It is obvious from Figure 6 that the maximum temperature $\left(T_{max}\right)$ and temperature difference (ΔT) of the liquid cooling plate under the three different discharges continued to decrease with the increase in plate thickness. Reason for analysis: Since the thermal conductivity of aluminum was much higher than that of the cooling liquid, increasing the thickness of the plate with the flow channel of the liquid cooling plate unchanged was equivalent to increasing the cross-sectional area of the aluminum plate. According to Fourier’s law of heat conduction, increasing the plate thickness was beneficial to the lateral diffusion of heat. Therefore, increasing the plate thickness was beneficial to improve the heat dissipation performance of the liquid cooling plate. For example, under 3C discharge, when the plate thickness increased from 3 mm to 4 mm, the maximum temperature (T_max) of the liquid cooling plate dropped from 305.24 K (32.09 °C) to 305.10 K (31.95 °C), which was a drop of 0.14 °C; the temperature difference (ΔT) dropped from 4.48 °C to 4.25 °C, which was a drop of 0.23 °C. When the plate thickness exceeded 4 mm, the maximum temperature ($T_{max}$) and temperature difference (ΔT) of the liquid cooling plate began to shrink. Considering the limited space for the layout of the power battery, in order to improve the cruising range of the power battery, more batteries should have been arranged in the limited space as much as possible, so that the thickness of the liquid cooling plate would be as small as possible. Based on the above analysis, the plate thickness of 4 mm could optimize the heat dissipation effect in a smaller space.

3.3. The Influence of Inner Tube Turning Radius on Heat Dissipation Performance

In order to compare the influence of the turning radius $R$ of the inner pipes of different flow channels on the heat dissipation performance of the liquid cooling plate, $R$ was designed to be 1 mm, 2 mm, 3 mm, 4 mm, 5 mm, 6 mm, 7 mm, 8 mm, 9 mm, 10 mm, 15 mm, and 20 mm in total. The research obtained the influence of radius $R$ on the maximum temperature ($T_{max}$) and temperature difference (ΔT) of the liquid cooling plate under the same boundary conditions. Figure 6 shows the relationship between the turning radius $R$ of the inner pipe of different flow channels and the heat dissipation performance within the working conditions of 300 K and 0.02 kg/s inlet mass flow rate.

From Figure 7a, it could be concluded that under 12 kinds of inner pipe turning radius conditions, the change trends of the maximum temperature ($T_{max}$) and temperature difference (ΔT) of the liquid cooling plate were basically the same, showing a change that first decreased and then increased. This trend of change was more obvious under 3C discharge. By analyzing the temperature change curve of the liquid cooling plate under 3C discharge, it could be found that when the inner pipe turning radius was 8 mm, the heat dissipation performance of the liquid cooling plate was the best. The maximum temperature ($T_{max}$) was 305.03 K (31.98 °C), and the temperature difference (ΔT) was 4.10 °C. Compared with the inner pipe turning radius of 1 mm, $T_{max}$ and ΔT decreased by 0.52 °C and 0.50 °C, respectively. Simultaneously, relative to the inner pipe turning radius of 20 mm, $T_{max}$ and ΔT decreased by 0.87 °C and 0.90 °C, respectively.

From Figure 7b, it could be concluded that the pressure drop (ΔP) difference of the liquid cooling plate showed a trend that first dropped rapidly, then rose slightly, and finally stabilized. When the turning radius of the inner pipe was 1 mm, ΔP was the largest, which was as high as 5203.8 Pa. The ΔP decreased with the increase in the radius. When the radius was 6 mm, ΔP dropped to a minimum of 4777.4 Pa, which was a drop of 426.4 Pa. When the turning radius continued to increase from 6 mm, ΔP rebound slightly, but finally stabilized. That was because the excessively large turning radius of the inner pipe shortened the straight-line flow distance of the coolant, and the increase in the distance of the bend caused a small increase in pressure loss. When the turning radius of the inner pipe exceeded a certain range, the pressure loss of the coolant flow began to stabilize, and, finally, the pressure difference between the inlet and outlet also tended to stabilize.

Based on the above analysis, the turning radius of the inner pipe of the channel had significant impact on the heat dissipation performance of the liquid cooling plate. Choosing a turning radius of 8 mm could effectively improve the maximum temperature ($T_{max}$) and temperature difference (ΔT) of the liquid cooling plate and effectively reduce the pressure drop (ΔP), which reduced the energy consumption of the cooling system. The temperature graph of the liquid cooling plate and the flow velocity graph at the coolant outlet under 3C discharge are shown in Figure 8.

3.4. The Influence of the Flow Channel Area at the Coolant Outlet on the Heat Dissipation Performance of the Liquid Cooling Plate

It can be seen from Figure 8 that the highest temperature region of the liquid cooling plate appeared at the outlet of the cooling liquid, especially the highest temperature on the right side of the outlet. By analyzing the flow velocity diagram at the coolant outlet, it was found that the flow on the right side of the coolant outlet was the smallest. It was found that there was a gradual change in the diameter of blood vessels at the entrance and exit, from large to small at the entrance and from small to large at the exit. Based on this, the flow channel at the outlet of the liquid cooling plate was subjected to variable width optimization processing. When the thickness of the flow channel was unchanged, the upper and lower width classification ratio was 0.8. We further discusses the effect of the flow channel area at the coolant outlet on the cooling performance of the liquid cooling plate. Taking 3C discharge as an example, the optimized coolant outlet channel is shown in Figure 9a, and the temperature diagram of the optimized liquid cooling plate under the same boundary conditions is shown in Figure 9b.

It can be seen from Figure 9b that the range of the maximum temperature region of the liquid cooling plate was reduced compared to Figure 8a. The maximum temperature ($T_{max}$) dropped from 305.03 K (31.88 °C) to 304.91 K (31.76 °C), which was a decrease of 0.12 °C. The temperature difference (ΔT) of the liquid cooling plate dropped from 4.10 °C to 3.97 °C, and decreased by 0.13 °C. The temperature uniformity of the liquid cooling plate was further improved. Reason for analysis: The optimized design of variable width at the coolant outlet essentially enlarged the area of the flow channel. Through this optimization, the flow rate could be better introduced to the outlet and the cooling liquid coverage area at the outlet increased, which greatly improved the heat dissipation performance of the liquid cooling plate.

3.5. The Influence of the Coolant Mass Flow Rate on the Heat Dissipation Performance of the Liquid Cooling Plate

The coolant mass flow rate is an important factor of the cooling performance of the liquid cooling plate. In order to analyze the impact of different flows on the cooling effect, six different inlet mass flows, which were 0.005 kg/s, 0.010 kg/s, 0.015 kg/s, 0.020 kg/s, 0.025 kg/s, and 0.030 kg/s, were designed in this section. According to the above research basis, the curves of the maximum temperature ($T_{max}$), temperature difference (ΔT), and Pressure drop (ΔP) of the liquid cooling plate with the flow rate under the same boundary conditions are shown in Figure 10.

It can be concluded from Figure 10 that the heat dissipation performance of the liquid cooling plate continued to increase with the increase in the coolant mass flow rate; especially when the mass flow rate increased from 0.005 kg/s to 0.010 kg/s, the temperature dropped the most, and then the temperature decline trend began to slow down. Taking 3C discharge as an example, when the coolant mass flow rate increased from 0.005 kg/s to 0.030 kg/s, the maximum temperature ($T_{max}$) of the liquid cooling plate dropped from 311.98 K (38.83 °C) to 304.24 K (31.09 °C), which reduced by 7.74 °C; the temperature difference (ΔT) dropped from 9.96 °C to 3.62 °C, which was a drop of 6.34 °C, and the drop rate was as high as 63.65%. When the coolant mass flow rate increased to 0.015 kg/s, the maximum temperature ($T_{max}$) and temperature difference (ΔT) of the liquid cooling plate were 305.69 K (32.54 °C) and 4.49 °C, respectively. At this time, the temperature of the liquid cold plate met the safe working temperature requirements of the power battery. With the continuous increase in the flow rate, the decreasing trend of the liquid cooling plate temperature began to slow down, while the pressure drop (ΔP) showed a tendency to increase exponentially. Compared with the mass flow rate of 0.030 kg/s and the flow rate of 0.020 kg/s, the maximum temperature ($T_{max}$) of the liquid cooling plate only decreased by 0.67 °C, and the temperature difference (ΔT) decreased by 0.35 °C. However, the pressure drop (ΔP) increased by 5928.5 Pa, which was an increase of 117.14%, and greatly expanded the energy consumption of the cooling pump under the specific heat dissipation requirement. Therefore, a moderate coolant mass flow rate should be selected according to the battery’s discharge rate and operating temperature to facilitate the best heat dissipation performance of the liquid cooling plate.

3.6. Experimental Verification

It can be seen from the above analysis that the temperature of the liquid cooling plate was the highest and most likely to exceed the safe working temperature condition of the power battery under 3C discharge. Therefore, in order to verify the accuracy of the simulation results, a 3C discharge verification experiment was designed. The liquid cooling plate shown in Figure 9a was processed using aluminum plates, the mass flow rate of the cooling liquid was 0.020 kg/s, and the ambient temperature and cooling liquid temperature were 300 K. The liquid cooling plate was divided into a base plate and a cover plate and glued together as a whole. Figure 11 shows the structure of the liquid cooling plate.

According to the simulation results, a total of 16 temperature checkpoints was arranged in this experiment, of which 15 checkpoints were arranged on the cooling plate and one checkpoint was the ambient temperature. Checkpoint 14 was the ambient temperature checkpoint, checkpoint 7 was placed at the coolant inlet, and checkpoint 6 was placed at the coolant outlet. The arrangement of the temperature checkpoints is shown in Figure 12a. The heat source was a silicon heating sheet pasted on the surface of the cooling plate as shown in Figure 12b. During the experiment, we put the liquid cooling plate into the environmental chamber and energized the heated silicon plate to detect the temperature change of the liquid cooling plate. The temperature curve of the 16 checkpoints obtained is shown in Figure 12c.

It can be seen from Figure 12c that the temperature at checkpoint 4 was the highest, and the corresponding position was the red high temperature area on the right side of the coolant outlet in Figure 8b. The maximum temperature ($T_{max}$) hardly changed after being reduced to 32.4 °C. The temperature at checkpoint 7 was the lowest and the temperature fluctuation was the smallest. This was because the checkpoint 7 layout at the inlet of the cooling liquid was cooling with excellent results. The temperature first rose slightly and then remained at 28.0 °C. By analyzing the experimental results, we found the maximum temperature ($T_{max}$) of the experiment to be 32.4 °C higher than the simulation result by 0.64 °C. The temperature difference (ΔT) was 4.4 °C, which was 0.43 °C higher than the simulation result, but the temperature difference (ΔT) was still less than 5 °C. The heat dissipation performance met the requirements of the battery operating temperature, and the maximum error between the experimental and simulation results was within 9.8%. The main reason for the error may have been the agricultural machinery glue used in the process of processing the liquid cooling plate, while the thermal conductivity of the agricultural machinery glue was much lower than that of the aluminum plate. Therefore, the difference between the simulation results and the experimental results was within the acceptable range, the experimental results were consistent with the simulation results, and the simulation results were accurate.

4. Conclusions

Based on bionics and the human blood vessel model, this study designed a liquid cooling plate with a bionic vascular structure of quasi-similar fractal. Under three different discharges of 1C, 2C, and 3C, Fluent software was used to study the pipe distance (A1 and A2) at the coolant outlet, the thickness of the liquid cooling plate, the turning radius R of the pipe in the channel, and the mass flow of the coolant on the heat dissipation performance. The results showed that the pipe distance (A1, A2), plate thickness, and inner pipe turning radius R had a significant effect on the heat dissipation effect of the liquid cooling plate, especially under 3C discharge. When A1 = 6 mm and A2 = 8 mm, the plate thickness was 4 mm, the inner pipe turning radius was 8 mm, the highest temperature ($T_{max}$) of the liquid cooling plate was 305.03 K (31.88 °C), and the temperature difference (ΔT) was 4.10 °C. At this time, the structure was more compact and the system energy consumption was lower while meeting the requirements of the safe working temperature of the power battery, which was more conducive to the standardization and practical application of the power battery liquid cooling plate.

By imitating the human blood vessel model, the cooling liquid outlet was optimized with a variable width, and the heat dissipation performance of the liquid cooling plate was greatly improved. The increase in the mass flow rate could improve the heat dissipation capacity, but would consume more cooling system energy. Therefore, a moderate mass flow of the coolant could be selected according to energy consumption and heat transfer targets.

For 3C discharge, a verification experiment was designed. The results showed that the error between the experimental and simulation results was maintained within 9.8%, the simulation of the cooling effect of the liquid cooling plate was accurate, and the cooling performance of the liquid cooling plate was obvious.