Quantifying the Effects of Stand and Climate Variables on Biomass of Larch Plantations Using Random Forests and National Forest Inventory Data in North and Northeast China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Plot and Climate Data
2.2. Random Forests Algorithm
2.3. Climate-Sensitive Stand Biomass Model Development
2.4. Model Validation and Evaluation
3. Results
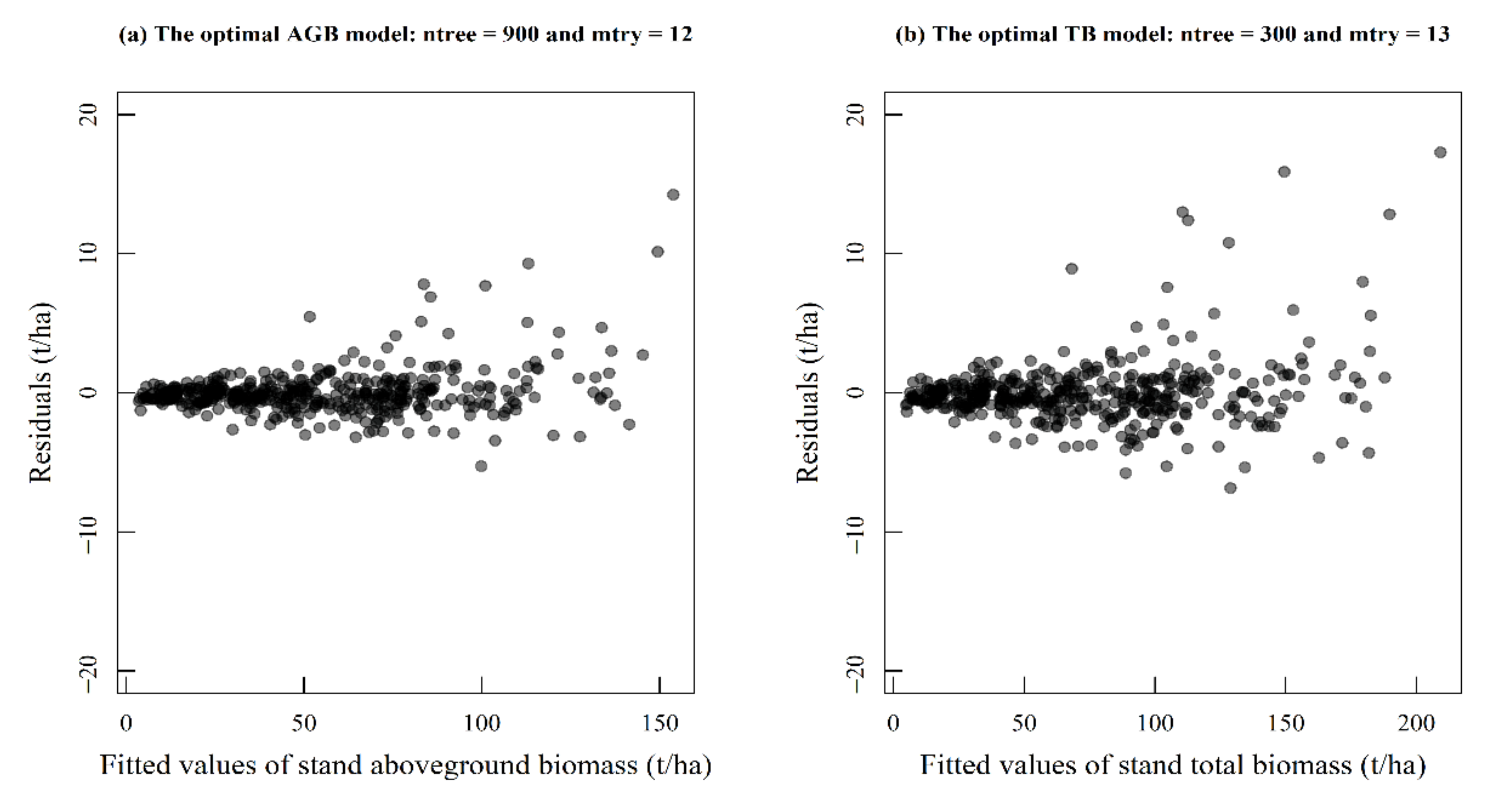
3.1. The Optimal Model
3.2. Relative Importance of Stand and Climate Factors
3.3. Partial Dependence of Stand Biomass on Stand and Climate Factors
4. Discussion
4.1. Applications of the Random Forests Algorithm for Estimating Stand Biomass
4.2. Relationship between Stand Factors and Stand Biomass
4.3. Relationship between Climate Factors and Stand Biomass
4.4. Uncertainty Analysis on Stand Biomass Estimation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Groot, R.S.; Alkemade, R.; Braat, L.; Hein, L.; Willemen, L. Challenges in integrating the concept of ecosystem services and values in landscape planning, management and decision making. Ecol. Complex. 2010, 7, 260–272. [Google Scholar] [CrossRef]
- Fang, J.; Chen, A.; Peng, C.; Zhao, S.; Ci, L. Changes in forest biomass carbon storage in China between 1949 and 1998. Science 2001, 292, 2320–2322. [Google Scholar] [CrossRef] [PubMed]
- Bi, H.; Long, Y.; Turner, J.; Lei, Y.; Snowdon, P.; Li, Y.; Harper, R.; Zerihun, A.; Ximenes, F. Additive prediction of aboveground biomass for Pinus radiata (D. Don) plantations. For. Ecol. Manag. 2010, 259, 2301–2314. [Google Scholar] [CrossRef]
- Jagodziński, A.M.; Dyderski, M.K.; Gęsikiewicz, K.; Horodecki, P. Tree-and stand-level biomass estimation in a Larix decidua Mill. Chronosequence. Forests 2018, 9, 587. [Google Scholar] [CrossRef] [Green Version]
- Jagodziński, A.M.; Dyderski, M.K.; Gęsikiewicz, K.; Horodecki, P. Tree and stand level estimations of Abies alba Mill. aboveground biomass. Ann. For. Sci. 2019, 76, 56. [Google Scholar] [CrossRef] [Green Version]
- Hu, M.; Lehtonen, A.; Minunno, F.; Mäkelä, A. Age effect on tree structure and biomass allocation in Scots pine (Pinus sylvestris L.) and Norway spruce (Picea abies [L.] Karst.). Ann. For. Sci. 2020, 77, 90. [Google Scholar] [CrossRef]
- Dong, L.; Zhang, L.; Li, F. Evaluation of stand biomass estimation methods for major forest types in the eastern Da Xing’an Mountains, Northeast China. Forests 2019, 10, 715. [Google Scholar] [CrossRef] [Green Version]
- Miettinen, J.; Ollikainen, M.; Nieminen, T.M.; Ukonmaanaho, L.; Laurén, A.; Hynynen, J.; Lehtonen, M.; Valsta, L. Whole-tree harvesting with stump removal versus stem-only harvesting in peatlands when water quality, biodiversity conservation and climate change mitigation matter. For. Policy Econ. 2014, 47, 25–35. [Google Scholar] [CrossRef]
- Bessaad, A.; Bilger, I.; Korboulewsky, N. Assessing Biomass Removal and Woody Debris in Whole-Tree Harvesting System: Are the Recommended Levels of Residues Ensured? Forests 2021, 12, 807. [Google Scholar] [CrossRef]
- Suchomel, C.; Pyttel, P.; Becker, G.; Bauhus, J. Biomass equations for sessile oak (Quercus petraea (Matt.) Liebl.) and hornbeam (Carpinus betulus L.) in aged coppiced forests in southwest Germany. Biomass Bioenergy 2012, 46, 722–730. [Google Scholar] [CrossRef]
- Fu, L.; Lei, X.; Hu, Z.; Zeng, W.; Tang, S.; Marshall, P.; Cao, L.; Song, X.; Yu, L.; Liang, J. Integrating regional climate change into allometric equations for estimating tree aboveground biomass of Masson pine in China. Ann. For. Sci. 2017, 74, 42. [Google Scholar] [CrossRef] [Green Version]
- Zeng, W.; Duo, H.; Lei, X.; Chen, X.; Wang, X.; Pu, Y.; Zou, W. Individual tree biomass equations and growth models sensitive to climate variables for Larix spp. in China. Eur. J. For. Res. 2017, 136, 233–249. [Google Scholar] [CrossRef]
- Cysneiros, V.C.; de Souza, F.C.; Gaui, T.D.; Pelissari, A.L.; Orso, G.A.; do Amaral Machado, S.; de Carvalho, D.C.; Silveira-Filho, T.B. Integrating climate, soil and stand structure into allometric models: An approach of site-effects on tree allometry in Atlantic Forest. Ecol. Indic. 2021, 127, 107794. [Google Scholar] [CrossRef]
- Rohner, B.; Waldner, P.; Lischke, H.; Ferretti, M.; Thürig, E. Predicting individual-tree growth of central European tree species as a function of site, stand, management, nutrient, and climate effects. Eur. J. For. Res. 2018, 137, 29–44. [Google Scholar] [CrossRef]
- Chave, J.; Réjou-Méchain, M.; Búrquez, A.; Chidumayo, E.; Colgan, M.S.; Delitti, W.B.; Duque, A.; Eid, T.; Fearnside, P.M.; Goodman, R.C. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Change Biol. 2014, 20, 3177–3190. [Google Scholar] [CrossRef]
- Schaphoff, S.; Reyer, C.P.; Schepaschenko, D.; Gerten, D.; Shvidenko, A. Tamm Review: Observed and projected climate change impacts on Russia’s forests and its carbon balance. For. Ecol. Manag. 2016, 361, 432–444. [Google Scholar] [CrossRef] [Green Version]
- Stegen, J.C.; Swenson, N.G.; Enquist, B.J.; White, E.P.; Phillips, O.L.; Jørgensen, P.M.; Weiser, M.D.; Monteagudo Mendoza, A.; Núñez Vargas, P. Variation in above-ground forest biomass across broad climatic gradients. Glob. Ecol. Biogeogr. 2011, 20, 744–754. [Google Scholar] [CrossRef]
- Usoltsev, V.A.; Shobairi, S.O.R.; Tsepordey, I.S.; Chasovskikh, V.P. Modeling the additive structure of stand biomass equations in climatic gradients of Eurasia. Environ. Qual. Manag. 2018, 28, 55–61. [Google Scholar] [CrossRef]
- Usoltsev, V.; Kovyazin, V.; Tsepordey, I.; Chasovskikh, V. What is a possible response of forest biomass to changes in Eurasian air temperature and precipitation? A special case for the genus Betula spp. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Saint Petersburg, Russian Federation, 16–18 June 2020; p. 012084. [Google Scholar]
- He, X.; Lei, X.-D.; Dong, L.-H. How large is the difference in large-scale forest biomass estimations based on new climate-modified stand biomass models? Ecol. Indic. 2021, 126, 107569. [Google Scholar] [CrossRef]
- Keith, H.; Mackey, B.G.; Lindenmayer, D.B. Re-evaluation of forest biomass carbon stocks and lessons from the world’s most carbon-dense forests. Proc. Natl. Acad. Sci. USA 2009, 106, 11635–11640. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Raich, J.W.; Russell, A.E.; Kitayama, K.; Parton, W.J.; Vitousek, P.M. Temperature influences carbon accumulation in moist tropical forests. Ecology 2006, 87, 76–87. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lei, X.; Zhang, H.; Mou, H. Compatible stand biomass models of Mongolia oak forests in over logged forest regions, Northeast China. Quat. Sci. 2010, 30, 559–565, (In Chinese with English Abstract). [Google Scholar]
- Ashraf, M.I.; Zhao, Z.; Bourque, C.P.-A.; MacLean, D.A.; Meng, F.-R. Integrating biophysical controls in forest growth and yield predictions with artificial intelligence technology. Can. J. For. Res. 2013, 43, 1162–1171. [Google Scholar] [CrossRef]
- Hamidi, S.K.; Zenner, E.K.; Bayat, M.; Fallah, A. Analysis of plot-level volume increment models developed from machine learning methods applied to an uneven-aged mixed forest. Ann. For. Sci. 2021, 78, 4. [Google Scholar] [CrossRef]
- Yousafzai, A.; Manzoor, W.; Raza, G.; Mahmood, T.; Rehman, F.; Hadi, R.; Shah, S.; Amin, M.; Akhtar, A.; Bashir, S. Forest yield prediction under different climate change scenarios using data intelligent models in Pakistan. Braz. J. Biol. 2021, 84. Available online: https://www.scielo.br/j/bjb/a/vBgTRjcxmgyFZR3TFqRVr8r/?lang=en (accessed on 1 March 2022). [CrossRef]
- Görgens, E.B.; Montaghi, A.; Rodriguez, L.C.E. A performance comparison of machine learning methods to estimate the fast-growing forest plantation yield based on laser scanning metrics. Comput. Electron. Agric. 2015, 116, 221–227. [Google Scholar] [CrossRef]
- Jachowski, N.R.; Quak, M.S.; Friess, D.A.; Duangnamon, D.; Webb, E.L.; Ziegler, A.D. Mangrove biomass estimation in Southwest Thailand using machine learning. Appl. Geogr. 2013, 45, 311–321. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, S.; Hogg, E.; Lieffers, V.; Qin, Y.; He, F. Estimating spatial variation in Alberta forest biomass from a combination of forest inventory and remote sensing data. Biogeosciences 2014, 11, 2793–2808. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Lu, D.; Li, G.; Wang, G.; Chen, Q.; Liu, L.; Li, D. Comparative analysis of modeling algorithms for forest aboveground biomass estimation in a subtropical region. Remote Sens. 2018, 10, 627. [Google Scholar] [CrossRef] [Green Version]
- Luo, M.; Wang, Y.; Xie, Y.; Zhou, L.; Qiao, J.; Qiu, S.; Sun, Y. Combination of Feature Selection and CatBoost for Prediction: The First Application to the Estimation of Aboveground Biomass. Forests 2021, 12, 216. [Google Scholar] [CrossRef]
- Puliti, S.; Hauglin, M.; Breidenbach, J.; Montesano, P.; Neigh, C.; Rahlf, J.; Solberg, S.; Klingenberg, T.; Astrup, R. Modelling above-ground biomass stock over Norway using national forest inventory data with ArcticDEM and Sentinel-2 data. Remote Sens. Environ. 2020, 236, 111501. [Google Scholar] [CrossRef]
- Hauglin, M.; Rahlf, J.; Schumacher, J.; Astrup, R.; Breidenbach, J. Large scale mapping of forest attributes using heterogeneous sets of airborne laser scanning and National Forest Inventory data. For. Ecosyst. 2021, 8, 65. [Google Scholar] [CrossRef]
- Vahedi, A.A. Artificial neural network application in comparison with modeling allometric equations for predicting above-ground biomass in the Hyrcanian mixed-beech forests of Iran. Biomass Bioenergy 2016, 88, 66–76. [Google Scholar] [CrossRef]
- Wu, C.; Chen, Y.; Peng, C.; Li, Z.; Hong, X. Modeling and estimating aboveground biomass of Dacrydium pierrei in China using machine learning with climate change. J. Environ. Manag. 2019, 234, 167–179. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Statistical modeling: The two cultures (with comments and a rejoinder by the author). Stat. Sci. 2001, 16, 199–231. [Google Scholar] [CrossRef]
- Calle, M.L.; Urrea, V. Stability of Random Forest importance measures. Brief. Bioinform. 2011, 12, 86–89. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Zhao, S.; Zhao, H.; Xu, M.; Zhang, L.; Wen, H.; Sheng, Q. Spatiotemporal Assessment of Forest Biomass Carbon Sinks: The Relative Roles of Forest Expansion and Growth in Sichuan Province, China. J. Environ. Qual. 2017, 46, 64–71. [Google Scholar] [CrossRef]
- Kindermann, G.E. The development of a simple basal area increment model. Nat. Preced. 2011, 127, 147–178. [Google Scholar] [CrossRef] [Green Version]
- Diamantopoulou, M.J.; Özçelik, R.; Yavuz, H. Tree-bark volume prediction via machine learning: A case study based on black alder’s tree-bark production. Comput. Electron. Agric. 2018, 151, 431–440. [Google Scholar] [CrossRef]
- Ou, Q.; Lei, X.; Shen, C. Individual tree diameter growth models of larch–spruce–fir mixed forests based on machine learning algorithms. Forests 2019, 10, 187. [Google Scholar] [CrossRef] [Green Version]
- Jevšenak, J.; Skudnik, M. A random forest model for basal area increment predictions from national forest inventory data. For. Ecol. Manag. 2021, 479, 118601. [Google Scholar] [CrossRef]
- State Forestry and Grassland Administration of China. Report of Forest Resources in China (2014–2018); China Forestry Publishing House: Beijing, China, 2019. [Google Scholar]
- Zhou, G.; Wang, Y.; Jiang, Y.; Yang, Z. Estimating biomass and net primary production from forest inventory data: A case study of China’s Larix forests. For. Ecol. Manag. 2002, 169, 149–157. [Google Scholar] [CrossRef]
- Dong, L.; Li, F. Additive stand-level biomass models for natural larch forest in the East of Daxing’ an Mountains. Sci. Silvae Sin. 2016, 52, 13–21, (In Chinese with English Abstract). [Google Scholar]
- Zang, H.; Lei, X.; Zeng, W. Height–diameter equations for larch plantations in northern and northeastern China: A comparison of the mixed-effects, quantile regression and generalized additive models. For. Int. J. For. Res. 2016, 89, 434–445. [Google Scholar] [CrossRef]
- Lei, X.; Yu, L.; Hong, L. Climate-sensitive integrated stand growth model (CS-ISGM) of Changbai larch (Larix olgensis) plantations. For. Ecol. Manag. 2016, 376, 265–275. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, H.; Lei, X. Application of the 3-PG model to predict growth of Larix olgensis plantations in northeastern China. For. Ecol. Manag. 2017, 406, 208–218. [Google Scholar] [CrossRef]
- Lei, X.; Tang, M.; Lu, Y.; Hong, L.; Tian, D. Forest inventory in China: Status and challenges. Int. For. Rev. 2009, 11, 52–63. [Google Scholar] [CrossRef]
- Zeng, W.; Tomppo, E.; Healey, S.P.; Gadow, K.V. The national forest inventory in China: History-results-international context. For. Ecosyst. 2015, 2, 23. [Google Scholar] [CrossRef] [Green Version]
- State Forestry Administration of China. Tree Biomass Models and Related Parameters to Carbon Accounting for Larix; Standards Press of China: Beijing, China, 2016. [Google Scholar]
- Wang, C. Biomass allometric equations for 10 co-occurring tree species in Chinese temperate forests. For. Ecol. Manag. 2006, 222, 9–16. [Google Scholar] [CrossRef]
- Wang, T.; Wang, G.; Innes, J.L.; Seely, B.; Chen, B. ClimateAP: An application for dynamic local downscaling of historical and future climate data in Asia Pacific. Front. Agric. Sci. Eng. 2017, 4, 448–458. [Google Scholar] [CrossRef] [Green Version]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013. [Google Scholar]
- Grömping, U. Variable importance assessment in regression: Linear regression versus random forest. Am. Stat. 2009, 63, 308–319. [Google Scholar] [CrossRef]
- Zhang, G.; Yue, C.; Zhao, X.; Luo, H.; Gu, L. Aboveground Biomass Estimation of Simao pinewith Stand Average Height and Density of Plantation. J. Northeast For. Univ. 2021, 49, 16–22, (In Chinese with English Abstract). [Google Scholar]
- Liu, K.; Wang, J.; Zeng, W.; Song, J. Comparison and evaluation of three methods for estimating forest above ground biomass using TM and GLAS data. Remote Sens. 2017, 9, 341. [Google Scholar] [CrossRef] [Green Version]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- Fukuda, S.; Yasunaga, E.; Nagle, M.; Yuge, K.; Sardsud, V.; Spreer, W.; Müller, J. Modelling the relationship between peel colour and the quality of fresh mango fruit using Random Forests. J. Food Eng. 2014, 131, 7–17. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Xia, Y.; Liu, C.; Li, Y.; Liu, N. A boosted decision tree approach using Bayesian hyper-parameter optimization for credit scoring. Expert Syst. Appl. 2017, 78, 225–241. [Google Scholar] [CrossRef]
- Fayed, H.A.; Atiya, A.F. Speed up grid-search for parameter selection of support vector machines. Appl. Soft Comput. 2019, 80, 202–210. [Google Scholar] [CrossRef]
- Sun, Y.; Ding, S.; Zhang, Z.; Jia, W. An improved grid search algorithm to optimize SVR for prediction. Soft Comput. 2021, 25, 5633–5644. [Google Scholar] [CrossRef]
- Roberts, D.R.; Bahn, V.; Ciuti, S.; Boyce, M.S.; Elith, J.; Guillera-Arroita, G.; Hauenstein, S.; Lahoz-Monfort, J.J.; Schröder, B.; Thuiller, W. Cross-validation strategies for data with temporal, spatial, hierarchical, or phylogenetic structure. Ecography 2017, 40, 913–929. [Google Scholar] [CrossRef]
- Usoltsev, V.A.; Shobairi, S.O.R.; Tsepordey, I.S.; Chasovkikh, V.P. Modelling forest stand biomass and net primary production with the focus on additive models sensitive to climate variables for two-needled Pines in Eurasia. J. Clim. Change 2019, 5, 41–49. [Google Scholar] [CrossRef]
- Castedo-Dorado, F.; Gómez-García, E.; Diéguez-Aranda, U.; Barrio-Anta, M.; Crecente-Campo, F. Aboveground stand-level biomass estimation: A comparison of two methods for major forest species in northwest Spain. Ann. For. Sci. 2012, 69, 735–746. [Google Scholar] [CrossRef]
- Cannell, M. Woody biomass of forest stands. For. Ecol. Manag. 1984, 8, 299–312. [Google Scholar] [CrossRef]
- Rahman, M.M.; Kabir, M.E.; Akon, A.J.U.; Ando, K. High carbon stocks in roadside plantations under participatory management in Bangladesh. Glob. Ecol. Conserv. 2015, 3, 412–423. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.N.I.; Shil, M.C.; Azad, M.S.; Sadath, M.N.; Feroz, S.; Mollick, A.S. Allometric relationships of stem volume and stand level carbon stocks at varying stand density in Swietenia macrophylla King plantations, Bangladesh. For. Ecol. Manag. 2018, 430, 639–648. [Google Scholar] [CrossRef]
- Khan, M.N.I.; Islam, M.R.; Rahman, A.; Azad, M.S.; Mollick, A.S.; Kamruzzaman, M.; Sadath, M.N.; Feroz, S.; Rakkibu, M.G.; Knohl, A. Allometric relationships of stand level carbon stocks to basal area, tree height and wood density of nine tree species in Bangladesh. Glob. Ecol. Conserv. 2020, 22, e01025. [Google Scholar] [CrossRef]
- Yuan, Z.; Ali, A.; Jucker, T.; Ruiz-Benito, P.; Wang, S.; Jiang, L.; Wang, X.; Lin, F.; Ye, J.; Hao, Z.; et al. Multiple abiotic and biotic pathways shape biomass demographic processes in temperate forests. Ecology 2019, 100, e02650. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.; Lei, X.; Guo, H.; Li, H.; Li, Y. Stand biomass model of Larix olgensis plantations based on multi-layer perceptron networks. J. Beijing For. Univ. 2019, 42, 97–107, (In Chinese with English Abstract). [Google Scholar]
- Ali, A.; Lin, S.-L.; He, J.-K.; Kong, F.-M.; Yu, J.-H.; Jiang, H.-S. Climate and soils determine aboveground biomass indirectly via species diversity and stand structural complexity in tropical forests. For. Ecol. Manag. 2019, 432, 823–831. [Google Scholar] [CrossRef]
- Gao, W.-Q.; Lei, X.-D.; Liang, M.-W.; Larjavaara, M.; Li, Y.-T.; Gao, D.-L.; Zhang, H.-R. Biodiversity increased both productivity and its spatial stability in temperate forests in northeastern China. Sci. Total Environ. 2021, 780, 146674. [Google Scholar] [CrossRef] [PubMed]
- Rudgers, J.A.; Hallmark, A.; Baker, S.R.; Baur, L.; Hall, K.M.; Litvak, M.E.; Muldavin, E.H.; Pockman, W.T.; Whitney, K.D. Sensitivity of dryland plant allometry to climate. Funct. Ecol. 2019, 33, 2290–2303. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, X.; Zhang, X.; Ren, Y.; Poorter, H. Variation in biomass expansion factors for China’s forests in relation to forest type, climate, and stand development. Ann. For. Sci. 2013, 70, 589–599. [Google Scholar] [CrossRef] [Green Version]
- Luo, H.; Zhang, C.; Wei, A. The Effect of Climate on the Biomass of Pinus yunnanensis Standing Forest. J. Southwest For. Univ. 2017, 37, 99–104, (In Chinese with English Abstract). [Google Scholar]
- Saatchi, S.S.; HOUGHTON, R.A.; Dos Santos Alvala, R.; Soares, J.V.; Yu, Y. Distribution of aboveground live biomass in the Amazon basin. Glob. Change Biol. 2007, 13, 816–837. [Google Scholar] [CrossRef]
- Ciais, P.; Reichstein, M.; Viovy, N.; Granier, A.; Ogée, J.; Allard, V.; Aubinet, M.; Buchmann, N.; Bernhofer, C.; Carrara, A. Europe-wide reduction in primary productivity caused by the heat and drought in 2003. Nature 2005, 437, 529–533. [Google Scholar] [CrossRef]
- Usoltsev, V.A.; Shobairi, S.O.R.; Petrovich, V. Modeling the additive stand biomass of Larix spp. for Eurasia. Ecol. Quest. 2019, 30, 35–46. [Google Scholar]
- Zhou, G.; Liu, Q.; Xu, Z.; Du, W.; Yu, J.; Meng, S.; Zhou, H.; Qin, L.; Shah, S. How can the shade intolerant Korean pine survive under dense deciduous canopy? For. Ecol. Manag. 2020, 457, 117735. [Google Scholar] [CrossRef]
- Wang, G.; Guan, D.; Xiao, L.; Peart, M. Forest biomass-carbon variation affected by the climatic and topographic factors in Pearl River Delta, South China. J. Environ. Manag. 2019, 232, 781–788. [Google Scholar] [CrossRef] [PubMed]
- Becknell, J.M.; Kucek, L.K.; Powers, J.S. Aboveground biomass in mature and secondary seasonally dry tropical forests: A literature review and global synthesis. For. Ecol. Manag. 2012, 276, 88–95. [Google Scholar] [CrossRef]
- Sileshi, G.W. A critical review of forest biomass estimation models, common mistakes and corrective measures. For. Ecol. Manag. 2014, 329, 237–254. [Google Scholar] [CrossRef]
- Fu, Y.; Lei, Y.; Zeng, W.; Hao, R.; Zhang, G.; Zhong, Q.; Xu, M. Uncertainty assessment in aboveground biomass estimation at the regional scale using a new method considering both sampling error and model error. Can. J. For. Res. 2017, 47, 1095–1103. [Google Scholar] [CrossRef] [Green Version]
- Lehtonen, A.; Cienciala, E.; Tatarinov, F.; Mäkipää, R. Uncertainty estimation of biomass expansion factors for Norway spruce in the Czech Republic. Ann. For. Sci. 2007, 64, 133–140. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Lei, X.; Liu, C.; Huang, H.; Zhou, C.; Peng, C. Re-estimating the changes and ranges of forest biomass carbon in China during the past 40 years. For. Ecosyst. 2019, 6, 51. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Yue, T.; Lei, Y.; Du, Z.; Zhao, M. Uncertainty of forest biomass carbon patterns simulation on provincial scale: A case study in Jiangxi Province, China. J. Geogr. Sci. 2016, 26, 568–584. [Google Scholar] [CrossRef] [Green Version]
- Garnett, M.H.; Ineson, P.; Stevenson, A.C.; Howard, D.C. Terrestrial organic carbon storage in a British moorland. Glob. Change Biol. 2001, 7, 375–388. [Google Scholar] [CrossRef] [Green Version]
- Abella, S.R.; Gering, L.R.; Shelburne, V.B. Slope correction of plot dimensions for vegetation sampling in mountainous terrain. Nat. Areas J. 2004, 24, 358–360. [Google Scholar]
- Chave, J.; Condit, R.; Aguilar, S.; Hernandez, A.; Lao, S.; Perez, R. Error propagation and scaling for tropical forest biomass estimates. Philos. Trans. R. Soc. London. Ser. B Biol. Sci. 2004, 359, 409–420. [Google Scholar] [CrossRef]
- Liu, C.; Zhou, X.; Lei, X.; Huang, H.; Zhou, C.; Peng, C.; Wang, X. Separating Regressions for model fitting to reduce the uncertainty in forest volume-biomass relationship. Forests 2019, 10, 658. [Google Scholar] [CrossRef] [Green Version]
- Keller, M.; Palace, M.; Hurtt, G. Biomass estimation in the Tapajos National Forest, Brazil: Examination of sampling and allometric uncertainties. For. Ecol. Manag. 2001, 154, 371–382. [Google Scholar] [CrossRef]
- Poorter, L.; Bongers, F.; Aide, T.M.; Almeyda Zambrano, A.M.; Balvanera, P.; Becknell, J.M.; Boukili, V.; Brancalion, P.H.; Broadbent, E.N.; Chazdon, R.L. Biomass resilience of Neotropical secondary forests. Nature 2016, 530, 211–214. [Google Scholar] [CrossRef] [PubMed]
- Anderson-Teixeira, K.J.; Davies, S.J.; Bennett, A.C.; Gonzalez-Akre, E.B.; Muller-Landau, H.C.; Joseph Wright, S.; Abu Salim, K.; Almeyda Zambrano, A.M.; Alonso, A.; Baltzer, J.L. CTFS-Forest GEO: A worldwide network monitoring forests in an era of global change. Glob. Change Biol. 2015, 21, 528–549. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rozendaal, D.M.; Suarez, D.R.; De Sy, V.; Avitabile, V.; Carter, S.; Yao, C.A.; Alvarez-Davila, E.; Anderson-Teixeira, K.; Araujo-Murakami, A.; Arroyo, L. Aboveground forest biomass varies across continents, ecological zones and successional stages: Refined IPCC default values for tropical and subtropical forests. Environ. Res. Lett. 2022, 17, 014047. [Google Scholar] [CrossRef]
- Bloomberg, M.; Mason, E.G.; Jarvis, P.; Sedcole, R. Predicting seedling biomass of radiata pine from allometric variables. New For. 2008, 36, 103–114. [Google Scholar] [CrossRef]
- Panda, M.R.; Oraon, P.R.; Tirkey, P. Distribution of woody biomass reserves in tropical dry Sal (Shorea robusta roth.) forests of Ranchi. Pharma Innov. J. 2020, 9, 477–482. [Google Scholar]
- Kaarakka, L.; Tamminen, P.; Saarsalmi, A.; Kukkola, M.; Helmisaari, H.-S.; Burton, A.J. Effects of repeated whole-tree harvesting on soil properties and tree growth in a Norway spruce (Picea abies (L.) Karst.) stand. For. Ecol. Manag. 2014, 313, 180–187. [Google Scholar] [CrossRef]
- Aherne, J.; Posch, M.; Forsius, M.; Lehtonen, A.; Härkönen, K. Impacts of forest biomass removal on soil nutrient status under climate change: A catchment-based modelling study for Finland. Biogeochemistry 2012, 107, 471–488. [Google Scholar] [CrossRef]
- Augusto, L.; Achat, D.L.; Bakker, M.R.; Bernier, F.; Bert, D.; Danjon, F.; Khlifa, R.; Meredieu, C.; Trichet, P. Biomass and nutrients in tree root systems–sustainable harvesting of an intensively managed Pinus pinaster (Ait.) planted forest. Gcb Bioenergy 2015, 7, 231–243. [Google Scholar] [CrossRef]
- Chave, J.; Condit, R.; Lao, S.; Caspersen, J.P.; Foster, R.B.; Hubbell, S.P. Spatial and temporal variation of biomass in a tropical forest: Results from a large census plot in Panama. J. Ecol. 2003, 91, 240–252. [Google Scholar] [CrossRef]





| Factors | Variables | Units | Mean | Min. | Max. | S.D. | Description |
|---|---|---|---|---|---|---|---|
| Stand | AGB | t/ha | 53.98 | 2.75 | 168.07 | 33.49 | Stand aboveground biomass |
| TB | t/ha | 72.05 | 3.74 | 226.50 | 44.53 | Stand total biomass | |
| H | m | 12.0 | 4.2 | 24.0 | 4.0 | Stand average height | |
| Dg | cm | 13.4 | 6.0 | 26.4 | 4.3 | Stand quadratic mean diameter at breast height | |
| V | m3/ha | 82.81 | 3.28 | 282.25 | 53.22 | Stand volume | |
| Ba | m2/ha | 13.55 | 0.93 | 38.48 | 7.63 | Stand basal area | |
| N | trees/ha | 1021 | 263 | 3933 | 595 | Stand density | |
| Age | a | 28 | 11 | 60 | 9 | Stand average age | |
| Climate | AHM | - | 22.5 | 11.7 | 39.8 | 4.9 | Annual heat-moisture index (MAT + 10)/(MAP/1000)) |
| CMD | - | 185 | 35 | 382 | 74 | Hargreaves climate moisture deficit | |
| DD_0 | days | 1537 | 425 | 3250 | 513 | Degree-days below 0 °C | |
| DD_18 | days | 5332 | 3601 | 7867 | 788 | Degree-days below 18 °C | |
| DD18 | days | 191 | 12 | 489 | 108 | Degree-days above 18 °C | |
| DD5 | days | 1882 | 1012 | 2707 | 354 | Degree-days above 5 °C | |
| EMT | °C | −30.5 | −43.8 | −17.7 | 4.2 | Extreme minimum temperature over a 30-year period | |
| EREF | °C | 701 | 510 | 912 | 60 | Extreme maximum temperature over a 30-year period | |
| EXT | - | 32.6 | 25.5 | 35.1 | 1.5 | Hargreaves reference evaporation | |
| MAP | mm | 625 | 382 | 1050 | 146 | Mean annual precipitation | |
| MAT | °C | 3.6 | −4.0 | 9.2 | 2.4 | Mean annual temperature | |
| MCMT | °C | −16.0 | −27.0 | −5.6 | 3.9 | Mean coldest month temperature | |
| MWMT | °C | 20.4 | 14.8 | 24.0 | 1.9 | Mean warmest month temperature | |
| NFFD | days | 171 | 111 | 224 | 20 | The number of frost-free days | |
| PAS | mm | 52 | 14 | 133 | 21 | Precipitation as snow between August in previous year and July in current year | |
| TD | °C | 36.4 | 25.0 | 45.2 | 3.8 | Temperature difference between MWMT and MCMT, or continentality |
| Model | RMSE (t ha−1) | RRMSE |
|---|---|---|
| AGB = 0.2249V0.9558AHM0.1536TD0.2228 | 5.2501 ± 1.1921 | 9.8075% ± 2.4826% |
| AGB = 0.7202BA0.9639H0.4079AHM−0.1341TD0.3287 | 4.9730 ± 0.6162 | 9.2079% ± 0.7672% |
| AGB model based on RF with ntree = 900 and mtry = 12 | 3.8008 ± 1.1350 | 7.0671% ± 2.1095% |
| TB = 0.2117V0.9471AHM0.1056TD0.3718 | 6.4483 ± 1.5948 | 9.0377% ± 2.5060% |
| TB = 0.7295BA0.9420H0.4296AHM−0.1687TD0.4362 | 6.9059 ± 0.9002 | 9.5804% ± 0.8853% |
| TB model based on RF with ntree = 300 and mtry = 13 | 5.1963 ± 1.5904 | 7.2418% ± 2.2730% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Lei, X.; Zeng, W.; Feng, L.; Zhou, C.; Wu, B. Quantifying the Effects of Stand and Climate Variables on Biomass of Larch Plantations Using Random Forests and National Forest Inventory Data in North and Northeast China. Sustainability 2022, 14, 5580. https://doi.org/10.3390/su14095580
He X, Lei X, Zeng W, Feng L, Zhou C, Wu B. Quantifying the Effects of Stand and Climate Variables on Biomass of Larch Plantations Using Random Forests and National Forest Inventory Data in North and Northeast China. Sustainability. 2022; 14(9):5580. https://doi.org/10.3390/su14095580
Chicago/Turabian StyleHe, Xiao, Xiangdong Lei, Weisheng Zeng, Linyan Feng, Chaofan Zhou, and Biyun Wu. 2022. "Quantifying the Effects of Stand and Climate Variables on Biomass of Larch Plantations Using Random Forests and National Forest Inventory Data in North and Northeast China" Sustainability 14, no. 9: 5580. https://doi.org/10.3390/su14095580
APA StyleHe, X., Lei, X., Zeng, W., Feng, L., Zhou, C., & Wu, B. (2022). Quantifying the Effects of Stand and Climate Variables on Biomass of Larch Plantations Using Random Forests and National Forest Inventory Data in North and Northeast China. Sustainability, 14(9), 5580. https://doi.org/10.3390/su14095580







