Two-Part Tariff of Pumped Storage Power Plants for Wind Power Accommodation
Abstract
:1. Introduction
- Study the two-part tariff mechanism of pumped storage power plants considering the wind power accommodation scenario and realize the rationality and economy of pumped storage charging and discharging strategy by using the peak-valley price difference of wind power, so as to improve the competitiveness of pumped storage power plants to participate in electricity market transactions.
- Determine the capacity tariff in the two-part pumped storage tariff through the approved operating period tariff method based on the principles of reasonable compensation of costs and reasonable determination of revenues and taxation in accordance with the law.
- Considering the economic advantages of “pumped storage + clean energy”, a pumped storage and wind power joint optimization scheduling model is to be established based on the original pumped storage pricing method. The pumped storage power electricity tariff is set on the basis of compensating variable costs through the optimal operation strategy obtained.
- Analyze and illustrate the feasibility of pumped storage power plants to reduce fossil energy consumption in several scenarios.
2. Two-Part Tariff
2.1. General Structure of the Two-Part Tariff System
2.2. Influencing Factors of the Two-Part Tariff
2.2.1. Influence of Different Operating Strategies
2.2.2. Influence of Uncertainty of New Energy Output
2.2.3. Influence of Seasonal Storage Changes in Pumped Storage Power Plants
3. Modeling of a Two-Part Tariff Setting Strategy for Pumped Storage Power Plants
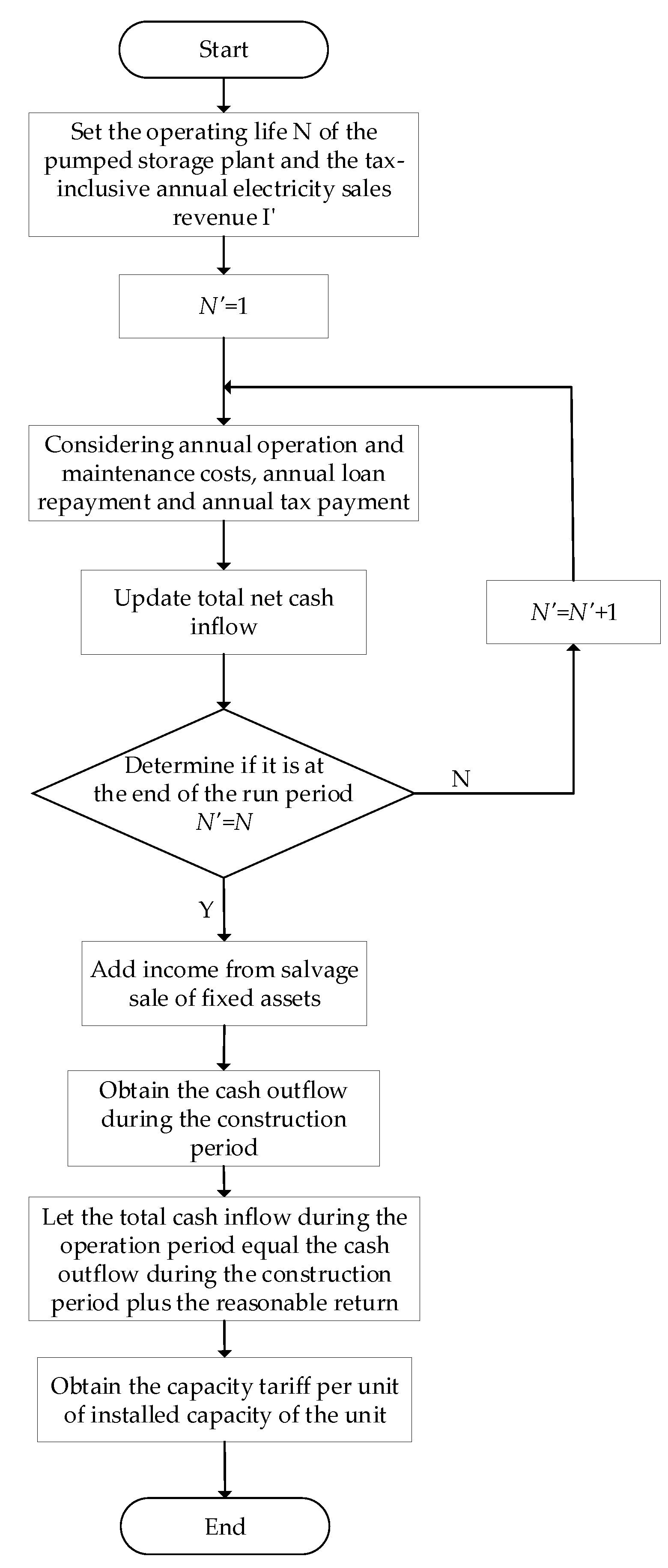
3.1. Methodology for Approving Capacity Tariffs
3.2. Modeling the Strategy for Setting Electricity Tariffs
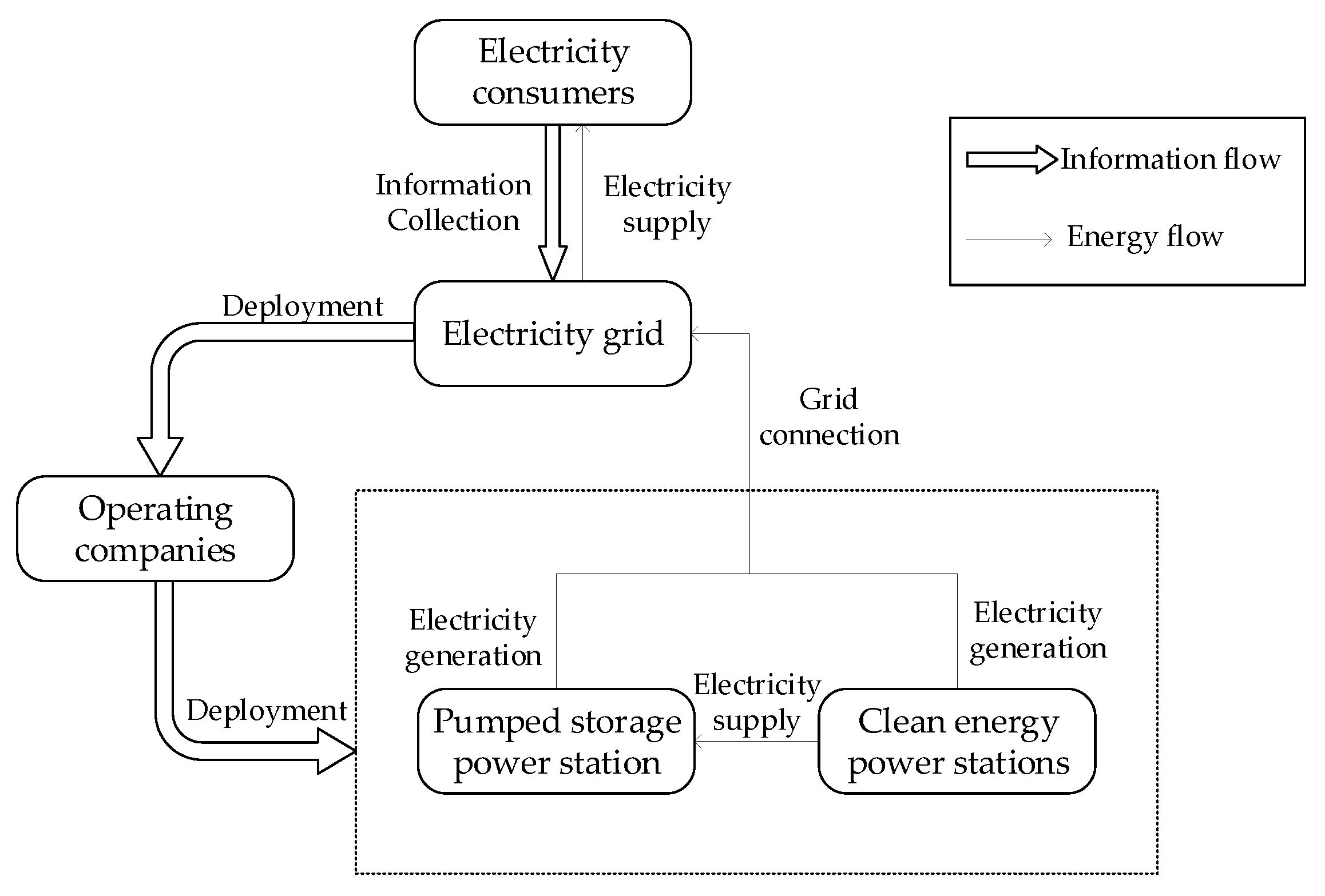
3.2.1. Background
3.2.2. Model
3.2.3. Constraints
3.2.4. Algorithm and Solving Process
4. Case Study and Discussion
4.1. Result Analysis
4.2. Analysis of Two-Part Tariff
4.2.1. Setting of the Scenarios
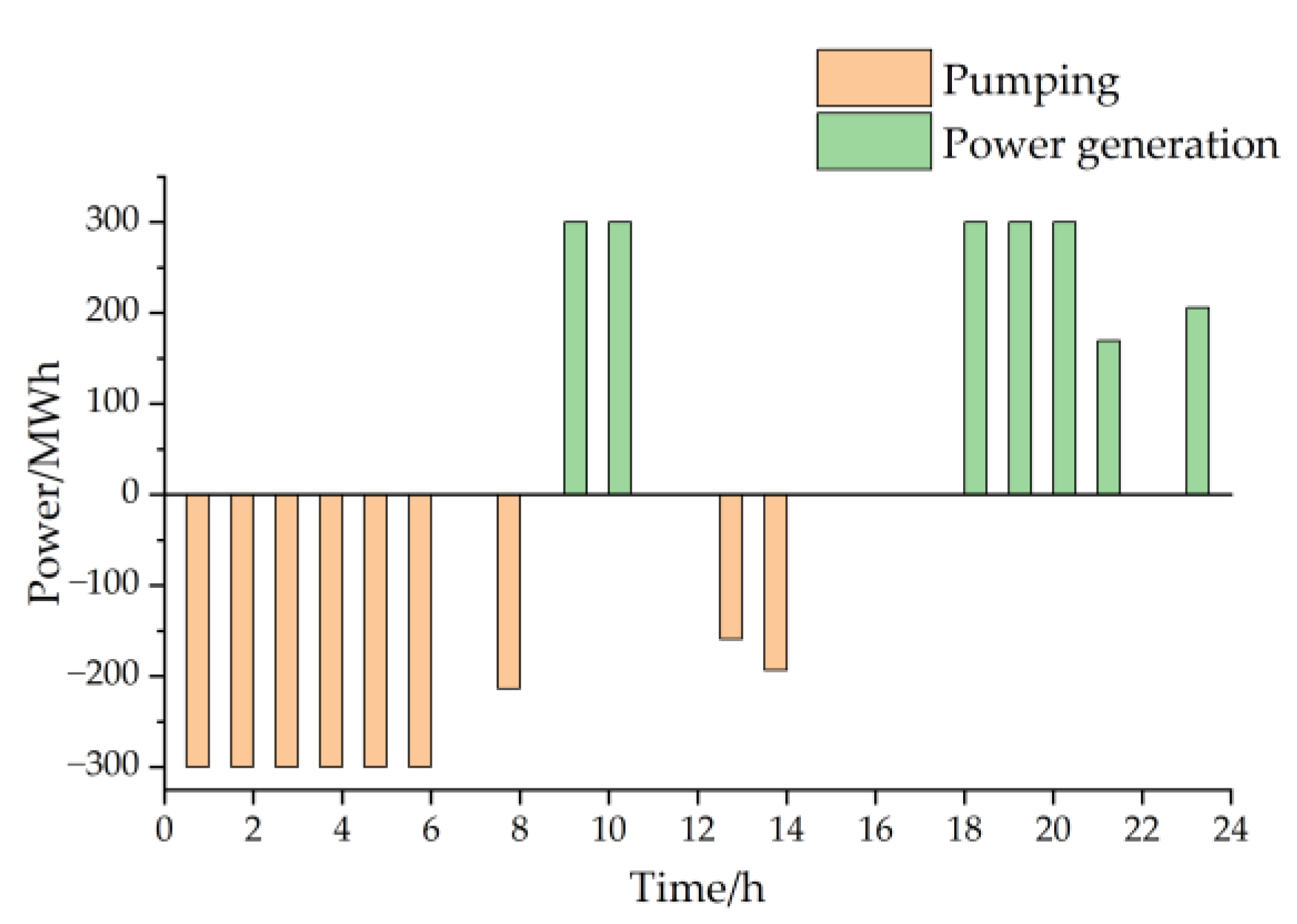
4.2.2. Analysis of Unit Output
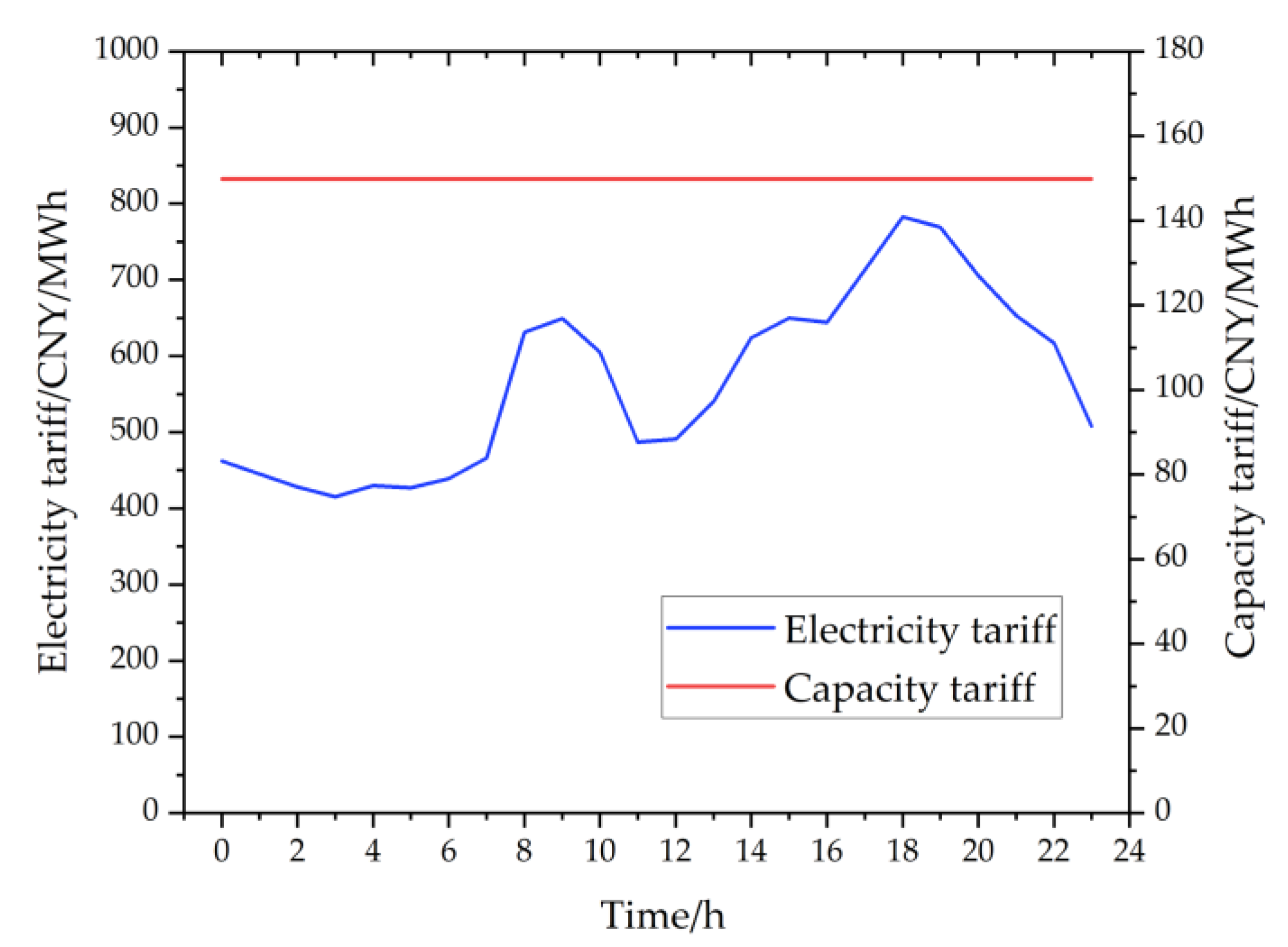
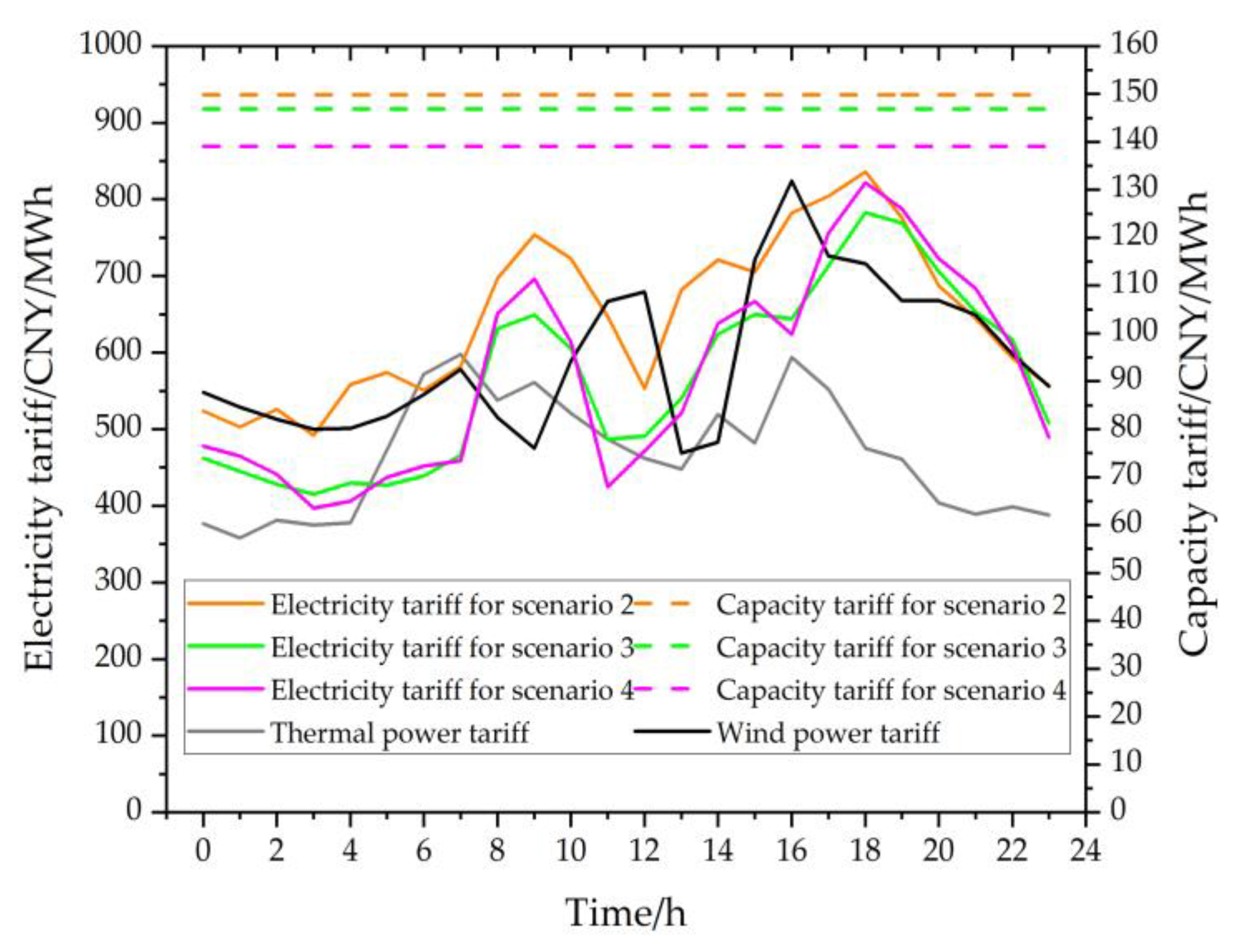
4.2.3. Analysis of Cost and Tariff
4.3. Sensitivity Analysis of Two-Part Tariff for Pumped Storage
4.3.1. Impact of Installed Capacity of Pumped Storage Units on Two-Part Tariff
4.3.2. Impact of Pumped Storage Plant Storage Capacity on Two-Part Tariff
5. Conclusions
- Pumped storage power plants combined with wind power plants to participate in the electricity market can increase the amount of wind power accommodation, reduce fossil energy consumption, and significantly improve the economy of the joint operation system.
- The electricity tariff of a pumped storage power plant is mainly determined by the pumping cost and the capacity electricity price is mainly determined by the capital investment and total generation capacity during the construction period. The electricity tariff and the capacity tariff are 560 CNY/MWh on average and 146.83 CNY/MWh, respectively, in the example.
- The electricity tariff of pumped storage power plants decreases as the installed capacity increases. The lowest electricity tariff is achieved when the appropriate reservoir capacity is selected, and the upper and lower initial reservoir capacity ratios are 1:1. The electricity tariff of a pumped storage power plant is lowest when the ratio of the capacity to the upper reservoir capacity is 1:6.37 (MW/million m3).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dong, J.; Liu, D.R.; Dou, X.H.; Li, B.; Lv, S.Y.; Jiang, Y.Z.; Ma, T.T. Key Issues and Technical Applications in the Study of Power Markets as the System Adapts to the New Power System in China. Sustainability 2021, 13, 13409. [Google Scholar] [CrossRef]
- Tan, K.M.; Babu, T.S.; Ramachandaramurthy, V.K.; Kasinathan, P.; Solanki, S.G.; Raveendran, S.K. Empowering smart grid: A comprehensive review of energy storage technology and application with renewable energy integration. J. Energy Storage 2021, 39, 102591. [Google Scholar] [CrossRef]
- Li, X.J.; Wang, S.X. Energy Management and Operational Control Methods for Grid Battery Energy Storage Systems. CSEE J. Power Energy Syst. 2021, 7, 1026–1040. [Google Scholar] [CrossRef]
- Steffen, B. Prospects for pumped-hydro storage in Germany. Energy Policy 2012, 45, 420–429. [Google Scholar] [CrossRef] [Green Version]
- Benato, A.; Stoppato, A. Pumped Thermal Electricity Storage: A technology overview. Therm. Sci. Eng. Prog. 2018, 6, 301–315. [Google Scholar] [CrossRef]
- Zhang, F.Q.; Xu, Z.C.; Jiao, B.Q.; Feng, J.S. Study on pricing mechanism of pumped hydro energy storage (PHES) under China’s electricity tariff reform. In Proceedings of the 4th International Conference on Energy Materials and Environment Engineering (ICEMEE), Kuala Lumpur, Malaysia, 13–15 April 2018. [Google Scholar]
- Guan, S.P.; Miao, X.Y.; Gao, Y.J.; Yang, P.P.; Wang, B.B.; Lu, J.W.; IEEE. Overview of the Electricity Futures Market. In Proceedings of the 3rd IEEE International Electrical and Energy Conference (CIEEC), Beijing, China, 7–9 September 2019; pp. 953–957. [Google Scholar]
- Ngan, H.W. Electricity regulation and electricity market reforms in China. Energy Policy 2010, 38, 2142–2148. [Google Scholar] [CrossRef]
- Rehman, S.; Al-Hadhrami, L.M.; Alam, M.M. Pumped hydro energy storage system: A technological review. Renew. Sustain. Energy Rev. 2015, 44, 586–598. [Google Scholar] [CrossRef]
- Luo, Y.H.; Nie, Q.B.; Yang, D.S.; Zhou, B.W. Robust Optimal Operation of Active Distribution Network Based on Minimum Confidence Interval of Distributed Energy Beta Distribution. J. Mod. Power Syst. Clean Energy 2021, 9, 423–430. [Google Scholar] [CrossRef]
- Yang, D.J.; Kim, J.; Kang, Y.C.; Muljadi, E.; Zhang, N.; Hong, J.; Song, S.H.; Zheng, T.Y. Temporary Frequency Support of a DFIG for High Wind Power Penetration. IEEE Trans. Power Syst. 2018, 33, 3428–3437. [Google Scholar] [CrossRef]
- Yang, D.J.; Jin, Z.Y.; Zheng, T.Y.; Jin, E.S. An adaptive droop control strategy with smooth rotor speed recovery capability for type III wind turbine generators. Int. J. Electr. Power Energy Syst. 2022, 135, 107532. [Google Scholar] [CrossRef]
- Sun, B.X.; Tian, S.P.; He, J.; Liu, L.D.; Wang, Z.Q.; Guo, J.W.; Xu, F.; Cheng, T.; Li, J.H. Review on Pumped Storage Power Station in High Proportion Renewable Energy Power System. In Proceedings of the 3rd IEEE Student Conference on Electrical Machines and Systems (SCEMS), Jinan, China, 4–6 December 2020; pp. 1001–1006. [Google Scholar]
- Li, J.Y.; Fu, J.; Gao, S.J. A conception of a new generation of pumped storage power station with multiple energy coupling. In Proceedings of the 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018. [Google Scholar]
- Rong, S.; Chen, X.G.; Guan, W.L.; Xu, M.Y. Coordinated dispatching strategy of multiple energy sources for wind power consumption. J. Mod. Power Syst. Clean Energy 2019, 7, 1461–1471. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.B.; Chen, D.Y.; Venkateshkumar, M.; Xiao, Y.; Yue, Y.; Xing, Y.Q.; Li, P.Q. Modeling a pumped storage hydropower integrated to a hybrid power system with solar-wind power and its stability analysis. Appl. Energy 2019, 248, 446–462. [Google Scholar] [CrossRef]
- Khani, H.; Farag, H.E.Z. Joint Arbitrage and Operating Reserve Scheduling of Energy Storage Through Optimal Adaptive Allocation of the State of Charge. IEEE Trans. Sustain. Energy 2019, 10, 1705–1717. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Xu, Y.; Yang, H.M.; Dong, Z.Y.; Zhang, R. Optimal Whole-Life-Cycle Planning of Battery Energy Storage for Multi-Functional Services in Power Systems. IEEE Trans. Sustain. Energy 2020, 11, 2077–2086. [Google Scholar] [CrossRef]
- Luo, Y.H.; Zhang, X.W.; Yang, D.S.; Sun, Q.Y. Emission Trading Based Optimal Scheduling Strategy of Energy Hub with Energy Storage and Integrated Electric Vehicles. J. Mod. Power Syst. Clean Energy 2020, 8, 267–275. [Google Scholar] [CrossRef]
- Qiu, T.; Xu, B.L.; Wang, Y.S.; Dvorkin, Y.; Kirschen, D.S. Stochastic Multistage Coplanning of Transmission Expansion and Energy Storage. IEEE Trans. Power Syst. 2017, 32, 643–651. [Google Scholar] [CrossRef]
- Ma, B.; Geng, S.P.; Tan, C.X.; Niu, D.X.; He, Z.J. Game Analysis of Wind Storage Joint Ventures Participation in Power Market Based on a Double-Layer Stochastic Optimization Model. Processes 2019, 7, 896. [Google Scholar] [CrossRef] [Green Version]
- Heussen, K.; Koch, S.; Ulbig, A.; Andersson, G. Unified System-Level Modeling of Intermittent Renewable Energy Sources and Energy Storage for Power System Operation. IEEE Syst. J. 2012, 6, 140–151. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Kambadkone, A.M.; Rong, G.D. Solution Study of Energy Storage for Renewable in Power Market. In Proceedings of the Asian Conference on Energy, Power and Transportation Electrification (ACEPT), Singapore, 24–26 October 2017. [Google Scholar]
- Xue, X.Q.; Wang, X.Y.; Liu, D.N.; Guo, J.H.; Li, L.; Li, X.T. The Enlightenment of Foreign Power Market Reform Experience to China’s Power Market Construction. In Proceedings of the 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; pp. 642–644. [Google Scholar]
- Wu, W.; Lin, B.Q. Application value of energy storage in power grid: A special case of China electricity market. Energy 2018, 165, 1191–1199. [Google Scholar] [CrossRef]
- Newbery, D.; Pollitt, M.G.; Ritz, R.A.; Strielkowski, W. Market design for a high-renewables European electricity system. Renew. Sustain. Energy Rev. 2018, 91, 695–707. [Google Scholar] [CrossRef] [Green Version]
- Fragkos, P.; van Soest, H.L.; Schaeffer, R.; Reedman, L.; Koberle, A.C.; Macaluso, N.; Evangelopoulou, S.; De Vita, A.; Sha, F.; Qimin, C.; et al. Energy system transitions and low-carbon pathways in Australia, Brazil, Canada, China, EU-28, India, Indonesia, Japan, Republic of Korea, Russia and the United States. Energy 2021, 216, 119385. [Google Scholar] [CrossRef]
- Li, F.; Xu, Q.; Zhou, C.; Lei, Z.; Ye, R.B. Joint Dispatching of Wind-thermal Power Considering Wind Power Consumption and Network Constraints. In Proceedings of the International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–8 November 2018; pp. 1921–1926. [Google Scholar]

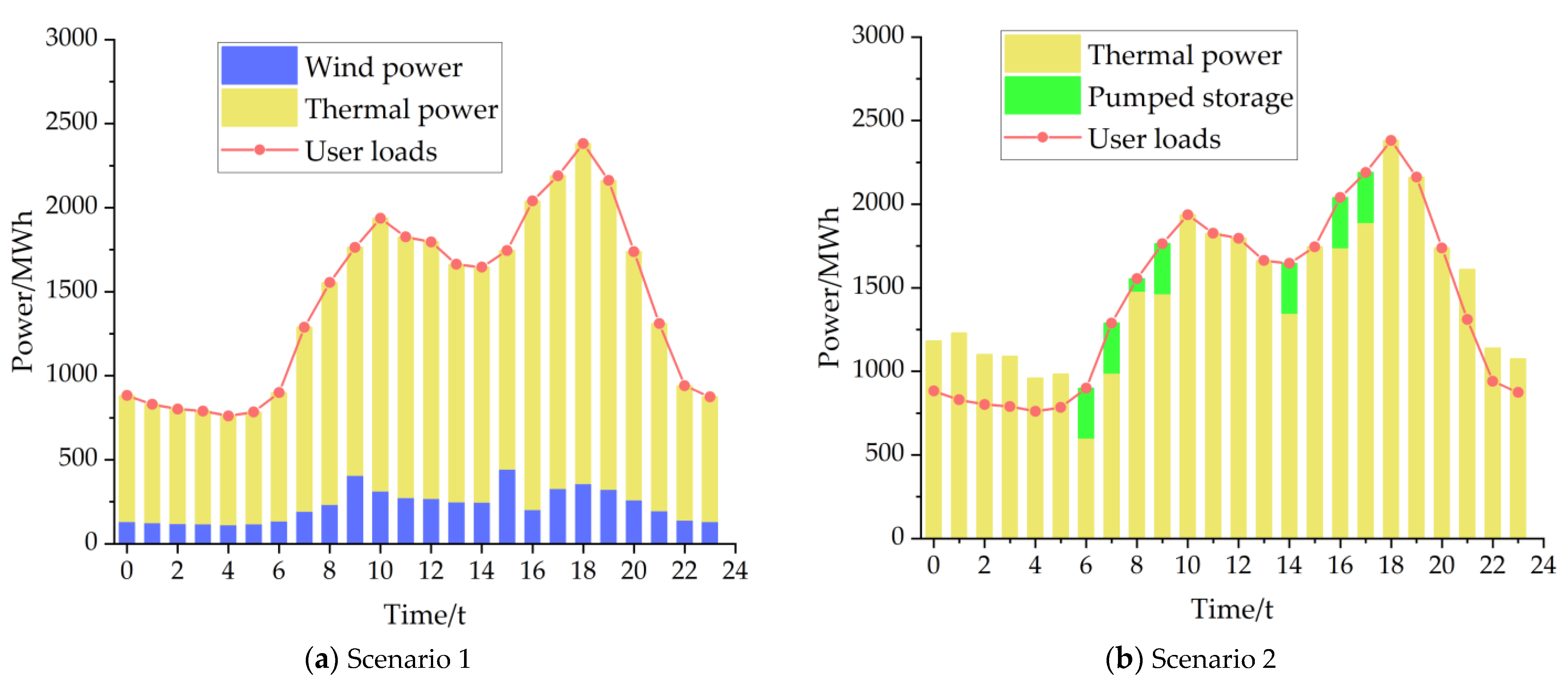
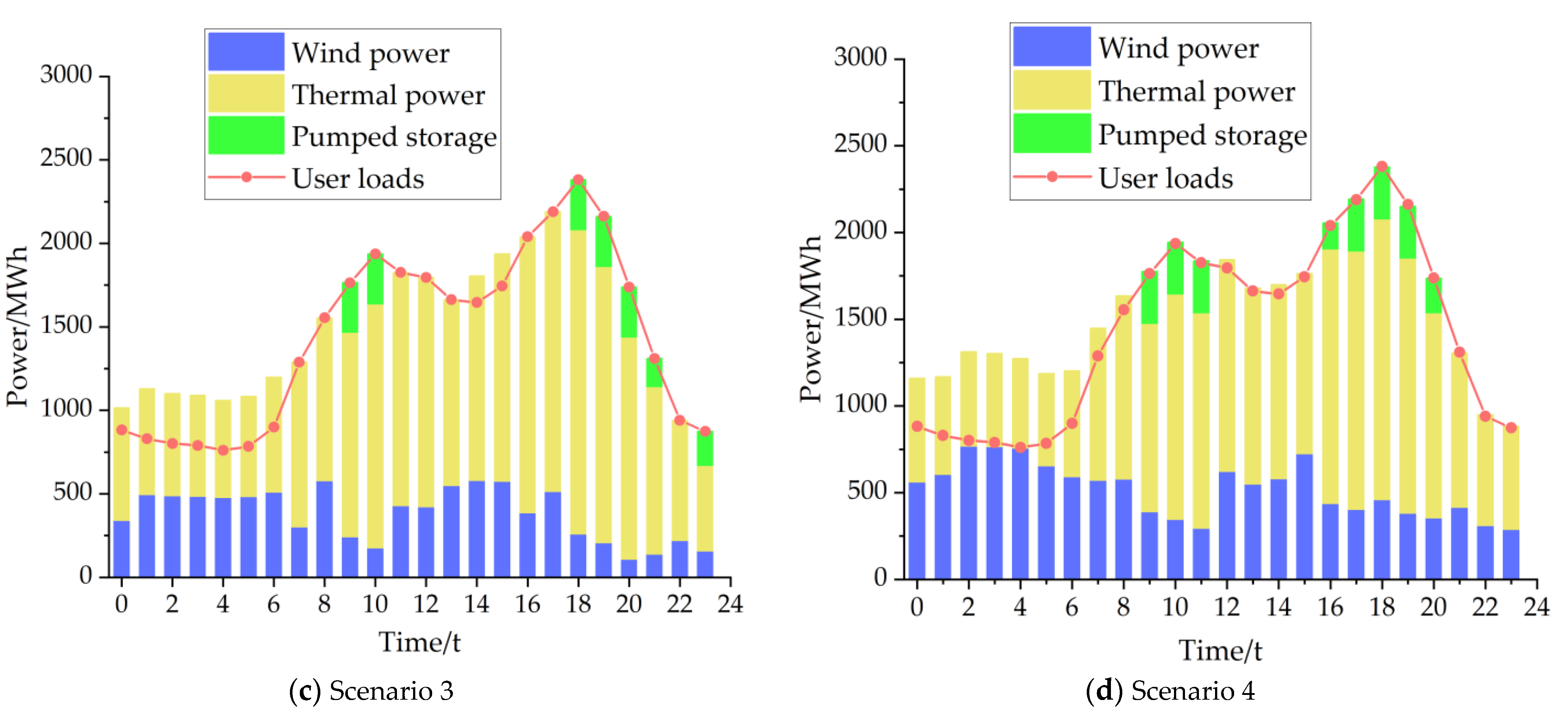
| Example Scenarios | Pumped Storage Units | Wind Turbine | Thermal Power Unit | Source of the Two-Part Tariff |
|---|---|---|---|---|
| 1 | × | √ | √ (100%) | — |
| 2 | √ | × | √ (100%) | pumped storage |
| 3 | √ | √ | √ (100%) | pumped storage + wind energy |
| 4 | √ | √ | √ (80%) | pumped storage + wind energy |
| Scenario | Daily Pumping Power/MWh | Daily Pumping Cost/×104CNY | Average Pumping Cost/CNY/MWh | Average Electricity Tariff/CNY/MWh | Average Capacity Tariff/CNY/MWh |
|---|---|---|---|---|---|
| 1 | — | 118.62 | 632.64 | 645.29 | — |
| 2 | 2500 | 115.54 | 462.16 | 624.21 | 149.81 |
| 3 | 2500 | 102.93 | 411.72 | 559.94 | 146.83 |
| 4 | 2700 | 111.46 | 412.81 | 561.43 | 139.11 |
| Installed Capacities | 200 | 250 | 300 | 400 |
| Pumping Costs | 106.41 | 104.07 | 102.93 | 101.68 |
| Storage Capacity Limit /×104 m3 | 3000 | 2500 | 2000 | 1500 | 1000 | |
|---|---|---|---|---|---|---|
| Upper and Lower Storage Capacity Ratio | ||||||
| 4:1 | 105.86 | 107.39 | 109.75 | — | — | |
| 2:1 | 102.93 | 103.39 | 104.21 | 105.94 | 109.75 | |
| 1:1 | 102.93 | 102.93 | 102.93 | 103.60 | 105.86 | |
| 1:2 | 103.27 | 103.60 | 104.58 | 106.26 | 109.75 | |
| 1:4 | 105.86 | 107.39 | 109.75 | — | — | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zheng, H.; Zhou, B.; Li, G.; Yang, B.; Hu, B.; Ma, M. Two-Part Tariff of Pumped Storage Power Plants for Wind Power Accommodation. Sustainability 2022, 14, 5603. https://doi.org/10.3390/su14095603
Li H, Zheng H, Zhou B, Li G, Yang B, Hu B, Ma M. Two-Part Tariff of Pumped Storage Power Plants for Wind Power Accommodation. Sustainability. 2022; 14(9):5603. https://doi.org/10.3390/su14095603
Chicago/Turabian StyleLi, Hua, Hongwei Zheng, Bowen Zhou, Guangdi Li, Bo Yang, Bo Hu, and Min Ma. 2022. "Two-Part Tariff of Pumped Storage Power Plants for Wind Power Accommodation" Sustainability 14, no. 9: 5603. https://doi.org/10.3390/su14095603
APA StyleLi, H., Zheng, H., Zhou, B., Li, G., Yang, B., Hu, B., & Ma, M. (2022). Two-Part Tariff of Pumped Storage Power Plants for Wind Power Accommodation. Sustainability, 14(9), 5603. https://doi.org/10.3390/su14095603








