Effect of Seismic Isolation on the Performance of High-Rise Buildings with Torsional Instability
Abstract
:1. Introduction
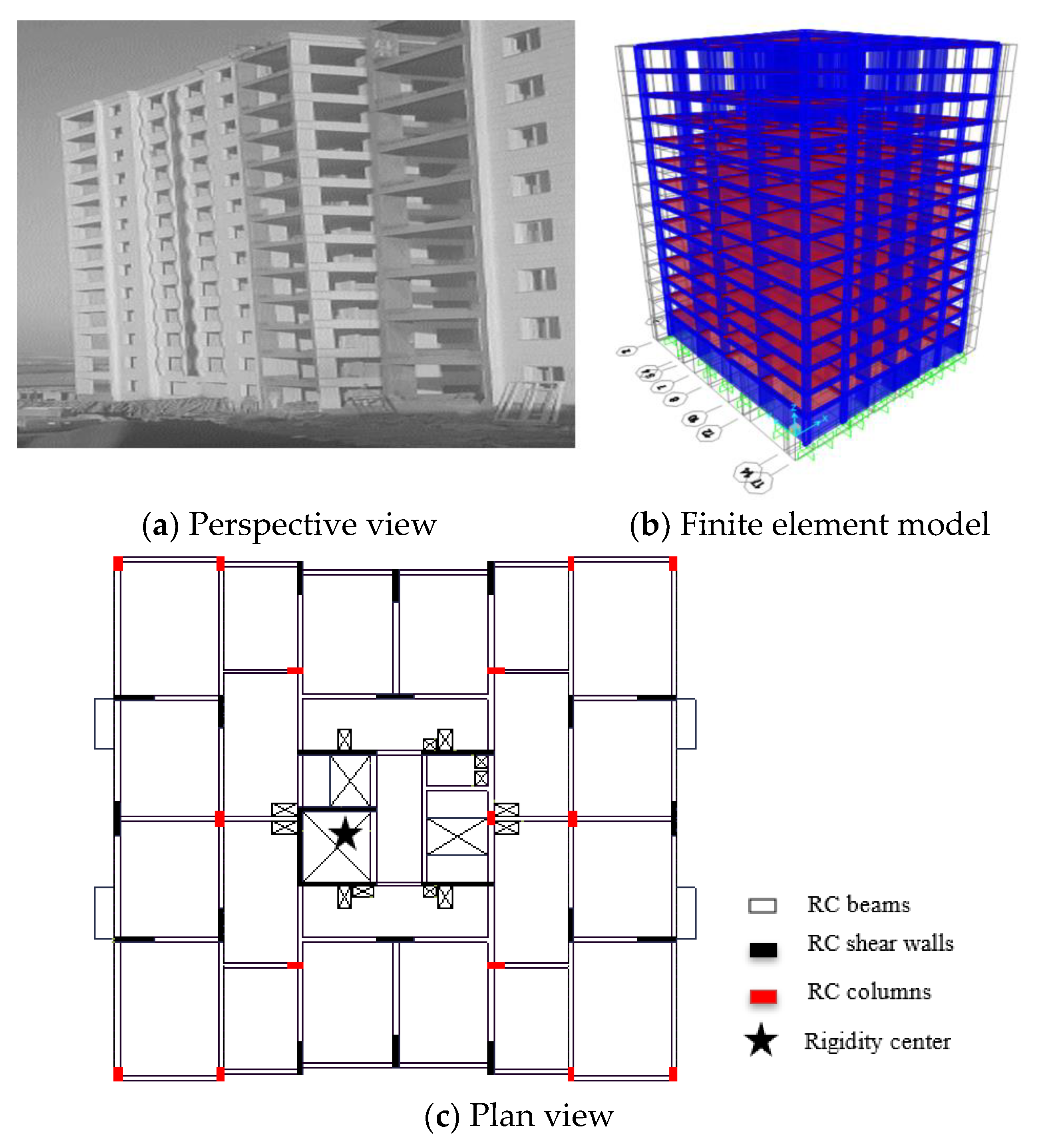
2. The Model Building System
3. Performance Based Analysis
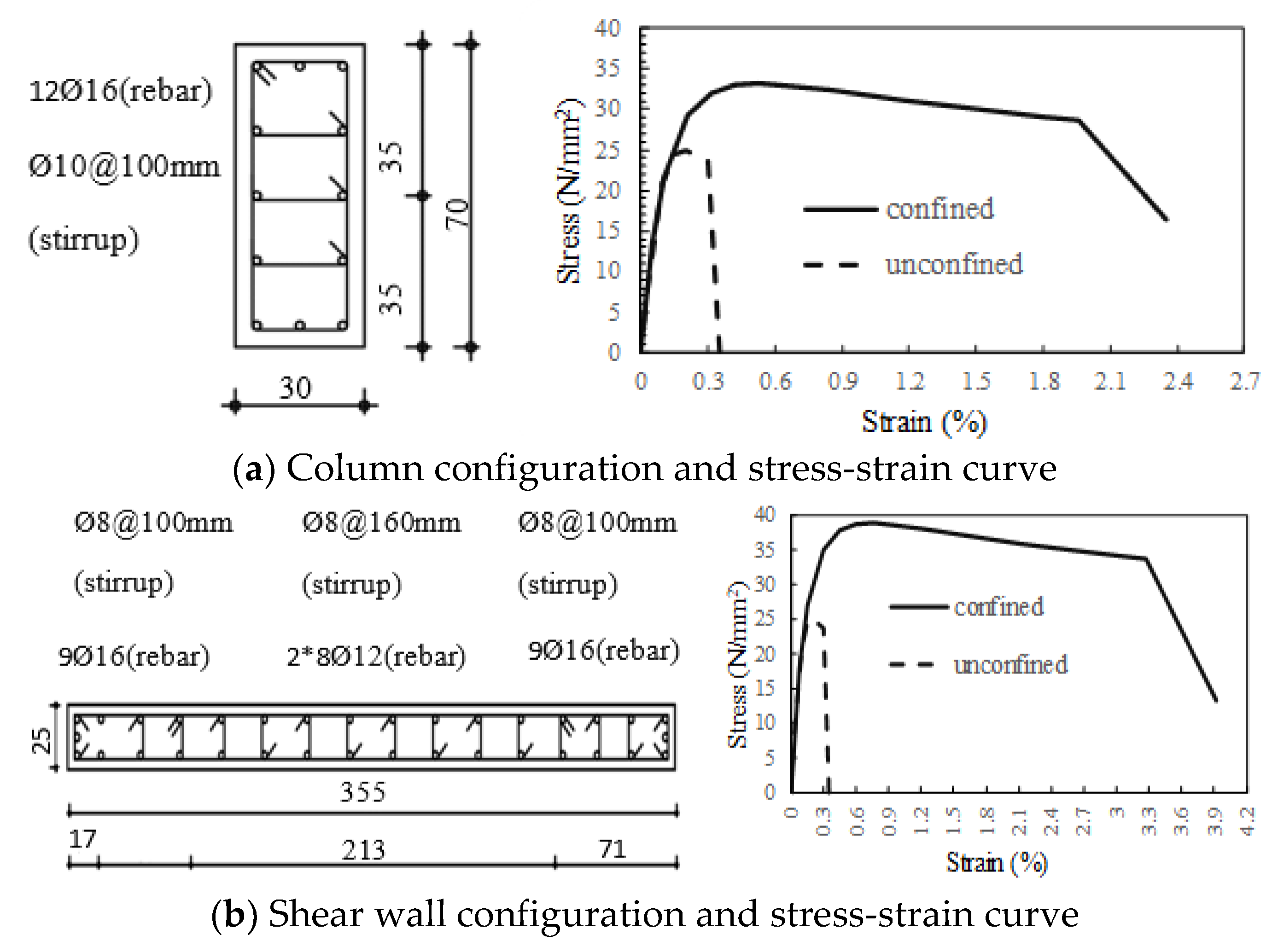
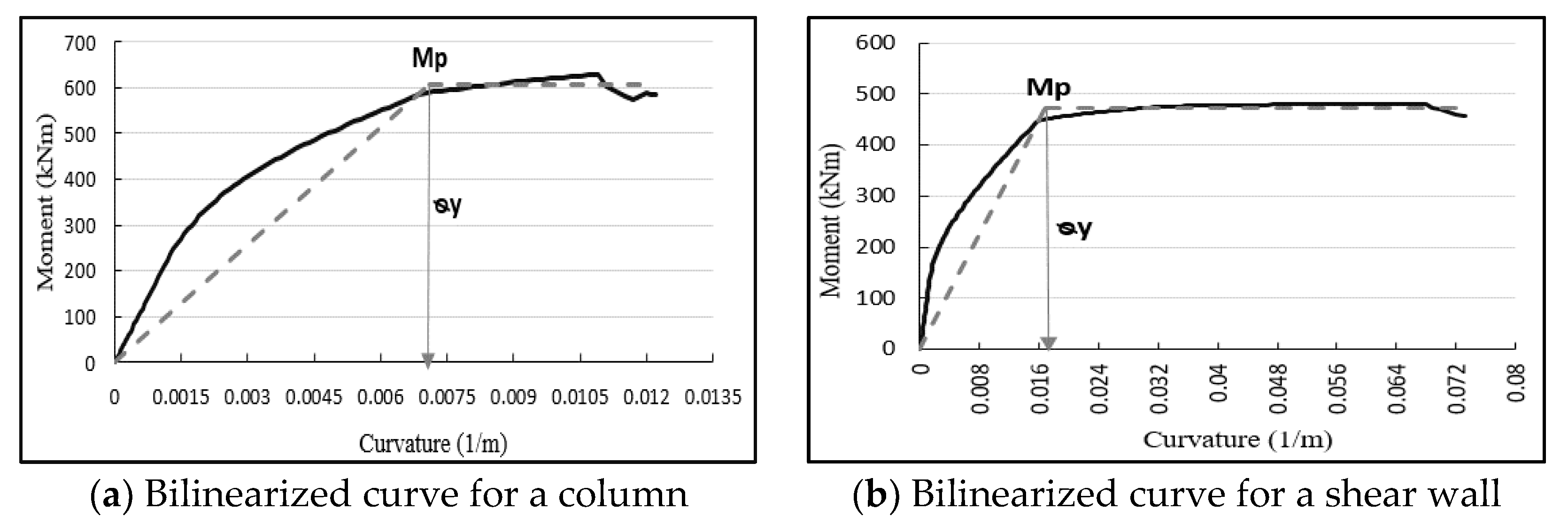
3.1. Moment-Curvature Relationship
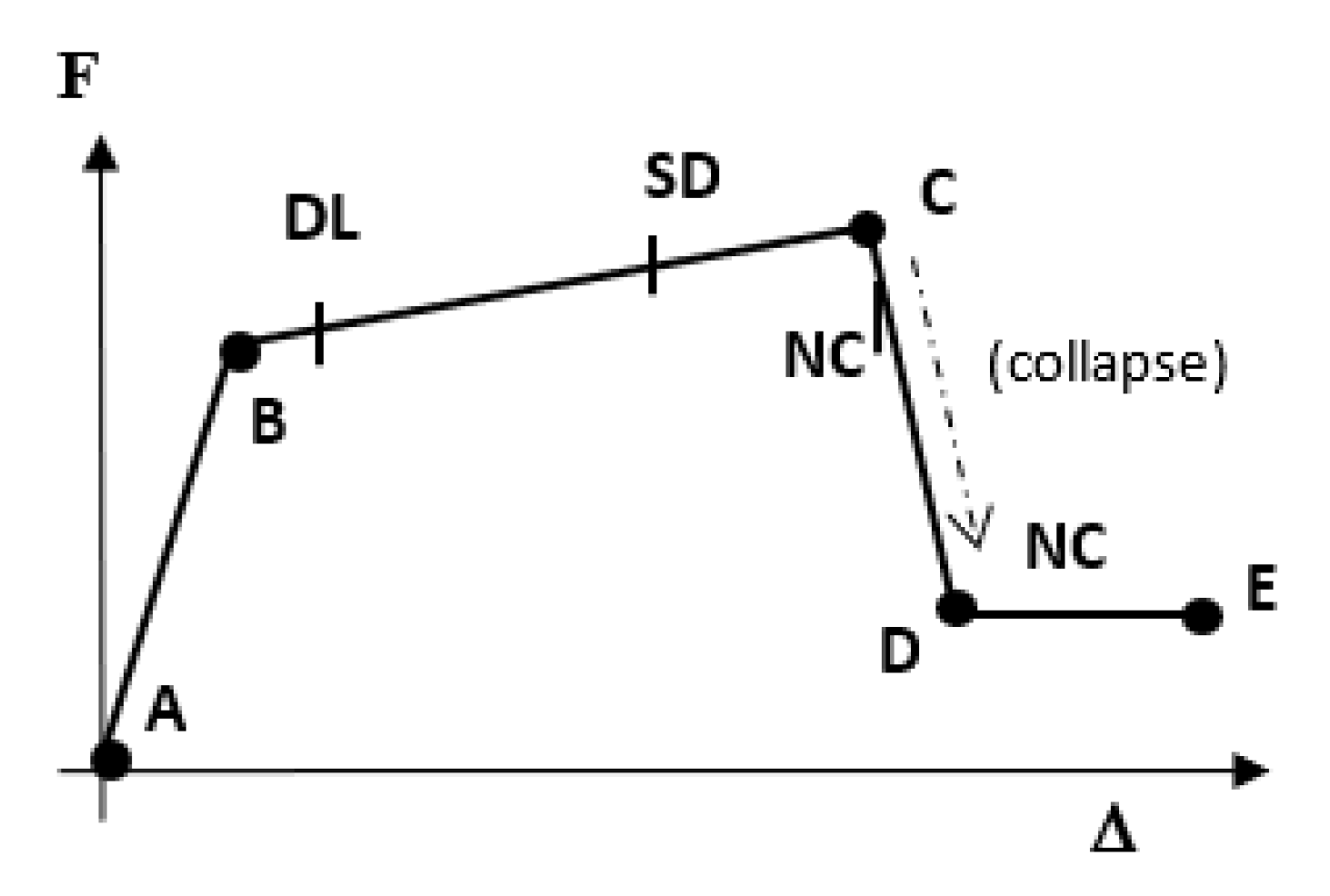
3.2. Nonlinear Static Analysis
3.3. Plastic Hinge Zone and Length
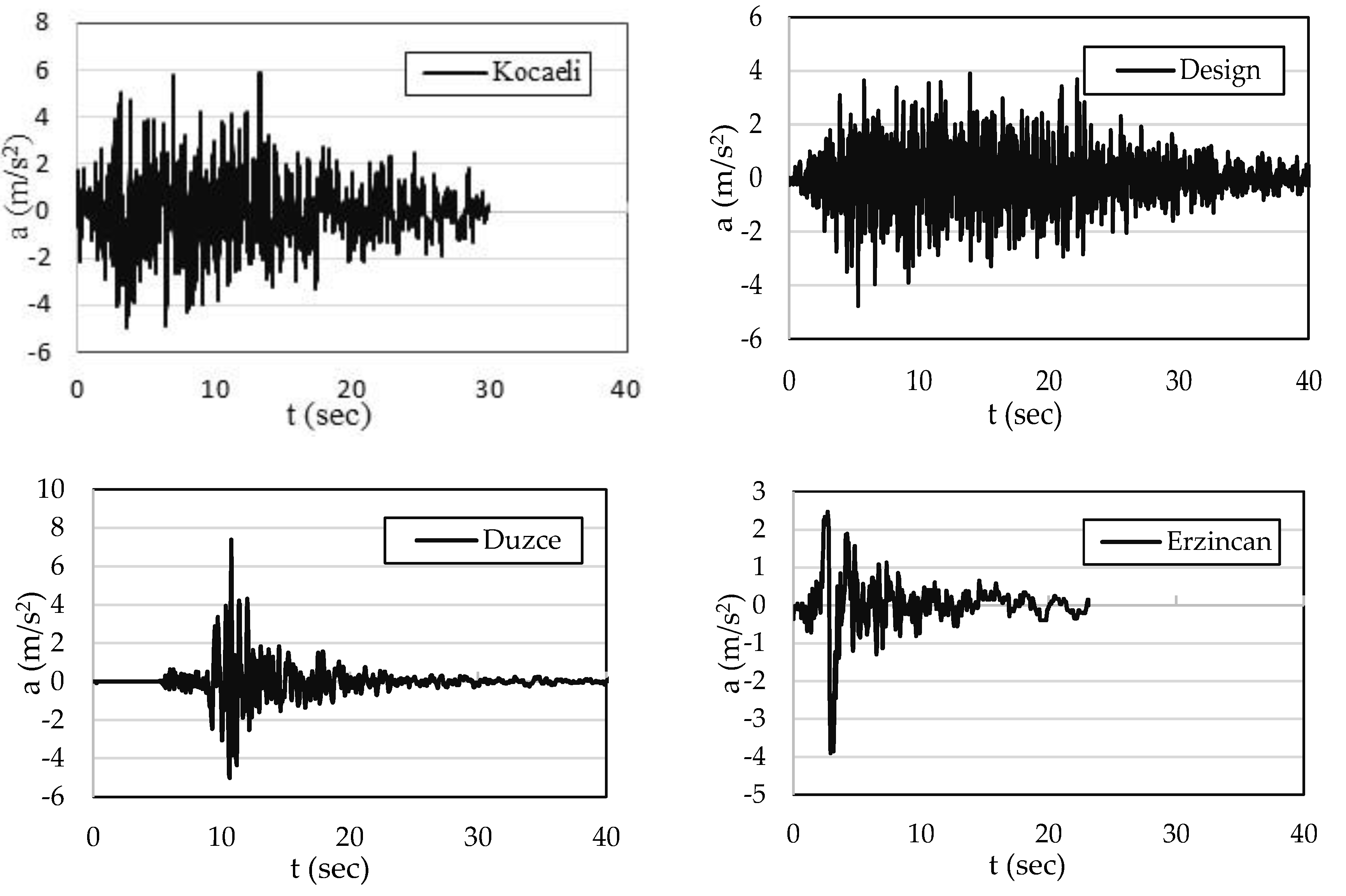
3.4. Time History Functions
4. Building Performance Assessment
5. Conclusions
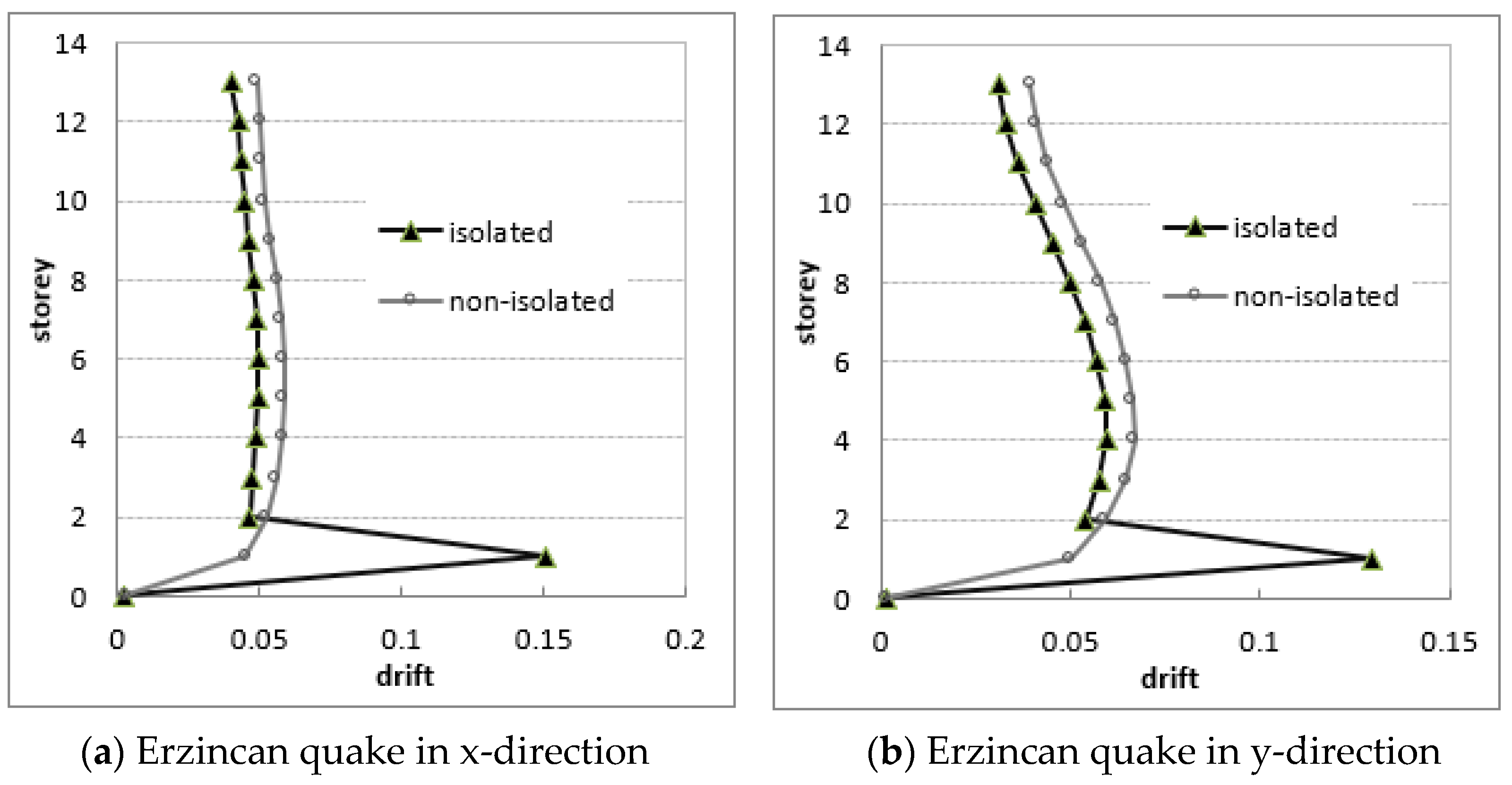
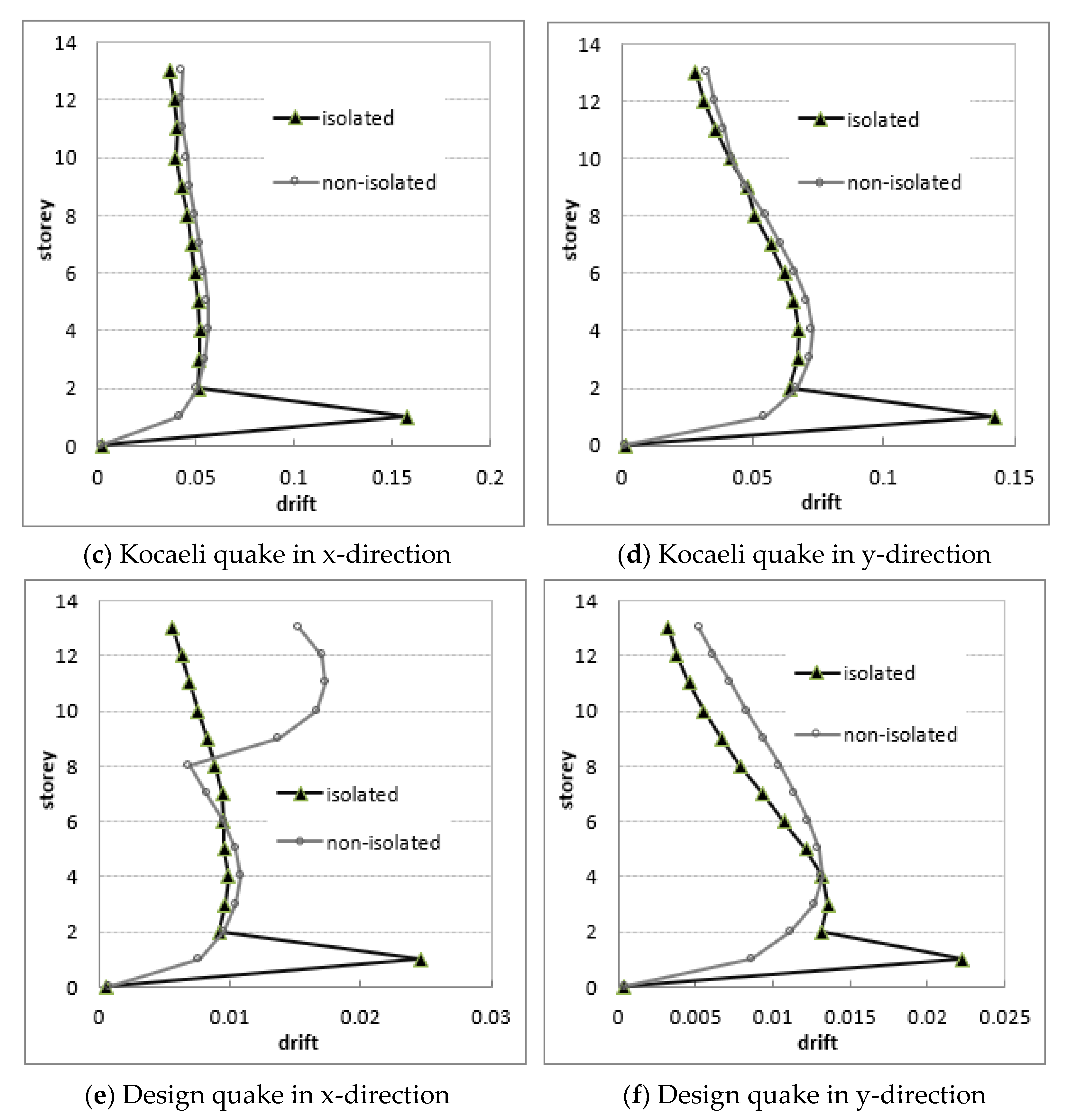
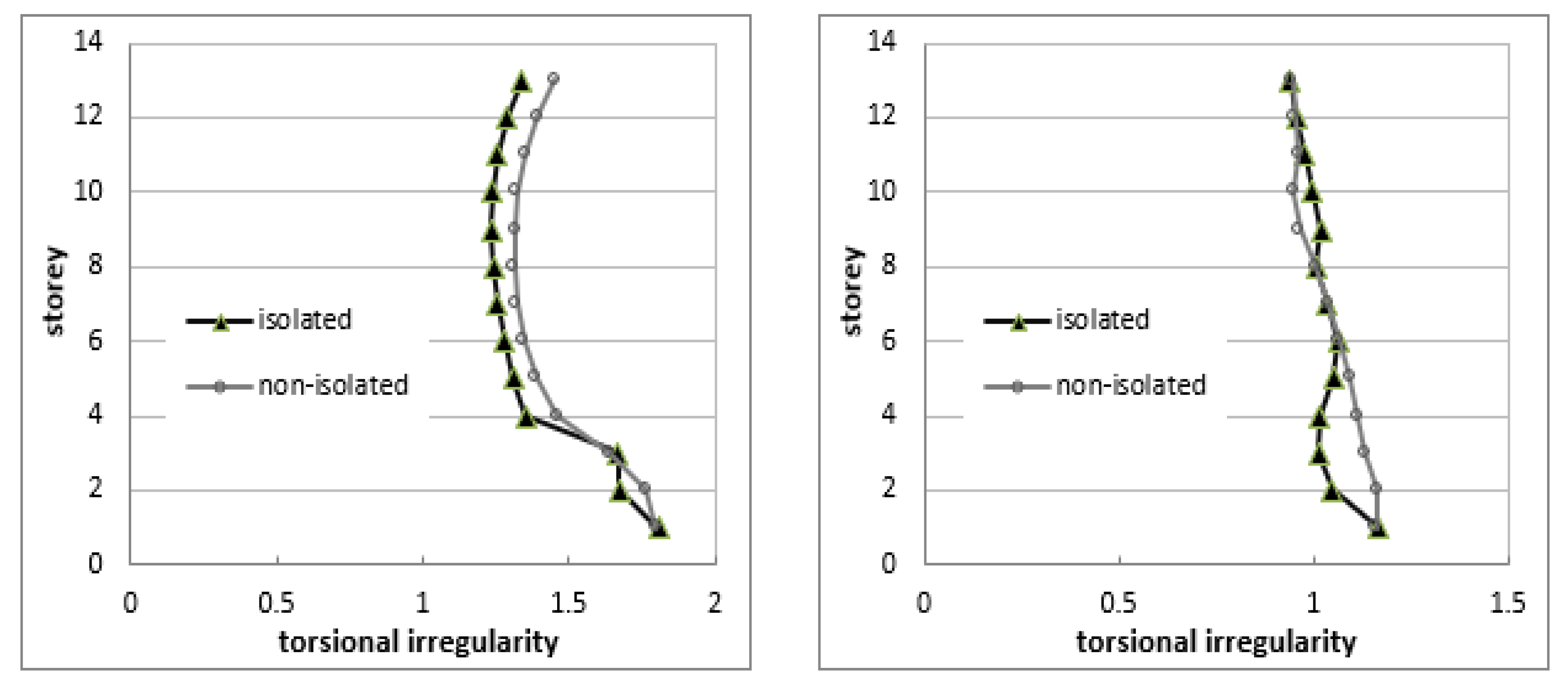
- The torsional irregularity is mainly caused by asymmetric placement of the shear walls in floor plan. Since center of mass of the investigated building differs greatly from center of rigidity, torsional effects have become very important factor over the seismic responses.
- To minimize torsional effects, proper design and placement of shear walls are more critical than design of alternative techniques such as rubber bearings. Therefore, special attentions should be paid in design process for preventing possible torsional issues.
- The base isolation system has partly improved the torsional irregularity. By using the rubber bearings, the torsional irregularity coefficients have remarkably dropped up to 7.6% for Erzincan earthquake and 10.7% for Kocaeli earthquake. In arrangement of bearings, the center of bearings should be coincided with mass-center of the structure in plan as much as possible. Some different displacement fluctuations in the responses have been observed and because the responses of LRB devices developed depending on the frequency content of the ground motion.
- It should be pointed that the seismic performance of the high-rise building has distinctly increased thanks to later installed rubber bearings. Although the undesirable torsional effects have decreased for the considered building, these effects may drastically increase for some buildings in case of unfavorable structural rigidity and soil conditions.
- The total base shear force effectively decreased with installment of base isolation system. A dimensionless response factor for seismic base shear force (Vbsc) stating the ratio of Vb/W is obtained to assess the isolation effects on the seismic forces. Reduction percentages in the base forces have resulted in the range of 20.2–39.1%. Decreases in roof displacements have been observed up to 48.4% and 37.5% reductions in relative roof displacements.
- Thanks to isolation system, very effective reductions have occurred in the floor displacements and especially in the rotations. Average relative floor displacements have decreased about 44.4% for design quake and 62.3% reductions for rotations.
- The effective reduction in the relative joint displacements on the same floor has developed up to 55% which shows how the values of relative displacements of the floors have decreased by means of the isolation system.
- Performance levels of the critical structural elements have been obtained for the considered ground motions. Valuable decreases in the damage have been seen with the use of the base isolation system. For the Kocaeli earthquake the number of heavily damaged elements has decreased from 6 to 4 for the SD-NC level and the collapsed members from 9 to 6 for beyond the NC level. The number of elements in slightly damaged zone (DL-SD), has decreased substantially from 110 to 55. The plastic rotations have generally limited in considerable quantities (up to 15%) but in the strongest earthquake (Kocaeli 1999) this variation has reversed for shear walls and the maximum plastic rotations have increased up to 12%.
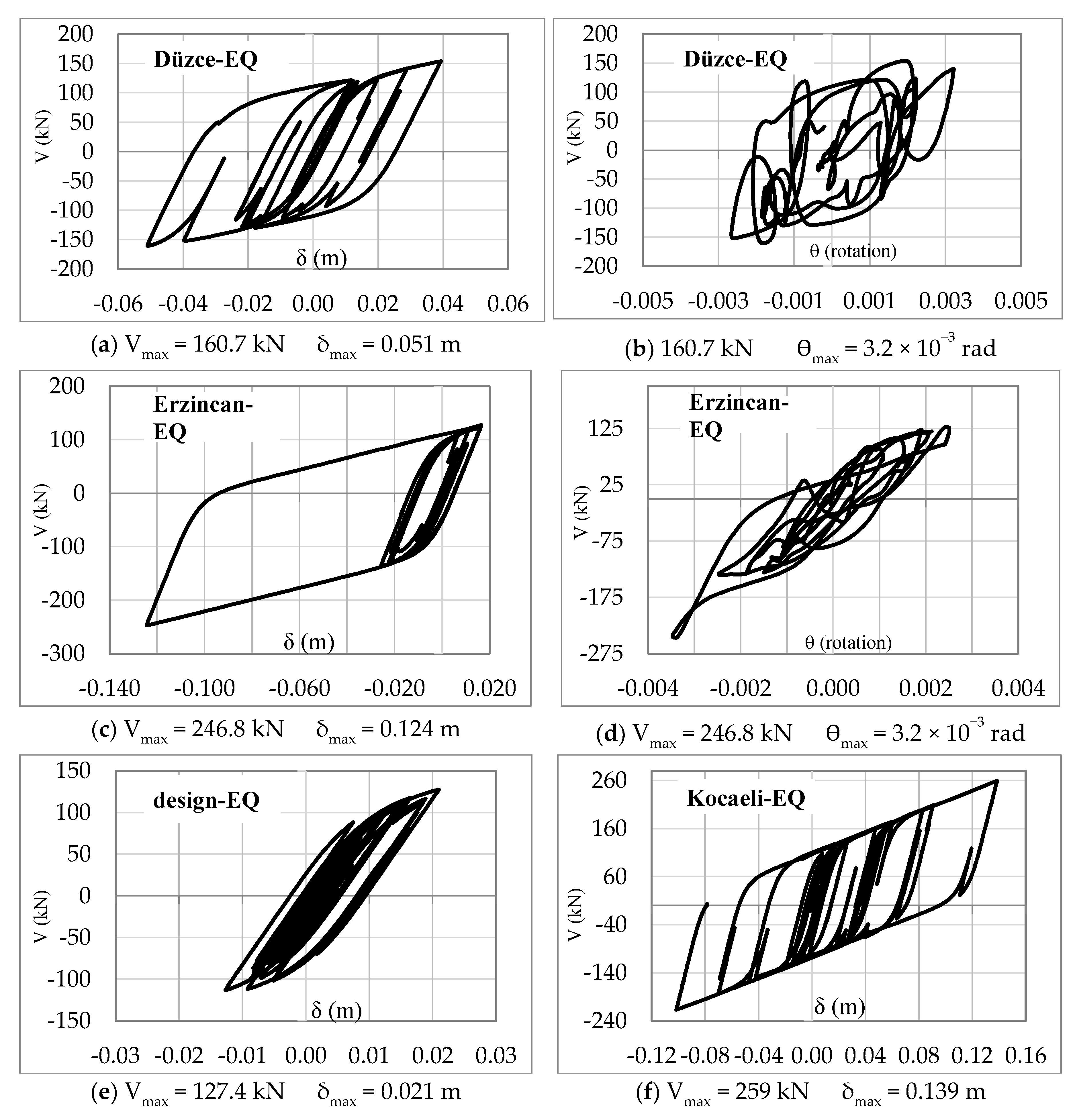
- The peak displacements of the LRB devices are 0.139 m for the Kocaeli earthquake and 0.124 m for Erzincan earthquake. The seismic deformation demand values of the LRB devices are the allowable design limit of 0.168 m where the LRB maximum displacement capacity is determined as 0.41 m by manufacturer company. While the peak shear strains (γs) of the LRB are limited by 150%, the maximum shear strain has been obtained as 68% for the strongest earthquake.
- With reference to the most unfavorable cases, the maximum allowable rotation of the LRB configuration is taken by 0.079 rad. In the analyses, the maximum bearing rotation is found as 0.006 in the Kocaeli EQ loading. While the rotations in the bearings are also in acceptable ranges for all earthquakes, the peak demand displacement in the Kocaeli EQ is in the region close to the allowable limit.
- It is important to note that although the analyses could present good performance for the LRB devices, deformations in bearings can exceed the allowable limits in case of a strong ground motion. Therefore, bearing displacement capacity plays a crucial role in designs and this critical issue should be checked for bearing rotations as well.
- The results have been presented here are only for the considered structural parameters and recorded ground motions. To generalize the results of the study, future research can focus on buildings that have various number of stories with different columns and shear wall types.
- In this study, the LRB devices have been designed directly to meet seismic demand forces. However, the results showed that the responses of LRB devices develop depending on the amplitudes and frequency contents of the ground motion. Investigating the optimum characteristics of LRB devices to find the more accurate solution would further limit damage and effectively minimize torsional effects.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bedirhanoglu, I.; Ilki, A.; Triantafillou, T.C. Seismic Behavior of Repaired and Externally FRP Jacketed Short Columns Built with Extremely Low-Strength Concrete. ASCE J. Compos. Constr. 2022, 26, 04021068. [Google Scholar] [CrossRef]
- Bedirhanoglu, I. The Behavior of Reinforced Concrete Columns and Joints with Low Strength Concrete under Earthquake Loads: An Investigation and Improvement. Ph.D. Thesis, Civil Engineering Faculty, Istanbul Technical University, Istanbul, Turkey, 2009. [Google Scholar]
- Bedirhanoglu, I.; Onal, T. 23 Ekim 2011 Van Depremi Ön Değerlendirme Raporu (Preliminary Evaluation Report for 23 October 2011 Van Earthquake); Chamber of Civil Engineers Diyarbakir Brach: Diyarbakir, Turkey, 2011. [Google Scholar] [CrossRef]
- Bedirhanoglu, I. Preliminary Report on 12 November 2017 Halabja Earthquake; Civil Engineering Department, Engineering Faculty, Dicle University: Diyarbakir, Turkey, 2017. [Google Scholar]
- Saritas, F. Performance-based seismic assessment of a base-isolated bridge-pier. Eur. J. Environ. Civ. Eng. 2019, 26, 21–38. [Google Scholar] [CrossRef]
- Saritas, F. Performance assessment of an isolated Multispan bridge. Arab. J. Sci. Eng. 2022, 47, 12993–13008. [Google Scholar] [CrossRef]
- Athanatopoulou, A.M. Critical orientation of three correlated seismic components. Eng. Struct. 2005, 27, 301–312. [Google Scholar] [CrossRef]
- Fontara, I.K.M.; Kostinakis, K.G.; Manoukas, G.E.; Athanatopoulou, A.M. Parameters affecting the seismic response of buildings under bi-directional excitation. Struct. Eng. Mech. 2015, 53, 957–979. [Google Scholar] [CrossRef]
- Askouni, P.K.; Karabalis, D.L. The Modification of the Estimated Seismic Behaviour of R/C Low-Rise Buildings Due to SSI. Buildings 2022, 12, 975. [Google Scholar] [CrossRef]
- Seo, J.; Hu, J.W. Seismic Response and Performance Evaluation of Self-Centering LRB Isolators Installed on the CBF Building under NF Ground Motions. Sustainability 2016, 8, 109. [Google Scholar] [CrossRef] [Green Version]
- Buzuk, J. Seismic Performance Evaluation Of 24 Story Rc Building By Nonlinear Time History Analysis Utilizing TBDY2018 And EC8. Master’s Thesis, Fen Bilimleri Enstitüsü, İstanbul Teknik Üniversitesi, Istanbul, Turkey, 2019. [Google Scholar]
- Turkish Building Earthquake Code (TBEC). Disaster and Emergency Management Presidency; T.C. Resmi Gazete; TBEC: Ankara, Turkey, 2018. [Google Scholar]
- EN 1998-1. Eurocode 8: Design of Structures for Earthquake Resistance—Part 1: General Rules, Seismic Actions and Rules for Buildings; [Authority: The European Union Per Regulation 305/2011, Directive 98/34/EC, Directive 2004/18/EC]; European Union: Maastricht, The Netherlands, 2004. [Google Scholar]
- Rahul, N.K. Effect of building height on torsional rotation of base isolated structures. Int. J. Recent Technol. Eng. 2019, 8, 1754–1760. [Google Scholar] [CrossRef]
- Nagarajaiah, S.; Reinhorn, A.M.; Constantinou, M.C. Torsion in base-isolated structures with elastomeric isolation systems. J. Struct. Eng. 1993, 119, 2932–2951. [Google Scholar] [CrossRef]
- Adibramezani, M.; Moghadam, A.S.; Ziyaeifar, M. Assessment of a technique for the torsional response reduction of isolated asymmetric structures. J. Appl. Sci. 2009, 9, 2653–2670. [Google Scholar] [CrossRef] [Green Version]
- Naderpour, H.; Naji, N.; Burkacki, D.; Jankowski, R. Seismic response of high-rise buildings equipped with base isolation and Non-traditional tuned mass dampers. Appl. Sci. 2019, 9, 1201. [Google Scholar] [CrossRef] [Green Version]
- Shiravand, M.R.; Ketabdari, H. Evaluating Seismic Response of Plan Irregular Buildings Using combination of Lead Rubber Bearing Isolator and Friction Pendulum System. JSCE 2021, 8, 141–163. [Google Scholar] [CrossRef]
- Konak, A. Nonlinear Performance Assessment of Rc Buildings Based on Displacement Design By Implementing TSC2018 with Comparison to the Eurocode. Master’s Thesis, Dicle University, Diyarbakir, Turkey, 2022. [Google Scholar]
- Naeim, F.; Kelly, J.M. Design of Seismic Isolated Structures: From Theory to Practice; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- CALTRANS. Caltrans Seismic Design Criteria Version 2.0; State of California Department of Transportation: Street Sacramento, CA, USA, 2019. [Google Scholar]
- FEMA-356. Update to ASCE/SEI-41 Concrete Provisions; Federal Emergency Management Agency: Washington, DC, USA, 2007. [Google Scholar]
- FEMA-356. Prestandard and Commentary for the Seismic Rehabilitation of Buildings; Federal Emergency Management Agency: Washington, DC, USA, 2000. [Google Scholar]
- DIN 4141-14. Structural Bearings, Laminated Elastomeric Bearings Design and Construction; Deutsche Institut für Normung: Berlin, Germany, 1985. [Google Scholar]
- AASHTO. LRFD Seismic Analysis and Design of Bridges Reference Manual; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2014. [Google Scholar]
- Kowalsky, M.J.; Priestley, M.J.N.; MacRae, G.A. Displacement Based Design—A Methodology for Seismic Design Applied to Single Degree of Freedom RC Structures; Structural Systems Research, University of California: San Diego, CA, USA, 1994; p. 131. [Google Scholar]
- Priestly, M.J.N.; Seible, F.; Calvi, G.M. Seismic Design and Retrofit of Bridges; John Wiley & Sons: New York, NY, USA, 1996; p. 704. [Google Scholar]
- Vision 2000. Performance Based Seismic Engineering for Buildings, Volume I and II; Structural Engineers Association of California: Sacramento, CA, USA, 1995. [Google Scholar]
- ATC-40. Seismic Evaluation and Retrofit of Concrete Buildings; Applied Technology Council, California Seismic Safety Commission: West Sacramento, CA, USA, 1996. [Google Scholar]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1998, 114, 1804–1826. [Google Scholar] [CrossRef] [Green Version]
- Bedirhanoglu, I.; Ilki, A. Theoretical Moment-Curvature Relationships for Reinforced Concrete Members and Comparison with Experimental Data. In Proceedings of the Sixth International Congress on Advances in Civil Engineering, Istanbul, Turkey, 6–8 October 2004; pp. 231–240. [Google Scholar]
- FEMA-440. Improvement of Nonlinear Static Seismic Analysis Procedures; Federal Emergency Management Agency: Washington, DC, USA, 2005. [Google Scholar]
- Chopra, A.K.; Goel, R.K. A modal pushover analysis procedure for estimating seismic demands for buildings. Earthq. Eng. Struct. Dyn. 2002, 31, 561–582. [Google Scholar] [CrossRef] [Green Version]
- Aydinoglu, M.N. An Incremental Response Spectrum Analysis Procedure Based on Inelastic Spectral Displacements for MultiMode Seismic Performance Evaluation. Bull. Earthq. Eng. 2003, 1, 3–36. [Google Scholar] [CrossRef]
- SAP 2000 CSI. Integrated Software for Structural Analysis and Design; Computers and Structures Inc.: Berkeley, CA, USA, 2020. [Google Scholar]
- AFAD. Ministry of Interior Disaster and Emergency Management Presidency: Ankara, Turkey. Available online: www.en.afad.gov.tr (accessed on 15 June 2022).
- PEER Data Base. Available online: https://ngawest2.berkeley.edu/site (accessed on 12 May 2022).






| Bearing Type | Bearing Diameter (m) | Hb (m) | S-Shape Factor | Tr (m) | Kd (kN/m) | Kv (kN/m) | Keff (kN/m) |
|---|---|---|---|---|---|---|---|
| type-1 | 0.70 | 0.205 | 14.48 | 0.112 | 900 | 261 × 104 | 1121 |
| type-2 | 0.70 | 0.205 | 15.60 | 0.112 | 1200 | 351 × 104 | 1464 |
| type-3 | 0.85 | 0.230 | 14.58 | 0.137 | 1400 | 328 × 104 | 1739 |
| Type | T1 | T2 | T3 |
|---|---|---|---|
| isolated | 3.89 | 3.78 | 3.65 |
| non-isolated | 2.94 | 2.75 | 2.55 |
| Type | Øy (rad) | Øu (rad) | Δy (m) | Δu (m) | μΔ | μØ |
|---|---|---|---|---|---|---|
| Column | 0.0069 | 0.0122 | 0.0066 | 0.01 | 1.62 | 1.768 |
| Shear wall | 0.0158 | 0.0732 | 0.0024 | 0.0058 | 2.45 | 4.63 |
| Shear-Wall | Column | ||||
|---|---|---|---|---|---|
| Point | Force | Rotation | Point | Force | Rotation |
| B | 1 | 0 | B | 1 | 0 |
| C | 1.24 | 0.019 | C | 1.048 | 0.028 |
| D | 0.2 | 0.019 | D | 0.2 | 0.028 |
| E | 0.2 | 0.029 | E | 0.2 | 0.038 |
| Limit State (LS) (Total) | |||
|---|---|---|---|
| Member | DL | SD | NC |
| ductile primary | θdl ≤ θy | θsd ≤ 0.75 | θNC ≤ |
| ductile secondary | θsd ≤ 0.75 | θNC ≤ | |
| (a) | |||||||||
| Section Strains | Computed Criteria | ||||||||
| Column No | Section | Lp (mm) | My (kNm) | Øy | Øu | N (kN) | DL | SD | NC |
| 1-2-3-4-12-13-14-15 | 30/70 | 329.5 | 582.1 | 0.00689 | 0.09167 | 1837.6 | 0 | 0.01099 | 0.0146 |
| 8 | 30/70 | 329.5 | 531.9 | 0.00644 | 0.07968 | 1522.3 | 0 | 0.01096 | 0.01461 |
| 5-6-10-11 | 70/30 | 249.5 | 265.7 | 0.02040 | 0.22000 | 1984.8 | 0 | 0.01464 | 0.01951 |
| 7 | 35/80 | 349.5 | 836.1 | 0.00630 | 0.085065 | 2565.6 | 0 | 0.01145 | 0.01526 |
| 9 | 40/80 | 349.5 | 1022.8 | 0.00608 | 0.08200 | 2993.6 | 0 | 0.01181 | 0.01574 |
| (b) | |||||||||
| Section Strains | Computed Criteria | ||||||||
| Column No | Section | Lp (mm) | My (kNm) | Øy | Øu | N (kN) | DL | SD | NC |
| 1-2-3-4-12-13-14-15 | 30/70 | 249.5 | 257.36 | 0.0196 | 0.241 | 1837.56 | 0 | 0.01504 | 0.02 |
| 8 | 30/70 | 249.5 | 237.393 | 0.01805 | 0.212 | 1522.30 | 0 | 0.0148 | 0.0198 |
| 5-6-10-11 | 70/30 | 329.5 | 600.769 | 0.007 | 0.084 | 1984.83 | 0 | 0.01068 | 0.0142 |
| 7 | 35/80 | 259.5 | 403.3 | 0.0163 | 0.169 | 2565.6 | 0 | 0.01464 | 0.0195 |
| 9 | 40/80 | 269.5 | 525.7 | 0.0138 | 0.161 | 2993.590 | 0 | 0.01344 | 0.0179 |
| Performance Values | Peak Values | ||||||
|---|---|---|---|---|---|---|---|
| Building System | V (kN) | Δp (m) | Sa | Sd (m) | βeff | Teff (s) | Δroof (m) |
| Isolated | 5289.85 | 0.156 | 0.062 | 0.116 | 0.096 | 2.743 | 0.95 |
| Non-isolated | 5933.88 | 0.133 | 0.076 | 0.101 | 0.087 | 2.312 | 0.477 |
| Columns | Shear Walls | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Non-Isolated | Isolated | Non-Isolated | Isolated | |||||||||||
| Floor Level | Number of Columns | DL-SD | SD-NC | >NC | DL-SD | SD-NC | >NC | Number of Shear Walls | DL-SD | SD-NC | >CP | DL-SD | LS-CP | >NC |
| 1 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 1 | 0 | 0 | 0 | 0 | 0 |
| 7 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 1 | 0 | 0 | 0 | 0 | 0 |
| 8 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 1 | 0 | 0 | 0 | 0 | 0 |
| 9 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 0 | 0 | 0 | 0 | 0 | 0 |
| 11 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 15 | 3 | 0 | 0 | 0 | 0 | 0 | 24 | 0 | 0 | 0 | 0 | 0 | 0 |
| Total | 180 | 3 | 0 | 0 | 0 | 0 | 0 | 288 | 4 | 0 | 0 | 0 | 0 | 0 |
| Columns | Shear Walls | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Non-Isolated | Isolated | Non-Isolated | Isolated | |||||||||||
| Floor Level | Number of Columns | DL-SD | SD-NC | >NC | DL-SD | SD-NC | >NC | Number of Shear Walls | DL-SD | SD-NC | >CP | DL-SD | LS-CP | >NC |
| 1 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 6 | 0 | 0 | 3 | 0 | 0 |
| 2 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 4 | 0 | 0 | 0 | 0 | 0 |
| 3 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 3 | 0 | 0 | 0 | 0 | 0 |
| 4 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 6 | 0 | 0 | 1 | 0 | 0 |
| 5 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 6 | 0 | 0 | 1 | 0 | 0 |
| 6 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 6 | 0 | 0 | 2 | 0 | 0 |
| 7 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 6 | 0 | 0 | 0 | 0 | 0 |
| 8 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 6 | 0 | 0 | 0 | 0 | 0 |
| 9 | 15 | 0 | 0 | 0 | 0 | 0 | 0 | 24 | 4 | 0 | 0 | 0 | 0 | 0 |
| 10 | 15 | 1 | 0 | 0 | 0 | 0 | 0 | 24 | 2 | 0 | 0 | 0 | 0 | 0 |
| 11 | 15 | 1 | 0 | 0 | 1 | 0 | 0 | 24 | 2 | 0 | 0 | 0 | 0 | 0 |
| 12 | 15 | 10 | 0 | 0 | 8 | 0 | 0 | 24 | 0 | 0 | 0 | 0 | 0 | 0 |
| Total | 180 | 12 | 0 | 0 | 9 | 0 | 0 | 288 | 51 | 0 | 0 | 7 | 0 | 0 |
| Columns | Shear Walls | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Non-Isolated | Isolated | Non-Isolated | Isolated | |||||||||||
| Floor Level | Number of Columns | DL-SD | SD-NC | >NC | DL-SD | SD-NC | >NC | Number of Shear Walls | DL-SD | SD-NC | >CP | DL-SD | LS-CP | >NC |
| 1 | 15 | 5 | 0 | 0 | 6 | 0 | 0 | 24 | 16 | 0 | 1 | 14 | 0 | 1 |
| 2 | 15 | 2 | 0 | 0 | 2 | 0 | 0 | 24 | 12 | 0 | 1 | 2 | 0 | 1 |
| 3 | 15 | 1 | 0 | 0 | 1 | 0 | 0 | 24 | 4 | 0 | 1 | 2 | 0 | 1 |
| 4 | 15 | 1 | 0 | 0 | 1 | 0 | 0 | 24 | 3 | 0 | 1 | 3 | 0 | 1 |
| 5 | 15 | 1 | 0 | 0 | 1 | 0 | 0 | 24 | 3 | 0 | 1 | 2 | 0 | 1 |
| 6 | 15 | 1 | 0 | 0 | 1 | 0 | 0 | 24 | 3 | 0 | 1 | 2 | 0 | 1 |
| 7 | 15 | 2 | 0 | 0 | 1 | 0 | 0 | 24 | 5 | 0 | 1 | 1 | 1 | 0 |
| 8 | 15 | 2 | 0 | 0 | 2 | 0 | 0 | 24 | 10 | 0 | 1 | 3 | 0 | 0 |
| 9 | 15 | 3 | 0 | 0 | 2 | 0 | 0 | 24 | 10 | 1 | 0 | 5 | 0 | 0 |
| 10 | 15 | 4 | 0 | 0 | 3 | 0 | 0 | 24 | 12 | 0 | 0 | 4 | 0 | 0 |
| 11 | 15 | 3 | 0 | 0 | 3 | 0 | 0 | 24 | 5 | 0 | 0 | 4 | 0 | 0 |
| 12 | 15 | 15 | 0 | 0 | 15 | 0 | 0 | 24 | 8 | 0 | 0 | 5 | 0 | 0 |
| Total | 180 | 40 | 0 | 0 | 38 | 0 | 0 | 288 | 91 | 1 | 8 | 47 | 1 | 6 |
| Columns | |||||||
|---|---|---|---|---|---|---|---|
| Non-Isolated | Isolated | ||||||
| Floor Level | Number of Beams | DL-SD | SD-NC | >NC | DL-SD | SD-NC | >NC |
| 1 | 63 | 46 | 10 | 3 | 47 | 9 | 0 |
| 2 | 63 | 40 | 10 | 6 | 43 | 10 | 3 |
| 3 | 63 | 51 | 10 | 6 | 43 | 9 | 4 |
| 4 | 63 | 41 | 10 | 7 | 42 | 9 | 4 |
| 5 | 63 | 39 | 10 | 7 | 41 | 9 | 4 |
| 6 | 63 | 42 | 10 | 6 | 42 | 9 | 4 |
| 7 | 63 | 44 | 11 | 4 | 42 | 11 | 2 |
| 8 | 63 | 43 | 11 | 4 | 47 | 7 | 1 |
| 9 | 63 | 45 | 9 | 2 | 48 | 6 | 0 |
| 10 | 63 | 49 | 8 | 0 | 48 | 4 | 0 |
| 11 | 63 | 49 | 6 | 0 | 48 | 3 | 0 |
| 12 | 63 | 44 | 3 | 0 | 41 | 1 | 0 |
| Total | 756 | 533 | 108 | 45 | 532 | 87 | 22 |
| Quake | δmax (m) | γi (%) | θmax | Vmax (kN) |
|---|---|---|---|---|
| Düzce | 0.051 | 30 | 0.003 | 160.7 |
| Erzincan | 0.124 | 61 | 0.003 | 246.8 |
| Kocaeli | 0.139 | 68 | 0.006 | 258.9 |
| Design | 0.021 | 5 | 0.001 | 127.4 |
| Quake | δfave (m) | θfmax (×10−3) | ||||
|---|---|---|---|---|---|---|
| Non-Isolated | Isolated | Reductions % | Non-Isolated | Isolated | Reductions % | |
| Erzincan | 0.027 | 0.023 | 14.8 | 6.63 × 10−3 | 4.11 × 10−3 | 25.2 |
| Kocaeli | 0.035 | 0.030 | 14.3 | 8.90 × 10−3 | 7.65 × 10−3 | 14.0 |
| Design | 0.009 | 0.005 | 44.4 | 2.47 × 10−3 | 0.93 × 10−3 | 62.3 |
| Loading | VBSC % | δrelative | δroof (m) | Columns | Shear Walls | Ɵmax (rad) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| (DL-SD) | (SD-NC) | (DL-SD) | (SD-NC) | (>NC) | Column | Shear-Wall | ||||
| Kocaeli Ex isolated | 13.25 | 0.012 | 0.708 | 22 | 0 | 54 | 0 | 0 | 0.0109 | 0.0083 |
| Kocaeli-Ex fixed | 17.26 | 0.014 | 0.64 | 32 | 0 | 88 | 1 | 2 | 0.0125 | 0.008 |
| Kocaeli Ey isolated | 13.43 | 0.009 | 0.764 | 33 | 0 | 65 | 4 | 6 | 0.00806 | 0.014 |
| Kocaeli-Ey fixed | 16.44 | 0.011 | 0.718 | 39 | 0 | 110 | 6 | 9 | 0.0095 | 0.0125 |
| Design Ex isolated | 5.88 | 0.002 | 0.126 | 2 | 0 | 0 | 0 | 0 | 0.00016 | 0 |
| Design Ex fixed | 9.6 | 0.005 | 0.15 | 3 | 0 | 0 | 0 | 0 | 0.00228 | 0 |
| Design Ey isolated | 5.47 | 0.001 | 0.126 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Design Ey fixed | 6.78 | 0.002 | 0.129 | 3 | 0 | 4 | 0 | 0 | 0.00074 | 0.00029 |
| Duzce Ex isolated | 8.63 | 0.005 | 0.269 | 9 | 0 | 7 | 0 | 0 | 0.00312 | 0.00057 |
| Duzce Ex fixed | 11.9 | 0.008 | 0.261 | 12 | 0 | 51 | 0 | 0 | 0.0044 | 0.0019 |
| Duzce Ey isolated | 12.22 | 0.004 | 0.294 | 12 | 0 | 8 | 0 | 0 | 0.002 | 0.000459 |
| Duzce Ey fixed | 15.84 | 0.006 | 0.273 | 18 | 0 | 28 | 0 | 0 | 0.0037 | 0.00205 |
| Erzincan Ex isolated | 7.18 | 0.013 | 0.708 | 22 | 0 | 59 | 0 | 0 | 0.0107 | 0.0064 |
| Erzincan Ex fixed | 9.84 | 0.016 | 0.702 | 27 | 0 | 76 | 1 | 0 | 0.0118 | 0.0066 |
| Erzincan Ey isolated | 6.04 | 0.01 | 0.708 | 38 | 0 | 47 | 1 | 6 | 0.0108 | 0.0108 |
| Erzincan Ey fixed | 8.63 | 0.013 | 0.719 | 40 | 0 | 91 | 1 | 8 | 0.0127 | 0.0125 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saritaş, F.; Bedirhanoglu, I.; Konak, A.; Keskin, M.S. Effect of Seismic Isolation on the Performance of High-Rise Buildings with Torsional Instability. Sustainability 2023, 15, 36. https://doi.org/10.3390/su15010036
Saritaş F, Bedirhanoglu I, Konak A, Keskin MS. Effect of Seismic Isolation on the Performance of High-Rise Buildings with Torsional Instability. Sustainability. 2023; 15(1):36. https://doi.org/10.3390/su15010036
Chicago/Turabian StyleSaritaş, Fevzi, Idris Bedirhanoglu, Arova Konak, and Mehmet Salih Keskin. 2023. "Effect of Seismic Isolation on the Performance of High-Rise Buildings with Torsional Instability" Sustainability 15, no. 1: 36. https://doi.org/10.3390/su15010036









