The Influence of Operation Platform on the Energy Consumption of Container Handling
Abstract
:1. Introduction
2. Literature Review
3. Problem Description
3.1. Work Scope and Process
3.2. Energy Consumption
3.3. Existing Problems
4. Theoretical Model
4.1. Assumptions of the Model
- (1)
- The study is carried out under ideal conditions, so there is no friction or energy loss.
- (2)
- All of the imported containers are 20 ft standard containers, and all of the quay cranes, yard cranes and trucks have the same dimensions.
- (3)
- If a container needs to cross over another container by yard crane, the vertical distance between the bottom of the upper container and the top of the lower container can be no less than the fixed value d1.
- (4)
- If the spreader needs to cross over a container, the vertical distance between the spreader and the container can be zero.
4.2. Model Building
- (1)
- Traditional low-platform operation mode
- (2)
- New high-platform operation mode
- (3)
- Model of energy consumption difference
5. Calculation and Analysis
5.1. Example Description
5.2. Model Calculation
5.3. Economic Benefit Estimation
6. Conclusions
- (1)
- We analyze the movement path of containers between the quay carne and the yard, and find that there are unnecessary energy-consuming paths in the vertical direction. As calculated in Section 3.3, the length of unnecessary energy-consuming paths is equal to X3 + 2X5.
- (2)
- To reduce the burden of unnecessary energy-consuming paths, we propose a new high-platform operation mode, where container trucks drive onto a high platform. By developing a model of energy consumption, we calculate that the new mode will be able to save 1.478 kWh of electricity compared to the traditional mode when handling a single container.
- (3)
- A terminal company in Tianjin Port is taken as an example to perform an economic benefit analysis. The results indicate that the electricity saved over about 12 years will be able to cover the cost of building the high platform.
Author Contributions
Funding
Conflicts of Interest
References
- Yang, L.; Cai, Y.; Wei, Y.; Huang, S. Choice of technology for emission control in port areas: A supply chain perspective. J. Clean. Prod. 2019, 240, 118105. [Google Scholar] [CrossRef]
- Kenan, N.; Jebali, A.; Diabat, A. The integrated quay crane assignment and scheduling problems with carbon emissions considerations. Comput. Ind. Eng. 2022, 165, 107734. [Google Scholar] [CrossRef]
- Wei, M.; He, J.; Tan, C.; Yue, J. Quay crane scheduling with time windows constraints for automated container port. Ocean. Coast. Manag. 2023, 231, 106401. [Google Scholar] [CrossRef]
- Sha, M.; Zhang, T.; Lan, Y.; Zhou, X. Scheduling optimization of yard cranes with minimal energy consumption at container terminals. Comput. Ind. Eng. 2017, 113, 704–713. [Google Scholar] [CrossRef]
- He, J.; Huang, Y.; Yan, W.; Wang, S. Integrated internal truck, yard crane and quay crane scheduling in a container terminal considering energy consumption. Expert Syst. Appl. 2015, 42, 2464–2487. [Google Scholar] [CrossRef]
- Zhu, S.; Tan, Z.; Yang, Z.; Cai, L. Quay crane and yard truck dual-cycle scheduling with mixed storage strategy. Adv. Eng. Inform. 2022, 54, 101722. [Google Scholar] [CrossRef]
- Zhao, N.; Fu, Z.; Sun, Y.; Pu, X. Digital-twin driven energy-efficient multi-crane scheduling and crane number selection in workshops. J. Clean. Prod. 2022, 336, 130175. [Google Scholar] [CrossRef]
- Gao, Y.; Ge, Y.-E. Integrated scheduling of yard cranes, external trucks, and internal trucks in maritime container terminal operation. Marit. Policy Manag. 2022, 10, 1–22. [Google Scholar] [CrossRef]
- Yue, L.; Fan, H.; Zhai, C. Joint Configuration and Scheduling Optimization of a Dual-Trolley Quay Crane and Automatic Guided Vehicles with Consideration of Vessel Stability. Sustainability 2020, 12, 24. [Google Scholar] [CrossRef] [Green Version]
- He, J. Berth allocation and quay crane assignment in a container terminal for the trade-off between time-saving and energy-saving. Adv. Eng. Inform. 2016, 30, 390–405. [Google Scholar] [CrossRef]
- Liu, D.; Ge, Y.-E. Modeling assignment of quay cranes using queueing theory for minimizing C02 emission at a container terminal. Transp. Res. Part D 2018, 61, 140–151. [Google Scholar] [CrossRef]
- Tan, C.; Yan, W.; Yue, J. Quay crane scheduling in automated container terminal for the trade-off between operation efficiency and energy consumption. Adv. Eng. Inform. 2021, 48, 101285. [Google Scholar] [CrossRef]
- Chung, R.; Li, C.; Lin, W. Interblock crane deployment in container terminals. Transp. Sci. 2002, 36, 79–93. [Google Scholar] [CrossRef]
- Zhang, X.; Zeng, Q.; Yang, Z. Modeling the mixed storage strategy for quay crane double cycling in container terminals. Transp. Res. Part E 2016, 94, 171–187. [Google Scholar] [CrossRef]
- He, J.; Huang, Y.; Yan, W. Yard crane scheduling in a container terminal for the trade-off between efficiency and energy consumption. Adv. Eng. Inform. 2015, 29, 59–75. [Google Scholar] [CrossRef]
- Nishimura, E.; Imai, A.; Papadimitriou, S. Yard trailer routing at a maritime container terminal. Transp. Res. Part E 2005, 41, 53–76. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Langevin, A.; Lu, Z. Integrated scheduling of crane handling and truck transportation in a maritime container terminal. Eur. J. Oper. Res. 2013, 225, 142–152. [Google Scholar] [CrossRef]
- Leonard, H.; Eduardo, L.-R.; Stefan, V. Multi-objective inter-terminal truck routing. Transp. Res. Part E 2017, 106, 178–202. [Google Scholar]
- Zhou, C.; Lee, B.K.; Li, H. Integrated optimization on yard crane scheduling and vehicle positioning at container yards. Transp. Res. Part E Logist. Transp. Rev. 2020, 138, 101966. [Google Scholar] [CrossRef]
- Gharehgozli, A.H.; Vernooij, F.G.; Zaerpour, N. A simulation study of the performance of twin automated stacking cranes at a seaport container terminal. Eur. J. Oper. Res. 2017, 261, 108–128. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.; Chang, D.; Shi, X.; Yuan, J. Analysis and Design of Typical Automated Container Terminals Layout Considering Carbon Emissions. Sustainability 2019, 11, 2957. [Google Scholar] [CrossRef]
- Kemme, N. Effects of storage block layout and automated yard crane systems on the performance of seaport container terminals. OR Spectr. 2012, 34, 563–591. [Google Scholar] [CrossRef]
- Niu, Y.; Yu, F.; Yao, H.; Yang, Y. Multi-equipment coordinated scheduling strategy of U-shaped automated container terminal considering energy consumption. Comput. Ind. Eng. 2022, 174, 108804. [Google Scholar] [CrossRef]
- Li, J.; Yang, J.; Xu, B.; Yang, Y. Hybrid Scheduling for Multi-Equipment at U-Shape Trafficked Automated Terminal Based on Chaos Particle Swarm Optimization. J. Mar. Sci. Eng. 2021, 9, 1080. [Google Scholar] [CrossRef]
- Xu, B.; Jie, D.; Li, J.; Yang, Y. Integrated scheduling optimization of U-shaped automated container terminal under loading and unloading mode. Comput. Ind. Eng. 2021, 162, 107695. [Google Scholar] [CrossRef]
- Xiang, X.; Liu, C.; Lee, L.H.; Chew, E.P. Performance Estimation and Design Optimization of a Congested Automated Container Terminal. IEEE Trans. Autom. Sci. Eng. 2022, 19, 2437–2449. [Google Scholar] [CrossRef]
- Budiyanto, M.A.; Huzaifi, M.H.; Sirait, S.J.; Prayoga, P.H.N. Evaluation of CO2 emissions and energy use with different container terminal layouts. Sci. Rep. 2021, 11, 5476. [Google Scholar] [CrossRef]
- Li, X.; Peng, Y.; Huang, J.; Wang, W. Simulation study on terminal layout in automated container terminals from efficiency, economic and environment perspectives. Ocean. Coast. Manag. 2021, 213, 105882. [Google Scholar] [CrossRef]

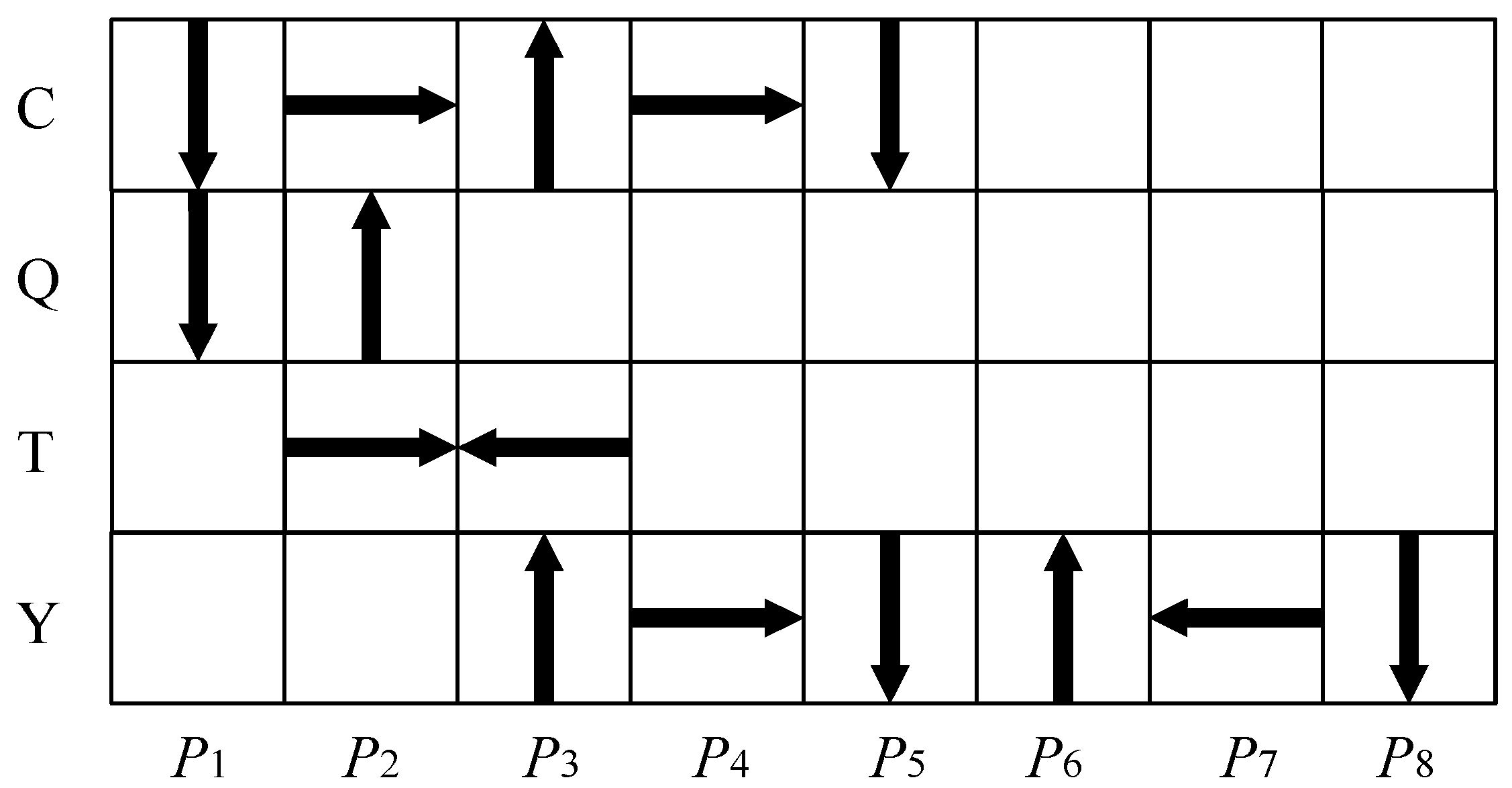

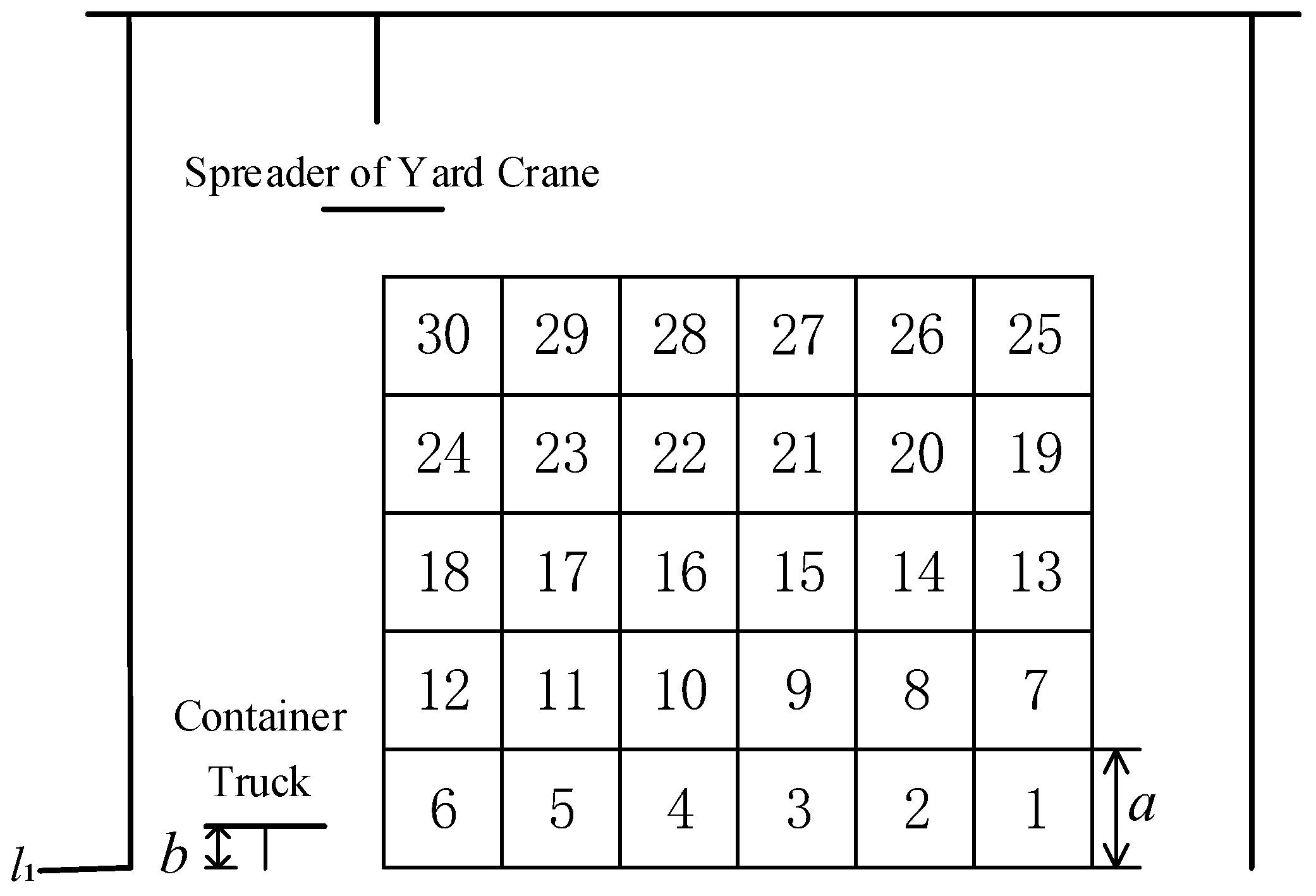
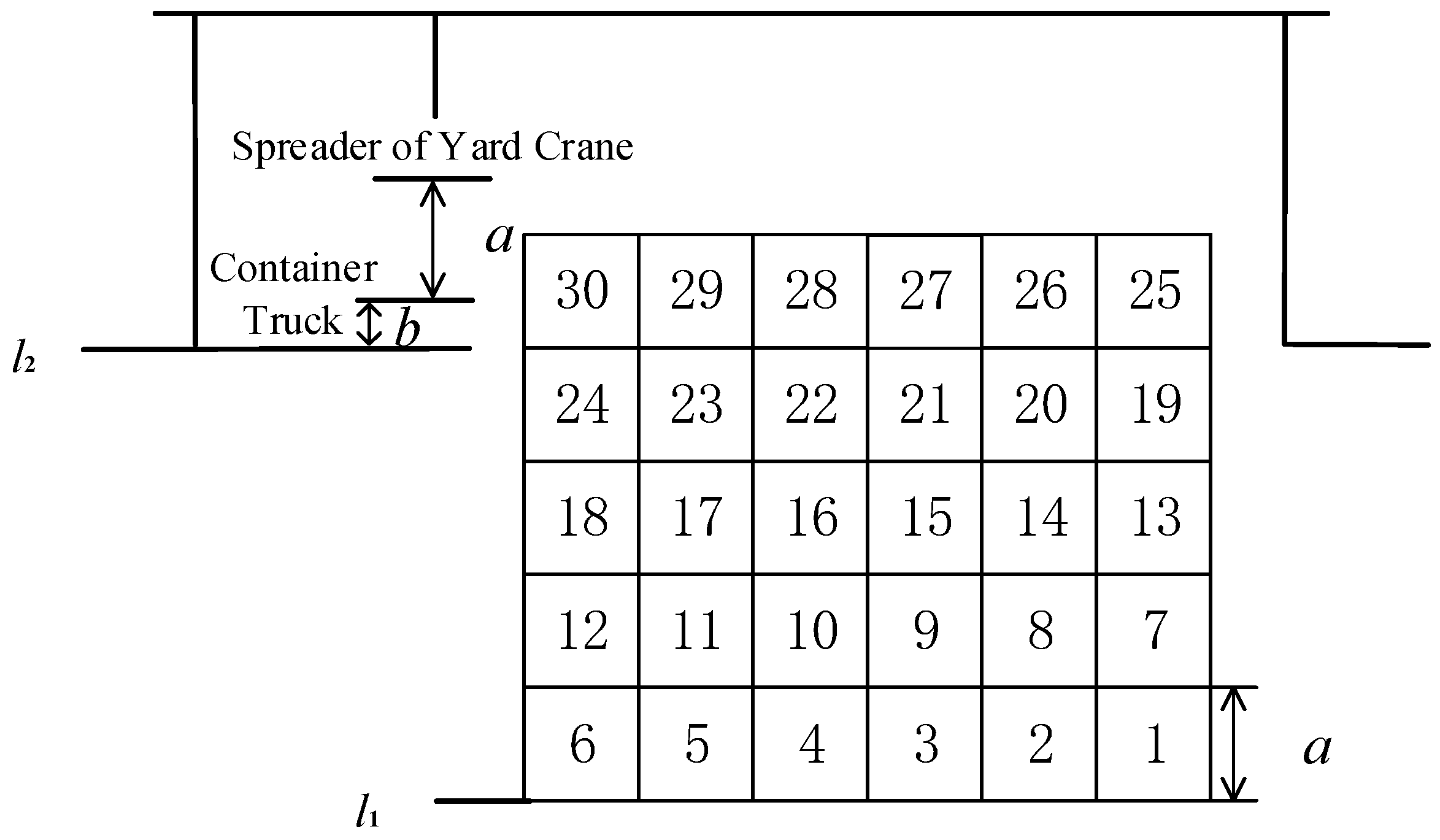

| Parameters (i) | 1 | 7 | 13 | 19 | 25 |
|---|---|---|---|---|---|
| d2 | d2 | d2 | d2 | d2 | |
| d2 | a − b + d1 | 2a − b + d1 | 3a − b + d1 | 4a − b + d1 | |
| 4a + b + d2 | 3a + b + d2 | 2a + b + d2 | a + b + d2 | b + d2 | |
| B + d2 | d1 | d1 | d1 | d1 | |
| 5a + b | 4a + b | 3a + b | 2a + b | a + b | |
| b | 0 | 0 | 0 | 0 | |
| 0 | a − b | 2a − b | 3a − b | 4a − b |
| Parameters | a | b | d1 | d2 | g | |||
|---|---|---|---|---|---|---|---|---|
| Numerical value | 2.59 m | 1.5 m | 0.3 m | 0.15 m | Heavy box: 20,000 kg Empty box: 2000 kg | 2000 kg | 2000 kg | 9.8 m/s2 |
| Parameter | a | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Numerical value | 1000 m | 390 m | 0.6 m | 10 | 5 | 8 m | 0.4 m | 4 m | 2.59 m | USD 104.167 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhou, R.; Zhu, L. The Influence of Operation Platform on the Energy Consumption of Container Handling. Sustainability 2023, 15, 385. https://doi.org/10.3390/su15010385
Li X, Zhou R, Zhu L. The Influence of Operation Platform on the Energy Consumption of Container Handling. Sustainability. 2023; 15(1):385. https://doi.org/10.3390/su15010385
Chicago/Turabian StyleLi, Xiaojun, Ran Zhou, and Lequn Zhu. 2023. "The Influence of Operation Platform on the Energy Consumption of Container Handling" Sustainability 15, no. 1: 385. https://doi.org/10.3390/su15010385
APA StyleLi, X., Zhou, R., & Zhu, L. (2023). The Influence of Operation Platform on the Energy Consumption of Container Handling. Sustainability, 15(1), 385. https://doi.org/10.3390/su15010385







