Analysis of Systemic Risk Scenarios and Stabilization Effect of Monetary Policy under the COVID-19 Shock and Pharmaceutical Economic Recession
Abstract
:1. Introduction
2. Theoretical Basis of Stabilizing Effect of Monetary Policy
2.1. Stabilization Goals
2.2. Stabilization Tools
2.2.1. Policy Rate
2.2.2. Open Market Operations
2.2.3. Standing Facilities
2.2.4. Statutory Deposit Reserve Ratio (SDRR)
2.3. Stabilization Channels
2.3.1. Neoclassical Conduction Channels
- (1)
- Interest Rate Channel (IRC)
- (2)
- Asset Price Channel (APC)
- (3)
- Exchange Rate Channel (ERC)
2.3.2. Non-Neoclassical Transmission Channels
- (1)
- Bank Lending Channel (BLC)
- (2)
- Broad Credit Channel (BCC)
3. Weakening Analysis of Stabilization Effect Based on IS–MP Model
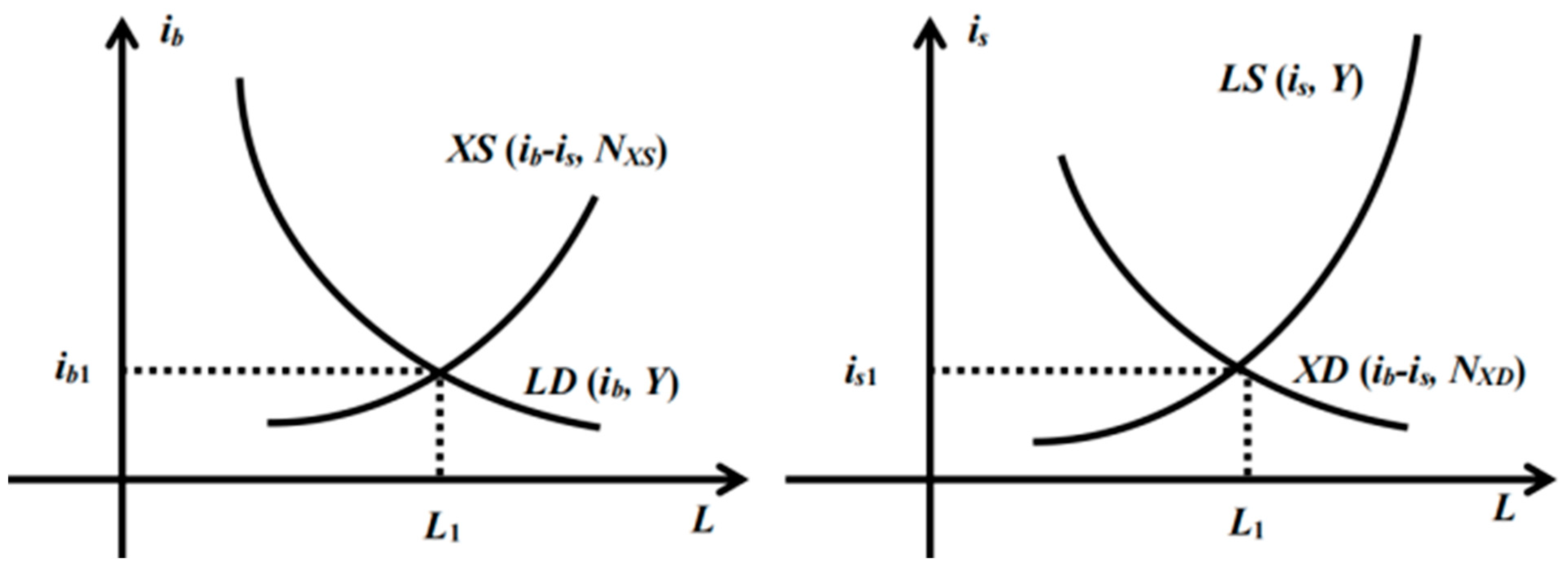
3.1. Model Construction
3.2. Model Analysis
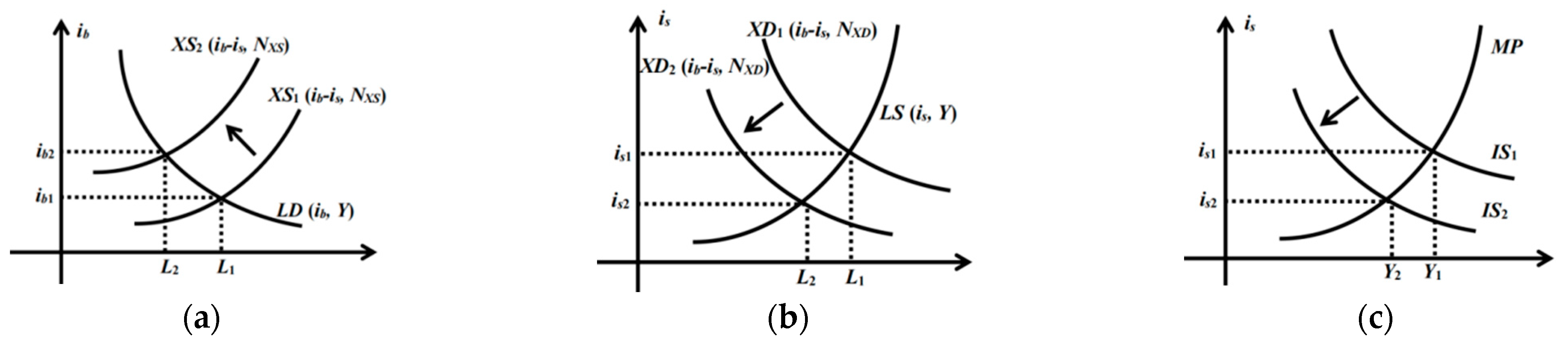
3.2.1. Impact of Financial Intermediary Credit Supply on Output in Systemic Risk Scenarios
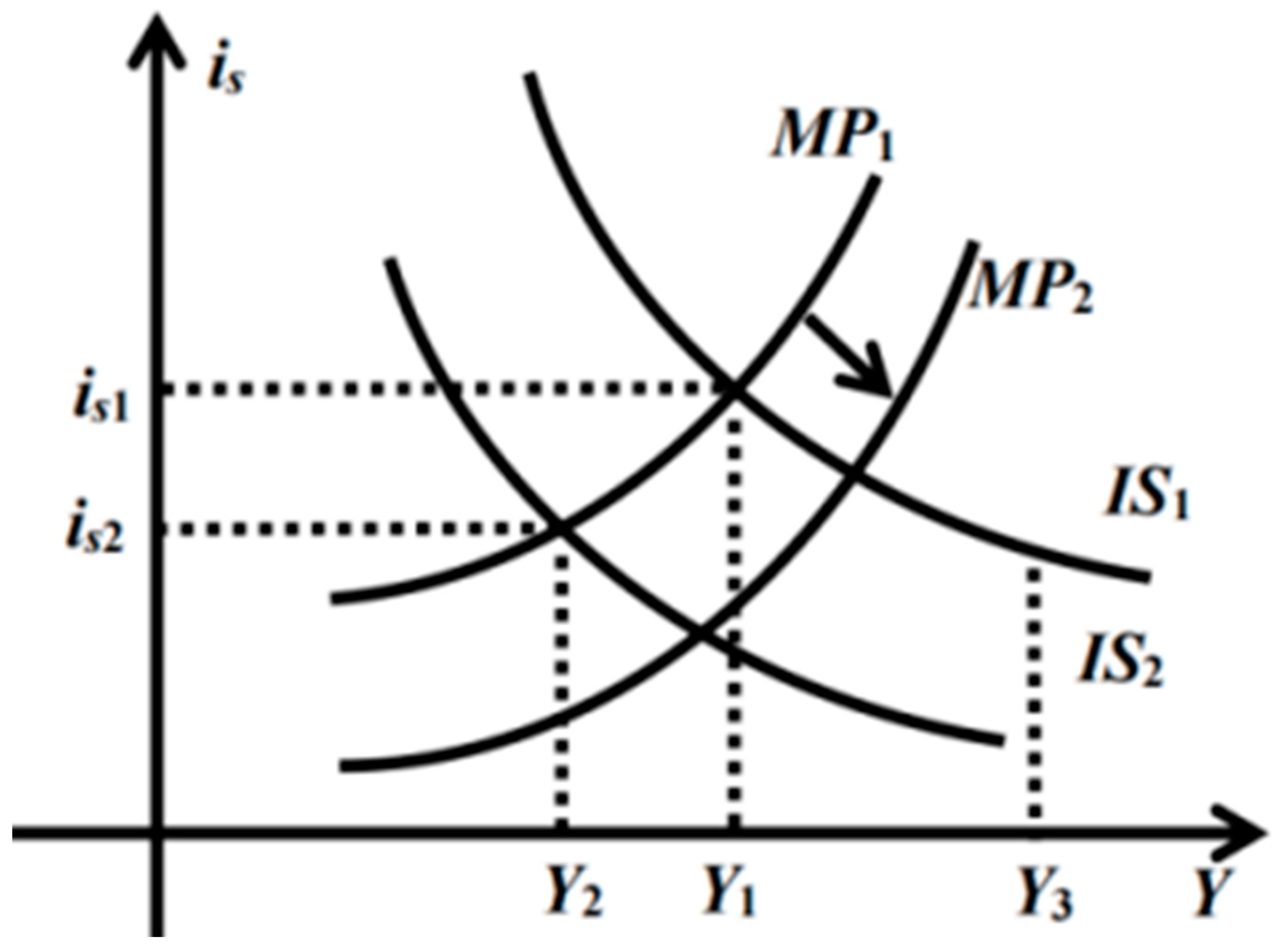
3.2.2. Weakening of the Stabilization Effect of Traditional Monetary Policy in Systemic Risk Scenarios
4. Quantitative Analysis of China’s Systemic Risks Based on the Financial Stress Index (FSI)
4.1. Indicator Selection
4.2. Financial Stress
4.2.1. Currency Market Financial Stress
4.2.2. Bond Market Financial Stress
4.2.3. Stock Market Financial Stress
4.2.4. Forex Market Financial Stress
4.2.5. Real Estate Market Financial Stress
4.3. Synthesis of CFSI Based on the Time-Varying Modified CRITIC Weighting Method
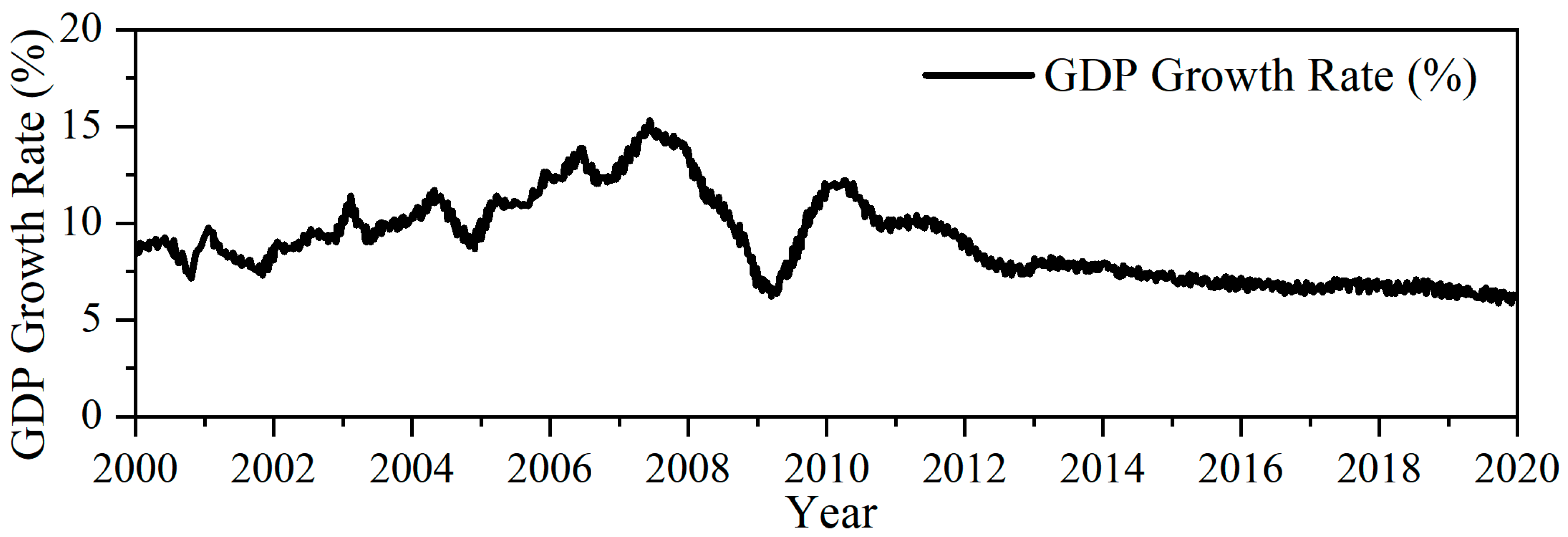
5. Characteristic Fact Investigation of the Stabilizing Effect of China’s Monetary Policy
6. Empirical Analysis of the Stabilization Effect of China’s Monetary Policy in the Systemic Risk Scenarios
6.1. Model Construction
6.2. Variable Selection
6.3. Model Estimation
6.3.1. Variable Stationarity Test
6.3.2. Form Determination of MS-VAR Model
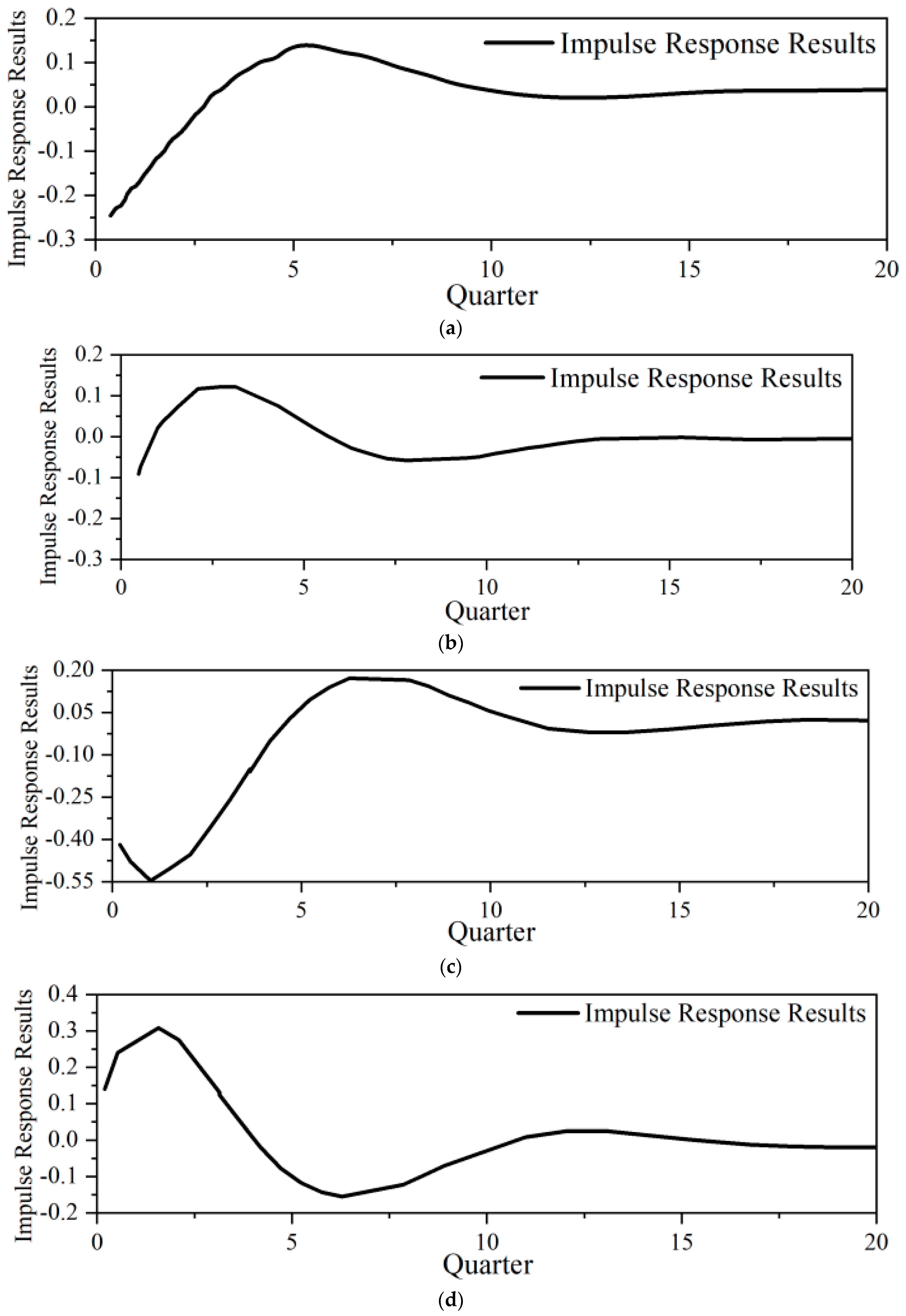
6.3.3. Estimated Results
6.4. Analysis of Measurement Results
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mallik, A.; Khan, T.A.; Biswas, N.A. Determinants of the Systematic Risk of the Cement Industry of Bangladesh. Int. J. Econ. Financ. 2022, 14, 1. [Google Scholar] [CrossRef]
- Filusch, T. Risk assessment for financial accounting: Modeling probability of default. J. Risk Financ. 2021, 22, 1–15. [Google Scholar] [CrossRef]
- Hsiao, C.Y.; Yan, Q.R.; Yang, D.; Zhu, R.-X. Corporate Governance against Systematic Risk during COVID-19—Empirical Findings Based on fs/QCA. J. Bus. Manag. Sci. 2022, 10, 30–38. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, Z.; Luo, Z. Research on Risk Prevention and Computer Modeling Optimization of Internet Financial Products. J. Phys. Conf. Ser. 2021, 1744, 032108. [Google Scholar] [CrossRef]
- Rahman, M.J.; Jia, L.; Sultana, R. Business strategy and systematic risk: Evidence from China. J. Corp. Account. Financ. 2021, 32, 99–117. [Google Scholar] [CrossRef]
- Li, Y.; Law, K. Systematic risk in pairs trading and dynamic parameterization. Econ. Lett. 2021, 202, 109842. [Google Scholar] [CrossRef]
- Mu, L.L.; Li, Y.; Cheng, Y.W. Risk Analysis of the Real Estate Financial Market Based on Risk Energy Theory. Int. J. Corp. Financ. Account. 2021, 8, 15–26. [Google Scholar]
- Qi, M.; Gu, Y.; Wang, Q. Internet financial risk management and control based on improved rough set algorithm. J. Comput. Appl. Math. 2021, 384, 113179. [Google Scholar] [CrossRef]
- Iannotta, G.; Pennacchi, G.; Santos, J. Ratings-Based Regulation and Systematic Risk Incentives. Rev. Financ. Stud. 2019, 32, 1374–1415. [Google Scholar] [CrossRef] [Green Version]
- Heo, W.; Rabbani, A.; Grable, J.E. An Evaluation of the Effect of the COVID-19 Pandemic on the Risk Tolerance of Financial Decision Makers. Financ. Res. Lett. 2021, 41, 101842. [Google Scholar] [CrossRef]
- Hussain, S.; Akbar, M.; Malik, Q.A.; Ahmad, T.; Abbas, N. Downside systematic risk in Pakistani stock market: Role of corporate governance, financial liberalization and investor sentiment. J. Asia Bus. Stud. 2022, 16, 137–160. [Google Scholar] [CrossRef]
- Kirchner, M.; Rieth, M. Sovereign Default Risk, Macroeconomic Fluctuations and Monetary—Fiscal Stabilization. IMF Econ. Rev. 2021, 69, 391–426. [Google Scholar] [CrossRef]
- Jesus, D.; Besarria, C.; Maia, S.F. The macroeconomic effects of monetary policy shocks under fiscal constrained: An analysis using a DSGE model. J. Econ. Stud. 2020, 47, 805–825. [Google Scholar] [CrossRef]
- Busetti, F.; Neri, S.; Notarpietro, A.; Pisani, M. Monetary policy strategies in the New Normal: A model-based analysis for the euro area. J. Macroecon. 2021, 70, 103366. [Google Scholar] [CrossRef]
- Diegel, M.; Nautz, D. Long-Term Inflation Expectations and the Transmission of Monetary Policy Shocks: Evidence from a SVAR Analysis. J. Econ. Dyn. Control 2021, 130, 104192. [Google Scholar] [CrossRef]
- Tomat, G.M. Central bank policy in a monetary union with heterogeneous member countries. Empirica 2021, 48, 759–773. [Google Scholar] [CrossRef]
- Chortareas, G.; Mavrodimitrakis, C. Policy conflict, coordination, and leadership in a monetary union under imperfect instrument substitutability. J. Econ. Behav. Organ. 2021, 183, 342–361. [Google Scholar] [CrossRef]
- Ottonello, P. Optimal exchange-rate policy under collateral constraints and wage rigidity. J. Int. Econ. 2021, 131, 103478. [Google Scholar] [CrossRef]
- Zulkhibri, M. Policy rate pass-through and the adjustment of retail interest rates: Empirical evidence from Malaysian financial institutions. J. Asian Econ. 2012, 23, 409–422. [Google Scholar] [CrossRef]
- Linzert, T.; Schmidt, S. What Explains the Spread Between the Euro Overnight Rate and the ECB’s Policy Rate? Int. J. Financ. Econ. 2011, 16, 275–289. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Liu, M.H. Interest rate liberalization and pass-through of monetary policy rate to bank lending rates in China. Front. Bus. Res. China 2019, 13, 8. [Google Scholar] [CrossRef]
- Bindseil, U. Over- and Underbidding in Central Bank Open Market Operations Conducted as Fixed Rate Tender. Ger. Econ. Rev. 2010, 6, 95–130. [Google Scholar] [CrossRef] [Green Version]
- Thornton, D.L. Open market operations and the federal funds rate. In Open Market Operations and Financial Markets; Routledge: London, UK, 2005; Volume 89, pp. 549–570. [Google Scholar]
- Demiralp, S.; Farley, D. Declining required reserves, funds rate volatility, and open market operations. J. Bank. Financ. 2003, 29, 1131–1152. [Google Scholar] [CrossRef] [Green Version]
- Judson, R.A.; Klee, E. Whither the liquidity effect: The impact of Federal Reserve open market operations in recent years. J. Macroecon. 2010, 32, 713–731. [Google Scholar] [CrossRef] [Green Version]
- Furfine, C. Standing Facilities and Interbank Borrowing: Evidence from the Federal Reserve’s New Discount Window. Int. Financ. 2003, 6, 329–347. [Google Scholar] [CrossRef] [Green Version]
- Quirós, G.P.; Mendizábal, H.R. Asymmetric Standing Facilities: An Unexploited Monetary Policy Tool. IMF Econ. Rev. 2012, 60, 43–74. [Google Scholar] [CrossRef] [Green Version]
- Vollmer, U.; Wiese, H. Central bank standing facilities, counterparty risk, and OTC-interbank lending. N. Am. J. Econ. Financ. 2016, 36, 101–122. [Google Scholar] [CrossRef]
- Theory, E. The effect of the central bank’s standing facilities on interbank lending and bank liquidity holding. Econ. Theory 2019, 68, 537–577. [Google Scholar]
- Metzger, C. Accounting of the German Statutory Pension Scheme: Balance Sheet, Cross-Sectional Internal Rate of Return and Implicit Tax Rate. Fisc. Stud. 2019, 40, 239–270. [Google Scholar] [CrossRef]
- Lin, C. Issue of Legal Digital Currency and Effectiveness of China’s Monetary Policy. J. Shenzhen Univ. Humanit. Soc. Sci. 2019, 36, 77–86. [Google Scholar]
- Ali, S.Z.; Anwar, S. Inflation and interest rates in the presence of a cost channel, wealth effect and agent heterogeneity. Econ. Model. 2013, 31, 286–296. [Google Scholar] [CrossRef]
- Chong, B.S.; Liu, M.H.; Shrestha, K. Monetary transmission via the administered interest rates channel. J. Bank. Financ. 2006, 30, 1467–1484. [Google Scholar] [CrossRef]
- Williams, M. The Impact of Quantitative Easing on Asset Price Comovement. Int. Financ. Mark. 2017, 13, 139–163. [Google Scholar]
- Horvath, J.; Rothman, P.; Lothian, J.R. Mortgage spreads, asset prices, and business cycles in emerging countries. J. Int. Money Financ. 2021, 115, 102370. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, M. Imports and RMB exchange rate pass-through: The role of quality sorting. J. Econ. Behav. Organ. 2021, 187, 470–487. [Google Scholar] [CrossRef]
- Kim, H.; Lin, Y.; Thompson, H. Exchange Rate Pass-Through to Consumer Prices: The Increasing Role of Energy Prices. Open Econ. Rev. 2021, 32, 395–415. [Google Scholar] [CrossRef]
- Akkay, R.C. The Real Effective Exchange Rate and Industrial Employment: The Turkish Case. Bus. Econ. J. 2021, 12, 491–507. [Google Scholar] [CrossRef]
- Gholampour, V. Unobservable Monetary Policy Surprises and Exchange Rates. Account. Financ. Res. 2021, 10, 11. [Google Scholar] [CrossRef]
- Gambacorta, L.; Altunbas, Y.; Marques-Ibanez, D. Securitisation and the bank lending channel. Eur. Econ. Rev. 2009, 53, 996–1009. [Google Scholar] [CrossRef] [Green Version]
- Gambacorta, L. Inside the bank lending channel. Eur. Econ. Rev. 2005, 49, 1737–1759. [Google Scholar] [CrossRef]
- Leonardo, G.; David, M.I. The bank lending channel: Lessons from the crisis. Econ. Policy 2011, 66, 135–182. [Google Scholar]
- Altunok, F.; Mitchell, K.; Pearce, D.K. The Trade Credit Channel and Monetary Policy Transmission: Empirical Evidence from U.S. Panel Data. Q. Rev. Econ. Financ. 2020, 78, 226–250. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.H.; Yang, B.Z. Applications of an IS-MP Model with Yield Curve. Front. Econ. China 2016, 11, 142–155. [Google Scholar]
- Hsing, Y. Extension of Romer’s IS-MP-IA model to small open economies. Atl. Econ. J. 2004, 32, 257. [Google Scholar] [CrossRef]
- Josheski, D.; Eftimoski, D. Application of Is-Mp-Ia Model and Taylor Rule to Cesee Economies. Econ. Cult. 2016, 13, 5–13. [Google Scholar] [CrossRef] [Green Version]
- Alavi, S.E.; Moshiri, S.; Sattarifar, M. An Analysis of the Efficiency of the Monetary and Fiscal Policies in Iran Economy Using IS-MP-AS Model. Procedia Econ. Financ. 2016, 36, 522–531. [Google Scholar] [CrossRef]
- Yu, H. Short-Term Output Fluctuations in Poland: An Application of the IS-MP-AS Model. Am. Econ. 2005, 49, 44–50. [Google Scholar]
- Yu, H. Application of the IS-MP-IA Model to the Slovene Economy and Policy Implications. Econ. Internazionale Int. Econ. 2005, 58, 167–177. [Google Scholar]
- Yu, H. Impacts of Macroeconomic Policies on Output in the Czech Republic: An Application of Romer’s IS-MP-IA Model. Prague Econ. Pap. 2004, 13, 339–345. [Google Scholar]
- Yu, H. Application of the IS-MP-IA model to the Singapore economy and policy implications. Econ. Bull. 2005, 15, 1–10. [Google Scholar]
- Ozcelebi, O. Assessing the impacts of financial stress index of developed countries on the exchange market pressure index of emerging countries. Int. Rev. Econ. Financ. 2020, 70, 288–302. [Google Scholar] [CrossRef]
- Ilesanmi, K.D.; Tewari, D.D. Financial Stress Index and Economic Activity in South Africa: New Evidence. Economies 2020, 8, 110. [Google Scholar] [CrossRef]
- Kim, H.; Shi, W.; Kim, H.H. Forecasting financial stress indices in Korea: A factor model approach. Empir. Econ. 2020, 59, 2895–2898. [Google Scholar] [CrossRef] [Green Version]
- Yao, X.; Le, W.; Sun, X.; Li, J. Financial stress dynamics in China: An interconnectedness perspective. Int. Rev. Econ. Financ. 2020, 68, 217–238. [Google Scholar] [CrossRef]
- Liu, R.; Chen, J.; Wen, F. The nonlinear effect of oil price shocks on financial stress: Evidence from China. N. Am. J. Econ. Financ. 2020, 55, 101317. [Google Scholar] [CrossRef]
- Valizadeh, T.; Rezakhah, S.; Basatini, F.M. On time-varying amplitude HGARCH model. Int. J. Financ. Econ. 2021, 26, 2538–2547. [Google Scholar] [CrossRef]
- Robiyanto, R.; Nugroho, B.A.; Huruta, A.D.; Frensidy, B.; Suyanto, S. Identifying the Role of Gold on Sustainable Investment in Indonesia: The DCC-GARCH Approach. Economies 2021, 9, 119. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, Z.; Sun, L.; Xie, G.; Lou, Q. Research on the evaluation index system of “new energy cloud” operation mode based on CRITIC weighting method and AHP method. IOP Conf. Ser. Earth Environ. Sci. 2021, 831, 012017. [Google Scholar] [CrossRef]
- Du, Y.; Yang, X.; Lei, S.; Guo, L.; Cao, B. Research on Green Comprehensive Evaluation Model of Urban Distribution Network Electric Energy Based on CRITIC-Order Relation Analysis Method Combination Weighting. E3S Web Conf. 2021, 233, 01145. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, X.; Yu, J.; Xue, L.; Yang, S. A Construction Schedule Robustness Measure Based on Improved Prospect Theory and the Copula-CRITIC Method. Appl. Sci. 2020, 10, 2013. [Google Scholar] [CrossRef]
- Lai, Y.; Hu, Y. Prediction of Stock Market Instability Based on MS-VAR Model. IOP Conf. Ser. Earth Environ. Sci. 2021, 714, 042021. [Google Scholar] [CrossRef]
- Bildirici, M.E. Economic growth and electricity consumption: MS-VAR and MS-Granger causality analysis. OPEC Energy Rev. 2013, 37, 447–476. [Google Scholar] [CrossRef]
- Le, C.; David, D. Asset price volatility and financial contagion: Analysis using the MS-VAR framework. Eurasian Econ. Rev. 2014, 4, 133–162. [Google Scholar] [CrossRef]
- Bildirici, M.; Alp, E.A.; Kayikçi, F. Relationship between hot money and economic growth: Tar-cointegration and MS-VAR analysis. Afr. J. Bus. Manag. 2011, 5, 1060–1075. [Google Scholar]


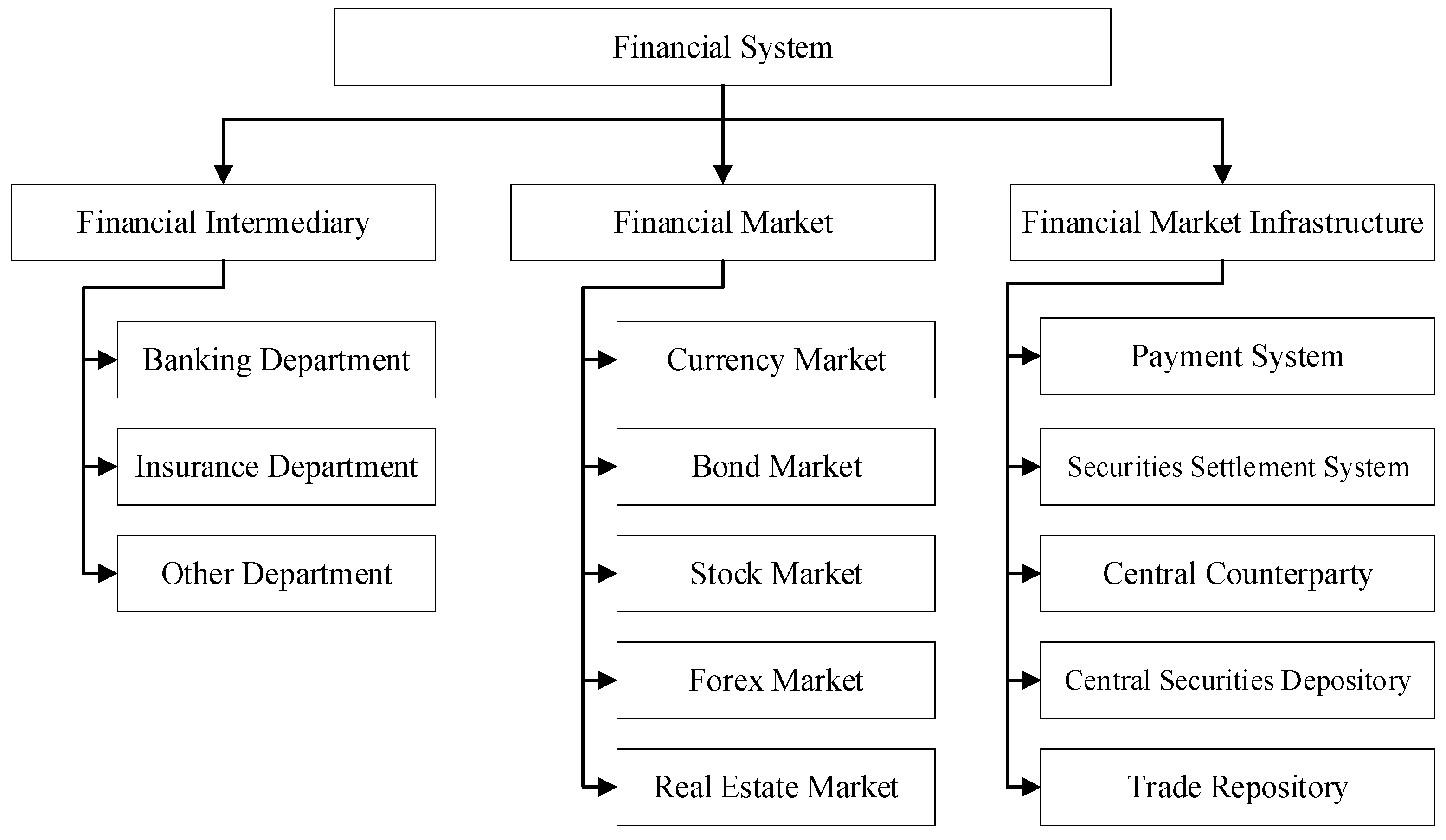
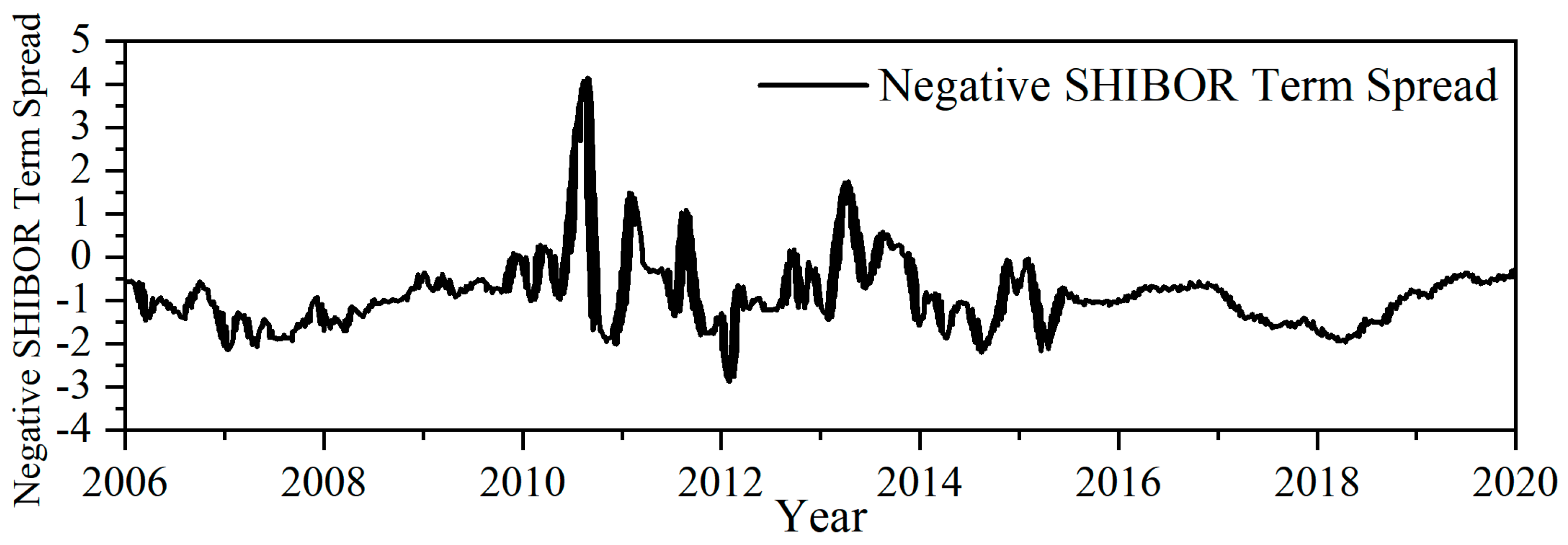
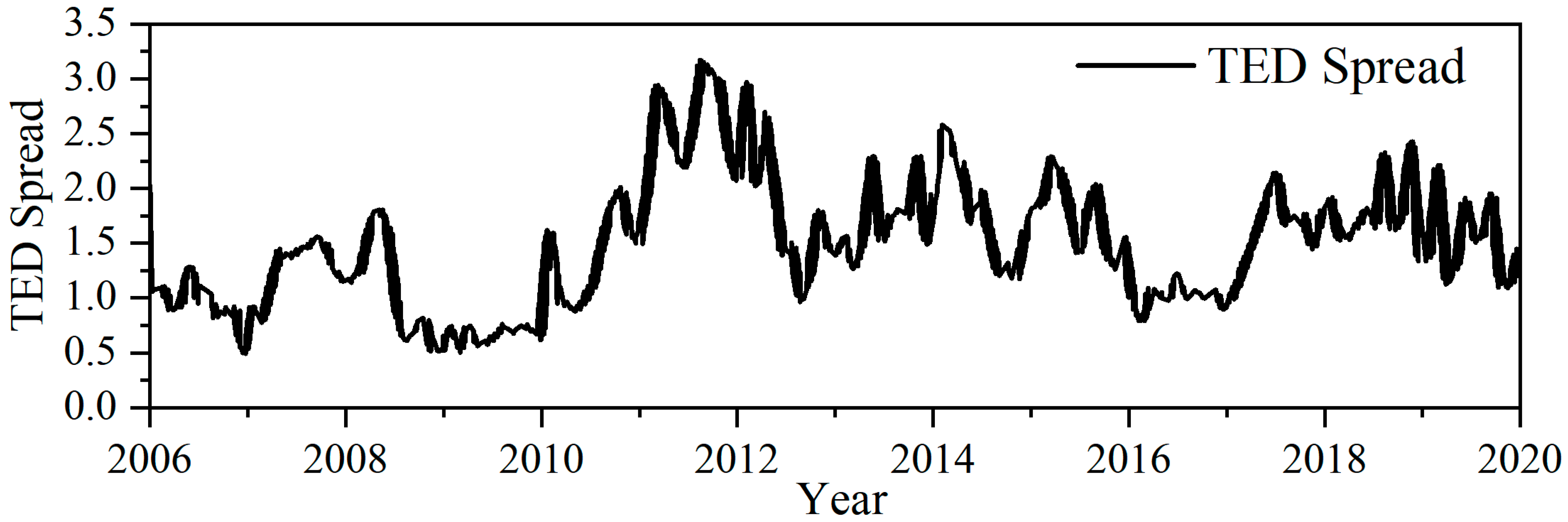
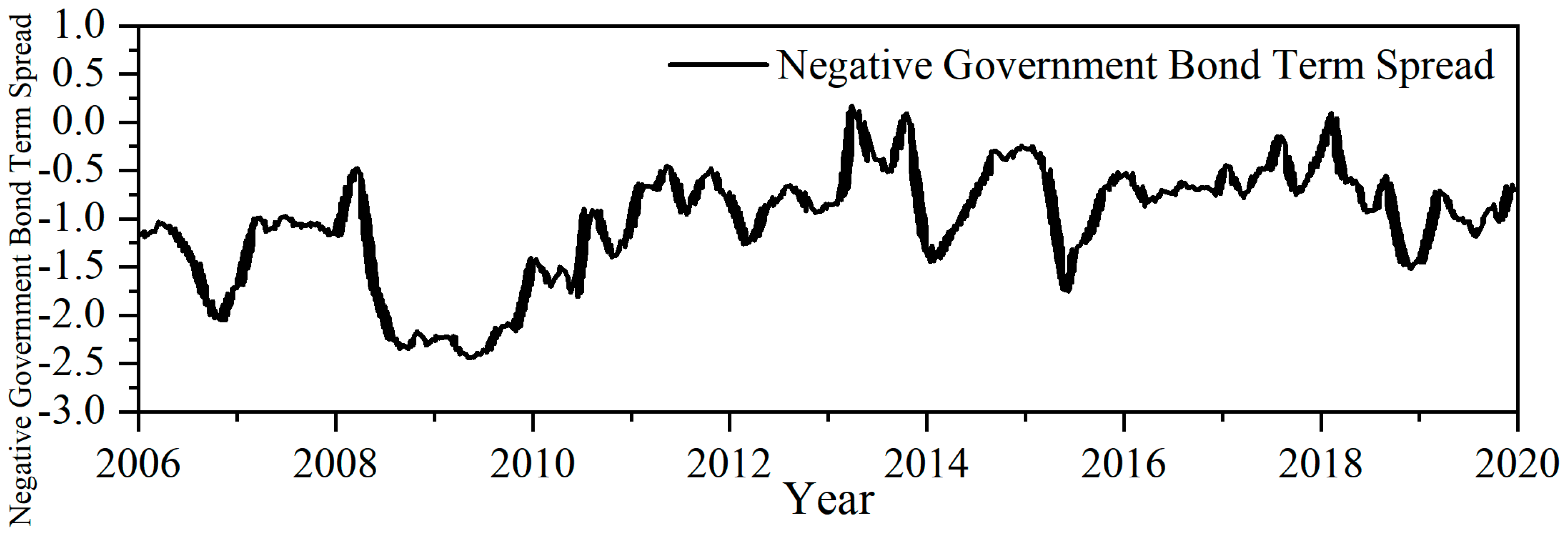
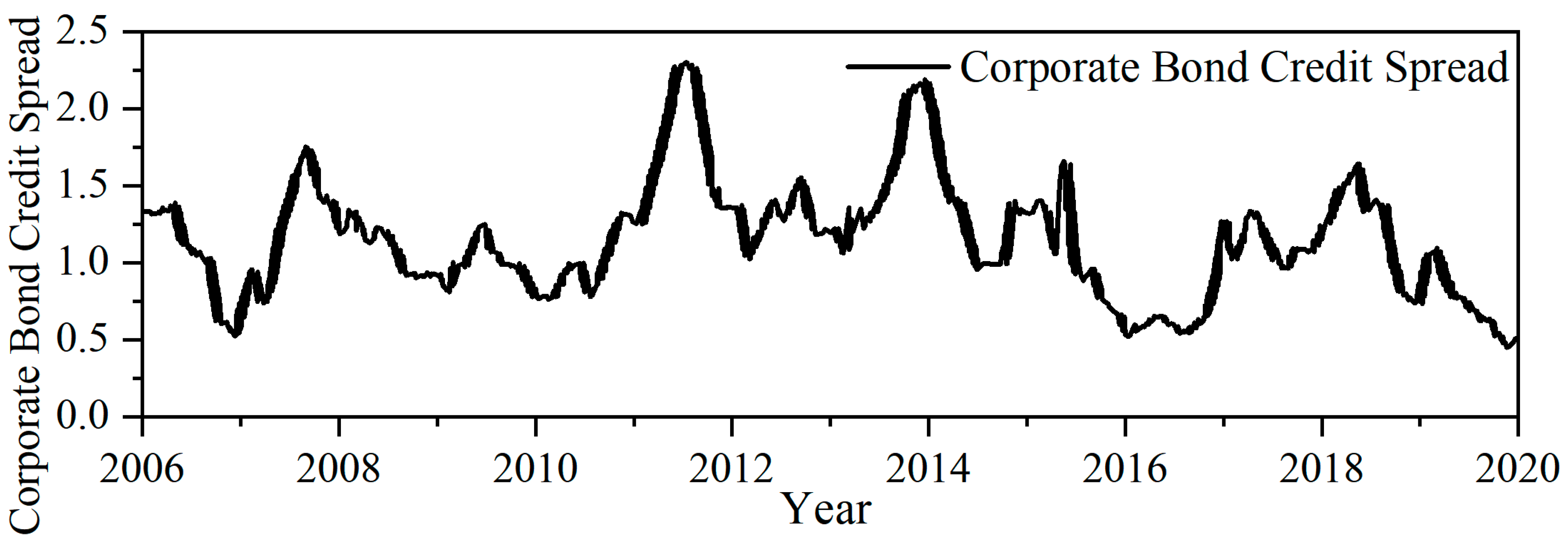
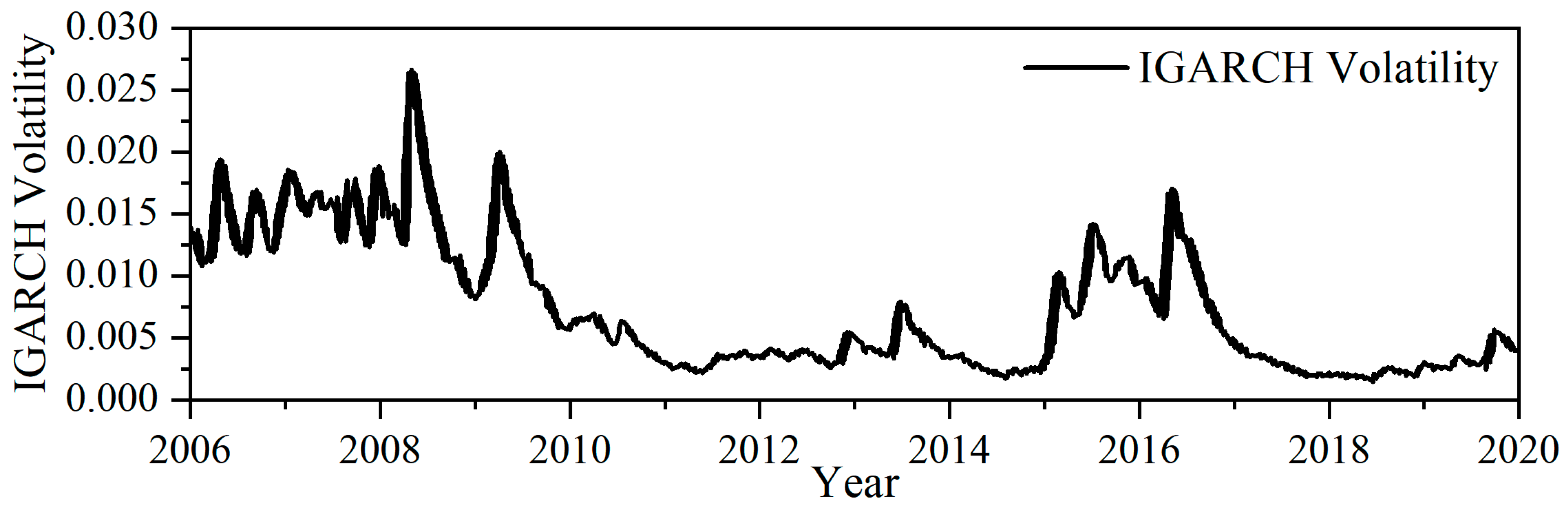


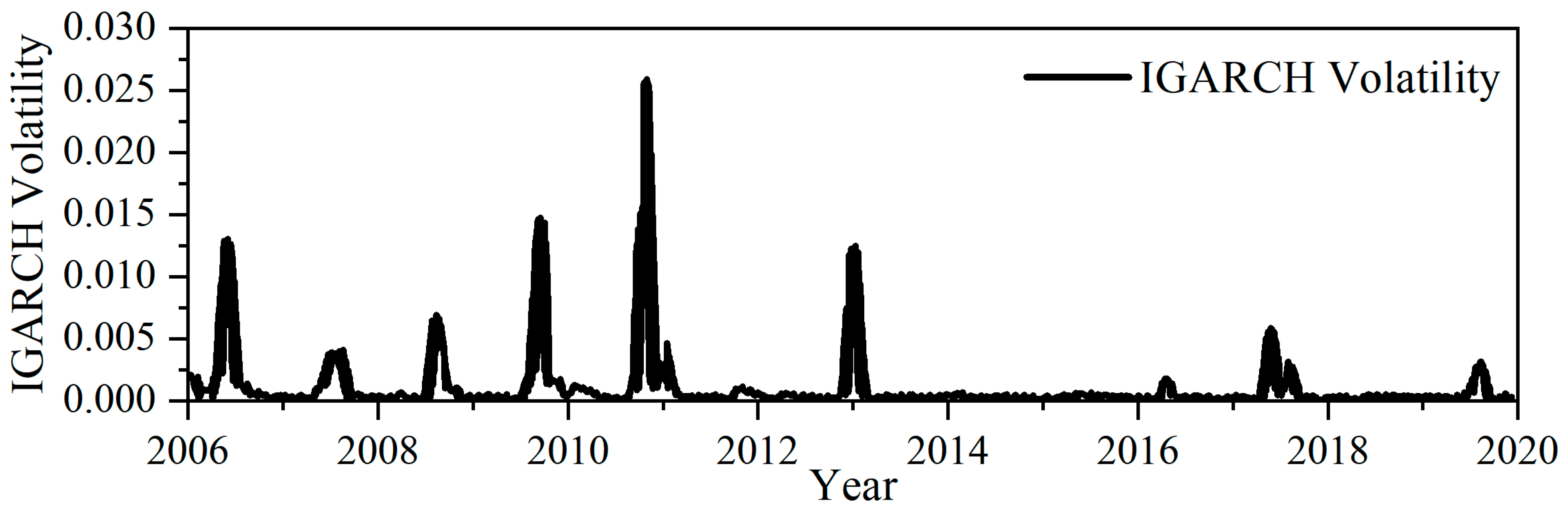





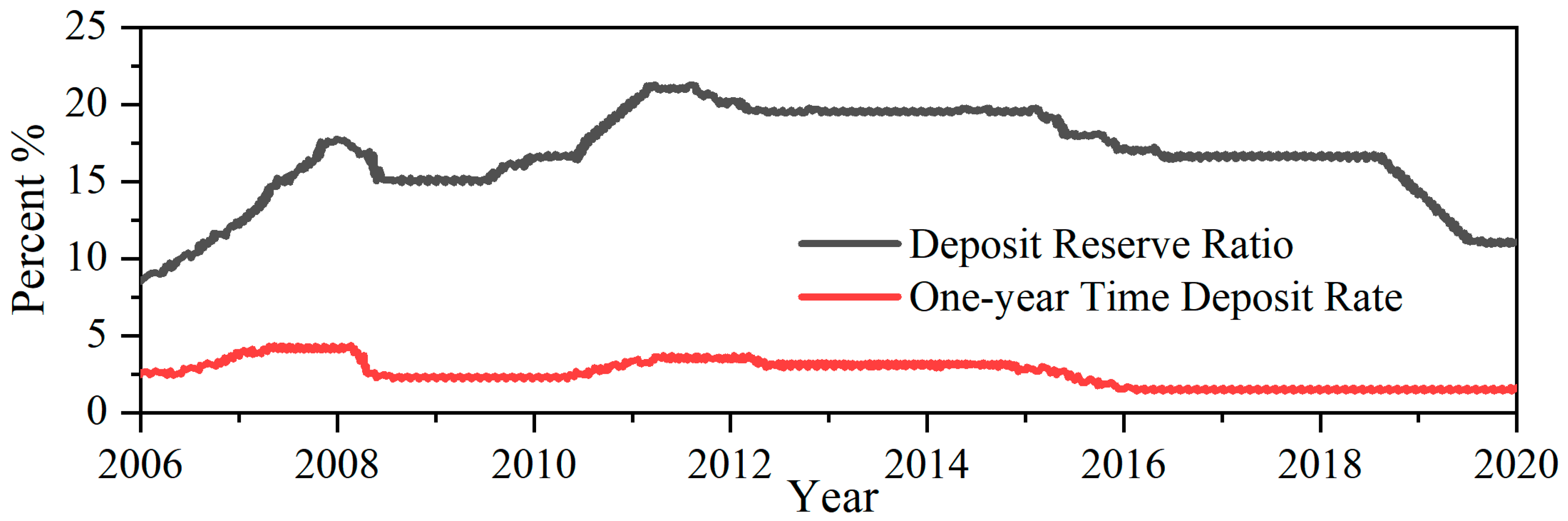
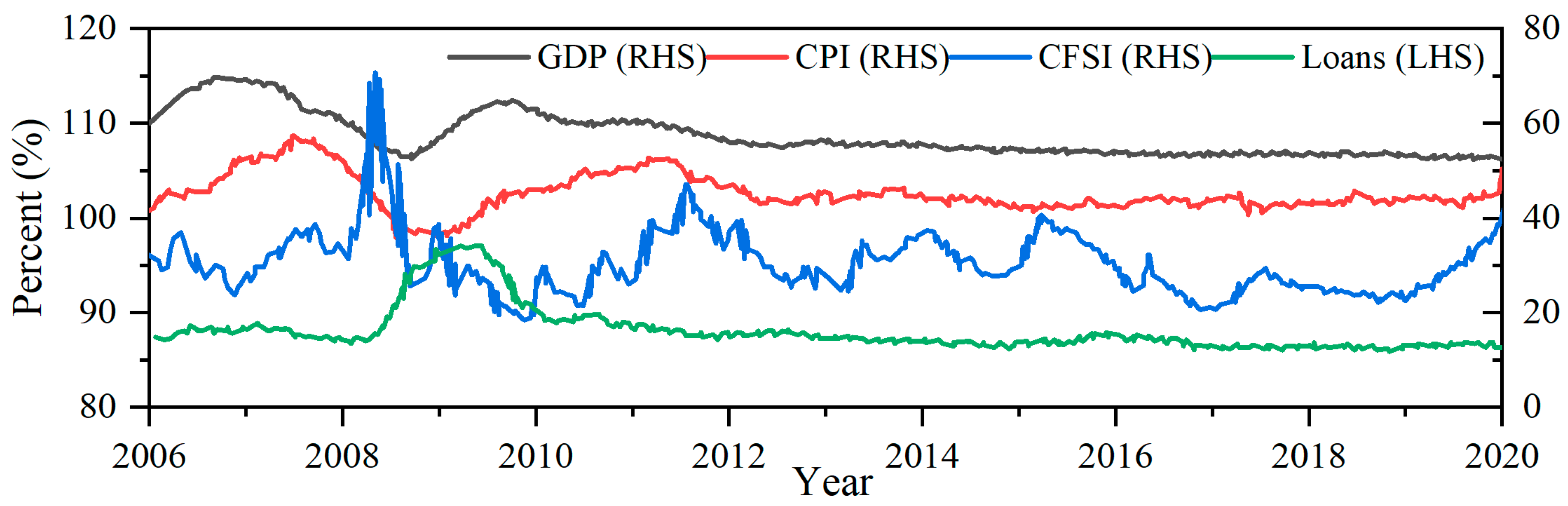



| Variable Name | Calculation Method | Influence Direction | |
|---|---|---|---|
| Currency market | SHIBOR term spread (M1) | The difference between 1-year period and 7-day SHIBOR | Negative |
| Spread between interbank offered rate and Treasury bond yield (M2) | The spread between the 3-month interbank offered rate and the 3-month Treasury bond maturity yield | Positive | |
| Bond market | Treasury bond maturity spread (B1) | The term spread between the 10-year Treasury bond and the 3-month Treasury bond yield to maturity | Negative |
| Spread between corporate bonds and government bonds (B2) | The difference between the yield to maturity of the 1-year AAA corporate bonds and the 1-year Treasury bonds | Positive | |
| Stock market | Stock price volatility (S1) | IGARCH volatility of the Shanghai Composite | Positive |
| Forex market | Real effective exchange rate volatility (F1) | IGARCH volatility of the real effective exchange rate | Positive |
| Exchange rate fluctuations (F2) | IGARCH volatility of RMB to USD | Positive | |
| Real estate market | House price volatility (H1) | IGARCH volatility of commodity housing sales prices | Positive |
| House price overvaluation level (H3) | Regression residuals of per capita disposable income and interest rates on real estate prices | Positive |
| Variable Selection | Variable Description | Data Sources | |
|---|---|---|---|
| Monetary policy variables | Real money supply (rM2_gro) | Year-on-year growth rate of M2 excluding price factors | CEIC |
| Real short-term rate (rR007) | R007 excluding price factors | CEIC | |
| Real economic variables | Actual output (rGDP_gro) | Year-on-year growth rate of real GDP | CEIC |
| Inflation (CPI) | CPI year-on-year growth rate | CEIC | |
| Systemic risk level | China Financial Stress Index (CFSI) | ||
| Variable Name | T Statistic | p-Value |
|---|---|---|
| rGDP_gro | −4.900567 *** | 0.0012 |
| CPI | −4.250878 *** | 0.0014 |
| CFSI | −3.183057 ** | 0.0271 |
| rR007 | −3.327355 ** | 0.0211 |
| rM2_gro | −4.655218 *** | 0.0027 |
| Variable Mean | Variable Intercept | ||
|---|---|---|---|
| Aj Constant | Constant Variance | Markov-Switching Mean Vector Auto-Regressive Model (MSM-VAR) | Markov-Switching Intercept Vector Auto-Regressive Model (MSI-VAR) |
| Variable Variance | Markov-Switching Mean Heteroskedastic Vector Auto-Regressive Model (MSMH-VAR) | Markov-Switching Intercept Heteroskedastic Vector Auto-Regressive Model (MSIH-VAR) | |
| Aj Variable | Constant Variance | Markov-Switching Mean Autoregressive Coefficient Vector Auto-Regressive Model (MSMA-VAR) | Markov-Switching Intercept Autoregressive Coefficient Vector Auto-Regressive Model (MSIA-VAR) |
| Variable Variance | Markov-Switching Mean Autoregressive Coefficient Heteroskedastic Vector Auto-Regressive Model (MSMAH-VAR) | Markov-Switching Intercept Autoregressive Coefficient Heteroskedastic Vector Auto-Regressive Model (MSIAH-VAR) |
| Model Form | Log Likelihood | AIC | HQ | SC |
|---|---|---|---|---|
| MSM(2)-VAR(1) | −85.499 | 5.6122 | 6.3739 | 7.6198 |
| MSMA(2)-VAR(1) | −351.0524 | 17.4715 | 18.5994 | 20.4444 |
| MSMH(2)-VAR(1) | −65.7095 * | 5.4167 * | 6.3981 * | 8.0035 * |
| MSMAH(2)-VAR(1) | −351.0524 | 18.0838 | 19.4314 | 21.6358 |
| MSI(2)-VAR(1) | −86.8419 | 5.667 | 6.4287 | 7.6747 |
| MSIA(2)-VAR(1) | −145.574 | 10.0234 | 11.4882 | 13.8843 |
| MSIH(2)-VAR(1) | −69.9882 | 5.5914 | 6.5728 | 8.1781 |
| Conversion Probability | Zone 1 | Zone 2 |
|---|---|---|
| Zone 1 | 0.9565 | 0.0435 |
| Zone 2 | 0.0769 | 0.9231 |
| Sample | Frequency | Duration | |
|---|---|---|---|
| Zone 1 | 24.0 | 0.6389 | 23.00 |
| Zone 2 | 25.0 | 0.3611 | 13.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, H.; Zheng, Y.; Li, N. Analysis of Systemic Risk Scenarios and Stabilization Effect of Monetary Policy under the COVID-19 Shock and Pharmaceutical Economic Recession. Sustainability 2023, 15, 880. https://doi.org/10.3390/su15010880
Dong H, Zheng Y, Li N. Analysis of Systemic Risk Scenarios and Stabilization Effect of Monetary Policy under the COVID-19 Shock and Pharmaceutical Economic Recession. Sustainability. 2023; 15(1):880. https://doi.org/10.3390/su15010880
Chicago/Turabian StyleDong, Hao, Yingrong Zheng, and Na Li. 2023. "Analysis of Systemic Risk Scenarios and Stabilization Effect of Monetary Policy under the COVID-19 Shock and Pharmaceutical Economic Recession" Sustainability 15, no. 1: 880. https://doi.org/10.3390/su15010880
APA StyleDong, H., Zheng, Y., & Li, N. (2023). Analysis of Systemic Risk Scenarios and Stabilization Effect of Monetary Policy under the COVID-19 Shock and Pharmaceutical Economic Recession. Sustainability, 15(1), 880. https://doi.org/10.3390/su15010880





