Spatially Varying Impacts of Built Environment on Transfer Ridership of Metro and Bus Systems
Abstract
:1. Introduction
2. Literature Review
3. Materials and Methods
3.1. Study Area and Data
3.1.1. Study Area
3.1.2. Identification of Transfer Passenger
3.1.3. Explanatory Variables
3.2. Spatial Autocorrelation
3.3. Global Model
3.4. Local Models
3.4.1. Geographically Weighted Regression (GWR)
3.4.2. Multiscale Geographically Weighted Regression (MGWR)
4. Results and Discussion
4.1. Validation and Analysis of Transfer Results
4.1.1. The Accuracy of Transfer Identification
4.1.2. Transfer Passenger Flow Characteristics
4.2. Model Results
4.2.1. OLS Model Results
4.2.2. Model Comparison and Performance
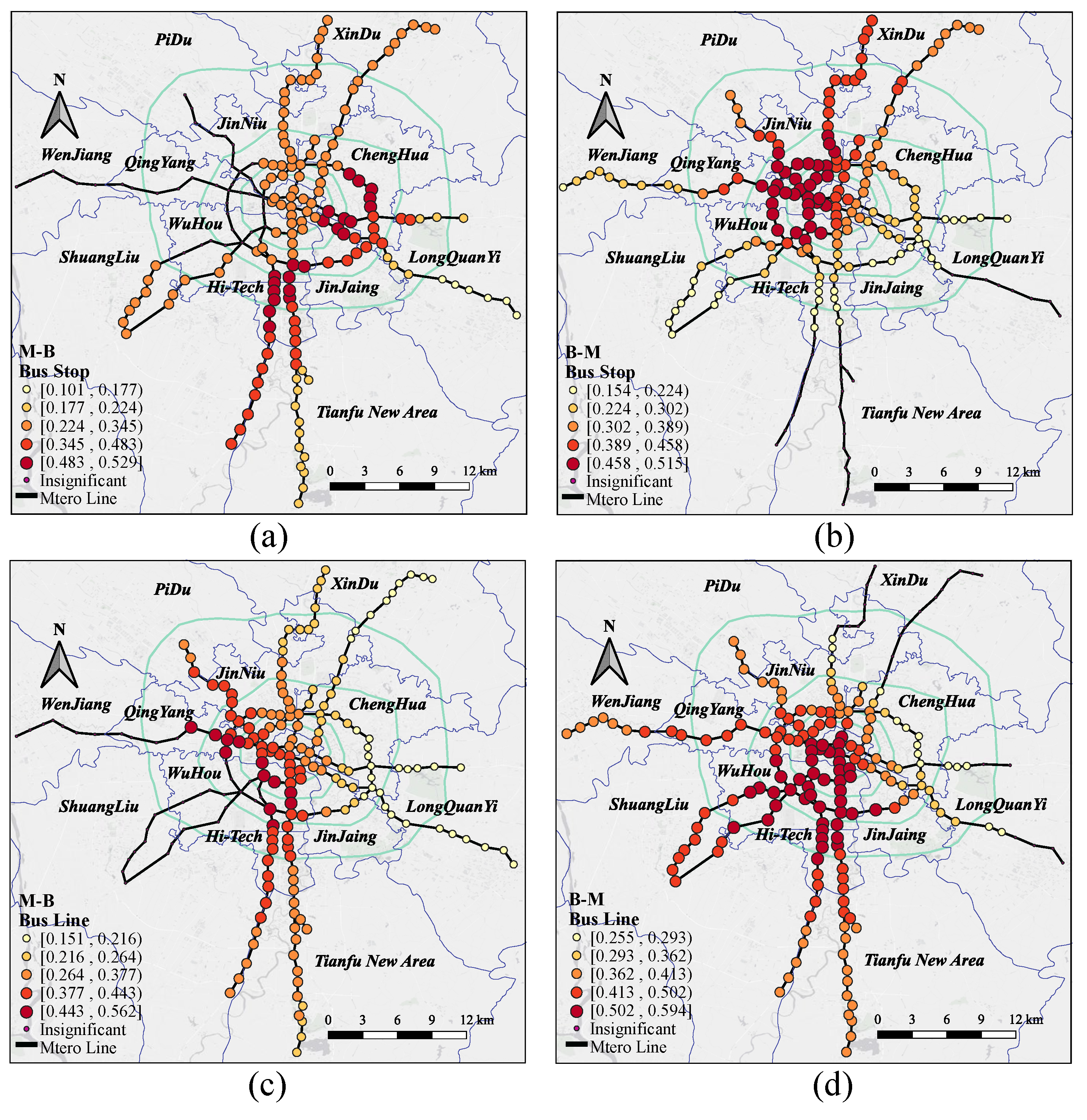
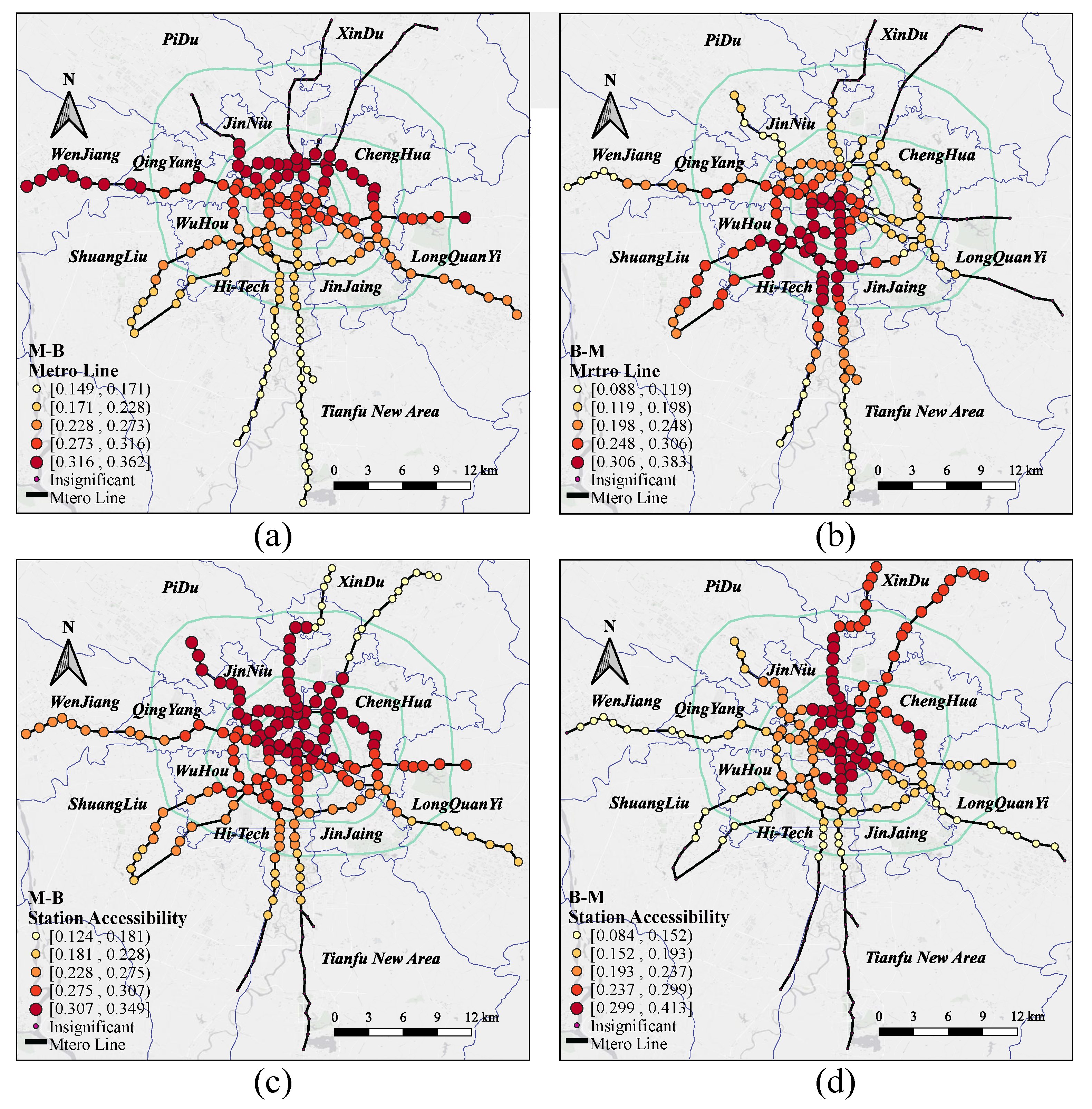
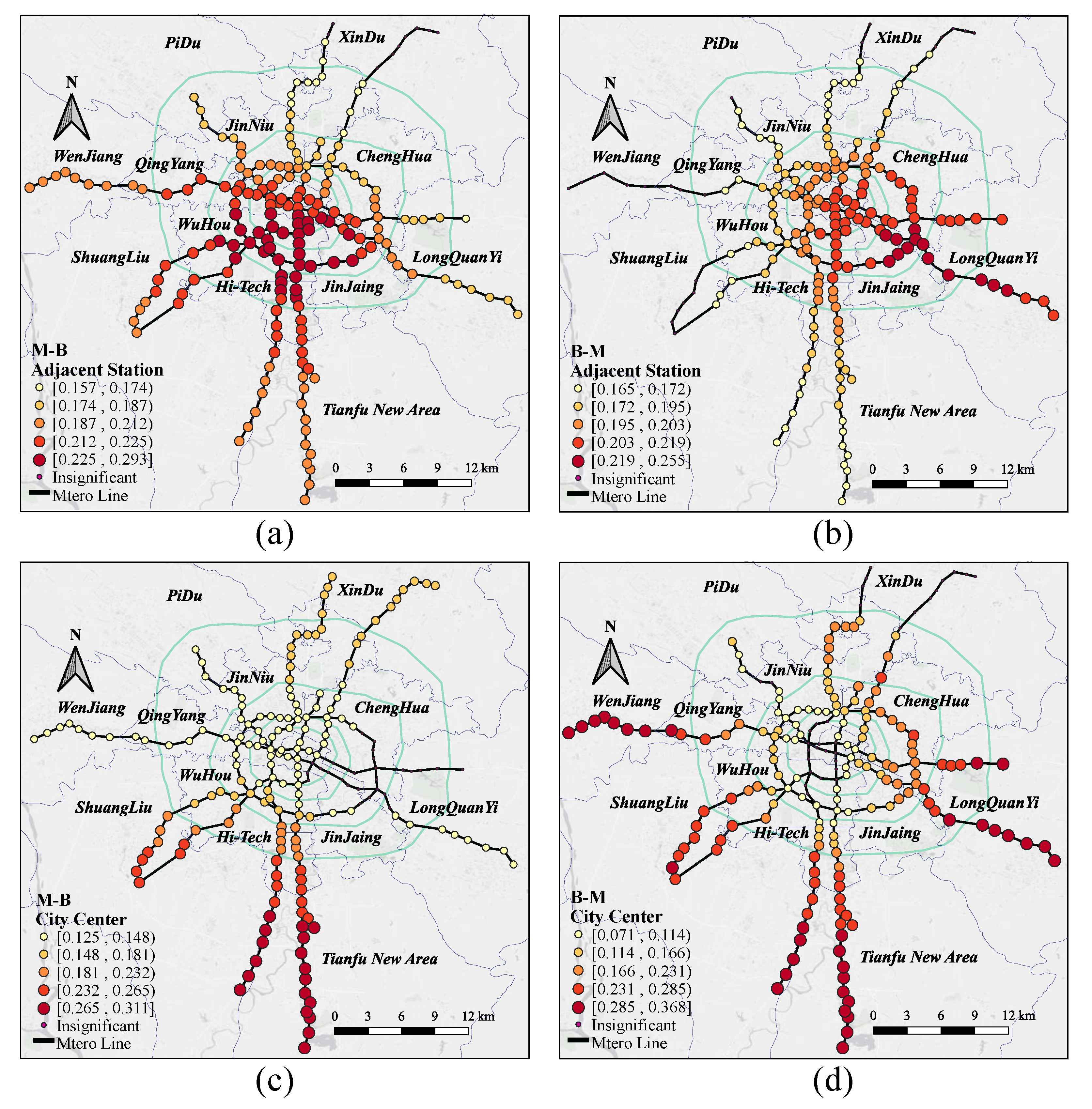
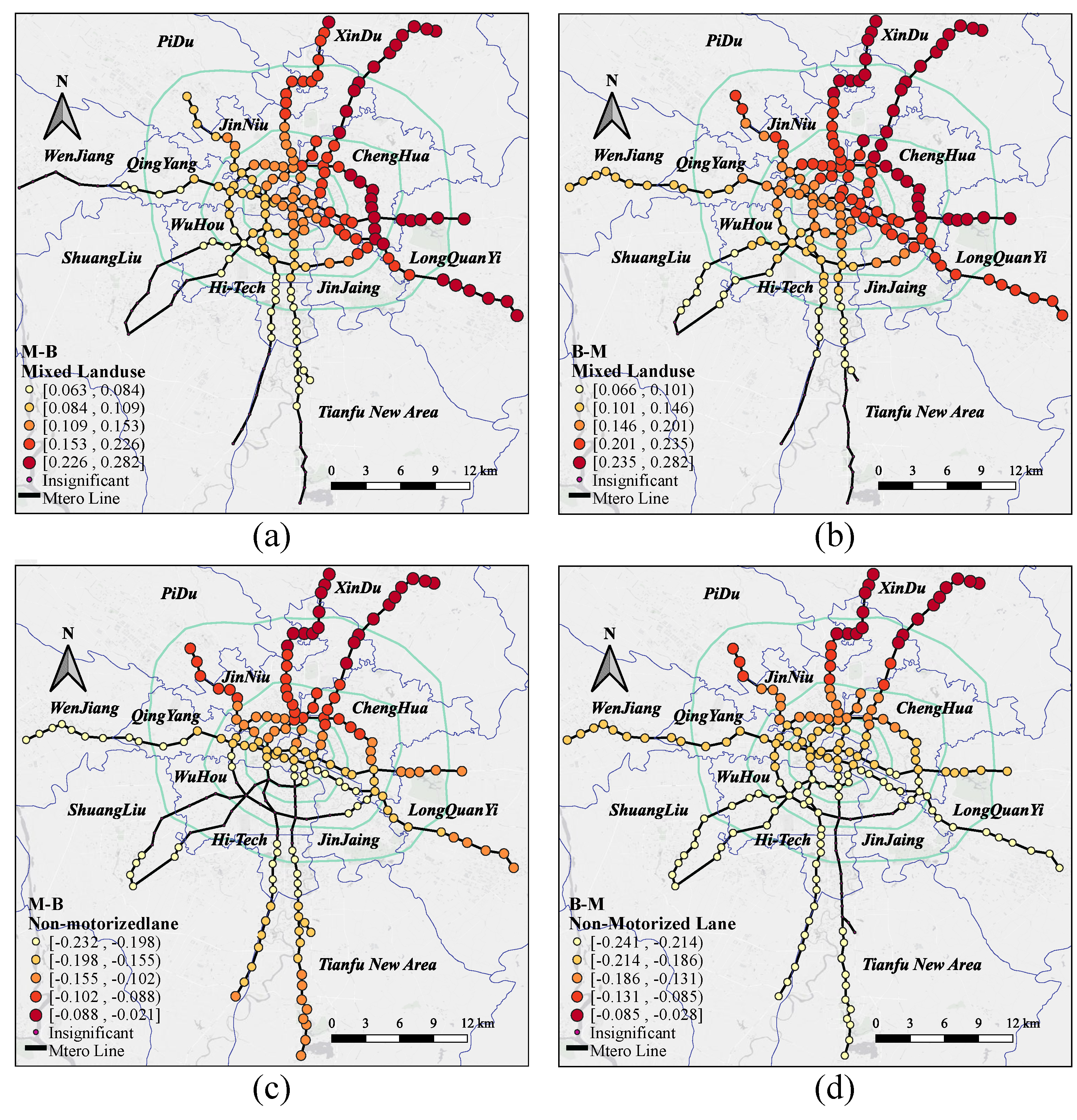
4.2.3. MGWR Model Results
5. Conclusions
- (1)
- Compared to OLS and GWR models, the MGWR model has demonstrated superior effectiveness in accounting for spatial heterogeneity at different scales. The inclusion of scale effects for built environment variables in the MGWR model allows for more precise local parameter estimates and more reliable estimation results, particularly for bus and metro transfer modes. The results show that the MGWR model outperforms the GWR model by 8.6% and 5.77% for the Adj.R2 for B-M and M-B transfer modes, respectively. In addition, the magnitude of the influence of built environment variables on metro and bus transfer modes is better represented by a 13.34% reduction in parameter AICc. This finding provides further evidence of the spatial heterogeneity of built environment variables and their influence on metro and bus transfer modes.
- (2)
- The spatial scale heterogeneity of built environment factors across different dimensions has a significant impact on metro and bus transfer modes. The results of the MGWR optimal bandwidth analysis show that the number of bus routes has the smallest scale of effect on both M-B and B-M modes while exhibiting the most significant spatial heterogeneity. In comparison, land use mix and non-highway density show a similar scale of effect to the global scale, with relatively less spatial heterogeneity.
- (3)
- The impact of the different variables differs between the M-B and B-M modes. The results show that the variables Bus Stop and Bus Line have a greater impact, while the variables Mixed land use and Non-motorized lane have the least impact, with variable Non-motorized lane having a significant negative impact. These results suggest that increasing the number of bus stops and lines around a metro station is the most effective way to increase metro and bus transfer passengers. Increasing the number of bus lines around the station is more effective than increasing the number of bus stops.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, P.; Xu, L.; Li, J.; Guo, H.; Huang, Z. Recognizing Real-Time Transfer Patterns between Metro and Bus Systems Based on Spatial–Temporal Constraints. J. Transp. Eng. Part A Syst. 2022, 148, 04022065. [Google Scholar] [CrossRef]
- Wang, D.; Zhou, M. The Built Environment and Travel Behavior in Urban China: A Literature Review. Transp. Res. Part D Transp. Environ. 2017, 52, 574–585. [Google Scholar] [CrossRef]
- Jiang, S.; Guan, W.; He, Z.; Yang, L. Exploring the Intermodal Relationship between Taxi and Subway in Beijing, China. J. Adv. Transp. 2018, 2018, 3981845. [Google Scholar] [CrossRef]
- Li, P.; Lu, Y.; Wang, J. The Effects of Fuel Standards on Air Pollution: Evidence from China. J. Dev. Econ. 2020, 146, 102488. [Google Scholar] [CrossRef]
- Wei, H. Impacts of China’s National Vehicle Fuel Standards and Subway Development on Air Pollution. J. Clean. Prod. 2019, 241, 118399. [Google Scholar] [CrossRef]
- Lin, D.; De Vos, J.; Maruyama, T.; Bobylev, N.; Cui, J. Metro-Related Transfers: A Review of Recent Literature. J. Urban Plan. Dev. 2022, 148, 03122002. [Google Scholar] [CrossRef]
- Seaborn, C.; Attanucci, J.; Wilson, N. Analyzing Multimodal Public Transport Journeys in London with Smart Card Fare Payment Data. Transp. Res. Rec. J. Transp. Res. Board 2009, 2121, 55–62. [Google Scholar] [CrossRef]
- Huang, Z.; Xu, L.; Lin, Y.; Wu, P.; Feng, B. Citywide Metro-to-Bus Transfer Behavior Identification Based on Combined Data from Smart Cards and GPS. Appl. Sci. 2019, 9, 3597. [Google Scholar] [CrossRef]
- Schakenbos, R.; Paix, L.L.; Nijenstein, S.; Geurs, K.T. Valuation of a Transfer in a Multimodal Public Transport Trip. Transp. Policy 2016, 46, 72–81. [Google Scholar] [CrossRef]
- Crane, R.; Scweitzer, L.A. Transport and Sustainability: The Role of the Built Environment. Built Environ. 2003, 29, 238–252. [Google Scholar] [CrossRef]
- Yu, L.; Xie, B.; Chan, E. How Does the Built Environment Influence Public Transit Choice in Urban Villages in China? Sustainability 2018, 11, 148. [Google Scholar] [CrossRef]
- Zhang, Y.; Thomas, T.; Brussel, M.; van Maarseveen, M. Exploring the Impact of Built Environment Factors on the Use of Public Bikes at Bike Stations: Case Study in Zhongshan, China. J. Transp. Geogr. 2017, 58, 59–70. [Google Scholar] [CrossRef]
- Van Acker, V.; Derudder, B.; Witlox, F. Why People Use Their Cars While the Built Environment Imposes Cycling. JTLU 2013, 6, 53–62. [Google Scholar] [CrossRef]
- Titze, S.; Stronegger, W.J.; Janschitz, S.; Oja, P. Association of Built-Environment, Social-Environment and Personal Factors with Bicycling as a Mode of Transportation among Austrian City Dwellers. Prev. Med. 2008, 47, 252–259. [Google Scholar] [CrossRef]
- Wey, W.-M.; Zhang, H.; Chang, Y.-J. Alternative Transit-Oriented Development Evaluation in Sustainable Built Environment Planning. Habitat Int. 2016, 55, 109–123. [Google Scholar] [CrossRef]
- Kamruzzaman, M.D.; Baker, D.; Washington, S.; Turrell, G. Advance Transit Oriented Development Typology: Case Study in Brisbane, Australia. J. Transp. Geogr. 2014, 34, 54–70. [Google Scholar] [CrossRef]
- Renne, J.L. From Transit-Adjacent to Transit-Oriented Development. Local Environ. 2009, 14, 1–15. [Google Scholar] [CrossRef]
- Cherry, T.; Townsend, C. Assessment of Potential Improvements to Metro–Bus Transfers in Bangkok, Thailand. Transp. Res. Rec. J. Transp. Res. Board 2012, 2276, 116–122. [Google Scholar] [CrossRef]
- Nesheli, M.M.; Ceder, A. (Avi) Improved Reliability of Public Transportation Using Real-Time Transfer Synchronization. Transp. Res. Part C Emerg. Technol. 2015, 60, 525–539. [Google Scholar] [CrossRef]
- Munizaga, M.A.; Carolina, P. Estimation of a Disaggregate Multimodal Public Transport Origin–Destination Matrix from Passive Smartcard Data from Santiago, Chile. Transp. Res. Part C Emerg. Technol. 2012, 24, 9–18. [Google Scholar] [CrossRef]
- Munizaga, M.A.; Gschwender, A.; Gallegos, N. Fare Evasion Correction for Smartcard-Based Origin-Destination Matrices. Transp. Res. Part A Policy Pract. 2020, 141, 307–322. [Google Scholar] [CrossRef]
- Sun, Y.; Shi, J.; Schonfeld, P.M. Identifying Passenger Flow Characteristics and Evaluating Travel Time Reliability by Visualizing AFC Data: A Case Study of Shanghai Metro. Public Transp. 2016, 8, 341–363. [Google Scholar] [CrossRef]
- Zhao, J.; Qu, Q.; Zhang, F.; Xu, C.; Liu, S. Spatio-Temporal Analysis of Passenger Travel Patterns in Massive Smart Card Data. IEEE Trans. Intell. Transport. Syst. 2017, 18, 3135–3146. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, W.; Woodburn, A.; Ryerson, M.S. Isolating High-Priority Metro and Feeder Bus Transfers Using Smart Card Data. Transportation 2017, 44, 1535–1554. [Google Scholar] [CrossRef]
- Arbab, P.; Martinez, J.; Amer, S.; Pfeffer, K. Toward Active Transport as a Utilitarian and Recreational Form of Sustainable Urban Mobility. In Advances in Mobility-as-a-Service Systems, Proceedings of the 5th Conference on Sustainable Urban Mobility, Virtual CSUM2020, Volos, Greece, 17–19 June 2020; Nathanail, E.G., Adamos, G., Karakikes, I., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 635–644. [Google Scholar]
- Ewing, R.; Cervero, R. Travel and the Built Environment: A Meta-Analysis. J. Am. Plan. Assoc. 2010, 76, 265–294. [Google Scholar] [CrossRef]
- Cervero, R.; Kockelman, K. Travel Demand and the 3Ds: Density, Diversity, and Design. Transp. Res. Part D Transp. Environ. 1997, 2, 199–219. [Google Scholar] [CrossRef]
- Yu, L.; Xie, B.; Chan, E.H.W. Exploring Impacts of the Built Environment on Transit Travel: Distance, Time and Mode Choice, for Urban Villages in Shenzhen, China. Transp. Res. Part E Logist. Transp. Rev. 2019, 132, 57–71. [Google Scholar] [CrossRef]
- Wang, X.; Shao, C.; Yin, C.; Dong, C. Exploring the Effects of the Built Environment on Commuting Mode Choice in Neighborhoods near Public Transit Stations: Evidence from China. Transp. Plan. Technol. 2021, 44, 111–127. [Google Scholar] [CrossRef]
- Gao, K.; Yang, Y.; Sun, L.; Qu, X. Revealing Psychological Inertia in Mode Shift Behavior and Its Quantitative Influences on Commuting Trips. Transp. Res. Part F Traffic Psychol. Behav. 2020, 71, 272–287. [Google Scholar] [CrossRef]
- Pan, H.; Li, J.; Shen, Q.; Shi, C. What Determines Rail Transit Passenger Volume? Implications for Transit Oriented Development Planning. Transp. Res. Part D Transp. Environ. 2017, 57, 52–63. [Google Scholar] [CrossRef]
- Zhao, J.; Deng, W.; Song, Y.; Zhu, Y. Analysis of Metro Ridership at Station Level and Station-to-Station Level in Nanjing: An Approach Based on Direct Demand Models. Transportation 2014, 41, 133–155. [Google Scholar] [CrossRef]
- Liu, D.; Rong, W.; Zhang, J.; Ge, Y.-E. (Ethan) Exploring the Nonlinear Effects of Built Environment on Bus-Transfer Ridership: Take Shanghai as an Example. Appl. Sci. 2022, 12, 5755. [Google Scholar] [CrossRef]
- An, R.; Wu, Z.; Tong, Z.; Qin, S.; Zhu, Y.; Liu, Y. How the Built Environment Promotes Public Transportation in Wuhan: A Multiscale Geographically Weighted Regression Analysis. Travel Behav. Soc. 2022, 29, 186–199. [Google Scholar] [CrossRef]
- Mainali, J.; Chang, H.; Chun, Y. A Review of Spatial Statistical Approaches to Modeling Water Quality. Prog. Phys. Geogr. Earth Environ. 2019, 43, 801–826. [Google Scholar] [CrossRef]
- Zhu, P.; Ho, S.N.; Jiang, Y.; Tan, X. Built Environment, Commuting Behaviour and Job Accessibility in a Rail-Based Dense Urban Context. Transp. Res. Part D Transp. Environ. 2020, 87, 102438. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Charlton, M.E.; Brunsdon, C. Geographically Weighted Regression: A Natural Evolution of the Expansion Method for Spatial Data Analysis. Environ. Plan A 1998, 30, 1905–1927. [Google Scholar] [CrossRef]
- Li, S.; Lyu, D.; Huang, G.; Zhang, X.; Gao, F.; Chen, Y.; Liu, X. Spatially Varying Impacts of Built Environment Factors on Rail Transit Ridership at Station Level: A Case Study in Guangzhou, China. J. Transp. Geogr. 2020, 82, 102631. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Yang, W.; Kang, W. Multiscale Geographically Weighted Regression (MGWR). Ann. Am. Assoc. Geogr. 2017, 107, 1247–1265. [Google Scholar] [CrossRef]
- Iyanda, A.E.; Osayomi, T. Is There a Relationship between Economic Indicators and Road Fatalities in Texas? A Multiscale Geographically Weighted Regression Analysis. GeoJournal 2021, 86, 2787–2807. [Google Scholar] [CrossRef]
- Chen, E.; Ye, Z.; Wang, C.; Zhang, W. Discovering the Spatio-Temporal Impacts of Built Environment on Metro Ridership Using Smart Card Data. Cities 2019, 95, 102359. [Google Scholar] [CrossRef]
- Kumar, P.; Khani, A.; He, Q. A Robust Method for Estimating Transit Passenger Trajectories Using Automated Data. Transp. Res. Part C Emerg. Technol. 2018, 95, 731–747. [Google Scholar] [CrossRef]
- Yang, H.; Li, X.; Li, C.; Huo, J.; Liu, Y. How Do Different Treatments of Catchment Area Affect the Station Level Demand Modeling of Urban Rail Transit? J. Adv. Transp. 2021, 2021, 2763304. [Google Scholar] [CrossRef]
- Jin, M.; Wang, M.; Gong, Y.; Liu, Y. Spatio-Temporal Constrained Origin-Destination Inferring Using Public Transit Fare Card Data. Phys. A Stat. Mech. Its Appl. 2022, 127642. [Google Scholar] [CrossRef]
- Gade, K. A Non-Singular Horizontal Position Representation. J. Navig. 2010, 63, 395–417. [Google Scholar] [CrossRef]
- Limpert, E.; Stahel, W.A.; Abbt, M. Log-Normal Distributions across the Sciences: Keys and Clues. BioScience 2001, 51, 341. [Google Scholar] [CrossRef]
- Wu, P.; Xu, L.; Zhong, L.; Gao, K.; Qu, X.; Pei, M. Revealing the Determinants of the Intermodal Transfer Ratio between Metro and Bus Systems Considering Spatial Variations. J. Transp. Geogr. 2022, 104, 103415. [Google Scholar] [CrossRef]
- Wang, C.; Qiu, Z.; Pan, R.; Wang, X.; Yan, Y. Exploring the Spatial Variation of Access/Egress Distances of Subway Stations Using Mobile Phone Positioning Data in Chengdu, China. J. Adv. Transp. 2023, 2023, e8008667. [Google Scholar] [CrossRef]
- Tao, T.; Wang, J.; Cao, X. Exploring the Non-Linear Associations between Spatial Attributes and Walking Distance to Transit. J. Transp. Geogr. 2020, 82, 102560. [Google Scholar] [CrossRef]
- El-Geneidy, A.; Grimsrud, M.; Wasfi, R.; Tétreault, P.; Surprenant-Legault, J. New Evidence on Walking Distances to Transit Stops: Identifying Redundancies and Gaps Using Variable Service Areas. Transportation 2014, 41, 193–210. [Google Scholar] [CrossRef]
- Wu, P.; Li, J.; Pian, Y.; Li, X.; Huang, Z.; Xu, L.; Li, G.; Li, R. How Determinants Affect Transfer Ridership between Metro and Bus Systems: A Multivariate Generalized Poisson Regression Analysis Method. Sustainability 2022, 14, 9666. [Google Scholar] [CrossRef]
- Bao, Z.; Lu, W. Applicability of the Environmental Kuznets Curve to Construction Waste Management: A Panel Analysis of 27 European Economies. Resour. Conserv. Recycl. 2023, 188, 106667. [Google Scholar] [CrossRef]
- Anselin, L.; Arribas-Bel, D. Spatial Fixed Effects and Spatial Dependence in a Single Cross-Section: Spatial Fixed Effects and Spatial Dependence. Pap. Reg. Sci. 2013, 92, 3–17. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. Geogr. Anal. 2010, 28, 281–298. [Google Scholar] [CrossRef]
- Liao, F.; Tian, Q.; Arentze, T.; Huang, H.-J.; Timmermans, H.J.P. Travel Preferences of Multimodal Transport Systems in Emerging Markets: The Case of Beijing. Transp. Res. Part A Policy Pract. 2020, 138, 250–266. [Google Scholar] [CrossRef]
- Hernandez, S.; Monzon, A. Key Factors for Defining an Efficient Urban Transport Interchange: Users’ Perceptions. Cities 2016, 50, 158–167. [Google Scholar] [CrossRef]
- Mollalo, A.; Vahedi, B.; Rivera, K.M. GIS-Based Spatial Modeling of COVID-19 Incidence Rate in the Continental United States. Sci. Total Environ. 2020, 728, 138884. [Google Scholar] [CrossRef] [PubMed]
- Oshan, T.M.; Smith, J.; Fotheringham, A.S. Targeting the Spatial Context of Obesity Determinants via Multiscale Geographically Weighted Regression; Open Science Framework: Charlottesville, VA, USA, 2020. [Google Scholar]
- Wang, S.; Noland, R.B. Variation in Ride-Hailing Trips in Chengdu, China. Transp. Res. Part D Transp. Environ. 2021, 90, 102596. [Google Scholar] [CrossRef]
- Liu, J.; Chau, K.W.; Bao, Z. Multiscale Spatial Analysis of Metro Usage and Its Determinants for Sustainable Urban Development in Shenzhen, China. Tunn. Undergr. Space Technol. 2023, 133, 104912. [Google Scholar] [CrossRef]
- Manville, M. Travel and the Built Environment: Time for Change. J. Am. Plan. Assoc. 2017, 83, 29–32. [Google Scholar] [CrossRef]
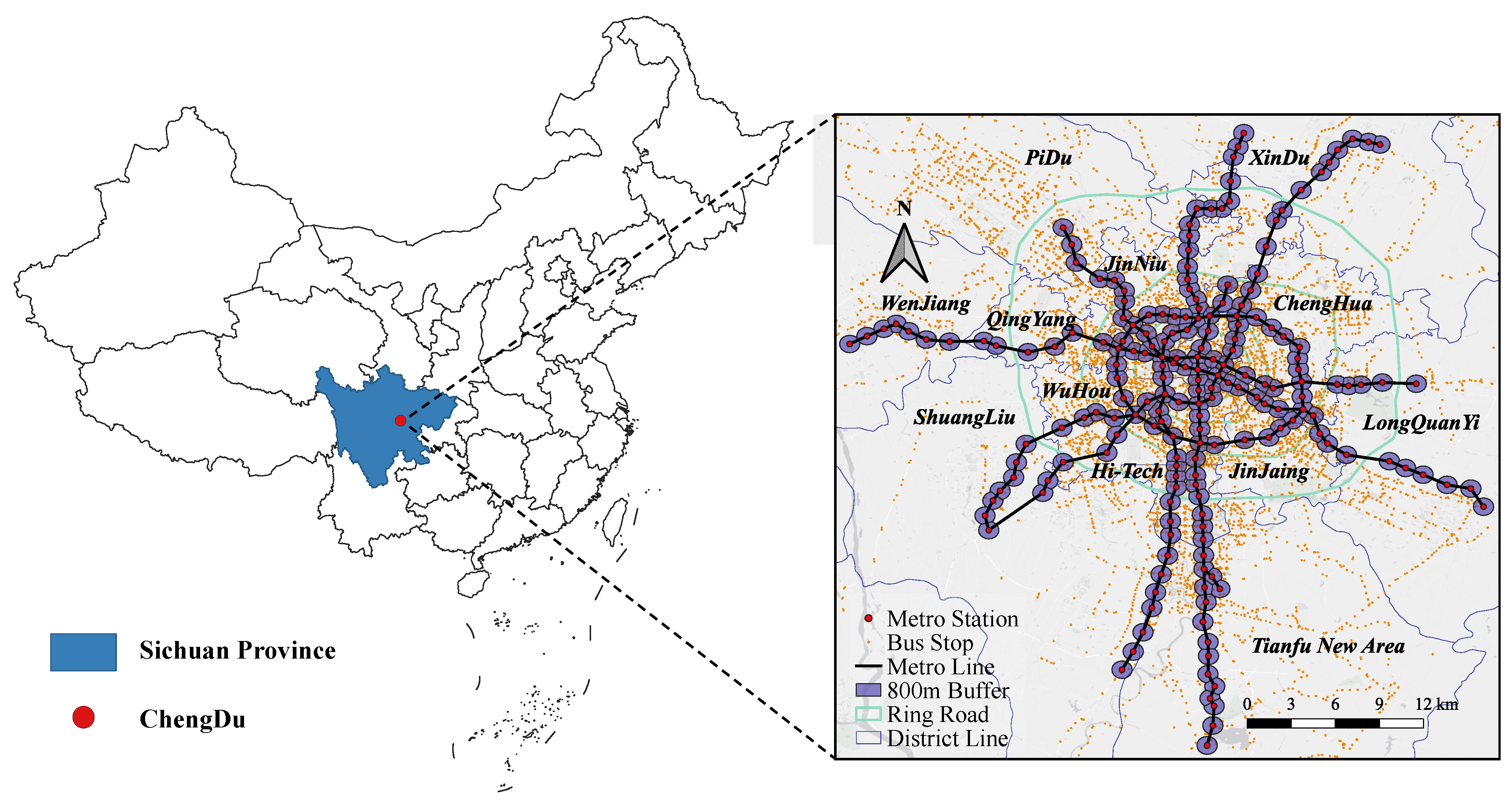
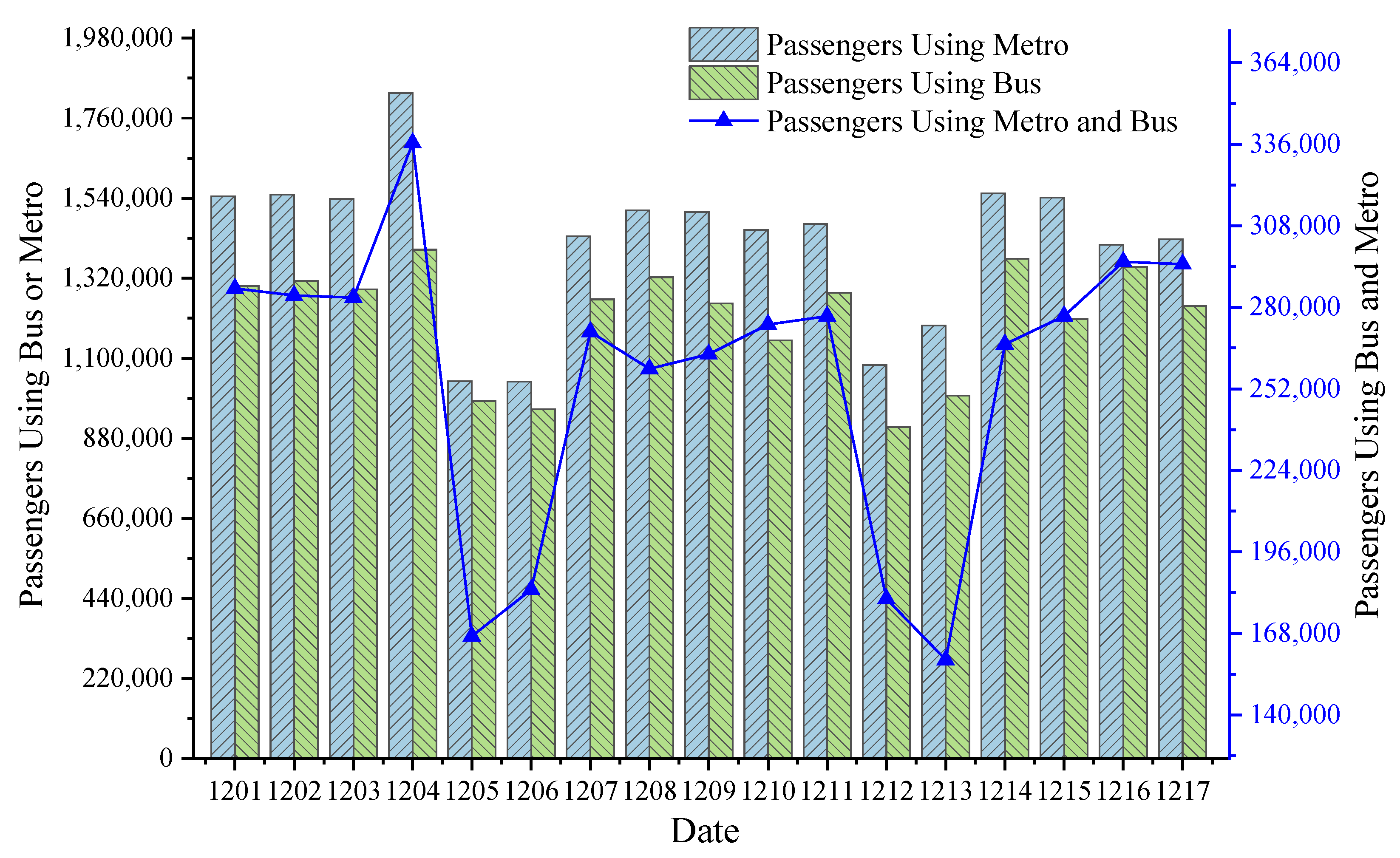
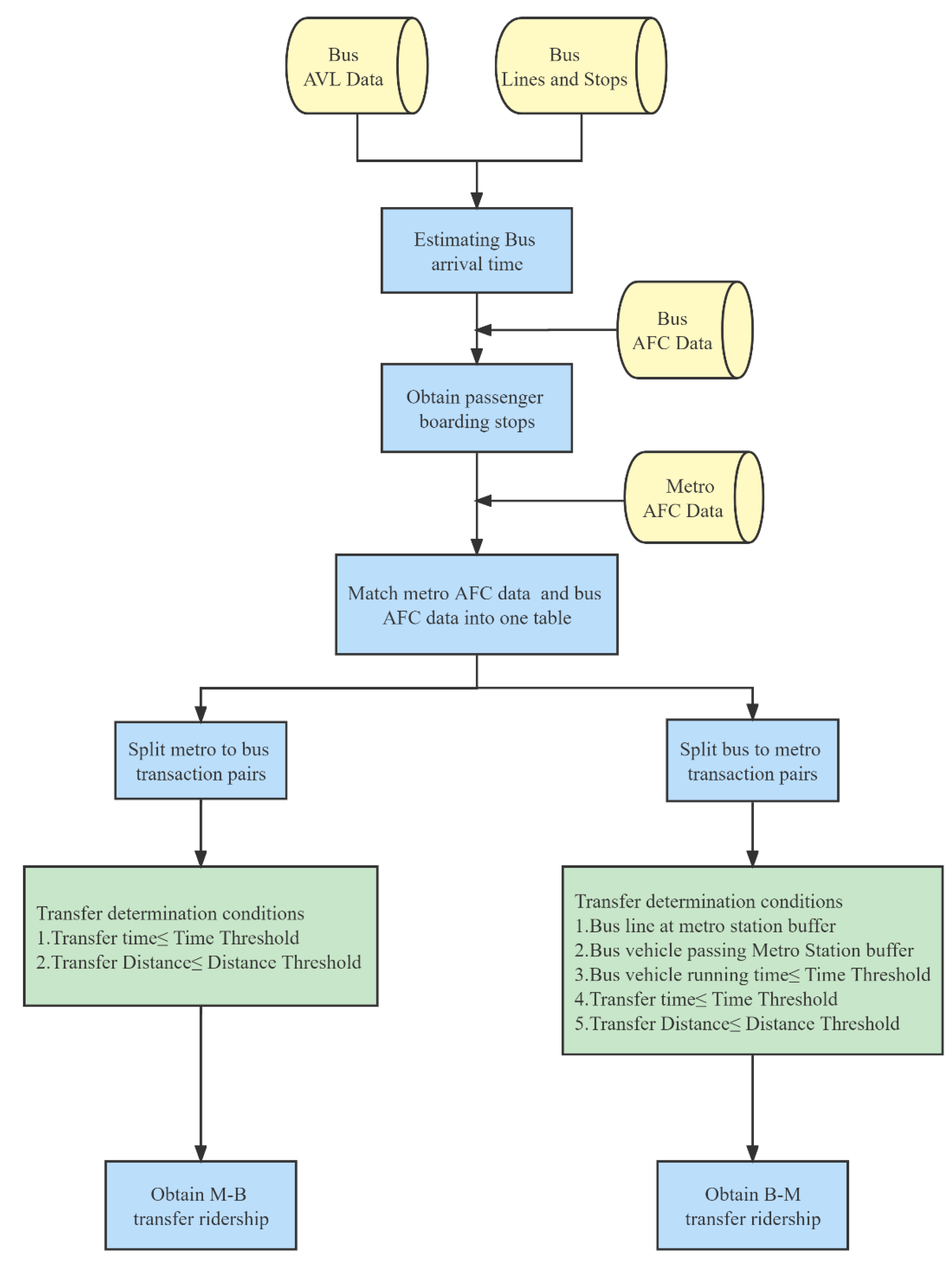

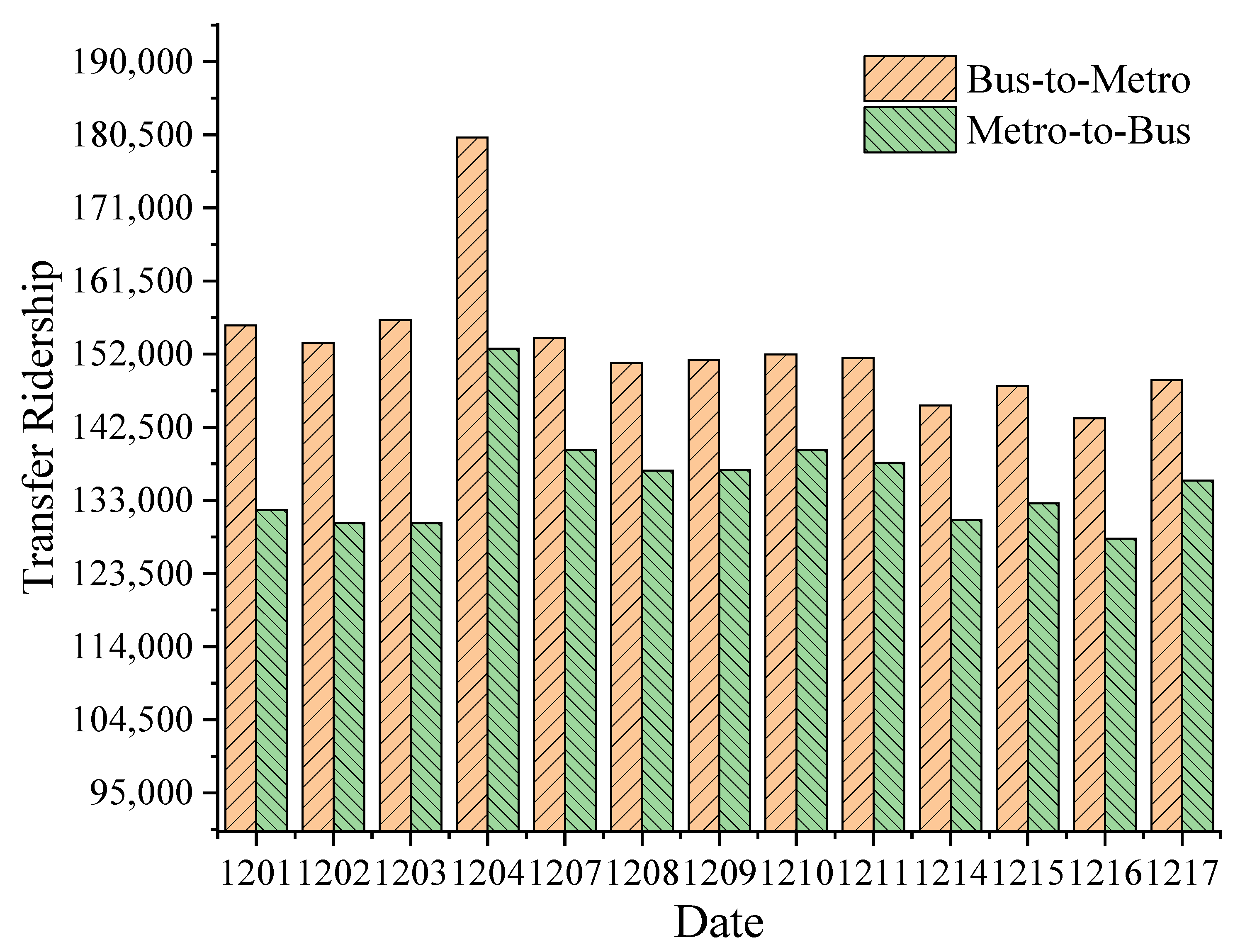
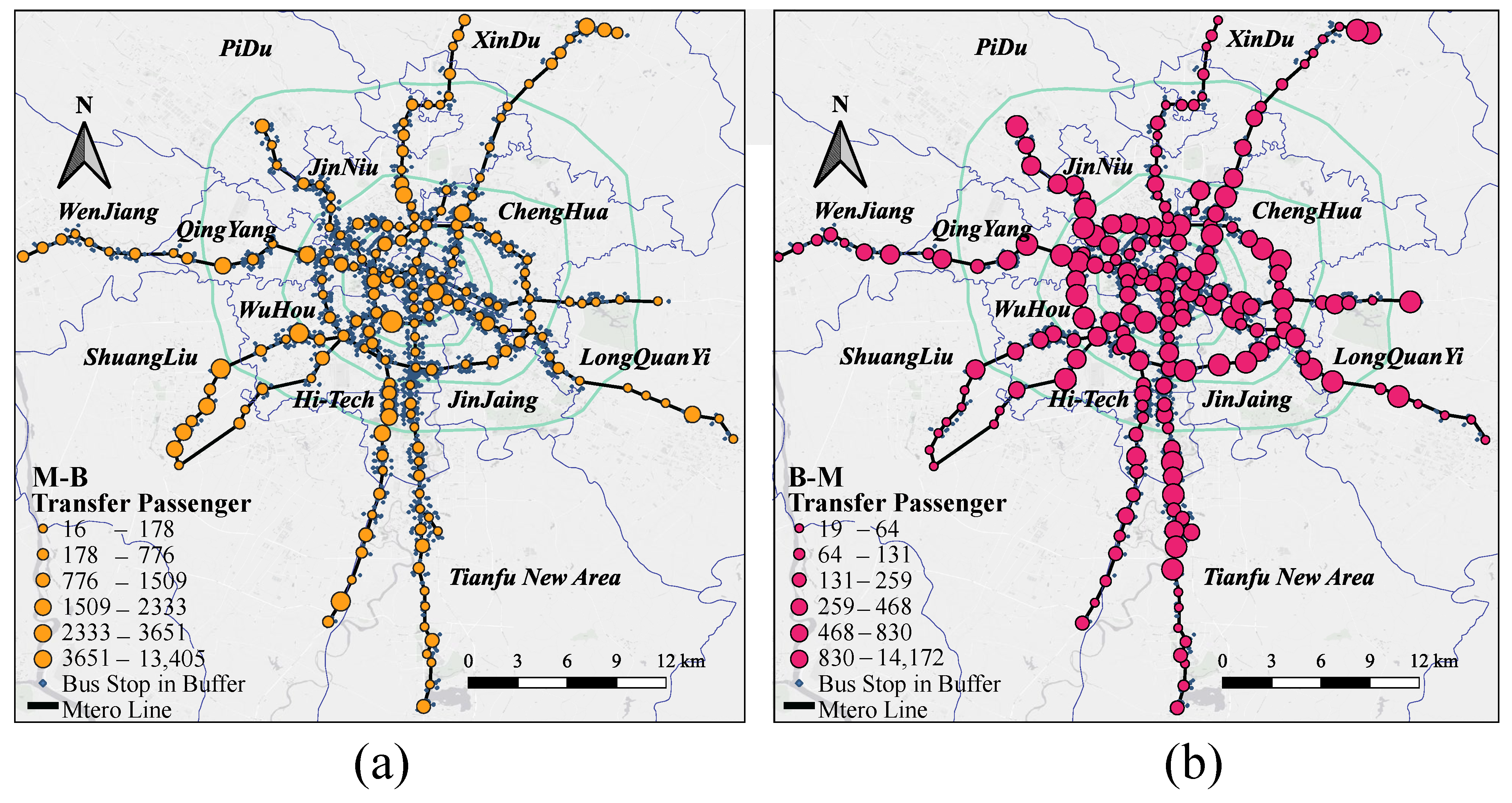
| Variables | Description | Mean | S.D | Source |
|---|---|---|---|---|
| Bus Stop | The number of bus stops | 21.40 | 13.20 | Chengdu Public Transport Group |
| Bus Line | The number of bus lines passing through | 21.98 | 17.64 | Chengdu Public Transport Group |
| Station Accessibility | The distance to other stations on the metro network | 14.15 | 3.79 | Chengdu Rail Transit Group |
| Metro Line | The number of metro lines passing through | 1.24 | 0.49 | ArcGIS |
| Terminal | Is it a terminal station? 1 means yes, 0 means no | 0.07 | 0.25 | ArcGIS |
| Adjacent station | The average distance to adjacent metro stations | 1.55 | 0.54 | ArcGIS |
| City Center | The straight line distance from the city center | 10.39 | 6.64 | ArcGIS |
| Non-motorized lane | The density of the non-motorized lane | 12.84 | 5.11 | Amap |
| Mixed land use | The Shannon entropy of POI categories | 0.63 | 0.10 | Amap |
| Bus Lines | Bus Vehicle Arrivals at Morning or Evening Peak | Morning or Evening Peak Boarding Passengers | ||||
|---|---|---|---|---|---|---|
| Time Interval | Maximum Error Number of Stops | Total Number of Error Stops | Real Passengers | Inferred Passengers | Error | |
| 49 | 14.45 s | 1 | 8 | 14.78 | 14.36 | −2.84 |
| 56 | 18.64 s | 1 | 4 | 29.08 | 29.63 | 1.89 |
| 73 | 13.25 s | 0 | 5 | 13.85 | 14.13 | 2.02 |
| Variables | Multicollinearity | Spatial Autocorrelation | |||
|---|---|---|---|---|---|
| VIFM-B | VIFB-M | Moran’s I | Z-Value | p-Value | |
| YM-B | — | — | 0.474 | 12.247 | <0.001 |
| YB-M | — | — | 0.409 | 10.574 | <0.001 |
| Bus Stop | 3.34 | 3.29 | 0.445 | 13.309 | <0.001 |
| Bus Line | 3.3 | 3.3 | 0.364 | 9.735 | <0.001 |
| Metro Line | 4.37 | 4.34 | 0.413 | 7.269 | <0.001 |
| Station Accessibility | 1.28 | 1.28 | 0.434 | 7.583 | <0.001 |
| Terminal | 1.17 | 1.19 | 0.361 | 6.508 | <0.001 |
| Adjacent station | 1.63 | 1.51 | 0.499 | 8.816 | <0.001 |
| City Center | 4.15 | 4.2 | 0.399 | 10.361 | <0.001 |
| Non-motorized lane | 2.34 | 2.18 | 0.431 | 11.175 | <0.001 |
| Mixed land use | 1.16 | 1.12 | 0.077 | 2.161 | <0.001 |
| Variables | M-B_OLS | B-M_OLS | ||||||
|---|---|---|---|---|---|---|---|---|
| Coefficient | T-Value | p-Value | VIF | Coefficient | T-Value | p-Value | VIF | |
| Intercept | 6.347 | 19.652 | 0.042 | — | 9.245 | 24.988 | 0.033 | — |
| Bus Stop | 0.184 * | 5.684 | 0.022 | 3.34 | 0.153 * | 8.097 | 0.015 | 3.29 |
| Bus Line | 0.237 * | 5.891 | 0.015 | 3.30 | 0.211 * | 3.426 | 0.018 | 3.30 |
| Metro Line | 0.151 * | 4.836 | 0.017 | 4.37 | 0.128 * | 6.135 | 0.035 | 4.34 |
| Station Accessibility | 0.222 ** | 4.003 | 0.004 | 1.28 | 0.149 * | 4.967 | 0.029 | 1.28 |
| Terminal | 0.094 * | 6.810 | 0.015 | 1.17 | 0.114 * | 7.358 | 0.011 | 1.19 |
| Adjacent station | 0.145 * | 3.177 | 0.033 | 1.63 | 0.201 * | 5.245 | 0.032 | 1.51 |
| City Center | 0.164 * | 5.160 | 0.014 | 4.15 | 0.178 ** | 2.382 | 0.006 | 4.20 |
| Non-motorized lane | −0.088 ** | −2.272 | 0.002 | 2.34 | −0.091 ** | −4.663 | 0.003 | 2.18 |
| Mixed land use | 0.155 * | 4.609 | 0.031 | 1.16 | 0.199 * | 2.504 | 0.023 | 1.12 |
| Variables | M-B_GWR | M-B_MGWR | B-M_GWR | B-M_MGWR | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | S.D | Mean | S.D | Mean | S.D | Mean | S.D | |
| Bus Stop | 0.221 * | 0.017 | 0.373 ** | 0.017 | 0.240 * | 0.015 | 0.368 ** | 0.017 |
| Bus Line | 0.276 * | 0.014 | 0.455 * | 0.018 | 0.297 * | 0.020 | 0.401 * | 0.013 |
| Metro Line | 0.203 * | 0.006 | 0.272 * | 0.008 | 0.183 * | 0.017 | 0.267 * | 0.014 |
| Station Accessibility | 0.213 * | 0.010 | 0.285 ** | 0.005 | 0.148 * | 0.003 | 0.278 ** | 0.014 |
| Terminal | 0.155 * | 0.003 | 0.227 * | 0.002 | 0.184 * | 0.011 | 0.203 * | 0.020 |
| Adjacent station | 0.193 * | 0.003 | 0.228 * | 0.002 | 0.216 * | 0.012 | 0.235 * | 0.009 |
| City Center | 0.217 * | 0.008 | 0.203 * | 0.003 | 0.164 ** | 0.015 | 0.212 ** | 0.005 |
| Non-motorized lane | −0.127 ** | 0.006 | −0.131 ** | 0.013 | −0.133 ** | 0.020 | -0.122 ** | 0.012 |
| Mixed land use | 0.211 * | 0.018 | 0.178 * | 0.002 | 0.238 * | 0.014 | 0.176 * | 0.015 |
| AICc | RSS | R2 | Adj.R2 | |
|---|---|---|---|---|
| M-B_OLS | 539.895 | 164.129 | 0.193 | 0.146 |
| M-B_GWR | 382.102 | 114.332 | 0.782 | 0.741 |
| M-B_MGWR | 322.856 | 39.532 | 0.799 | 0.754 |
| B-M_OLS | 539.321 | 163.641 | 0.235 | 0.192 |
| B-M_GWR | 359.164 | 71.578 | 0.788 | 0.77 |
| B-M_MGWR | 311.25 | 33.967 | 0.811 | 0.783 |
| Bandwidth | B-M | M-B | ||
|---|---|---|---|---|
| MGWR | GWR | MGWR | GWR | |
| Bus Stop | 87 | 79 | 96 | 79 |
| Bus Line | 47 | 79 | 38 | 79 |
| Metro Line | 129 | 79 | 134 | 79 |
| Station Accessibility | 156 | 79 | 156 | 79 |
| Terminal | 84 | 79 | 92 | 79 |
| Adjacent station | 68 | 79 | 75 | 79 |
| City Center | 93 | 79 | 93 | 79 |
| Non-motorized lane | 138 | 79 | 138 | 79 |
| Mixed land use | 144 | 79 | 144 | 79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Yan, Q.; Ma, Y.; Luo, C. Spatially Varying Impacts of Built Environment on Transfer Ridership of Metro and Bus Systems. Sustainability 2023, 15, 7891. https://doi.org/10.3390/su15107891
Li X, Yan Q, Ma Y, Luo C. Spatially Varying Impacts of Built Environment on Transfer Ridership of Metro and Bus Systems. Sustainability. 2023; 15(10):7891. https://doi.org/10.3390/su15107891
Chicago/Turabian StyleLi, Xiang, Qipeng Yan, Yafeng Ma, and Chen Luo. 2023. "Spatially Varying Impacts of Built Environment on Transfer Ridership of Metro and Bus Systems" Sustainability 15, no. 10: 7891. https://doi.org/10.3390/su15107891
APA StyleLi, X., Yan, Q., Ma, Y., & Luo, C. (2023). Spatially Varying Impacts of Built Environment on Transfer Ridership of Metro and Bus Systems. Sustainability, 15(10), 7891. https://doi.org/10.3390/su15107891


_Chen.png)




