Assessing Environmental Sustainability Based on the Three-Dimensional Emergy Ecological Footprint (3D EEF) Model: A Case Study of Gansu Province, China
Abstract
1. Introduction
2. Materials and Methods
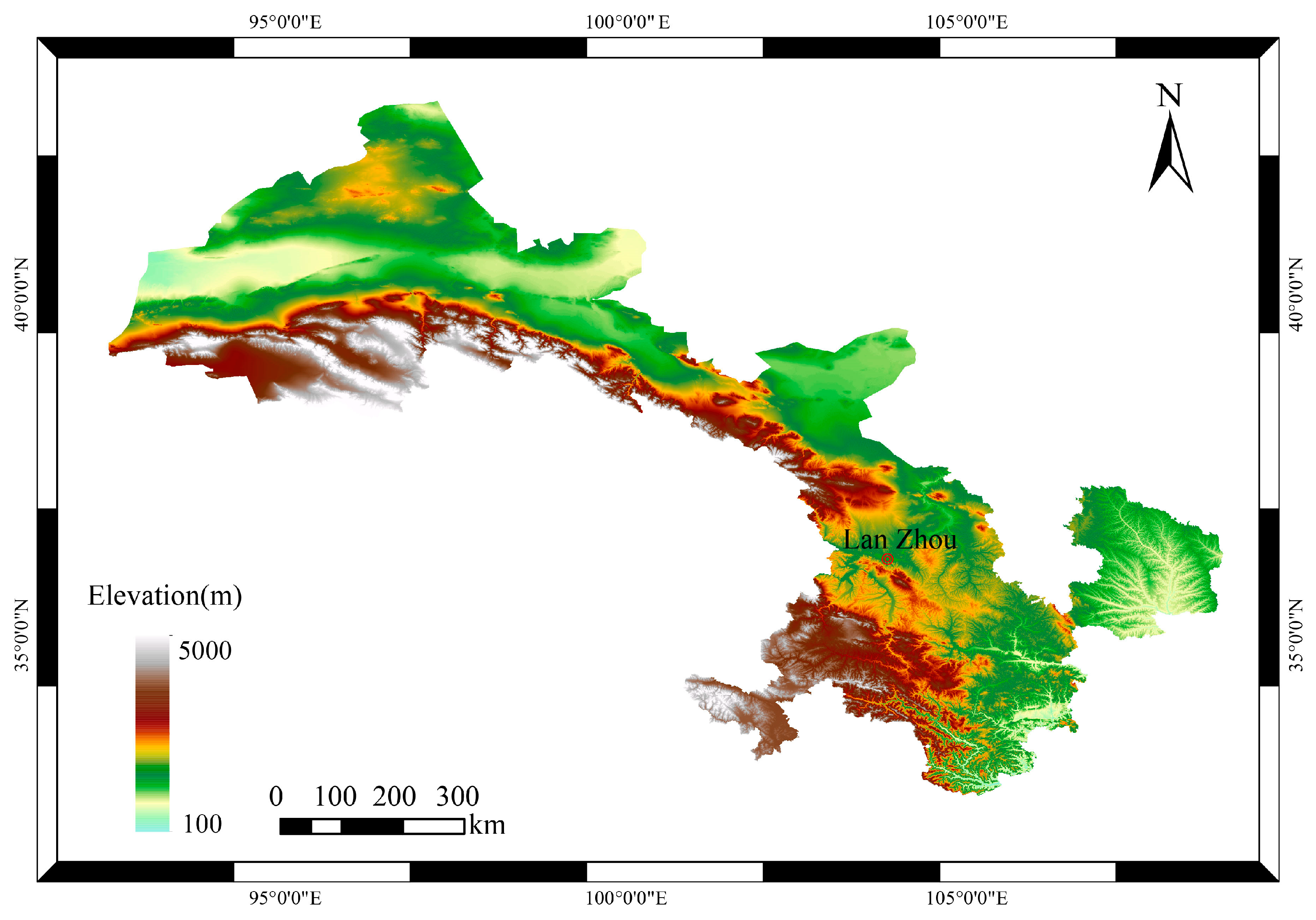
2.1. Study Area
2.2. Data Source
2.3. Methods
2.3.1. Emergy Analysis Theory
2.3.2. 3D EEF Model
2.3.3. ARIMA Model
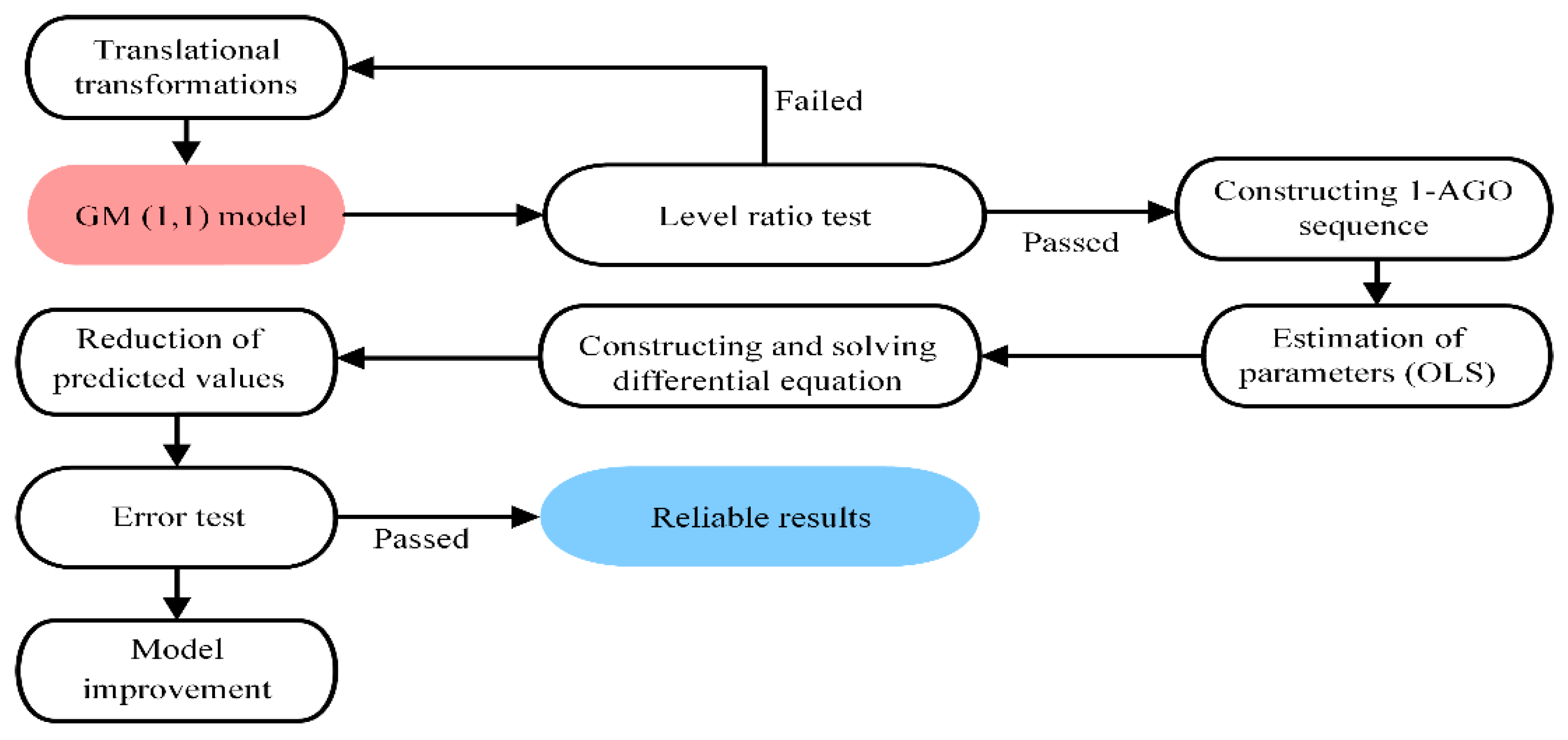
2.3.4. Gray Model
3. Results
3.1. Calculation Results
3.1.1. Calculation of ecc in Gansu Province in 2020
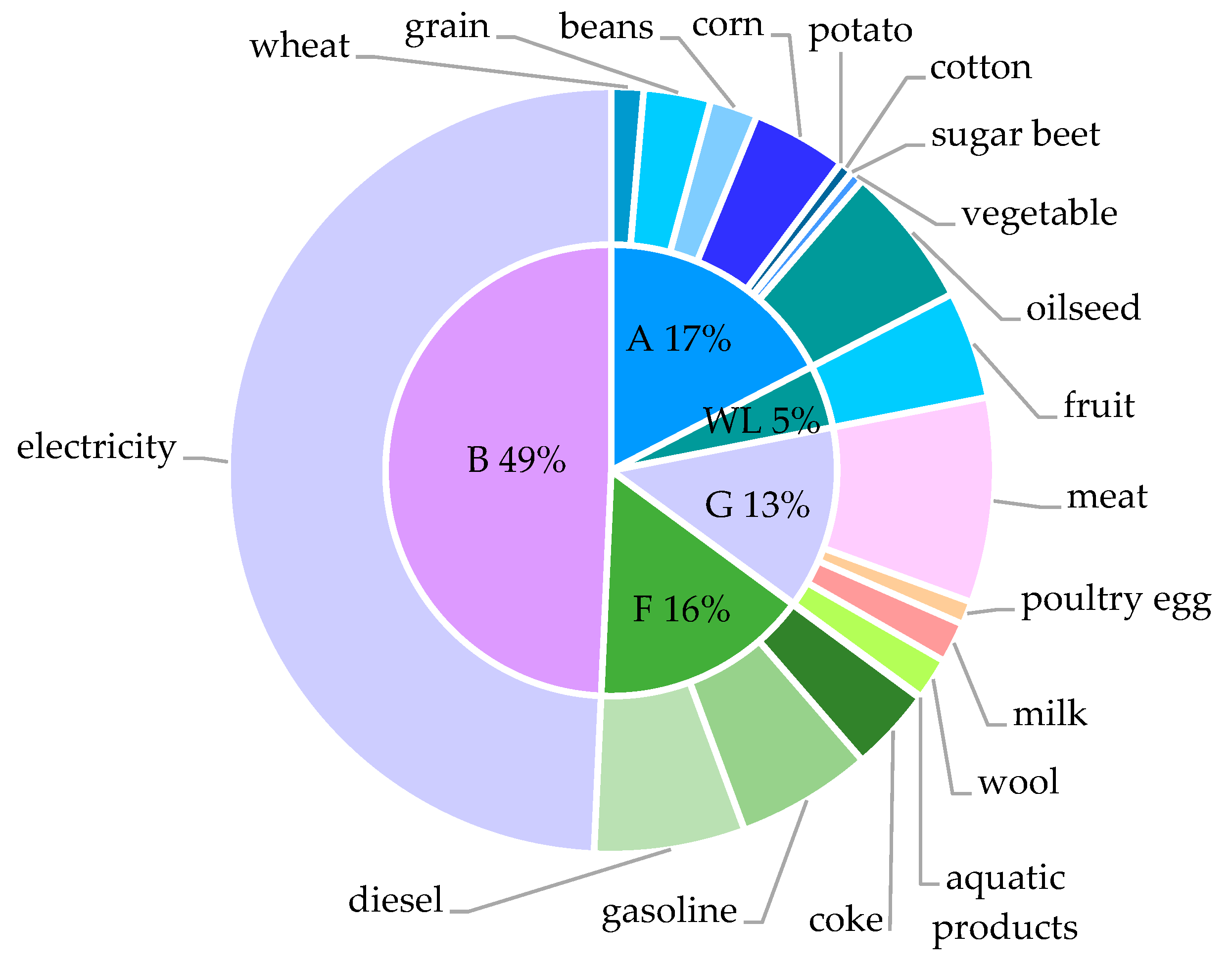
3.1.2. Calculation of eef in Gansu Province for 2020
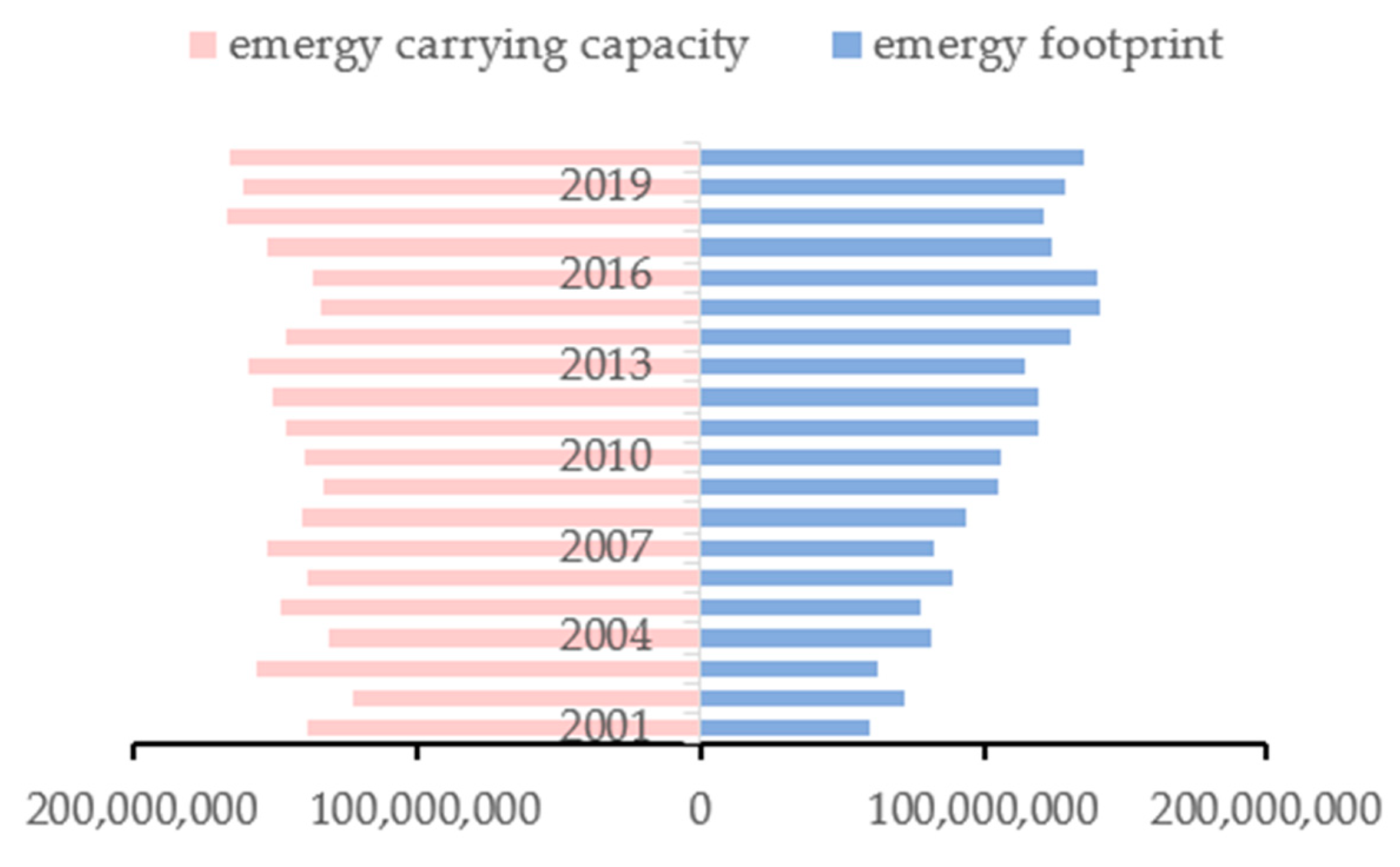
3.1.3. Calculation of EEF3D in Gansu Province from 2001 to 2020
3.2. Predicted Results
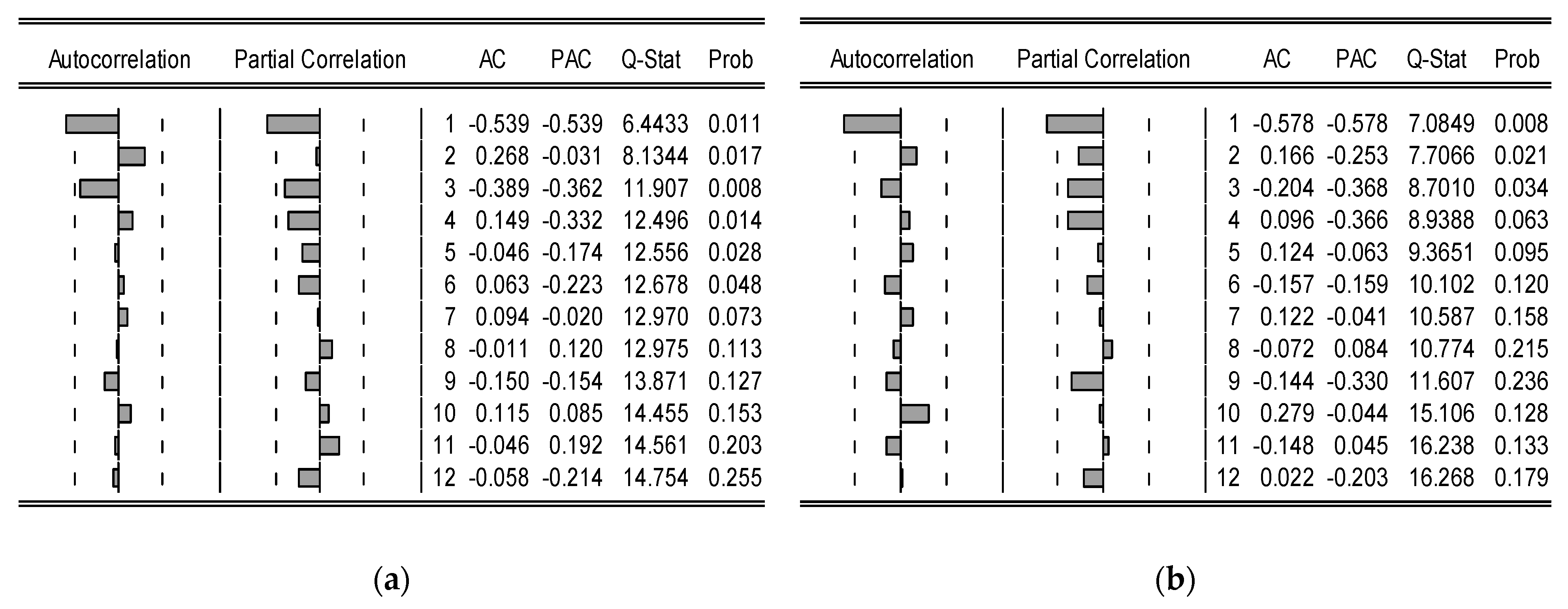
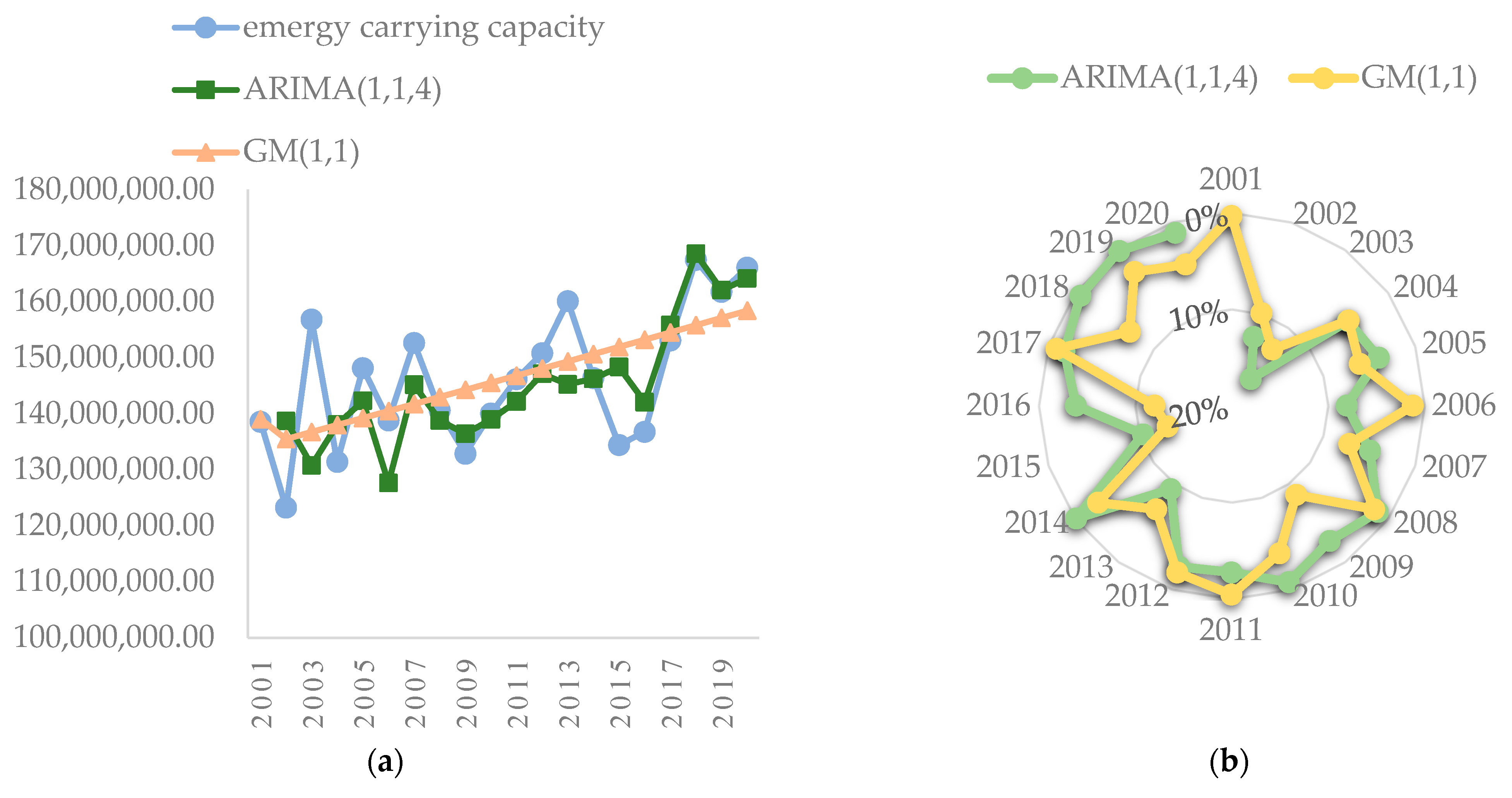
3.2.1. Predicted Results of the ECC
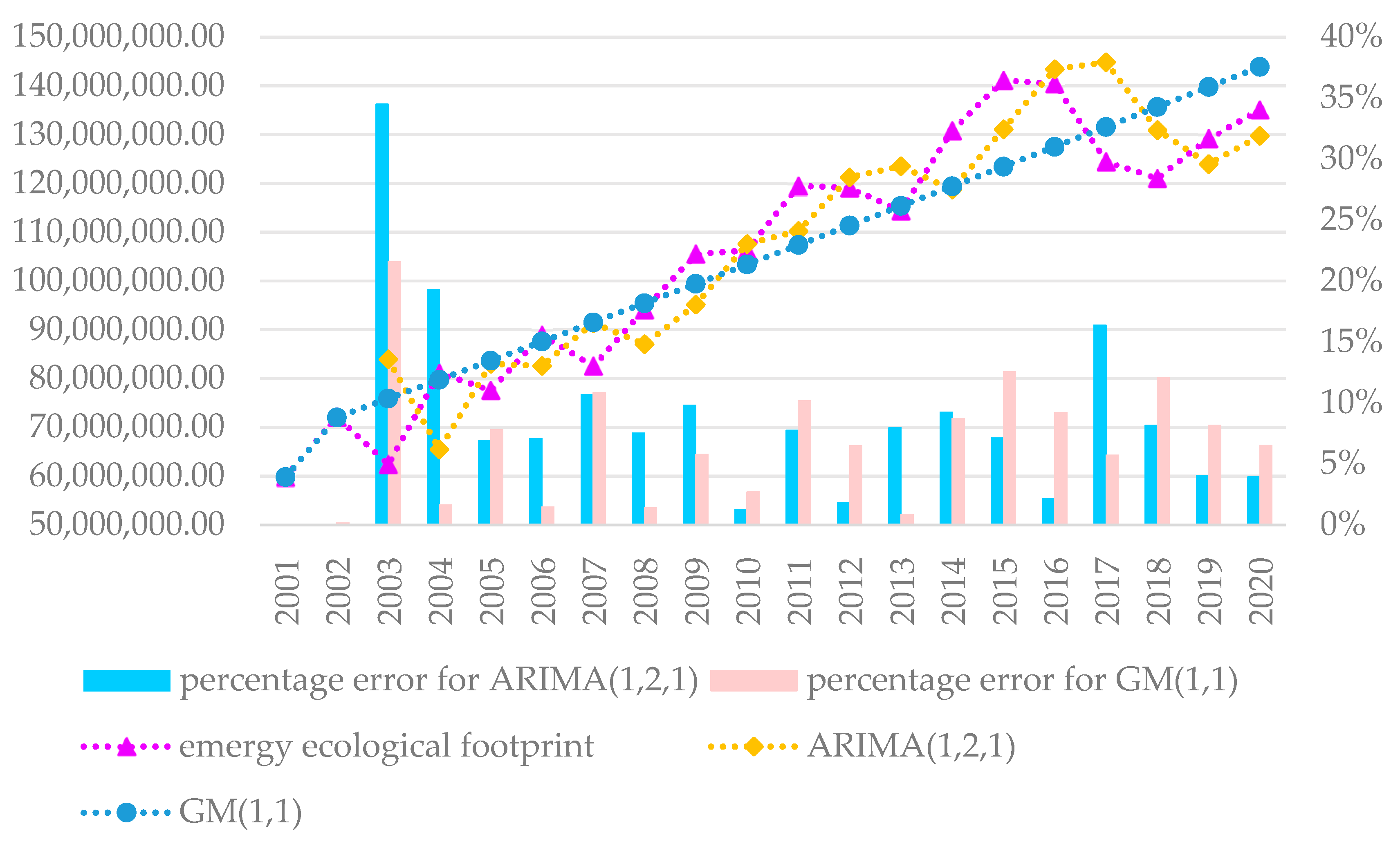
3.2.2. Predicted Results of the EEF
3.2.3. Predicted Results of the EEF3D
4. Discussion
4.1. Analysis of Results and Comparison
4.2. Limitations and Applications of the Model
4.3. Policy Implications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, H.J.; Qu, J.S.; Pang, J.X.; Xu, L.; Han, J.Y. Spatial-temporal synthetic measurement of coupling coordination and sustainable development of population-economy-society-resource-environment system in Gansu Province. J. Arid Land 2020, 43, 1622–1634. [Google Scholar]
- Peng, W.J.; Wang, X.M.; Li, X.K.; He, C.C. Sustainability evaluation based on the emergy ecological footprint method: A case study of Qingdao, China, from 2004 to 2014. Ecol. Indic. 2018, 85, 1249–1261. [Google Scholar] [CrossRef]
- Liu, H.; Wei, Y.M.; Jin, X. Emergy footprint analysis of gannan Tibet an autonomous prefecture ecological-economic systems. In Ecosystem Assessment and Fuzzy Systems Management; Springer: Cham, Switzerland, 2014; pp. 53–61. [Google Scholar]
- Odum, H.T. Systems Ecology: An Introduction; John Wiley & Sons: New York, NY, USA, 1983. [Google Scholar]
- Wackernagel, M.; Rees, W. Our Ecological Footprint: Reducing Human Impact on the Earth; New Society Publishers: Gabriola Island, BC, Canada, 1998. [Google Scholar]
- Zhao, S.; Li, Z.Z.; Li, W.L. A modified method of ecological footprint calculation and its application. Ecol. Model. 2005, 185, 65–75. [Google Scholar] [CrossRef]
- Zhao, S.; Song, K.; Gui, F.; Cai, H.W.; Jin, W.H.; Wu, C.W. The emergy ecological footprint for small fish farm in China. Ecol. Indic. 2013, 29, 62–67. [Google Scholar] [CrossRef]
- Chen, B.; Chen, G.Q. Ecological footprint accounting based on emergy—A case study of the Chinese society. Ecol. Model. 2006, 198, 101–114. [Google Scholar] [CrossRef]
- Chen, C.F.; Wang, H.Y.; Xiao, D.N.; Wang, D.Q. Comparison of sustainable development status in Heilongjiang Province based on traditional ecological footprint method and emergy ecological footprint method. J. Appl. Ecol. 2008, 19, e2544–e2549. [Google Scholar]
- Mancini, M.S.; Galli, A.; Niccolucci, V.; Lin, D.; Bastianoni, S.; Wackernagel, M.; Marchettini, N. Ecological footprint: Refining the carbon footprint calculation. Ecol. Indic. 2016, 61, 390–403. [Google Scholar] [CrossRef]
- Lin, Q.P.; Feng, Z.S.; Liu, N.H.; Mei, Y. Modified Model of Ecological Footprint Accounting and Its Application to Cropland in Jiangsu, China. Pedosphere 2008, 18, 9. [Google Scholar]
- Liu, X.M.; Fu, J.Y.; Jiang, D.J.; Luo, J.W.; Sun, C.X.; Liu, H.M.; Wen, R.; Wang, X. Improvement of ecological footprint model in national nature reserve based on net primary production (NPP). Sustainability 2018, 11, 2. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, D. Natural capital utilization based on a three-dimensional ecological footprint model: A case study in northern Shaanxi, China. Ecol. Indic. 2018, 87, 178–188. [Google Scholar] [CrossRef]
- Fang, K. Ecological footprint depth and size: New indicators for a 3D model. Acta Ecol. Sin. 2013, 33, 0267–0274. [Google Scholar] [CrossRef]
- Zhang, L.; Dzakpasu, M.; Chen, R.; Wang, X.C. Validity and utility of ecological footprint accounting: A state-of-the-art review. Sustain. Cities Soc. 2017, 32, 411–416. [Google Scholar] [CrossRef]
- Niccolucci, V.; Bastianoni, S.; Tiezzi, E.B.P.; Wackernagel, M.; Marchettini, N. How deep is the footprint? A 3D representation. Ecol. Model. 2009, 220, 2819–2823. [Google Scholar] [CrossRef]
- Niccolucci, V.; Galli, A.; Reed, A.; Neri, E.; Wackernagel, M.; Bastianoni, S. Towards a 3D national ecological footprint geography. Ecol. Model. 2011, 222, 2939–2944. [Google Scholar] [CrossRef]
- Fang, K.; Reinout, H. A review on three-dimensional ecological footprint model for natural capital accounting. Prog. Geogr. 2012, 31, 1700–1707. [Google Scholar]
- Fang, K.; Li, H.C. Provincial Pattern of China’s Natural Capital Use: A Modification and Application of Ecological Footprint Depth and Size. J. Nat. Resour. Policy Res. 2012, 27, 1995–2005. [Google Scholar]
- Fang, K. Changes in the spatial distribution of natural capital use among G20 countries from 1999 to 2008. Resour. Sci. 2014, 36, 793–800. [Google Scholar]
- Fang, K. Assessing the natural capital use of eleven nations: An application of a revised three-dimensional model of ecological footprint. Acta Ecol. Sin. 2015, 35, 3766–3777. [Google Scholar]
- Li, P.H.; Zhang, R.Q.; Xu, L.P. Three-dimensional ecological footprint based on ecosystem service value and their drivers: A case study of Urumqi. Ecol. Indic. 2021, 131, 108117. [Google Scholar] [CrossRef]
- Peng, J.; Du, Y.Y.; Ma, J.; Liu, Z.W.; Liu, Y.X.; Wei, H. Sustainability evaluation of natural capital utilization based on 3D EF model: A case study in Beijing City, China. Ecol. Indic. 2015, 58, 254–266. [Google Scholar] [CrossRef]
- Rudolph, A.; Figge, L. Determinants of Ecological Footprints: What is the role of globalization? Ecol. Indic. 2017, 81, 348–361. [Google Scholar] [CrossRef]
- Wackernagel, M.; Monfreda, C.; Erb, K.H.; Haberl, H.; Schulz, N.B. Ecological footprint time series of Austria, the Philippines, and South Korea for 1961-1999: Comparing the conventional approach to an ‘actual land area’ approach. Land Use Policy 2004, 21, 261–269. [Google Scholar] [CrossRef]
- Wu, F.F.; Yang, X.H.; Shen, Z.Y.; Bian, D.H.; Babuna, P. Exploring sustainability and decoupling effects of natural capital utilization in China: Evidence from a provincial three-dimensional ecological footprint. J. Clean. Prod. 2021, 295, 126486. [Google Scholar] [CrossRef]
- Wang, Z.H.; Lin, Y.G.; Yin, J.H.; Zhang, B. Assessment and prediction of environmental sustainability in China based on a modified ecological footprint model. Resour. Conserv. Recycl. 2017, 132, 301–313. [Google Scholar] [CrossRef]
- Lin, D.; Hanscom, L.; Murthy, A.; Galli, A.; Evans, M.; Neill, E.; Mancini, M.S.; Martindill, J.; Medouar, F.Z.; Huang, S.; et al. Ecological Footprint Accounting for Countries: Updates and Results of the National Footprint Accounts, 2012–2018. Resources 2018, 7, 58. [Google Scholar] [CrossRef]
- Long, X.Y.; Yu, H.J.; Sun, M.X.; Wang, X.C.; Kleme, J.J.; Xie, W.; Wang, C.; Li, W.; Wang, Y. Sustainability evaluation based on the Three-dimensional Ecological Footprint and Human Development Index: A case study on the four island regions in China. J. Environ. Manag. 2020, 265, 110509. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.H.; Yuan, J.H.; Chen, L. Water ecological footprint size, depth and its spatial pattern correlation in the “Four-city Area in Middle China”. Ecol. Indic. 2021, 133, 108387. [Google Scholar] [CrossRef]
- Sun, C.Z.; Zhang, Z.X. Assessment of water ecological footprint size, depth, and spatial pattern in China. Acta Ecol. Sin. 2017, 37, 7048–7060. [Google Scholar]
- Poongodi, M.; Vijayakumar, V.; Chilamkurti, N. Bitcoin price prediction using ARIMA model. J. Internet Technol. 2020, 10, 396–406. [Google Scholar] [CrossRef]
- Wang, G.; Wang, J.L.; Su, B.L. Dynamic simulation and prediction of ecological footprint in Liaohe River Basin based on ARIMA model. J. Ecol. Environ. 2013, 22, 632–638. [Google Scholar]
- Zhang, B.; Liu, X.L. Dynamic ecological footprint simulation and prediction based on ARIMA Model: A case study of Gansu Province, China. Sheng Tai Xue Bao 2011, 31, 6251–6260. [Google Scholar]
- Ma, M.L.; Wang, Z.Z. Prediction of the energy consumption variation trend in South Africa based on ARIMA, NGM and NGM-ARIMA models. Energies 2019, 13, 10. [Google Scholar] [CrossRef]
- Li, J.X.; Chen, Y.N.; Xu, C.C.; Li, Z. Evaluation and analysis of ecological security in arid areas of Central Asia based on the emergy ecological footprint (EF) model. J. Clean. Prod. 2019, 235, 664–677. [Google Scholar] [CrossRef]
- Deng, J.L. Control problems of grey systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar]
- Chen, H.S. Evaluation and analysis of eco-security in environmentally sensitive areas using an emergy ecological footprint. Int. J. Environ. Res. Public Health 2017, 14, 136. [Google Scholar] [CrossRef]
- Liu, H.; Li, D.Y.; Ma, R.; Ma, M. Assessing the ecological risks based on the three-dimensional ecological footprint model in Gansu Province. Sustainability 2022, 14, 16995. [Google Scholar] [CrossRef]
- National Energy Administration. Available online: http://www.nea.gov.cn/2021-07/23/c_1310080005.htm (accessed on 21 March 2023).
- The Editorial Board of Gansu Statistical Yearbook in Gansu Province. In Gansu Statistical Yearbook 2001–2020; Statistics Press: Beijing, China, 2021.
- Odum, H.T. Self-organization, transformity, and information. Science 1988, 242, 1132–1139. [Google Scholar] [CrossRef]
- Guizhou Energy Administration. Available online: http://nyj.guizhou.gov.cn/zxfw/nyzs/ (accessed on 22 March 2023).
- Odum, H.T. Environment Accounting: Energy and Environment Decision Making; John Wiley: New York, NY, USA, 1996. [Google Scholar]
- Wang, Z.X.; Li, D.D.; Zheng, H.H. Model comparison of GM (1, 1) and DGM (1, 1) based on Monte-Carlo simulation. Phys. A 2020, 542, 123341. [Google Scholar] [CrossRef]
- Lin, X.F.; Liu, H.; Wei, J.H. Research on Sustainable Development in Gansu Province Based on Three-Dimensional Energy Footprint. In Proceedings of the 3rd International Conference on Green Energy, Environment and Sustainable Development (GEESD2022), Online, 29 June 2022, 3rd ed.; IOS Press BV: Amsterdam, The Netherlands, 2022; pp. 422–428. [Google Scholar]
- Global Footprint Network. Obtenido de Global Footprint Network. Available online: http://www.footprintnetwork.org (accessed on 22 March 2023).
- Galli, A.; Halle, M.; Grunewald, N. Physical limits to resource access and utilisation and their economic implications in Mediterranean economies. Environ. Sci. Policy 2015, 51, 125–136. [Google Scholar] [CrossRef]
- Niccolucci, V.; Pulselli, F.M.; Tiezzi, E. Strengthening the threshold hypothesis: Economic and biophysical limits to growth. Ecol. Econ. 2007, 60, 667–672. [Google Scholar] [CrossRef]
- Bastianoni, S.; Niccolucci, V.; Neri, E.; Cranston, G.; Galli, A.; Wackernagel, M. Sustainable Development: Ecological Footprint in Accounting. In Encyclopedia of Environmental Management; CRC Press: Boca Raton, FL, USA, 2013; pp. 2467–2481. [Google Scholar]
- Hau, J.L.; Bakshi, B.R. Promise and problems of emergy analysis. Ecol Model. 2004, 178, 215–225. [Google Scholar] [CrossRef]

| Account Type | Land Type | Indicators | Data Source |
|---|---|---|---|
| Biological account | Agricultural land | Wheat, grain, beans, corn, potatoes, cotton, sugar beets, vegetables, and oilseed | Gansu Statistical Yearbook (2001–2020) [41] |
| Building land | Electricity | ||
| Fuel land | Coke, gasoline, and diesel | ||
| Grassland | Meat, poultry eggs, milk, and wool | ||
| Water area | Aquatic products | ||
| Woodland | Fruits |
| Item | Original Data J | Emergy Transformity sej/J | Solar Emergy sej | Per-Capita Emergy sej/cap | ecc hm2/cap |
|---|---|---|---|---|---|
| Solar radiant energy | 2.38 × 1021 | 1.00 | 2.38 × 1021 | 9.52 × 1013 | 0.31 |
| Wind energy | 3.30 × 1018 | 6.32 × 102 | 2.09 × 1021 | 8.35 × 1013 | 0.27 |
| Rain potential energy | 4.56 × 1018 | 8.89 × 103 | 4.06 × 1022 | 1.62 × 1015 | 5.23 |
| Chemical energy of rainwater | 1.07 × 1018 | 1.82 × 104 | 1.94 × 1022 | 7.75 × 1014 | 2.50 |
| Energy of Earth’s rotation | 6.18 × 1017 | 2.90 × 104 | 1.79 × 1022 | 7.16 × 1014 | 2.31 |
| Total emergy of the region | 5.85 × 1022 |
| Productive Land Type | Subject | Conversion Factor | Original Data | Emergy Transformity sej/J | Solar Emergy /sej | ci/sej | eef /hm2 |
|---|---|---|---|---|---|---|---|
| A * | wheat | 1.38 × 1010 | 2.69 × 106 | 6.80 × 104 | 2.52 × 1021 | 1.01 × 1014 | 7.36 × 10-2 |
| grain | 1.55 × 1010 | 9.42 × 106 | 3.59 × 104 | 5.24 × 1021 | 2.10 × 1014 | 1.53 × 10−1 | |
| beans | 2.07 × 1010 | 3.72 × 105 | 6.90 × 105 | 5.31 × 1021 | 2.13 × 1014 | 1.09 × 10−1 | |
| corn | 1.46 × 1010 | 6.17 × 106 | 5.81 × 104 | 5.23 × 1021 | 2.09 × 1014 | 2.17 × 10−1 | |
| potatoes | 4.20 × 109 | 2.23 × 106 | 2.70 × 103 | 2.53 × 1019 | 1.01 × 1012 | 7.37 × 10−4 | |
| cotton | 1.88 × 1010 | 3.01 × 104 | 1.90 × 106 | 1.08 × 1021 | 4.30 × 1013 | 3.14E × 10−2 | |
| sugar beets | 2.50 × 109 | 2.24 × 105 | 8.49 × 104 | 4.76 × 1019 | 1.90 × 1012 | 1.39E × 10−3 | |
| vegetables | 2.51 × 109 | 1.48 × 107 | 2.70 × 104 | 1.00 × 1021 | 4.01 × 1013 | 2.92 × 10−2 | |
| oilseed | 2.64 × 1010 | 6.15 × 105 | 6.90 × 105 | 1.12 × 1022 | 4.48 × 1014 | 3.27 × 10−1 | |
| WL * | fruits | 3.30 × 109 | 4.81 × 106 | 5.30 × 105 | 8.41 × 1021 | 3.36 × 1014 | 2.46 × 10−1 |
| G * | meat | 4.60 × 109 | 1.10 × 106 | 3.17 × 106 | 1.61 × 1022 | 6.42 × 1014 | 4.69 × 10−1 |
| poultry eggs | 4.60 × 109 | 1.98 × 105 | 2.00 × 106 | 1.82 × 1021 | 7.28 × 1013 | 5.32 × 10−2 | |
| milk | 3.20 × 109 | 5.84 × 105 | 1.70 × 106 | 3.18 × 1021 | 1.27 × 1014 | 9.28 × 10−2 | |
| wool | 2.09 × 1010 | 3.56 × 104 | 4.40 × 106 | 3.27 × 1021 | 1.31 × 1014 | 9.55 × 10−2 | |
| W * | aquatic products | 4.61 × 109 | 1.41 × 104 | 2.00 × 106 | 1.30 × 1020 | 5.18 × 1012 | 3.78 × 10−3 |
| F * | coke | 3.18 × 1010 | 5.17 × 106 | 3.98 × 104 | 6.54 × 1021 | 2.62 × 1014 | 1.91 × 10−1 |
| gasoline | 4.66 × 1010 | 4.51 × 106 | 5.04 × 104 | 1.06 × 1022 | 4.23 × 1014 | 3.09 × 10−1 | |
| diesel | 3.30 × 1010 | 5.43 × 106 | 6.60 × 104 | 1.18 × 1022 | 4.72 × 1014 | 3.45 × 10−1 | |
| B * | electricity | 3.60 × 106 | 1.60 × 1011 | 1.59 × 105 | 9.17 × 1022 | 3.66 × 1015 | 2.67 |
| eef/hm2 | 5.40 |
| Time | ECC/hm2 | EEF/hm2 | EEFsize/hm2 | EEFdepth | EEF3D/hm2 | Ecological Status |
|---|---|---|---|---|---|---|
| 2001 | 1.39 × 108 | 5.98 × 107 | 5.98 × 107 | 1 | 5.98 × 107 | surplus |
| 2002 | 1.23 × 108 | 7.21 × 107 | 7.21 × 107 | 1 | 7.21 × 107 | surplus |
| 2003 | 1.57 × 108 | 6.24 × 107 | 6.24 × 107 | 1 | 6.24 × 107 | surplus |
| 2004 | 1.31 × 108 | 8.11 × 107 | 8.11 × 107 | 1 | 8.11 × 107 | surplus |
| 2005 | 1.48 × 108 | 7.76 × 107 | 7.76 × 107 | 1 | 7.76 × 107 | surplus |
| 2006 | 1.39 × 108 | 8.89 × 107 | 8.89 × 107 | 1 | 8.89 × 107 | surplus |
| 2007 | 1.53 × 108 | 8.26 × 107 | 8.26 × 107 | 1 | 8.26 × 107 | surplus |
| 2008 | 1.41 × 108 | 9.41 × 107 | 9.41 × 107 | 1 | 9.41 × 107 | surplus |
| 2009 | 1.33 × 108 | 1.06 × 108 | 1.06 × 108 | 1 | 1.06 × 108 | surplus |
| 2010 | 1.40 × 108 | 1.06 × 108 | 1.06 × 108 | 1 | 1.06 × 108 | surplus |
| 2011 | 1.46 × 108 | 1.19 × 108 | 1.19 × 108 | 1 | 1.19 × 108 | surplus |
| 2012 | 1.51 × 108 | 1.19 × 108 | 1.19 × 108 | 1 | 1.19 × 108 | surplus |
| 2013 | 1.60 × 108 | 1.14 × 108 | 1.14 × 108 | 1 | 1.14 × 108 | surplus |
| 2014 | 1.46 × 108 | 1.31 × 108 | 1.31 × 108 | 1 | 1.31 × 108 | surplus |
| 2015 | 1.34 × 108 | 1.41 × 108 | 1.34 × 108 | 1.050 | 1.41 × 108 | deficit |
| 2016 | 1.37 × 108 | 1.40 × 108 | 1.37 × 108 | 1.027 | 1.40 × 108 | deficit |
| 2017 | 1.53 × 108 | 1.24 × 108 | 1.24 × 108 | 1 | 1.24 × 108 | surplus |
| 2018 | 1.67 × 108 | 1.21 × 108 | 1.21 × 108 | 1 | 1.21 × 108 | surplus |
| 2019 | 1.62 × 108 | 1.29 × 108 | 1.29 × 108 | 1 | 1.29 × 108 | surplus |
| 2020 | 1.66 × 108 | 1.35 × 108 | 1.35 × 108 | 1 | 1.35 × 108 | surplus |
| Sequence | ADF Statistic (t-Statistic) | Critical Values | Prob | ||
|---|---|---|---|---|---|
| 1% | 5% | 10% | |||
| ECC | −4.067 | −4.886 | −3.829 | −3.363 | 0.035 |
| EEF | −3.547 | −5.125 | −3.933 | −3.420 | 0.085 |
| Year | EEFsize/hm2 | EEFdepth/hm2 | EEF3D/hm2 | Ecological Status |
|---|---|---|---|---|
| 2021 | 1.48 × 108 | 1.00 | 1.48 × 108 | surplus |
| 2022 | 1.52 × 108 | 1.00 | 1.52 × 108 | surplus |
| 2023 | 1.56 × 108 | 1.00 | 1.56 × 108 | surplus |
| 2024 | 1.60 × 108 | 1.00 | 1.60 × 108 | surplus |
| 2025 | 1.65 × 108 | 1.00 | 1.65 × 108 | surplus |
| 2026 | 1.69 × 108 | 1.00 | 1.69 × 108 | surplus |
| 2027 | 1.73 × 108 | 1.00 | 1.73 × 108 | surplus |
| 2028 | 1.77 × 108 | 1.00 | 1.77 × 108 | surplus |
| 2029 | 1.82 × 108 | 1.00 | 1.82 × 108 | surplus |
| 2030 | 1.86 × 108 | 1.00 | 1.86 × 108 | surplus |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Lin, X.; Wei, J.; Hu, L. Assessing Environmental Sustainability Based on the Three-Dimensional Emergy Ecological Footprint (3D EEF) Model: A Case Study of Gansu Province, China. Sustainability 2023, 15, 8007. https://doi.org/10.3390/su15108007
Liu H, Lin X, Wei J, Hu L. Assessing Environmental Sustainability Based on the Three-Dimensional Emergy Ecological Footprint (3D EEF) Model: A Case Study of Gansu Province, China. Sustainability. 2023; 15(10):8007. https://doi.org/10.3390/su15108007
Chicago/Turabian StyleLiu, Hua, Xiaofen Lin, Jinhuan Wei, and Lei Hu. 2023. "Assessing Environmental Sustainability Based on the Three-Dimensional Emergy Ecological Footprint (3D EEF) Model: A Case Study of Gansu Province, China" Sustainability 15, no. 10: 8007. https://doi.org/10.3390/su15108007
APA StyleLiu, H., Lin, X., Wei, J., & Hu, L. (2023). Assessing Environmental Sustainability Based on the Three-Dimensional Emergy Ecological Footprint (3D EEF) Model: A Case Study of Gansu Province, China. Sustainability, 15(10), 8007. https://doi.org/10.3390/su15108007





