Cyclic Bond-Slip Behavior of Partially Debonded Tendons for Sustainable Design of Non-Emulative Precast Segmental Bridge Columns
Abstract
:1. Introduction
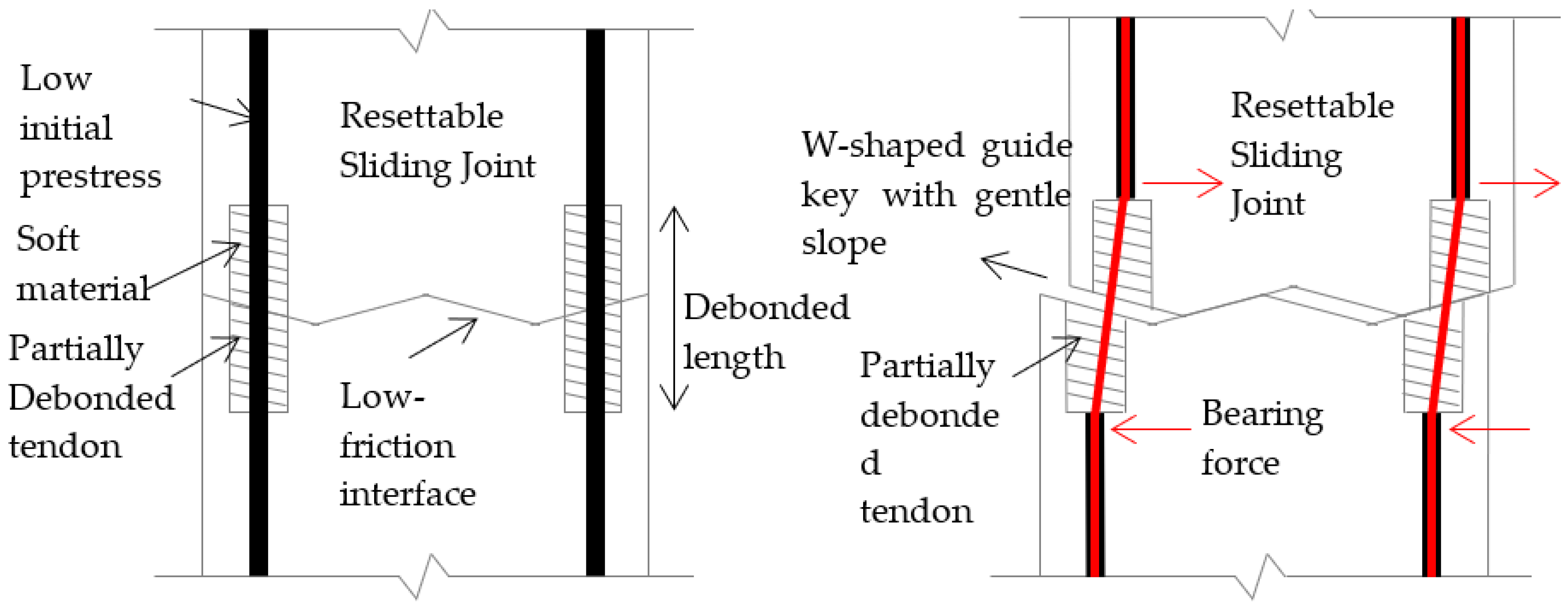
2. PSBC with Resettable Sliding Joints
2.1. Overall Design
2.2. Partially Debonded Tendons
3. Cyclic Bond-Slip Behavior of Partially Debonded Tendons
3.1. Bond Behavior of Tendons
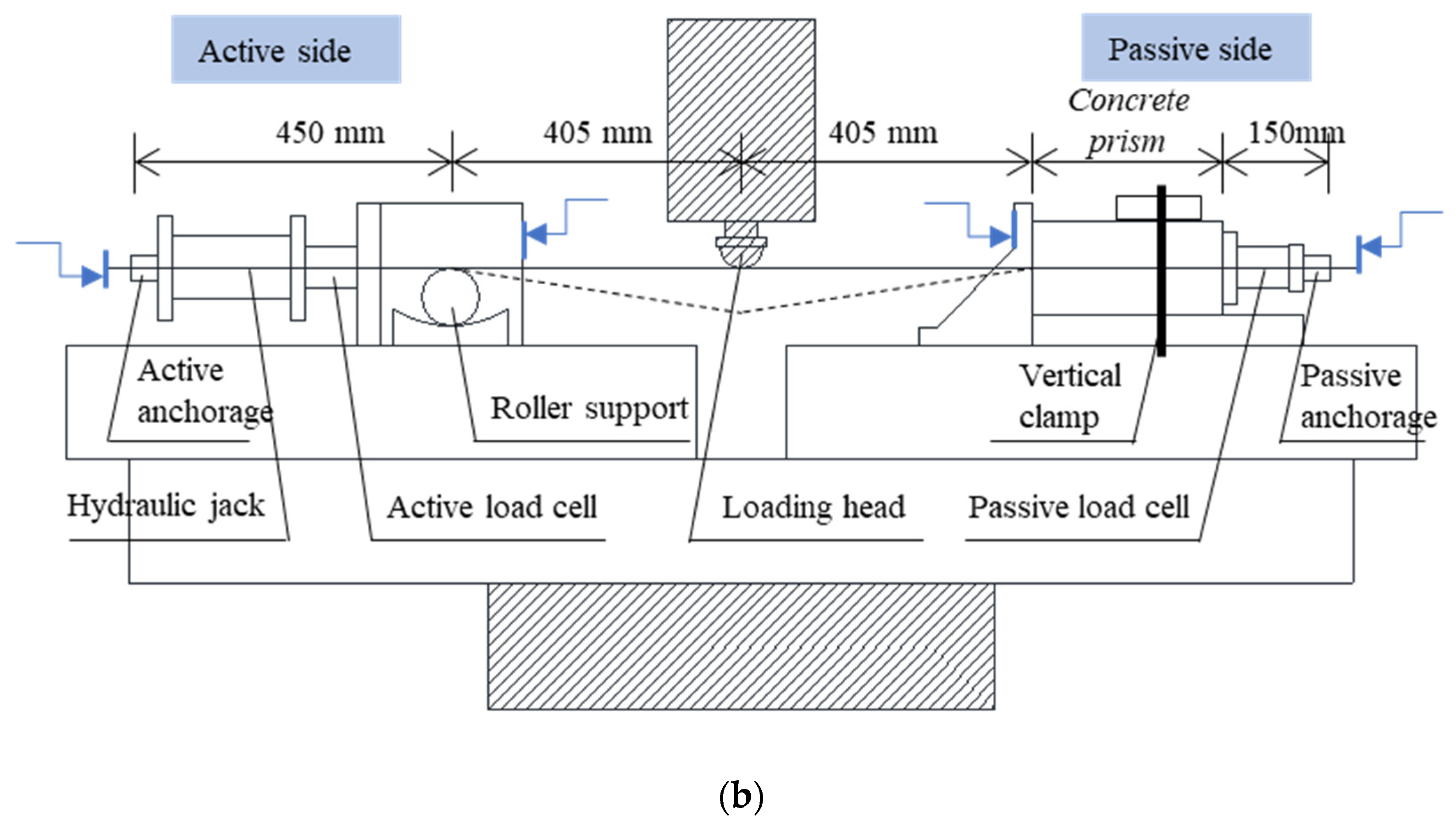
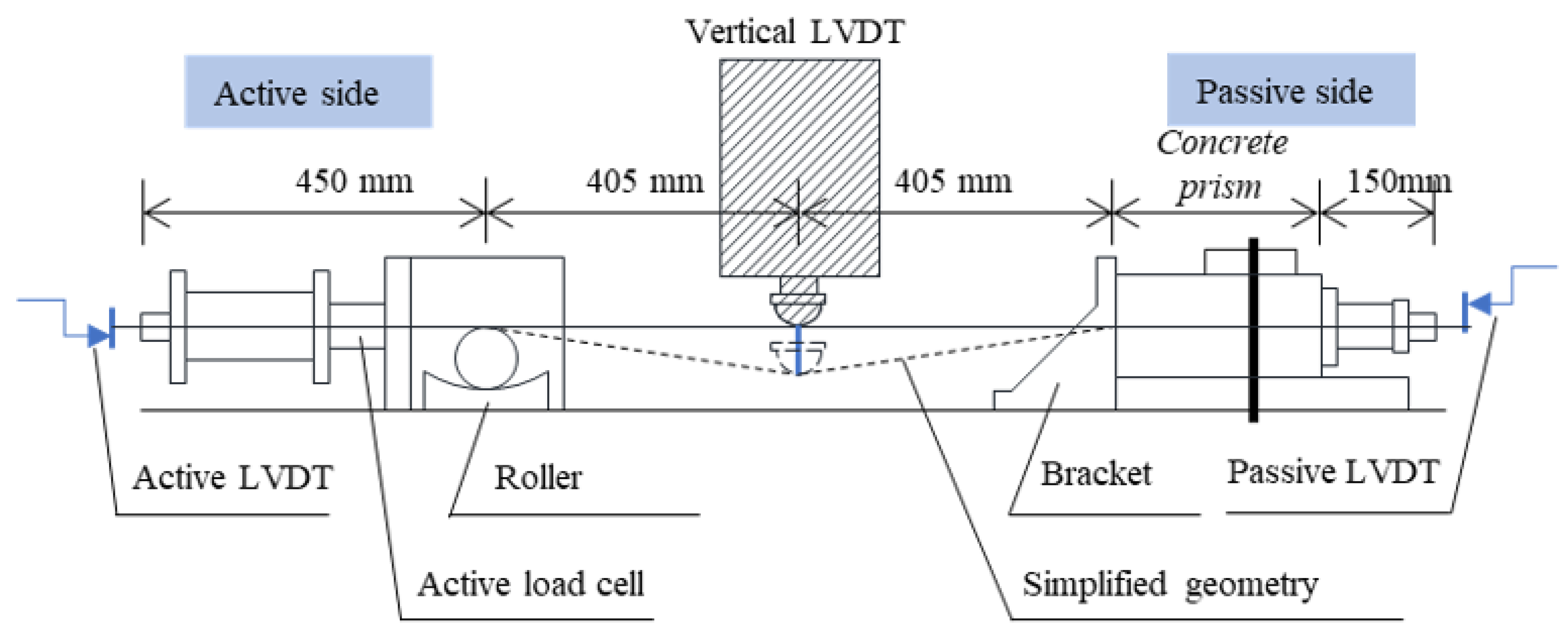
3.2. Overview of Test Setup
3.2.1. Setup and Experiment Design
3.2.2. Design of Specimens
3.2.3. Fabrication of Specimens
3.2.4. Testing Procedures
4. Evaluation of Testing Results
4.1. Specimens
4.2. Bond Performance
4.2.1. Bond Parameters
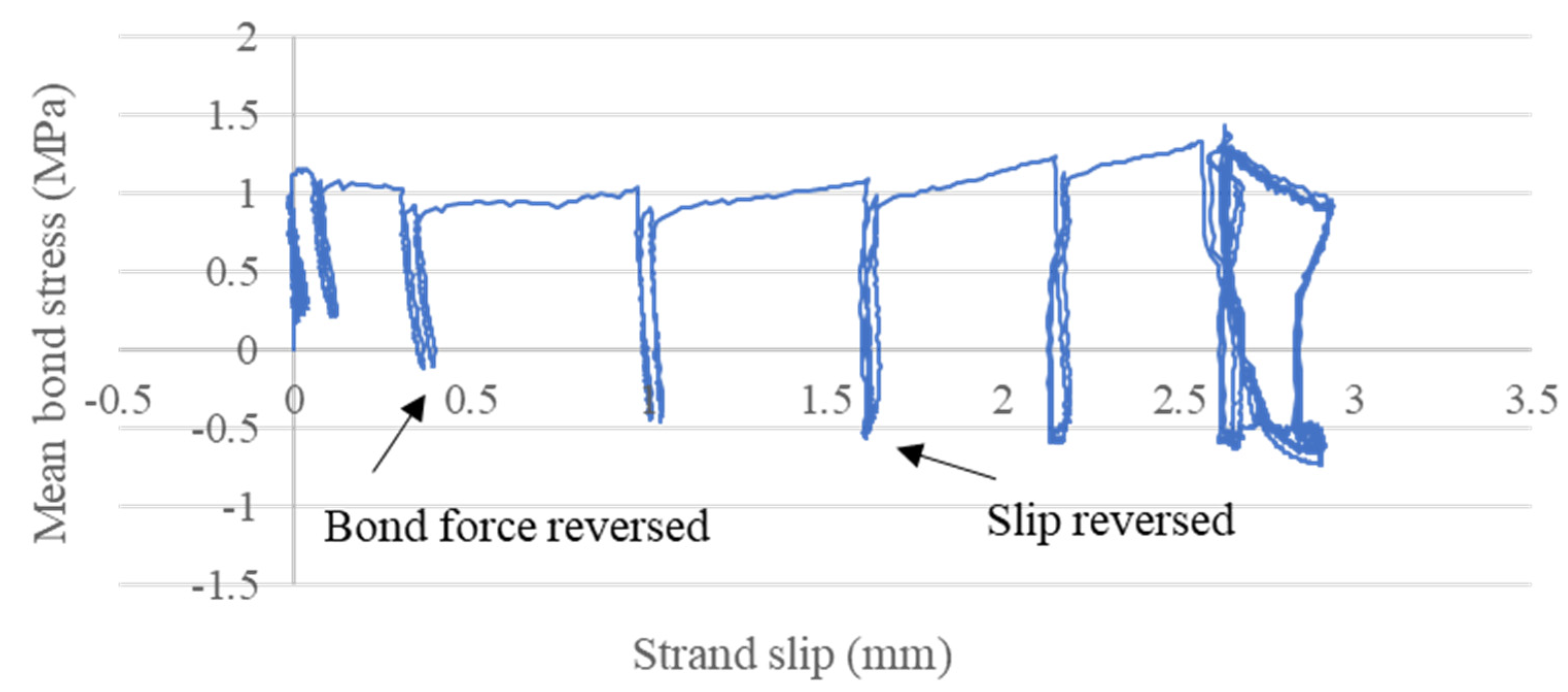
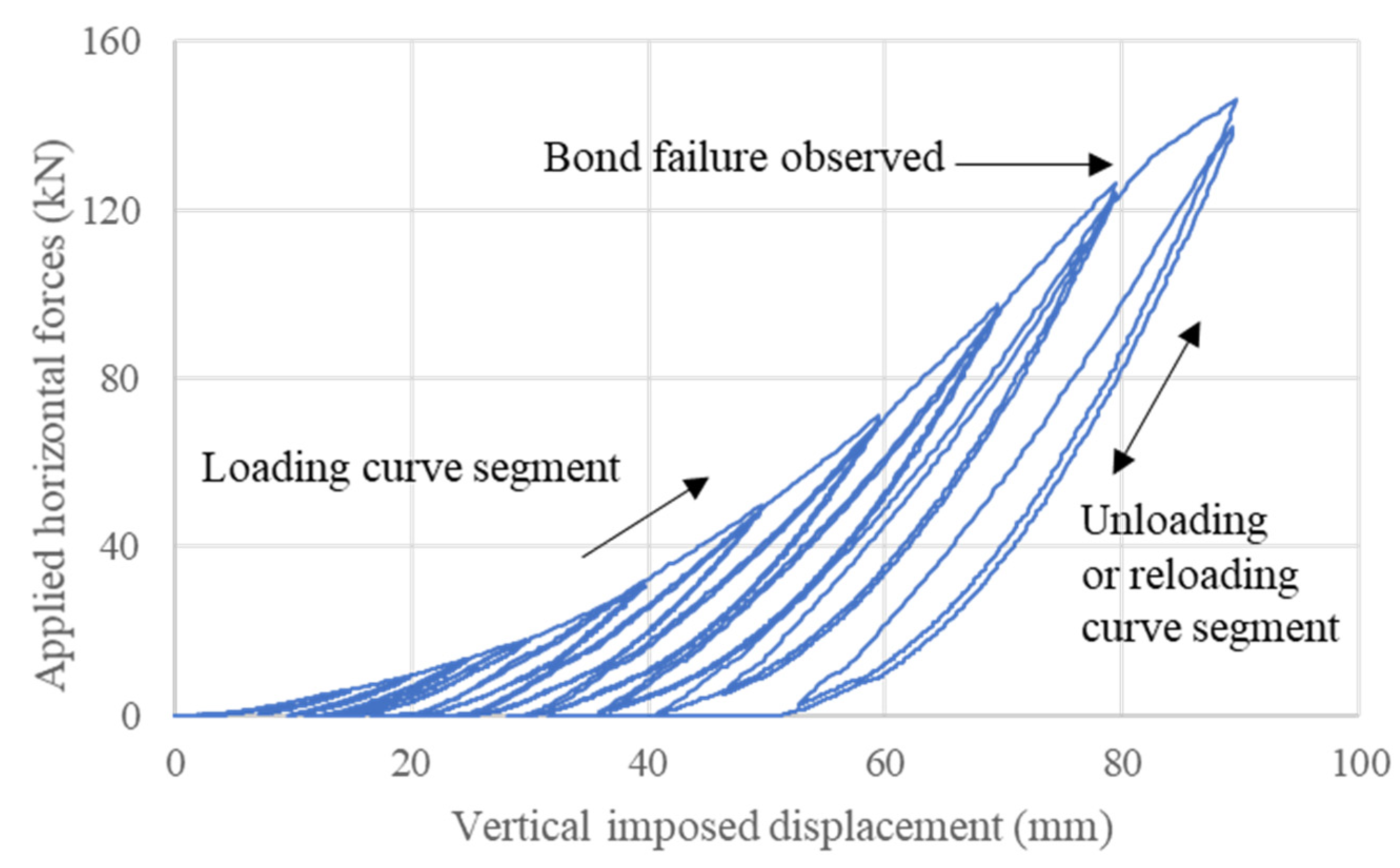
4.2.2. Cyclic Bond-Slip Performance
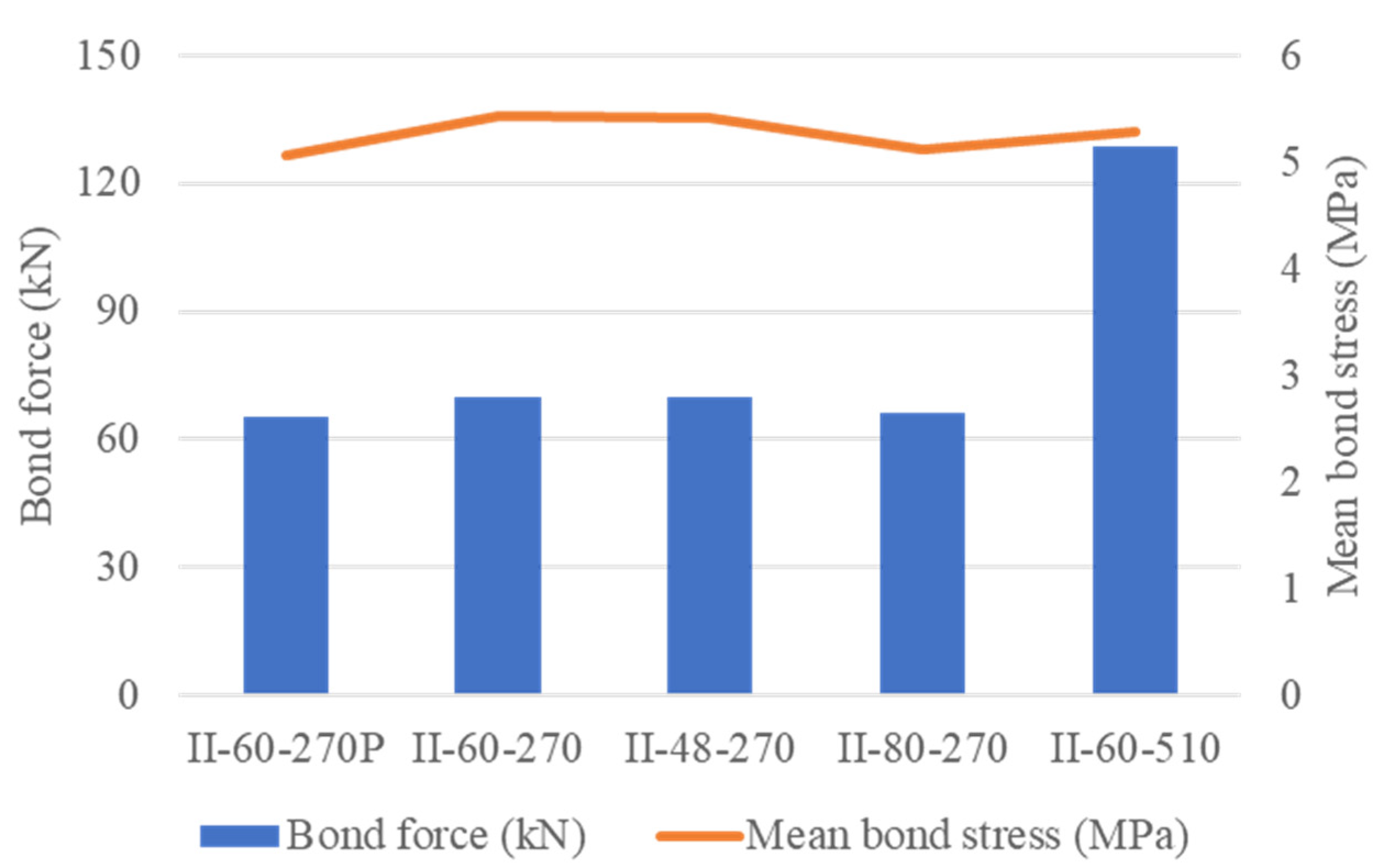
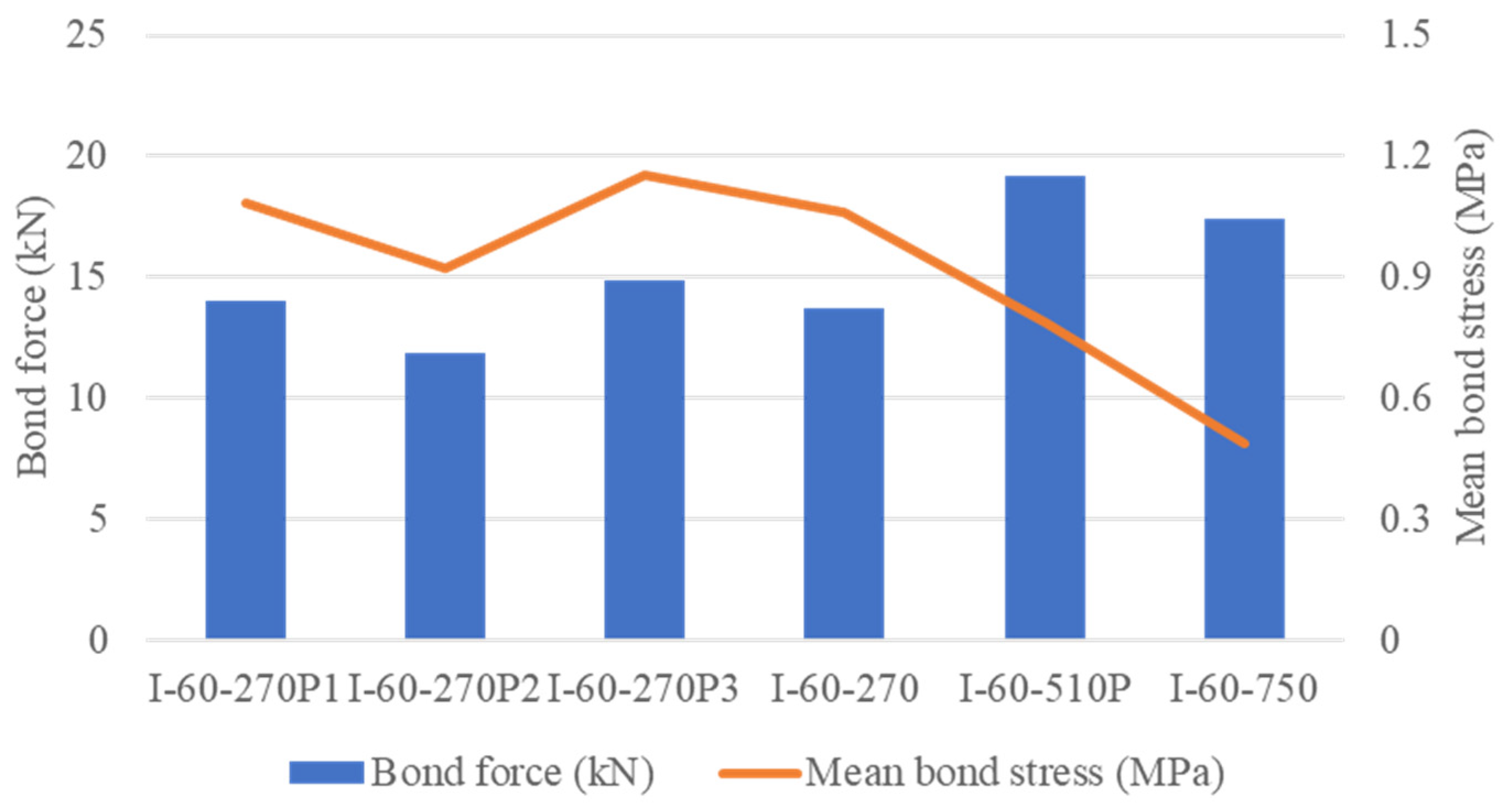
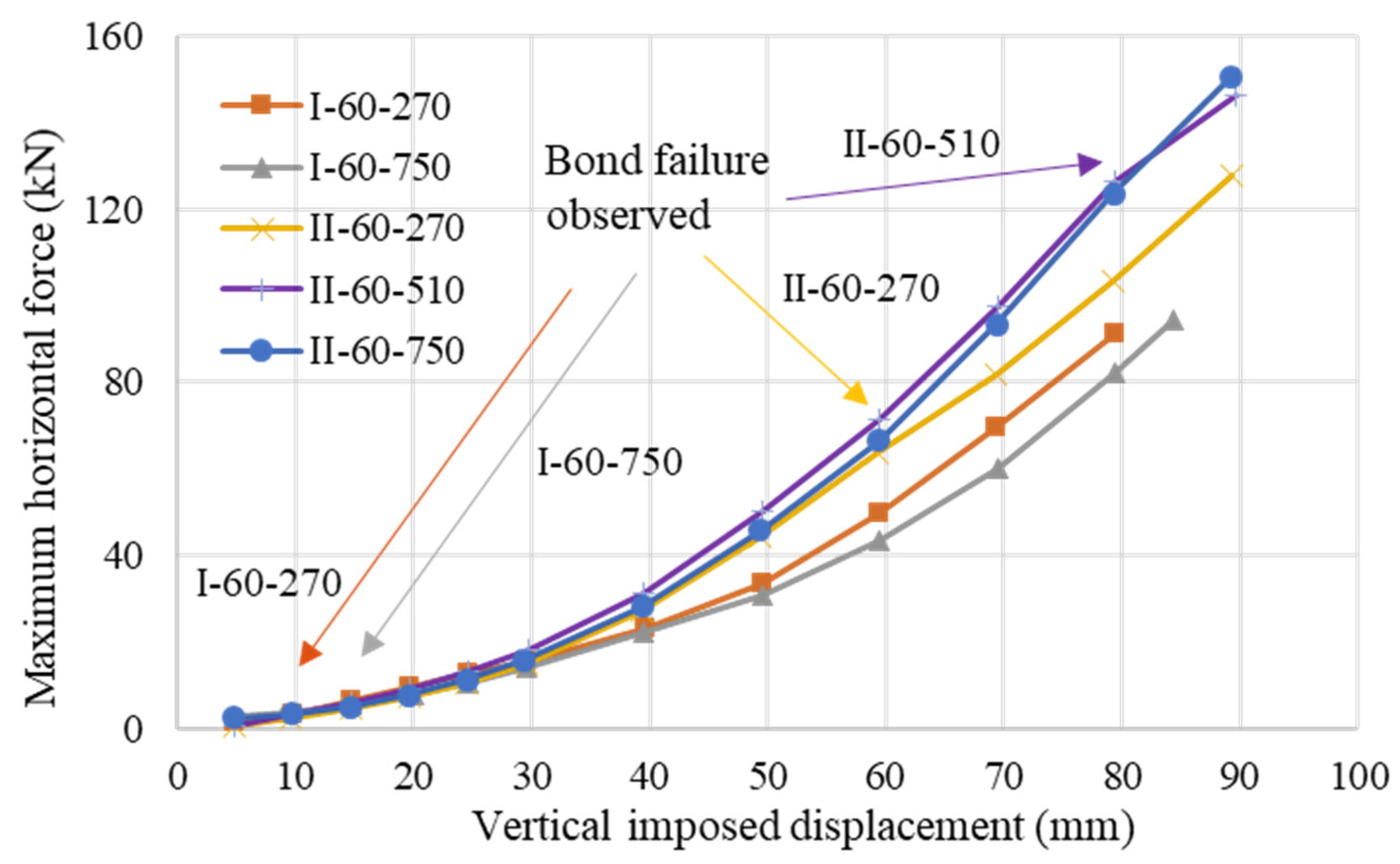
4.2.3. Mean Bond Stress and Bond Force
4.3. Cyclic Bond Behaviors
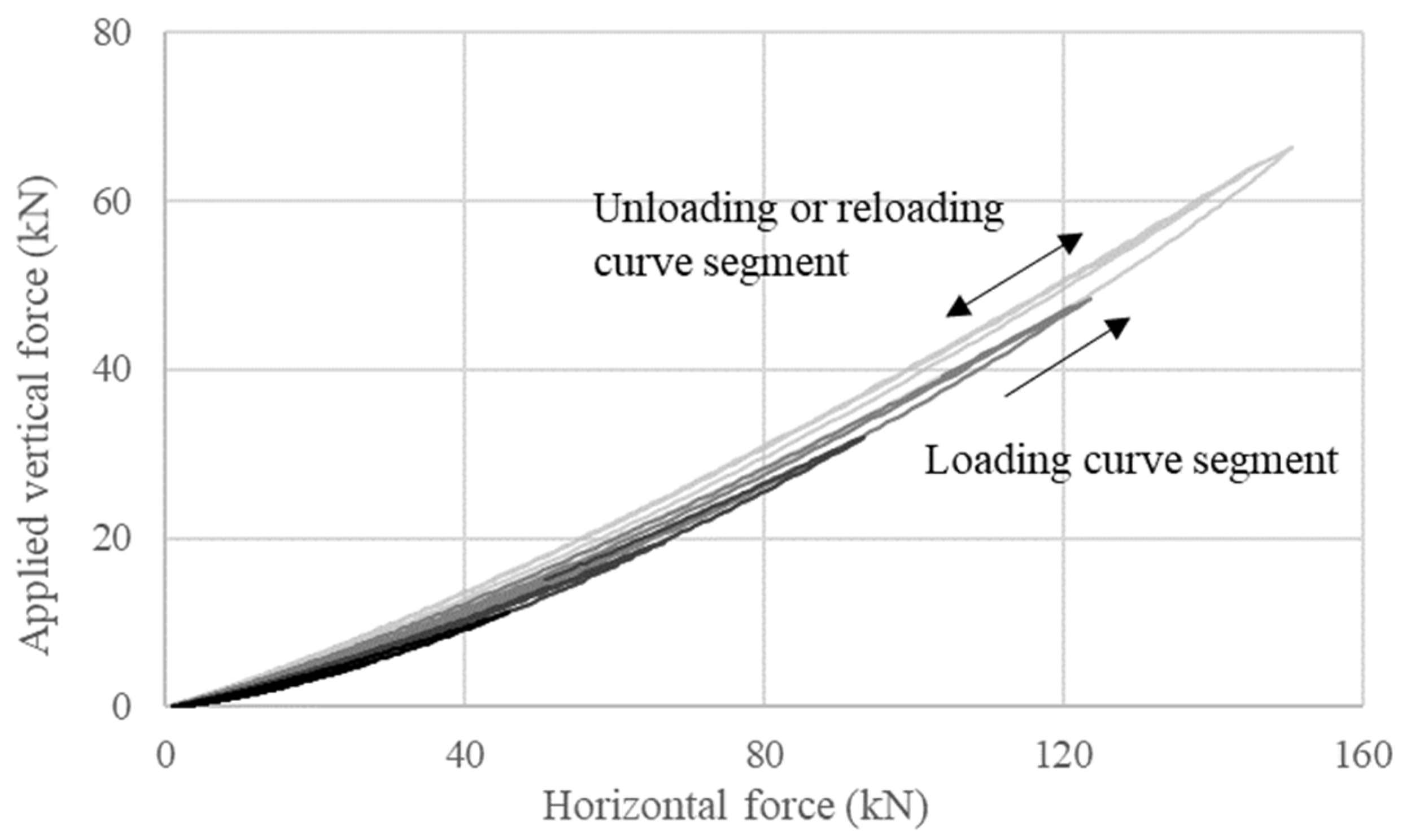
4.3.1. Vertical Forces
4.3.2. Horizontal Forces at Different Vertical Loading Conditions
5. Further Evaluation of Testing Results
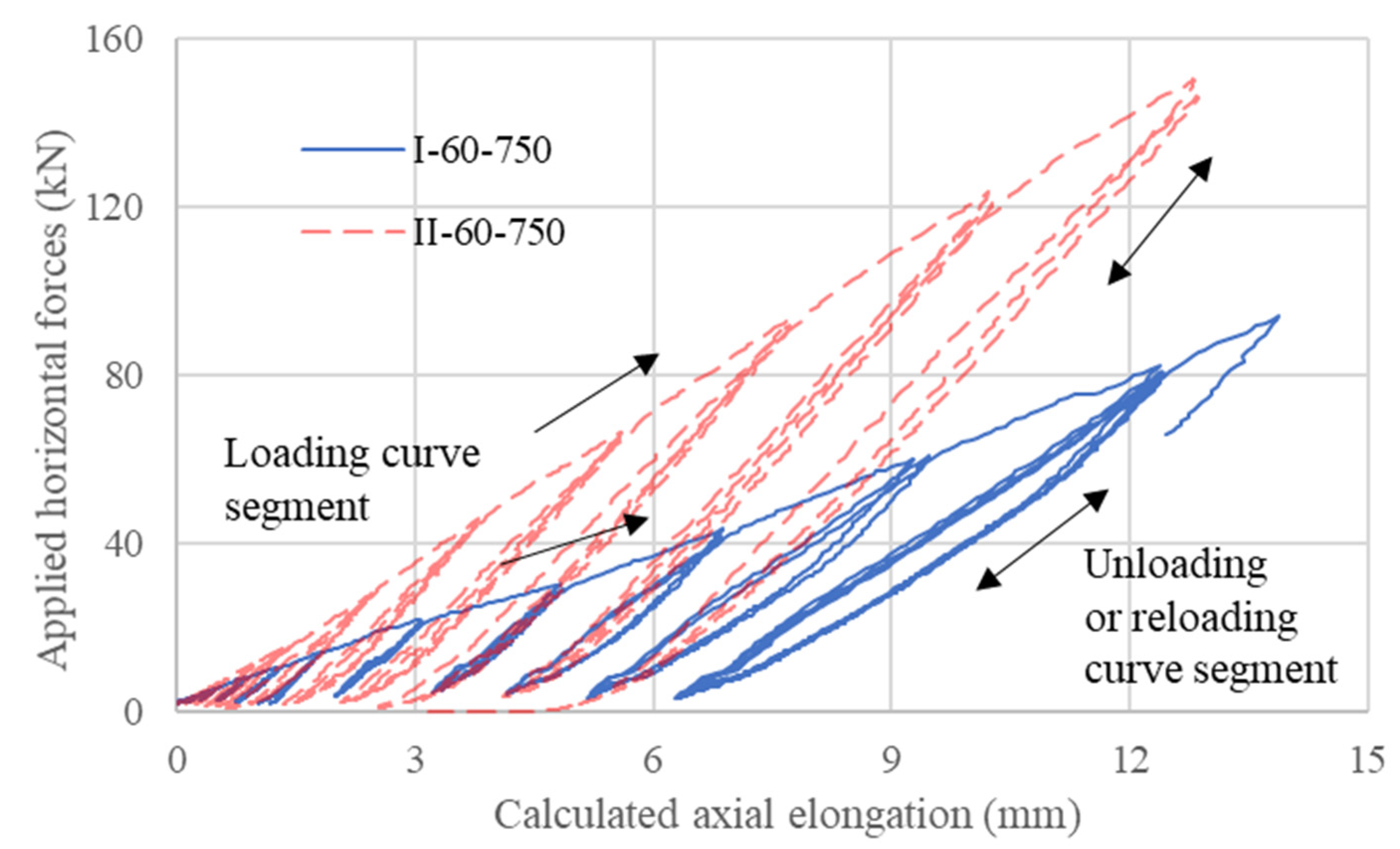
5.1. Calculated Axial Elongation
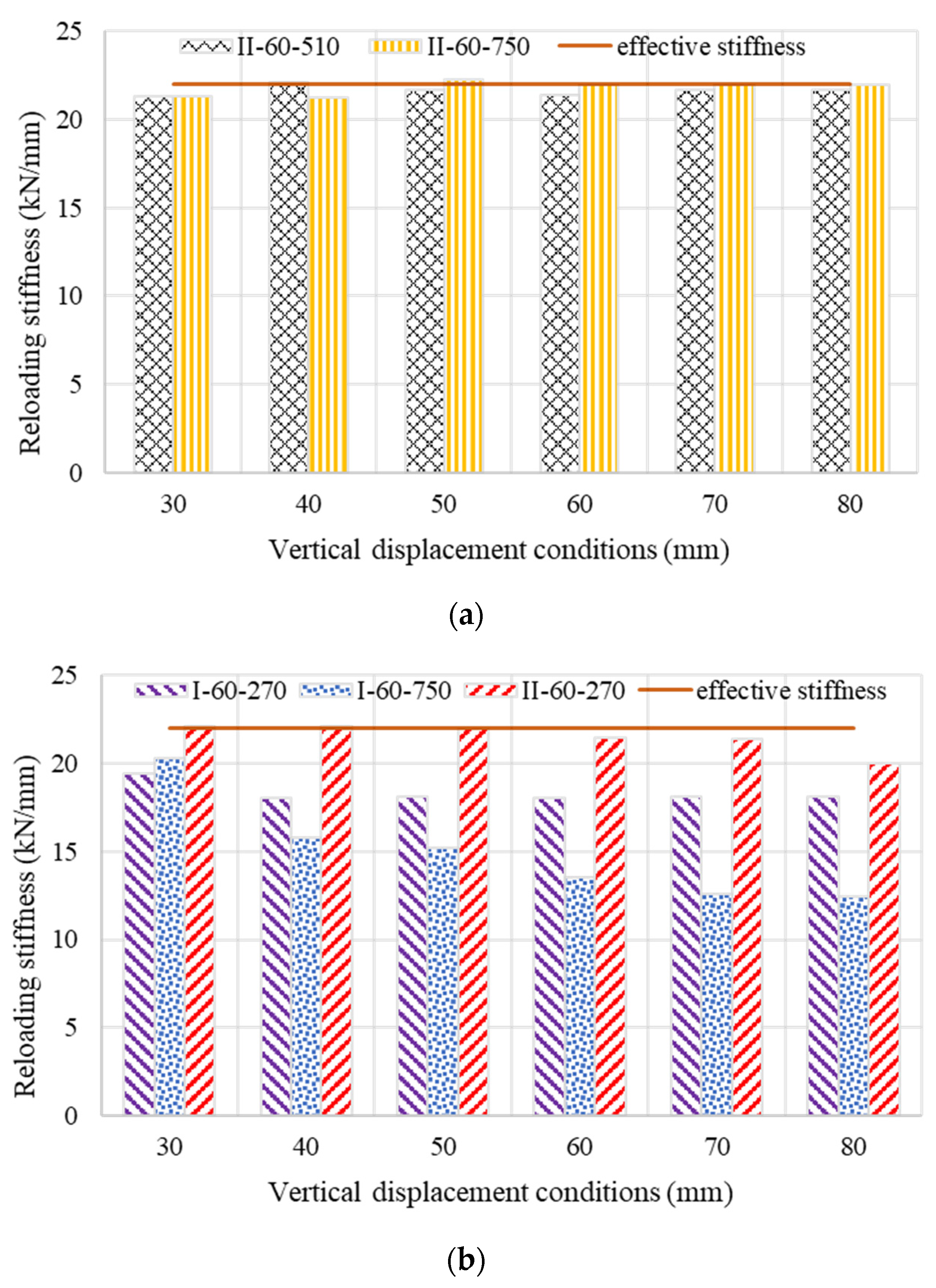
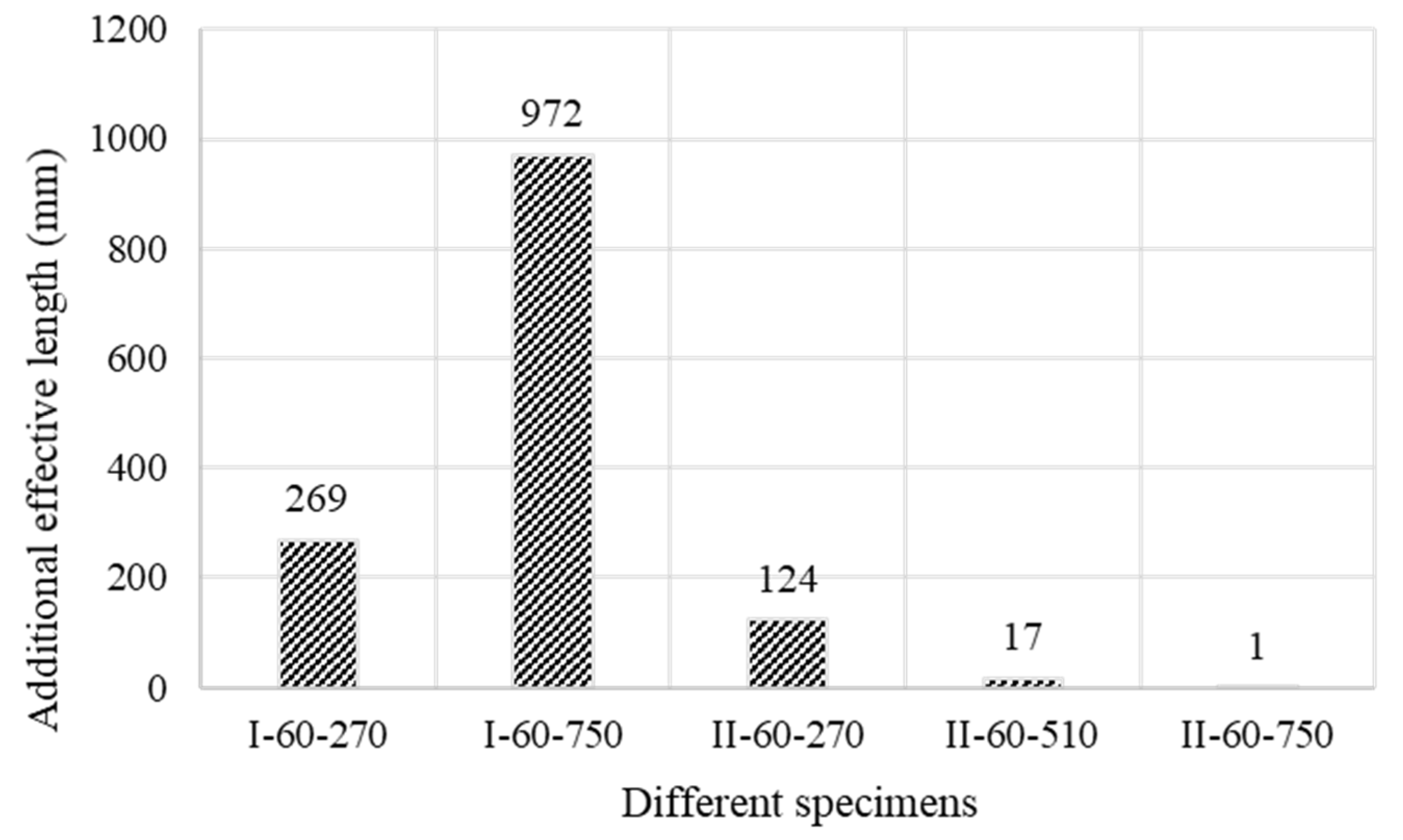
5.2. Deterioration of Fixity Due to Bond Failure
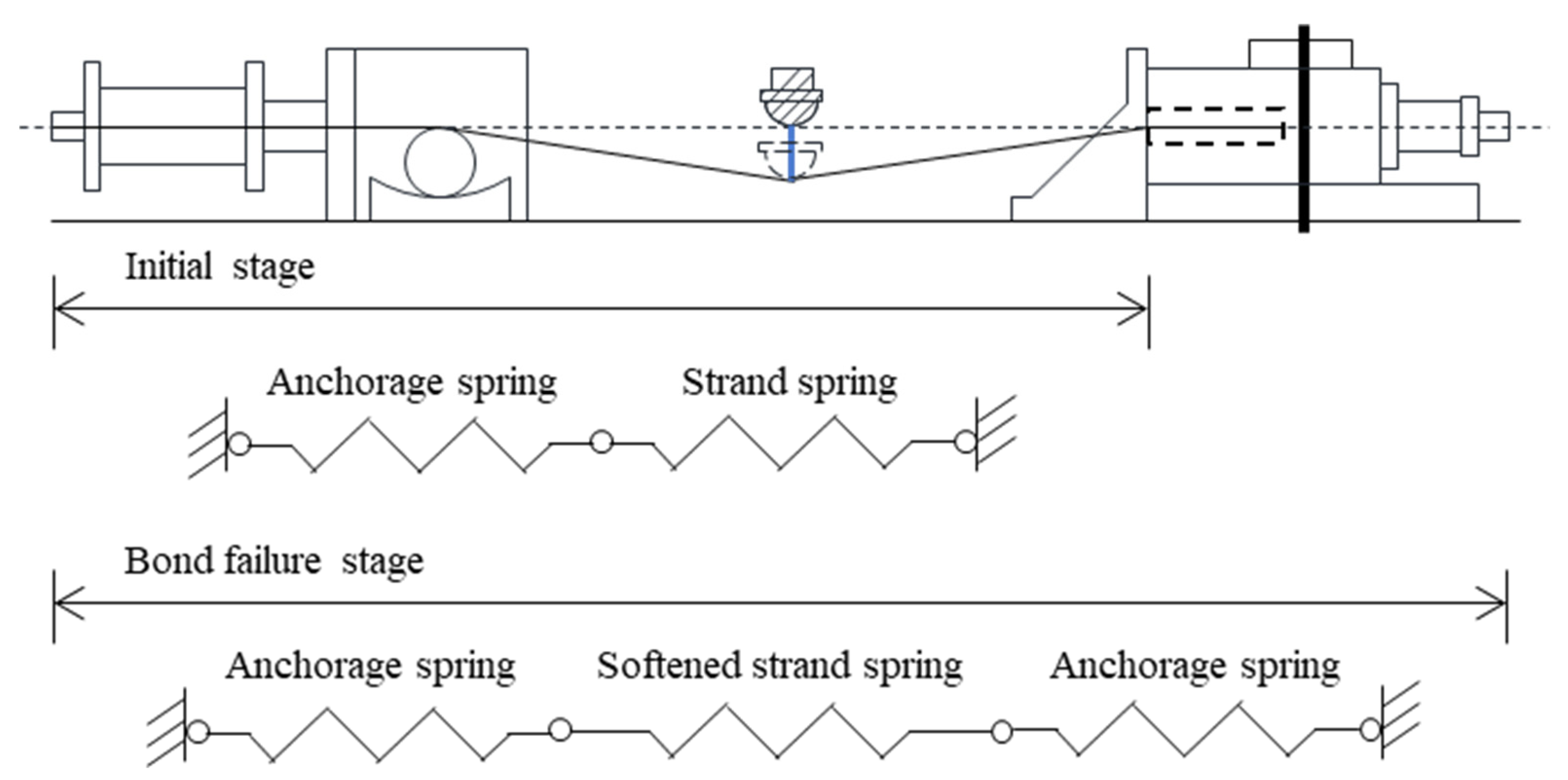
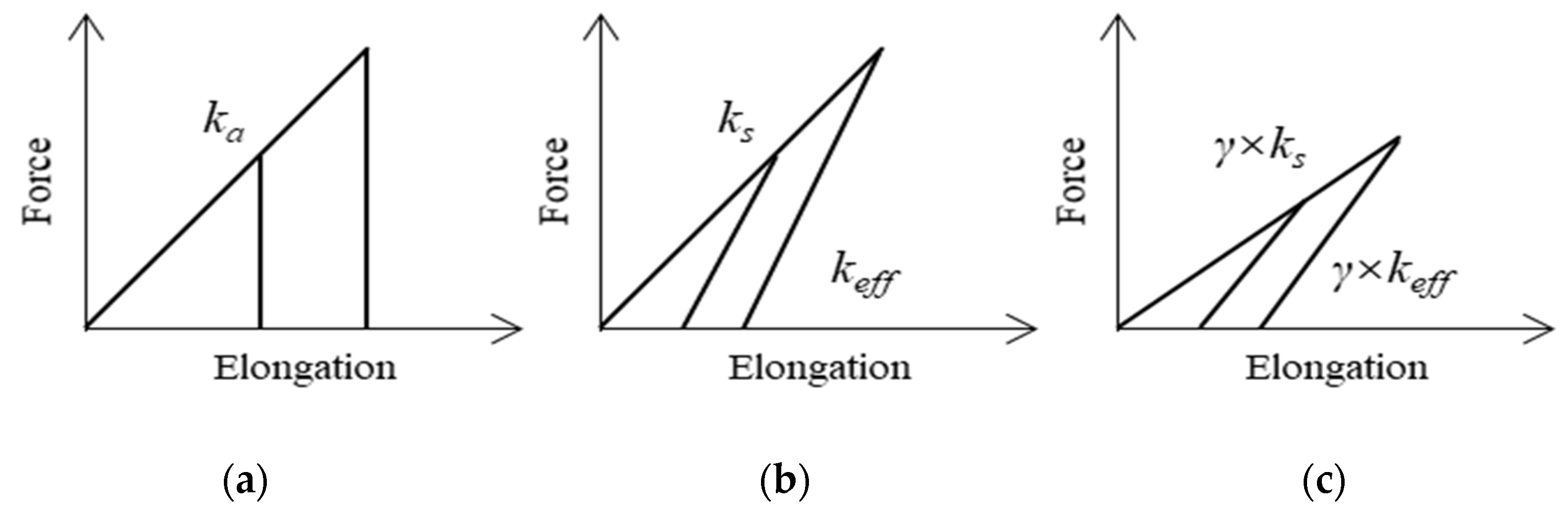
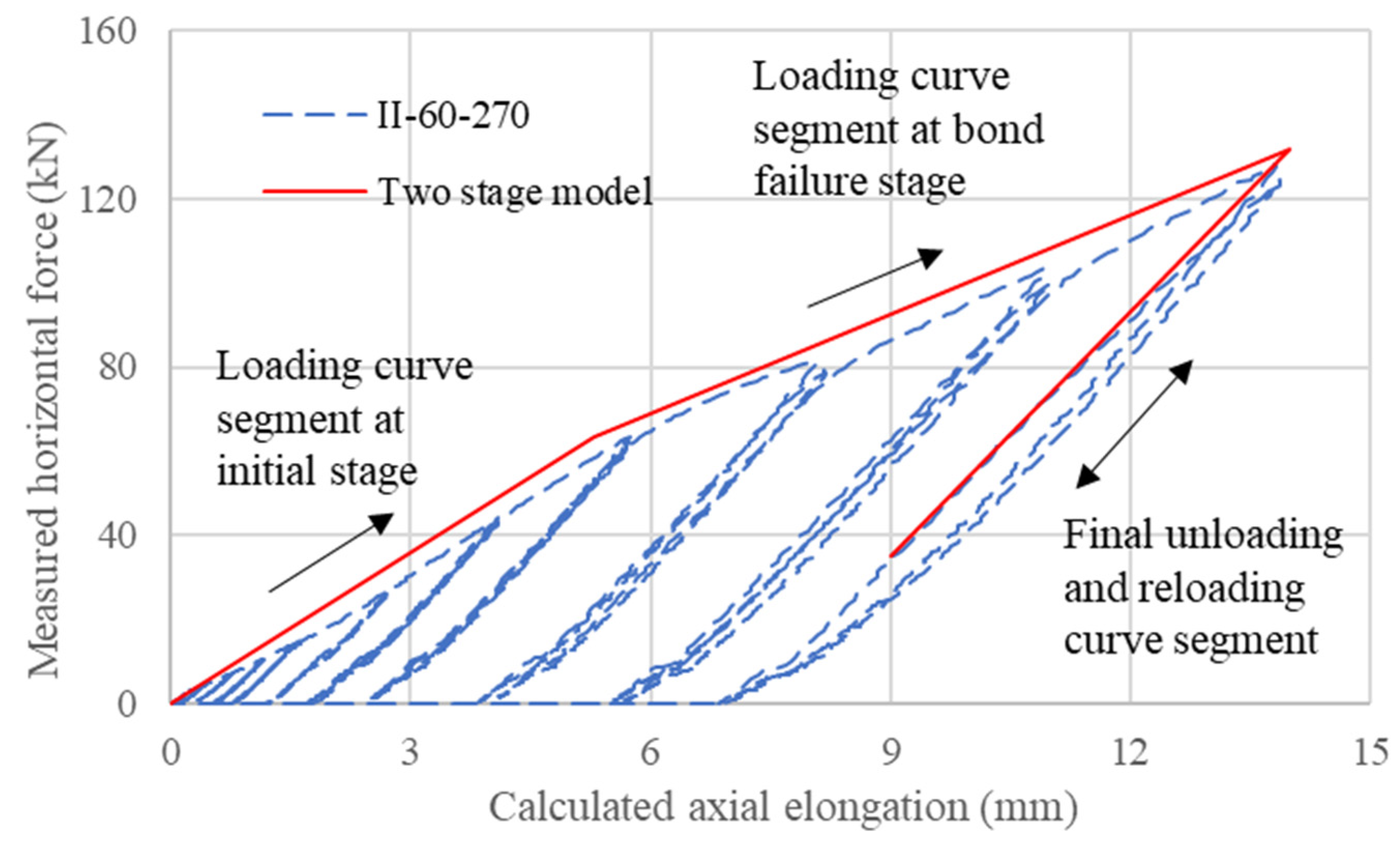
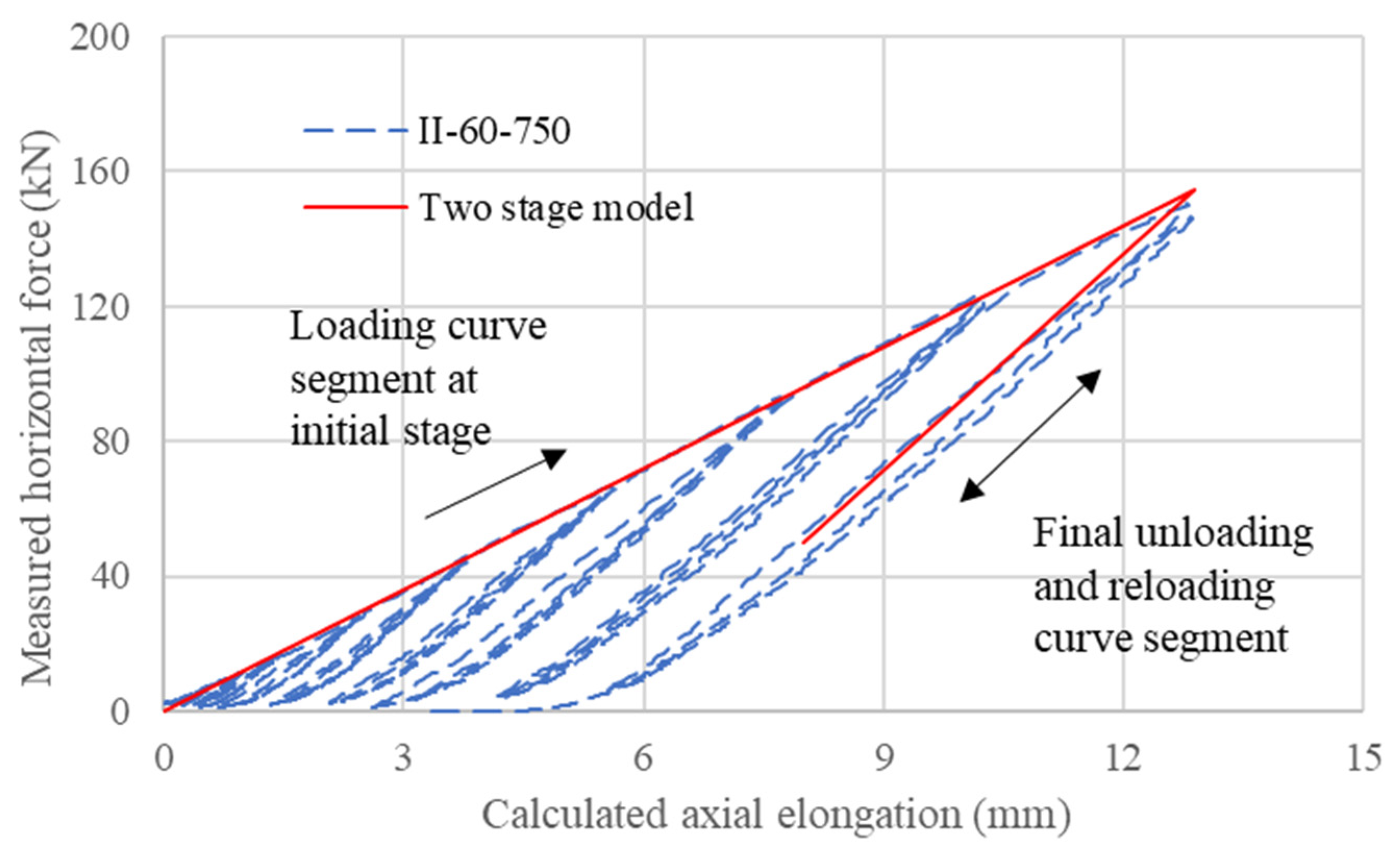
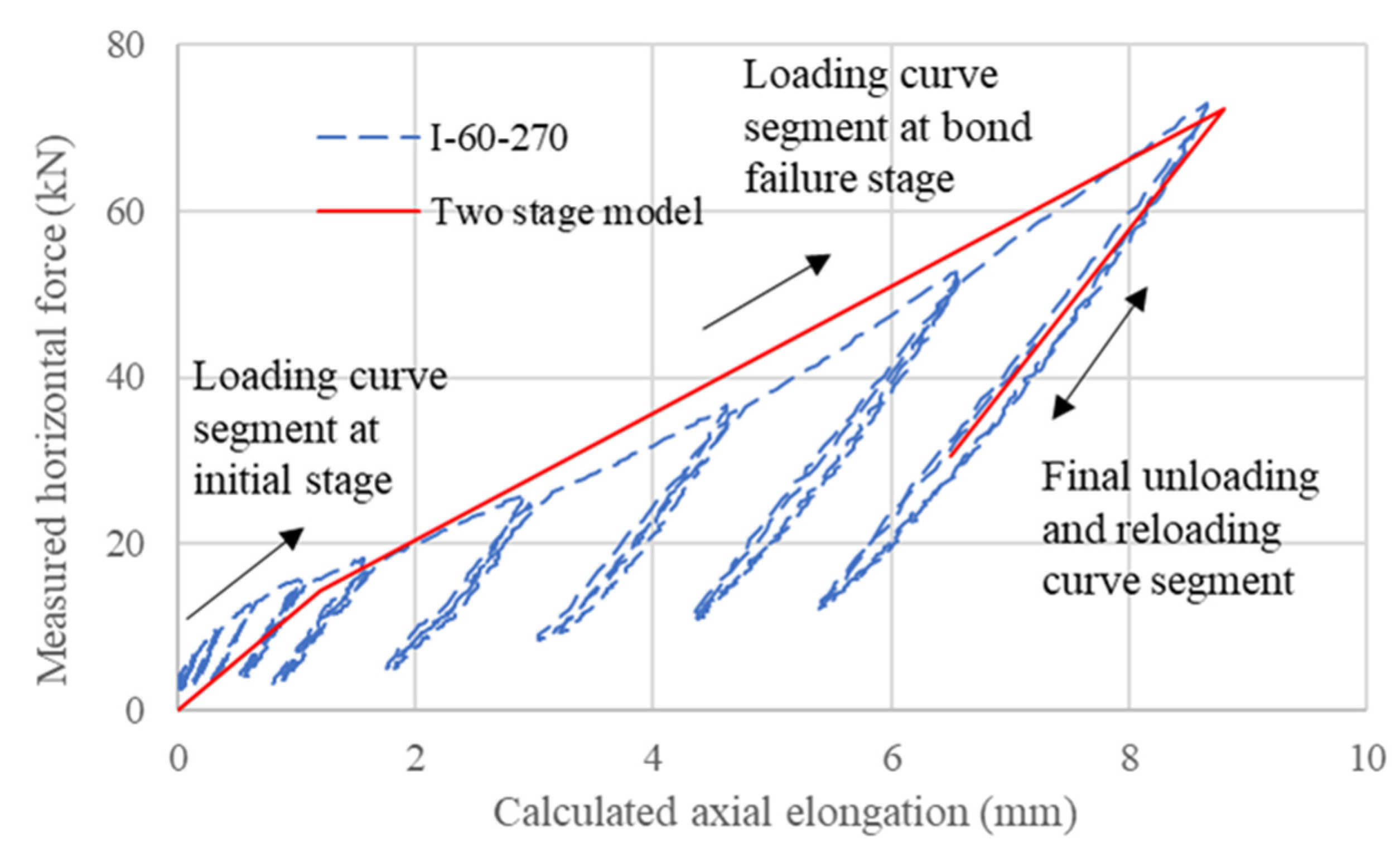
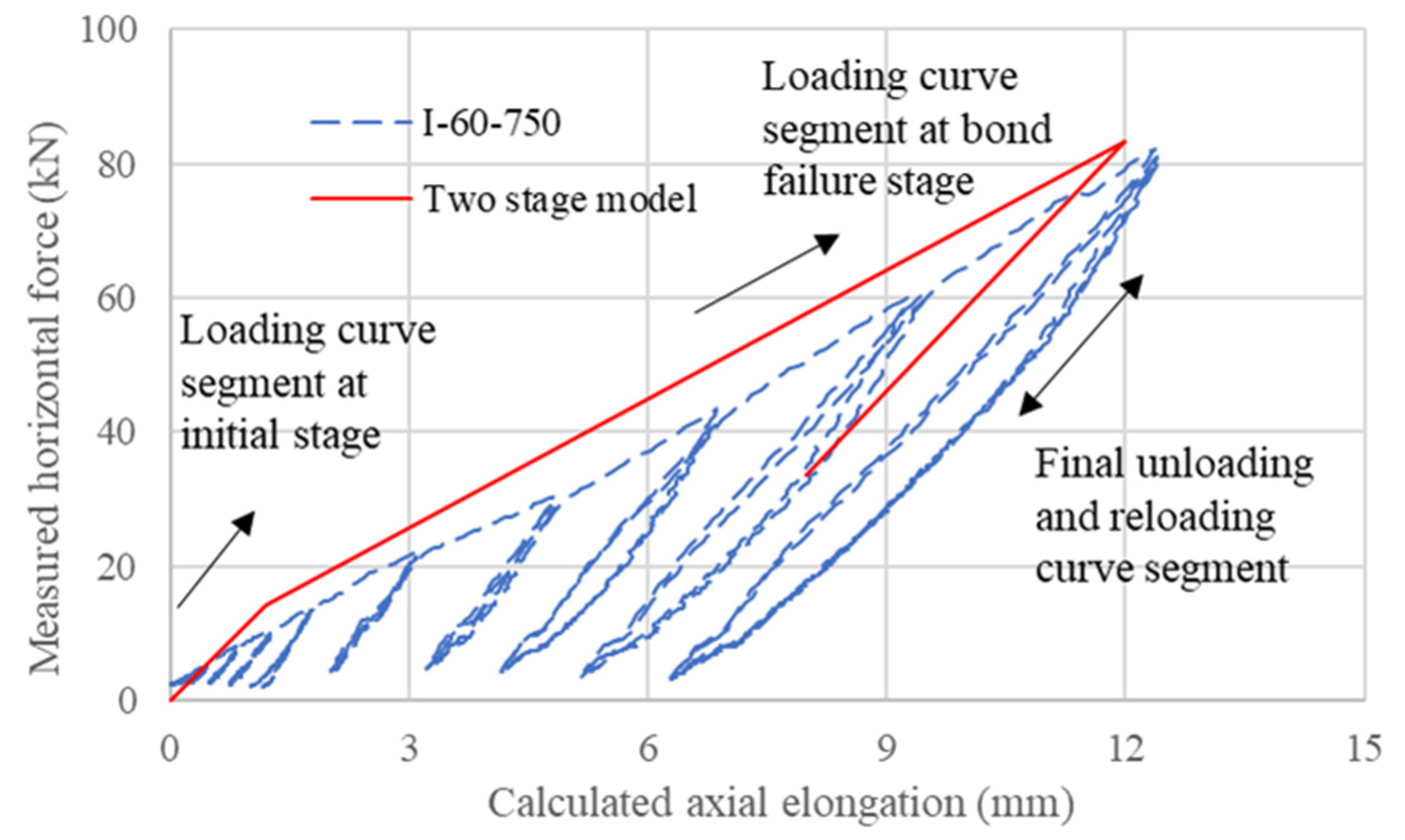
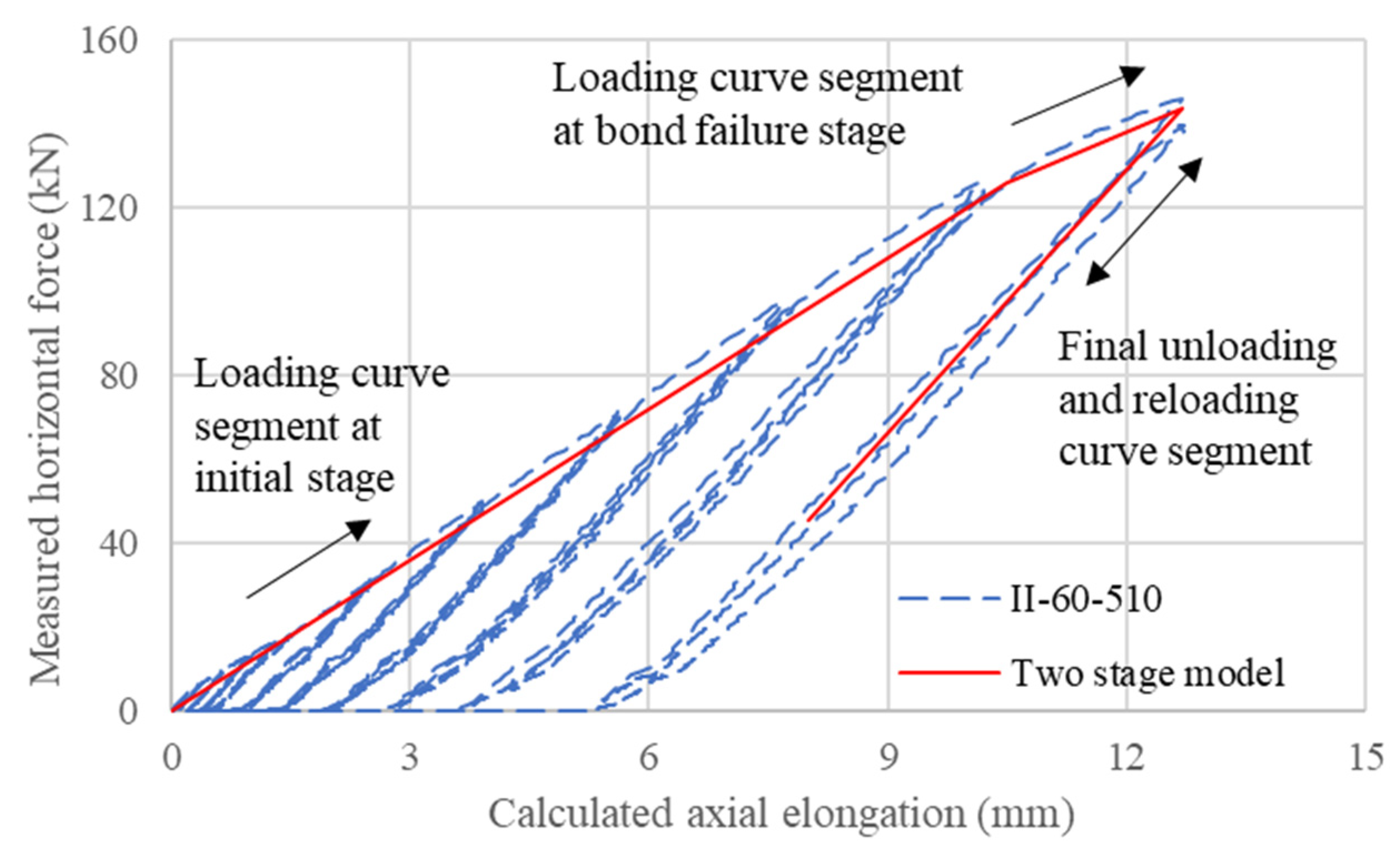
5.3. Two-Stage Numerical Model for Partially Debonded Tendon System
5.3.1. Establishment of the Model
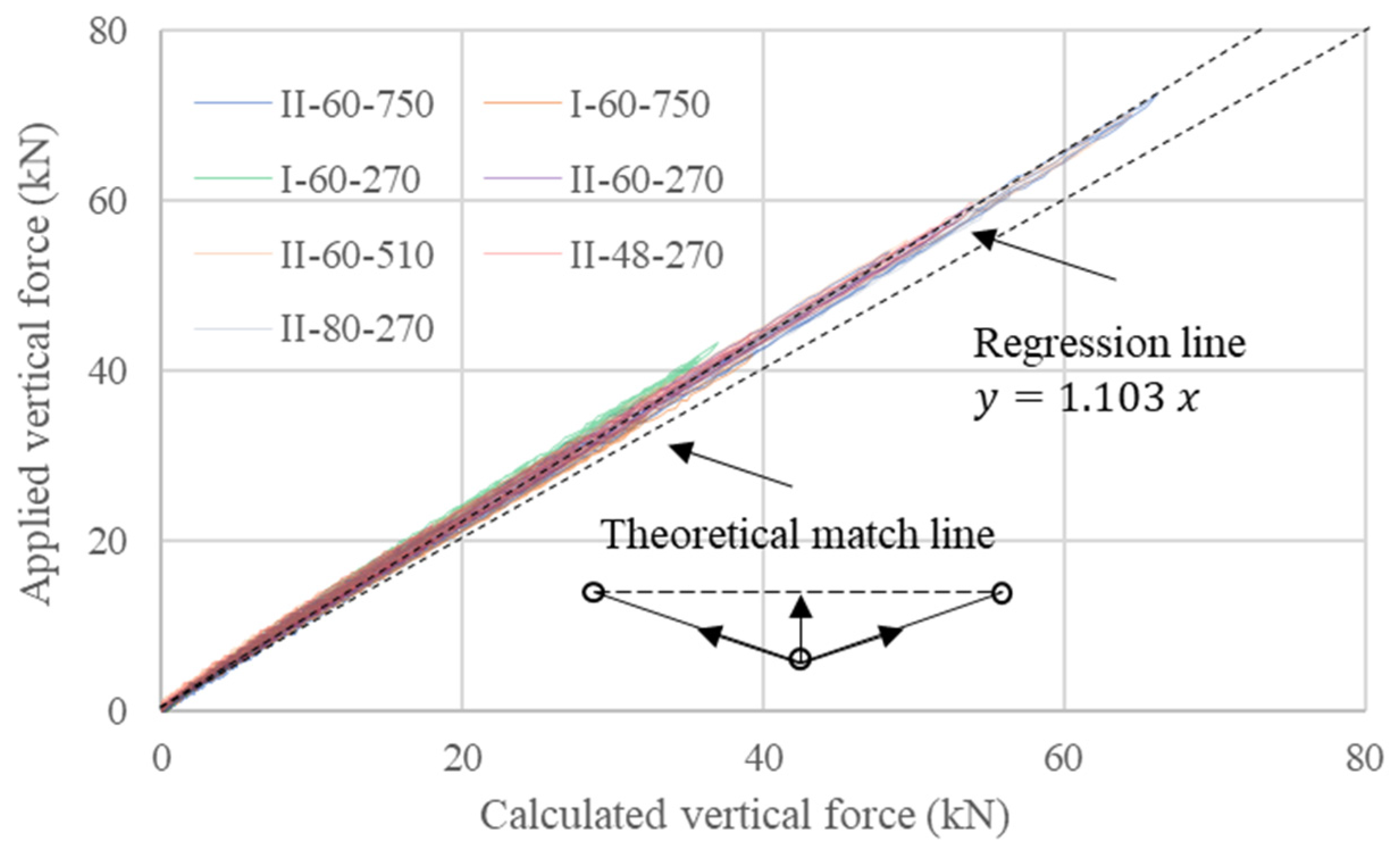
5.3.2. Calibration of the Models
5.3.3. Comparison of Calibrated Model with Other Results
6. Conclusions
- The established setup of the simplified bond testing is suitable to study the cyclic bond behavior of partially debonded tendons. For tendons with relatively low bond stresses, the stirrups in the specimens hardly affect the debonding between the tendon and grout. The direct axial tension and cyclic orthogonal displacement provide comparable values of bond strength.
- The deterioration of reloading stiffnesses can be represented by an additional effective debonded length caused by a bond failure in specimens. For partially debonded tendons with low initial prestress, the gradual fastening of the end anchorages must be considered as the loading stiffness during analysis.
- With proper calibration, a two-stage numerical model with a series of anchorage and strand springs can satisfactorily capture the envelope of the responses of the partially debonded tendon system.
- Despite the observation of permanent transverse deformation after testing, the 7-wire strand performs essentially elastically under large imposed vertical displacement (maximum orthogonal curvature at ) in the simplified cyclic bond testing, and the anchorage slip helps to dissipate energy. The proposed partially debonded tendon system can be a suitable option for precast segmental bridge columns with RSJs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| concrete cover to reinforcement in concrete prism | |
| stiffness of anchorage and strand, respectively | |
| effective stiffness of steel mono-strand | |
| transient stiffness of steel mono-strand | |
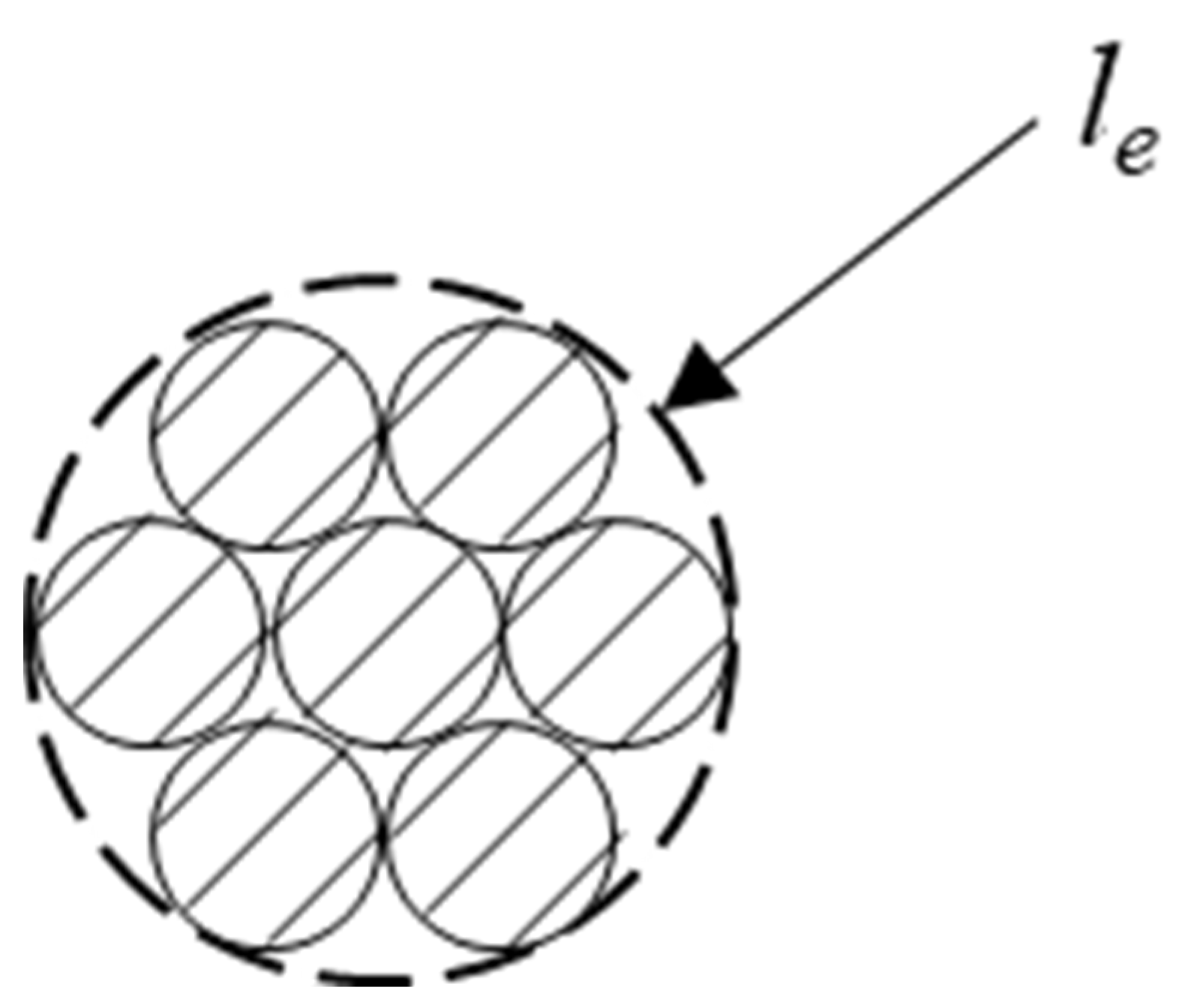
| additional fixity length induced by strand bond failure | |
| original fixity length determined by the setup | |
| axial elongation of strand induced by vertical loading | |
| debonded length of partially debonded tendons | |
| free length of the strand in cyclic bond testing | |
| total length of concrete prism | |
| measurement recorded in active LVDT | |
| measurement recorded in passive LVDT | |
| measurement recorded in vertical LVDT | |
| stiffness softening factor of strand due to bond failures | |
| ABC | accelerated bridge construction |
| LVDT | linear variable differential transformer |
| PSBC | precast segmental bridge columns |
| RSJ | resettable sliding joint |
References
- Priestley, M.N. Overview of PRESSS research program. PCI J. 1991, 36, 50–57. [Google Scholar] [CrossRef]
- Arai, T.; Hishiki, Y.; Suda, K.; Yamamoto, T.; Takizawa, S.; Onabe, T. Development of a New Precast Segmental PC Pier; KaTRI Annual Report VOL.48; KAJIMA Corporation: Tokyo, Japan, 2000. (In Japanese) [Google Scholar]
- Chang, K.C.; Loh, C.H.; Chiu, H.S.; Hwang, J.S.; Cheng, C.B.; Wang, J.C. Seismic Behavior of Precast Segmental Bridge Columns and Design Methodology for Applications in Taiwan; Taiwan Area National Expressway Engineering Bureau: Taipei, Taiwan, 2002. (In Chinese) [Google Scholar]
- Priestley, M.N.; Tao, J.R. Seismic Response of Precast Prestressed Concrete Frames with Partially Debonded Tendons. PCI J. 1993, 38, 58–69. [Google Scholar] [CrossRef]
- Priestley, M.N.; Sritharan, S.; Conley, J.R.; Pampanin, S. Preliminary results and conclusions from the PRESSS five-story precast concrete test building. PCI J. 1999, 44, 42–67. [Google Scholar] [CrossRef]
- Wang, J.C.; Ou, Y.C.; Chang, K.C.; Lee, G.C. Large-scale seismic tests of tall concrete bridge columns with precast segmental construction. Earthq. Eng. Struct. Dyn. 2008, 37, 1449–1465. [Google Scholar] [CrossRef]
- Ou, Y.C.; Wang, P.H.; Tsai, M.S.; Chang, K.C.; Lee, G.C. Large-Scale Experimental Study of Precast Segmental Unbonded Posttensioned Concrete Bridge Columns for Seismic Regions. J. Struct. Eng. 2010, 136, 255–264. [Google Scholar] [CrossRef]
- Ou, Y.C.; Tsai, M.S.; Chang, K.C.; Lee, G.C. Cyclic behavior of precast segmental concrete bridge columns with high performance or conventional steel reinforcing bars as energy dissipation bars. Earthq. Eng. Struct. Dyn. 2010, 39, 1181–1198. [Google Scholar] [CrossRef]
- Chou, C.C.; Chang, H.J.; Hewes, J.T. Two-plastic-hinge and two dimensional finite element models for post-tensioned precast concrete segmental bridge columns. Eng. Struct. 2013, 46, 205–217. [Google Scholar] [CrossRef]
- Li, C.; Hao, H.; Bi, K. Seismic performance of precast concrete-filled circular tube segmental column under biaxial lateral cyclic loadings. Bull. Earthq. Eng. 2018, 17, 271–296. [Google Scholar] [CrossRef]
- Shim, C.S.; Chung, C.H.; Kim, H.H. Experimental evaluation of seismic performance of precast segmental bridge piers with a circular solid section. Eng. Struct. 2008, 30, 3782–3792. [Google Scholar] [CrossRef]
- Bu, Z.Y.; Ou, Y.C.; Song, J.W.; Lee, G.C. Hysteretic modeling of unbonded posttensioned precast segmental bridge columns with circular section based on cyclic loading test. J. Bridge Eng. 2016, 21, 04016016. [Google Scholar] [CrossRef]
- Bu, Z.Y.; Ou, Y.C.; Song, J.W.; Zhang, N.S.; Lee, G.C. Cyclic loading test of unbonded and bonded posttensioned precast segmental bridge columns with circular section. J. Bridge Eng. 2016, 21, 04015043. [Google Scholar] [CrossRef]
- Cai, Z.K.; Zhou, Z.; Wang, Z. Influencing factors of residual drifts of precast segmental bridge columns with energy dissipation bars. Adv. Struct. Eng. 2019, 22, 126–140. [Google Scholar] [CrossRef]
- Thapa, D.; Pantelides, C.P. Self-centering bridge bent with stretch length anchors as a tension-only hysteretic hybrid system. J. Struct. Eng. 2021, 147, 04021163. [Google Scholar] [CrossRef]
- Dangol, I.; Pantelides, C.P. Resilient posttensioned bridge bent with buckling restrained brace. J. Bridge Eng. 2022, 27, 04021107. [Google Scholar] [CrossRef]
- Marriott, D.; Pampanin, S.; Palermo, A. Quasi-static and pseudo-dynamic testing of unbonded post-tensioned rocking bridge piers with external replaceable dissipaters. Earthq. Eng. Struct. Dyn. 2009, 38, 331–354. [Google Scholar] [CrossRef]
- ElGawady, M.A.; Sha’lan, A. Seismic behavior of selfcentering precast segmental bridge bents. J. Bridge Eng. 2011, 16, 328–339. [Google Scholar] [CrossRef]
- ElGawady, M.A.; Booker, A.J.; Dawood, H.M. Seismic behavior of posttensioned concrete-filled fiber tubes. J. Compos. Constr. 2010, 14, 616–628. [Google Scholar] [CrossRef]
- Nikoukalam, M.T.; Sideris, P. Resilient bridge rocking columns with polyurethane damage-resistant end segments and replaceable energy-dissipating links. J. Bridge Eng. 2017, 22, 04017064. [Google Scholar] [CrossRef]
- Li, C.; Bi, K.; Hao, H.; Zhang, X. Cyclic test and numerical study of precast segmental concrete columns with BFRP and TEED. Bull. Earthq. Eng. 2019, 17, 3475–3494. [Google Scholar] [CrossRef]
- Sideris, P.; Aref, A.J.; Filiatrault, A. Quasi-static cyclic testing of a large-scale hybrid sliding-rocking segmental column with slip-dominant joints. J. Bridge Eng. 2014, 19, 04014036. [Google Scholar] [CrossRef]
- Sideris, P.; Aref, A.J.; Filiatrault, A. Large-scale seismic testing of a hybrid sliding-rocking posttensioned segmental bridge system. J. Struct. Eng. 2014, 140, 04014025. [Google Scholar] [CrossRef]
- Au, F.T.K.; Liu, Y.Q.; Yuan, Y.; Su, R.K.L.; Lam, N.T.K. Seismic Performance of Precast Segmental Bridge Columns with Resettable Sliding Joints: Feasibility Study. In Proceedings of the Bridge Engineering Institute Conference—Frontiers of Bridge Engineering, Honolulu, HI, USA, 22–25 July 2019. [Google Scholar]
- Liu, Y.Q.; Liang, F.; Au, F.T.K. Precast segmental bridge columns with resettable sliding joints—An inspiration from ancient Chinese pagodas. Structures 2021, 33, 615–626. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Liang, F.; Au, F.T.K. Experimental study of durable low-friction concrete contacts for precast segmental columns with resettable sliding joints. Constr. Build. Mater. 2022, 318, 126192. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Yuan, Y.; Liang, F.; Au, F.T.K. Resetting Response of Precast Segments with Gently Keyed Interface under Seismic Action. Earthq. Eng. Struct. Dyn. 2021, 50, 601–618. [Google Scholar] [CrossRef]
- Janney, J.R. Nature of Bond in Pre-Tensioned Prestressed Concrete; ACI: Farmington Hills, MI, USA, 1954. [Google Scholar]
- ASTM (American Society for Testing Materials). A1081/A1081M: Standard Test Method for Evaluating Bond of Seven Wire Steel Prestressing Strand; ASTM International: West Conshohocken, PA, USA, 2012. [Google Scholar]
- Laldji, S. Bond Characteristics of Prestressing Strand in Grout. Master’s Thesis, University of Leicester, Leicester, UK, 1987. [Google Scholar]
- ACI (American Concrete Institute) Committee 408. Bond and Development of Straight Reinforcing Bars in Tension; Report No. 408R-03; ACI: Farmington Hills, MI, USA, 2003. [Google Scholar]
- Borzovič, V.; Laco, J. Bond stress–slip behaviour of prestressing units coated with corrosion protection. Trans. VŠB–Tech. Univ. Ostrava. Civ. Eng. Series. 2013, 23, 13–20. [Google Scholar] [CrossRef]
- CEN (European Committee for Standardisation). EN 197-1: Cement-Part 1: Composition, Specifications and Conformity Criteria for Common Cements; CEN: Brussels, Belgium, 2011. [Google Scholar]
- SikaGrout-214 HK. Product Data Sheet of Multi-Purpose Non-Shrink (Shrinkage Compensated) Cementitious Grout; Version 02.01; Sika Hongkong Ltd.: Hongkong, China, 2020. [Google Scholar]
- BSI (British Standards Institution). BS 5896: Specification for High Tensile Steel Wire and Strand for the Prestressing of Concrete; BSI: London, UK, 2012. [Google Scholar]
- Zhang, L.; Wei, Y.; Au, F.T.K.; Li, J. Mechanical properties of prestressing steel in and after fire. Mag. Concr. Res. 2017, 69, 379–388. [Google Scholar] [CrossRef]
- Wu, X.Q.; Huang, T.; Zhang, L.; Au, F.T.K. Bond performance of grouted tendons at elevated temperatures. Proc. Inst. Civ. Eng.-Struct. Build. 2021, 174, 791–803. [Google Scholar] [CrossRef]
- Wu, X.Q.; Huang, T.; Au, F.T.K.; Li, J. Post-tensioned Concrete Bridge Beams Exposed to Hydrocarbon Fire. Journal of Structural Engineering-ASCE. J. Struct. Eng. 2020, 146, 04020210. [Google Scholar] [CrossRef]
- Wu, X.Q.; Huang, T.; Au, F.T.K.; Li, J. A Localized Fire Model for Predicting the Surface Temperature of Box Girder Bridges Subjected to Tanker Truck Fire. Fire Technol. 2020, 56, 2059–2087. [Google Scholar] [CrossRef]
- Sideris, P. Seismic Analysis and Design of Precast Concrete Segmental Bridges. Ph.D. Thesis, Department of Civil, Structural and Environmental Engineering, State University of New York at Buffalo, Buffalo, NY, USA, 2012. [Google Scholar]








| Batch | Grade | Cement | Water (kg/m3) | Fine Aggregate (kg/m3) | 10 mm Aggregate (kg/m3) | 28-Day Cylinder Strength (MPa) | 28-Day Cube Strength (Mpa) |
|---|---|---|---|---|---|---|---|
| (kg/m3) | |||||||
| First | C45 | 501 | 256 | 857 | 701 | 45.0 | 50.1 |
| Second | C45 | 501 | 256 | 857 | 701 | 44.6 | 51.0 |
| No. | Batch | Label | Strand Surface Condition | Stirrup | Grout | Length (mm) | Notes |
|---|---|---|---|---|---|---|---|
| 1 | First batch | I-60-270P1 | coated with oil | 60 | w/c = 0.4 | 270 | axial only |
| 2 | I-60-270P2 | 60 | w/c = 0.4 | 270 | axial only | ||
| 3 | I-60-270P3 | 60 | w/c = 0.4 | 270 | axial only | ||
| 4 | I-60-510P | 60 | w/c = 0.4 | 510 | axial only | ||
| 5 | I-60-270 | 60 | w/c = 0.4 | 270 | vertical cyclic | ||
| 6 | I-60-750 | 60 | w/c = 0.4 | 750 | vertical cyclic | ||
| 7 | Second batch | II-60-270P | dry and clean | 60 | w/sika = 0.2 | 270 | axial only |
| 8 | II-48-270 | 48 | w/sika = 0.2 | 270 | vertical cyclic | ||
| 9 | II-80-270 | 80 | w/sika = 0.2 | 270 | vertical cyclic | ||
| 10 | II-60-270 | 60 | w/sika = 0.2 | 270 | vertical cyclic | ||
| 11 | II-60-510 | 60 | w/sika = 0.2 | 510 | vertical cyclic | ||
| 12 | II-60-750 | 60 | w/sika = 0.2 | 750 | vertical cyclic |
| Stage | Cycles | Loading Rate (mm/min) | Loading and Reloading | Unloading |
|---|---|---|---|---|
| Displacement Control (mm) | Force Control (kN) | |||
| 1 | 2 | 10 | 5 | to zero |
| 2 | 10 | to zero | ||
| 3 | 15 | to zero | ||
| 4 | 20 | to zero | ||
| 5 | 25 | to zero | ||
| 6 | 15 | 30 | to zero | |
| 7 | 40 | to zero | ||
| 8 | 50 | to zero | ||
| 9 | 60 | to zero | ||
| 10 | 70 | to zero | ||
| 11 | 80 | to zero | ||
| 12 | 90 | to zero | ||
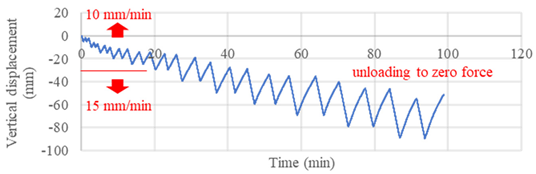 Typical time history for one-way cyclic loading | ||||
| Unit | II-60-270 | II-60-750 | |
|---|---|---|---|
| maximum bond force | kN | 63 | 154 |
| maximum horizontal force | kN | 130 | 154 |
| anchorage stiffness | kN/mm | 26.3 | 26.3 |
| strand stiffness | kN/mm | 22.2 | 22.2 |
| additional effective length | mm | 180 | 0 |
| softening factor | - | 0.875 | 1 |
| Unit | I-60-270 | I-60-750 | II-60-510 | |
|---|---|---|---|---|
| maximum bond force | kN | 14 | 63 | 126 |
| maximum horizontal force | kN | 73 | 130 | 145 |
| anchorage stiffness | kN/mm | 26.3 | 26.3 | 26.3 |
| strand stiffness | kN/mm | 22.2 | 22.2 | 22.2 |
| additional effective length | mm | 270 | 970 | 70 |
| softening factor | - | 0.824 | 0.565 | 0.947 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, L.; Hu, H.; Guan, S.; Shah, Y.I.; Liu, Y. Cyclic Bond-Slip Behavior of Partially Debonded Tendons for Sustainable Design of Non-Emulative Precast Segmental Bridge Columns. Sustainability 2023, 15, 8128. https://doi.org/10.3390/su15108128
Xia L, Hu H, Guan S, Shah YI, Liu Y. Cyclic Bond-Slip Behavior of Partially Debonded Tendons for Sustainable Design of Non-Emulative Precast Segmental Bridge Columns. Sustainability. 2023; 15(10):8128. https://doi.org/10.3390/su15108128
Chicago/Turabian StyleXia, Leilei, Hongcheng Hu, Shiyu Guan, Yasir Ibrahim Shah, and Yingqi Liu. 2023. "Cyclic Bond-Slip Behavior of Partially Debonded Tendons for Sustainable Design of Non-Emulative Precast Segmental Bridge Columns" Sustainability 15, no. 10: 8128. https://doi.org/10.3390/su15108128
APA StyleXia, L., Hu, H., Guan, S., Shah, Y. I., & Liu, Y. (2023). Cyclic Bond-Slip Behavior of Partially Debonded Tendons for Sustainable Design of Non-Emulative Precast Segmental Bridge Columns. Sustainability, 15(10), 8128. https://doi.org/10.3390/su15108128







