Tunnel Face Stability Considering the Influence of Excess Slurry Pressure
Abstract
:1. Introduction
2. Problem and Methodology
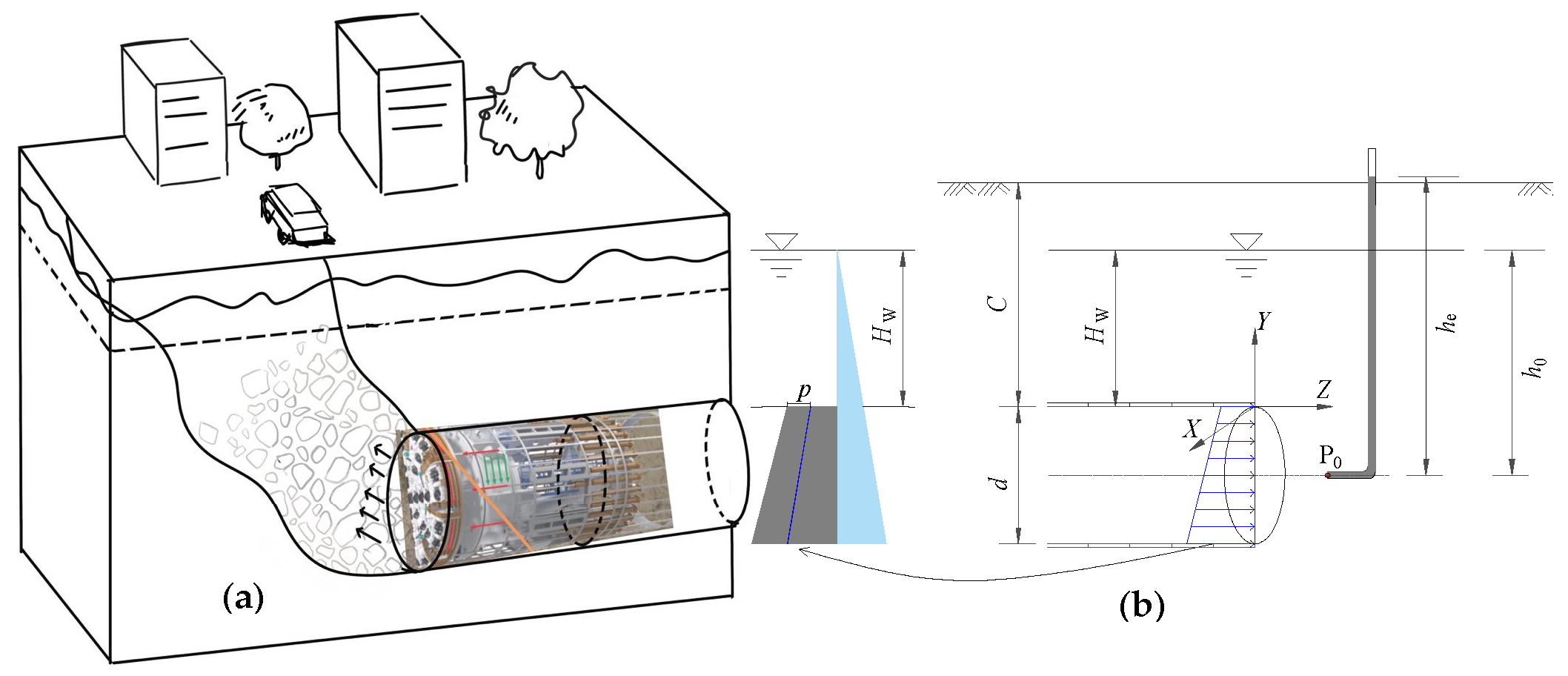
2.1. Depiction of Tunnel Faces Subjected to Excess Slurry Pressures
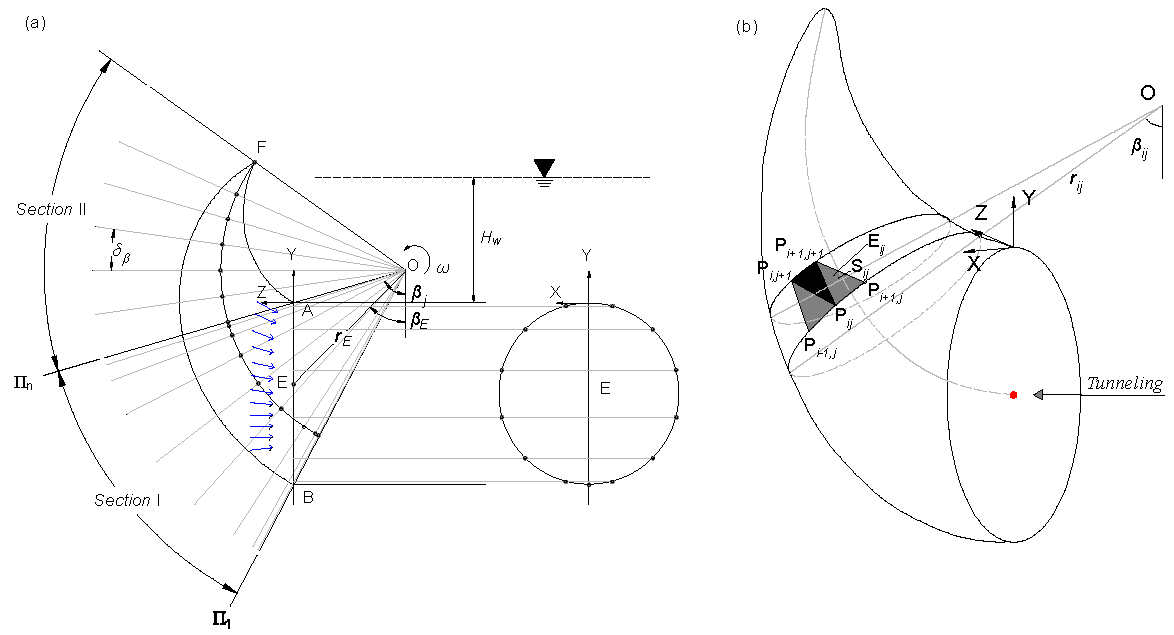
2.2. Kinematical Analysis of the Tunnel Face
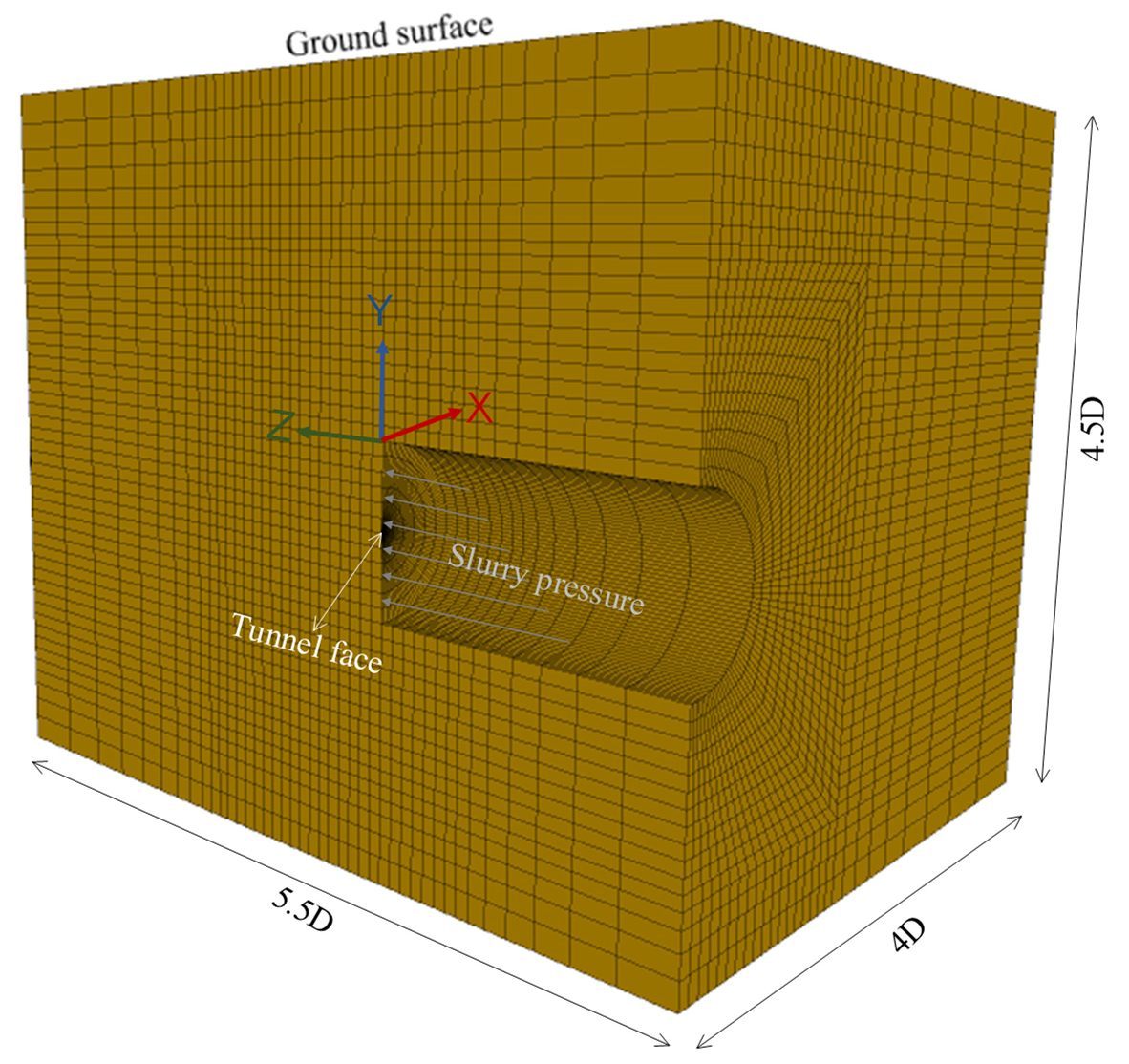
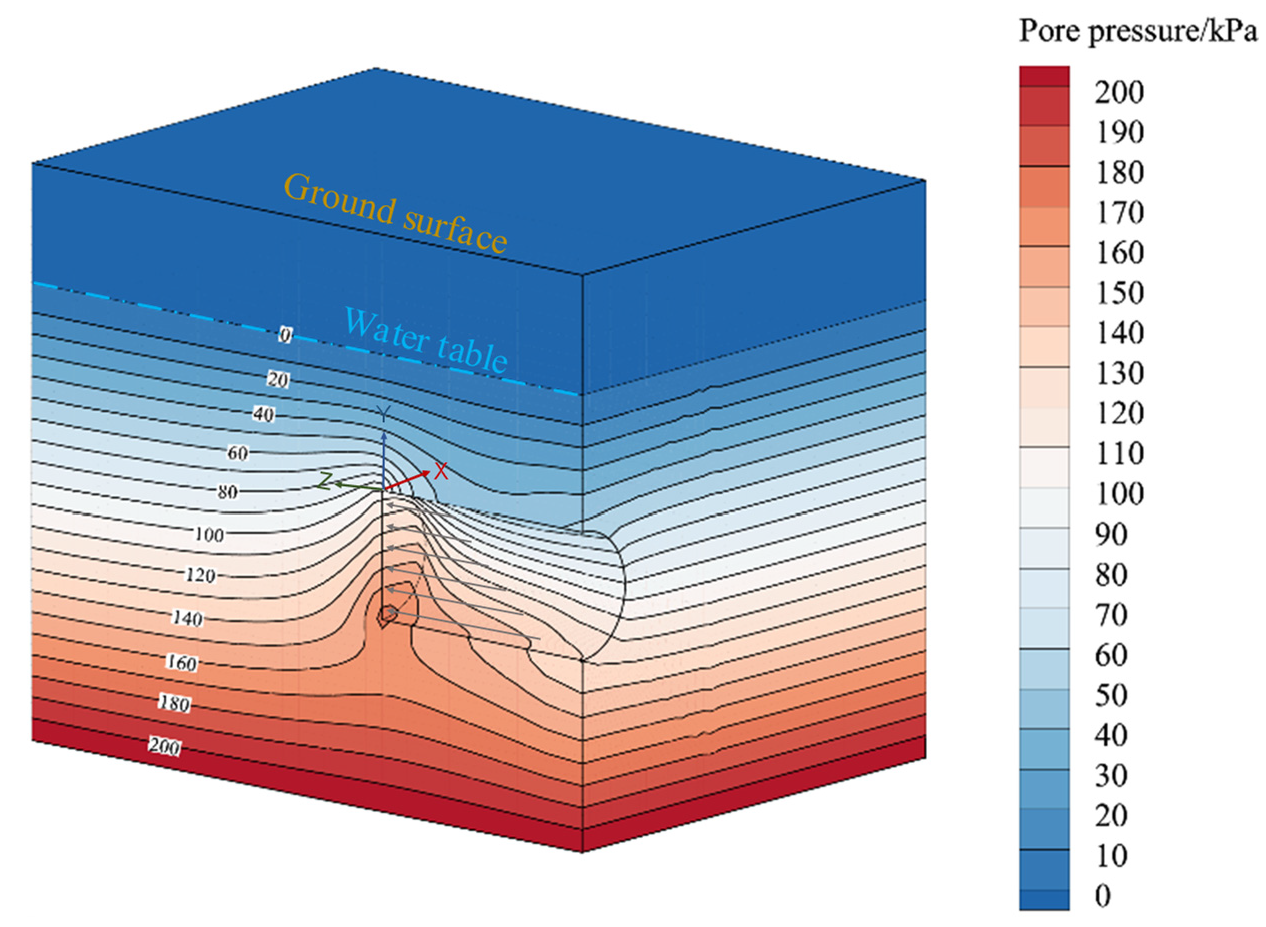
2.3. Numerical Simulation of Seepage Flow Due to Excess Slurry Pressure
2.4. Empirical Formulas for Approximating the Piezometric Head under the Slurry Infiltration
2.5. Flow Diagram of Solving Safety Factor
3. Comparison
4. Parametric Study
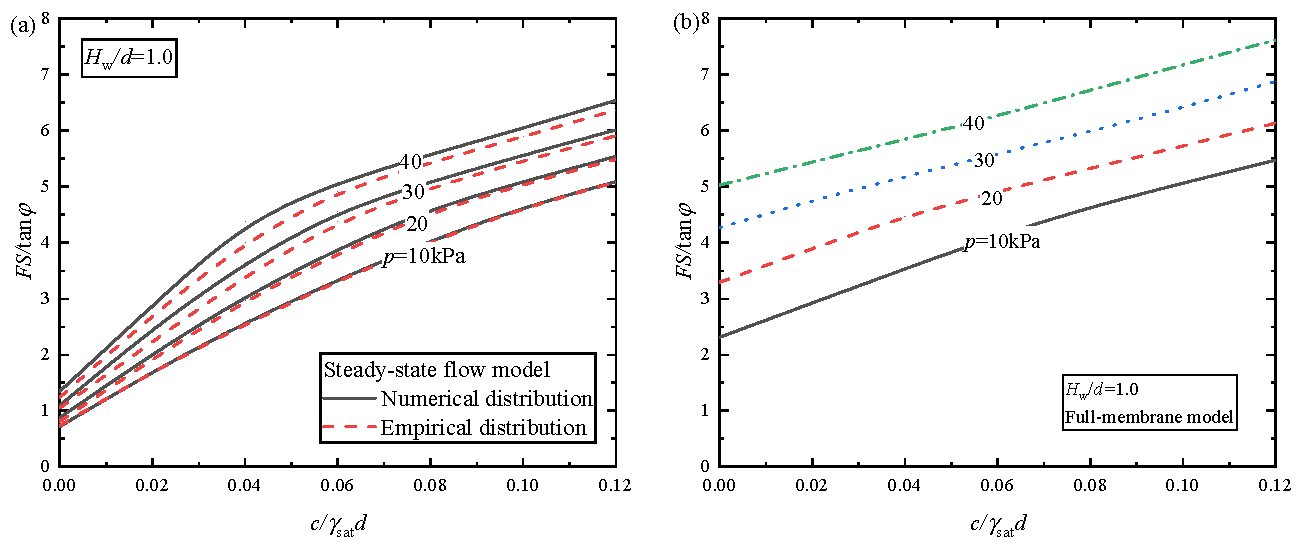
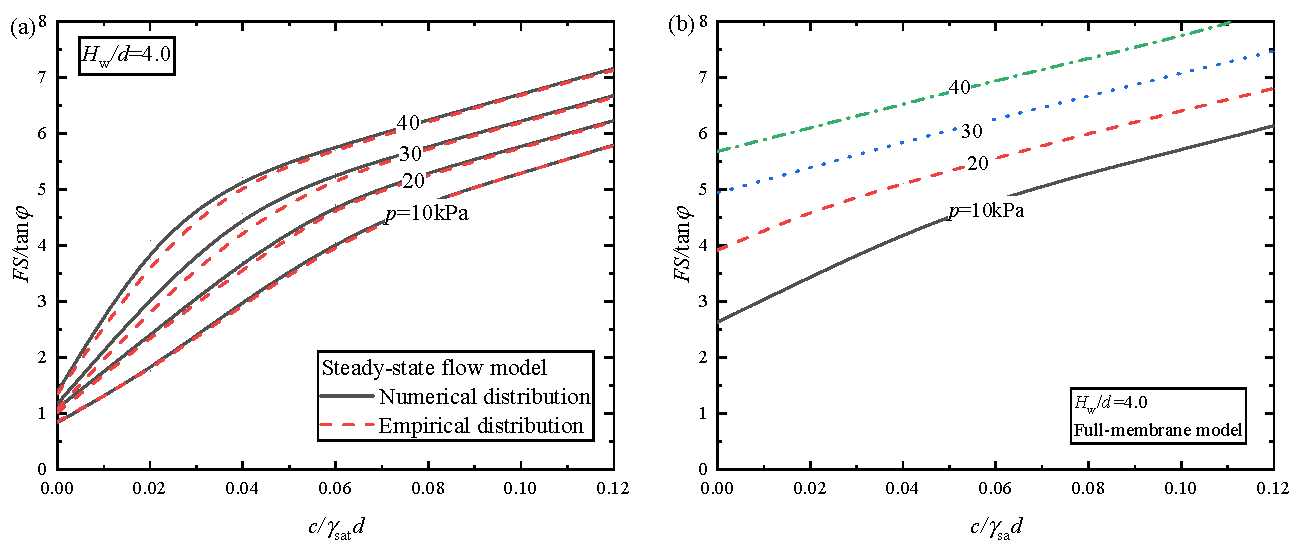
4.1. The Impact of Excess Slurry Pressure
4.2. The Impact of the Coefficient
4.3. Design Diagrams of Normalized Safety Factor
4.4. Discussion
5. Conclusions
- (1)
- The results based on the empirical distribution are a little more conservative than those based on the numerical distribution, which verifies the effectiveness of the proposed empirical formulas. Compared to numerically simulating the seepage, employing the empirical distribution allows a significantly higher computational efficiency with acceptable accuracy;
- (2)
- The results of the flow case show that with increasing excess slurry pressures, the safety factor shows a noticeable non-linear increasing trend in low cohesion cases, which turns into a linear increasing trend in large cohesion cases. As the excess slurry pressure increases, the critical failure mechanism becomes closer to the tunnel face and the ground;
- (3)
- Compared to the full-membrane model, safety factors of the steady-state flow model are much more conservative and exhibit a more distinct non-linearity with the increasing normalized cohesion, particularly for the low normalized cohesion cases. With the increase in , a coefficient representing the residual excess slurry pressure after the pressure drop over the filter cake, the safety factor decreases almost linearly. According to the state of the filter cakes in practical engineering, the tunnel face stability can be referenced with the results of the normalized charts.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Pressure drop coefficient | |
| Polar coordinates of point E | |
| , | Effective cohesion and internal friction angle |
| C | Buried depth |
| D,R | Tunnel diameter and tunnel radius |
| Angular interval of Section II in the failure mechanism | |
| FS | Safety factor |
| Location of water table with respect to the tunnel crown | |
| Permeability coefficient | |
| Dimensionless coefficients denoting contribution of cohesion, soil gravity, pore pressure, and slurry pressure | |
| Piezometric head of a point ahead of the tunnel | |
| Excess slurry pressure at tunnel crown | |
| Uniform excess slurry pressure | |
| Extra required uniform support pressure | |
| Average slurry pressure over the tunnel face | |
| Slurry infiltration velocity | |
| TBM velocity | |
| Unit slurry weight, unit water weight, and unit saturated weight |
References
- Chen, R.; Li, J.; Kong, L.; Tang, L. Experimental Study on Face Instability of Shield Tunnel in Sand. Tunn. Undergr. Space Technol. 2013, 33, 12–21. [Google Scholar] [CrossRef]
- Jin, D.; Yuan, D.; Li, X.; Zheng, H. Analysis of the Settlement of an Existing Tunnel Induced by Shield Tunneling Underneath. Tunn. Undergr. Space Technol. 2018, 81, 209–220. [Google Scholar] [CrossRef]
- Li, Y.; Emeriault, F.; Kastner, R.; Zhang, Z.X. Stability Analysis of Large Slurry Shield-Driven Tunnel in Soft Clay. Tunn. Undergr. Space Technol. 2009, 24, 472–481. [Google Scholar] [CrossRef]
- Kim, S.H.; Tonon, F. Face Stability and Required Support Pressure for TBM Driven Tunnels with Ideal Face Membrane—Drained Case. Tunn. Undergr. Space Technol. 2010, 25, 526–542. [Google Scholar] [CrossRef]
- Anagnostou, G.; Kovári, K. The Face Stability of Slurry-Shield-Driven Tunnels. Tunn. Undergr. Space Technol. 1994, 9, 165–174. [Google Scholar] [CrossRef]
- Thewes, M.; Schoesser, B.; Zizka, Z. Transient Face Support in Slurry Shield Tunneling Due to Different Time Scales for Excavation Sequence of Cutting Tools and Penetration Time of Support Fluid. In Proceedings of the ITA World Tunnel Congress, San Francisco, CA, USA, 22–28 April 2016. [Google Scholar]
- Xu, T.; Bezuijen, A. Analytical Methods in Predicting Excess Pore Water Pressure in Front of Slurry Shield in Saturated Sandy Ground. Tunn. Undergr. Space Technol. 2018, 73, 203–211. [Google Scholar] [CrossRef]
- Bezuijen, A.; van Lottum, H. (Eds.) Tunnelling: A Decade of Progress: GeoDelft 1995–2005; Taylor & Francis: London, UK; New York, NY, USA, 2006; ISBN 978-0-415-39133-7. [Google Scholar]
- Broere, W. Infuence of Excess Pore Pressures on the Stability of the Tunnel Face. Reclaiming the Underground Space. 2002, Volume 2, pp. 759–765. Available online: https://www.taylorfrancis.com/chapters/edit/10.1201/9780203741177-31/influence-excess-pore-pressures-stability-tunnel-face-broere (accessed on 4 April 2023).
- Min, F.; Zhu, W.; Han, X. Filter Cake Formation for Slurry Shield Tunneling in Highly Permeable Sand. Tunn. Undergr. Space Technol. 2013, 38, 423–430. [Google Scholar] [CrossRef]
- Zhou, Z.; Ling, T.; Huang, F.; Zhang, M. The Face Stability Analysis of Shield Tunnels Subjected to Seepage Based on the Variational Principle. Sustainability 2022, 14, 16538. [Google Scholar] [CrossRef]
- Anagnostou, G.; Kovári, K. Face Stability in Slurry and EPB Shield Tunnelling; Progressive Media Markets, Ltd.: London, UK, 1996. [Google Scholar]
- Broere, W.; van Tol, A.F. Time-Dependant Infiltration and Groundwater Flow in a Face Stability Analysis. In Modern Tunneling Science and Technology; Adachi, T., Tateyama, K., Kimura, M., Eds.; CRC Press: Boca Raton, FL, USA, 2020; pp. 629–634. ISBN 978-1-00-307753-4. [Google Scholar]
- Talmon, A.M.; Bezuijen, A. Simulating the Consolidation of TBM Grout at Noordplaspolder. Tunn. Undergr. Space Technol. 2009, 24, 493–499. [Google Scholar] [CrossRef]
- Zizka, Z.; Schoesser, B.; Thewes, M.; Schanz, T. Slurry Shield Tunneling: New Methodology for Simplified Prediction of Increased Pore Pressures Resulting from Slurry Infiltration at the Tunnel Face Under Cyclic Excavation Processes. Int. J. Civ. Eng. 2019, 17, 113–130. [Google Scholar] [CrossRef]
- Talmon, A.M.; Mastbergen, D.R.; Huisman, M. Invasion of pressurized clay suspensions into granular soil. J. Porous Media 2013, 16, 351–365. [Google Scholar] [CrossRef]
- Xu, T.; Bezuijen, A. Bentonite Slurry Infiltration into Sand: Filter Cake Formation under Various Conditions. Geotechnique 2019, 69, 1095–1106. [Google Scholar] [CrossRef]
- Bezuijen, A.; Steeneken, S.P.; Ruigrok, J.A.T. Monitoring and analysing pressures around a tbm. In Proceedings of the 13th International Conference Underground Construction, Prague, Czech Republic, 23–25 May 2016; Volume 1, pp. 1–9. [Google Scholar]
- Steeneken, S.P. Excess Pore Pressures Near a Slurry Tunnel Boring Machine: Modelling and Measurements. 2016. Available online: https://repository.tudelft.nl/islandora/object/uuid:b8f3db81-7143-4b93-a059-c9bd4d92210a (accessed on 4 April 2023).
- Soranzo, E.; Guardiani, C.; Wu, W. A Soft Computing Approach to Tunnel Face Stability in a Probabilistic Framework. Acta Geotech. 2022, 17, 1219–1238. [Google Scholar] [CrossRef]
- Qin, C.; Li, Y.; Yu, J.; Chen Chian, S.; Liu, H. Closed-Form Solutions for Collapse Mechanisms of Tunnel Crown in Saturated Non-Uniform Rock Surrounds. Tunn. Undergr. Space Technol. 2022, 126, 104529. [Google Scholar] [CrossRef]
- Wang, C.; Xiao, J.; Liu, W.; Ma, Z. Unloading and Reloading Stress-Strain Relationship of Recycled Aggregate Concrete Reinforced with Steel/Polypropylene Fibers under Uniaxial Low-Cycle Loadings. Cem. Concr. Compos. 2022, 131, 104597. [Google Scholar] [CrossRef]
- Wang, C.; Wu, H.; Li, C. Hysteresis and Damping Properties of Steel and Polypropylene Fiber Reinforced Recycled Aggregate Concrete under Uniaxial Low-Cycle Loadings. Constr. Build. Mater. 2022, 319, 126191. [Google Scholar] [CrossRef]
- Qin, C.; Zhou, J. On the Seismic Stability of Soil Slopes Containing Dual Weak Layers: True Failure Load Assessment by Finite-Element Limit-Analysis. Acta Geotech. 2023, 1–23. [Google Scholar] [CrossRef]
- Qin, C.-B.; Chian, S.C. Kinematic Analysis of Seismic Slope Stability with a Discretisation Technique and Pseudo-Dynamic Approach: A New Perspective. Géotechnique 2018, 68, 492–503. [Google Scholar] [CrossRef]
- Gong, W.; Juang, C.H.; Wasowski, J. Geohazards and Human Settlements: Lessons Learned from Multiple Relocation Events in Badong, China—Engineering Geologist’s Perspective. Eng. Geol. 2021, 285, 106051. [Google Scholar] [CrossRef]
- Li, T.Z.; Pan, Q.; Dias, D. Active Learning Relevant Vector Machine for Reliability Analysis. Appl. Math. Model. 2021, 89, 381–399. [Google Scholar] [CrossRef]
- Subrin, D.; Wong, H. Tunnel face stability in frictional material: A new 3D failure mechanism. C. R. Mec. 2002, 330, 513–519. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A.-H. Face Stability Analysis of Circular Tunnels Driven by a Pressurized Shield. J. Geotech. Geoenviron. Eng. 2010, 136, 215–229. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A.-H. Rotational Failure Mechanisms for the Face Stability Analysis of Tunnels Driven by a Pressurized Shield. Int. J. Numer. Anal. Meth. Geomech. 2011, 35, 1363–1388. [Google Scholar] [CrossRef]
- Bezuijen, A.; Pruiksma, J.P.; van Meerten, H.H. Pore Pressures in Front of Tunnel, Measurements, Calculations and Consequences for Stability of Tunnel Face. Modern Tunneling Science and Technology. 2001. Available online: https://www.taylorfrancis.com/chapters/edit/10.1201/9781003077534-35/pore-pressures-front-tunnel-measurements-calculations-consequences-stability-tunnel-face-adam-bezuijen-jitse-pruiksma-hans-van-meerten (accessed on 4 April 2023).
- Kaalberg, F.J.; Ruigrok, J.A.T.; De Nijs, R. TBM face stability & excess pore pressures in close proximity of piled bridge foundations controlled with 3D FEM. In Proceedings of the 8th International Symposium on Geotechnical Aspects of Underground Construction in Soft Ground, London, UK, 25–27 August 2014; pp. 555–560. [Google Scholar]
- Bezuijen, A. Keynote Lecture: Soil-water-tunnel interaction at the front face of a TBM. In Geotechnics for Sustainable Infrastructure Development; Springer: Singapore, 2020; pp. 207–220. [Google Scholar]
- Xu, T.; Bezuijen, A. Experimental Study on the Mechanisms of Bentonite Slurry Penetration in Front of a Slurry TBM. Tunn. Undergr. Space Technol. 2019, 93, 103052. [Google Scholar] [CrossRef]
- Rotaru, A.; Bejan, F.; Almohamad, D. Sustainable Slope Stability Analysis: A Critical Study on Methods. Sustainability 2022, 14, 8847. [Google Scholar] [CrossRef]
- Qin, C.; Chian, S.C.; Du, S. Revisiting Seismic Slope Stability: Intermediate or below-the-Toe Failure? Géotechnique 2020, 70, 71–79. [Google Scholar] [CrossRef]
- Li, T.; Gong, W.; Tang, H.; Zhang, L. A Meshed Kinematical Approach for 3D Slope Stability Analysis. Num. Anal. Meth. Geomech. 2022, 46, 2913–2930. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Zhu, J.Q.; Yang, X.L. Three-Dimensional Active Earth Pressures for Unsaturated Backfills with Cracks Considering Steady Seepage. Int. J. Geomech. 2023, 23, 04022270. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Yang, X.L. Pseudodynamic Analysis of Three-Dimensional Fissured Slopes Reinforced with Piles. Int. J. Geomech. 2023, 23, 04022315. [Google Scholar] [CrossRef]
- Hou, C.; Zhong, J.; Yang, X. Three-Dimensional Stability Assessments of a Non-Circular Tunnel Face Reinforced by Bolts under Seepage Flow Conditions. Tunn. Undergr. Space Technol. 2023, 131, 104831. [Google Scholar] [CrossRef]
- Zizka, Z. Stability of Slurry Supported Tunnel Face Considering the Transient Support Mechanism during Excavation in Non-Cohesive Soil. 2019. Available online: https://hss-opus.ub.ruhr-uni-bochum.de/opus4/frontdoor/index/index/docId/6514 (accessed on 4 April 2023).
- Bakker, K.J.; de Boer, F.; Kuiper, J.C. Extensive independent research programs on second Heinenoord Tunnel and Botlek Rail Tunnel. In Proceedings of the Twelfth European Conference on Soil Mechanics and Geotechnical Engineering, Amsterdam, The Netherlands, 7–10 June 1999. [Google Scholar]
- Leca, E.; Dormieux, L. Upper and Lower Bound Solutions for the Face Stability of Shallow Circular Tunnels in Frictional Material. Géotechnique 1990, 40, 581–606. [Google Scholar] [CrossRef]
- Qin, S.; Xu, T.; Zhou, W.-H.; Bezuijen, A. Infiltration Behaviour and Microstructure of Filter Cake from Sand-Modified Bentonite Slurry. Transp. Geotech. 2023, 40, 100963. [Google Scholar] [CrossRef]
- Hou, C.; Pan, Q.; Xu, T.; Huang, F.; Yang, X. Three-Dimensional Tunnel Face Stability Considering Slurry Pressure Transfer Mechanisms. Tunn. Undergr. Space Technol. 2022, 125, 104524. [Google Scholar] [CrossRef]
- Zizka, Z.; Schoesser, B.; Thewes, M. Investigations on Transient Support Pressure Transfer at the Tunnel Face during Slurry Shield Drive Part 1: Case A—Tool Cutting Depth Exceeds Shallow Slurry Penetration Depth. Tunn. Undergr. Space Technol. 2021, 118, 104168. [Google Scholar] [CrossRef]

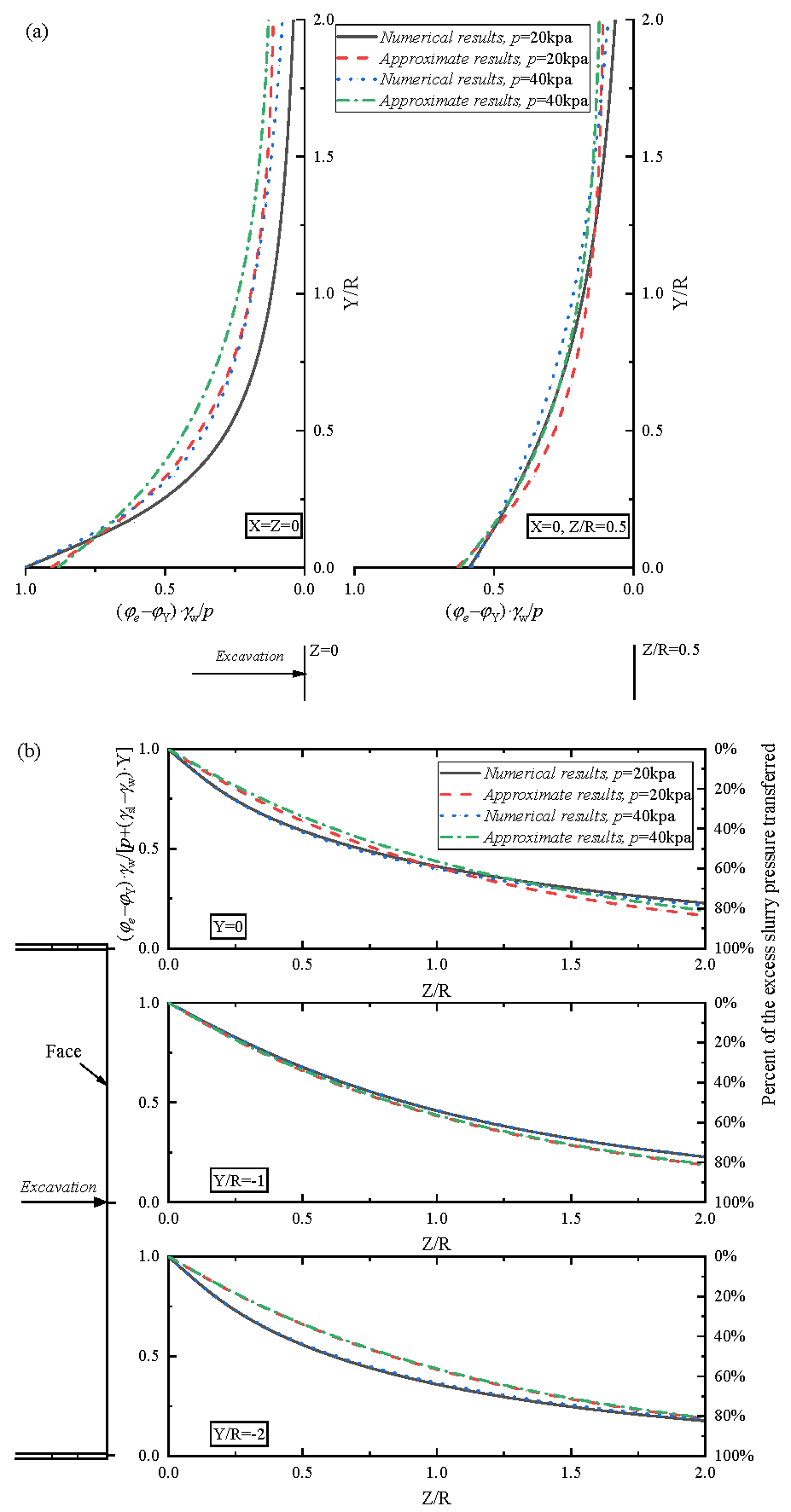

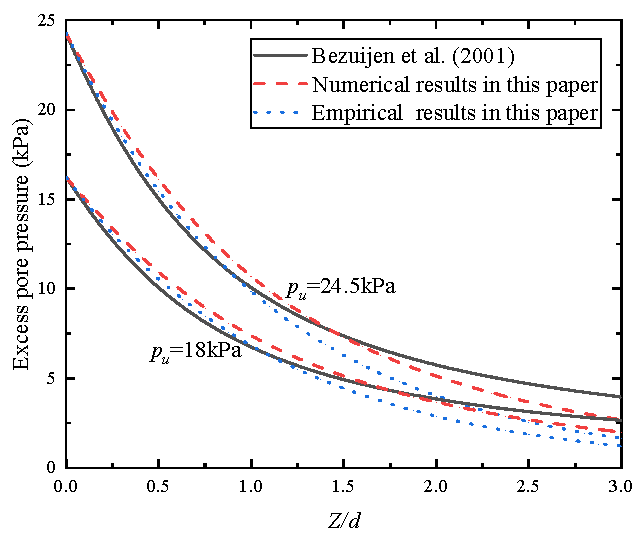
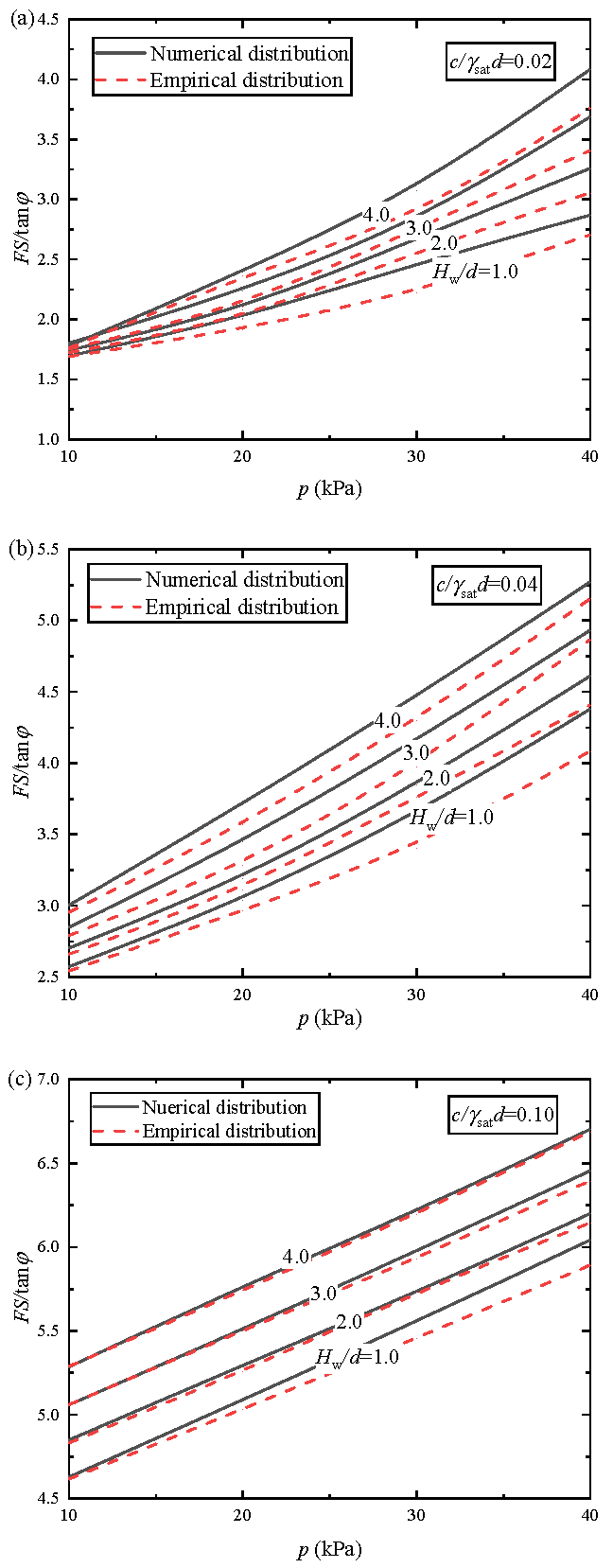
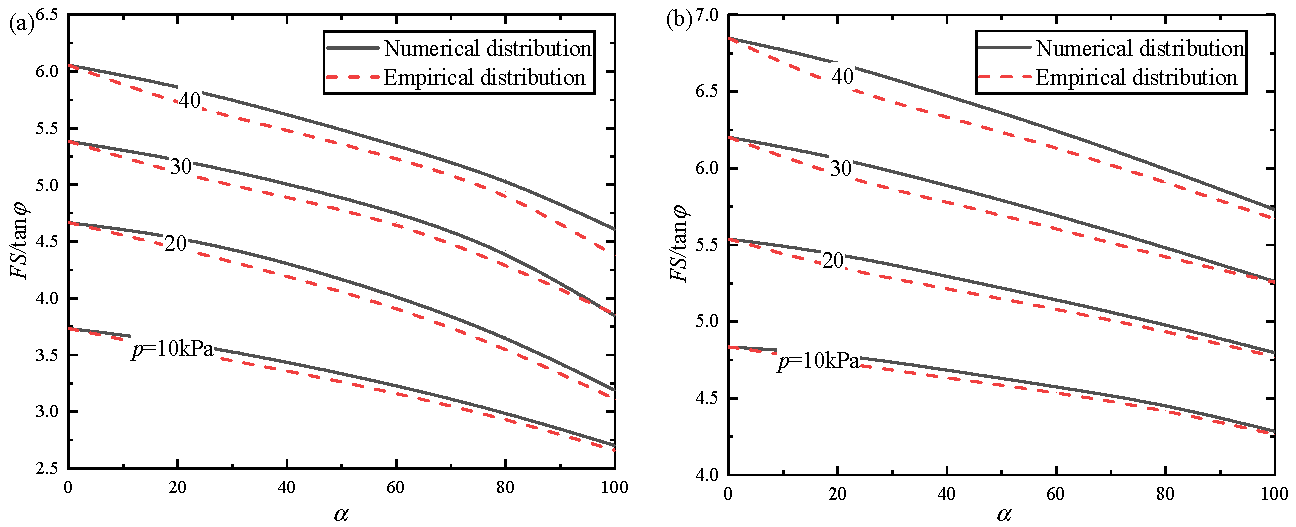
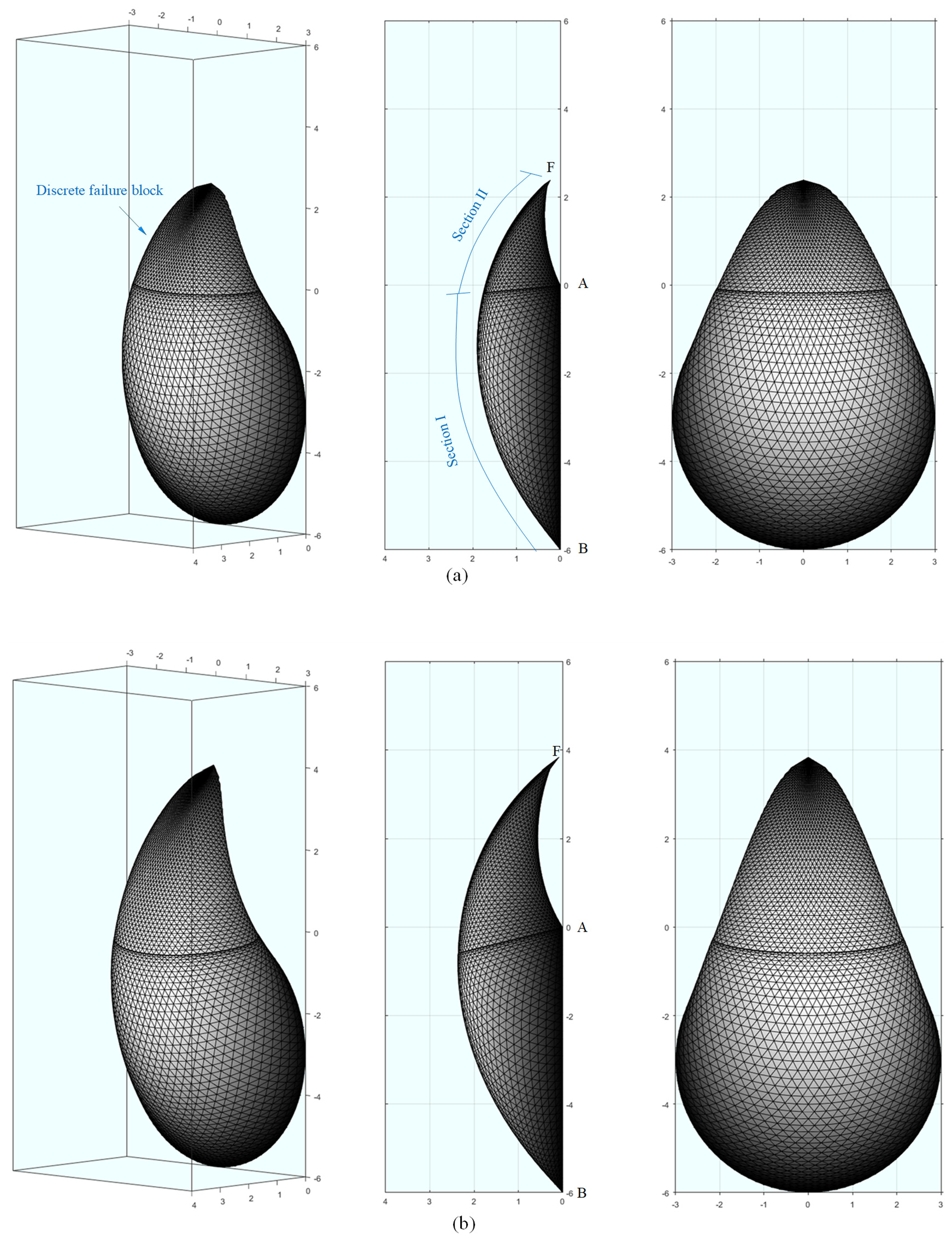
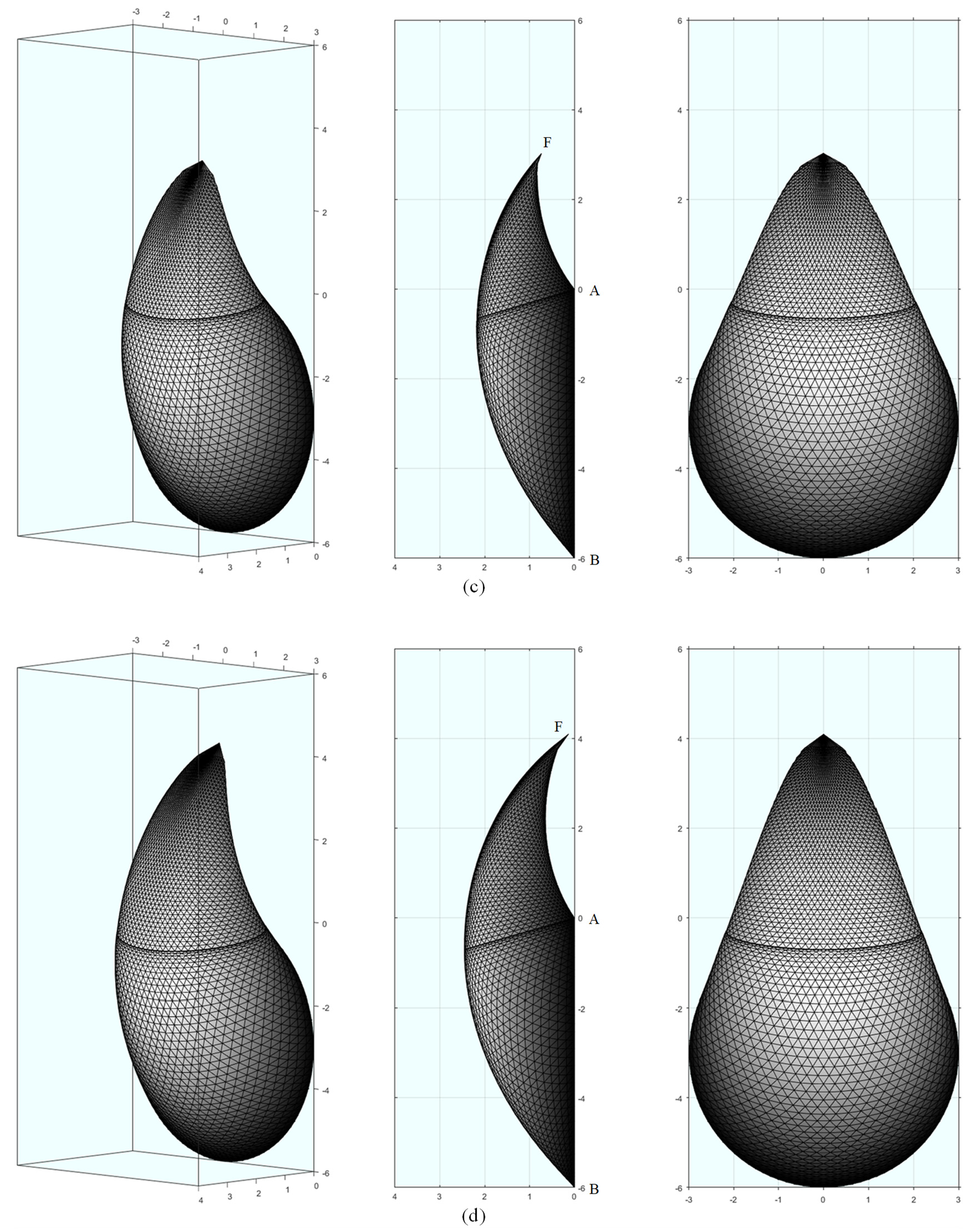


| Scenarios | Solution of Bezuijen et al. [31] | Presented Solution with Numerical Pore Pressure | Presented Solution with Empirical Pore Pressure |
|---|---|---|---|
| , , , | 1.00 | 1.00 | 0.97 |
| , , , | 1.00 | 0.97 | 0.95 |
| Parameters | p = 10 kPa | p = 20 kPa | p = 30 kPa | p = 40 kPa |
|---|---|---|---|---|
| 0.856 | 0.840 | 0.834 | 0.832 | |
| 2.969 | 2.213 | 1.940 | 1.801 | |
| 0.882 | 0.805 | 0.784 | 0.776 | |
| 0.758 | 2.039 | 3.193 | 4.295 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, J.; Zhao, S.; Wang, P.; Hou, C. Tunnel Face Stability Considering the Influence of Excess Slurry Pressure. Sustainability 2023, 15, 8230. https://doi.org/10.3390/su15108230
Zhong J, Zhao S, Wang P, Hou C. Tunnel Face Stability Considering the Influence of Excess Slurry Pressure. Sustainability. 2023; 15(10):8230. https://doi.org/10.3390/su15108230
Chicago/Turabian StyleZhong, Junhao, Shihe Zhao, Pengqin Wang, and Chuantan Hou. 2023. "Tunnel Face Stability Considering the Influence of Excess Slurry Pressure" Sustainability 15, no. 10: 8230. https://doi.org/10.3390/su15108230
APA StyleZhong, J., Zhao, S., Wang, P., & Hou, C. (2023). Tunnel Face Stability Considering the Influence of Excess Slurry Pressure. Sustainability, 15(10), 8230. https://doi.org/10.3390/su15108230








