Prioritization of Off-Grid Hybrid Renewable Energy Systems for Residential Communities in China Considering Public Participation with Basic Uncertain Linguistic Information
Abstract
:1. Introduction
2. Geographical Feature and Assessment of Load Demand
2.1. Study Area
2.2. Load Estimation
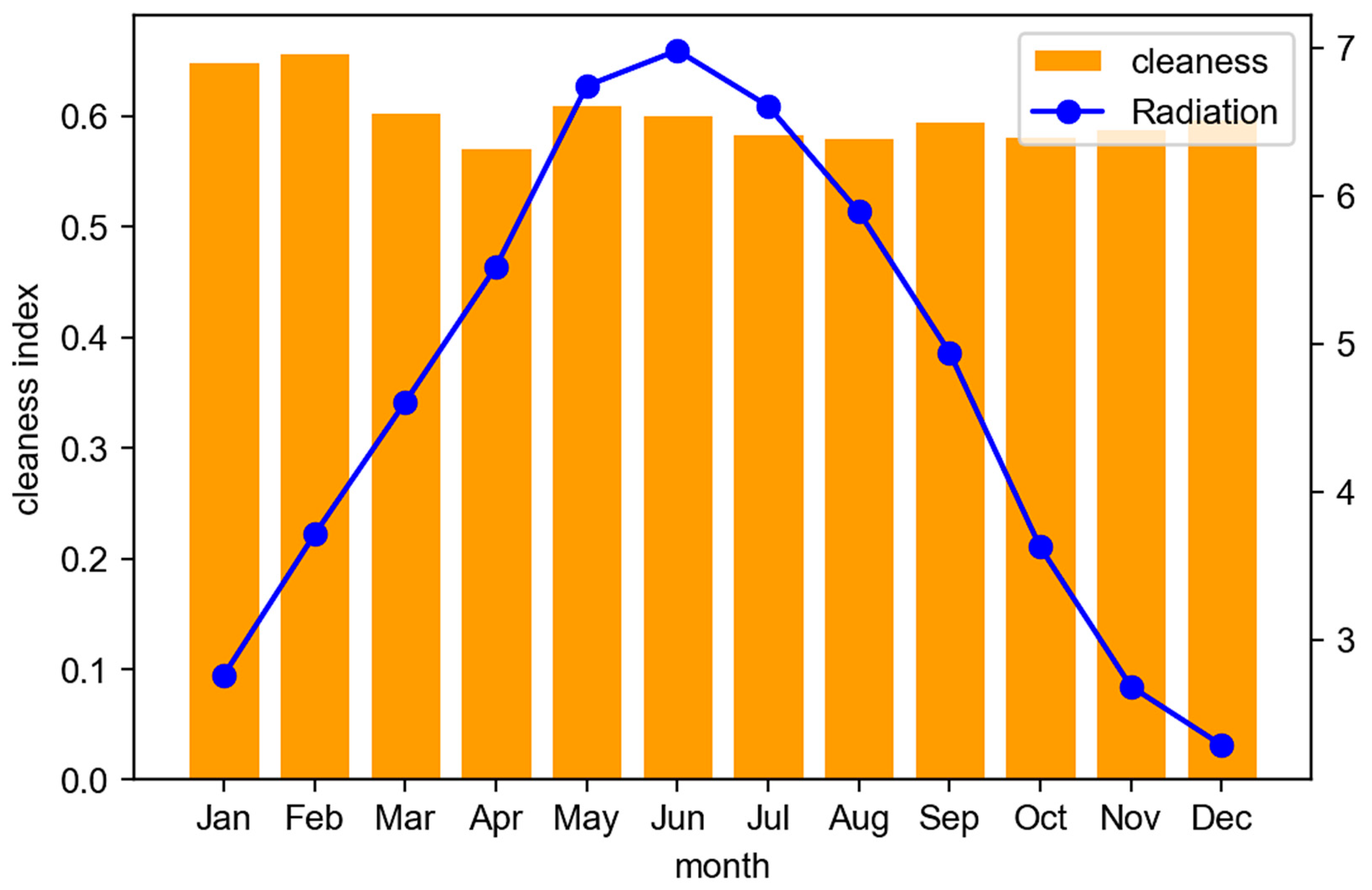
2.3. Resource Assessment
2.4. Component Configuration
2.5. Global Parameter Settings
2.6. Control Strategies
3. Optimization Method
3.1. Preliminary and Problem Description
3.2. Basic Uncertain Linguistic Information (BULI)
- if , then is smaller than ;
- if , then
- (a)
- if , then and represent the same information;
- (b)
- if , then is smaller then .
- (1)
- (2)
- (3)
3.3. Indicator System
3.3.1. Economic Indicators
- Initial investment (Q1)
- O&M cost (Q2)
- Levelized cost of energy (Q3)
3.3.2. Environmental Indicators
- Carbon emissions (Q4)
- Area requirement (Q5)
- Environmental impact (Q6)
3.3.3. Technology Indicators
- Energy variability (Q7)
- Technology Maturity (Q8)
3.3.4. Social Indicators
- Economic Contribution (Q9)
- Policy Support (Q10)
- Public Acceptance (Q11)
3.4. The BULI-EDAS Multi-Criteria Decision-Making Method
- Determination of indicator weights considering public preferences;
- The BULI-EDAS decision-making method.
3.4.1. Determination of Indicator Weights Considering Public Preferences
3.4.2. MCDM for Alternative Selection
4. Simulation Results and Discussion
4.1. Design Optimization Results
4.1.1. Feasible System Configuration
4.1.2. Qualitative Indicator Scores
4.2. Multicriteria Decision Results
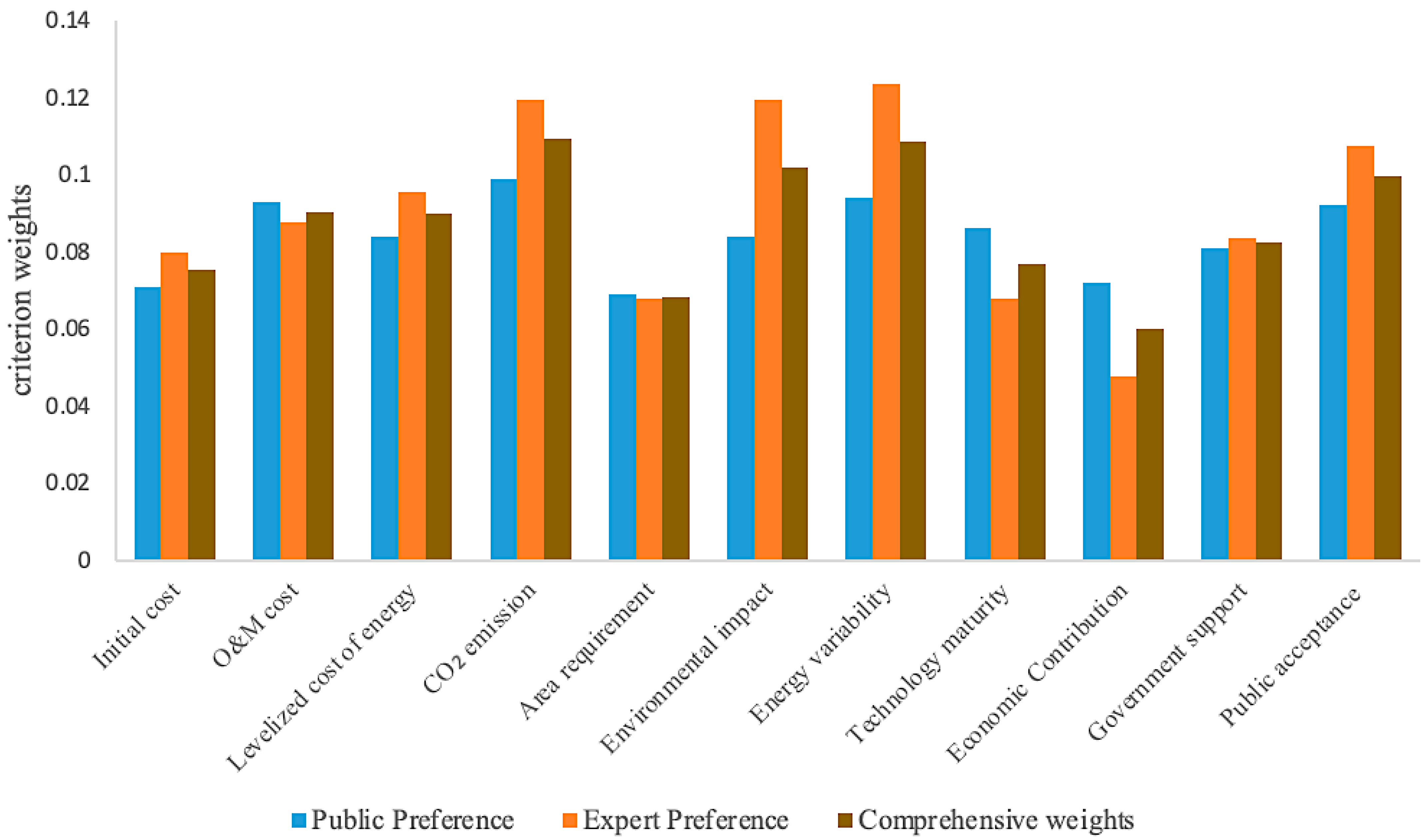
4.2.1. Criteria Weights
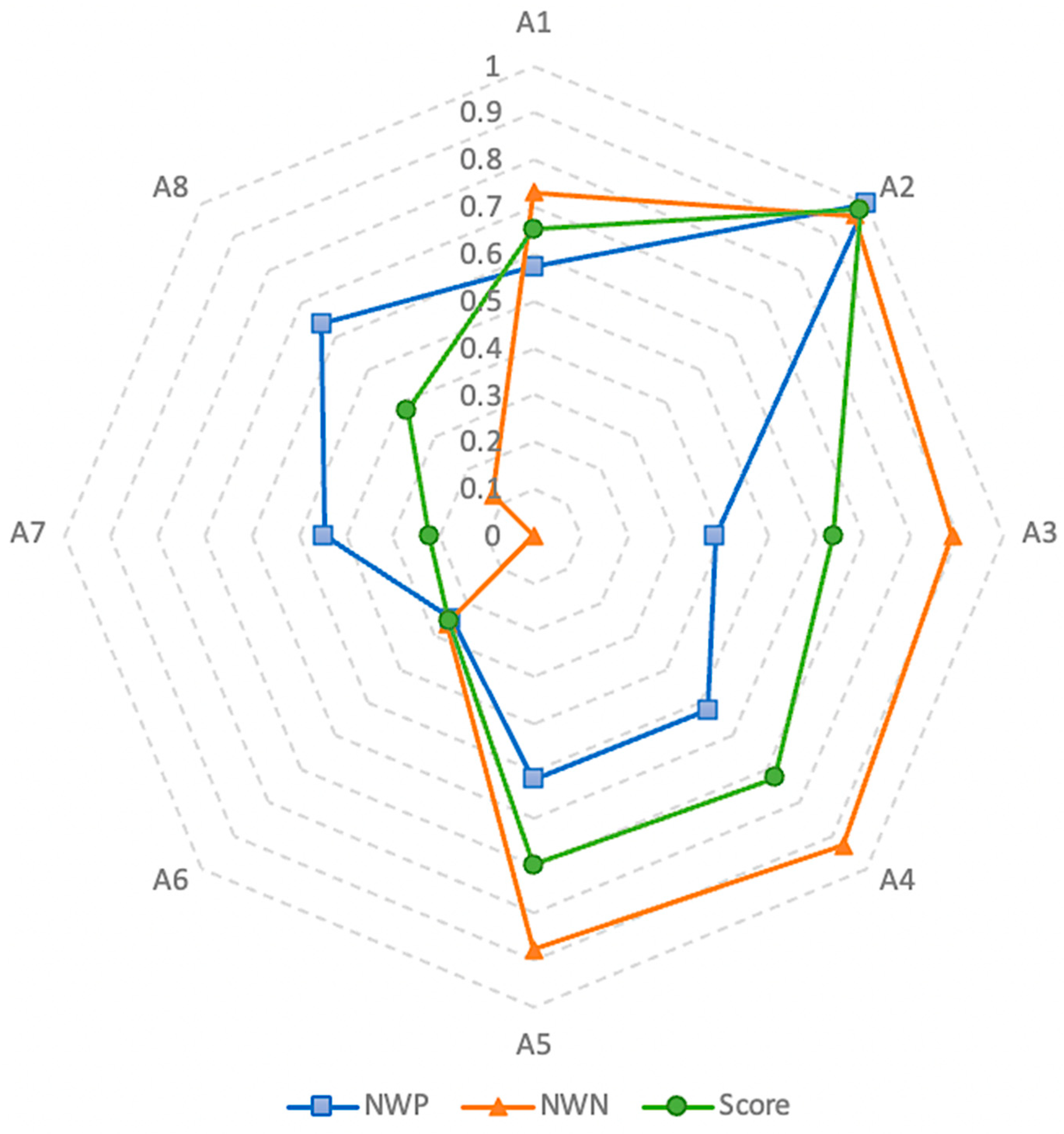
4.2.2. Alternative Scores
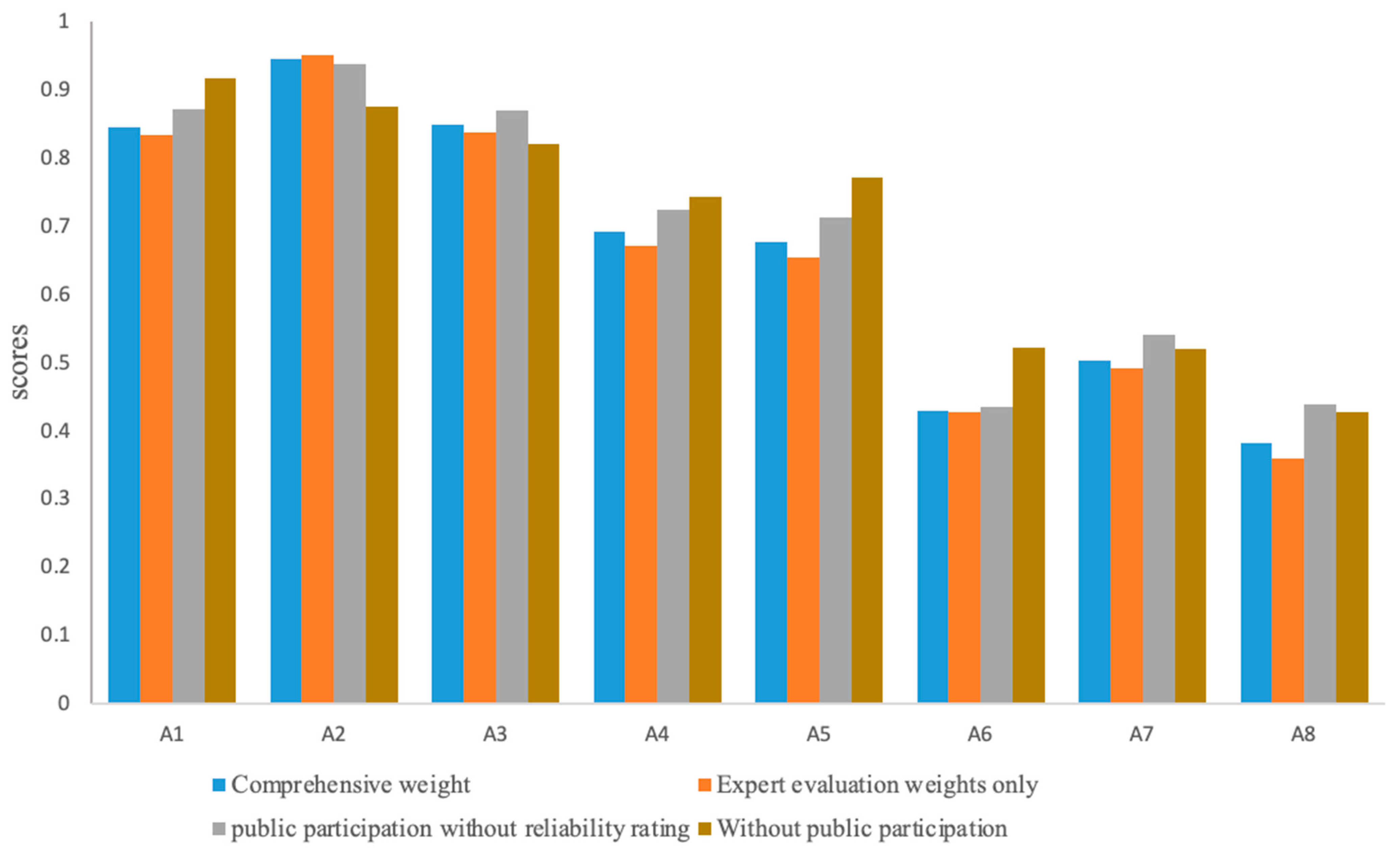
4.3. Comparative Analysis
4.4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Policy Support | Energy Variability | Environmental Impact | Economic Contribution | Technology Maturity | |
|---|---|---|---|---|---|
| Policy Support | Energy Variability | Environmental Impact | Economic Contribution | Technology Maturity | |
|---|---|---|---|---|---|
| Policy Support | Energy Variability | Environmental Impact | Economic Contribution | Technology Maturity | |
|---|---|---|---|---|---|
| Policy Support | Energy Variability | Environmental Impact | Economic Contribution | Technology Maturity | |
|---|---|---|---|---|---|
| Policy Support | Energy Variability | Environmental Impact | Economic Contribution | Technology Maturity | |
|---|---|---|---|---|---|
| Policy Support | Energy Variability | Environmental Impact | Economic Contribution | Technology Maturity | |
|---|---|---|---|---|---|
| Policy Support | Energy Variability | Environmental Impact | Economic Contribution | Technology Maturity | |
|---|---|---|---|---|---|
Appendix B
| ||||
|
|
|
|
|
| ||||
|
|
|
|
|
| ||||
|
|
|
|
|
| ||||
|
|
|
|
|
| ||||
|
|
|
|
|
| ||||
|
|
|
|
|
| ||||
|
|
|
|
|
| ||||
|
|
|
|
|
| ||||
|
|
|
|
|
| ||||
|
|
|
|
|
| ||||
|
|
|
|
|
| ||||
|
|
|
|
|
| ||||
| ( ) Please enter a number between 0 and 1 | ||||
| ||||
|
|
|
|
|
| ||||
| ( ) Please enter a number between 0 and 1 | ||||
| ||||
|
|
|
|
|
| ||||
| ( ) Please enter a number between 0 and 1 | ||||
| ||||
|
|
|
|
|
| ||||
| ( ) Please enter a number between 0 and 1 | ||||
| ||||
|
|
|
|
|
| ||||
| ( ) Please enter a number between 0 and 1 | ||||
| ||||
|
|
|
|
|
| ||||
| ( ) Please enter a number between 0 and 1 | ||||
| ||||
|
|
|
|
|
| ||||
| ( ) Please enter a number between 0 and 1 | ||||
| ||||
|
|
|
|
|
| ||||
| ( ) Please enter a number between 0 and 1 | ||||
| ||||
|
|
|
|
|
| ||||
| ( ) Please enter a number between 0 and 1 | ||||
| ||||
|
|
|
|
|
| ||||
| ( ) Please enter a number between 0 and 1 | ||||
| ||||
|
|
|
|
|
| ||||
| ( ) Please enter a number between 0 and 1 | ||||
| ||||
|
|
|
|
|
| ||||
| ( ) Please enter a number between 0 and 1 | ||||
| ||||
|
|
|
|
|
| ||||
| ( ) Please enter a number between 0 and 1 | ||||
| ||||
|
|
|
|
|
| ||||
| ( ) Please enter a number between 0 and 1 | ||||
| ||||
|
|
|
|
|
| ||||
| ( ) Please enter a number between 0 and 1 | ||||
| ||||
|
|
|
|
|
| ||||
| ( ) Please enter a number between 0 and 1 | ||||
| ||||
|
|
|
|
|
| ||||
| ( ) Please enter a number between 0 and 1 | ||||
Appendix C
| Component | Item | Value |
|---|---|---|
| PV | Model type | Generic flat plate PV |
| Rated power | 1 kW/panel | |
| Derating factor | 80% | |
| Lifetime | 25 years | |
| WT | Model type | Eocycle E010 |
| Rated power | 10 kw | |
| Cut-in velocity | 2.75 m/s | |
| Cut-off velocity | 20 m/s | |
| Rated velocity | 6.5 m/s | |
| Hub height | 16 m | |
| Lifetime | 20 years | |
| BioGen | Fuel curve slope | 2.0 L/h/kW output |
| Intercept coefficient | 0.10 L/h/kW rated | |
| Lifetime | 20,000 h | |
| Carbon monoxide | 2 g/kg of fuel | |
| Nitrogen oxides | 1.25 g/kg of fuel | |
| Available biomass | 1.4287 tones/day | |
| Gasification ratio | 0.7 kg | |
| Generator | Fuel curve intercept | 25.9 L/h |
| Fuel curve slope | 0.236 L/h/kw | |
| CO2 | 16.5 g/L fuel | |
| Fuel price | 1USD/L | |
| Lifetime | 20,000 h | |
| Battery | Battery type | Lead Acid |
| Minimal voltage | 12 V | |
| Minimal capacity | 200 Ah | |
| Convert | Capacity | 1 kW |
| Lifetime | 15 years | |
| Inverter input efficiency | 95% | |
| Relative capacity | 100% | |
| Rectifier input efficiency | 95% | |
| Electrolyzer | Capacity optimization | {0,100,200,300} |
| Lifetime | 15 years | |
| Efficiency | 85% | |
| Minimum load ratio | 0% |
References
- Hu, J.; Harmsen, R.; Crijns-Graus, W.; Worrell, E. Barriers to investment in utility-scale variable renewable electricity (VRE) generation projects. Renew. Energy 2018, 121, 730–744. [Google Scholar] [CrossRef]
- Madurai Elavarasan, R.; Afridhis, S.; Vijayaraghavan, R.; Subramaniam, U.; Nurunnabi, M. SWOT analysis: A framework for comprehensive evaluation of drivers and barriers for renewable energy development in significant countries. Energy Rep. 2020, 6, 1838–1864. [Google Scholar] [CrossRef]
- Umamaheswaran, S.; Rajiv, S. Financing large scale wind and solar projects—A review of emerging experiences in the Indian context. Renew. Sustain. Energy Rev. 2015, 48, 166–177. [Google Scholar] [CrossRef]
- Bahramara, S.; Moghaddam, M.P.; Haghifam, M.R. Optimal planning of hybrid renewable energy systems using HOMER: A review. Renew. Sustain. Energy Rev. 2016, 62, 609–620. [Google Scholar] [CrossRef]
- Cuesta, M.A.; Castillo-Calzadilla, T.; Borges, C.E. A critical analysis on hybrid renewable energy modeling tools: An emerging opportunity to include social indicators to optimise systems in small communities. Renew. Sustain. Energy Rev. 2020, 122, 109691. [Google Scholar] [CrossRef]
- Ye, B.; Zhou, M.; Yan, D.; Li, Y. Multi-Objective Decision-Making for Hybrid Renewable Energy Systems for Cities: A Case Study of Xiongan New District in China. Energies 2020, 13, 6223. [Google Scholar] [CrossRef]
- Niu, D.; Zhen, H.; Yu, M.; Wang, K.; Sun, L.; Xu, X. Prioritization of renewable energy alternatives for China by using a hybrid FMCDM methodology with uncertain information. Sustainability 2020, 12, 4649. [Google Scholar] [CrossRef]
- Qiu, T.; Faraji, J. Techno-economic optimization of a grid-connected hybrid energy system considering electric and thermal load prediction. Energy Sci. Eng. 2021, 9, 1313–1336. [Google Scholar] [CrossRef]
- Ullah, Z.; Elkadeem, M.R.; Kotb, K.M.; Taha, I.B.M.; Wang, S. Multi-criteria decision-making model for optimal planning of on/off grid hybrid solar, wind, hydro, biomass clean electricity supply. Renew. Energy 2021, 179, 885–910. [Google Scholar] [CrossRef]
- Dawood, F.; Shafiullah, G.M.; Anda, M. Stand-Alone Microgrid with 100% Renewable Energy: A Case Study with Hybrid Solar PV-Battery-Hydrogen. Sustainability 2020, 12, 2047. [Google Scholar] [CrossRef]
- Jackson, T.; Oliver, M. Wind energy comes of age: Paul Gipe John Wiley, New York, 1995. Energy Policy 1996, 24, 491–492. [Google Scholar] [CrossRef]
- Diógenes, J.R.F.; Claro, J.; Rodrigues, J.C.; Loureiro, M.V. Barriers to onshore wind energy implementation: A systematic review. Energy Res. Soc. Sci. 2020, 60, 101337. [Google Scholar] [CrossRef]
- Estévez, R.A.; Espinoza, V.; Ponce Oliva, R.D.; Vásquez-Lavín, F.; Gelcich, S. Multi-Criteria Decision Analysis for Renewable Energies: Research Trends, Gaps and the Challenge of Improving Participation. Sustainability 2021, 13, 3515. [Google Scholar] [CrossRef]
- Zelt, O.; Krüger, C.; Blohm, M.; Bohm, S.; Far, S. Long-Term Electricity Scenarios for the MENA Region: Assessing the Preferences of Local Stakeholders Using Multi-Criteria Analyses. Energies 2019, 12, 3046. [Google Scholar] [CrossRef]
- Zhou, J.; Wu, Y.; Dong, H.; Tao, Y.; Xu, C. Proposal and comprehensive analysis of gas-wind-photovoltaic-hydrogen integrated energy system considering multi-participant interest preference. J. Clean. Prod. 2020, 265, 121679. [Google Scholar] [CrossRef]
- Dong, H.; Wu, Y.; Zhou, J.; Chen, W. Optimal selection for wind power coupled hydrogen energy storage from a risk perspective, considering the participation of multi-stakeholder. J. Clean. Prod. 2022, 356, 131853. [Google Scholar] [CrossRef]
- Zhang, Z.; Liao, H.; Tang, A. Renewable energy portfolio optimization with public participation under uncertainty: A hybrid multi-attribute multi-objective decision-making method. Appl. Energy 2022, 307, 118267. [Google Scholar] [CrossRef]
- Mesiar, R.; Borkotokey, S.; Jin, L.; Kalina, M. Aggregation Under Uncertainty. IEEE Trans. Fuzzy Syst. 2018, 26, 2475–2478. [Google Scholar] [CrossRef]
- Herrera, F.; Martinez, L. A 2-tuple fuzzy linguistic representation model for computing with words. IEEE Trans. Fuzzy Syst. 2000, 8, 746–752. [Google Scholar] [CrossRef]
- Chen, Z.-S.; Martínez, L.; Chang, J.-P.; Wang, X.-J.; Xionge, S.-H.; Chin, K.-S. Sustainable building material selection: A QFD- and ELECTRE III-embedded hybrid MCGDM approach with consensus building. Eng. Appl. Artif. Intell. 2019, 85, 783–807. [Google Scholar] [CrossRef]
- Li, J.; Liu, P.; Li, Z. Optimal design and techno-economic analysis of a hybrid renewable energy system for off-grid power supply and hydrogen production: A case study of West China. Chem. Eng. Res. Des. 2022, 177, 604–614. [Google Scholar] [CrossRef]
- Li, X.; Gao, J.; You, S.; Zheng, Y.; Zhang, Y.; Du, Q.; Xie, M.; Qin, Y. Optimal design and techno-economic analysis of renewable-based multi-carrier energy systems for industries: A case study of a food factory in China. Energy 2022, 244, 123174. [Google Scholar] [CrossRef]
- Mudasar, R.; Kim, M.-H. Experimental study of power generation utilizing human excreta. Energy Convers. Manag. 2017, 147, 86–99. [Google Scholar] [CrossRef]
- Yang, Y.; Bao, W.; Xie, G.H. Estimate of restaurant food waste and its biogas production potential in China. J. Clean. Prod. 2019, 211, 309–320. [Google Scholar] [CrossRef]
- Barber, S.; Boller, S.; Nordborg, H. Feasibility study for 100% renewable energy microgrids in Switzerland. Wind Energ. Sci. Discuss. 2019, 16. [Google Scholar] [CrossRef]
- Chauhan, A.; Saini, R.P. Techno-economic feasibility study on Integrated Renewable Energy System for an isolated community of India. Renew. Sustain. Energy Rev. 2016, 59, 388–405. [Google Scholar] [CrossRef]
- Baruah, A.; Basu, M.; Amuley, D. Modeling of an autonomous hybrid renewable energy system for electrification of a township: A case study for Sikkim, India. Renew. Sustain. Energy Rev. 2021, 135, 110158. [Google Scholar] [CrossRef]
- Rad, M.A.V.; Ghasempour, R.; Rahdan, P.; Mousavi, S.; Arastounia, M. Techno-economic analysis of a hybrid power system based on the cost-effective hydrogen production method for rural electrification, a case study in Iran. Energy 2020, 190, 116421. [Google Scholar] [CrossRef]
- Akhtari, M.R.; Baneshi, M. Techno-economic assessment and optimization of a hybrid renewable co-supply of electricity, heat and hydrogen system to enhance performance by recovering excess electricity for a large energy consumer. Energy Convers. Manag. 2019, 188, 131–141. [Google Scholar] [CrossRef]
- Ramezanzade, M.; Saebi, J.; Karimi, H.; Mostafaeipour, A. A new hybrid decision-making framework to rank power supply systems for government organizations: A real case study. Sustain. Energy Technol. Assess. 2020, 41, 100779. [Google Scholar] [CrossRef]
- Jing, R.; Wang, M.; Brandon, N.; Zhao, Y. Multi-criteria evaluation of solid oxide fuel cell based combined cooling heating and power (SOFC-CCHP) applications for public buildings in China. Energy 2017, 141, 273–289. [Google Scholar] [CrossRef]
- Li, T.; Li, A.; Guo, X. The sustainable development-oriented development and utilization of renewable energy industry—A comprehensive analysis of MCDM methods. Energy 2020, 212, 118694. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, T.; Gao, R.; Wu, C. Portfolio planning of renewable energy with energy storage technologies for different applications from electricity grid. Appl. Energy 2021, 287, 116562. [Google Scholar] [CrossRef]
- Saraswat, S.K.; Digalwar, A.; Yadav, S.S. Development of assessment model for selection of sustainable energy source in India: Hybrid fuzzy MCDM approach. In International Conference on Intelligent and Fuzzy Systems; Springer: Berlin/Heidelberg, Germany, 2020; pp. 649–657. [Google Scholar]
- Zhang, L.; Zhou, P.; Newton, S.; Fang, J.; Zhou, D.; Zhang, L. Evaluating clean energy alternatives for Jiangsu, China: An improved multi-criteria decision making method. Energy 2015, 90, 953–964. [Google Scholar] [CrossRef]
- Zavadskas, E.K. Multi-Criteria Inventory Classification Using a New Method of Evaluation Based on Distance from Average Solution (EDAS). Informatica 2015, 26, 435–451. [Google Scholar] [CrossRef]
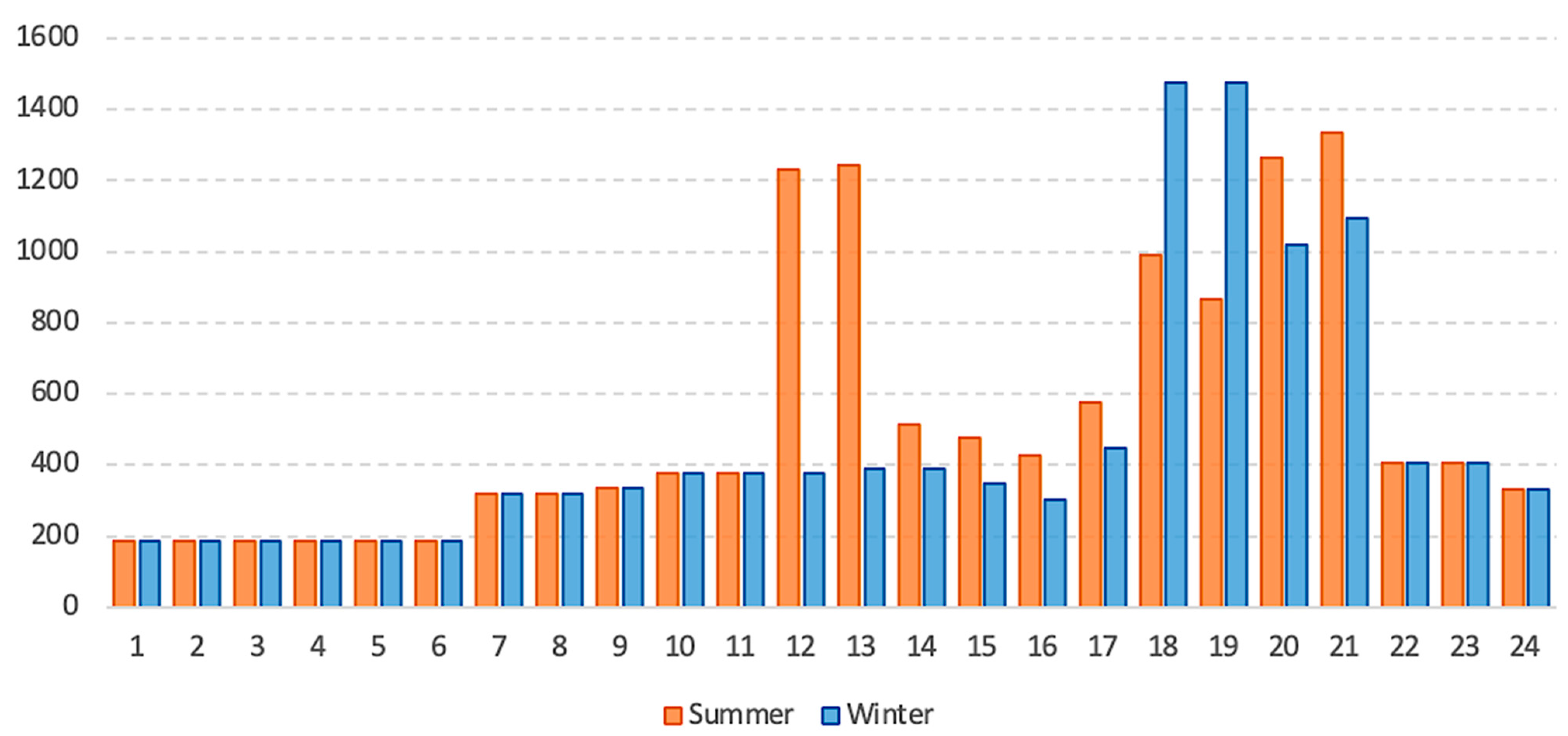





| Item | Consumption (W/Unit) | Qty (Unit) | Summer | Winter | ||
|---|---|---|---|---|---|---|
| Daily Operating Hours (h) | kWh/day | Daily Operating Hours (h) | kWh/day | |||
| Lights (CFLs) | 24 | 5 | 8 | 0.96 | 8 | 0.96 |
| TV | 60 | 1 | 4 | 0.24 | 4 | 0.24 |
| Cell phone charger | 10 | 3 | 2 | 0.06 | 1 | 0.03 |
| Refrigerator | 150 | 1 | 24 | 3.6 | 24 | 3.6 |
| Air conditioner | 800 | 2 | 2 | 3.2 | 0 | 0 |
| Fan | 50 | 2 | 5 | 0.5 | 0 | 0 |
| Water pumps | 175 | 1 | 1 | 0.175 | 2 | 0.35 |
| Iron | 1000 | 1 | 0 | 0 | 2 | 2 |
| Total load of household (kWh/day) Total public demand (kWh/day) | 8.97 | 8.42 | ||||
| 10,970.3 | 10,297.66 | |||||
| Public Demand | |||||
|---|---|---|---|---|---|
| Energy Consumption Sector | Item | Consumption (W/Unit) | Qty (Unit) | Daily Operating Hours Summer/Winter | Energy Demand (kWh) Summer/Winter |
| School | Lights (CFL) | 24 | 60 | 5/5 | 14.4/14.4 |
| Fan | 50 | 60 | 5/0 | 15/0 | |
| Computer | 20 | 30 | 8/8 | 60/60 | |
| Hospital | Lights (CFL) | 24 | 30 | 10/10 | 7.2/7.2 |
| Fan | 50 | 30 | 5/0 | 7.5/0 | |
| Computer | 250 | 18 | 8/8 | 36/36 | |
| Refrigerator | 150 | 5 | 24/24 | 18/18 | |
| Commercial/industrial | |||||
| Flourmill | 3750 | 4 | 8/8 | 120/120 | |
| Mini dairy plant | 5000 | 4 | 8/8 | 160/160 | |
| Shop | 20 | 10/8 | 99.2/99.2 | ||
| Agricultural use | |||||
| Agricultural: | Irrigation pump | 5000 | 8 | 6/6 | 240/240 |
| Crop threshing machine | 1400 | 8 | 3/3 | 33.6/33.6 | |
| Lights (CFL) | 24 | 10 | 6/6 | 1.44/1.44 | |
| Total Energy demand (kWh/day) | 812.34/789.84 | ||||
| Type of Raw Material | Number of Heads | Raw Material Available per Head per Day (kg) | Collection Coefficient | Daily Total Biomass Production (ton) |
|---|---|---|---|---|
| Human Excreta | 3140 | 0.35 | 0.7 | 0.7693 |
| Kitchen Waste | 3140 | 0.3 | 0.7 | 0.6594 |
| Total Biomass Production | 1.4287 |
| Component | Area Required | Ref. |
|---|---|---|
| PV System | 180 W/m2 | [24] |
| Wind Turbine | 0.92 m2/turbine | [25] |
| Biogas System | 13.44 m2/kW | [25] |
| Battery | 0.095 m2/unit | [26] |
| Converter | 464 m2/unit | [26] |
| Component | Capital (USD) | Replacement (USD) | Maintenance (USD) | Lifetime | Ref. |
|---|---|---|---|---|---|
| Diesel generator | 300/kw | 300/kw | 0.01/h | 90,000 h | [27] |
| Wind Turbine | 20,000/turbine | 18,000/turbine | 600/year | 20 years | [10] |
| PV System | 900/kw | 850/kw | 10/year | 20 years | [21] |
| Hydrogen Tank | 600/kg | 600/kg | 10/year | 20 years | [28] |
| Electrolyzer | 1500/kw | 1500/kw | 0.05/h | 10 years | [28] |
| Biogas System | 1500/kw | 1500/kw | 0.01/h | 200 h | [10] |
| Boiler | 54/kw | 54/kw | 0/kw | 20 years | [29] |
| Converter | 300/kw | 300/kw | 0/kw | 15 years | [29] |
| Battery | 500/kw | 500/kw | 0/hour | 15 years | [21] |
| System Parameter Setting | |
|---|---|
| Interest Rate | 8% |
| Inflation Rate | 2% |
| Carbon Price | 3 USD/t |
| Project Life | 25 years |
| Annual Capacity Shortage | 0% |
| Dimensions | Indicator | Attribute Type | Ref. |
|---|---|---|---|
| Economy | Initial cost (Q1) | Quantitative | [30] |
| O&M cost (Q2) | Quantitative | [27] | |
| Levelized cost of energy (Q3) | Quantitative | [31] | |
| Environment | CO2 emissions (Q4) | Quantitative | [30] |
| Area requirement (Q5) | Quantitative | [27] | |
| Environmental impact (Q6) | Qualitative | [32] | |
| Technology | Energy variability (Q7) | Qualitative | [32] |
| Technology maturity (Q8) | Qualitative | [33] | |
| Society | Economic contribution (Q9) | Qualitative | [16] |
| Policy support (Q10) | Qualitative | [7,34] | |
| Public acceptance (Q11) | Qualitative | [35] |
| Alternative | PV (kW) | EO10 (10 kW) | Gen (kW) | Bio (kW) | 1 kWh LA | Electrolyzer (kW) | HTank (kg) | Converter (kW) |
|---|---|---|---|---|---|---|---|---|
| A1 | 1453.84 | 96 | 300 | 18,441 | 100 | 150 | 1356 | |
| A2 | 1005.14 | 80 | 1700 | 300 | 16,371 | 200 | 150 | 1327 |
| A3 | 1231.79 | 79 | 1700 | 17,188 | 200 | 150 | 1633 | |
| A4 | 108 | 1700 | 300 | 14,969 | 200 | 200 | 1268 | |
| A5 | 136 | 1700 | 15,796 | 100 | 200 | 1496 | ||
| A6 | 13,915.17 | 200 | 21,733 | 200 | 50 | 1658 | ||
| A7 | 1700 | 100 | 629 | 100 | 300 | 253 | ||
| A8 | 1700 | 1145 | 100 | 50 | 200 |
| Alternative | COE (USD/kWh) | Initial Capital (USD) | O&M (USD/yr) | CO2 (kg/yr) | Area (m2) |
|---|---|---|---|---|---|
| A1 | 0.123 | 5,072,642 | 87,581.09 | 454.149 | 84,171.53 |
| A2 | 0.126 | 5,244,210 | 86,301.13 | 45,305.56 | 75,108.58 |
| A3 | 0.129 | 5,257,085 | 79,652.28 | 66,507.76 | 75,144.60 |
| A4 | 0.133 | 4,858,919 | 106,969.8 | 139,374.3 | 80,255.15 |
| A5 | 0.139 | 5,078,761 | 104,909.4 | 161,908.8 | 88,975.04 |
| A6 | 0.317 | 14,401,370 | 161,052.1 | 41.655 | 79,879.87 |
| A7 | 0.523 | 1,387,371 | 441,537.8 | 3,422,660 | 378.26 |
| A8 | 0.553 | 1,147,346 | 460,347.8 | 3,671,213 | 134.28 |
| Government Support | Energy Variability | Environmental Impact | Economic Contribution | Technology Maturity | |
|---|---|---|---|---|---|
| Government Support | Energy Variability | Environmental Impact | Economic Contribution | Technology Maturity | |
|---|---|---|---|---|---|
| A1 | |||||
| A2 | |||||
| A3 | |||||
| A4 | |||||
| A5 | |||||
| A6 | |||||
| A7 | |||||
| A8 |
| Criterion | Public Preference | Expert Preference | Comprehensive Weights |
|---|---|---|---|
| Initial cost (Q1) | 0.071 | 0.07968 | 0.07534 |
| O&M cost (Q2) | 0.093 | 0.08764 | 0.09032 |
| Levelized cost of energy (Q3) | 0.084 | 0.0956 | 0.0898 |
| CO2 emissions (Q4) | 0.099 | 0.1195 | 0.10925 |
| Area requirement (Q5) | 0.069 | 0.06772 | 0.06836 |
| Environmental impact (Q6) | 0.084 | 0.1195 | 0.10175 |
| Energy variability (Q7) | 0.094 | 0.1235 | 0.10875 |
| Technology maturity | 0.086 | 0.06772 | 0.07686 |
| Economic contribution (Q9) | 0.072 | 0.0478 | 0.0599 |
| Policy support (Q10) | 0.081 | 0.08366 | 0.08233 |
| Public acceptance (Q11) | 0.092 | 0.1075 | 0.09975 |
| Alternative | Weighted Sum of PDA | Weighted Sum of NDA | Weighted Normalized PDA | Weighted Normalized NDA | EDAS SCORE | Rank |
|---|---|---|---|---|---|---|
| A1 | 0.1657 | 0.0595 | 0.8539 | 0.8354 | 0.8447 | 3 |
| A2 | 0.1940 | 0.0397 | 1 | 0.8901 | 0.9450 | 1 |
| A3 | 0.1512 | 0.02934 | 0.7796 | 0.9190 | 0.8493 | 2 |
| A4 | 0.1022 | 0.05176 | 0.5268 | 0.8569 | 0.6918 | 4 |
| A5 | 0.1139 | 0.08533 | 0.5869 | 0.7642 | 0.6755 | 5 |
| A6 | 0.0905 | 0.22024 | 0.4667 | 0.3914 | 0.4291 | 7 |
| A7 | 0.1479 | 0.27477 | 0.7626 | 0.2407 | 0.5017 | 6 |
| A8 | 0.1483 | 0.36192 | 0.7644 | 0 | 0.3822 | 8 |
| Method | Ranking of Alternatives |
|---|---|
| Comprehensive weights | A2 > A3 > A1 > A4 > A5 > A7 > A6 > A8 |
| Expert evaluation weights only | A2 > A3 > A1 > A4 > A5 > A7 > A6 > A8 |
| Public participation without reliability rating | A2 > A1 > A3 > A4 > A5 > A7 > A8 > A6 |
| Without public participation | A1 > A2 > A3 > A5 > A4 > A6 > A7 > A8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Chen, X.; Yang, Y.; Yang, J.; Chen, J. Prioritization of Off-Grid Hybrid Renewable Energy Systems for Residential Communities in China Considering Public Participation with Basic Uncertain Linguistic Information. Sustainability 2023, 15, 8454. https://doi.org/10.3390/su15118454
Liu L, Chen X, Yang Y, Yang J, Chen J. Prioritization of Off-Grid Hybrid Renewable Energy Systems for Residential Communities in China Considering Public Participation with Basic Uncertain Linguistic Information. Sustainability. 2023; 15(11):8454. https://doi.org/10.3390/su15118454
Chicago/Turabian StyleLiu, Limei, Xinyun Chen, Yi Yang, Junfeng Yang, and Jie Chen. 2023. "Prioritization of Off-Grid Hybrid Renewable Energy Systems for Residential Communities in China Considering Public Participation with Basic Uncertain Linguistic Information" Sustainability 15, no. 11: 8454. https://doi.org/10.3390/su15118454
APA StyleLiu, L., Chen, X., Yang, Y., Yang, J., & Chen, J. (2023). Prioritization of Off-Grid Hybrid Renewable Energy Systems for Residential Communities in China Considering Public Participation with Basic Uncertain Linguistic Information. Sustainability, 15(11), 8454. https://doi.org/10.3390/su15118454







