Hybrid Renewable Energy System Design: A Machine Learning Approach for Optimal Sizing with Net-Metering Costs
Abstract
:1. Introduction
- The proposal of a new data-driven framework integrating AI and hybrid metaheuristics for HRES capacity optimization;
- The development and comparison of various ML models for the prediction of solar radiation, air temperature and LD;
- A comparison of multiple hybrid optimization algorithms for the optimal capacity sizing of HRES, most of which have not been previously investigated for this application.
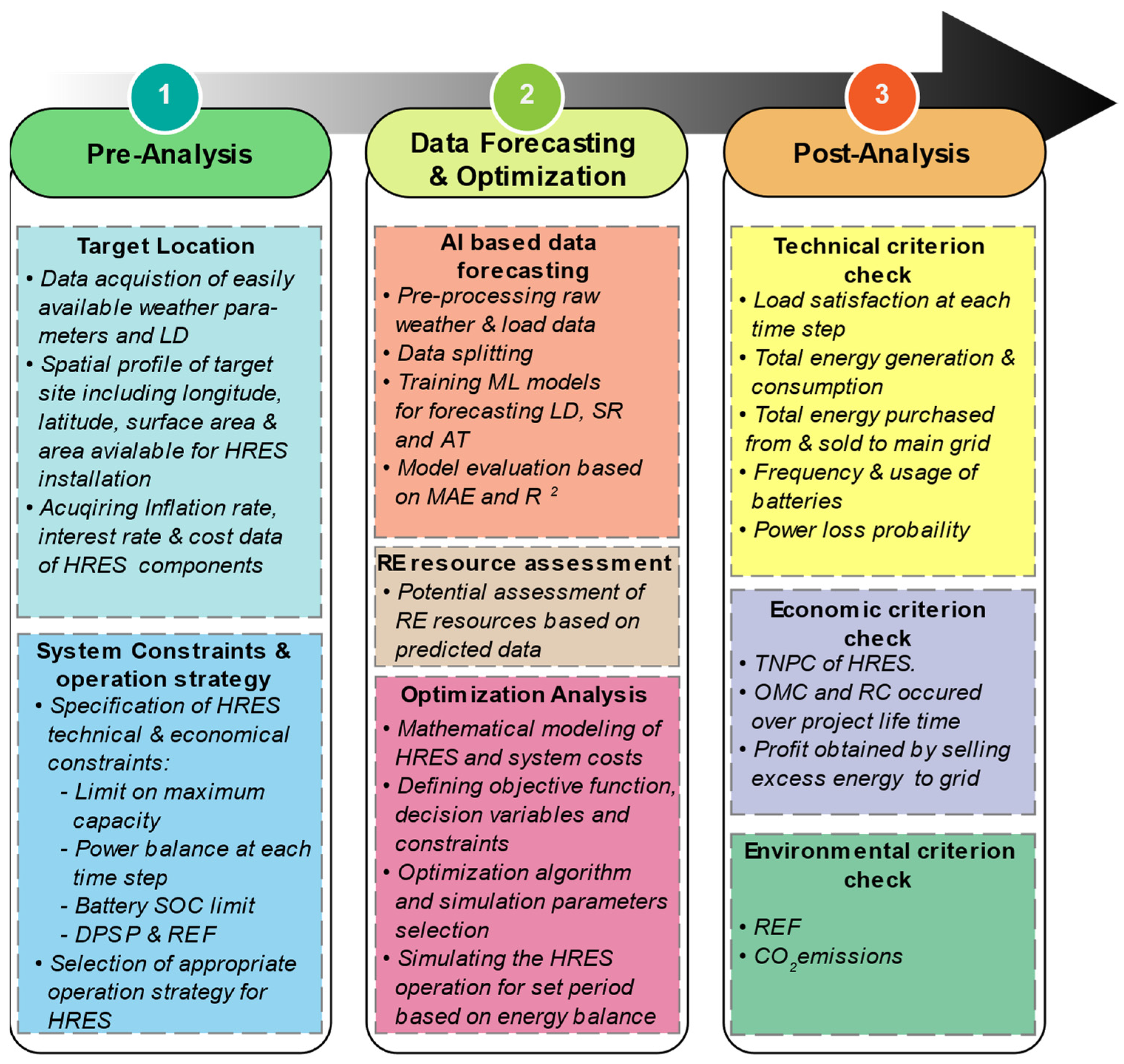
2. Materials and Methods
2.1. Problem Statement and Objective of Study
2.2. Description of the Target Location
2.3. Machine Learning Framework
2.3.1. Data Collection
2.3.2. Data Pre-Processing
2.3.3. Machine Learning Algorithms, Hyperparameter Tuning and Performance Evaluation
3. Mathematical Modeling of Renewable Energy System Components
3.1. PV System Model
3.2. Battery ESS Model
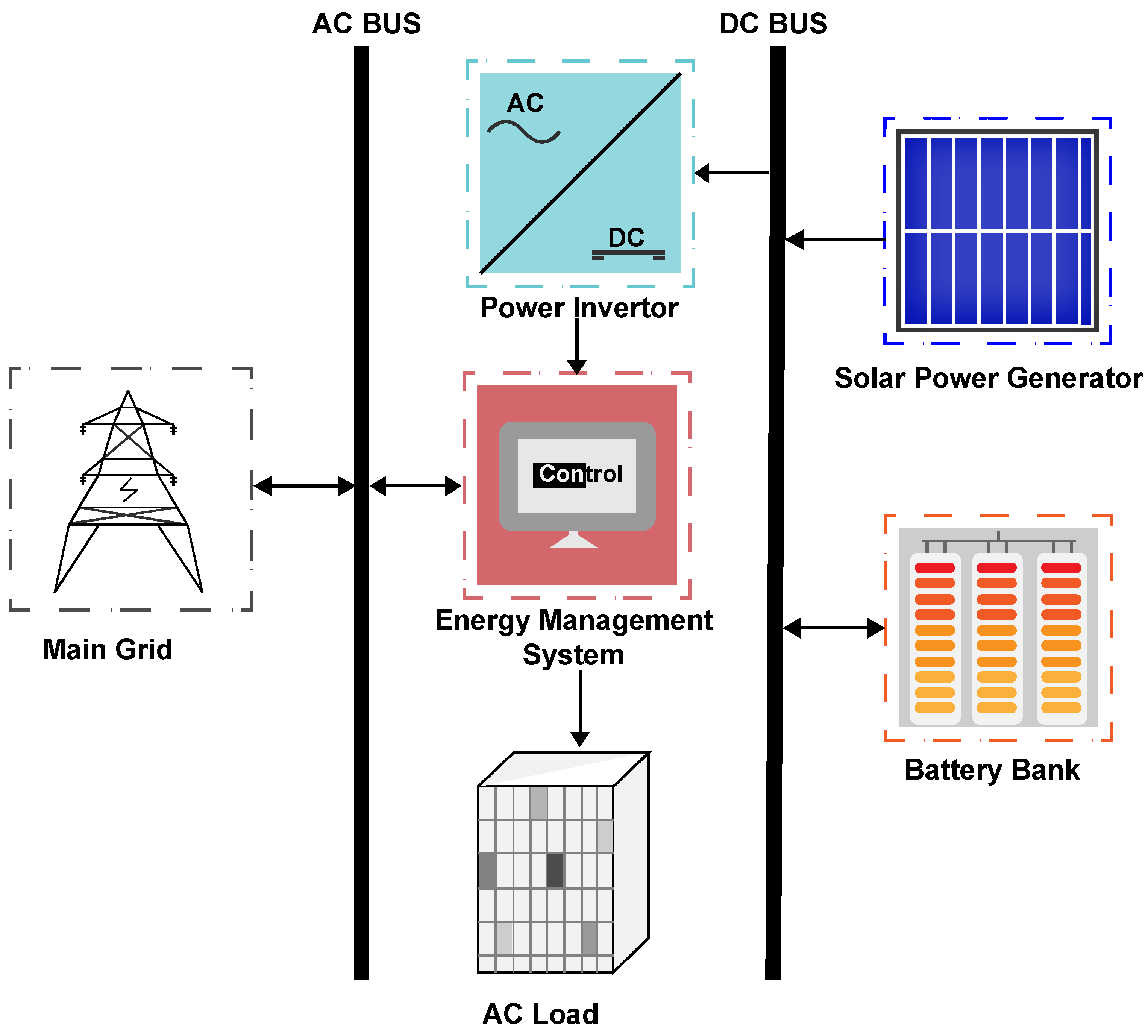
3.3. Inverter Model
3.4. Grid Interaction Model
3.5. Techno-Enviro-Economic Performance Evaluation Criteria
3.6. Hybrid Optimization Algorithms
3.7. Optimization Problem Formulation
3.8. Energy Management Strategy
- 1.
- When TREG is greater than or equal to the LD, then, after satisfying the LD,
- (a)
- The remaining energy is first utilized to charge the battery pack;
- (b)
- The excess energy is then sold to the main electric grid.
- 2.
- When the LD becomes greater than TREG at t,
- (a)
- The battery is discharged to satisfy the LD fully or partially until it reaches the minimum capacity limit;
- (b)
- If discharging the battery pack cannot satisfy the LD, the remaining LD is satisfied by purchasing electricity from the main grid.
4. Results and Discussion
4.1. Performance Assessment of Ensemble Methods for Forecasting of Solar Radiation, Air Temperature and Load Demand
4.2. Comparative Performance Evaluation of Optimization Algorithms
4.3. Optimal Sizing of HRES
4.4. Operation Simulation Analysis of Optimal HRES
4.5. Comparison of Sizing Results against 15-Year and 1-Year Scenarios
5. Conclusions
- The novel data-driven HRES capacity optimization framework considered as the first scenario proposed in this study was found to result in a different optimal HRES size compared to the second scenario. The difference is reflected by the obtained values of the HRES constraints at the end of optimization, including REF and DRPSP, with values of 30% and 0.0128, respectively, for the first scenario. On the other hand, the system obtained through the second scenario resulted in a 25% REF, which was 5% less than the set limit, as well as a DRPSP of 0.0134, which was larger than the set limit of 0.0130. In addition, the first system also purchased 4% less and sold 86% more power to the main electrical grid, respectively, with 4% less CO2 emissions.
- The comparison of results found that when optimizing the HRES capacity, it is better to utilize simulation input data spanning the whole life of the targeted HRES. However, further investigation is required to confirm whether the proposed data-driven approach provides more realistic HRES sizing results than the conventional yearly-based simulations.
- The comparative performance analysis of the optimization algorithms showed that the dFDBMRFO algorithm is the best in terms of computational time, while the CPSOGSA algorithm finds the lowest HRES cost within a reasonable time.
- The optimal HRES, under the constraint of DRPSPmax of 1.3%, consists of 305 PV panels, 21 batteries and 10 power inverters, with a TNPC of USD 1.46 million, including grid interaction costs. The proposed system satisfies all the constraints such that the values of DRPSP and REF obtained are 0.013 and 0.3, respectively, both of which satisfy the specified limits.
- The comparison of various proposed HRES based on the environmental impact and power supply reliability revealed that minimizing the environmental impact increases the HRES capacity and corresponding TNPC by as much as 25%. The TNPC value almost triples for HRES with zero probability of a deficient power supply over the project lifespan.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Prediction Target | Input Features | |||
|---|---|---|---|---|
| Basic Variables | Timestamp Derived Variables | Time Difference and Lag Variables | Statistical Variables | |
| SR | AT H WS WD SS TC | Hour of day | SRC(t) SRC(t − 1) SRC(t − 2) | - |
| AT | GT AT H | Hour of day | AT(t − 1) AT(t − 2) AT(t − 3) | GT/DPT Rolling mean of T |
| LD | AT H Pr | Hour of day Day of year Hour angle | - | SR expanding mean, H expanding mean, Cosine (day of year) |
| ML Models | Hyperparameters | SR Prediction Task | AT Prediction Task | LD Prediction Task |
|---|---|---|---|---|
| XGB | Colsample by tree | 0.06 | 0.96 | 0.33 |
| Gamma | 0.85 | 0.23 | 0.46 | |
| Learning rate | 0.03 | 0.02 | 0.10 | |
| Max. depth | 8.00 | 2.00 | 2.00 | |
| Min. child weight | 7.00 | 9.00 | 8.00 | |
| Estimators (102) | 13.00 | 80.00 | 90.00 | |
| Objective function | Squared error | Absolute error | Absolute error | |
| Alpha | 0.99 | 0.78 | 0.11 | |
| Lambda | 0.50 | 0.78 | 0.45 | |
| Subsample | 0.44 | 0.83 | 0.10 | |
| LGBM | Bagging fraction | 0.60 | 0.50 | 0.40 |
| Bagging frequency (102) | 1.00 | 4.00 | 5.00 | |
| Boosting | Dart | Dart | Gbdt | |
| Feature fraction | 0.80 | 0.70 | 0.37 | |
| Learning rate | 0.10 | 0.10 | 0.14 | |
| Max. depth | 10.00 | 40.00 | 10.00 | |
| Min. data in leaf | 15.00 | 50.00 | 20.00 | |
| Estimators (102) | 50.00 | 10.00 | 70.00 | |
| Number of leaves | 45.00 | 60.00 | 20.00 | |
| Objective function | Mean absolute error | Mean absolute error | - | |
| CBR | Bagging temperature | 0.16 | 0.06 | 0.95 |
| Border count (102) | 1.90 | 2.44 | 1.48 | |
| Depth | 10.00 | 4.00 | 6.00 | |
| Iterations (102) | 10.00 | 7.00 | 3.00 | |
| L2 leaf | 7.28 | 9.87 | 8.12 | |
| Learning rate | 0.07 | 0.38 | 0.04 | |
| Od type | IncToDec | Iter | IncToDec | |
| Od wait | 15.00 | 22.00 | 28.00 | |
| Random strength | 3.57 | 1.53 | 51.50 |
References
- United Nations Department of Economic and Social Affairs, Population Division. World Population Prospects 2022: Summary of Results; United Nations: New York, NY, USA, 2022; p. 52. [Google Scholar]
- International Energy Agency. World Energy Outlook; IEA: Paris, France, 2021; p. 386. [Google Scholar]
- Caetano, N.S.; Mata, T.M.; Martins, A.A.; Felgueiras, M.C. New Trends in Energy Production and Utilization. Energy Procedia 2017, 107, 7–14. [Google Scholar] [CrossRef]
- Capuano, D.L. International Energy Outlook 2018 (IEO2018); U.S. Energy Information Administration: Washington, DC, USA, 2018; p. 21.
- Clarke, B.; Otto, F.; Stuart-Smith, R.; Harrington, L. Extreme Weather Impacts of Climate Change: An Attribution Perspective. Environ. Res. Clim. 2022, 1, 012001. [Google Scholar] [CrossRef]
- Konisky, D.M.; Hughes, L.; Kaylor, C.H. Extreme Weather Events and Climate Change Concern. Clim. Chang. 2016, 134, 533–547. [Google Scholar] [CrossRef]
- International Energy Agency. Net Zero by 2050—A Roadmap for the Global Energy Sector; IEA: Paris, France, 2021; p. 224. [Google Scholar]
- Stram, B.N. Key Challenges to Expanding Renewable Energy. Energy Policy 2016, 96, 728–734. [Google Scholar] [CrossRef]
- Ciupageanu, D.-A.; Barelli, L.; Lazaroiu, G. Real-Time Stochastic Power Management Strategies in Hybrid Renewable Energy Systems: A Review of Key Applications and Perspectives. Electr. Power Syst. Res. 2020, 187, 106497. [Google Scholar] [CrossRef]
- Sinsel, S.R.; Riemke, R.L.; Hoffmann, V.H. Challenges and Solution Technologies for the Integration of Variable Renewable Energy Sources—A Review. Renew. Energy 2020, 145, 2271–2285. [Google Scholar] [CrossRef]
- Adnan, M.; Tariq, M.; Zhou, Z.; Poor, H.V. Load Flow Balancing and Transient Stability Analysis in Renewable Integrated Power Grids. Int. J. Electr. Power Energy Syst. 2019, 104, 744–771. [Google Scholar] [CrossRef]
- IRENA; ILO. Renewable Energy and Jobs Annual Review; International Renewable Energy Agency International Labour Organization: Abu Dhabi, Geneva, 2021; ISBN 978-92-9260-364-9. [Google Scholar]
- Alberizzi, J.C.; Frigola, J.M.; Rossi, M.; Renzi, M. Optimal Sizing of a Hybrid Renewable Energy System: Importance of Data Selection with Highly Variable Renewable Energy Sources. Energy Convers. Manag. 2020, 223, 113303. [Google Scholar] [CrossRef]
- Memon, S.A.; Patel, R.N. An Overview of Optimization Techniques Used for Sizing of Hybrid Renewable Energy Systems. Renew. Energy Focus 2021, 39, 1–26. [Google Scholar] [CrossRef]
- Siddaiah, R. A Review on Planning, Configurations, Modeling and Optimization Techniques of Hybrid Renewable Energy Systems for off Grid Applications. Renew. Sustain. Energy Rev. 2016, 58, 376–396. [Google Scholar] [CrossRef]
- Kellogg, W.D.; Nehrir, M.H.; Venkataramanan, G.; Gerez, V. Generation Unit Sizing and Cost Analysis for Stand-Alone Wind, Photovoltaic, and Hybrid Wind/PV Systems. IEEE Trans. Energy Convers. 1998, 13, 70–75. [Google Scholar] [CrossRef]
- Diaf, S.; Notton, G.; Belhamel, M.; Haddadi, M.; Louche, A. Design and Techno-Economical Optimization for Hybrid PV/Wind System under Various Meteorological Conditions. Appl. Energy 2008, 85, 968–987. [Google Scholar] [CrossRef]
- Hocaoğlu, F.O.; Gerek, Ö.N.; Kurban, M. A Novel Hybrid (Wind–Photovoltaic) System Sizing Procedure. Sol. Energy 2009, 83, 2019–2028. [Google Scholar] [CrossRef]
- Al-falahi, M.D.A.; Jayasinghe, S.D.G.; Enshaei, H. A Review on Recent Size Optimization Methodologies for Standalone Solar and Wind Hybrid Renewable Energy System. Energy Convers. Manag. 2017, 143, 252–274. [Google Scholar] [CrossRef]
- Khan, T.; Yu, M.; Waseem, M. Review on Recent Optimization Strategies for Hybrid Renewable Energy System with Hydrogen Technologies: State of the Art, Trends and Future Directions. Int. J. Hydrogen Energy 2022, 47, 25155–25201. [Google Scholar] [CrossRef]
- Das, M.; Singh, M.A.K.; Biswas, A. Techno-Economic Optimization of an off-Grid Hybrid Renewable Energy System Using Metaheuristic Optimization Approaches—Case of a Radio Transmitter Station in India. Energy Convers. Manag. 2019, 185, 339–352. [Google Scholar] [CrossRef]
- Gazijahani, F.S.; Ravadanegh, S.N.; Salehi, J. Stochastic Multi-Objective Model for Optimal Energy Exchange Optimization of Networked Microgrids with Presence of Renewable Generation under Risk-Based Strategies. ISA Trans. 2018, 73, 100–111. [Google Scholar] [CrossRef]
- Ramli, M.A.M.; Bouchekara, H.R.E.H.; Alghamdi, A.S. Efficient Energy Management in a Microgrid with Intermittent Renewable Energy and Storage Sources. Sustainability 2019, 11, 3839. [Google Scholar] [CrossRef]
- Fares, D.; Fathi, M.; Mekhilef, S. Performance Evaluation of Metaheuristic Techniques for Optimal Sizing of a Stand-Alone Hybrid PV/Wind/Battery System. Appl. Energy 2022, 305, 117823. [Google Scholar] [CrossRef]
- Kharrich, M.; Kamel, S.; Hassan, M.H.; ElSayed, S.K.; Taha, I.B.M. An Improved Heap-Based Optimizer for Optimal Design of a Hybrid Microgrid Considering Reliability and Availability Constraints. Sustainability 2021, 13, 10419. [Google Scholar] [CrossRef]
- Guo, X.; Zhou, L.; Guo, Q.; Rouyendegh, B.D. An Optimal Size Selection of Hybrid Renewable Energy System Based on Fractional-Order Neural Network Algorithm: A Case Study. Energy Rep. 2021, 7, 7261–7272. [Google Scholar] [CrossRef]
- Sadollah, A.; Nasir, M.; Geem, Z.W. Sustainability and Optimization: From Conceptual Fundamentals to Applications. Sustainability 2020, 12, 2027. [Google Scholar] [CrossRef]
- Tezer, T.; Yaman, R.; Yaman, G. Evaluation of Approaches Used for Optimization of Stand-Alone Hybrid Renewable Energy Systems. Renew. Sustain. Energy Rev. 2017, 73, 840–853. [Google Scholar] [CrossRef]
- Lei, G.; Song, H.; Rodriguez, D. Power Generation Cost Minimization of the Grid-Connected Hybrid Renewable Energy System through Optimal Sizing Using the Modified Seagull Optimization Technique. Energy Rep. 2020, 6, 3365–3376. [Google Scholar] [CrossRef]
- Khan, A.A.; Minai, A.F.; Pachauri, R.K.; Malik, H. Optimal Sizing, Control, and Management Strategies for Hybrid Renewable Energy Systems: A Comprehensive Review. Energies 2022, 15, 6249. [Google Scholar] [CrossRef]
- Eriksson, E.L.V.; Gray, E.M. Optimization and Integration of Hybrid Renewable Energy Hydrogen Fuel Cell Energy Systems—A Critical Review. Appl. Energy 2017, 202, 348–364. [Google Scholar] [CrossRef]
- Pang, M.; Shi, Y.; Wang, W.; Pang, S. Optimal Sizing and Control of Hybrid Energy Storage System for Wind Power Using Hybrid Parallel PSO-GA Algorithm. Energy Explor. Exploit. 2019, 37, 558–578. [Google Scholar] [CrossRef]
- Fatih Güven, A.; Mahmoud Samy, M. Performance Analysis of Autonomous Green Energy System Based on Multi and Hybrid Metaheuristic Optimization Approaches. Energy Convers. Manag. 2022, 269, 116058. [Google Scholar] [CrossRef]
- Vyas, M.; Yadav, V.K.; Vyas, S.; Joshi, R.R.; Tirole, R. A Review of Algorithms for Control and Optimization for Energy Management of Hybrid Renewable Energy Systems. In Intelligent Renewable Energy Systems; Priyadarshi, N., Bhoi, A.K., Padmanaban, S., Balamurugan, S., Holm-Nielsen, J.B., Eds.; Wiley: Hoboken, NJ, USA, 2022; pp. 131–155. ISBN 978-1-119-78627-6. [Google Scholar]
- Rahman, M.M.; Shakeri, M.; Tiong, S.K.; Khatun, F.; Amin, N.; Pasupuleti, J.; Hasan, M.K. Prospective Methodologies in Hybrid Renewable Energy Systems for Energy Prediction Using Artificial Neural Networks. Sustainability 2021, 13, 2393. [Google Scholar] [CrossRef]
- Bansal, A.K. Sizing and Forecasting Techniques in Photovoltaic-Wind Based Hybrid Renewable Energy System: A Review. J. Clean. Prod. 2022, 369, 133376. [Google Scholar] [CrossRef]
- Houssein, E.H.; Ibrahim, I.E.; Kharrich, M.; Kamel, S. An Improved Marine Predators Algorithm for the Optimal Design of Hybrid Renewable Energy Systems. Eng. Appl. Artif. Intell. 2022, 110, 104722. [Google Scholar] [CrossRef]
- Tamjid Shabestari, S.; Kasaeian, A.; Vaziri Rad, M.A.; Forootan Fard, H.; Yan, W.-M.; Pourfayaz, F. Techno-Financial Evaluation of a Hybrid Renewable Solution for Supplying the Predicted Power Outages by Machine Learning Methods in Rural Areas. Renew. Energy 2022, 194, 1303–1325. [Google Scholar] [CrossRef]
- Piotrowski, P.; Baczyński, D.; Kopyt, M.; Gulczyński, T. Advanced Ensemble Methods Using Machine Learning and Deep Learning for One-Day-Ahead Forecasts of Electric Energy Production in Wind Farms. Energies 2022, 15, 1252. [Google Scholar] [CrossRef]
- Ministry of Land, Infrastructure and Transport. Building Energy Information. Real-Time Electricity Usage Information for Buildings in Seo-gu, Gwangju; Ministry of Land, Infrastructure and Transport: Sejong City, Republic of Korea, 2018.
- Korean Meteorological Association (KMA). Hourly Synoptic Meteorological Observations; KMA: Seoul, Republic of Korea, 2021.
- Rafati, A.; Joorabian, M.; Mashhour, E.; Shaker, H.R. High Dimensional Very Short-Term Solar Power Forecasting Based on a Data-Driven Heuristic Method. Energy 2021, 219, 119647. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Statist. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Natekin, A.; Knoll, A. Gradient Boosting Machines, a Tutorial. Front. Neurorobot. 2013, 7, 21. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: San Francisco, CA, USA, 2016; pp. 785–794. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased Boosting with Categorical Features 2019. In Advances in Neural Information Processing Systems; IEEE: New York, NY, USA, 2019. [Google Scholar]
- Sagi, O.; Rokach, L. Ensemble Learning: A Survey. WIREs Data Min. Knowl Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Albuquerque, P.H.M.; Peng, Y.; Silva, J.P.F.D. Making the Whole Greater than the Sum of Its Parts: A Literature Review of Ensemble Methods for Financial Time Series Forecasting. J. Forecast. 2022, 41, 1701–1724. [Google Scholar] [CrossRef]
- Bergstra, J.; Yamins, D.; Cox, D.D. Making a Science of Model Search: Hyperparameter Optimization in Hundreds of Dimensions for Vision Architectures. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013. [Google Scholar]
- Seshia, S.A.; Sadigh, D.; Sastry, S.S. Toward Verified Artificial Intelligence. Commun. ACM 2022, 65, 46–55. [Google Scholar] [CrossRef]
- Krichen, M.; Mihoub, A.; Alzahrani, M.Y.; Adoni, W.Y.H.; Nahhal, T. Are Formal Methods Applicable To Machine Learning And Artificial Intelligence? In Proceedings of the 2022 2nd International Conference of Smart Systems and Emerging Technologies (SMARTTECH), Riyadh, Saudi Arabia, 9–11 May 2022; IEEE: Riyadh, Saudi Arabia, 2022; pp. 48–53. [Google Scholar]
- Ali, S.; Jang, C.-M. Optimum Design of Hybrid Renewable Energy System for Sustainable Energy Supply to a Remote Island. Sustainability 2020, 12, 1280. [Google Scholar] [CrossRef]
- Kaluthanthrige, R.; Rajapakse, A.D.; Lamothe, C.; Mosallat, F. Optimal Sizing and Performance Evaluation of a Hybrid Renewable Energy System for an Off-Grid Power System in Northern Canada. Technol Econ Smart Grids Sustain Energy 2019, 4, 4. [Google Scholar] [CrossRef]
- Bae, J.; Lee, S.; Kim, H. Comparative Study on the Economic Feasibility of Nanogrid and Microgrid Electrification: The Case of Jeju Island, South Korea. Energy Environ. 2021, 32, 168–188. [Google Scholar] [CrossRef]
- Traoré, A.; Elgothamy, H.; Zohdy, M.A. Optimal Sizing of Solar/Wind Hybrid Off-Grid Microgrids Using an Enhanced Genetic Algorithm. JPEE 2018, 06, 64–77. [Google Scholar] [CrossRef]
- Dahiru, A.T.; Tan, C.W. Optimal Sizing and Techno-Economic Analysis of Grid-Connected Nanogrid for Tropical Climates of the Savannah. Sustain. Cities Soc. 2020, 52, 101824. [Google Scholar] [CrossRef]
- Borhanazad, H. Techno Economic Analysis of Stand-Alone Hybrid Renewable Energy System; Universiti Malaya: Federal Territory of Kuala Lumpur, Malaysia, 2015. [Google Scholar]
- Korea Electric Power Corporation. Korean Electricty Price Structure; Korea Electric Power Corporation: Naju-si, Republic of Korea, 2022. [Google Scholar]
- Niaz, H.; Lakouraj, M.M.; Liu, J. Techno-Economic Feasibility Evaluation of a Standalone Solar-Powered Alkaline Water Electrolyzer Considering the Influence of Battery Energy Storage System: A Korean Case Study. Korean J. Chem. Eng. 2021, 38, 1617–1630. [Google Scholar] [CrossRef]
- Abdelaziz Mohamed, M.; Eltamaly, A.M. Modeling and Simulation of Smart Grid Integrated with Hybrid Renewable Energy Systems; Studies in Systems, Decision and Control; Springer International Publishing: Cham, Switzerland, 2018; Volume 121, ISBN 978-3-319-64794-4. [Google Scholar]
- Statistics Korea. Consumer Price Index(CPI); Statistics Korea: Seo-gu, Republic of Korea, 2022.
- Husein, M.; Hau, V.; Chung, I.-Y.; Chae, W.-K.; Lee, H.-J. Design and Dynamic Performance Analysis of a Stand-Alone Microgrid—A Case Study of Gasa Island, South Korea. J. Electr. Eng. Technol. 2017, 12, 1777–1788. [Google Scholar]
- Lian, J.; Zhang, Y.; Ma, C.; Yang, Y.; Chaima, E. A Review on Recent Sizing Methodologies of Hybrid Renewable Energy Systems. Energy Convers. Manag. 2019, 199, 112027. [Google Scholar] [CrossRef]
- Papaefthymiou, S.V.; Papathanassiou, S.A. Optimum Sizing of Wind-Pumped-Storage Hybrid Power Stations in Island Systems. Renew. Energy 2014, 64, 187–196. [Google Scholar] [CrossRef]
- Aydilek, İ.B. A Hybrid Firefly and Particle Swarm Optimization Algorithm for Computationally Expensive Numerical Problems. Appl. Soft Comput. 2018, 66, 232–249. [Google Scholar] [CrossRef]
- Rather, S.A.; Bala, P.S. Hybridization of Constriction Coefficient Based Particle Swarm Optimization and Gravitational Search Algorithm for Function Optimization. In Proceedings of the International Conference on Advances in Electronics, Electrical & Computational Intelligence, Prayagraj, India, 31 May–1 June 2019; Elsevier: Prayagraj, India, 2019. [Google Scholar]
- Zhang, M.; Long, D.; Qin, T.; Yang, J. A Chaotic Hybrid Butterfly Optimization Algorithm with Particle Swarm Optimization for High-Dimensional Optimization Problems. Symmetry 2020, 12, 1800. [Google Scholar] [CrossRef]
- Sharma, S.; Kapoor, R.; Dhiman, S. A Novel Hybrid Metaheuristic Based on Augmented Grey Wolf Optimizer and Cuckoo Search for Global Optimization. In Proceedings of the 2021 2nd International Conference on Secure Cyber Computing and Communications (ICSCCC), Jalandhar, India, 21–23 May 2021; IEEE: Jalandhar, India, 2021; pp. 376–381. [Google Scholar]
- Meena, N.K.; Parashar, S.; Swarnkar, A.; Gupta, N.; Niazi, K.R. Improved Elephant Herding Optimization for Multiobjective DER Accommodation in Distribution Systems. IEEE Trans. Ind. Inf. 2018, 14, 1029–1039. [Google Scholar] [CrossRef]
- Shehadeh, H.A. A Hybrid Sperm Swarm Optimization and Gravitational Search Algorithm (HSSOGSA) for Global Optimization. Neural Comput. Applic. 2021, 33, 11739–11752. [Google Scholar] [CrossRef]
- Aras, S.; Gedikli, E.; Kahraman, H.T. A Novel Stochastic Fractal Search Algorithm with Fitness-Distance Balance for Global Numerical Optimization. Swarm Evol. Comput. 2021, 61, 100821. [Google Scholar] [CrossRef]
- Duman, S.; Kahraman, H.T.; Sonmez, Y.; Guvenc, U.; Kati, M.; Aras, S. A Powerful Meta-Heuristic Search Algorithm for Solving Global Optimization and Real-World Solar Photovoltaic Parameter Estimation Problems. Eng. Appl. Artif. Intell. 2022, 111, 104763. [Google Scholar] [CrossRef]
- Kahraman, H.T.; Bakir, H.; Duman, S.; Katı, M.; Aras, S.; Guvenc, U. Dynamic FDB Selection Method and Its Application: Modeling and Optimizing of Directional Overcurrent Relays Coordination. Appl Intell 2022, 52, 4873–4908. [Google Scholar] [CrossRef]
- Rolls Battery Engineering. Rolls Battery User Manual; Rolls Battery Engineering: Springhill, NS, Canada, 2018. [Google Scholar]











| Dataset | Raw Data Variables | Missing Data (%) | Temporal Resolution | Input Variables | Target Variable |
|---|---|---|---|---|---|
| Meteorological data | AT [C] | 4.16 | 1 h | AT GT H Pr WS WD TC SS | SR AT |
| H [%] | 26.17 | ||||
| GT [C] | |||||
| Pr [mm] | 88.81 | ||||
| WS [m/s] | 0.04 | ||||
| WD [deg] | 0.04 | ||||
| TC | |||||
| SS [h] | |||||
| SR [MJ/m2] | |||||
| Electric power consumption data | LD [kW] | 4.10 | 15 min | SR SS | LD |
| Performance Metric | Mathematical Expression |
|---|---|
| MAE | |
| R2 |
| PV MODULE | |
|---|---|
| Technical Specifications | |
| Manufacturer | Hanwha |
| Cell Type | Q Cell |
| Surface Area (m2) | 1.7943 |
| Rated Power (W) | 360 |
| Short-Circuit Current (Amp.) | 11.04 |
| Open-Circuit Voltage (V) | 41.18 |
| Module Efficiency (%) | 20.1 |
| Temperature Coefficient of Rated Power (%/K) | −0.34 |
| Nominal Cell Operating Temperature (K) | 316 |
| Cost Data | |
| Capital Investment ($/W) | 1.5 |
| Replacement Cost ($/W) | 1.2 |
| Operation and Maintenance ($/W/year) | 0.03 |
| Life (years) | 25 |
| Battery | |
|---|---|
| Technical Specifications | |
| Manufacturer | Rolls/Surrette |
| Type | Surrette 6CS25P |
| Maximum Capacity (Ah) | 1150 |
| Capacity (Ah) | 820 |
| Rated Voltage (V) | 6 |
| Rated Current (Amp.) | 152 |
| Charge/Discharge Efficiency (%) | 89.4 |
| Round Trip Efficiency (%) | 80 |
| Cost Data | |
| Capital Investment ($/W) | 0.25 |
| Replacement Cost ($/W) | 0.25 |
| Operation and Maintenance ($/W/year) | 0.001 |
| Life (years) | 20 |
| Inverter | |
|---|---|
| Technical Specifications | |
| Manufacturer | LEONICS |
| Type | MTP-413F 25 kW |
| Rated Power (kW) | 25 |
| Maximum Input voltage (V) | 240 |
| Rated Voltage (V) | 240 DC |
| Rated Current (Amp.) | 72 |
| Maximum efficiency (%) | 95 |
| Cost Data | |
| Capital Investment ($/W) | 0.8 |
| Replacement Cost ($/W) | 0.8 |
| Operation and Maintenance ($/kW/year) | 0.01 |
| Life (years) | 10 |
| Algorithm Name | Search Process | New Position Update |
|---|---|---|
| HFPSO | After initialization, the algorithm starts with a global search using the PSO algorithm, which provides fast convergence in exploration. Then, the firefly algorithm is used for a local search to avoid becoming trapped in local minima. The light attraction of each particle is mutated by a PSO operator to balance exploration and exploitation. This process helps to increase the particle diversity and achieve a faster convergence ability in the hybrid HFPSO algorithm. | After the search process, if a particle’s fitness value is more than or equal to the previous global best, it is anticipated that a local search will begin and a new position will be calculated by an imitative FA; otherwise, the particle will be handled by PSO, which will carry on with its regular operations with this particle. |
| CPSOGSA | PSO uses a combination of its velocity and position update equations, along with the inertia weight and constriction coefficient, to exploit new regions of the search space. The coefficient ensures that the search agents do not move far away from the promising local regions of the search space. GSA contributes to exploitation by using gravitational forces between agents to converge towards the global optimum. | The positions of particles are updated based on the current position and velocity calculated by a new equation, which is constructed by merging the velocity equation of GSA in the PSO equation. |
| HPSOBOA | PSO is used to update particle velocities (global exploration), while BOA is used to update positions and perform local search by allowing each particle to explore its immediate neighborhood in detail by use of an adaptive parameter. | BOA uses a probabilistic model to generate a new position for each dimension of each particle’s position vector based on its previous values and those of other particles in its neighbor, and the process continues until maximum iterations. |
| AGWOCS | Performs global search using AGWO by updating the positions of wolves based on its augmented position update equation, facilitating faster exploration by allowing wolves to jump at random positions throughout search space. Local search is carried out by CS for efficiency by using Levy flights. | After local search is done, the optimal positions of some wolves as found in AGWO are updated by CS results and the final positions are achieved and are evaluated for OF. If there is no improvement in the OF value, the whole process starts again till maximum iterations are reached. |
| EHOTOPSIS | IEHO generates a population of elephants and updates their positions in the exploration phase by moving them toward their best positions found so far. It promotes diversity by replacing the worst elephant with a new baby elephant. The exploitation phase selects promising solutions and updates them to move toward better solutions with small variations to promote diversity. | Best and worst elephant position is updated based on local search, while all other elephants are positioned based on their neighbors (output of global search). |
| HSSOGSA | The GSA assigns masses to solutions and calculates gravitational force to explore new regions. SSO exploits promising regions by simulating a sperm swarm that moves toward promising solutions. The algorithm updates its population based on the selected solutions. | HSSOGSA uses a weighted sum approach to combine the positions updated by GSA and SSO. The weights are determined by a parameter called the “exploration factor,” which controls the balance between exploration and exploitation before calculating new Pbest and GBest. |
| FDBSFS | In the exploration phase, a Gaussian Walk method generates new particles from diffusion applied to all points in the population. The exploitation phase selects particles based on fitness and distances from each other using the FDB method, which balances both factors by sorting and penalizing close particles. | The selected particles are then updated using a velocity equation that considers their current position, their best position so far and the best position of all particles in the population, which helps to refine existing solutions by moving particles toward better positions in the search space. |
| FDBTLABC | The ABC algorithm uses learning-based onlooker and generalized oppositional scout bee stages for exploration, while the teaching-based bee stage is used for exploitation. Onlooker bees choose a solution based on probability, while scout bees generate new solutions. Teacher bees improve the quality of solutions by sharing their knowledge. | The algorithm updates bee positions via a greedy selection method. Bees generate new solutions by modifying their positions based on a bee selected at random. The best solution replaces the current best if it has a better fitness value. The employed and onlooker bee stages use teaching and learning mechanisms, respectively. |
| Regression Task | ML Algorithm | Performance Metric | |
|---|---|---|---|
| MAE | R2 | ||
| SR prediction | XGB | 0.1573 | 0.9139 |
| LGBM | 0.0945 | 0.9433 | |
| CBR | 0.0985 | 0.9422 | |
| AT prediction | XGB | 0.0241 | 0.9999 |
| LGBM | 0.2967 | 0.9956 | |
| CBR | 0.0637 | 0.9998 | |
| LD prediction | XGB | 11.4073 | 0.7366 |
| LGBM | 10.8954 | 0.6996 | |
| CBR | 11.4797 | 0.7280 | |
| DRPSPmax | Optimization Algorithm | Average Time (s) | Time Standard Deviation | Average TNPC (Million $) | TNPC Standard Deviation |
|---|---|---|---|---|---|
| 0% | AGWOCS | 219.1 | 4.1 | 3.262 | 0.000 |
| CPSOGSA | 219.9 | 5.4 | 3.262 | 0.000 | |
| dFDBMRFO | 6.5 | 0.1 | 3.262 | 0.000 | |
| EHOTOPSIS | 219.4 | 5.1 | 3.546 | 0.148 | |
| FDBSFS | 876.8 | 18.7 | 3.262 | 0.000 | |
| FDBTLABC | 6.5 | 0.2 | 3.262 | 0.000 | |
| HFPSO | 222.4 | 5.9 | 3.285 | 0.036 | |
| HPSOBOA | 346.8 | 8.3 | 3.591 | 0.173 | |
| HSSOGSA | 219.3 | 3.9 | 3.262 | 0.000 |
| DRPSPmax | Optimization Algorithm | Average Time (s) | Time Standard Deviation | Average TNPC (Million $) | TNPC Standard Deviation |
|---|---|---|---|---|---|
| 1.3% | AGWOCS | 216.3 | 4.2 | 1.465 | 0.241 |
| CPSOGSA | 216.8 | 5.0 | 1.461 | 0.000 | |
| dFDBMRFO | 6.3 | 0.2 | 1.461 | 0.641 | |
| EHOTOPSIS | 215.5 | 7.0 | 2.723 | 0.000 | |
| FDBSFS | 862.5 | 15.5 | 1.461 | 0.641 | |
| FDBTLABC | 6.3 | 0.1 | 1.461 | 0.460 | |
| HFPSO | 218.3 | 6.2 | 1.571 | 0.000 | |
| HPSOBOA | 335.0 | 6.9 | 1.676 | 0.217 | |
| HSSOGSA | 216.8 | 4.8 | 1.461 | 0.209 |
| DRPSPmax | Optimization Algorithm | Average Time (s) | Time Standard Deviation | Average TNPC (Million $) | TNPC Standard Deviation |
|---|---|---|---|---|---|
| 2% | AGWOCS | 219.5 | 4.7 | 1.315 | 0.028 |
| CPSOGSA | 221.4 | 6.1 | 1.313 | 0.000 | |
| dFDBMRFO | 6.4 | 0.1 | 1.313 | 0.000 | |
| EHOTOPSIS | 220.6 | 5.4 | 2.385 | 0.000 | |
| FDBSFS | 881.3 | 23.2 | 1.313 | 0.075 | |
| FDBTLABC | 6.4 | 0.2 | 1.313 | 0.032 | |
| HFPSO | 221.1 | 4.5 | 1.374 | 0.025 | |
| HPSOBOA | 342.3 | 7.9 | 1.338 | 0.163 | |
| HSSOGSA | 219.4 | 5.0 | 1.371 | 0.031 |
| DRPSPmax | Optimization Algorithm | Average Time (s) | Time Standard Deviation | Average TNPC (Million $) | TNPC Standard Deviation |
|---|---|---|---|---|---|
| 5% | AGWOCS | 218.3 | 5.1 | 1.103 | 0.000 |
| CPSOGSA | 217.4 | 3.8 | 1.103 | 0.000 | |
| dFDBMRFO | 6.3 | 0.2 | 1.103 | 0.000 | |
| EHOTOPSIS | 217.8 | 5.9 | 2.720 | 0.014 | |
| FDBSFS | 864.5 | 16.6 | 1.105 | 0.115 | |
| FDBTLABC | 6.3 | 0.2 | 1.126 | 0.000 | |
| HFPSO | 221.5 | 6.0 | 1.103 | 0.000 | |
| HPSOBOA | 336.4 | 8.6 | 1.103 | 0.000 | |
| HSSOGSA | 217.1 | 4.4 | 1.103 | 0.000 |
| Algorithm | Iterations to Convergence | Average Computational Time | Results Stability (Avg. Standard Deviation) | Lowest Cost Achieved (Million $) |
|---|---|---|---|---|
| AGWOCS | 31 | 218.290 | 0.067 | 1.103 |
| CPSOGSA | 37 | 218.850 | 0.000 | 1.103 |
| dFDBMRFO | 100 | 6.370 | 0.160 | 1.103 |
| EHOTOPSIS | 100 | 218.310 | 0.003 | 2.720 |
| FDBSFS | 88 | 871.260 | 0.207 | 1.105 |
| FDBTLABC | 45 | 6.380 | 0.123 | 1.126 |
| HFPSO | 23 | 220.820 | 0.015 | 1.103 |
| HPSOBOA | 6 | 340.130 | 0.130 | 1.103 |
| HSSOGSA | 30 | 218.130 | 0.060 | 1.103 |
| DRPSPmax | Optimization Algorithm | NPV | NBAT | NINV | REF | DRPSP | CO2 (ton/MWh) | TNPC (106 $) |
|---|---|---|---|---|---|---|---|---|
| 0% | AGWOCS | 303 | 115 | 31 | 0.301 | 0.000 | 1757 | 3.262 |
| CPSOGSA | 303 | 115 | 31 | 0.301 | 0.000 | 1757 | 3.262 | |
| dFDBMRFO | 303 | 115 | 31 | 0.301 | 0.000 | 1757 | 3.262 | |
| EHOTOPSIS | 329 | 127 | 34 | 0.332 | 0.000 | 1703 | 3.546 | |
| FDBSFS | 303 | 115 | 31 | 0.301 | 0.000 | 1757 | 3.262 | |
| FDBTLABC | 303 | 115 | 31 | 0.301 | 0.000 | 1757 | 3.262 | |
| HFPSO | 305 | 116 | 31 | 0.303 | 0.000 | 1753 | 3.285 | |
| HPSOBOA | 304 | 132 | 35 | 0.302 | 0.000 | 1755 | 3.591 | |
| HSSOGSA | 303 | 115 | 31 | 0.301 | 0.000 | 1757 | 3.262 |
| DRPSPmax | Optimization Algorithm | NPV | NBAT | NINV | REF | DRPSP | CO2 (ton/MWh) | TNPC (×106 $) |
|---|---|---|---|---|---|---|---|---|
| 1.3% | AGWOCS | 307 | 21 | 10 | 0.303 | 0.013 | 1755 | 1.465 |
| CPSOGSA | 305 | 21 | 10 | 0.301 | 0.013 | 1759 | 1.461 | |
| dFDBMRFO | 305 | 21 | 10 | 0.301 | 0.013 | 1759 | 1.461 | |
| EHOTOPSIS | 672 | 48 | 22 | 0.729 | 0.004 | 1238 | 2.723 | |
| FDBSFS | 305 | 21 | 10 | 0.301 | 0.013 | 1759 | 1.461 | |
| FDBTLABC | 305 | 21 | 10 | 0.301 | 0.013 | 1759 | 1.461 | |
| HFPSO | 321 | 25 | 11 | 0.320 | 0.011 | 1726 | 1.571 | |
| HPSOBOA | 325 | 30 | 12 | 0.325 | 0.010 | 1715 | 1.676 | |
| HSSOGSA | 305 | 21 | 10 | 0.301 | 0.013 | 1759 | 1.461 |
| DRPSPmax | Optimization Algorithm | NPV | NBAT | NINV | REF | DRPSP | CO2 (ton/MWh) | TNPC (×106 $) |
|---|---|---|---|---|---|---|---|---|
| 2% | AGWOCS | 309 | 13 | 8 | 0.302 | 0.020 | 1759 | 1.315 |
| CPSOGSA | 308 | 13 | 8 | 0.301 | 0.020 | 1761 | 1.313 | |
| dFDBMRFO | 308 | 13 | 8 | 0.301 | 0.020 | 1761 | 1.313 | |
| EHOTOPSIS | 952 | 4 | 17 | 0.901 | 0.018 | 1358 | 2.385 | |
| FDBSFS | 308 | 13 | 8 | 0.301 | 0.020 | 1761 | 1.313 | |
| FDBTLABC | 308 | 13 | 8 | 0.301 | 0.020 | 1761 | 1.313 | |
| HFPSO | 458 | 1 | 8 | 0.430 | 0.020 | 1616 | 1.374 | |
| HPSOBOA | 330 | 12 | 8 | 0.323 | 0.020 | 1726 | 1.338 | |
| HSSOGSA | 446 | 2 | 8 | 0.421 | 0.020 | 1621 | 1.371 |
| DRPSPmax | Optimization Algorithm | NPV | NBAT | NINV | REF | DRPSP | CO2 (ton/MWh) | TNPC (×106 $) |
|---|---|---|---|---|---|---|---|---|
| 5% | AGWOCS | 320 | 1 | 6 | 0.300 | 0.021 | 1771 | 1.103 |
| CPSOGSA | 320 | 1 | 6 | 0.300 | 0.021 | 1771 | 1.103 | |
| dFDBMRFO | 320 | 1 | 6 | 0.300 | 0.021 | 1771 | 1.103 | |
| EHOTOPSIS | 949 | 21 | 21 | 0.942 | 0.010 | 1250 | 2.72 | |
| FDBSFS | 321 | 1 | 6 | 0.301 | 0.021 | 1770 | 1.105 | |
| FDBTLABC | 322 | 2 | 6 | 0.304 | 0.021 | 1765 | 1.126 | |
| HFPSO | 320 | 1 | 6 | 0.300 | 0.021 | 1771 | 1.103 | |
| HPSOBOA | 320 | 1 | 6 | 0.300 | 0.021 | 1771 | 1.103 | |
| HSSOGSA | 320 | 1 | 6 | 0.300 | 0.021 | 1771 | 1.103 |
| Inflation Rate | Interest Rate | Grid Purchase Unit Price | Grid Sellback Unit Price | PV Efficiency | Battery DOD |
|---|---|---|---|---|---|
| 5% | 3.26% | 0.07 $/kWh | 0.098 $/kWh | 20.1% | 80% |
| DRPSPmax | Optimization Algorithm | NPV | NBAT | NINV | REF | DRPSP | CO2 (ton/MWh) | TNPC (×106 $) |
|---|---|---|---|---|---|---|---|---|
| 0% | AGWOCS | 265 | 114 | 30 | 0.301 | 0.000 | 1731 | 3.179 |
| CPSOGSA | 264 | 114 | 30 | 0.300 | 0.000 | 1733 | 3.177 | |
| dFDBMRFO | 264 | 114 | 30 | 0.300 | 0.000 | 1733 | 3.177 | |
| EHOTOPSIS | 697 | 125 | 40 | 0.970 | 0.000 | 817 | 4.262 | |
| FDBSFS | 264 | 114 | 30 | 0.300 | 0.000 | 1733 | 3.177 | |
| FDBTLABC | 264 | 114 | 30 | 0.300 | 0.000 | 1733 | 3.177 | |
| HFPSO | 293 | 114 | 31 | 0.340 | 0.000 | 1661 | 3.235 | |
| HPSOBOA | 310 | 128 | 34 | 0.364 | 0.000 | 1619 | 3.538 | |
| HSSOGSA | 264 | 114 | 30 | 0.300 | 0.000 | 1733 | 3.177 |
| DRPSPmax | Optimization Algorithm | NPV | NBAT | NINV | REF | DRPSP | CO2 (ton/MWh) | TNPC (×106 $) |
|---|---|---|---|---|---|---|---|---|
| 1.3% | AGWOCS | 266 | 21 | 9 | 0.302 | 0.013 | 1730 | 1.395 |
| CPSOGSA | 265 | 21 | 9 | 0.301 | 0.013 | 1732 | 1.393 | |
| dFDBMRFO | 265 | 21 | 9 | 0.301 | 0.013 | 1732 | 1.393 | |
| EHOTOPSIS | 460 | 28 | 14 | 0.554 | 0.008 | 1367 | 1.909 | |
| FDBSFS | 265 | 21 | 9 | 0.301 | 0.013 | 1732 | 1.393 | |
| FDBTLABC | 265 | 21 | 9 | 0.301 | 0.013 | 1732 | 1.393 | |
| HFPSO | 303 | 25 | 11 | 0.351 | 0.011 | 1642 | 1.546 | |
| HPSOBOA | 265 | 32 | 12 | 0.301 | 0.009 | 1731 | 1.604 | |
| HSSOGSA | 265 | 21 | 9 | 0.301 | 0.013 | 1732 | 1.393 |
| DRPSPmax | Optimization Algorithm | NPV | NBAT | NINV | REF | DRPSP | CO2 (ton/MWh) | TNPC (×106 $) |
|---|---|---|---|---|---|---|---|---|
| 2% | AGWOCS | 351 | 2 | 6 | 0.388 | 0.020 | 1607 | 1.191 |
| CPSOGSA | 351 | 2 | 6 | 0.388 | 0.020 | 1607 | 1.191 | |
| dFDBMRFO | 351 | 2 | 6 | 0.388 | 0.020 | 1607 | 1.191 | |
| EHOTOPSIS | 289 | 38 | 14 | 0.334 | 0.007 | 1671 | 1.768 | |
| FDBSFS | 351 | 2 | 6 | 0.388 | 0.020 | 1607 | 1.191 | |
| FDBTLABC | 351 | 2 | 6 | 0.388 | 0.020 | 1607 | 1.191 | |
| HFPSO | 352 | 1 | 6 | 0.387 | 0.020 | 1610 | 1.173 | |
| HPSOBOA | 337 | 4 | 7 | 0.376 | 0.020 | 1620 | 1.203 | |
| HSSOGSA | 351 | 2 | 6 | 0.388 | 0.020 | 1607 | 1.191 |
| DRPSPmax | Optimization Algorithm | NPV | NBAT | NINV | REF | DRPSP | CO2 (ton/MWh) | TNPC (×106 $) |
|---|---|---|---|---|---|---|---|---|
| 5% | AGWOCS | 273 | 1 | 5 | 0.300 | 0.021 | 1739 | 1.022 |
| CPSOGSA | 273 | 1 | 5 | 0.300 | 0.021 | 1739 | 1.022 | |
| dFDBMRFO | 273 | 1 | 5 | 0.300 | 0.021 | 1739 | 1.022 | |
| EHOTOPSIS | 755 | 33 | 20 | 0.908 | 0.005 | 1096 | 2.560 | |
| FDBSFS | 273 | 1 | 5 | 0.300 | 0.021 | 1739 | 1.022 | |
| FDBTLABC | 273 | 1 | 5 | 0.300 | 0.021 | 1739 | 1.022 | |
| HFPSO | 274 | 1 | 5 | 0.301 | 0.021 | 1737 | 1.024 | |
| HPSOBOA | 282 | 2 | 5 | 0.312 | 0.021 | 1719 | 1.059 | |
| HSSOGSA | 273 | 1 | 5 | 0.300 | 0.021 | 1739 | 1.022 |
| Scenario | Simulation Duration | Simulated System | Obtained DRPSP | Obtained REF | CO2 Emissions | Grid Power Purchased | Grid Power Sold | Battery Utility |
|---|---|---|---|---|---|---|---|---|
| First Based on 15-year data | 15 years | NPV: 305, NBAT: 21, NPI: 10 | 0.0128 | 30% | 1759 tons/MWh | 429 MW | 15929 kW | 11% |
| Second Based on repeat of 1-year data | 15 years | NPV: 265, NBAT: 21, NPI: 9 | 0.0134 | 25% | 1732 tons/MWh | 448 MW | 2224 kW | 8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdullah, H.M.; Park, S.; Seong, K.; Lee, S. Hybrid Renewable Energy System Design: A Machine Learning Approach for Optimal Sizing with Net-Metering Costs. Sustainability 2023, 15, 8538. https://doi.org/10.3390/su15118538
Abdullah HM, Park S, Seong K, Lee S. Hybrid Renewable Energy System Design: A Machine Learning Approach for Optimal Sizing with Net-Metering Costs. Sustainability. 2023; 15(11):8538. https://doi.org/10.3390/su15118538
Chicago/Turabian StyleAbdullah, Hafiz Muhammad, Sanghyoun Park, Kwanjae Seong, and Sangyong Lee. 2023. "Hybrid Renewable Energy System Design: A Machine Learning Approach for Optimal Sizing with Net-Metering Costs" Sustainability 15, no. 11: 8538. https://doi.org/10.3390/su15118538
APA StyleAbdullah, H. M., Park, S., Seong, K., & Lee, S. (2023). Hybrid Renewable Energy System Design: A Machine Learning Approach for Optimal Sizing with Net-Metering Costs. Sustainability, 15(11), 8538. https://doi.org/10.3390/su15118538








