Damage Detection of High-Speed Railway Box Girder Using Train-Induced Dynamic Responses
Abstract
:1. Introduction
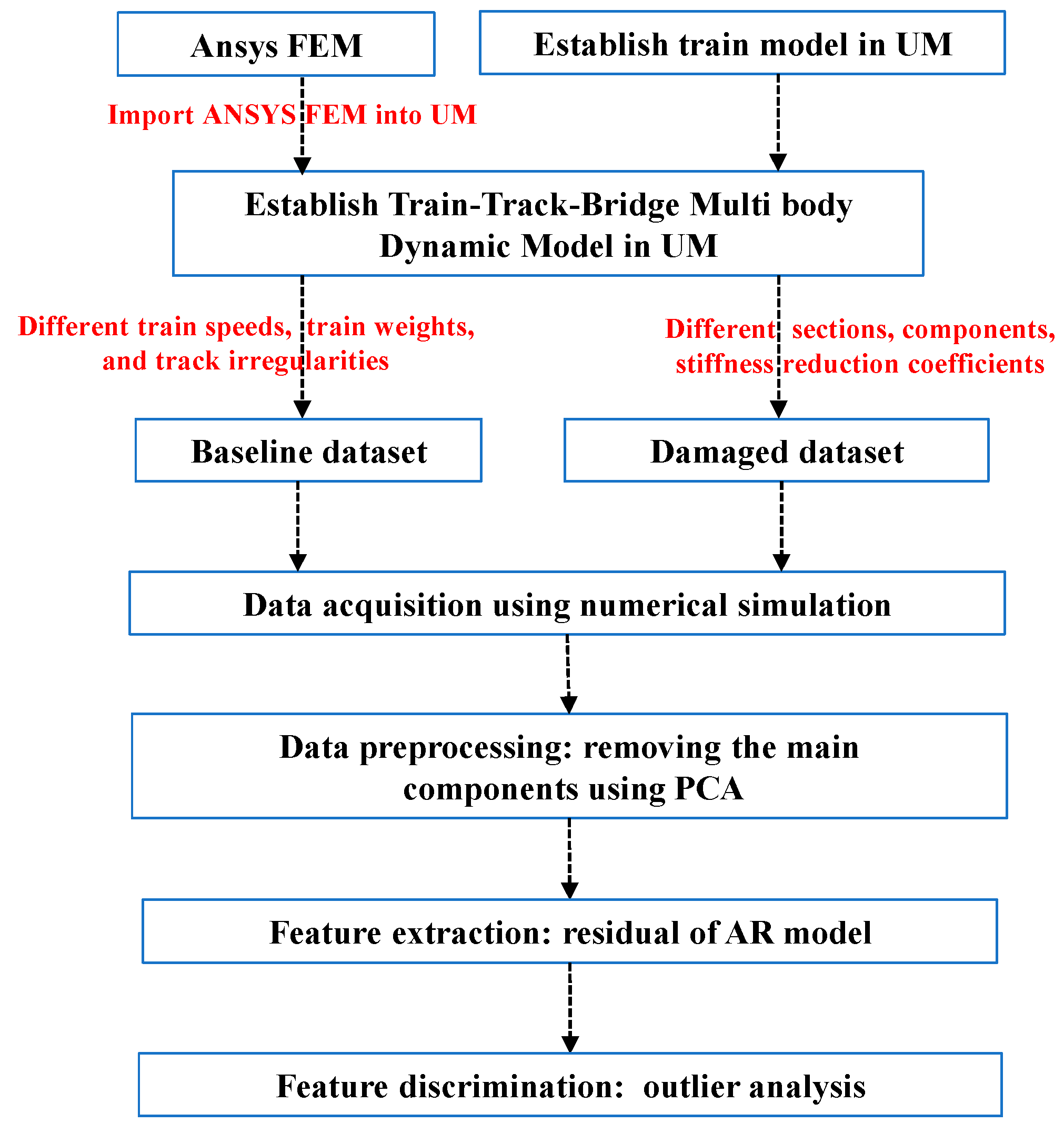
2. Damage Detection Methodology
2.1. Analysis of the Removal of Principal Components
2.2. Feature Extraction
2.3. Outlier Analysis Based on a Newly Proposed Damage Index
3. Numerical Simulation and Validation of the Proposed Algorithm
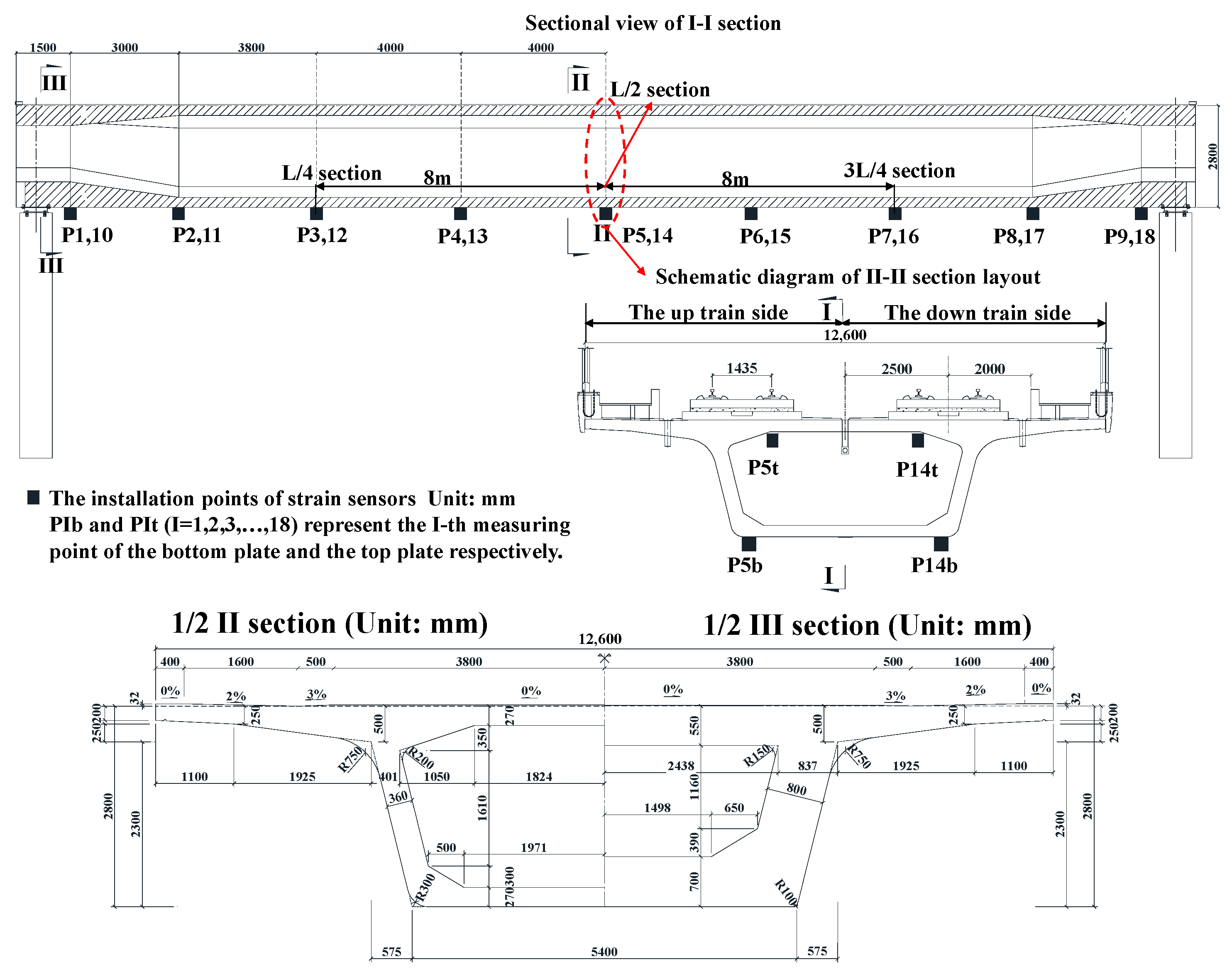
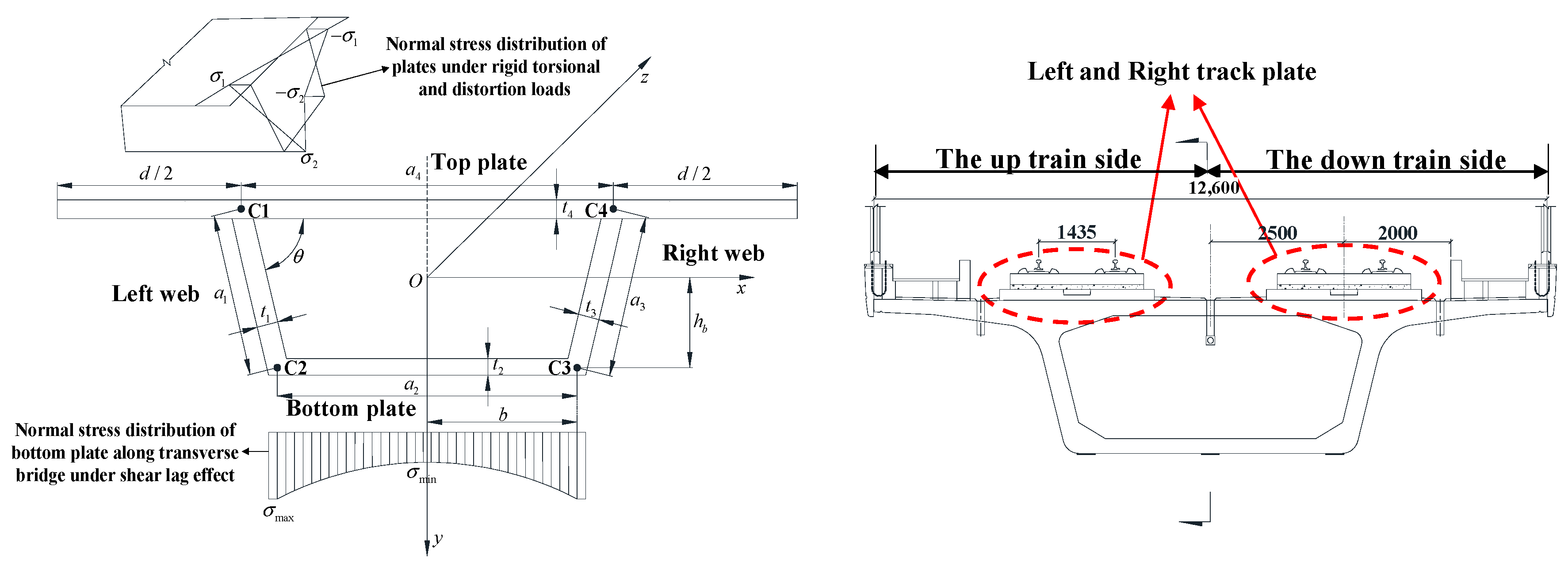
3.1. FEM of the Widely Used Simply Supported Box Girder
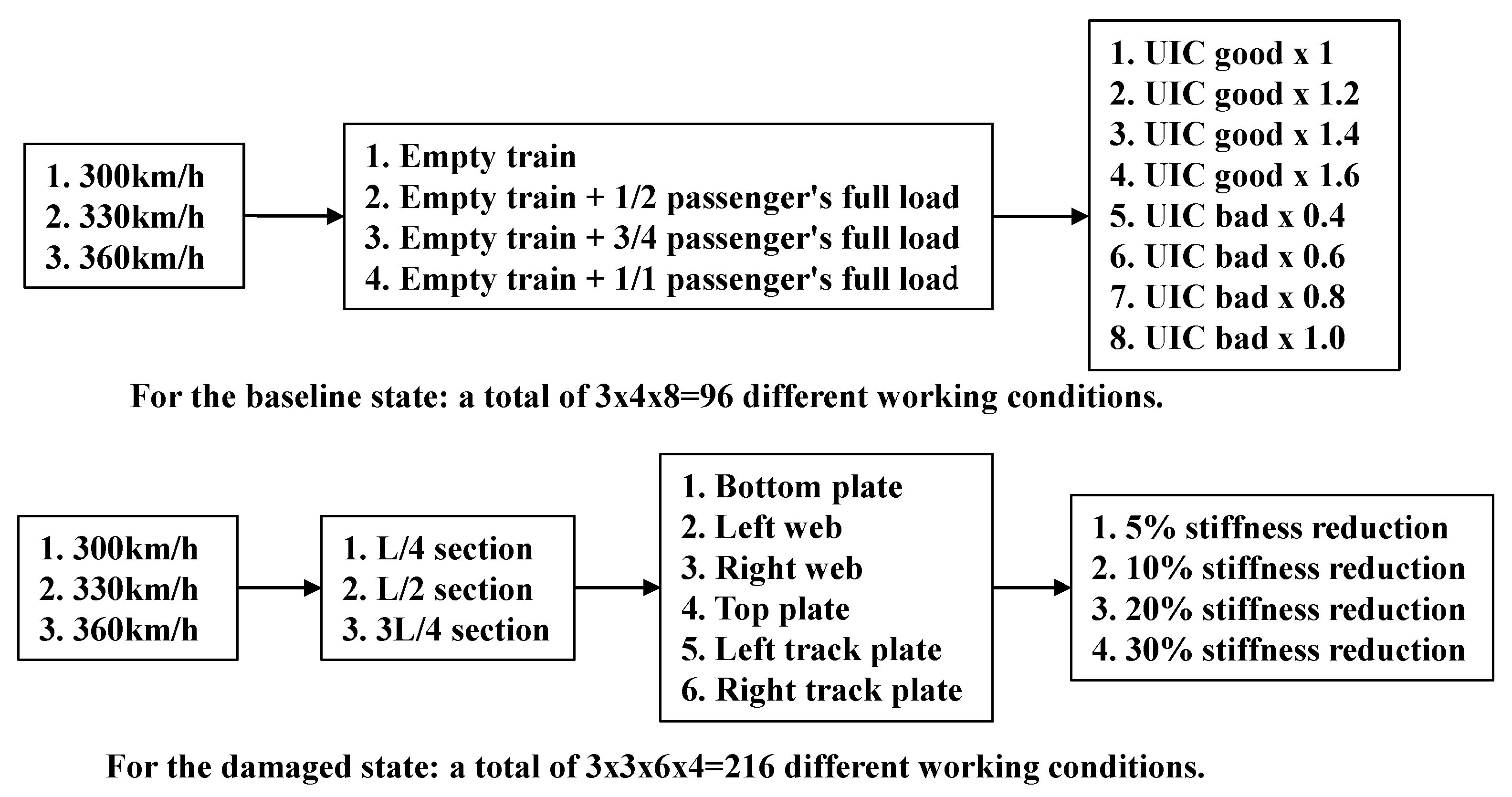
3.2. Realistic Simulation of Damage Conditions
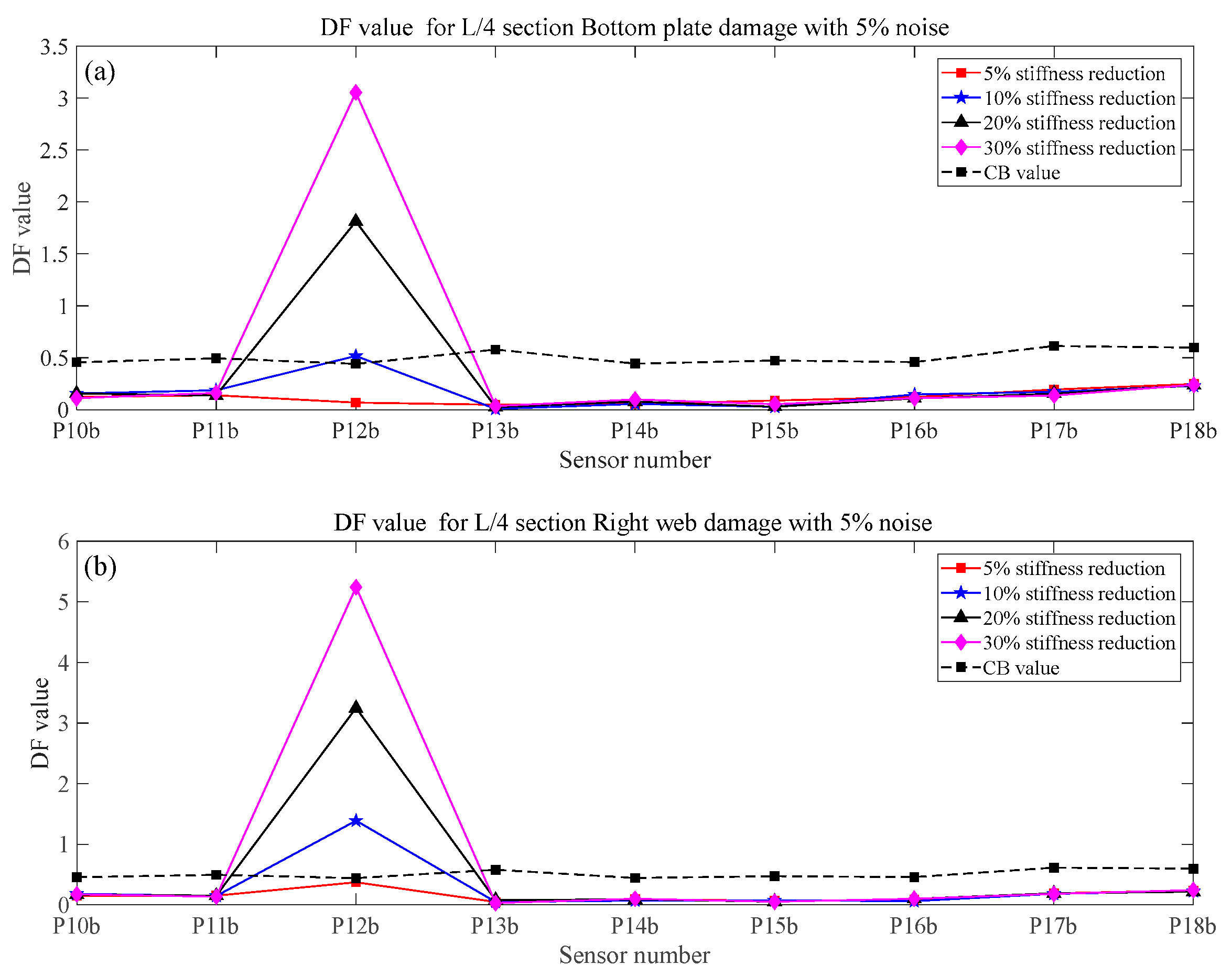
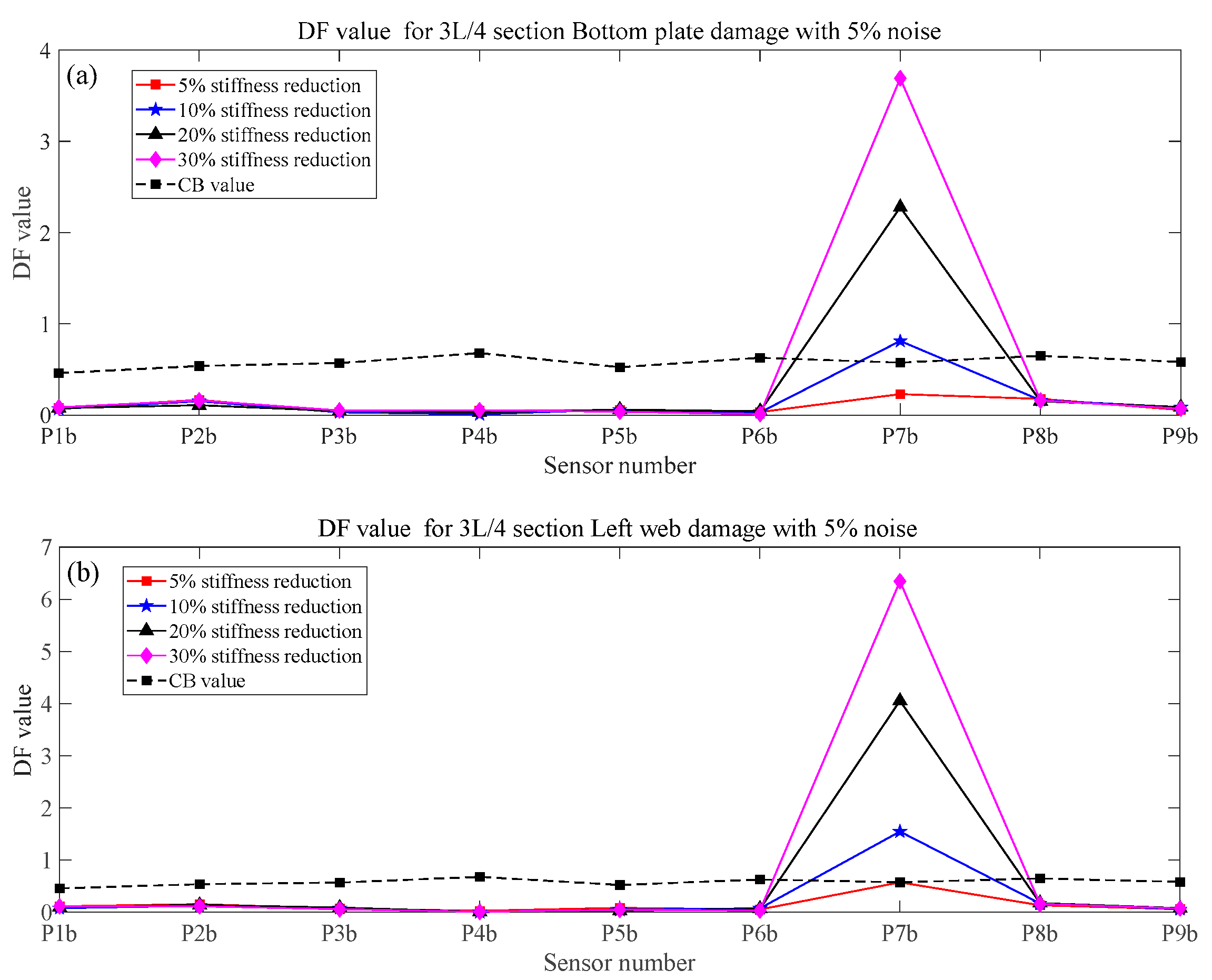
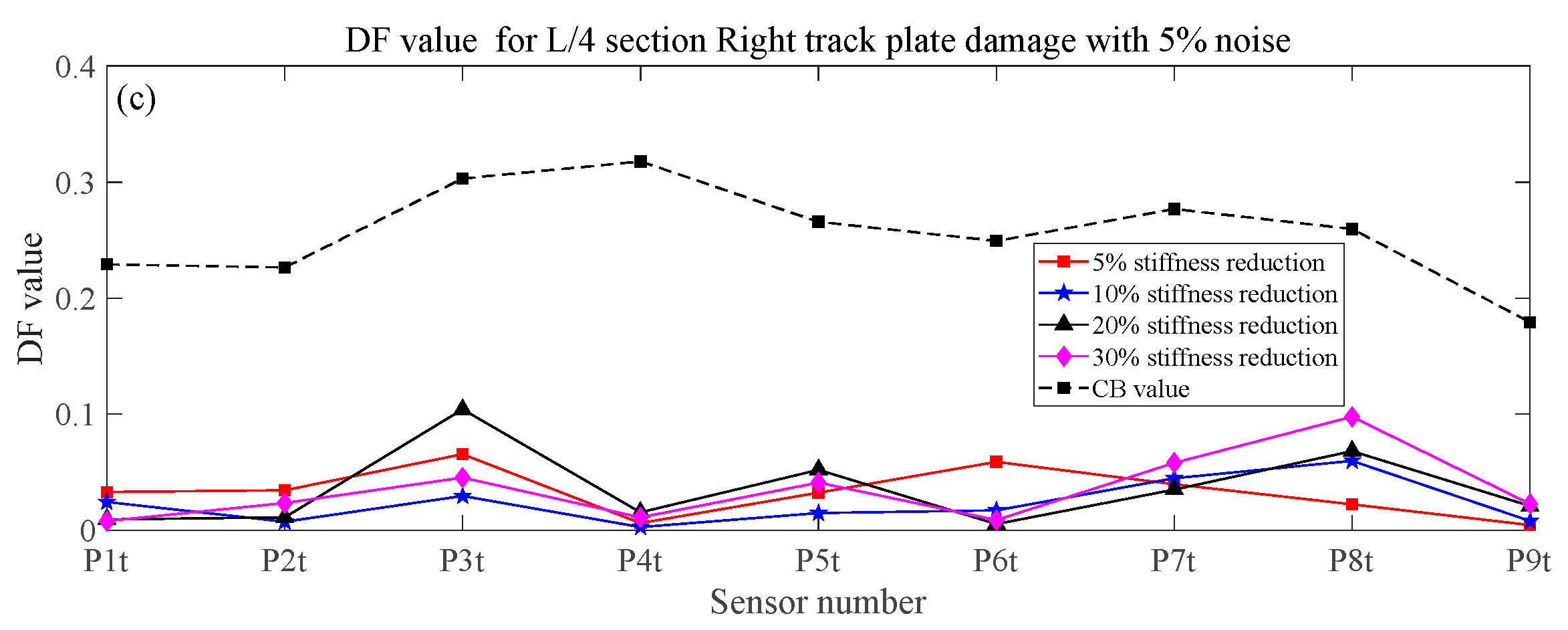
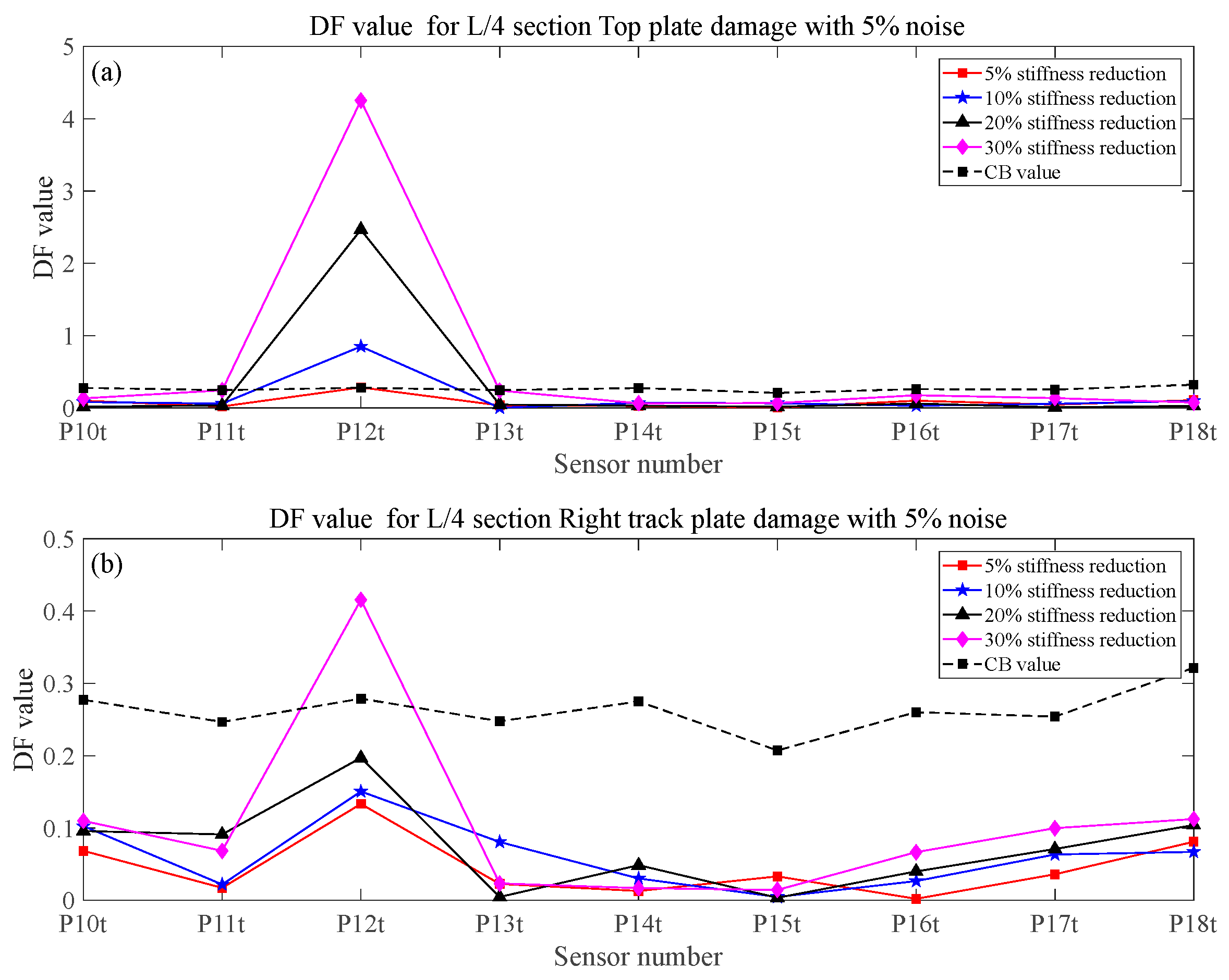
3.3. Verification of Proposed Method
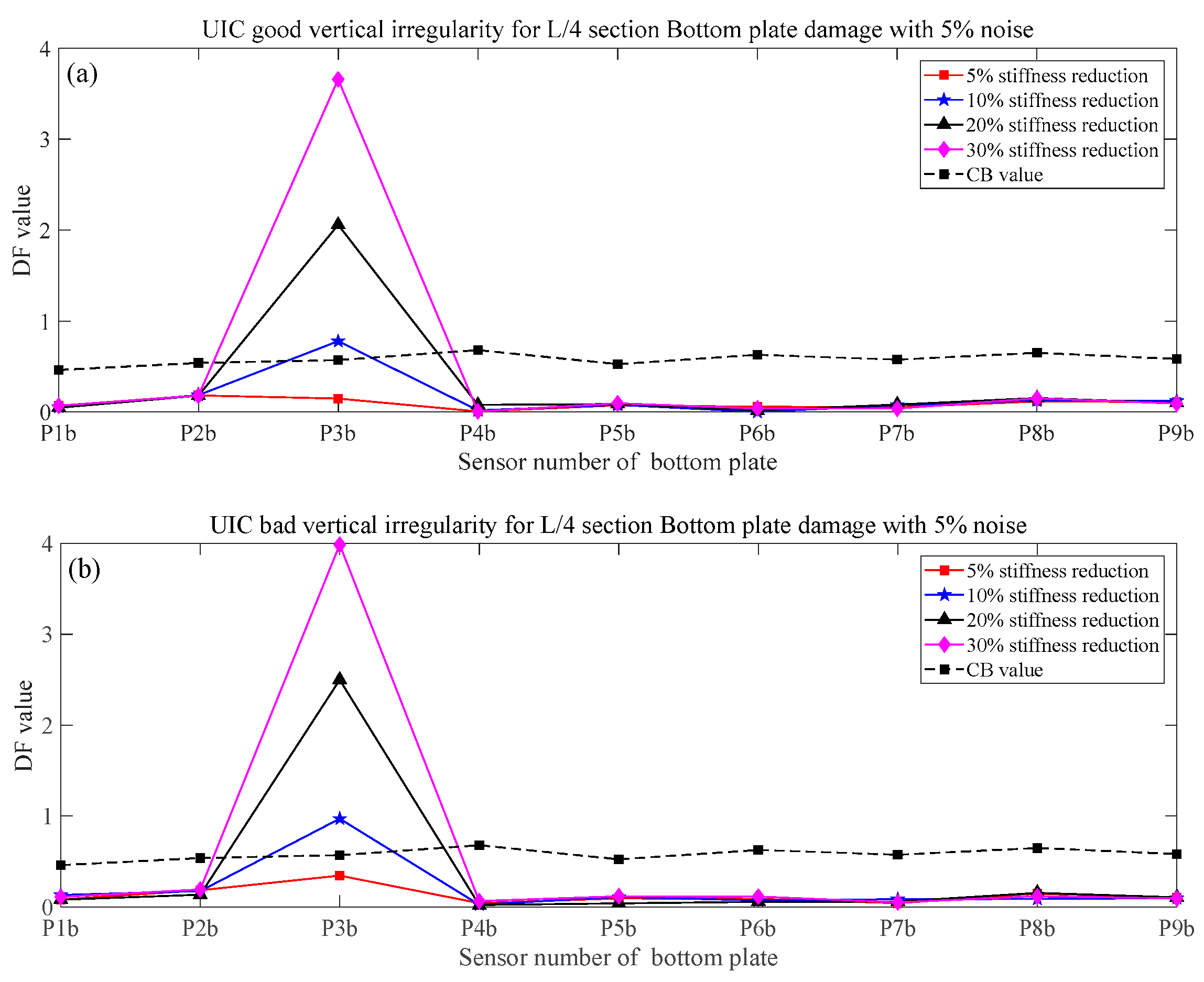
3.4. Effect of Different Vertical Track Irregularities, Train Weights, and Speeds
4. Conclusions
- Under the coupling effects of bending and torsion, the deformation of the box girder does not conform to the Euler beam bending theory. The global response of the box girder cannot reflect the local damage characteristics, and the traditional damage detection method based on the Euler beam theory cannot be applied. In this paper, the box girder section is divided into different components based on the plate element analysis method. The proposed method in this paper can successfully identify the potential damage of all components for a section by using four strain sensors.
- The numerical simulation results show that the proposed method in this paper is sensitive to train speed, so the train speed needs to be calculated first by using a radar speedometer or the related algorithm. Even under the effect of noise, different train weights, and vertical track irregularity conditions, when the stiffness reduction factor of components is large enough, the proposed method in this paper can effectively identify, locate, and quantify the damage.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Li, Z.; Zhuo, Y.; Di, H.; Wei, J.; Li, Y.; Li, S. Indirect displacement monitoring of high-speed railway box girders consider bending and torsion coupling effects. Smart Struct. Syst. 2021, 28, 827–838. [Google Scholar] [CrossRef]
- Azim, M.R.; Gul, M. Damage detection framework for truss railway bridges utilizing statistical analysis of operational strain response. Struct. Control. Health Monit. 2020, 27, e2573. [Google Scholar] [CrossRef]
- Huang, Y.; Beck, J.L.; Li, H. Bayesian system identification based on hierarchical sparse Bayesian learning and Gibbs sampling with application to structural damage assessment. Comput. Methods Appl. Mech. Eng. 2017, 318, 382–411. [Google Scholar] [CrossRef]
- Li, H.; Mao, C.-X.; Ou, J.-P. Experimental and theoretical study on two types of shape memory alloy devices. Earthq. Eng. Struct. Dyn. 2008, 37, 407–426. [Google Scholar] [CrossRef]
- Li, S.; Zhu, S.; Xu, Y.-L.; Chen, Z.-W.; Li, H. Long-term condition assessment of suspenders under traffic loads based on structural monitoring system: Application to the Tsing Ma Bridge. Struct. Control. Health Monit. 2012, 19, 82–101. [Google Scholar] [CrossRef]
- Li, S.; Wei, S.; Bao, Y.; Li, H. Condition assessment of cables by pattern recognition of vehicle-induced cable tension ratio. Eng. Struct. 2018, 155, 1–15. [Google Scholar] [CrossRef]
- Bao, Y.; Shi, Z.; Beck, J.L.; Li, H.; Hou, T.Y. Identification of time-varying cable tension forces based on adaptive sparse time-frequency analysis of cable vibrations. Struct. Control. Health Monit. 2017, 24, e1889. [Google Scholar] [CrossRef]
- Li, H.; Lan, C.M.; Ju, Y.; Li, D.S. Experimental and Numerical Study of the Fatigue Properties of Corroded Parallel Wire Cables. J. Bridge Eng. 2012, 17, 211–220. [Google Scholar] [CrossRef]
- Meixedo, A.; Santos, J.; Ribeiro, D.; Calcada, R.; Todd, M. Damage detection in railway bridges using traffic-induced dynamic responses. Eng. Struct. 2021, 238, 112189. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Y.; Yu, K. Steady-State Data Baseline Model for Nonstationary Monitoring Data of Urban Girder Bridges. Sustainability 2022, 14, 12134. [Google Scholar] [CrossRef]
- Zhou, Z.; Dong, K.; Fang, Z.; Liu, Y. A Two-Stage Approach for Damage Diagnosis of Structures Based on a Fully Distributed Strain Mode under Multigain Feedback Control. Sustainability 2022, 14, 10019. [Google Scholar] [CrossRef]
- He, X.; Tan, G.; Chu, W.; Zhang, S.; Wei, X. Reliability Assessment Method for Simply Supported Bridge Based on Structural Health Monitoring of Frequency with Temperature and Humidity Effect Eliminated. Sustainability 2022, 14, 9600. [Google Scholar] [CrossRef]
- Gao, X.; Duan, G.; Lan, C. Bayesian Updates for an Extreme Value Distribution Model of Bridge Traffic Load Effect Based on SHM Data. Sustainability 2021, 13, 8631. [Google Scholar] [CrossRef]
- Li, Z.; Ji, W.; Zhang, Y.; Ge, S.; Bing, H.; Zhang, M.; Ye, Z.; Lv, B. Study on the Reliability Evaluation Method and Diagnosis of Bridges in Cold Regions Based on the Theory of MCS and Bayesian Networks. Sustainability 2022, 14, 13786. [Google Scholar] [CrossRef]
- Glaser, S.D.; Tolman, A. Sense of Sensing: From Data to Informed Decisions for the Built Environment. J. Infrastruct. Syst. 2008, 14, 4–14. [Google Scholar] [CrossRef]
- Posenato, D.; Lanata, F.; Inaudi, D.; Smith, I.F.C. Model-free data interpretation for continuous monitoring of complex structures. Adv. Eng. Inform. 2008, 22, 135–144. [Google Scholar] [CrossRef]
- Yan, A.M.; Kerschen, G.; De Boe, P.; Golinval, J.C. Structural damage diagnosis under varying environmental conditions—Part I: A linear analysis. Mech. Syst. Signal Process. 2005, 19, 847–864. [Google Scholar] [CrossRef]
- Alvandi, A.; Cremona, C. Assessment of vibration-based damage identification techniques. J. Sound Vib. 2006, 292, 179–202. [Google Scholar] [CrossRef]
- Alves, V.; Meixedo, A.; Ribeiro, D.; Calcada, R.; Cury, A. Evaluation of the performance of different damage indicators in railway bridges. In Proceedings of the 1st International Conference on Structural Integrity (ICSI), Funchal, Portugal, l–4 September 2015; Volume 114, pp. 746–753. [Google Scholar]
- Santos, J.P.; Cremona, C.; Orcesi, A.D.; Silveira, P. Multivariate statistical analysis for early damage detection. Eng. Struct. 2013, 56, 273–285. [Google Scholar] [CrossRef]
- Cury, A.; Cremona, C. Assignment of structural behaviours in long-term monitoring: Application to a strengthened railway bridge. Struct. Health Monit. Int. J. 2012, 11, 422–441. [Google Scholar] [CrossRef]
- Posenato, D.; Kripakaran, P.; Inaudi, D.; Smith, I.F.C. Methodologies for model-free data interpretation of civil engineering structures. Comput. Struct. 2010, 88, 467–482. [Google Scholar] [CrossRef]
- Entezami, A.; Shariatmadar, H. An unsupervised learning approach by novel damage indices in structural health monitoring for damage localization and quantification. Struct. Health Monit. Int. J. 2018, 17, 325–345. [Google Scholar] [CrossRef]
- Adams, D.E.; Farrar, C.R. Classifying Linear and Nonlinear Structural Damage Using Frequency Domain ARX Models. Struct. Health Monit. Int. J. 2002, 1, 185–201. [Google Scholar] [CrossRef]
- Sohn, H.; Allen, D.W.; Worden, K.; Farrar, C.R. Statistical Damage Classification Using Sequential Probability Ratio Tests. Struct. Health Monit. 2003, 2, 57–74. [Google Scholar] [CrossRef]
- Bao, C.; Hao, H.; Li, Z. Vibration-based structural health monitoring of offshore pipelines: Numerical and experimental study. Struct. Control. Health Monit. 2013, 20, 769–788. [Google Scholar] [CrossRef]
- Ay, A.M.; Wang, Y. Structural damage identification based on self-fitting ARMAX model and multi-sensor data fusion. Struct. Health Monit. Int. J. 2014, 13, 445–460. [Google Scholar] [CrossRef]
- Mujica, L.E.; Gharibnezhad, F.; Rodellar, J.; Todd, M. Considering temperature effect on robust principal component analysis orthogonal distance as a damage detector. Struct. Health Monit. Int. J. 2020, 19, 781–795. [Google Scholar] [CrossRef]
- Cavadas, F.; Smith, I.F.C.; Figueiras, J. Damage detection using data-driven methods applied to moving-load responses. Mech. Syst. Signal Process. 2013, 39, 409–425. [Google Scholar] [CrossRef]
- Peeters, B.; De Roeck, G. One-year monitoring of the Z24-Bridge: Environmental effects versus damage events. Earthq. Eng. Struct. Dyn. 2001, 30, 149–171. [Google Scholar] [CrossRef]
- de Lautour, O.R.; Omenzetter, P. Damage classification and estimation in experimental structures using time series analysis and pattern recognition. Mech. Syst. Signal Process. 2010, 24, 1556–1569. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. An introduction to structural health monitoring. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 303–315. [Google Scholar] [CrossRef]
- Gonzalez, I.; Karoumi, R. BWIM aided damage detection in bridges using machine learning. J. Civ. Struct. Health Monit. 2015, 5, 715–725. [Google Scholar] [CrossRef]
- Nie, Z.; Lin, J.; Li, J.; Hao, H.; Ma, H. Bridge condition monitoring under moving loads using two sensor measurements. Struct. Health Monit. Int. J. 2020, 19, 917–937. [Google Scholar] [CrossRef]
- Magalhaes, F.; Cunha, A.; Caetano, E. Vibration based structural health monitoring of an arch bridge: From automated OMA to damage detection. Mech. Syst. Signal Process. 2012, 28, 212–228. [Google Scholar] [CrossRef]
- Ribeiro, D.; Leite, J.; Meixedo, A.; Pinto, N.; Calcada, R.; Todd, M. Statistical methodologies for removing the operational effects from the dynamic responses of a high-rise telecommunications tower. Struct. Control. Health Monit. 2021, 28, e2700. [Google Scholar] [CrossRef]
- Entezami, A.; Shariatmadar, H.; Karamodin, A. Data-driven damage diagnosis under environmental and operational variability by novel statistical pattern recognition methods. Struct. Health Monit. Int. J. 2019, 18, 1416–1443. [Google Scholar] [CrossRef]
- Datteo, A.; Busca, G.; Quattromani, G.; Cigada, A. On the use of AR models for SHM: A global sensitivity and uncertainty analysis framework. Reliab. Eng. Syst. Saf. 2018, 170, 99–115. [Google Scholar] [CrossRef]
- Yeager, M.; Gregory, B.; Key, C.; Todd, M. On using robust Mahalanobis distance estimations for feature discrimination in a damage detection scenario. Struct. Health Monit. Int. J. 2019, 18, 245–253. [Google Scholar] [CrossRef]
- Zhai, W.; Xia, H. Train-Track-Bridge Dynamic Interaction: Theory and Engineering Application, 1st ed.; Science Press: Beijing, China, 2011. [Google Scholar]
- Pan, C.-D.; Yu, L.; Liu, H.-L.; Chen, Z.-P.; Luo, W.-F. Moving force identification based on redundant concatenated dictionary and weighted l(1)-norm regularization. Mech. Syst. Signal Process. 2018, 98, 32–49. [Google Scholar] [CrossRef]
- Hou, R.; Xia, Y.; Bao, Y.; Zhou, X. Selection of regularization parameter for l(1)-regularized damage detection. J. Sound Vib. 2018, 423, 141–160. [Google Scholar] [CrossRef]
- Wang, H.; Zhu, Q.; Li, J.; Mao, J.; Hu, S.; Zhao, X. Identification of moving train loads on railway bridge based on strain monitoring. Smart Struct. Syst. 2019, 23, 263–278. [Google Scholar] [CrossRef]



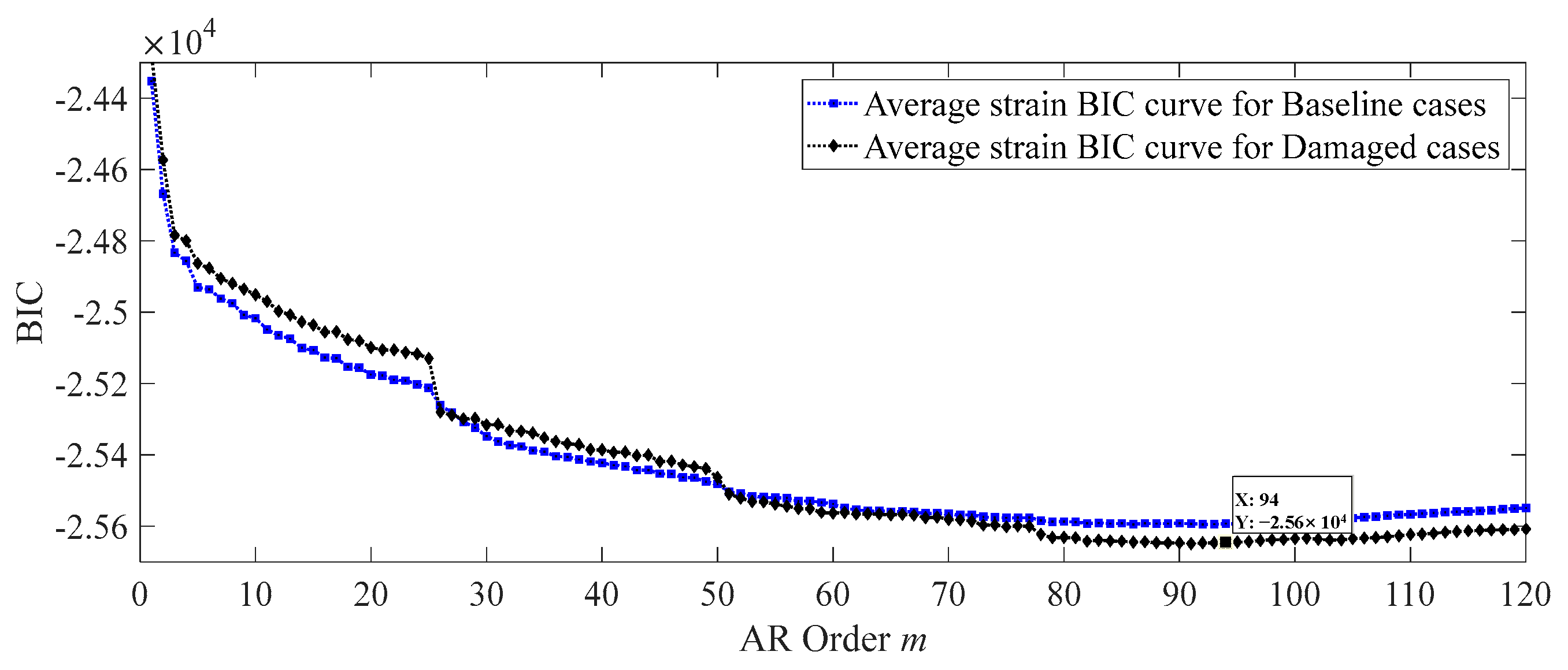

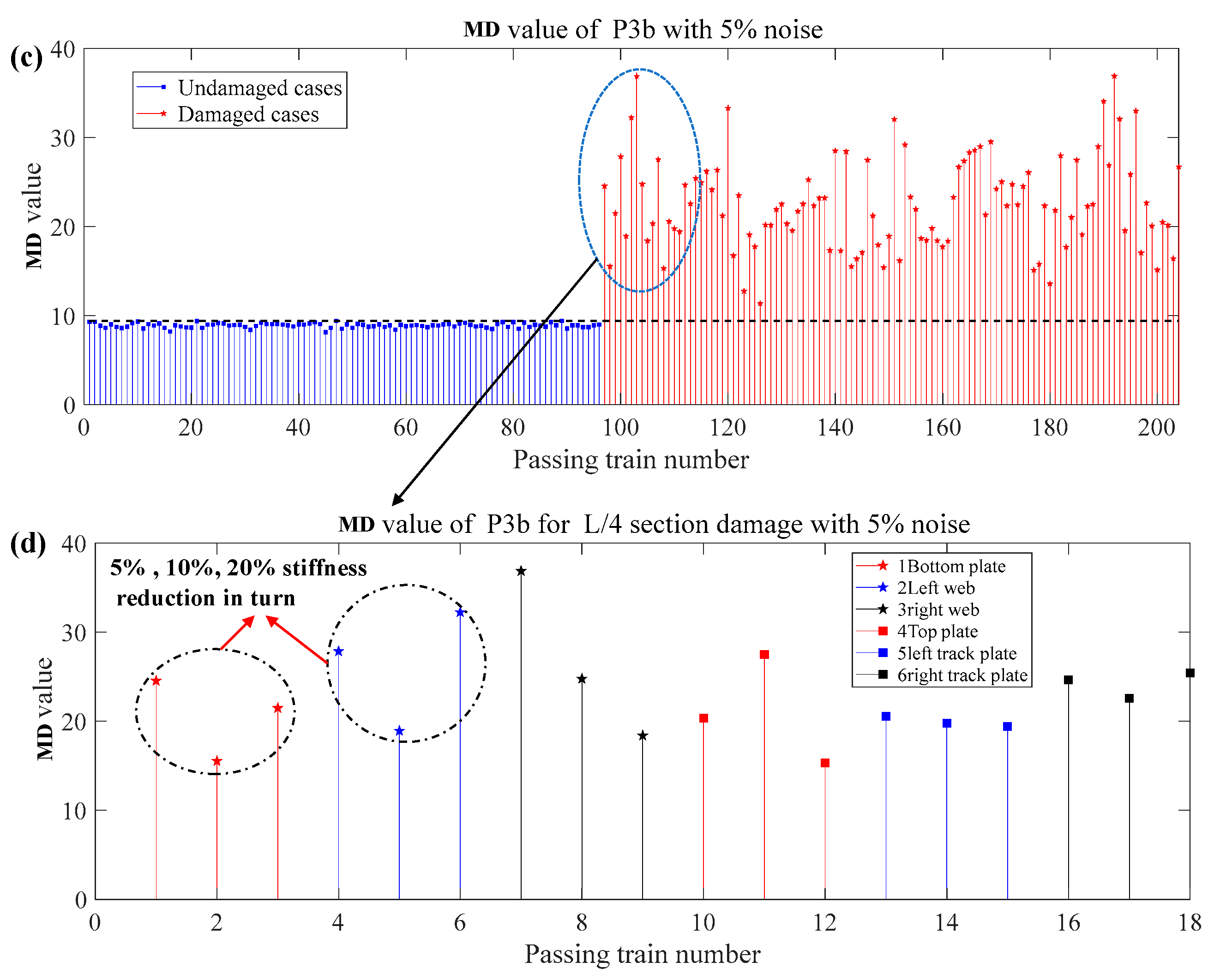
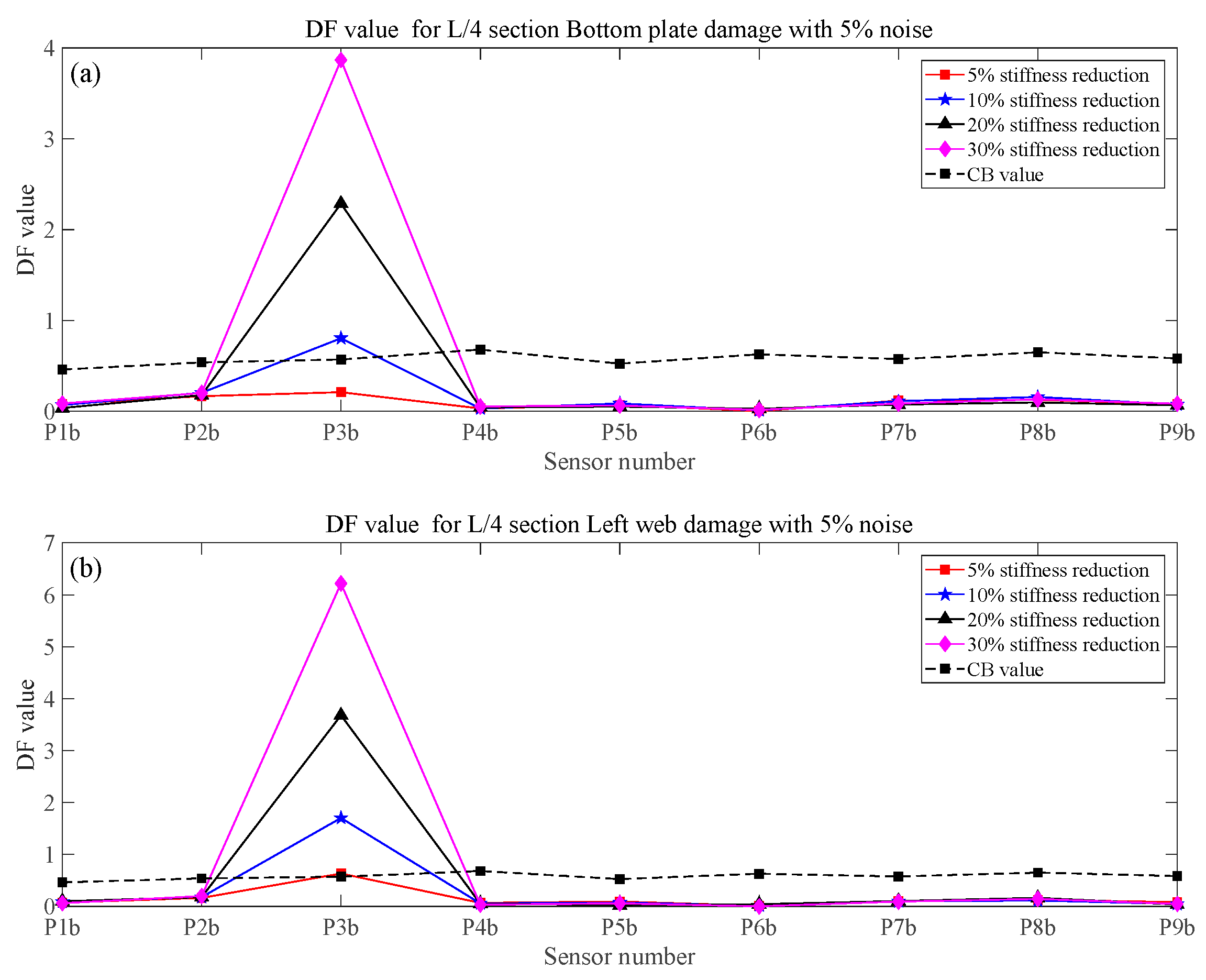
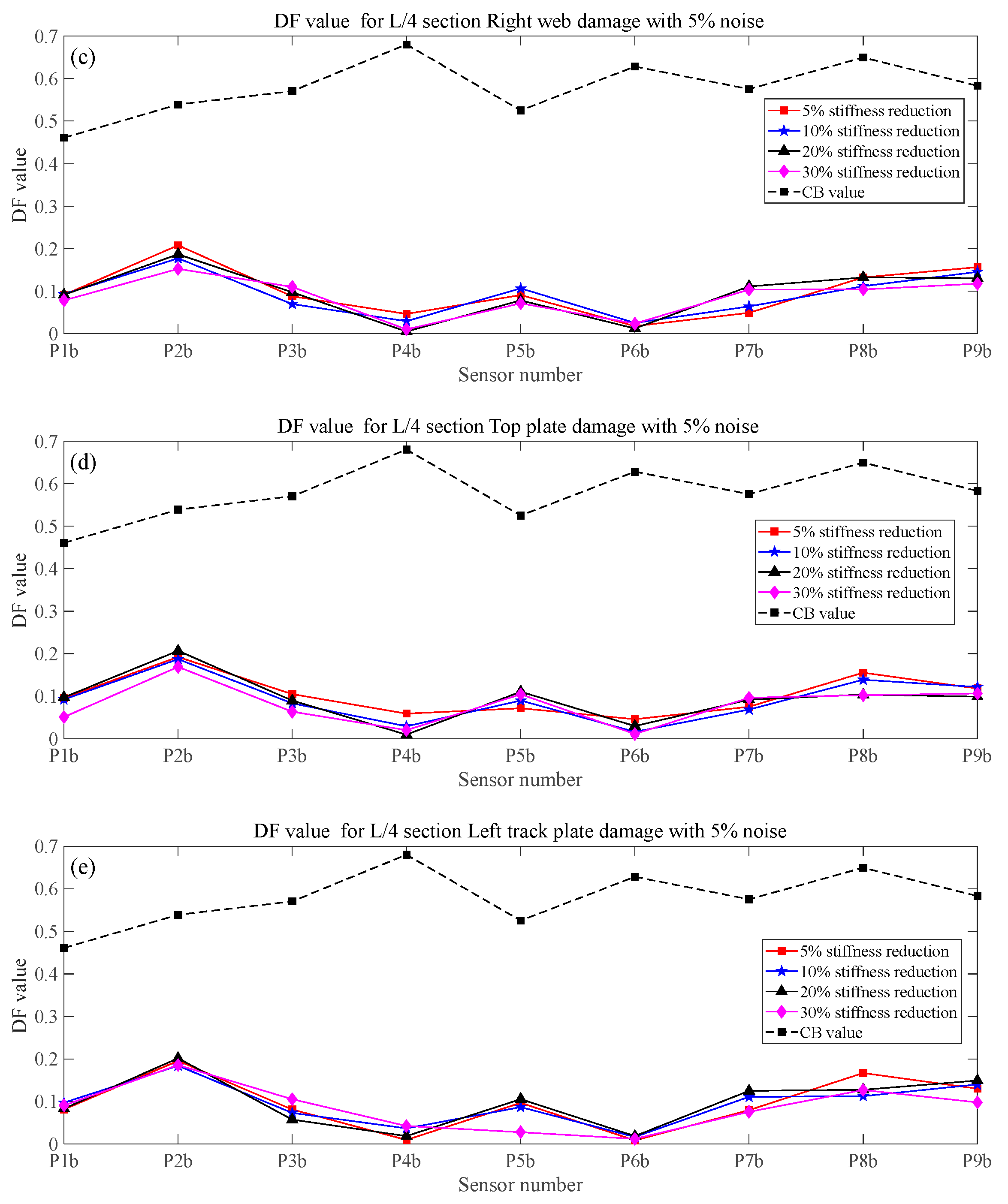




| Item | Element Type | Density (kg/m3) | Poisson’s Ratio | Elastic Modulus (N/m2) | |
|---|---|---|---|---|---|
| Main girder | Solid65 | 2681 | 0.202 | 4.29 × 1010 | |
| self-compacting concrete filling layer | 3.79 × 1010 | ||||
| Track plate | 4.06 × 1010 | ||||
| Other secondary dead loads | Element type | Value (N/m) | Elastic modulus(N/m2) | ||
| Mass21 | 6.702 × 104 | / | |||
| Prestressed steel | Element type | Density (kg/m3) | Poisson’s ratio | Elastic modulus (N/m2) | Coefficient of linear expansion |
| Link8 | 8005 | 0.3 | 1.95 × 1011 | 1.2 × 10−5 | |
| Rail | Element type | Density (kg/m3) | Poisson’s ratio | Elastic modulus (N/m2) | |
| Beam 188 | 7800 | 0.3 | 2.06 × 1011 | ||
| Spring fasteners | Item | Element type | Vertical | Longitudinal | Transverse |
| Elastic stiffness (N/m) | Combin14 | 5 × 107 | 3 × 107 | 3 × 107 | |
| Damping coefficient (N/(m/s)) | 6 × 104 | 6 × 104 | 7.5 × 104 | ||
| Train Number | Empty Train Weight (kN) | Number of Passengers | Total Weight (kN) | Average Axle Weight (kN) |
|---|---|---|---|---|
| M1 | 548.8 | 33 | 574.3 | 143.6 |
| T2 | 599.8 | 85 | 666.4 | 166.6 |
| M3 | 585.1 | 85 | 651.7 | 162.9 |
| T4 | 541.0 | 75 | 599.8 | 149.9 |
| T5 | 563.5 | 63 | 612.5 | 153.1 |
| M6 | 599.8 | 85 | 666.4 | 166.6 |
| T7 | 588.0 | 85 | 654.6 | 163.7 |
| M8 | 536.1 | 45 | 571.3 | 142.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhuo, Y.; Li, S. Damage Detection of High-Speed Railway Box Girder Using Train-Induced Dynamic Responses. Sustainability 2023, 15, 8552. https://doi.org/10.3390/su15118552
Wang X, Zhuo Y, Li S. Damage Detection of High-Speed Railway Box Girder Using Train-Induced Dynamic Responses. Sustainability. 2023; 15(11):8552. https://doi.org/10.3390/su15118552
Chicago/Turabian StyleWang, Xin, Yi Zhuo, and Shunlong Li. 2023. "Damage Detection of High-Speed Railway Box Girder Using Train-Induced Dynamic Responses" Sustainability 15, no. 11: 8552. https://doi.org/10.3390/su15118552
APA StyleWang, X., Zhuo, Y., & Li, S. (2023). Damage Detection of High-Speed Railway Box Girder Using Train-Induced Dynamic Responses. Sustainability, 15(11), 8552. https://doi.org/10.3390/su15118552








