Economic Loss Assessment for Losses Due to Earthquake under an Integrated Building, Lifeline, and Transportation Nexus: A Spatial Computable General Equilibrium Approach for Shelby County, TN

Abstract

Earthquakes have caused tremendous losses worldwide. Though unpredictable, comprehensive assessment of their impact on urban areas can facilitate effectiveness in mitigation strategies. This paper builds a spatial general equilibrium (SCGE) model for Shelby County, Tennessee, an area located in the most active seismic zone in the central and eastern U.S. Starting from the building, lifeline and transportation damages, this paper also develops means by which such damages can be integrated into the SCGE model for prompt effect estimation. Using novel approaches to represent substitution and shifting behaviors intra-regionally within the county, the model estimated a total of loss over $8 billion in domestic supply due to a hypothetical earthquake. Compared with the outcomes from the model without these behaviors, the magnitude of the losses is smaller in the model with these behaviors. This implies the resistance, resourcefulness and flexibility from economic resilience, as the level of physical damages do vary intra-regionally. Interestingly, although the percentage of losses in domestic supply varies almost linearly with the percentage loss in physical damage intra-regionally, the losses in employment are relatively evenly distributed. This also emphasizes the importance of the shifting and substitution behaviors which make the model profoundly spatial.

1. Introduction

Natural hazards occur frequently, and the costs associated with these events run well into billions of dollars [1]. During the last century, from 1900 to 1999, a total of 1248 destructive earthquakes have been estimated to have caused, in sum, more than USD 1 trillion in damage at modern values [2]. What needs to be noticed is the fact that, with earthquakes, modern technology has not made it possible to prevent them or give forewarning [3]. However, proper preparation and mitigation strategies can help decrease the losses generated from earthquakes, and these require improved assessment of the performance of the engineering, social and economic systems after the shocks.

In 1986, the National Science Foundation established a national center to promote earthquake studies at the State University of New York, Buffalo (Multidiscipline Center for Earthquake Engineering Research, MCEER). The objective was to conduct research using a multidisciplinary approach to provide an integrated understanding of the factors that can result in resilience within a community in response to an earthquake. To this end, economists at the center started by quantifying the direct and indirect losses, then turned to further developing methods to assess resilience for economic systems. Economic resilience was defined by Rose [4] as being the inherent and adaptive capacity to respond to hazards that allows communities to avoid potential loss and/or to recover from shocks more quickly.

Over the years, research testbeds such as the Memphis Metropolitan Area (New Madrid Seismic Zone) and the Portland Metropolitan Area (ocean floor Cascadian Subduction Zone) have been created. Studies on economic losses are back-ended, and probability distributions of the states of damage to existing structures and infrastructure corresponding to an earthquake is on the front end. However, due to multiple types of physical damages, integrated estimation is rare. Against this background, in 2014, the National Institute of Standards and Technologies (NIST) funded a ten-year grant to create a Center for Risk-Based Community Resilience Planning (CRBCRP). The center was unique in merging the disciplines of civil engineering, sociology, and economics to model community resilience comprehensively. Different from the MCEER center mentioned above, CRBCRP worked on multiple types of disasters, from earthquake to tornado, hurricane and flood. What remained unchanged was the testbed for projected earthquakes, which was the largest major population center potentially affected by major earthquakes in the New Madrid Seismic Zone. The regional boundary in the hazardous zone now extends outward from the city of Memphis to the whole county: Shelby County. The New Madrid Seismic Zone is the most active seismic zone in the central and eastern United States [5]; historically, very large earthquakes have occurred in this zone, such as the 1811–1812 sequence, and they are likely to occur in the future [6,7,8]. These facts make it urgent to assess the losses and understand the mechanisms of the losses in Shelby County relative to potential earthquakes.

As mentioned earlier, methods and models typically used to estimate the impact of earthquakes or other kinds of disasters have rarely managed to integrate all types of physical damages. Recent work has been performed in CRBCRP by engineers, including simulated outcomes in Shelby County, making such data readily available and internally consistent for such an integration. Additionally, current studies in disaster loss estimations have made improvements in incorporating dynamic or spatial features [9,10,11,12]. Nonetheless, the spatial feature for the model of the moment is inadequate regarding the spatial adjustment of workers and consumers in the aftermath of the shock.

Hence, this paper fills the gaps mentioned above. Work performed in this paper has the following contributions: firstly, it builds a spatial general equilibrium model (SCGE) for Shelby County, and improves the spatial aspect in the model to a larger extent, with behavior changes of firms prompting substitution of the same types of intermediate input materials among regions, and the behavior changes of households working and consuming among regions, given post-disaster conditions; secondly, it provides more detailed and more comprehensive descriptions of the means that integrate engineering and the economic model; thirdly, it examines jointly the economic impact from building damages, electricity transmission and water/wastewater pipeline damages, and transportation network disruptions, given the limitations of previous studies which only looked at one type of these physical damages at a time.

Results in this paper suggest that modeling the above behaviors allows the model to better mimic the real-world responses of the agents after external shocks. Adjusting to the spatial damages and shifting demand/supply to areas that are less damaged helps to reduce the loss for the economy. Moreover, such behaviors echo the concept of inherent resilience that was brought up by Rose [4], through which the local communities have their potential to avoid additional losses after any external shocks.

Meanwhile, when looking at the joint impact from building, utility and transportation network damages, the results suggest that the total impact could be overestimated by examining the impacts individually and then summing the losses together. The intuitive response is the Leontief production function, which reduces the efficiency level of a second and third type of physical damages. Trying to estimate the losses from one aspect of the damages in natural disasters by assuming other conditions stay the same would not provide the most accurate representation of the influences from such external shocks.

This paper is organized as follows: Section 2 reviews the current literature on economic impact analysis due to natural hazards; Section 3 describes the corresponding SCGE model; Section 4 illustrates steps transforming engineering outputs into economic inputs to simulate our SCGE model for short-run influences; Section 5 presents the simulated results concerning changes in major economic variables after the earthquake, Section 6 discusses the implications of the results, the limitations of the model and possible studies in the future; and Section 7 concludes the paper.

2. Literature Review

The history of measuring economic losses due to earthquakes started with the work accomplished by Cochrane et al. [13]. He used an input–output model to study the economic impact of a hypothetical earthquake in California. In such models, industries or firms are linearly linked with intermediate inputs based on the input–output (I–O) coefficients, coefficients that describe the value of inputs required from all industries to produce a certain value of outputs in each industry. When industries are directly damaged by the earthquake, it creates a supply bottleneck to other undamaged industries. Cochrane calculated this additional loss to be about $4 billion, followed by the direct loss of $10 billion worth of outputs. Following this direction, researchers have extended the context of the model under spatial and dynamic scenarios [14,15,16]. For instance, Hallegatte [16] developed an adaptive regional I–O mode to analyze both the reduction and recovery in capital stock after Hurricane Katrina.

Downsides to I–O models include linearity, rigidity and lack of behavior content. For example, I–O models do not allow for substitution between factor inputs or consumption outputs. Some researchers then transitioned to a computable general equilibrium (CGE) model; among them, one of the most representative works was from Adam Rose and his team. In Rose and Liao [17], the authors specified that there are several advantages of using a CGE model to analyze the economic impact of natural hazards.

First, CGE models not only contain features from other modeling techniques such as the input–output model or linear programming, but also allow for substitution between inputs (intermediate inputs, land, labor, and capital). In other words, CGE models can be disaggregated to different industries or production sectors in a manner similar to that of an I–O model, allowing industries to adjust between various types of inputs. Second, CGE models can address the roles of price and scarcity, which are used by firms and consumers to adjust their behavior accordingly. Last, CGE models are better in evaluating the roles of lifelines and infrastructure by placing a valuation on such services. Hence, CGE models are more realistic than I–O models because of the former’s behavioral adjustments and valuation processes for lifeline and infrastructure.

One limitation of Rose’s work is that it only provides losses from one aspect of the adverse condition after disasters, such as water and electricity outage, and other conditions like building damages or transportation network damages are not considered. Part of the limitation is resolved by Chang and Chamberlin [18], where they were able to integrate the building damages and water and electricity outages in an index called “Business Disruptiveness.” Still, the adverse impact from road network damages was not included, and, for areas such as Los Angeles that are densely populated, the normal functioning of the road network is essential.

Even though improvements have been made under the different categories discussed above, there have been few models that could consider how physical, economic, and social infrastructure systems interact and affect the responses to external shocks. To further facilitate integrated analysis in natural disasters, the NIST-funded Center for Risk-Based Community Resilience Planning has generated research that merges the disciplines of engineering, social sciences and economics [19]. Additionally, the types of disasters have extended from earthquakes to other risks such as tornados, hurricanes and tsunamis (see: Alam et al. [20]; Nofal et al. [21]; and Wang and van de Lindt, [22]). The work from the NIST-funded center mentioned above has created a platform called “IN-CORE” that allows multidisciplinary collaboration to happen (see: Attary et al. [23]; Roohi et al. [24]; and Wang et al. [25]). Using data from the engineering team at NIST, methods to jointly estimate the economic losses from building, utility and transportation damages can be developed. Nevertheless, multidisciplinary collaboration involves the complex work required to translate and transform the inputs and outputs for both the engineering and economic models, and the detailed description for this work has not been updated since Cutler et al. [19].

In the meantime, CGE studies on the topic of natural disasters have been improved in four categories: the first one is validating key model parameters using real-world observations [9]; the second one is building a spatial CGE model to better capture multiplier/spillover impacts due to business interruption [26]; the third one is the extension in natural hazards type (such as flooding or extreme weather events) [27,28,29] or damage type (from lifeline disruption to road/highway damages) [30]; the last one is extending the CGE model to a dynamic framework, so that both immediate damage and the long-run recovery process can be studied [11,12]. What is worth noticing is the concept of a spatial model. Most studies have extended the model to include intra-regional trade flows [10,27,31,32,33], but they neglect the intra-regional labor flows and their associated consumption behaviors. One possible explanation is the scope of the study areas; specifically, study areas are often spatially connected at the province or city level, where intra-provincial labor flows are rare. For metropolitan areas that are at high levels of mobility in commuting and consumption, though, further research is required in incorporating such behaviors.

In light of the limitations in the literature, our study introduced a novel approach to capture the spatial substitution behavior of firms and households, given post-disaster conditions. In addition, our work provides a detailed and comprehensive theoretical framework that can be translated, both to engineers and economists, regarding how bridges are built, allowing it to transform output from engineering models to economic models in hazard loss assessment. Its comprehensiveness in integrating building, water and electricity, and road network damages to disturbances in the regional economy has offered an opportunity to reveal the mechanisms within the general equilibrium model.

3. Shelby County, TN and the SCGE Model

3.1. Study Area and Data

Shelby County is in the southwest corner of Tennessee, and adjacent to the borders of Arkansas and Mississippi. One important feature of Shelby County is its commuting pattern, within and in/out of the area. To illustrate this, Figure 1 divided Shelby County into eight PUMA (public used micro-areas) regions. Using LODES (longitudinal employer–household dynamics (LEHD) origin–destination employment statistics) 2012 data which describe where people reside and work for the eight PUMA regions,

Table 1. Commuting pattern for Shelby County, TN (2012).

Work	A	B	C	D	E	F	G	H
Live
A (3201)	18%	12%	9%	6%	7%	5%	9%	10%
B (3202)	12%	19%	11%	8%	10%	8%	11%	8%
C (3203)	9%	9%	16%	12%	10%	6%	7%	7%
D (3204)	10%	8%	15%	23%	12%	7%	8%	6%
E (3205)	10%	11%	13%	16%	21%	12%	11%	7%
F (3206)	11%	11%	7%	9%	12%	28%	16%	12%
G (3207)	8%	9%	8%	5%	8%	10%	13%	13%
H (3208)	7%	5%	4%	3%	4%	4%	6%	12%
Outside	15%	14%	17%	18%	17%	20%	19%	27%
Total	100%	100%	100%	100%	100%	100%	100%	100%

presents the commuting pattern for the county. For example, in column 1, among the people who work in PUMA region A, 18 percent of them live in that region, 15 percent of them live outside the county, and the remaining 68 percent live in PUMA regions B to H.

Regarding the potential earthquake risks, Shelby County is in the so-called New Madrid Seismic Zone, with its northwest corner close to the epicenter. Zhang et al. [34] illustrated a hypothetical earthquake scenario for Shelby County. From their work, a higher level of ground motion due to earthquake is concentrated in the northwest corner of the county, while the southeast area only experiences a low-to-moderate level of ground motion. This implies the eight PUMA regions in the county will be impacted differently by natural hazards such as earthquakes.

Operationalizing the SCGE model requires a social accounting matrix (SAM) with the transaction flowing through all actors in the model and being balanced (

Table 2. Section and data flows in a social accounting matrix.

Sections in the SAM	Flow Segments	Data Sources
Firms	Sales Income (from Firms)	National Input Output Coefficients; Location Quotients
	Sales Income (from Households)	Consumer Expenditure Survey (CEX)
	Investments	Bureau of Economic Analysis
	Intermediate Input Payments	National Input Output Coefficients; Location Quotients (Bureau of Economic Analysis)
	Wage Payment	American Community Survey (ACS)
	Rental Rate of Capital Payment	County Assessors Data
	Tax Payment	Comprehensive Annual Financial Reports (CAFR)
Households	Wages Received	American Community Survey (ACS); Origin–Destination Employment Statistics (LODES)
	Rental Rate Received	County Assessors Data
	Expenditure and Saving	Consumer Expenditure Survey (CEX)
Government	Sales and Property Tax Received	Comprehensive Annual Financial Reports (CAFR)
	Public Expenditure	Comprehensive Annual Financial Reports (CAFR)
	Wage Payment by Public Sector	American Community Survey (ACS)
ROW (Rest of the World)	Import and Export	Bureau of Economic Analysis
	Income Outflow	Authors’ Calculation
	Public Transfers	Authors’ Calculation

). (A complete description of SAM can be found in Schwarm and Cutler [35]). The SAM is an integrated system of accounts in which wage and capital income inflows, consumption and investment outflows, and the public finance and expenditures are consistent. Since earthquakes impact the regions unevenly, it is necessary to construct a spatial SAM. Five data sources are utilized to present the spatial wage flows and capital stock as well as intermediate input demand. We start with the worker flow and their wage constructions, which are obtained by using the combination of LODES (longitudinal employer–household dynamics origin–destination employment statistics) and ACS (American Community Survey) data (Note that both LODES and ACS are publicly available.)

First, ACS provided micro-level information on households at the PUMA level. Households in each PUMA region were assigned into five groups, based on the income thresholds outlined in Appendix A 

Table A1. Thresholds for labor and household groups.

Labor Groups

L1 < $15,000

$15,001 < L2 ≤ $40,000

$40,000 < L3

Household Groups

HH1 ≤ 15,000

$15,001 < HH2 ≤ $35,000

$35,000 < HH3 ≤ $70,000

$70,000 < HH4 ≤ $120,000

$120,000 < HH5

. We then assigned all workers in each household their associated labor groups (L1, L2, and L3) according to the annual wage income thresholds defined in Appendix A Table A1. The microdata was then aggregated, and details can be found at Appendix A 

Table A2. Total wages and number of workers by household groups.

	Total Wages (in Millions)			Number of Workers
	L1	L2	L3	L1	L2	L3
HH1A	48.70	0.00	0.00	7054	0	0
HH2A	28.32	177.90	0.00	3513	8293	0
HH3A	17.26	180.11	209.16	2590	7101	4677
HH4A	4.96	64.37	344.54	761	2754	6502
HH5A	4.14	7.37	754.33	706	330	5713
HH1B	35.36	2.63	0.00	4479	123	0
HH2B	43.21	154.13	0.00	4958	7243	0
HH3B	29.59	156.99	191.87	3217	5652	4075
HH4B	13.78	85.65	374.98	1919	3469	6510
HH5B	0.64	22.87	731.41	66	890	6339
HH1C	15.79	0.00	0.00	2021	0	0
HH2C	17.20	133.34	0.00	2280	6195	0
HH3C	30.53	185.12	190.62	4241	7368	4225
HH4C	13.43	97.68	247.02	1351	3710	4604
HH5C	2.08	13.58	268.39	394	532	2596
HH1D	4.96	0.00	0.00	915	0	0
HH2D	12.09	53.88	0.00	1768	2629	0
HH3D	20.86	167.80	116.35	2568	6168	2486
HH4D	6.57	89.62	580.43	887	3605	10,215
HH5D	8.59	52.70	760.76	1591	2052	9004
HH1E	6.10	0.00	0.00	920	0	0
HH2E	21.06	88.86	0.00	2430	4048	0
HH3E	14.50	145.59	233.46	2701	6101	4881
HH4E	13.06	106.14	656.15	1790	4239	10,672
HH5E	1.55	55.18	921.50	329	2259	10,054
HH1F	1.80	0.00	0.00	161	0	0
HH2F	1.54	52.42	0.00	304	2442	0
HH3F	14.26	126.04	277.46	2382	4436	5615
HH4F	29.86	125.29	634.55	4793	4674	10,549
HH5F	16.59	55.94	2158.99	2977	2424	17,843
HH1G	25.65	0.00	0.00	2716	0	0
HH2G	31.28	185.73	0.00	3614	8697	0
HH3G	25.05	177.16	203.21	3237	7110	4482
HH4G	2.79	137.27	267.47	565	5039	4705
HH5G	5.26	11.67	332.60	673	498	2825
HH1H	28.80	0.00	0.00	3222	0	0
HH2H	16.55	124.30	0.00	2590	5347	0
HH3H	19.45	161.68	141.79	1923	6909	3185
HH4H	7.95	38.12	179.36	948	1343	3634
HH5H	4.75	19.60	144.26	476	763	1453

(For workers who work in Shelby County but live outside the county, ACS data was also collected and aggregated using the same labor group distinctions).

Next, the LODES data was utilized to link the labor groups with different commercial sectors spatially. The LODES data describes commuting flows for different groups of workers between each possible pair of census block of residence and census block of work. For confidentiality purposes, the workers are aggregated into three composite sectors: “Goods”, “Trade” and “Other”, which we will refer to as “commercial sectors” in our model (see Appendix A 

Table A4. Percent Increase in Travel Time for Each PUMA Pair.

PUMA	A	B	C	D	E	F	G	H
A	0%	—	—	—	—	—	—	—
B	3%	0%	—	—	—	—	—	—
C	12%	18%	0%	—	—	—	—	—
D	12%	50%	2%	0%	—	—	—	—
E	12%	20%	12%	4%	0%	—	—	—
F	5%	5%	11%	16%	4%	0%	—	—
G	10%	18%	22%	19%	8%	6%	0%	—
H	8%	5%	14%	14%	8%	5%	4%	0%

of crosswalks between the three sectors “Goods”, “Trade” and “Other” sectors and the NAICS (North American Industry Classification System) two-digit sectors). The LODES data was then aggregated from census block level to PUMA level using geographic crosswalks provided by the Census Bureau.

Besides the spatial information on laborers, spatial information on capital stocks was also needed. The Shelby County assessor’s office keeps records on each parcel of land in the county, such as the address, the assessed value, and the use of the structure (commercial and residential buildings). The residential properties or homes are grouped into three different residential groups (HS1, HS2, and HS3) based on the property value (HS1 ≤ $100,000, HS2 > $100,000, HS3—rentals) (Households demand services from these properties, such as maintaining the house, paying the mortgage or rent, repairing the house.) The commercial properties were aggregated into the “Goods”, “Trade” and “Other” sectors of the eight PUMAs in Shelby County, after being augmented with the Quarterly Census of Employment and Wages (QCEW) data. (QCEW data supply the address of each firm, the number of workers, the total wage bill, and the NAICS industry classification code.)

The firms’ intermediate input demands or I–O matrices come from the Bureau of Economic Analysis, which supplies a national I–O matrix based on NAICS codes. This was then scaled to a local I-O matrix using the location quotient (LQ) for Shelby County; LQ is an index that measures the level of concentration for an industry in a region.

For earthquakes, we used a hypothetical earthquake with a magnitude of 7.7 and an epicenter located at 35.3 N; 90.3 W. An engineering team in the NIST project developed the parcel-level damages for buildings and utilities, which were then aggregated at the PUMA level. They also provided the PUMA-to-PUMA travel efficiency losses due to road network damages. The engineering data is described in detail in Section 4.

3.2. The SCGE Model

Cutler et al. [36] described in detail the foundations of the CGE model used in this paper, and this provides a basic understanding of how the CGE model responds to economic shocks. However, in this paper, a substantial spatial component has been added to reflect the impact of an earthquake, which has important spatial characteristics. Given Figure 1 and Table 1 above, Shelby County has been divided into eight regions, in which workers can both reside and work in any of the regions. Therefore, if the spatial characteristics of the earthquake are changed, then the initial impact of the eight-region model will be different, resulting in an altered impact of economic outcomes. Our description of the model focuses on the equations that are impacted by the spatial characteristics of Shelby County.

3.2.1. Households

The SCGE model has forty household groups, which are categorized by income (indexed by $h, h\in H, H=\left(H1, H2,\dots ,H5\right)$) and PUMA region, as illustrated in Figure 1 (indexed by $s or r,s and r \in \mathrm{S}, \mathrm{S}=\left(\mathrm{PUMA} \mathrm{region} \mathrm{A}, \mathrm{B},\dots \mathrm{H}\right))$. Households will consume not only in their region of residence but also in the other seven regions. For simplicity, it is assumed that consumption outside their region of residence only comes from their workplace region. For example, households which both live and work in PUMA region A will not consume outside PUMA region A, but households who live in PUMA region A and work in PUMA region B will consume in PUMA region A and B in fixed proportions. Hence their utility maximization problem can be expressed in Equations (1)–(3) below:

$${\mathrm{V}}_{\mathrm{h}}^{\mathrm{s}}=\max U\left(F_{j,h}^{r,s}\right)$$

(1)

$$\mathrm{s}.\mathrm{t}. {\displaystyle \sum }_{r\in S}{\displaystyle \sum }_{j\in N}{P}_j^r{F}_{j,h}^{r,s}=I_h^s$$

(2)

$$for each r and r^{\prime }\in S \frac{P_j^r{F}_{j,h}^{r,s}}{P_j^{r^{\prime }}{F}_{j,h}^{r^{\prime },s}}=f\left(R{w}_h^{r,r^{\prime }}, {\delta }_h^s\right).$$

(3)

where ${\mathrm{V}}_{\mathrm{h}}^{\mathrm{s}}$ is an indirect utility function, $U_h^s$ is a direct utility function, $F_{j,h}^{r,s}$ is the quantity demanded from sector $j$ in region $r$ for households $h$ who live in region $s$, $P_j^r$ is the price for outputs produced by sector $j$ in region $r$, $R{w}_h^{r,r^{\prime }}$ is the relative proportions of households working in region $r$ versus $r^{\prime }$, and ${\delta }_h^s$. is the percentage of total consumption that goes to the place of work, when households live in region $s$ and work in other regions.

Equation (3) implies that for all households who live in region $s$ their consumption in region $r$ and $r^{\prime }$ depends on the relative ratio of households who work in region $r$ and $r^{\prime }$, respectively. Additionally, households who work outside their region of residence only spend part of their income in the region where they work; the remaining portion $\left(1-{\delta }_h^s\right)$. stays in the region they live, as suggested by Equation (3).

When disaster happens, the distribution of households working in different regions $\left(R{w}_h^{r,r^{\prime }}\right)$ will change, and their decision to work in one region versus another depends on the labor demand status as well as the convenience of commuting after the earthquake. This behavior change will be explained and modeled in detail in Section 4.

3.2.2. Firms

Firms use labor services and capital stock as inputs; labor is measured in the number of workers, while capital is measured in real dollar terms. The capital stock is essential, as substantial portions of it consist of buildings and types of equipment that will be damaged or destroyed. Firms also require intermediate inputs, but different from traditional non-spatial CGE models or the spatial model in Cutler et al. (2016) [19], firms can obtain the same type of intermediate inputs, say, agriculture inputs, from different PUMA regions with certain levels of substitution. Figure 2 below illustrates firms’ production techniques.

The level of final products at the first layer of Figure 2 is determined by inputting composite goods and value added based on the Leontief production function below:

$${\mathrm{DS}}_j^s=\min (\frac{V_j^s}{a_{vj}^s},\frac{x_{1j}^s}{a_{1j}^s},\dots \frac{x_{Nj}^s}{a_{Nj}^s})$$

(4)

where ${\mathrm{DS}}_j^s$ is the total output produced in sector $j$ region s, $V_j^s$ is the amount of value-added, $x_{ij}^s$ represents the intermediate inputs demanded by sector $j$ from sector $i$, and $a_{vj}^s$, $a_{ij}^s$ are the I–O coefficients. $V_j^s$ is determined by solving the cost-minimization problem in Equations (5)–(7) below:

$$V_j^s=min {\mathrm{w}}_{\mathrm{j}}^s{L}_j^s+r_j^s{K}_j^s$$

(5)

$$\mathrm{s}.\mathrm{t}. f(L_j^s,K_j^s)={{\eta }_j^s\{{\alpha }_L{\left(L_j^s\right)}^{\rho }+{\alpha }_K{\left(K_j^s\right)}^{\rho }\}}^{1/\rho }$$

(6)

$$L_j^s\le \overline{L{S}_j^s}; K_j^s\le \overline{K{S}_j^s}$$

(7)

where ${\eta }_j^s$ is total factor productivity, ${\alpha }_L$ and ${\alpha }_K$ are share parameters of labor and capital inputs, and $(1/(1-\rho \left)\right)$ is the elasticity of substitution between labor and capital. $\overline{L{S}_j^s}$ and $\overline{K{S}_j^s}$ are the initial endowments of labor and capital stock in region $s$.

Composite goods on the left-hand side at the second tier of Figure 2 are assumed to follow the CES production techniques, and the composite goods consist of the same type of intermediate inputs from all eight PUMA regions. The use of each type of intermediate input from each region is determined by the cost-minimization problem in Equations (8) and (9):

$$min {\displaystyle \sum }_{r\in S}{P}_i^r{x}_{ij}^{rs}$$

(8)

$$s.t. x_{ij}^s={\varnothing }_{ij}^s{({\displaystyle \sum }_{r\in S}{\beta }_{ij}^{rs}{(x_{ij}^{rs})}^{\phi })}^{1/\phi }$$

(9)

where ${\varnothing }_{ij}^s$ is the scale parameter, ${\beta }_{ij}^{rs}$ is the share parameter, and ($1/\left(1-\mathsf{\phi }\right)\equiv \mathsf{\epsilon }$) is the elasticity-of-substitution parameter.

Solving for the cost-minimization problem in Equations (8) and (9) gives the optimal demand on product $i$ produced in region $r$. The solution is described in Equations (10) and (11) below:

$$x_{ij}^{r,s}={\mathsf{\Gamma }}_{ij}^{rs}{\left[{\displaystyle \sum }_{r\in S}{({\beta }_{ij}^{r,s})}^{\epsilon }{\left(P{R}_i^{r,s}\right)}^{\epsilon \phi }\right]}^{-\frac{1}{\phi }}$$

(10)

$$where {\mathsf{\Gamma }}_{ij}^{rs}=\frac{1}{{\varnothing }_{ij}^s}{\left[{\beta }_{ij}^{rs}\right]}^{\epsilon }\left(a_{ij}^{s}D{S}_j^s\right);P{R}_i^{r,s}=P_i^r/P_i^s$$

(11)

When external shocks are spatially distributed, firms located in region $r$ can re-adjust their intermediate input demand on product $i$ produced in region $r$ – $x_{ij}^{rs}$, based on the relative prices of the same product $i$ produced in all other regions $\left(P{R}_i^{r,s}, r=A,B,\dots ,H\right)$.

3.2.3. Government

The government is de-composed as federal, state, and local governments. The federal government collects federal income taxes from local households, while the state government collects sales and income taxes from firms and households separately. The local government collects property taxes, local sales tax, and all other taxes and fees, such as license taxes and permits. Governments also buy commodities produced from commercial sectors and demand labor. In the model, the governments run a balanced budget, meaning that they do not run any type of deficits or surpluses.

3.2.4. Rest of the World (ROW)

Shelby County trades with neighboring local economies as well as foreign sectors to import goods and services that are consumed by local households. Additionally, it demands workers from neighboring economies, and these workers will bring their wage income outside of the county. Similarly, local households who commute to work outside the area will bring income into Shelby County. (For the year 2012, 84,014 was the number of workers who went out of Shelby County for work, which is about 18.5% of the number of workers in Shelby County, and they brought a total of USD 1882 million of income into Shelby County, which also means on average, each worker brought in about USD 22,401 annual income.)

3.2.5. Spatial Behaviors in Labor Market and Model Closure

Different from previous spatial CGE models that only allowed for the intra-regional trade of intermediate inputs, the model in this paper also allows for intra-regional commuting of workers. As a result, the supply of labor depends on wages provided both locally and outside Shelby County. Equation (12) is the labor supply decision made by households:

$$L{S}_h^s=F\left(w{a}_h^s, w_{co }, t,g\right)$$

(12)

where $w{a}_h^s$ is the average wage received in household group $h$ who lives in region $s$, $w_{co }$ is the wage offered outside the Shelby County, $t$ is the income tax rate, and $g$ is government transfer.

The modified labor-supply equation takes wage, total government transfer, and taxes into account. It is different from the conventional CGE model, in that out-commuting wages are considered. If wages outside Shelby County increase, denoted by $w_{co}$, the proportion of working households will also increase because of this change.

Markets closure conditions include:

(a)

The factor demand and factor supply (including intermediate inputs) are equal;

(b)

The supply of goods equals the demand for goods in each sector;

(c)

The government sector’s budget is balanced.

Next, general equilibrium systems were finalized with realistic utility and production functions and parameters, and we then ran the model until the equations of the model exactly reproduced the data and the benchmark equilibrium in our social accounting matrix. Recall that we have built a social accounting matrix (SAM) in Section 3.1, which described how firms, households, and the relevant government entity interact with each other to create a functioning economic region. After calibration was performed successfully, the model was used to run simulations describing different shocks in the aftermath of an earthquake, and Section 4 below describes in detail the framework and the methods used to simulate the model.

4. Modeling Earthquake Impact

This section presents the frameworks through which different types of physical damage can result in economic losses, and how the physical damages data are translated as external shocks to the SCGE model for loss assessment. As illustrated in Figure 3 below, earthquake can cause three types of physical damages, which are building damages, water and electricity outages, and transportation network damages. For regional economies, these physical damages become two channels of disturbances to firms and households in the economy. The first channel of disturbance comes from building functionality loss, and the second channel of disturbance comes from travel efficiency loss. Within the economic system, we renamed these separate disturbances as reduction in capital stock and rise in travel costs. The two disturbances generated four kinds of responses for firms and households. Finally, these responses lead to reductions in regional aggregate supply and aggregate demand, which are accompanied by losses in output, income and employment (rate). Hence, we will describe in detail in the rest of this section how the outputs provided by the engineers were mathematically turned into external shocks in order to enter the SCGE model.

4.1. Functionality Loss for Buildings

4.1.1. Commercial Buildings

There are two situations in which commercial buildings cannot operate properly for production: ① The buildings are not damaged, but the water pipelines or electricity transmission lines are damaged. (For almost all states, when water or electricity is not functioning for commercial buildings, state regulations prevent commercial businesses from opening, and we model this as a loss in capital stock.); ② The buildings are physically damaged to a safety-threatening condition, regardless of the availability of the utilities. For a SCGE model, commercial buildings are treated as a factor of production called capital stock. To use the capital stock, firms must pay the rental rate, which is similar to the wages paid to the workers.

Understanding the above situations, we now identify to what extent the capital stock will be reduced for industries in each PUMA region. At the parcel level, building damages were indexed to different levels of functionality status, and the engineers defined and described five functionality states as (Lin and Wang [37], p. 98):

• Restricted Entry (RE): Extensive structural or non-structural damage that threatens life or safety regardless of utility availability.
• Restricted Use (RU): Moderate structural or non-structural damage that does not threaten life or safety, regardless of utility availability
• Ro-occupancy (RO): Minor to moderate structural and non-structural damage, but utilities are unavailable.
• Baseline Functionality (BF): Minor cosmetic structural and nonstructural damage with critical utilities available (power, water, fire sprinklers, lighting, and HVAC systems).
• Full Functionality (FF): No damage, and all utilities are available.

In the above definitions, buildings under RE and RU are consistent with situation ②, and buildings under RO are consistent with situation ①. A building under functionality status RE, RU, or RO is not going to be used as an operational factor of production, so its value as capital is zero. Subtracting these zero-valued capital entities from the initial endowment will give the post-disaster level of capital stock. In the simulation, the new level of endowment in capital stock, $\overline{K{S}_j^{s\left(1\right)}}$, will go back to Equations (5)–(7), for re-optimization.

$${\zeta }_j^{s\left(1\right)}=1-\overline{K{S}_j^{s\left(1\right)}}/\overline{K{S}_j^{s\left(0\right)}}$$

(13)

where $\overline{K{S}_j^{s\left(0\right)}}$ is the capital stock endowment for sector $j$ in the region $s$ before the earthquake.

Again, we assume that buildings that are under the categories of no damage, or minor structural damage, except for unavailability of utilities are not functional. Even though in reality, such buildings may be in a situation where some types of utilities are available, but not all of them. This may allow them to maintain some level of production at smaller capacities if it is legal to do so. At this point, we are not able to incorporate this scenario, and there may be no need to capture such margins.

4.1.2. Residential Buildings

When residential buildings are damaged, people may be forced to migrate out of the county, and such reduction in population will lead to a decrease in aggregate demand and labor supply. To model this, the same logic used in Section 4.1.1 is used to calculate the loss ratio of residential building, and this is summarized in Equation (15) below:

$${\zeta }_h^{s\left(1\right)}=1-\overline{N_h^{s\left(1\right)}}/\overline{N_h^{s\left(0\right)}}$$

(14)

where $\overline{N_h^{s\left(0\right)}}$ and $\overline{N_h^{s\left(1\right)}}$ are the total number of functional buildings in the region $s$ for household group $h$ before and after the earthquake.

Then this loss ratio is going to impact household migration. Based on Berck et al. [38], household migration is a function of disposable income and unemployment rate. Here we extend the function to include residential building damage. In fact, several studies that looked at New Orleans’ evacuees and their decision to return after Hurricane Katrina have found that the probabilities of returning to New Orleans did relate to housing damages. (Paxon and Rouse, [39]; Fussell et al. [40]; Groen and Polivka [41]). Hence, household migration can be expressed in Equation (15) below:

$$H{H}_h^{s\left(1\right)}=f\left({\zeta }_h^{s\left(1\right)},Y{D}_h^{s\left(1\right)},U{E}_h^{s\left(1\right)};H{H}_h^{s\left(0\right)}\right)$$

(15)

4.2. Travel Efficiency Loss (TEL)

The civil engineering team used the travel time and travel efficiency for each PUMA pair to portray the transportation network damages after the earthquake. For example, as given in Appendix A Table A4, the estimated travel efficiency between PUMA region A and PUMA region C is 88 percent of the pre-disaster condition, i.e., the travel time is increased by 12 percent. This increase in travel time is denoted by variable $T{T}^{r, s \left(1\right)}$.

4.2.1. Firms’ Response to TEL

For firms, the damaged transportation network increases the shipping costs among regions as well as the waiting times to obtain materials needed for production. To model these impacts, a perceived price inflator ($P{I}_j^{r,s\left(1\right)}$) was used to reflect the rising travel costs of intermediate inputs in each origin–destination pair. Recall, from Equation (10) in Section 3, that firms’ demand for intermediate inputs is a function of their own prices and the prices of the substitutes. We multiplied the prices by the perceived price inflator to capture the impact from road network damages, as firms would be re-adjusting to post-disaster conditions.

Imagine that $P{I}^{r,s\left(1\right)}>1$ and $P{I}^{r^{\prime }, s\left(1\right)}=1, for r^{\prime }\ne r$, which implies only the road to region $r$ is damaged. Then the perceived price on product $i$ produced in region $r$ goes up, meaning that firm $j$ now would want to substitute more product $i$ from another region $r^{\prime } \left(r^{\prime }\ne r\right)$ instead, and this is equivalent to $\frac{\partial x_{ij}^{r^{\prime }s\left(1\right)}}{\partial P{I}^{rs\left(1\right)}}\ge 0, r^{\prime }\ne r$ and $\frac{\partial x_{ij}^{rs\left(1\right)}}{\partial P{I}^{rs\left(1\right)}}\le 0$.

The price inflator for the firms is calculated using Equation (16) below:

$$P{I}_j^{r,s\left(1\right)}=\left(1+{\tau }_j\times {\mathrm{TT}}^{r,s}\right)$$

(16)

where ${\tau }_j$ measures the contribution of shipping time in the valuation of the intermediate inputs. According to the empirical work performed by Hummels and Schaur [42], a one-day (5%) delay of the transit time is equivalent to 0.6 to 2 percent value of the good, based on the US monthly import data from 1991 to 2005. Hence, it is equivalent to saying that a 1% increase in shipping time is equivalent to 0.12 to 0.4 percent value of the good. The high-end value of 0.4 was applied in the simulation.

Meanwhile, the damaged road networks can extend the time in which firms receive their intermediate inputs, and as a result, reduce the total factor productivity (TFP) of firms. Since the intermediate inputs come from all eight PUMA regions, only the inputs that arrive the latest will matter in influencing the firms’ production process. The shock to the total factor productivity ${\eta }_j^s$ is modeled in Equation (17) below:

$$\mathrm{TFP}\equiv {\eta }_j^{s\left(1\right)}={\eta }_j^{s\left(0\right)}(1-{\tau }^{TFP}\times \underset{r}{\max }{\mathrm{TT}}^{r,s})$$

(17)

where the ${\eta }_j^{s\left(0\right)}$ and ${\eta }_j^{s\left(1\right)}$ are the level of TFP for firm $j$ in region $s$ before and after the earthquake, and ${\tau }^{TFP}$ is the contribution of transportation for TFP. For the value of ${\tau }^{TFP}$, a survey of literature by Isaksson [43] suggested that infrastructure contributes 15% to TFP changes, or ${\tau }^{TFP}=0.15$.

4.2.2. Households’ Response to TEL

For households who commute to work, TEL will change the likelihood that households will supply labor to other PUMA regions. For example, when under the same/similar wage rate, if an earthquake increases the cost of travel to region B more than to region A, households would prefer to work in A instead, and firms in PUMA region B would need to pay higher wages to attract workers. To model this, the relative proportions of households working in region $r$ versus $r^{\prime }$, or variable $R{w}_h^{r,r^{\prime }}$, was determined as a function of commuting time, as well as of the firms’ ability to maintain their employment levels. Equation (18) below gives the functional form.

$$R{w}^{r,r^{\prime }\left(1\right)}=\frac{1+{ϵ}_h{\mathrm{TT}}^{r,s}}{1+{ϵ}_h{\mathrm{TT}}^{r^{\prime },s}}\times \frac{F{D}^{r\left(1\right)}}{F{D}^{{r^{\prime }}^{\left(1\right)}}}$$

(18)

where ${ϵ}_h$ is the responsiveness of labor supply with respect to commuting time for household $h$.

For a reasonable estimate of the responsiveness of labor supply decisions to changes in commuting time, Black et al. [44] found that a 1-min (2%) increase in commuting time is associated with a 0.3 and 0.15 percent reduction in the labor force participation rate for high-school graduates and those with a bachelor’s degree, respectively. (The Federal Reserve Bank of St. Louis calculated the daily average commuting time for workers by year in Shelby County, and in 2018, this number was 46 min, which implies that a 1-min increase in commuting time is equivalent to 2 percent increase from the average commuting time.) Therefore, the elasticity of the labor supply decision to commuting time ranges from −0.075 to −0.15 in the simulation. For household groups 4 and 5, whose annual income is above $70,000, we apply the responsiveness value of −0.075, as they are more likely to have a bachelor’s degree. For household groups 1 to 3, the responsiveness value of −0.15 is used.

To model the consumption demand change, a price inflator ($P{I}_h^{r,s\left(1\right)}$) was also imposed on the household’s consumption function, with the same idea as the price inflator imposed in the firms’ intra-regional demand on intermediate inputs. The calculation of the price inflator for households is also similar to Equation (16), but with a different level of ${ϵ}^{dr}$, which measures the contribution of travel time in the perceived value of commodities by households. To quantify ${ϵ}^{dr}$, we first obtained estimates on the percentage of gasoline spending relative to total consumption expenditure. (Note that consumption behavior also includes leisure-related activities.) Then, the relative ratio of driving time spent on consumption (about 79%) was calculated from the American Time Use Survey. (Detailed information about time spent in primary activities from American Time Use Survey were accessed 23 April 2022 at the Bureau of Labor Statistics via the link https://www.bls.gov/tus/a1-2018.pdf.) As a result, the process of calculating the perceived price inflator for households can be summarized in Equation (19) below:

$$P{I}_h^{r,s\left(1\right)}=\left(1+{ϵ}^{dr}\times {\mathrm{TT}}^{r,s}\right)$$

(19)

5. Results

This section has two subsections. Section 5.1 focuses on the simulation results due to building damages using the current model and compares it to either the old model in Cutler et al. [19], or the old model in the present study. Current specifications consider the spatial behavior of firms purchasing intermediate inputs from different regions, and the commuting behavior at sub-county-level as well as the spatial consumption behavior of households in different regions. Detailed differences between the two models are listed in

Table 3. Differences between the old model and the new model.

	Highlighted Features	Old Model	New Model
For Firms	Intraregional substitution in intermediate inputs	No	Yes
	Shipping costs in decision-making	No	Yes
	CES production function	Yes	Yes
For Households	Intraregional labor supply decision	No	Yes
	Consumption adjustment by place of work	Yes	Yes
	Consumption decision based on travel time	No	Yes

below. The comparation between the two reveals the resilience behind these behaviors. Section 5.2 provides the simulation results under both building functionality loss and transportation network damage using the new model.

5.1. Results with Current Model and the Old Model

Table 4. Simulation results for the original model and the new model.

Major Economic Variables		Current Model	Old Model
		(1)	(2)
Domestic Supply	Change (million USD)	−8010.64	−8160.67
	Percent change	−12.27%	−12.50%
Employment	Change (number)	−30,815.95	−32,187.27
	Percent change	−6.79%	−7.09%
Household Income	Change (million USD)	−574.29	−482.29
	Percent change	−2.57%	−2.16%
Unemployment Rate	Change	1.95%	2.18%
Outmigration	Change (number)	−16,059.35	16,058.44
	Percent change	−4.64%	−4.64%

presents the simulation results in terms of major economic variables in Shelby County, with damages to buildings/capital stock. (Detailed numbers on the level of damage can be found in Appendix A 

Table A5. Capital Stock Destruction as A Percent of Initial Value (Production Sector).

Commercial Sectors	PUMA Regions	Capital Stock Destruction (%)
Goods-Producing Industries (Goods sector)	A	29.40%
	B	25.30%
	C	20.20%
	D	28.60%
	E	11.60%
	F	11.30%
	G	0.00%
	H	31.90%
Trade, Transportation, and Utilities (Trade sector)	A	44.90%
	B	33.60%
	C	35.40%
	D	32.60%
	E	23.60%
	F	17.30%
	G	25.50%
	H	31.90%
Other sectors	A	44.80%
	B	35.00%
	C	33.00%
	D	31.10%
	E	12.40%
	F	19.30%
	G	16.70%
	H	26.40%

and

Table A6. Capital stock destruction as a percent of initial value (Housing Sector).

Residential Sectors	PUMA Regions	Capital Stock Destruction (%)
HS1 (Single Family Homes that are below the median market value)	A	45%
	B	42%
	C	45%
	D	44%
	E	38%
	F	33%
	G	39%
	H	41%
HS2 (Single Family Homes that are above the median market value)	A	44%
	B	40%
	C	41%
	D	41%
	E	36%
	F	33%
	G	37%
	H	40%
HS3 (Rental Homes)	A	47%
	B	45%
	C	46%
	D	44%
	E	34%
	F	29%
	G	34%
	H	43%

.) Before comparing the differences between our current model with the old model, the common, or general, theme indicates that, when Shelby County experiences an earthquake, the total output produced/domestic supply falls, as well as the employment and household income. People also migrate out of the county due to housing damages. When looking at the magnitude of the impact, the percentage loss in total output is the largest and the percentage loss in household income is the smallest. The intuition is that there are offsetting effects from wages and the rental rate of capital. When the buildings are damaged and the households are forced to leave, capital and labor inputs both become more expensive for firms. The rise in wage rates and the rate of return on capital offsets the drops of employment and capital regarding household income.

Generally speaking, if firms and households could adjust their behavior accordingly after the earthquake, then these behavior adjustments, or the idea of inherent resiliencies defined in Rose [4], could reduce losses to some extent. Comparing column (2) versus column (1) of Table 4, as we expected, the inclusion of the behavior adjustment for firms to substitute their input demand as to the same type of product from more damaged regions to less damaged regions helped to reduce the total loss in firms’ output and employment. The rise in the unemployment rate for households is also smaller in the new model compared to the original model. Unlike what one might expect, though, the current model comes with a larger fall in household income (from USD 482 million to USD 574 million.).

To understand the additional income loss, recall the fact that both the rise in wages and the rental rate of capital offsets the loss in household income. With the current model, the re-adjustment that workers flow to regions where they can maintain the level of labor demand as much as possible makes firms able to more easily obtain labor inputs. This has two impacts: when firms find it easier to hire workers, the wage rate will not go up as much compared to the conventional model; meanwhile, it allows firms to substitute easily into labor, which offsets some of the negative impact from losses in capital, and the rental rate of capital will rise by a smaller amount. (For the original model, the weighted rise in rental rate of capital and wage rate are 3.74% and 13%, but the rise in rental rate of capital and wage rate in the new model are 3.69% and 12%, smaller than the rise compared to the original model.) Therefore, when the wage and rental rate rise at a smaller pace, the current model brings a larger fall in household income, which is more realistic.

Table 5. Distributional impacts on output, income and employment.

PUMA Regions	Capital Stock Destruction (Commercial)	Domestic Supply Loss	Household Income Loss	Employment Loss
	(1)	(2)	(3)	(4)
A	41.84%	−12.88%	−9.20%	−7.24%
B	33.42%	−12.66%	−4.37%	−7.66%
C	33.39%	−12.75%	−4.95%	−7.78%
D	31.41%	−11.79%	−3.00%	−7.45%
E	17.48%	−8.60%	0.30%	−7.40%
F	16.22%	−7.48%	3.57%	−6.30%
G	19.35%	−8.69%	−1.34%	−7.20%
H	31.30%	−11.27%	−5.70%	−7.15%
Correlation coefficient	—	0.96	0.94	0.49

continues with the distributional impacts on total output and household income by PUMA regions. First, we can observe that larger capital stock damages come with a larger fall in total output produced, and larger capital stock damages imply larger household income fall.

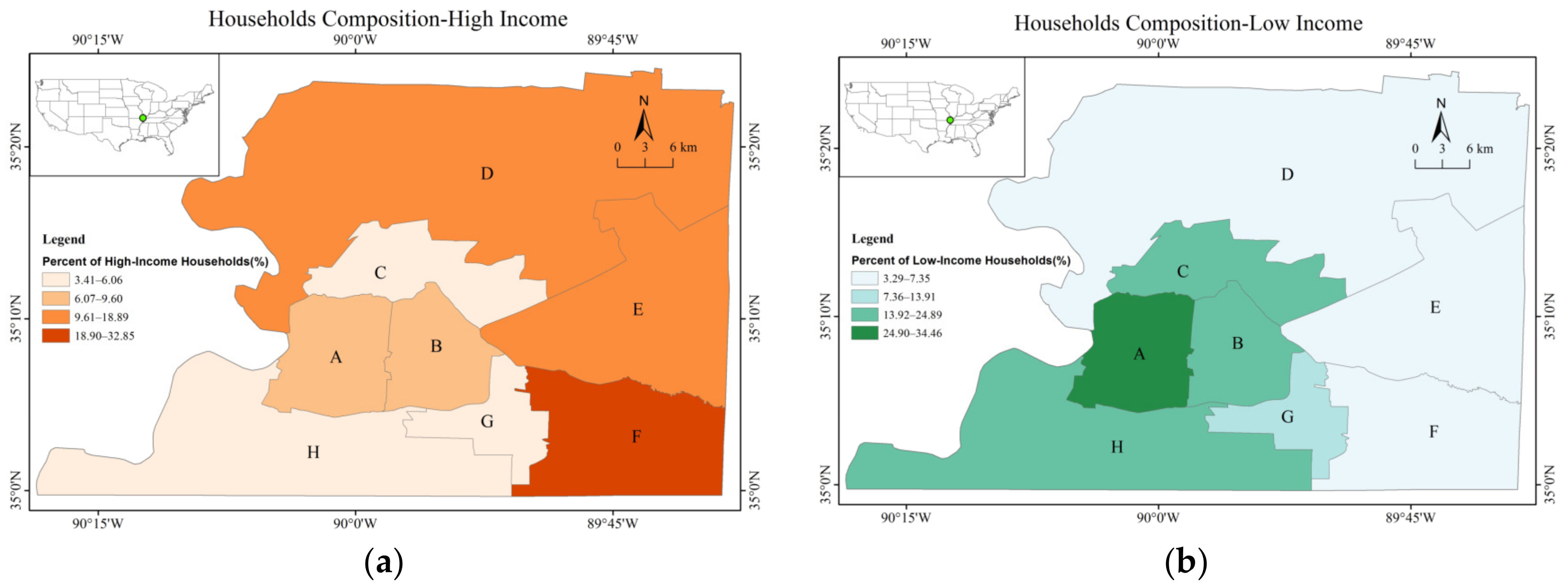
An interesting result in Table 5 column (3) is that, while households in region A and H experience the largest income fall, households in region F experience an income rise after the simulation. For households, their income comes from both labor and capital income; Appendix A 

Table A7. Household Income Loss by Labor and Capital Income.

PUMA Regions	Household Income Loss	From Labor Income	From Capital Income
A	−9.20%	−7.52%	−1.68%
B	−4.37%	−4.48%	0.11%
C	−4.95%	−4.81%	−0.14%
D	−3.00%	−3.70%	0.70%
E	0.30%	−1.45%	1.75%
F	3.57%	0.90%	2.67%
G	−1.34%	−2.22%	0.88%
H	−5.70%	−4.87%	−0.83%

suggests that the regional difference in household income losses mainly comes from the difference in capital incomes.

For capital income, Figure 4 presents the distributions for low-income and high-income households by each region before the earthquake. It indicates that region F is a rich community with more high-income households whose income relies heavily on the return on capital. When capital is damaged, the rate of return for the remaining capital skyrockets. This leads to a rise in nominal capital income, and households in region F benefit the most from this rise, as they owned more capital stock than households in other regions. For labor income, since PUMA region F is the region with the smallest extent of damage in both commercial and residential capital, its total net-outmigration (about 2%) is the smallest. Meanwhile, the wage rate rises after the earthquake because of the reduction in labor supply. With the average wage rise around 8 percent, the combination of a smaller loss in employment and a larger rise in wages produced a small labor income rise instead of fall in region F.

Column (4) of Table 3 provides the employment loss by region; unlike the output and income losses, in which their correlation coefficient with respect to the damage in capital stock is over 0.9, the correlation coefficient of loss in employment with respect to damages in capital stock is only 0.5. This can be explained by the substitution effect between labor and capital. Specifically, Equations (20) and (21) solve for the optimal level of labor demand using the cost minimization problem expressed in Equations (5)–(7) in Section 3.2.2

$$L_j^s=\left(\frac{\overline{Y_j^s}}{{\eta }_j^s}\right){\left({\alpha }_k^{\frac{1}{1-\rho }}{r}_j^s{}^{\frac{\rho }{\rho -1}}+{\alpha }_L^{\frac{1}{1-\rho }}{w}_j^s{}^{\frac{\rho }{\rho -1}}\right)}^{-\frac{1}{\rho }}{\left(\frac{w_j^s}{{\alpha }_L}\right)}^{\frac{1}{\rho -1}}$$

(20)

$$where \overline{Y_j^s}={\eta }_j^s{\left\{{\alpha }_L{\left(\overline{L_j^s}\right)}^{\rho }+{\alpha }_K{\left(\overline{K_j^s}\right)}^{\rho }\right\}}^{1/\rho }$$

(21)

When capital ($\overline{K_j^s}$) is damaged, firm’s level of output ($\overline{Y_j^s}$) is reduced and this is the output loss we see in column (2) of Table 3. The loss in output leads to a reduction in labor demand. Meanwhile, the price of the rest of the available capital stock ($r_j^s$) goes up to reflect scarcity. Then the change in relative costs of factor inputs will drive firms to substitute capital into labor, and this leads to an increase in labor demand. This substitution effect can make the final employment loss, in general, to be smaller compared to total output loss, and the larger the capital stock damage is, the larger the substitution effect will be to offset the negative employment loss.

When looking at the losses in employment, initial capital stock damage can only partially explain the outcome. Other features, such as mobility of workers and the commuting patterns among regions, will also impact firms’ ability to maintain their level of labor demanded after the earthquake shock.

5.2. Results from Joint Estimation

Now with the model developed in this paper, we run two additional simulations in this subsection, which are the simulations that only consider the transportation network damages or the building damages (column (3) in

Table 6. Simulation results under different types of damages.

Economic Variables		Scenario (Building)	Scenario (Transportation)	New Model (Building and Transportation)
		(1)	(2)	(3)
Domestic Supply	Change (million USD)	−8010.64	−77.59	−8068.93
	percent change	−12.27%	−0.12%	−12.36%
Employment	Change (number)	−30,815.95	−673.95	−31,349.42
	percent change	−6.79%	−0.15%	−6.91%
Household Income	Change (million USD)	−574.29	−2.53	−575.30
	percent change	−2.57%	−0.01%	−2.57%
Outmigration	Change (number)	−16,059.35	−35.41	−16,087.35
	percent change	−4.64%	−0.01%	−4.65%

). Column (1) in Table 6 presents the previous results of the simulation which only considered the capital stock destructions, which is also listed here for comparison.

When summing column (1) and column (2) in Table 6, the estimated loss is larger than the results in column (3). This implies that the joint impact from building functionality loss and transportation network damages doesn’t simply equal to the sum of running the two simulations individually. Adding the two individual simulation results would lead to a small overestimation of the negative impact.

An explanation for the above situation is that, recall from Figure 2, at the upper level of the production tier, the technology is a Leontief Type, which suggests that the production capacity is determined not by total resources available, but by the scarcest resource (limiting factor inputs). When the road network is damaged, trade flow across regions is limited, and as a result, firms will also reduce their demand for capital and labor due to their Leontief Type production technology. When adding additional restrictions due to building damage, the efficient level of reduction in capital stock is smaller, as firms’ demand on capital has already been reduced due to the road-network damages. As mentioned in the literature review, previous studies often focused on one type of physical damage, and few papers would consider these impacts jointly. The results here imply that it is worthwhile to consider all channels of the negative impacts that an earthquake can bring at the same time, to avoid overestimation when considering these impacts individually.

6. Discussion

When the spatial behavior responses are included in the new model, results compared with the old model indicate the total damages are smaller in most variables, as suggested by Table 4. We interpreted this finding as a property called “resilience”. Since 1973, when Hollings introduced resilience in Ecology to represent the ability to absorb the disturbance in the system [45], up to recently when scholars have extended the understanding of resilience to represent the ability to resist, adapt and transform [46], the understanding and the definition of resilience are more profound and comprehensive.

The disturbance here to the economic systems is the reduction in production factors in terms of labor force and capital. Given this, Rose [47] proposed that resilience can be attained by means such as input substitution and relocation. More importantly, the spatially-distributed disturbances provided some level of intra-regional unevenness, which can then be used by firms and households to efficiently allocate the resources remaining after the disaster. For instance, PUMA region E and F experienced the least relative losses in capital; with the adjustment we made in the model, agents can now shift to purchase intermediate inputs, find job opportunities, and increase consumption in these regions. This is consistent with resistance, resourcefulness, flexibility and even the redundancy feature in resilience [48]. Additionally, the spatial feature of the model and the adjustment mechanism can be viewed as an extension to the definition and concept of resilience regarding its dimension in space, when a system/organization is unevenly shocked, spatial connectivity is a way to release resources to a larger boundary.

Although most economic variables have exhibited a smaller magnitude of losses within the current model’s specification, household income variable is the outlier. As we impose a current level of disturbances/shocks to the economy, the general equilibrium feature inherently within both the old and current model will allow the rental rate of capital to rise accordingly, in order to satisfy market-clearing conditions where quantity supplied and demanded are equal. Additionally, there is no upper bound limit in this rise. Therefore, the rise in the return of capital offsets the income fall, and this effect is especially stronger when the possibility of resilience is not fully considered in the old model. This has two implications, firstly, the new model is more realistic in mimicking real-world responses, even though these responses have trade-offs that are unexpected. Secondly, with respect to how far the price skyrocketing process can proceed, both models have limitations in taking the market shortage as a closing condition. In fact, several studies found the phenomenon of price gouging, in disasters such as Hurricane Katrina or COVID-19 [49,50], but government intervention and regulation, company reputation and other factors may impose restrictions or price-ceiling to regional economy, and future studies can improve the model in such manners.

Interestingly, the distributional impacts in Table 5 suggest that regions with the least relative disturbances witnessed a rise in household income; coincidentally, these regions are where the rich reside. In other words, earthquakes have made the rich richer. This partially comes from the fact the rich communities are geographically further away from the epicenter, plus the fact that the rich own more in capital. However, the current setting of the earthquake does not allow us to test if the opposite were to happen, i.e., if the rich reside in areas that are closer to the epicenter, the disproportionate effect remains unchanged. The current literatures has not reached consensus in the relationship between natural disaster and income inequality. For example, Mutter [51] found that Hurricane Katrina widened the rich-poor gap, with New Orleans’s poorest district being the slowest to recover. In developing countries such as Myanmar, Warr and Aung [52] found that cyclone reduced inequality between regions. Here, the outcome of this model offered an insight from the perspective of the rental rate of capital, to facilitate future studies in this topic.

Understanding the instantaneous impacts where the economy managed to limit the immediate losses is the first step. Resilience literature has recognized that the dynamic features, or the ability to undergo adaptation and transformation, is equally important [51]. While we have focused on the static responses of an economy facing external shocks, extending current model to a dynamic pattern is necessary. Especially for the concept of transformation, future studies can possibly alter the equilibrium defined to include other routes for the growth and change of reginal economy. Except for CGE models, dynamic stochastic general equilibrium (DSGE) models are another set of general equilibrium models with infinitely-lived households and household-owned firms, and monetary authorities, who make decisions over time [52]. The major differences between the two are the level of aggregation and the aims. While CGE models can make heterogeneous the households by income, residence, or race, the DSGE model is often operated under one representative agent. Additionally, DSGE models focused on analyzing macroeconomic policies such as monetary policy [53]. For studies that examined country-wide disasters, for example, the mitigation monetary policy for COVID-19, DSGE would be a good choice, but for other studies that examined localized hazards, the dynamic CGE model would be more appropriate.

Finally, the usefulness of this study may be gauged in two separate ways. First, the general equilibrium model and the analytical framework in integrating physical damages to the economic system could be applied to other hazards and other geographical areas. Second, the results in this study have policy implications that are associated with the spatial feature of natural disasters. From the findings above, policy makers will want to allocate resources to protect key sectors in regions where the relative building damages are the largest, and in this special case, would be leveraging mitigation efforts in PUMA region A. Moreover, a highly spatialized model would be the foundation of goal setting to distinguish between primary and secondary urgency when designing coping strategies.

7. Conclusions

In this paper, a SCGE model was developed based on the model in Cutler et al. [19], and it extended the spatial feature of the model by considering two behavioral changes, with the first one being the firms’ substitution among the same type of intermediate input produced in different regions and the second one being households’ decision of where to work and consume based on endogenous changes in labor demand conditions after the earthquake. Then we described both in theory and in practice how the physical damages from an earthquake can be used to simulate the economic losses in the SCGE model.

When applying our new model with the two behavior changes, we find that the losses to firms and households are reduced concerning the total output and unemployment rate. We also find that regions with less damage, or regions that are more resilient to damage, would have better performance from modeling these two behavioral changes. Both findings are consistent with the fact that communities have the potential to reduce the losses after the natural hazards, or the idea of inherent resilience brought up by Rose [4].

In addition, when we simulate jointly the impact from the combinations of building, utility, and transportation network damage, we find that the total losses are smaller than the sum of the simulations by the damage types individually. This implies that the economy is working together to cope with different damages, and all components in the economy are impacting each other to produce the best results for the whole economy when facing external shocks.

We also find that when different regions within the economy are damaged differently by the earthquake, some economic variable and associated consequences are highly correlated with the level of capital stock damages to each region, such as regional output, while other types of losses are less correlated with the level of capital stock damage to each region, such as employment, because of the substitution between labor and capital due to relative change in factor prices.

Finally, policy makers and regional planners should pay special attention in preparing and utilizing the redundant resources in the aftermath of natural disasters, to ensure smaller influences to the economy. Future studies may want to extend the current framework developed in this paper to other types of external shocks, ranging from different types of natural hazards to man-made hazards.