Adaptability Evaluation of the Spatiotemporal Fusion Model of Sentinel-2 and MODIS Data in a Typical Area of the Three-River Headwater Region
Abstract
:1. Introduction
2. Materials and Methods
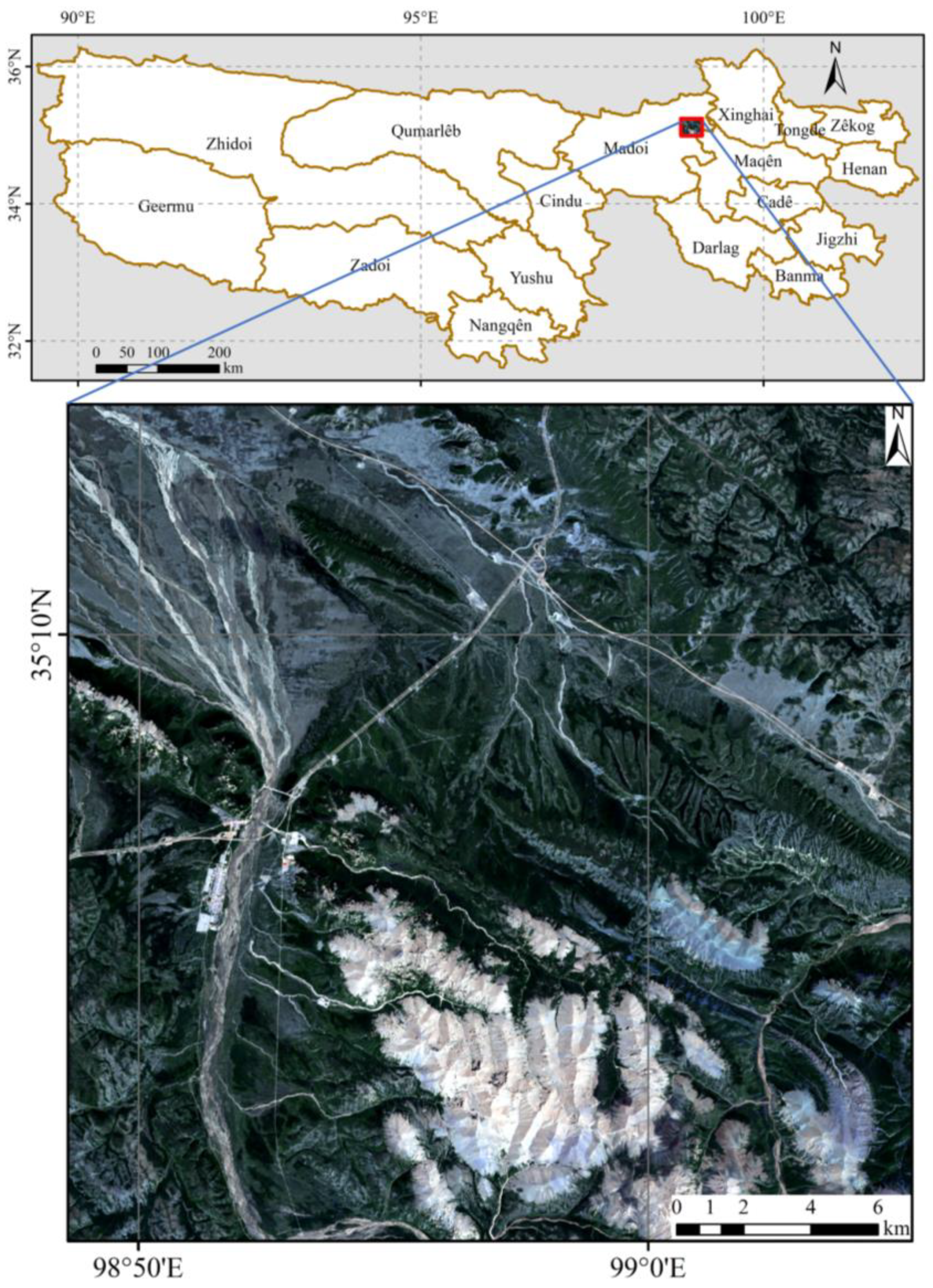
2.1. Study Area
2.2. Data
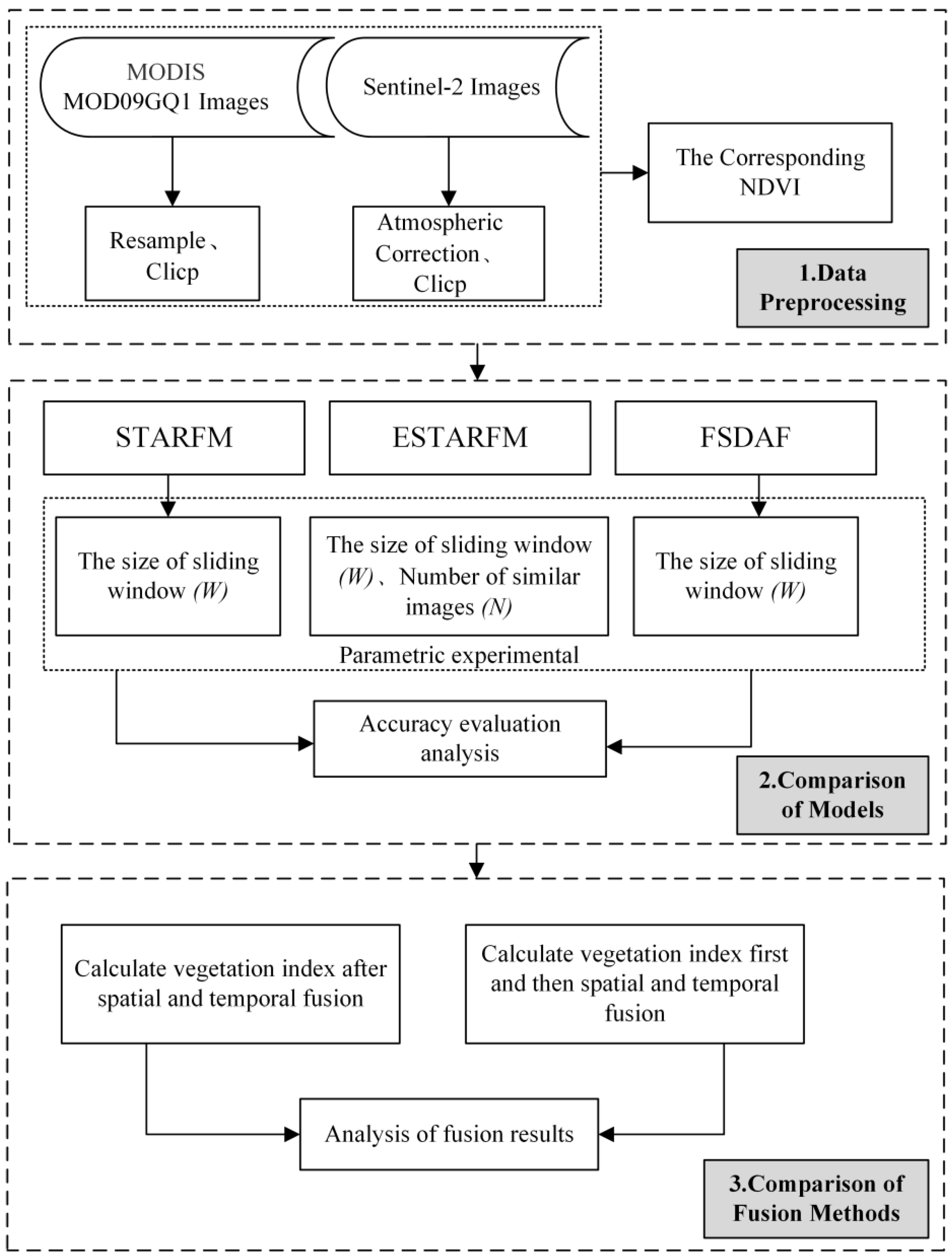
2.3. Methods
- (i)
- Data pre-processing. The pre-processing of the acquired raw Sentinel-2 and MODIS data to obtain the red and near-red band data and NDVI data with a uniform resolution and projection coordinates in the study area.
- (ii)
- Experimental analysis of the fusion models. The parameters of the STARFM, ESTARFM, and FSDAF model were set using the control variable method, and the fused red band, near-red band, and NDVI data were obtained under various combinations of parameters. The accuracy indexes of the fused data of each model were compared separately, and their applicability and optimal parameter range in the typical area of the TRHR were analyzed.
- (iii)
- Comparative analysis of the fusion schemes. Based on the best parameters for the fusion model experiments, a comparative experimental scheme was designed based on the NDVI (in experiment Ⅰ the band fusion was performed first and then the vegetation index was calculated; in experiment Ⅱ the vegetation index was calculated first and then the spatiotemporal fusion was performed) to compare the fusion results of experiments Ⅰ and Ⅱ and to discuss the feasibility of conducting spatiotemporal fusion experiments based directly on the vegetation index data products.
2.3.1. Fusion Method
- 1.
- STARFM
- 2.
- ESTARFM
- 3.
- FSDAF
2.3.2. Fusion Model Parameter Sensitivity Experiments
2.3.3. Accuracy Evaluation Method
2.3.4. Fusion Solution Analysis
3. Results
3.1. Parameter Sensitivity Experimental Results
3.1.1. The Size of the Sliding Window
3.1.2. The Number of Similar Pixels
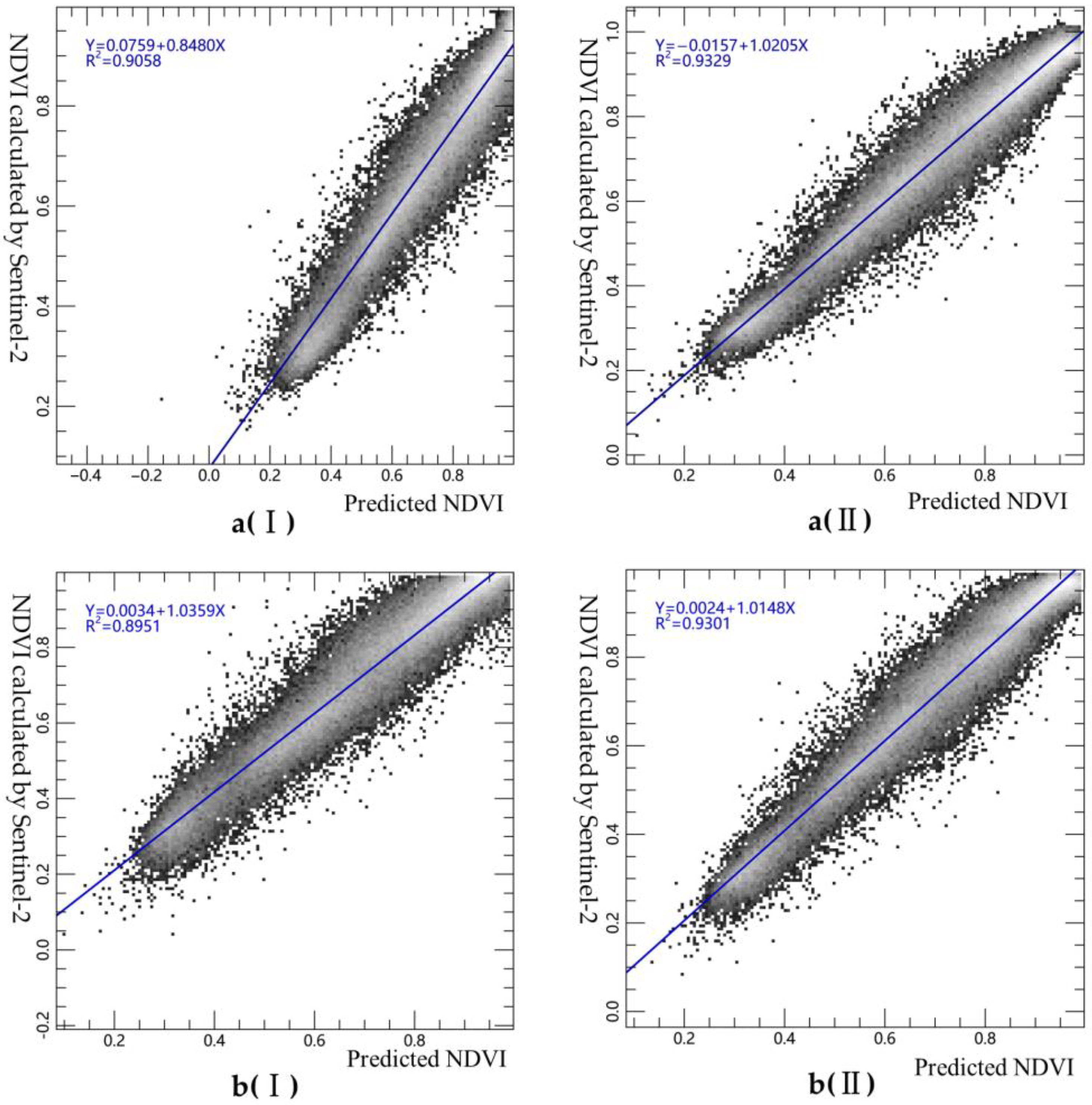
3.1.3. The Fusion Effect of the Comparison Experiment
4. Discussion
5. Conclusions
- (1)
- The accuracy of the spatiotemporal fusion models involved in this study was influenced by the parameters. With a gradual increase in the size of the sliding window, the fusion accuracy of all three models showed a trend of increasing first and then leveling off. Considering the influence of the size of the sliding window on the running time of the fusion model, the sliding window size was set to 50 pixels. For the ESTARFM, the fusion accuracy increased with an increase in the number of similar pixels and stabilized after the number of similar pixels became greater than 80 when the window size was constant.
- (2)
- According to the results of the study, compared to the ESTARFM, the STARFM and FSADF model had better fusion effects and higher accuracies. We recommend the use of the STARFM and FSDAF model for spatiotemporal fusion in this study area.
- (3)
- The comparison of the experimental results showed that the order of the fusion and calculation of the NDVI had an influence on the accuracy of the final vegetation index. The calculation of the vegetation index followed by the spatiotemporal integration produced a higher accuracy. In other words, it is possible to perform spatiotemporal data fusion directly on the vegetation index data products, which can simultaneously save time and obtain high-precision data.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- An, R.; Lu, C.; Wang, H.; Jiang, D.; Sun, M.; Jonathan Arthur Quaye, B. Remote Sensing Identification of Rangeland Degradation Using Hyperion Hyperspectral Image in a Typical Area for Three-River Headwater Region, Qinghai, China. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 399–405. [Google Scholar]
- Pan, L.; Xia, H.; Yang, J.; Niu, W.; Wang, R.; Song, H.; Guo, Y.; Quin, Y. Geoinformation, Mapping cropping intensity in Huaihe basin using phenology algorithm, all Sentinel-2 and Landsat images in Google Earth Engine. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102376. [Google Scholar]
- Raffini, F.; Bertorelle, G.; Biello, R.; D’Urso, G.; Russo, D.; Bosso, L.J.S. Supplementary Materials–From Nucleotides to Satellite Imagery: Approaches to Identify and Manage the Invasive Pathogen Xylella fastidiosa and Its Insect Vectors in Europe. Sustainability 2020, 12, 4508. [Google Scholar] [CrossRef]
- Huang, B.; Jiang, X. An enhanced unmixing model for spatiotemporal image fusion. J. Remote Sens. 2021, 25, 241–250. [Google Scholar]
- Hu, Y.F.; Wang, H.; Niu, X.Y.; Shao, W.; Yang, Y.C. Comparative Analysis and Comprehensive Trade-Off of Four Spatiotemporal Fusion Models for NDVI Generation. Remote Sens. 2022, 14, 5996. [Google Scholar] [CrossRef]
- Zhu, X.; Helmer, E.H.; Gao, F.; Liu, D.; Chen, J.; Lefsky, M.A. A flexible spatiotemporal method for fusing satellite images with different resolutions. Remote Sens. Environ. 2016, 172, 165–177. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Wu, M.; Niu, Z.; Wang, C. Assessing the Accuracy of Spatial and Temporal Image Fusion Model of Complex area in South China. J. Geo-Inf. Sci. 2014, 16, 776–783. [Google Scholar]
- He, X.; Jing, Y.S.; Gu, X.H.; Huang, W.J. A Province-Scale Maize Yield Estimation Method Based on TM and Modis Time-Series Interpolation. Sens. Lett. 2010, 8, 2–5. [Google Scholar] [CrossRef]
- Wu, M.; Niu, Z.; Wang, C.; Wu, C.; Wang, L. Use of MODIS and Landsat time series data to generate high-resolution temporal synthetic Landsat data using a spatial and temporal reflectance fusion model. J. Appl. Remote Sens. 2012, 6, 63507. [Google Scholar]
- Shi, Y.-C.; Yang, G.-J.; Li, X.-C.; Song, J.; Wang, J.-H.; Wang, J.-D. Intercomparison of the different fusion methods for generating high spatial-temporal resolution data. J. Infrared Millim. Waves 2015, 34, 92–99. [Google Scholar]
- Ibn El Hobyb, A.; Radgui, A.; Tamtaoui, A.; Er-Raji, A.; El Hadani, D.; Merdas, M.; Smiej, F.M. Evaluation of spatiotemporal fusion methods for high resolution daily NDVI prediction. In Proceedings of the 5th International Conference on Multimedia Computing and Systems (ICMCS), Marrakech, Morocco, 29 September–1 October 2016; pp. 121–126. [Google Scholar]
- Jun, L.I.; Yunfei, L.I.; Lin, H.E.; Chen, J.; Plaza, A. Spatio-temporal fusion for remote sensing data:an overview and new benchmark. Sci. China Inf. Sci. 2020, 63, 7–23. [Google Scholar]
- Zhang, K.; Wei, W.; Zhou, J.; Yin, L.; Xia, J. Spatial-temporal Evolution Characteristics and Mechanism of ”Three-Function Space” in the Three-Rivers Headwaters’ Region from 1992 to 2020. J. Geo-Inf. Sci. 2022, 24, 1755–1770. [Google Scholar]
- Zhang, Y.; Zhang, C.; Wang, Z.; Yang, Y.; Zhang, Y.; Li, J.; An, R. Quantitative assessment of relative roles of climate change and human activities on grassland net primary productivity in the Three-River Source Region, China. Acta Prataculturae Sinica 2017, 26, 1–14. [Google Scholar]
- Guan, Q.; Ding, M.; Zhang, H. Spatiotemporal Variation of Spring Phenology in Alpine Grassland and Response to Climate Changes on the Qinghai-Tibet, China. Mt. Res. 2019, 37, 639–648. [Google Scholar]
- Claverie, M.; Ju, J.; Masek, J.G.; Dungan, J.L.; Vermote, E.F.; Roger, J.-C.; Skakun, S.V.; Justice, C. The Harmonized Landsat and Sentinel-2 surface reflectance data set. Remote Sens. Environ. 2018, 219, 145–161. [Google Scholar] [CrossRef]
- Zhao, Q.; Ding, J.; Han, L.; Jin, X.; Hao, J. Exploring the application of MODIS and Landsat spatiotemporal fusion images in soil salinization: A case of Ugan River-Kuqa River Delta Oasis. Arid. Land Geogr. 2022, 45, 1155–1164. [Google Scholar]
- Yin, X.; Zhu, H.; Gao, J.; Gao, J.; Guo, L.; Gou, Z. NPP Simulation of Agricultural and Pastoral Areas Based on Landsat and MODIS Data Fusion. Trans. Chin. Soc. Agric. Mach. 2020, 51, 163–170. [Google Scholar]
- Ge, Y.; Li, Y.; Sun, K.; Li, D.; Chen, Y.; Li, X. Two-way fusion experiment of Landsat and MODIS satellite data. Sci. Surv. Mapp. 2019, 44, 107–114. [Google Scholar]
- Guan, Q.; Ding, M.; Zhang, H.; Wang, P. Analysis of Applicability about ESTARFM in the Middle-Lower Yangtze Plain. J. Geo-Inf. Sci. 2021, 23, 1118–1130. [Google Scholar]
- Li, S.H.; Yu, D.Y.; Huang, T.; Hao, R.F. Identifying priority conservation areas based on comprehensive consideration of biodiversity and ecosystem services in the Three-River Headwaters Region, China. J. Clean Prod. 2022, 359, 13. [Google Scholar] [CrossRef]
- Wei, X.Y.; Mao, X.F.; Wang, W.Y.; Tao, Y.Q.; Tao, Z.F.; Wu, Y.; Ling, J.K. Measuring the Effectiveness of Four Restoration Technologies Applied in a Degraded Alpine Swamp Meadow in the Qinghai-Tibet Plateau, China. J. Environ. Account. Manag. 2021, 9, 59–74. [Google Scholar] [CrossRef]
- Zhou, W.; Li, H.; Shi, P.; Xie, L.; Yang, H. Spectral Characteristics of Vegetation of Poisonous Weed Degraded Grassland in the ”Three-River Headwaters” Region. J. Geo-Inf. Sci. 2020, 22, 1735–1742. [Google Scholar]
- Lei, C.; Meng, X.; Shao, F. Spatio-temporal fusion quality evaluation based on Point-Line-Planeaspects. J. Remote Sens. 2021, 25, 791–802. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Sheikh, H.R.; Bovik, A.C. Image information and visual quality. IEEE Trans. Image Process. 2006, 15, 430–444. [Google Scholar] [CrossRef]
- Li, W.; Xu, J.; Yao, Y.; Zhang, Z. Temporal and Spatial Changes in the Vegetation Cover (NDVI) in the Three-River Headwater Region, Tibetan Plateau, China under Global Warming. Mt. Res. 2021, 39, 473–482. [Google Scholar]
- Sun, X.P.; Xiao, Y. Vegetation Growth Trends of Grasslands and Impact Factors in the Three Rivers Headwater Region. Land 2022, 11, 2201. [Google Scholar] [CrossRef]
- Hu, Y.; Dao, R.; Hu, Y. Vegetation Change and Driving Factors: Contribution Analysis in the Loess Plateau of China during 2000-2015. Sustainability 2019, 11, 1320. [Google Scholar] [CrossRef]
- Liu, S.; Sun, Y.; Zhao, H.; Liu, Y.; Li, M. Grassland dynamics and their driving factors associated with ecological construction projects in the Three-River Headwaters Region based on multi-source data. Acta Ecol. Sin. 2021, 41, 3865–3877. [Google Scholar]
- Gao, S.; Dong, G.; Jiang, X.; Nie, T.; Guo, X.; Dang, S. Analysis of Vegetation Coverage Changes and Natural Driving Factors in the Three-River Headwaters Region Based on Geographical Detector. Res. Soil Water Conserv. 2022, 29, 336–343. [Google Scholar]
- Ruan, Y.; Ruan, B.; Zhang, X.; Ao, Z.; Xin, Q.; Sun, Y.; Jing, F. Toward 30 m Fine-Resolution Land Surface Phenology Mapping at a Large Scale Using Spatiotemporal Fusion of MODIS and Landsat Data. Sustainability 2023, 15, 3365. [Google Scholar] [CrossRef]
- Sun, Q.; Liu, W.; Gao, Y.; Li, J.; Yang, C.J.S. Spatiotemporal Variation and Climate Influence Factors of Vegetation Ecological Quality in the Sanjiangyuan National Park. Sustainability 2020, 12, 6634. [Google Scholar] [CrossRef]
- Lu, Y.; Wu, P.; Ma, X.; Li, X.J.E.M. Assessment, Detection and prediction of land use/land cover change using spatiotemporal data fusion and the Cellular Automata–Markov model. Environ. Monit. Assess. 2019, 191, 1–19. [Google Scholar] [CrossRef]
- Li, S.; Zhang, W.; Yang, S. Intelligence fusion method research of multisource high-resolution remote sensing images. J. Remote Sens. 2017, 21, 415–424. [Google Scholar]



| Data Set | Band | Spatial Resolution/(m) | Temporal Resolution/(day) |
|---|---|---|---|
| Sentinel-2 Level-1C | Band4 (R) | 10 | 5 |
| Band8 (NIR) | 10 | 5 | |
| MODIS MOD09GQ1 | Band1 (R) | 250 | 1 |
| Band2 (NIR) | 250 | 1 |
| Method | Input Data | Validation Data | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Sentinel-2 | MODIS | Sentinel-2 | |||||||
| Band | Resolution | Date | Band | Resolution | Date | Band | Resolution | Date | |
| STRAFM | R/NIR | 10 m | 25 July 2019 | R/NIR | 250 m | 25 July 2019 | R/NIR | 10 m | 30 July 2019 |
| - | 30 July 2019 | ||||||||
| ESTARFM | R/NIR | 10 m | 26 April 2019 | R/NIR | 250 m | 25 April 2019 | R/NIR | 10 m | 30 July 2019 |
| 25 July 2019 | 25 July 2019 | ||||||||
| - | 30 July 2019 | ||||||||
| FSDAF | R/NIR | 10 m | 25 July 2019 | R/NIR | 250 m | 25 July 2019 | R/NIR | 10 m | 30 July 2019 |
| - | 30 July 2019 | ||||||||
| Method | Accuracy Indicators for the Different Bands | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R | NIR | NDVI | ||||||||||
| PSNR | R2 | SSIM | VIF | PSNR | R2 | SSIM | VIF | PSNR | R2 | SSIM | VIF | |
| STRAFM | 34.419 | 0.905 | 0.570 | 0.177 | 27.846 | 0.880 | 0.754 | 0.172 | 31.257 | 0.934 | 0.868 | 0.938 |
| ESTRAFM | 33.523 | 0.812 | 0.546 | 0.164 | 28.124 | 0.708 | 0.650 | 0.200 | 30.124 | 0.919 | 0.839 | 0.928 |
| FSDAF | 34.697 | 0.895 | 0.586 | 0.164 | 27.753 | 0.868 | 0.725 | 0.161 | 30.903 | 0.931 | 0.856 | 0.931 |
| Experimental Data | Spatial Resolution (m) | Time Resolution (D) | |
|---|---|---|---|
| Before fusion | Sentinel-2 | 10 | 5 |
| MODIS | 250 | <1 | |
| After fusion | 10 | <1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, M.; Ma, D.; Huang, X.; An, R. Adaptability Evaluation of the Spatiotemporal Fusion Model of Sentinel-2 and MODIS Data in a Typical Area of the Three-River Headwater Region. Sustainability 2023, 15, 8697. https://doi.org/10.3390/su15118697
Fan M, Ma D, Huang X, An R. Adaptability Evaluation of the Spatiotemporal Fusion Model of Sentinel-2 and MODIS Data in a Typical Area of the Three-River Headwater Region. Sustainability. 2023; 15(11):8697. https://doi.org/10.3390/su15118697
Chicago/Turabian StyleFan, Mengyao, Dawei Ma, Xianglin Huang, and Ru An. 2023. "Adaptability Evaluation of the Spatiotemporal Fusion Model of Sentinel-2 and MODIS Data in a Typical Area of the Three-River Headwater Region" Sustainability 15, no. 11: 8697. https://doi.org/10.3390/su15118697
APA StyleFan, M., Ma, D., Huang, X., & An, R. (2023). Adaptability Evaluation of the Spatiotemporal Fusion Model of Sentinel-2 and MODIS Data in a Typical Area of the Three-River Headwater Region. Sustainability, 15(11), 8697. https://doi.org/10.3390/su15118697





