Frequency Regulation of Interlinked Microgrid System Using Mayfly Algorithm-Based PID Controller
Abstract
:1. Introduction
1.1. Research Gap and Motivation
1.2. Innovation of the Article
1.3. The Main Contribution of the Article
- Developing a microgrid and a multimicrogrid incorporated with RESs (PV and wind) and an energy storage system;
- Developing a suitable secondary controller (PID) for the proposed power system;
- Utilizing the projected Mayfly algorithm for controller gain parameter tuning in order to regulate the system’s operation during sudden load demand situations;
- Explaining the enhanced response of the MA-optimized controller (over the GA, PSO, and DE method-designed controllers);
- Conducting robust and sensitivity analyses in order to demonstrate the supremacy of the proposed algorithm for tuning the gain values of the controller in certain situations.
1.4. Implication of the Article
- Investigating the RES-based microgrid;
- Utilizing the Mayfly algorithm in order to optimize the proposed auxiliary controller;
- Providing both SLP and random load pattern (RLP) load interruption to the system, and the response comparison against the GA, PSO, and DE techniques. Also, robustness test conducted to prove the reliability of the MA-PID controller.
2. Proposed System Modelling
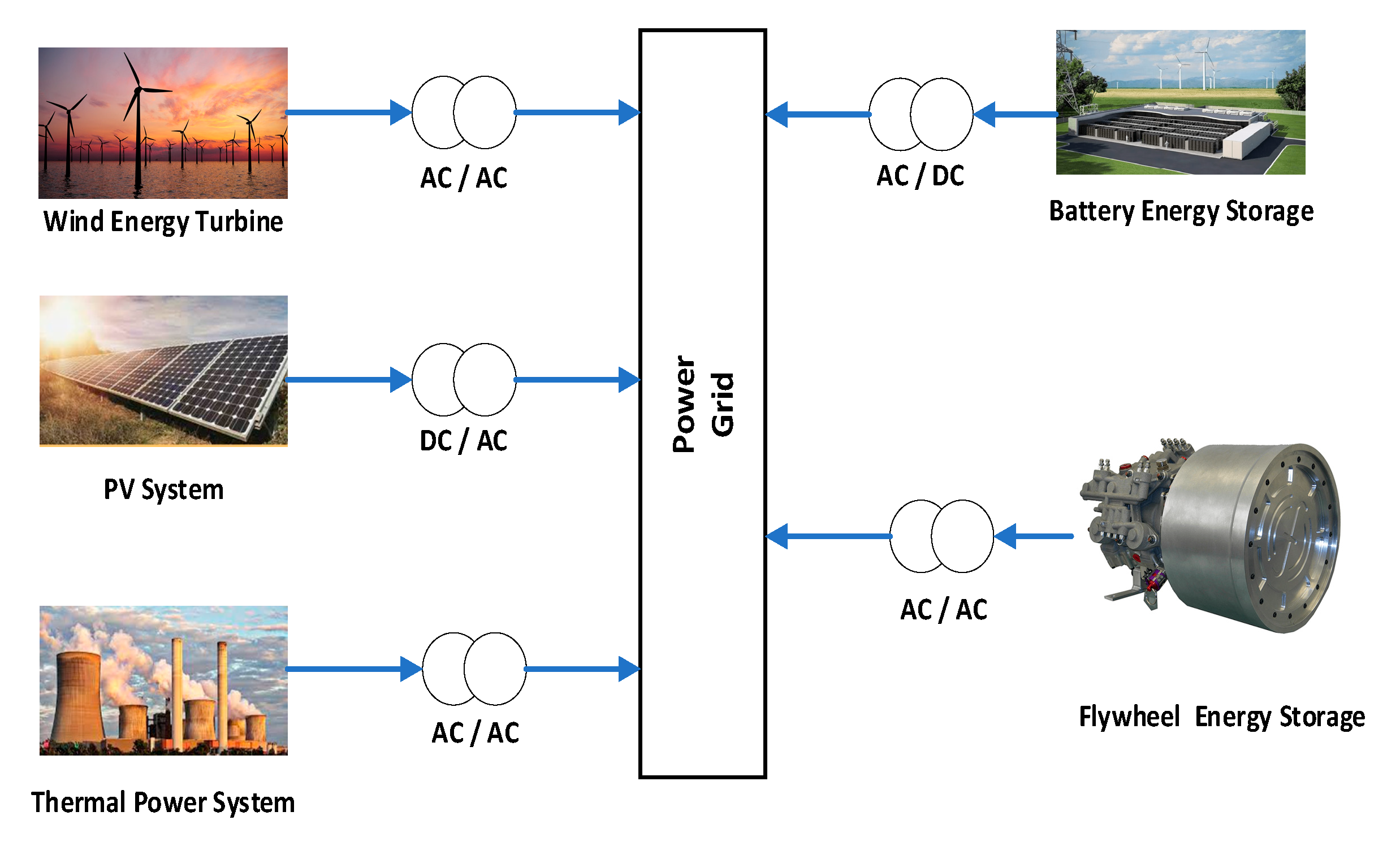
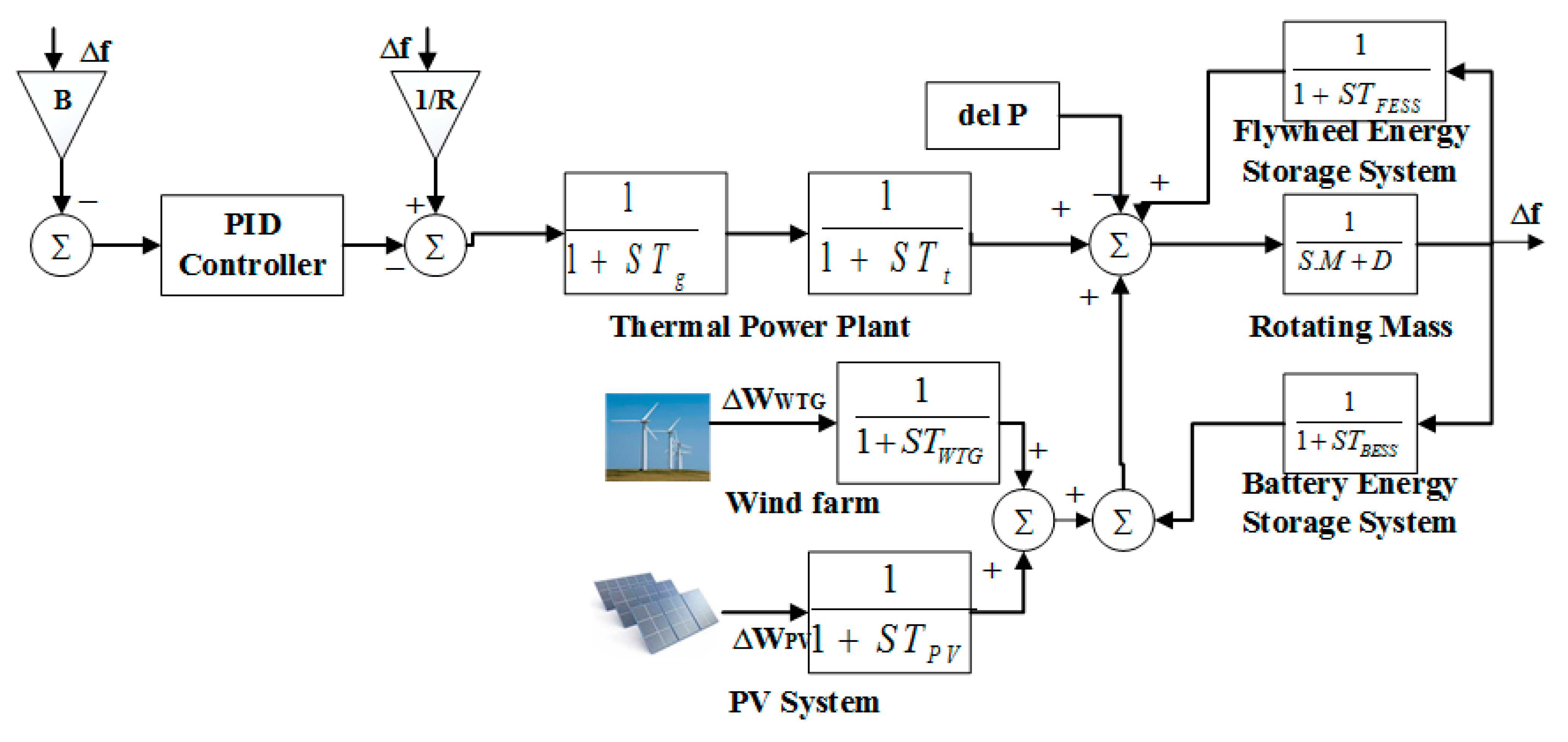
2.1. Microgrid (MG)
2.2. Thermal Power Plant
2.3. PV System
2.4. Energy Storage Units
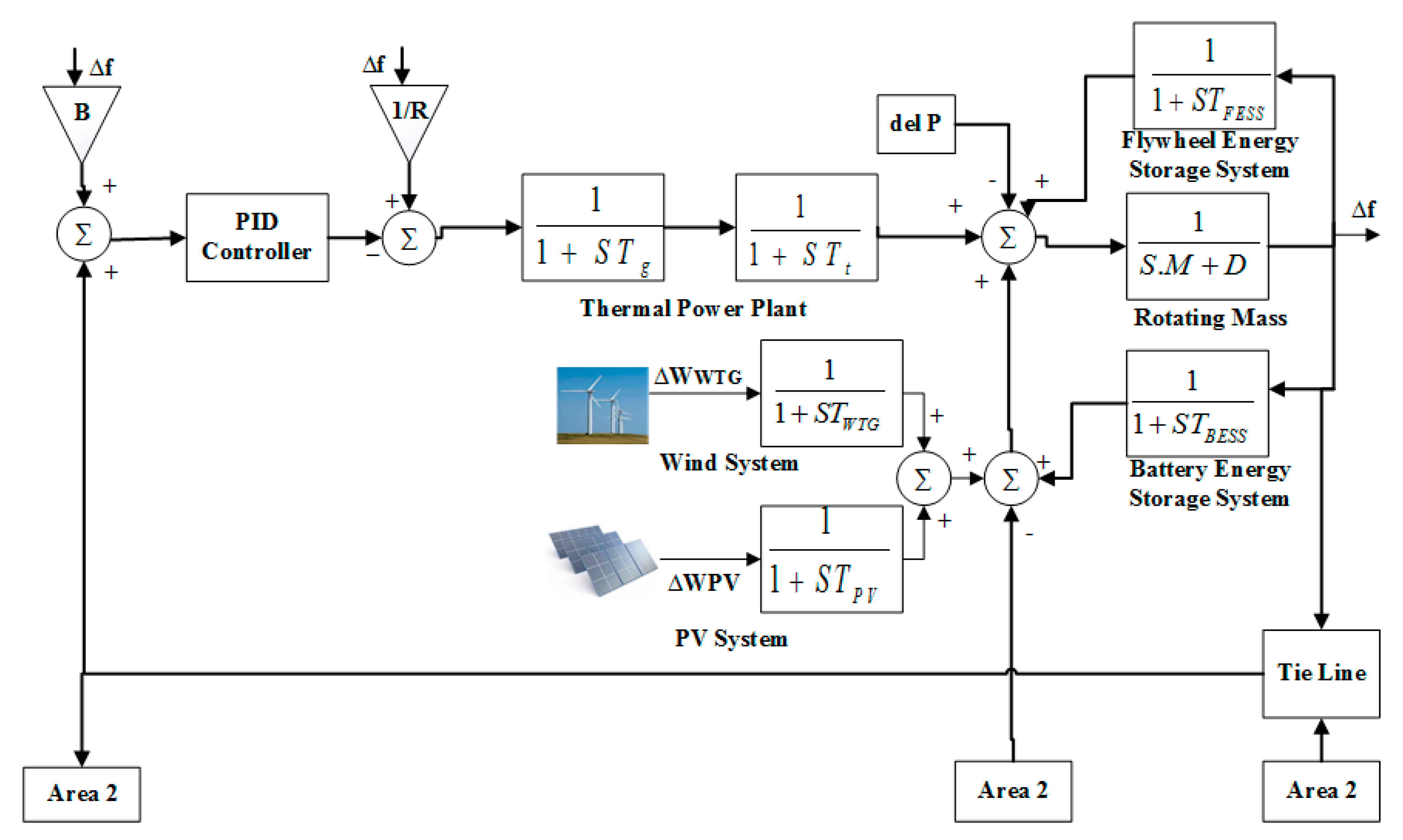
2.5. Multi-MG
3. Controller Design and Methodology
3.1. PID Controller
3.2. Mayfly Algorithm
3.2.1. Male Mayfly Movement
- = Velocity of Mayfly (ith at time t).
- ij = Dimension in search space.
- = Fly position at time t.
- a1, a2 = Coefficients of social effects.
- Pbestij = Local best value.
- Gbesti = Best location of Mayfly.
3.2.2. Female Mayfly Movement
- MA has a fast convergence and a fast convergence rate;
- The nuptial dance and random flying contribute to the equilibrium between exploitation and exploration.
4. Performance Analysis of MG with SLP and RLP
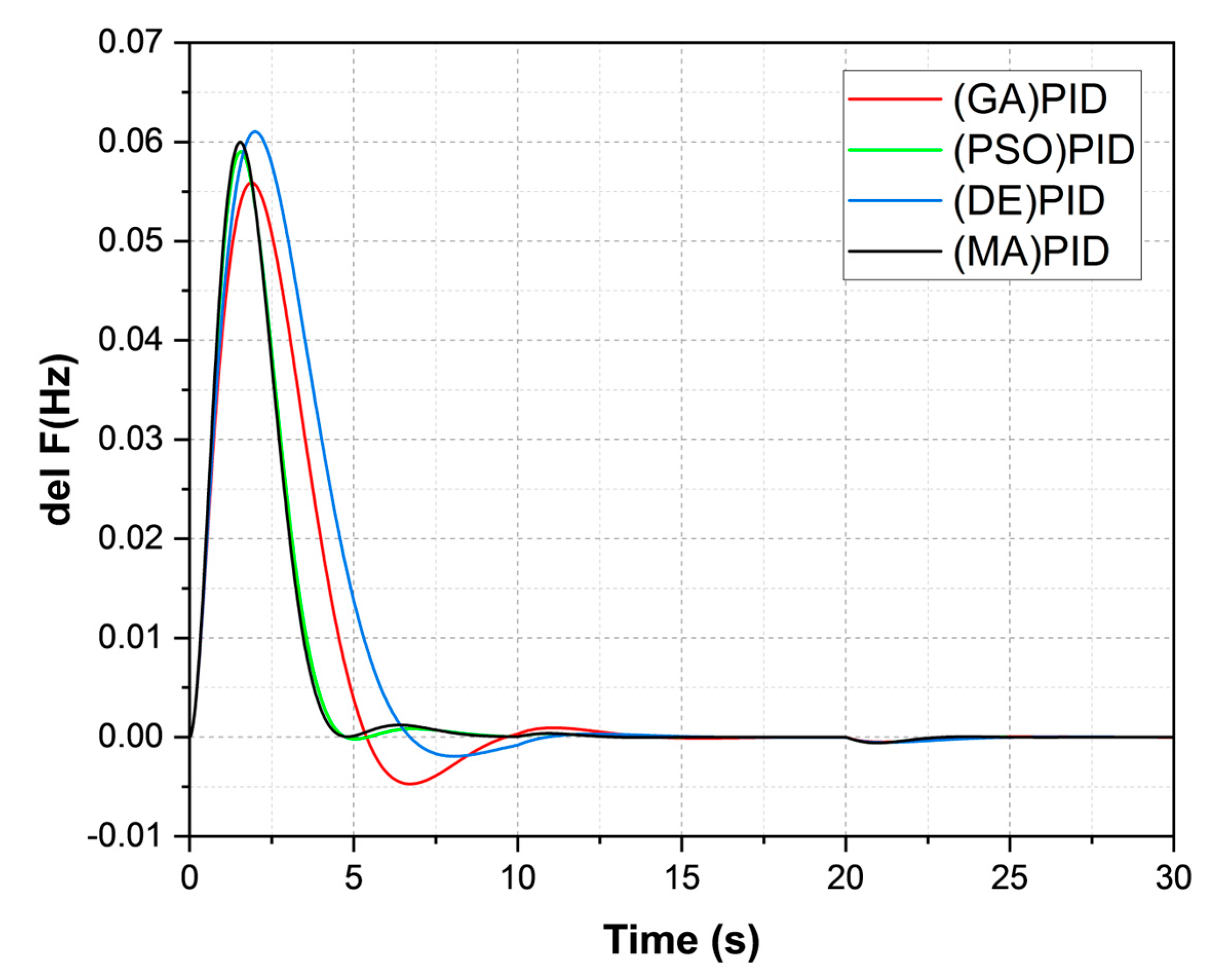
4.1. Case 1: MG with SLP
4.2. Case 2: MG with RLP
5. Performance Analysis of MMG with SLP and RLP
5.1. Case 1: MMG with SLP
5.2. Case 2: MMG with RLP
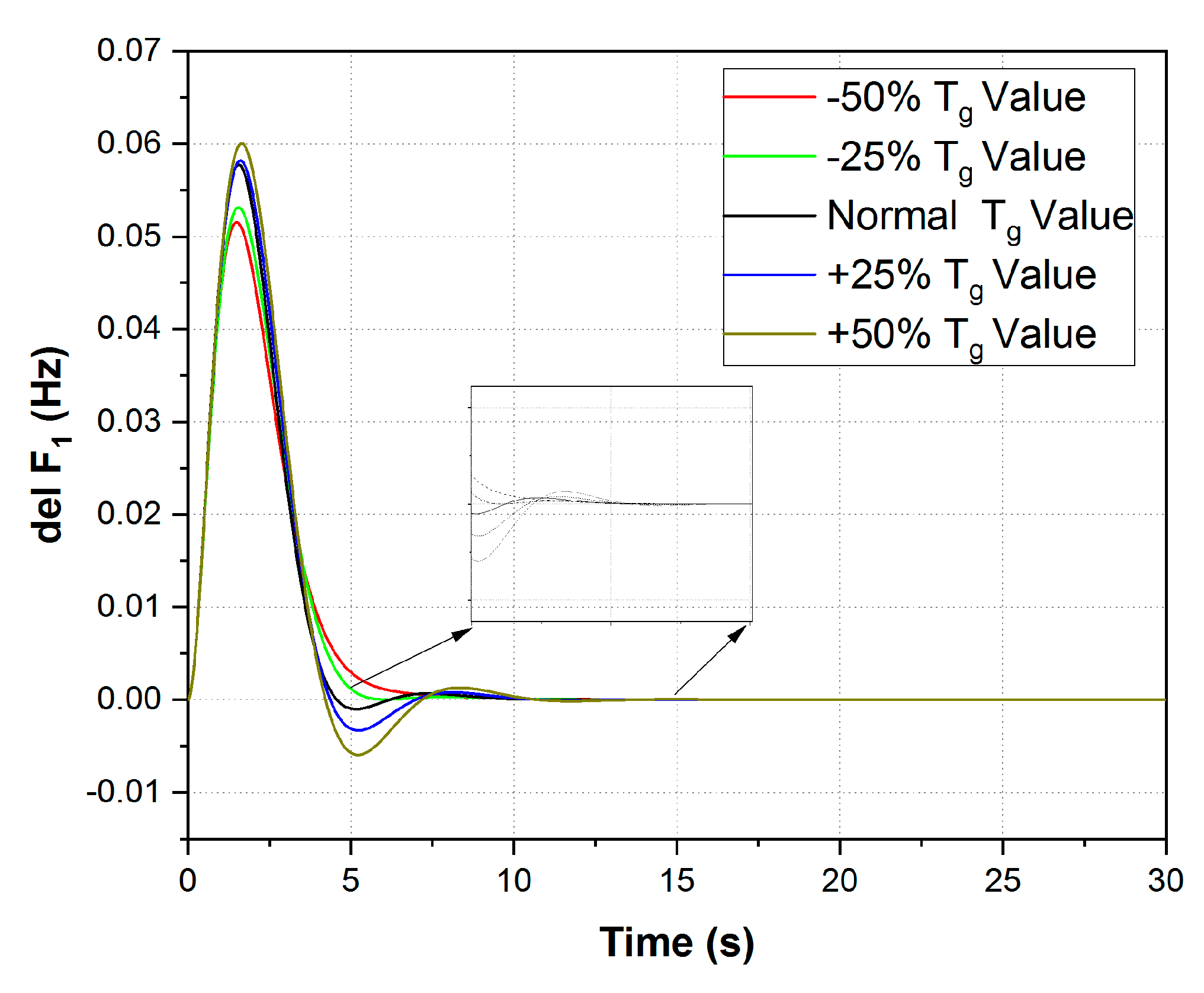
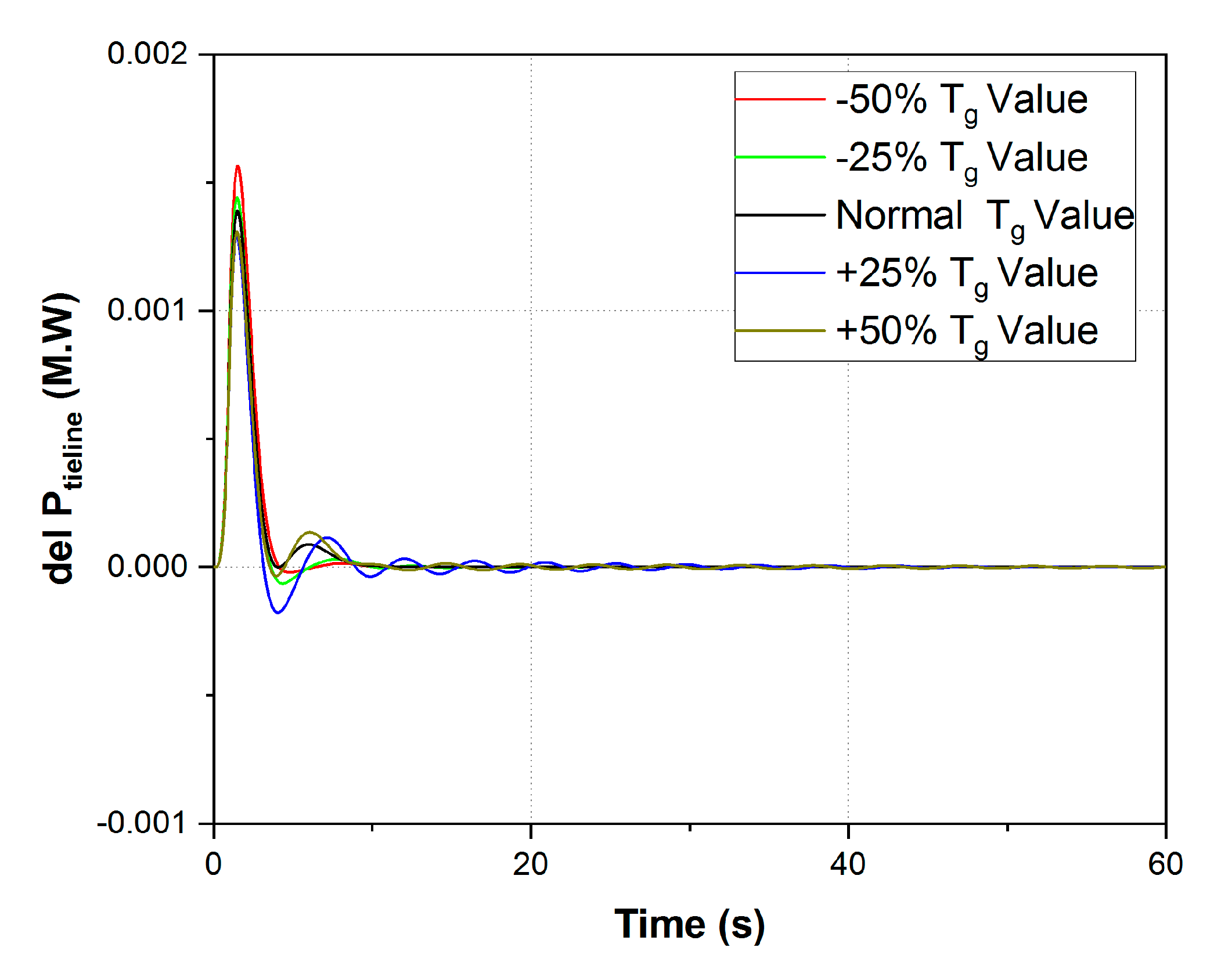
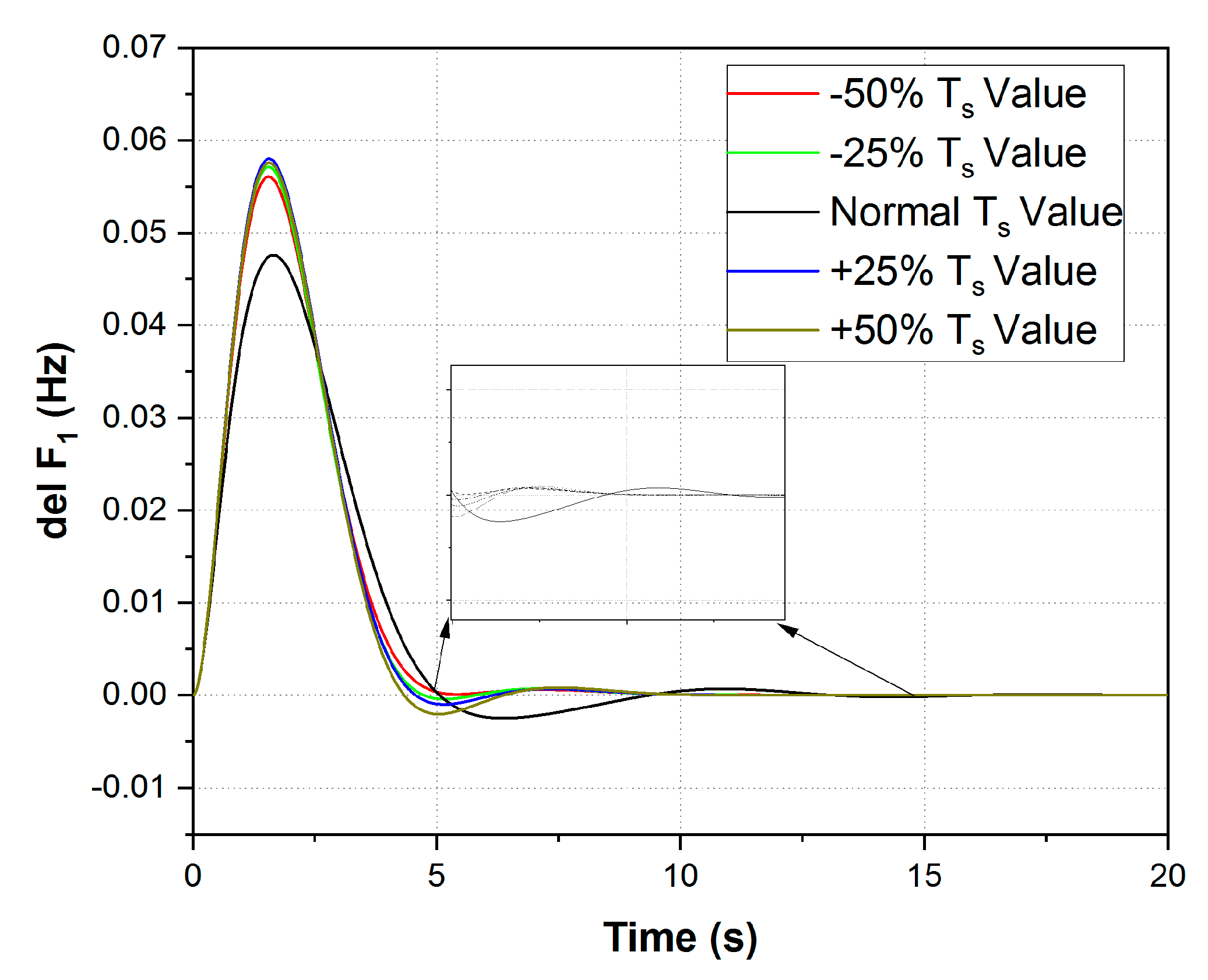
6. Robustness Analysis
6.1. 1%, 2%, 5%, and 10% Load
6.2. Sensitivity Analysis
7. Conclusions
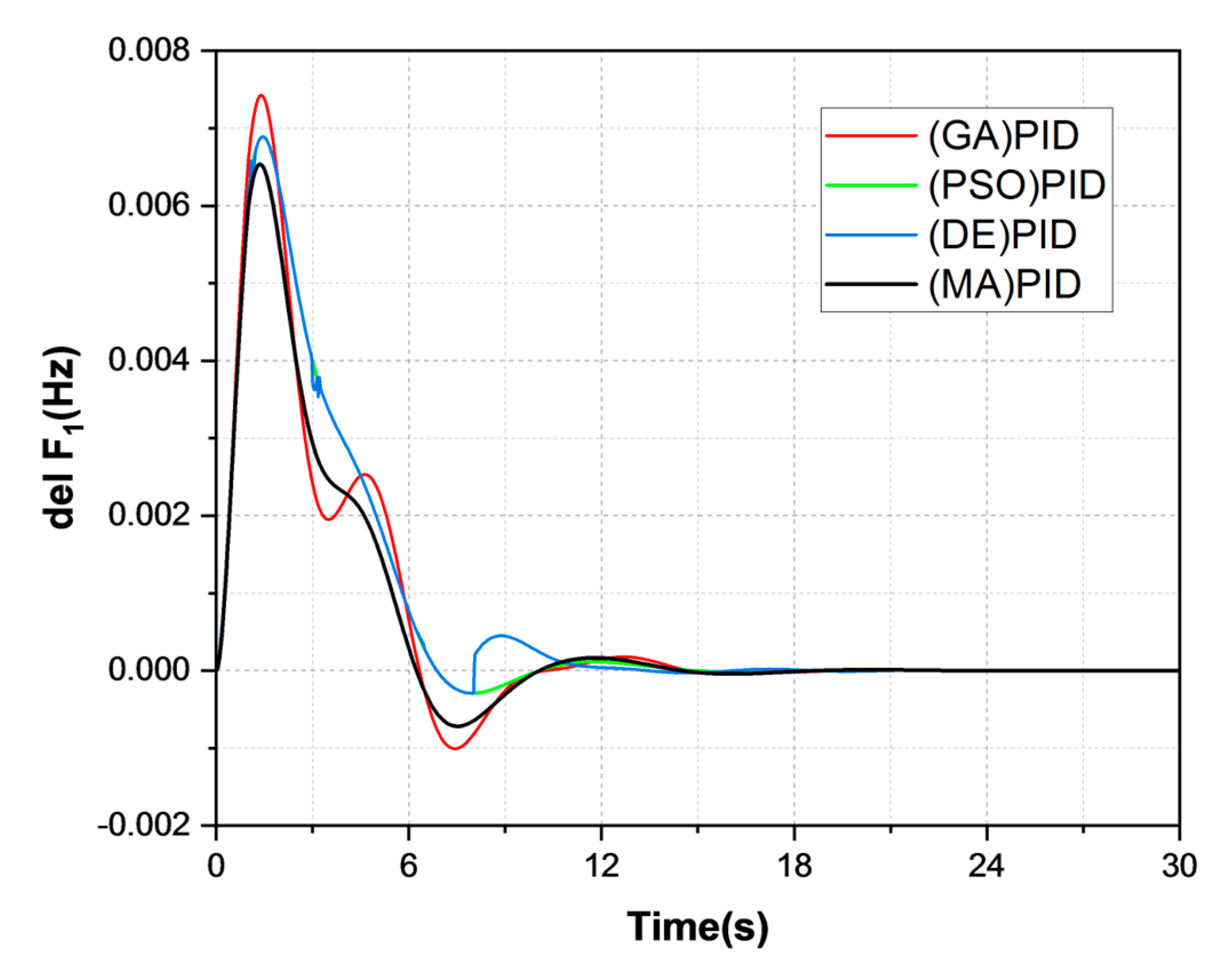
- The MA-PID controller was examined an isolated MG system with 1% SLP. The performance of the projected technique-tuned controller was compared with those of GA, DE, and PSO-PID controllers. The performance of systems del F1, del F2, and del Ptieline showed that the projected MA-PID produces a better outcome with minimal settling time (8 s = MA < 10 s = DE < PSO = 10.5 s < GA = 11 s) over GA, PSO, and DE controllers.
- RLP was used to examine the single-area MG system, and the frequency was affected at the initialization time of loading, but it returned to normal operating conditions after 10 s.
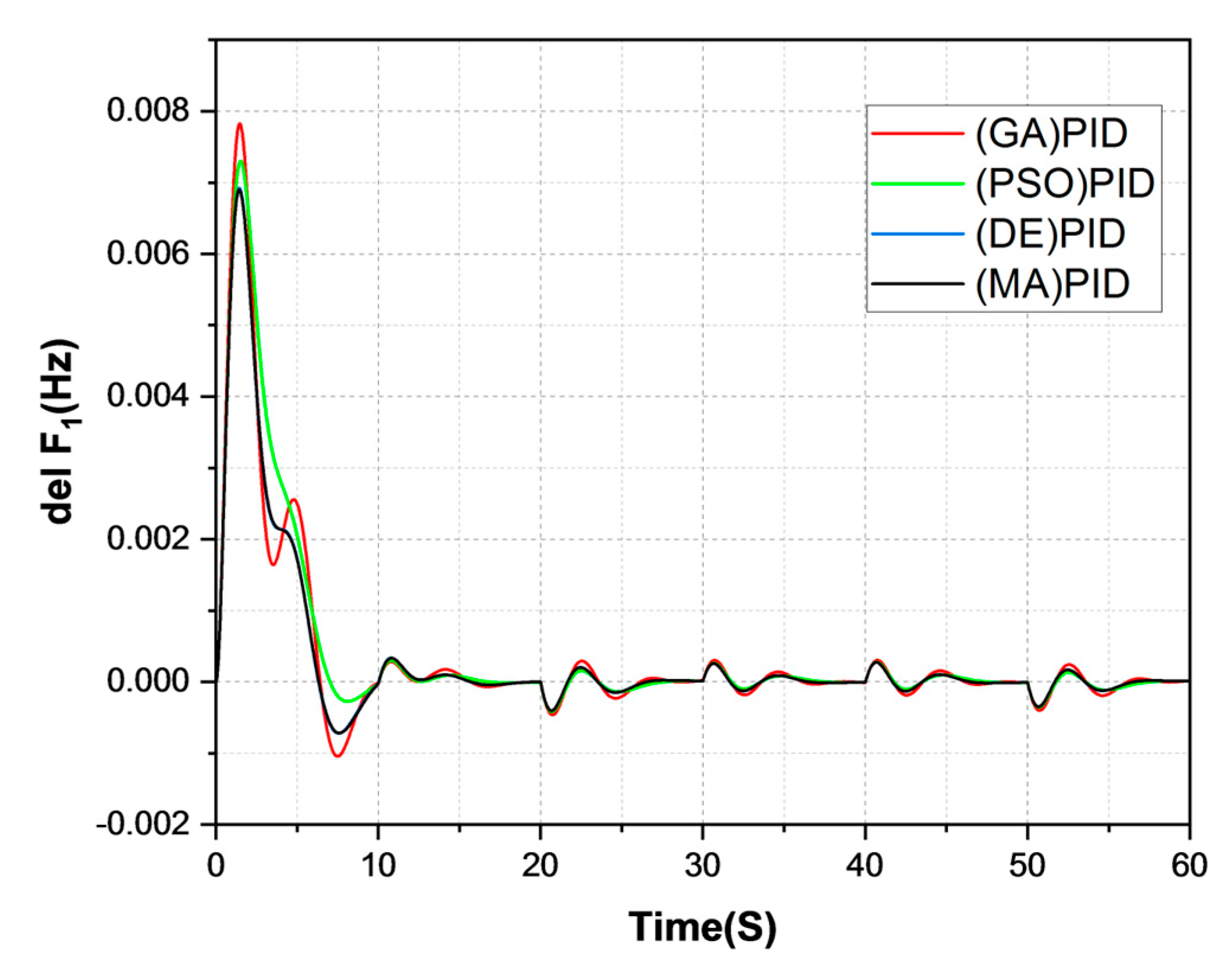
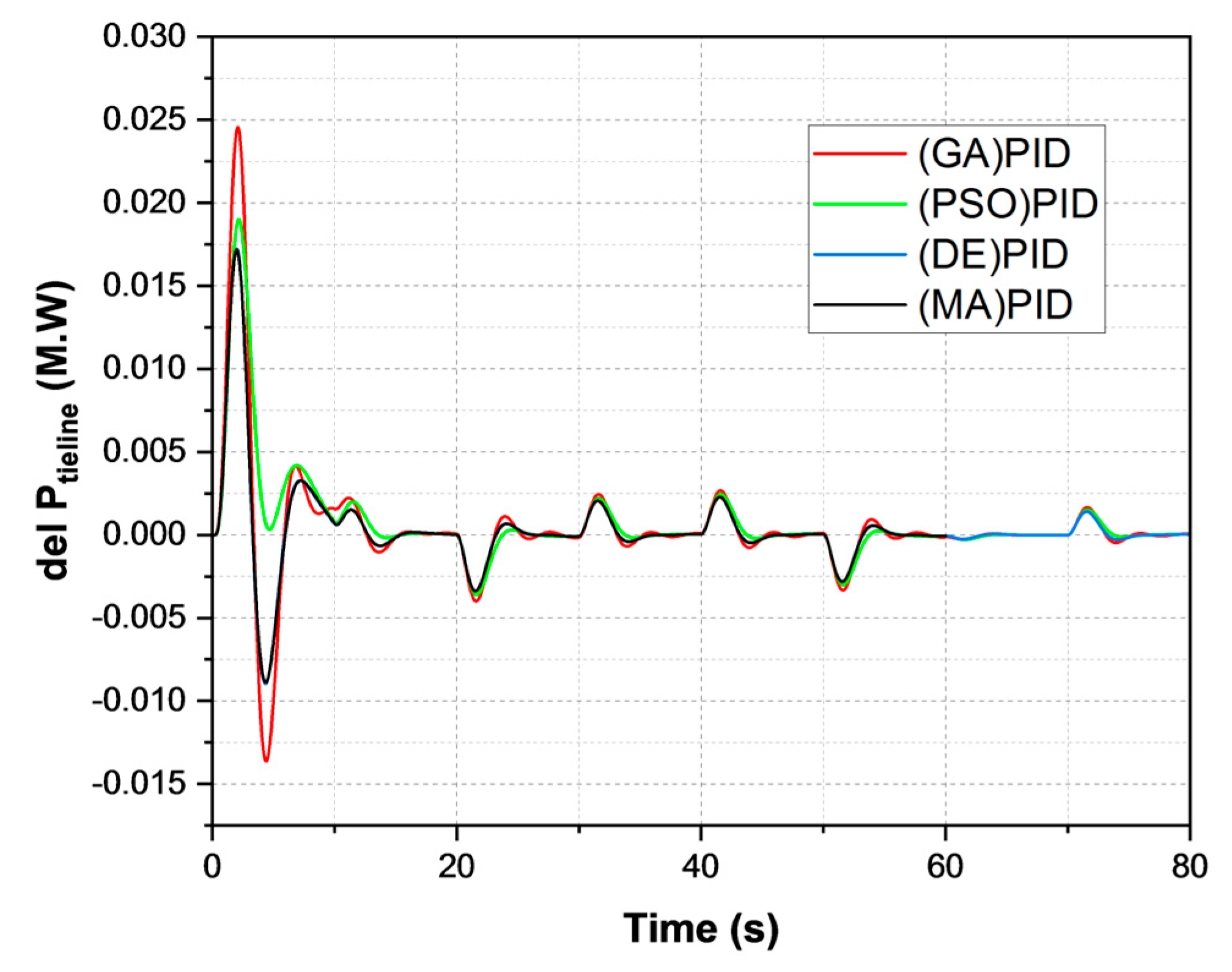
- SLP was used to analyse the performance of the projected MA-PID controller in the MMG system. In terms of oscillation control of the system frequency, the MA-PID controller performed more quickly in del F1 (22 s > 19 s > 19 s > 18 s), del F2 (23 s > 19 s > 18.5 s > 18 s), and del Ptieline (20s > 19 s > 19 s > 18.5 s) than GA, PSO, and DE controllers.
- RLP was employed in the MMG to legalize the performance of the MA-PID controller within the MMG’s LFC. It was effectively evident that the MA-PID controller improved performance by reducing the steady-state error in the system frequency with minimal settling time (in del F1 = 20 s).
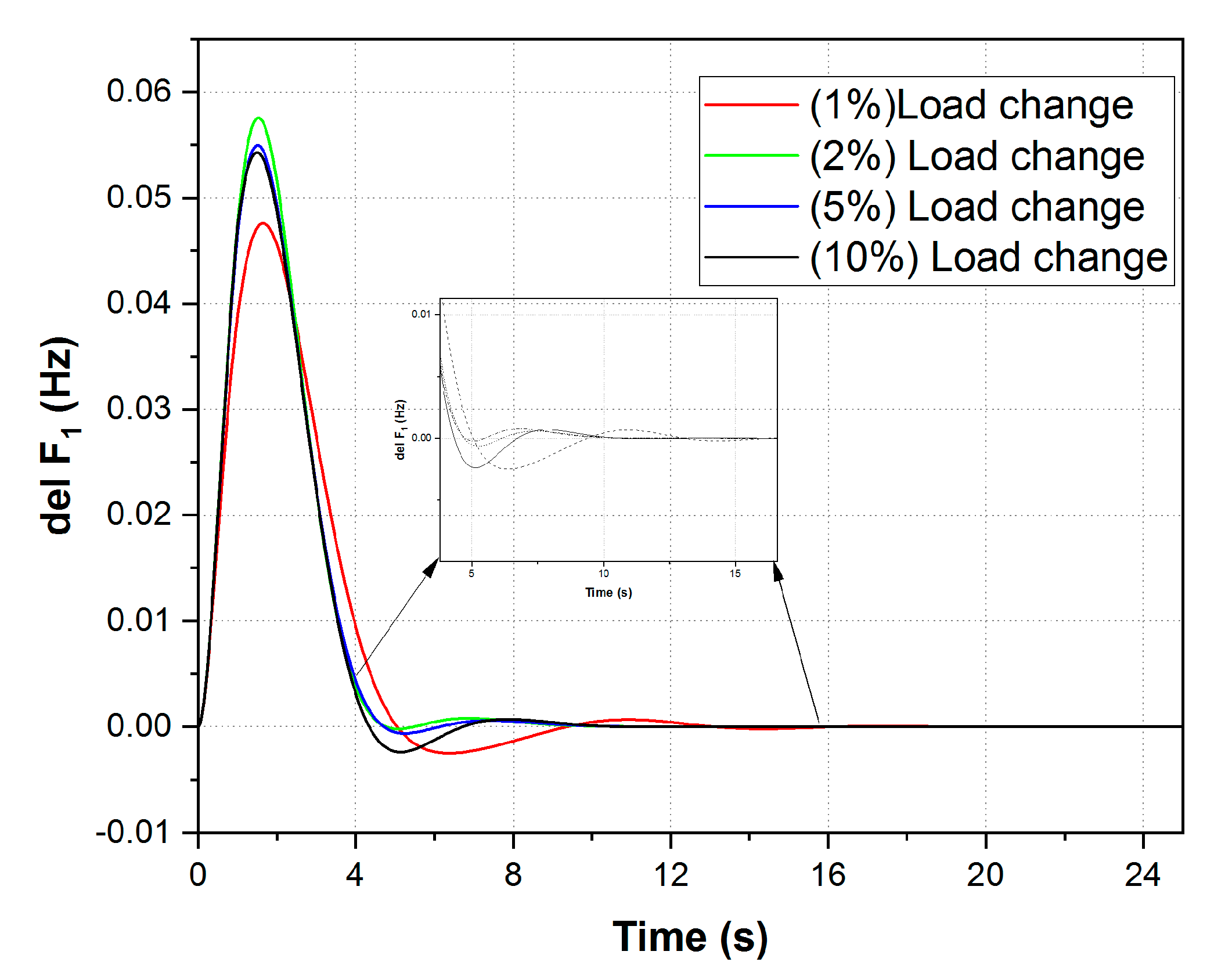
- Various load disturbance situations and system parameter variations were conducted in the robustness test, and the sensitivity analysis test clearly proved that the projected MA-PID controller functioned admirably under all crucial conditions for solving the LFC crisis.
8. Recommendation and Future Scope
- The system size may vary, and the performance of the secondary controller can be analysed;
- Conduct an investigation by changing the optimization technique and controller.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Kumar, M.; Hote, Y.V. Maximum sensitivity-constrained coefficient diagram method-based PIDA controller design: Application for load frequency control of an isolated microgrid. Electr. Eng. 2021, 103, 2415–2429. [Google Scholar] [CrossRef]
- Gheisarnejad, M.; Khooban, M.H. Secondary load frequency control for multimicrogrids: HiL real-time simulation. Soft Comput. 2019, 23, 5785–5798. [Google Scholar] [CrossRef]
- Ramesh, M.; Yadav, A.K.; Pathak, P.K. Intelligent adaptive LFC via power flow management of integrated standalone microgrid system. ISA Trans. 2021, 112, 234–250. [Google Scholar] [CrossRef] [PubMed]
- Patel, S.; Mohanty, B.; Hasanien, H.M. Competition over resources optimized fuzzy TIDF controller for frequency stabilization of hybrid micro-grid system. Int. Trans. Electr. Energy Syst. 2020, 30, e12513. [Google Scholar] [CrossRef]
- Khokhar, B.; Dahiya, S.; Singh Parmar, K.P. A robust cascade controller for load frequency control of a standalone microgrid incorporating electric vehicles. Electr. Power Compon. Systems 2020, 48, 711–726. [Google Scholar] [CrossRef]
- Xu, Y.; Li, C.; Wang, Z.; Zhang, N.; Peng, B. Load frequency control of a novel renewable energy integrated microgrid containing pumped hydropower energy storage. IEEE Access 2018, 6, 29067–29077. [Google Scholar] [CrossRef]
- Veronica, A.J.; Kumar, N.S.; Gonzalez-Longatt, F. Design of load frequency control for a microgrid using D-partition method. Int. J. Emerg. Electr. Power Syst. 2020, 21, 20190175. [Google Scholar] [CrossRef]
- Sahoo, B.P.; Panda, S. Chaotic multi verse optimizer based fuzzy logic controller for frequency control of microgrids. Evol. Intell. 2021, 14, 1597–1618. [Google Scholar] [CrossRef]
- Ali, H.; Magdy, G.; Xu, D. A new optimal robust controller for frequency stability of interconnected hybrid microgrids considering noninertia sources and uncertainties. Int. J. Electr. Power Energy Syst. 2021, 128, 106651. [Google Scholar] [CrossRef]
- Boopathi, D.; Saravanan, S.; Jagatheesan, K.; Anand, B. Performance estimation of frequency regulation for a microgrid power system using PSO-PID controller. Int. J. Appl. Evol. Comput. (IJAEC) 2021, 12, 36–49. [Google Scholar] [CrossRef]
- Khooban, M.H.; Niknam, T.; Shasadeghi, M.; Dragicevic, T.; Blaabjerg, F. Load frequency control in microgrids based on a stochastic noninteger controller. IEEE Trans. Sustain. Energy 2017, 9, 853–861. [Google Scholar] [CrossRef]
- Dhanasekaran, B.; Kaliannan, J.; Baskaran, A.; Dey, N.; Tavares, J.M.R. Load Frequency Control Assessment of a PSO-PID Controller for a Standalone Multi-Source Power System. Technologies 2023, 11, 22. [Google Scholar] [CrossRef]
- Jagatheesan, K.; Samanta, S.; Boopathi, D.; Anand, B. Frequency Stability Analysis of Microgrid interconnected Thermal Power Generating System with GWO tuned PID controller. In Proceedings of the 2021 9th IEEE International Conference on Power Systems (ICPS), Kharagpur, India, 16–18 December 2021; pp. 1–5. [Google Scholar]
- Yang, J.; Zeng, Z.; Tang, Y.; Yan, J.; He, H.; Wu, Y. Load frequency control in isolated microgrids with electrical vehicles based on multivariable generalized predictive theory. Energies 2015, 8, 2145–2164. [Google Scholar] [CrossRef]
- Prusty, U.C.; Nayak, P.C.; Prusty, R.C.; Panda, S. Impact of Vehicle to Grid mode Electric Vehicles in standalone Microgrid for frequency regulation. In Proceedings of the 2020 IEEE International Symposium on Sustainable Energy, Signal Processing and Cyber Security (iSSSC), Gunupur Odisha, India, 16–17 December 2020; pp. 1–6. [Google Scholar]
- Nayak, P.C.; Prusty, U.C.; Prusty, R.C.; Panda, S. Imperialist competitive algorithm optimized cascade controller for load frequency control of multimicrogrid system. Energy Sources Part A Recovery Util. Environ. Eff. 2021, 1–23. [Google Scholar]
- Kumarakrishnan, V.; Vijayakumar, G.; Jagatheesan, K.; Boopathi, D.; Anand, B.; Kanendra Naidu, V. PSO Optimum Design-PID Controller for Frequency Management of Single Area Multi-Source Power Generating System. In Contemporary Issues in Communication, Cloud and Big Data Analytics; Springer: Singapore, 2022; pp. 373–383. [Google Scholar]
- Sahoo, B.P.; Panda, S. Load frequency control of solar photovoltaic/wind/biogas/biodiesel generator based isolated microgrid using harris hawks optimization. In Proceedings of the 2020 First International Conference on Power, Control and Computing Technologies (ICPC2T), Raipur, India, 3–5 January 2020; pp. 188–193. [Google Scholar]
- Elkasem, A.H.; Khamies, M.; Magdy, G.; Taha, I.; Kamel, S. Frequency stability of AC/DC interconnected power systems with wind energy using arithmetic optimization algorithm-based fuzzy-PID controller. Sustainability 2021, 13, 12095. [Google Scholar] [CrossRef]
- Kumarakrishnan, V.; Vijayakumar, G.; Boopathi, D.; Jagatheesan, K.; Saravanan, S.; Anand, B. Frequency Regulation of Interconnected Power Generating System Using Ant Colony Optimization Technique Tuned PID Controller. In Control and Measurement Applications for Smart Grid; Springer Nature Singapore: Singapore, 2021; pp. 129–141. [Google Scholar]
- Magdy, G.; Mohamed, E.A.; Shabib, G.; Elbaset, A.A.; Mitani, Y. SMES based a new PID controller for frequency stability of a real hybrid power system considering high wind power penetration. IET Renew. Power Gener. 2018, 12, 1304–1313. [Google Scholar] [CrossRef]
- Muthukumar, T.; Jagatheesan, K.; Samanta, S. Mayfly Algorithm-Based PID Controller for LFC of Multisources Single Area Power System. In Intelligence Enabled Research; Springer: Singapore, 2022; pp. 53–64. [Google Scholar]
- Shaheen, M.A.; Hasanien, H.M.; El Moursi, M.S.; El-Fergany, A.A. Precise modelling of PEM fuel cell using improved chaotic MayFly optimization algorithm. Int. J. Energy Res. 2021, 45, 18754–18769. [Google Scholar] [CrossRef]
- Wei, D.; Ji, J.; Fang, J.; Yousefi, N. Evaluation and optimization of PEM Fuel Cell-based CCHP system based on Modified Mayfly Optimization Algorithm. Energy Rep. 2021, 7, 7663–7674. [Google Scholar] [CrossRef]
- Hu, C.; Bi, L.; Piao, Z.; Wen, C.; Hou, L. Coordinative optimization control of microgrid based on model predictive control. Int. J. Ambient. Comput. Intell. (IJACI) 2018, 9, 57–75. [Google Scholar] [CrossRef]
- Selim, A.; Kamel, S.; Jurado, F.; Nasrat, L. Voltage stability assessment of radial distribution systems including optimal allocation of distributed generators. Int. J. Interact. Multimed. Artif. Intell. 2020, 6, 32–40. [Google Scholar] [CrossRef]
- Kamel, S.; Jurado, F.; Rashad, A.; Ibrahim, Y.; Nasrat, L. Performance Enhancement of Wind Farms Using Tuned SSSC Based on Artificial Neural Network. Int. J. Interact. Multim. Artif. Intell 2019, 5, 118–124. [Google Scholar]
- Rezk, H.; Arfaoui, J.; Gomaa, M.R. Optimal parameter estimation of solar PV panel based on hybrid particle swarm and grey wolf optimization algorithms. Int. J. Interact. Multim. Artif. Intell 2021, 6, 145–155. [Google Scholar] [CrossRef]
- Mishra, S.; Nayak, P.C.; Prusty, R.C.; Panda, S. Performance analysis of multistage PID controller for frequency regulation of multi microgrid system using atom search optimization. Int. J. Ambient. Energy 2022, 43, 7186–7371. [Google Scholar] [CrossRef]
- Nisha, G.; Jamuna, K. Frequency Stabilization of Stand-Alone Microgrid with Tuned PID Controller. ECS Trans. 2022, 107, 773. [Google Scholar]
- Mahakur, A.; Mohanty, D. Frequency Control of SPV/Wind/Biogas/Biodiesel-Based Microgrid Using Fuzzy-Aided PID Controllers. In Sustainable Energy and Technological Advancements; Springer: Singapore, 2022; pp. 611–624. [Google Scholar]
- Nikhil, M.; Ruchitha, B.N.; Gotur, P.; Ravinand, M.P.; Reddy, G.H. Frequency Control of Renewables/Biodiesel/Biogas/Battery Energy Storage based Isolated Microgrid using the Honey Badger Algorithm. In Proceedings of the 2022 4th International Conference on Energy, Power and Environment (ICEPE), Shillong, India, 29 April–1 May 2022; pp. 1–6. [Google Scholar]
- Armghan, H.; Yang, M.; Ali, N.; Armghan, A.; Alanazi, A. Quick reaching law based global terminal sliding mode control for wind/hydrogen/battery DC microgrid. Applied Energy 2022, 316, 119050. [Google Scholar] [CrossRef]
- Poudyal, R.; Loskot, P.; Parajuli, R. Techno-economic feasibility analysis of a 3-kW PV system installation in Nepal. Renew. Wind. Water Sol. 2020, 8, 5. [Google Scholar] [CrossRef]
- Poudyal, R.; Khadka, S.K.; Loskot, P. Understanding energy crisis in nepal: Assessment of the country’s energy demand and supply in 2016. In Proceedings of the 2017 International Electrical Engineering Congress (iEECON), Pattaya, Thailand, 8–10 March 2017; pp. 1–4. [Google Scholar]
- Poudyal, R.; Loskot, P.; Nepal, R.; Parajuli, R.; Khadka, S.K. Mitigating the current energy crisis in Nepal with renewable energy sources. Renew. Sustain. Energy Rev. 2019, 116, 109388. [Google Scholar] [CrossRef]
- Mishra, S.; Patel, S.; Prusty, R.C.; Panda, S. MVO optimized hybrid FOFPID-LQG controller for load frequency control of an AC microgrid system. World J. Eng. 2020, 16, 675–686. [Google Scholar] [CrossRef]
- Boopathi, D.; Jagatheesan, K.; Anand, B.; Kumarakrishnan, V.; Samanta, S. Effect of Sustainable Energy Sources for Load Frequency Control (LFC) of Single-Area Wind Power Systems. In Industrial Transformation; CRC Press: Boca Raton, FL, USA, 2022; pp. 87–98. [Google Scholar]
- Liu, C.; Li, Q.; Tian, X.; Wei, L.; Chi, Y.; Li, C. Multi-Objective Mayfly Optimization-Based Frequency Regulation for Power Grid With Wind Energy Penetration. Front. Energy Res. 2022, 10, 848966. [Google Scholar] [CrossRef]
- Zervoudakis, K.; Tsafarakis, S. A mayfly optimization algorithm. Comput. Ind. Eng. 2020, 145, 106559. [Google Scholar] [CrossRef]





| Ref. No | Optimizer | Controller | Control Area | Source | Comparative Study |
|---|---|---|---|---|---|
| [6] | Artificial Sheep algorithm | PI | Microgrid | Pumped storage, RESs | Robustness study |
| [9] | Chaotic crow search algorithm | PID | two areas MG | Thermal, solar, wind, EV, ESS | Conventional I controller |
| [10] | Particle swarm optimization | PID | Isolated MG | PV, wind, FC, BESS | Conventional PID |
| [11] | Black hole optimization | FPID | Isolated MG | Wind, PV, flywheel, EV | Multi-objective PID |
| [13] | Grey wolf optimization | PID | hybrid MG | Thermal, PV, BESS, wind | GA-PID, PSO-PID |
| [16] | Imperialist Competitive Algorithm | PID | multi-MG | Thermal, DEG, FESS, BESS | GA and CSA-PID |
| [17] | Particle swarm optimization | PID | Single area | Thermal, solar, wind | Conventional PID |
| [18] | Harris hawks optimization | PI | Isolated MG | PV, wind, biogas, biodiesel | GOA, CSA and GA-PID |
| [20] | Ant colony optimization | PID | hybrid MG | Thermal, FC, HAE, ESS | Conventional-PID |
| [21] | Moth swarm algorithm | PID | Single area | Wind | Effect of SMES |
| [22] | Mayfly Algorithm | PID | Single area | Thermal, hydro, gas | GA, PSO-PID |
| [29] | Atom search optimization | PID | Multi-MG | PV, wind, diesel | GA, PSO-PID |
| [30] | Ziegler Nichols | PID | Single area | Wind, Solar | Conventional-PID |
| [31] | Slap swarm optimization | FPID | Isolated MG | PV, wind, biogas | SSO-PID |
| [32] | Honey Badger Algorithm | PID | Isolated MG | PV, wind, biogas, biodiesel | Conventional-PID |
| [33] | Quick reaching law | PID | Isolated MG | Wind, battery | Conventional-PID |
| System Modelling/ Optimized Gain Parameter | Controller 1 | Controller 2 | ||||
|---|---|---|---|---|---|---|
| (Kp) | (Ki) | (Kd) | (Kp) | (Ki) | (Kd) | |
| Microgrid (SLP) | 0.9750 | 0.9999 | 0.0017 | - | - | - |
| Microgrid (RLP) | 0.9999 | 0.9999 | 0.0624 | - | - | - |
| Multi-MG (SLP) | 0.9805 | 0.9998 | 0.1456 | 0.6691 | 0.8088 | 0.0747 |
| Multi-MG (RLP) | 0.9999 | 0.9999 | 0.3037 | 0.9999 | 0.9999 | 0.9999 |
| Controlled Parameters/Optimization Technique | Ts | POS | PUS |
|---|---|---|---|
| GA-PID | 12 | 0.057 | 2 × 10−3 |
| PSO-PID | 11 | 0.057 | 0.6 × 10−3 |
| DE-PID | 10 | 0.060 | 0 |
| MA-PID | 08 | 0.062 | 2.5 × 10−4 |
| Controlled Parameters/Optimization Technique | del F1 | del F2 | del Ptieline | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ts | POS (10−3) | PUS (10−3) | Ts | POS (10−3) | PUS (10−3) | Ts | POS (10−3) | PUS (10−3) | |
| GA-PID | 20 | 7.5 | 1 | 21 | 6.1 | 0.7 | 20 | 0.021 | 0.013 |
| PSO-PID | 19 | 6.9 | 0.3 | 18.5 | 6 | 0.1 | 19 | 0.016 | 0.0002 |
| DE-PID | 19 | 7.0 | 0.3 | 18.5 | 6.2 | 0.1 | 19 | 0.001 | 0.001 |
| MA-PID | 18.6 | 6.5 | 0.75 | 18 | 5.8 | 0.6 | 18 | 0.015 | 0.007 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boopathi, D.; Jagatheesan, K.; Anand, B.; Samanta, S.; Dey, N. Frequency Regulation of Interlinked Microgrid System Using Mayfly Algorithm-Based PID Controller. Sustainability 2023, 15, 8829. https://doi.org/10.3390/su15118829
Boopathi D, Jagatheesan K, Anand B, Samanta S, Dey N. Frequency Regulation of Interlinked Microgrid System Using Mayfly Algorithm-Based PID Controller. Sustainability. 2023; 15(11):8829. https://doi.org/10.3390/su15118829
Chicago/Turabian StyleBoopathi, Dhanasekaran, Kaliannan Jagatheesan, Baskaran Anand, Sourav Samanta, and Nilanjan Dey. 2023. "Frequency Regulation of Interlinked Microgrid System Using Mayfly Algorithm-Based PID Controller" Sustainability 15, no. 11: 8829. https://doi.org/10.3390/su15118829
APA StyleBoopathi, D., Jagatheesan, K., Anand, B., Samanta, S., & Dey, N. (2023). Frequency Regulation of Interlinked Microgrid System Using Mayfly Algorithm-Based PID Controller. Sustainability, 15(11), 8829. https://doi.org/10.3390/su15118829





