Next Article in Journal
Antimicrobial Potential of Biosynthesized Zinc Oxide Nanoparticles Using Banana Peel and Date Seeds Extracts
Previous Article in Journal
Prediction of Cooling Load of Tropical Buildings with Machine Learning
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Sustainability
Volume 15
Issue 11
10.3390/su15119059
sustainability-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Evaluation of Soil Loss and Sediment Yield Based on GIS and Remote Sensing Techniques in a Complex Amazon Mountain Basin of Peru: Case Study Mayo River Basin, San Martin Region

by
Katherine del Carmen Camacho-Zorogastúa
1,*,
Julio Cesar Minga
2,
Jhon Walter Gómez-Lora
2,
Víctor Hugo Gallo-Ramos
3,4 and
Victor Garcés Díaz
1
1
Facultad de Ingeniería, Universidad Católica Sedes Sapientiae (UCSS), Los Olivos 15301, Peru
2
Facultad de Ingeniería Geográfica, Ambiental y Ecoturismo, Universidad Nacional Federico Villarreal (UNFV), Cercado de Lima 15082, Peru
3
Instituto Especializado de Investigación y Gestión del Agua (INEIGA), Universidad Nacional Federico Villarreal (UNFV), Lima 15082, Peru
4
Environmental and Hydrologic Engineering, Chorrillos 15064, Peru
*
Author to whom correspondence should be addressed.
Sustainability 2023, 15(11), 9059; https://doi.org/10.3390/su15119059
Submission received: 13 April 2023 / Revised: 25 May 2023 / Accepted: 31 May 2023 / Published: 3 June 2023
(This article belongs to the Special Issue Soil Erosion Risk Assessment)
Browse Figures
Review Reports Versions Notes

Abstract

:
This study aims to estimate the average annual rate of soil loss by rainfall in terms of spatial distribution and sediment rate using RUSLE and GIS techniques. Additionally, remote sensing and available soil property information are applied for erosion analysis. The work reveals a very severe type of soil erosion, with the highest mean rate in the steep areas. Annual mean erosion in many parts of the basin is in the range of 0 to 9237.0 t/km2/year with an average of 403 t/km2/year. Approximately 45% (in the upper basin) of the total area has moderate to high soil loss by water, especially in five catchments, namely Serranoyacu, Naranjos, Naranjillo, Yuracyacu, and Tonchima at 886.8 t/km2/yr, 985.1 t/km2/yr, 691.3 t/km2/yr, 567.3 t/km2/yr, and 506.9 t/km2/yr, respectively. Catchment-wise soil loss estimates suggest that these areas are experiencing much higher soil loss in comparison to others; hence, these catchments are prioritized for soil conservation efforts. Sediment rate assessments indicate high sediment deposition along the flow direction of the mainstream of the catchment; in the upper Mayo part, the highest sediment rates are in Yuracyacu, Serranoyacu and Tonchima. Finally, the parts most vulnerable to increased erosion rate are the central part of the basin, which indicates progressive sediment deposition.

1. Introduction

Soil loss is a major environmental problem and plays a pivotal role in land degradation [1,2,3,4].
Recently, land degradation has become a major environmental concern in many regions of the world [5], particularly in developing countries where agriculture is a main activity [6,7,8,9,10]. At a global level, nearly 85% of land degradation is primarily caused by soil erosion [11]. Soil erosion and land degradation are additionally becoming a significant challenge for food production in many parts of the world. Rapid increase in population growth, cultivation on steep slopes, clearing of vegetation, and overgrazing are the key factors that accelerate soil erosion and land degradation [12].
Soil erosion or soil loss has become a serious issue in almost all parts of the globe [13,14,15], affecting land and water resources [16]. In this sense, Oliveira [17] observed that runoff from mountain catchments toward regions of lower elevations increases the rate of erosion of an area.
Land use and land cover (LULC) changes in many parts of river basins have caused water shortages, flood risks, land degradation, soil loss, biodiversity loss, and ecosystem deterioration. LULC change and topography are the main factors that cause land degradation and soil erosion [18].
Global estimates of soil erosion vary from as low as 12–15 billion tn/y (Biggelaar et al., 2004) to about 25–40 billion tn/y [19] and even as high as 75 billion metric tons, and is estimated to cost around USD 400 billion [20].
The Amazon is a territory shared by eight countries, with an estimated extension of 7.4 million km2 (5% of the world’s continental area), and is one of the territories with the greatest biodiversity [21]. It is considered the largest tropical rainforest in the world, covering a total area of approximately 7 million km2, which represents about 56% of the tropical forests on planet Earth [22]. The Amazon is one of the areas most vulnerable to climate change, which has caused water deficits and low retention and alteration of humidity, which consequently alters vegetation cover and land use because there is high pressure on ecosystems that threatens their stability due to anthropogenic activities, mainly deforestation [23]. Peru recorded, in 2016, a total of 164,662 ha of deforestation in Amazon rainforests (5.2% higher than that of 2015); during the years from 2001 to 2016, there was a total loss of 1,974,209.0 ha of Amazon rainforests, which represents an annual average of 123,388 ha [24]. In the Peruvian Amazon, the department of San Martin has a large number of forested areas [25,26], which, over the years, have lost significant areas of vegetation cover due to deforestation for agricultural activities (136,926.83 ha, representing 20%) and implementation of pastures (73,695.08 ha, representing 6.25%) [27]. This phenomenon results in increased vulnerability to water erosion processes, and consequently causes significant soil loss [28]. Some studies, such as Garcia and Camacho [29,30] conducted in similar areas (Chachapoyas and Lamas-San Martín), determined average to severe erosion rates of 300 t/ha/y and 50 t/ha/y, respectively. Soil erosion affects the environment and its natural resources, resulting in low agricultural productivity, ecological collapse, and high sedimentation [31]. Worldwide, more than 80% of degraded soils are associated with environmental problems related to water and wind erosion processes [31,32,33]. Water erosion exceeds 2000 t/km2/year, and this type of erosion is the most frequent in croplands in tropical areas [34], as is the case in Amazonian climates. Models for estimating water erosion are tools capable of quantitatively estimating the rates of soil loss and sediment deposition, and thus help propose effective erosion control practices [35].
The need for soil erosion modelling has been well recognized and a significant increase has been observed in the efforts made, especially in the last decade [36]. There are several models available for assessment of soil erosion, including: (1) empirical equations such as the universal soil loss equation (USLE) developed by Wischmeier and Smith (1978); a revised model of the USLE known as the revised universal soil loss equation (RUSLE) [37]; and (2) process-based models such as the USDA-Water Erosion Prediction Project (WEPP) [38], European soil erosion model (EUROSEM) [39], and large scale catchment model (LASCAM) [40].
However, selection of a soil erosion model may be based on its applicability in terms of input data and relatively good reliability of estimates [41].
Geospatial data integrated with geographic information system (GIS) provides useful monitoring capabilities for the identification of erosion and its measurement [36].
To evaluate the soil loss by water from river basins, managers must estimate the risk of soil erosion and forecast potential future scenarios. To achieve this, numerous methods, techniques, and innovative approaches have been initiated and developed by specialists throughout the globe [42]. Indeed, Rohit used Google Earth Engine to estimate erosion rate using combined geographic information systems and remote sensing techniques [36]. Others, such as (Elaloui et al., 2023), Garcia et al. (2021), and Camacho–Zorogastúa and Gómez–Lora (2018) [29,30,42], used GIS and satellite imagery to understand erosion rates in watersheds with diverse climatic conditions and scarce environmental data.
The soil erosion process is the main and initial part of sediment delivery to rivers, where displaced soil particles are transformed into sediments by the influence of an erosion agent. A consequence of the presence of sediment can be to decrease the potential storage capacity of reservoirs and the performance of hydraulic structures [43]. In this regard, it is important to have quantitative information on the rate of water erosion in areas with high rainfall, particularly forested areas affected by deforestation with moderate to steep slopes and predominantly clay soils, as these are the most vulnerable.
The Mayo river basin is a bi-regional basin located in the northern amazon of Peru. This basin faces a rapid socioeconomic development, mainly due to the agricultural activities that are developed, the tourist attractions, and the potential development of hydroelectric plants. In addition, there are substantial factors, such as soil, rainfall, soil properties, and agricultural activity that affect soil and are highly susceptible to erosion and sediment rate. With this background, the objective of this study was to determine soil loss by water and sediment rates in the Mayo river basin, located in the Department of San Martin, Peruvian Amazon, using geographic information systems (GIS) and remote sensing techniques, the revised soil loss equation (RUSLE), and the soil water assessment tool (SWAT) model for sediment estimation.

2. Materials and Methods

The boundaries of the Mayo basin and its catchments have been delineated using automatic procedures in the GIS environment by using SWAT tool in QGIS 3.16 software and then corrected according to the guidelines of [44].
The RUSLE model integrated with Google Earth Engine and GIS platforms has been used to estimate mean annual soil loss.
Official vectorial datasets were obtained from different sources (Table 1). On the other side, the soil information was extracted from Soilgrids (https://soilgrids.org/ accessed on 3 February 2023) and the precipitation of the ground stations used was acquired from SENAMHI and analyzed via Rstudio. Finally, the maps of the RUSLE factors were developed in QGIS.

2.1. Study Area

The Mayo river basin is bi-regional and covers the Amazonas and San Martin departments (Figure 1). The Mayo river originates at the confluence of the Serranoyacu and Huasta rivers. It is one of the main tributaries of the Huallaga river and follows a northwest to southeast direction [47].
It is elongated in shape, and from its headwaters it adopts a progressively widened structure, which forms an extensive and densely populated valley. The upper and middle zone of the basin includes the provinces of Rioja, Moyobamba, and Rodriguez de Mendoza; in the lower zone, there are important towns such as Shapaja, Tabalosos, Lamas, Cacatachi, Zapatero, Tarapoto, and Juan Guerra [48].
The Mayo river has an approximate length of 300 km from its source to its mouth; morphologically, it is characterized by being meandering, and its hydrological regime is permanent. Its average annual flow at the Shanao station is 410 m3/s and controls an area of 8482 km2 [49]. Altitudinally, it varies from 180 m a.s.l. to 4000 m a.s.l. There are 12 gauging stations in the basin that record the main hydrometeorological variables in the basin; they are distributed in the lower part between 200 and 900 m a.s.l., which means that there are no measurements in important areas of the upper middle part. Its cover is dominated by primary forests, which contribute to soil water retention. During periods of heavy rainfall, the Mayo river carries a high concentration of suspended and bottom solids, due to the erosion of unprotected or deforested slopes, increasing bank erosion processes and local scour of hydraulic structures, particularly bridges and culverts.
Table 2 shows some of the important physiographic characteristics of the basins that form the Mayo river hydrographic system.

2.2. Revised Universal Soil Loss Equation (RUSLE)

The RUSLE is an empirical model recognized as a standard method for calculating average soil loss. It is also the most popular model for estimating average soil erosion by water [50] and is simple to integrate with GIS and remote sensing [51].
A = R   ×   K   ×   LS   ×   C   ×   P
where A is the average annual soil loss (t/ha.y), R is the rainfall erosivity factor (MJ·mm/ha·hr·y), K is the erodibility factor (t·hr/MJ·mm), LS is the topographic factor (dimensionless), C is the crop management factor (dimensionless) and P is the conservation practices factor (dimensionless).
The evaluation of soil loss in the Mayo river basin can be classified into 4 levels according to the FAO classification [52].

2.2.1. R Factor (Erosivity)

Precipitation plays a fundamental role in the process of soil erosion and sedimentation resulting in water erosion, gully erosion, and splash erosion caused by water flows. Soil particles are detached by the action of raindrops and transported by water currents in the watersheds [53]. In the Peruvian Amazon, this is further aggravated by the high rainfall intensities typical of this region.
Therefore, potential erosion can be determined by rainfall intensities and storm duration. For the calculation of the R factor, the ratio between the total energy of the stI (E) and the maximum intensity of 30 min (I30) is considered [54].
However, due to the limitation of precipitation data over the Mayo river basin, the R factor is derived from monthly total precipitation measurements from meteorological stations supplemented with gridded information from the PISCO product (Peruvian Interpolated Spatiotemporal Climatological Observations), which corresponds to the period 1981–2021 and was developed by SENAMHI.
For the conditions of the Mayo river basin, the R-factor equation of Arnouldus (1980) [55], based on the work of Fourier, was considered in this study.
R = ∑ i = 1 12 ( p i 2 P t )
where pi is the monthly precipitation and Pt is the annual precipitation, both expressed in millimeters (mm).

2.2.2. Soil Erodibility Factor (K)

The effect of soil characteristics and properties on erosion can be represented by the soil erodibility factor (K), since this factor shows the physical and chemical properties of the soil through equations related to soil texture, organic matter, and percentages of sand, silt, and clay.
Observed data on local soil properties in the Mayo river basin are extremely difficult to obtain. Therefore, the soil information in this study was derived from data provided by SoilGrids developed by ISRIC-World Soil Information.
The calculation of the K-factor using the SoilGrids data was performed by using the equations described in [56,57,58].
K USLE = f csand ×   f cl − si ×   f orgC ×   f hisand  
K RUSLE = K USLE   × 0.1317
f csand = [ 0.2 + 0.3   ×   exp ( − 0.256   ×   m s × ( 1 − m silt 100 ) ) ]
f cl − si = ( m silt m c + m silt ) 0.3
f orgC = [ 1 − 0.25 × orgC orgC + exp [ 3.72 − 2.95 × orgC ] ]
f hisand = ( 1 − 0.7 × ( 1 − m s 100 ) ( 1 − m s 100 ) +   exp [ − 5.51 + 22.9 × ( 1 − m s 100 ) ] )
where ms is % sand; msilt is % silt; mc is % clay; orgC is organic carbon fraction (%).
In this sense, the data were downloaded from https://soilgrids.org/ (accessed on 3 February 2023), then the geospatial analysis was performed in QGIS to obtain the raster files of sand, silt, clay, and organic matter. Finally, the raster calculator was used to enter the equations and obtain the K factor.

2.2.3. Topographic Factor (LS)

This factor includes slope length (L) and slope steepness (S), which are 2 important factors influencing soil erosion. GIS and remote sensing techniques were applied to obtain the LS factor in the RUSLE equation using a digital elevation model (DEM) [59]. Changes in DEM grid size affect slope values. The L factor depends on the size of the grid and the slope, while the S factor depends only on the slope. Therefore, if the DEM has a high resolution, then the result can increase the accuracy of the LS factor in the RUSLE model [60,61].
DEM images at 12.5 m resolution were downloaded from https://search.asf.alaska.edu/#/ (accessed on 3 February 2023). The calculation of the LS factor was based on the RUSLE using GIS software, as explained in the references. SAGA GIS was used to determine the LS factor, where each grid cell was coupled into the following Equation:
LS = ( 1.4 ) × ( Flowacc 22.13 ) 0.4 × ( sin θ 0.0896 ) 1.3
where Flowacc is the flow accumulation of cells flowing because of slopes; θ is expressed in degrees and represents the slope.

2.2.4. Factor C

This factor represents the capacity of the vegetation to prevent soil detachment by the action of a storm, since, if the soil remains bare during the rainy season, the detachment and dragging of the material is higher than if it had some type of vegetation cover [62]. Vegetation cover is one of the most important factors affecting erosion processes and river development [53]. In that sense, this factor, in the RUSLE method, is the second most important factor controlling the risk of soil erosion [63] and reflects the effect of cropping and management practices on the rate of soil erosion [64]. In general, the C factor varies between zero (0) and one (1). C equal to 1 indicates that there is no cover present, and the surface is treated as barren land; when C is close to 0, it indicates strong cover effects and protected soil [65].
This factor was determined using satellite images by calculating the NDVI. The image search was performed with the following criteria: (i) percentage of clouds in the scene between 10 and 20%, (ii) the time frame chosen was 2019, and (iii) the selected satellites were Landsat 8 and Sentinel 2A.
For this purpose, Google Earth Engine was used, which is a very robust cloud platform capable of processing hundreds of images quickly and efficiently. To process the images, we used a code written in Javascript, which allows us to search for a collection of specific images and perform filters by date (temporality), cloud filter, and area or region of interest.
After performing the necessary filters according to the requirements for the present work, we performed the calculations with the bands of interest. Sentinel 2 bands 8 and 4 were used for NDVI. The C factor was determined using NDVI analysis for Landsat and Sentinel 2 satellite images, which was calculated for each image pixel with the equation described by Turkey [66]. The NDVI assumes value “from “−” to +1”, with high values in areas with abundant vegetation.
NDVI = ( NIR − red ) ( NIR + red )
The NDVI and the method proposed by Durigon were used for areas under tropical climatological conditions with intense rainfall [67]. In that sense, for areas of high vegetation cover, NDVI values t “nd” to “+1” and C factor val “e” to “0”. Accordingly, these values were transformed by the following Equation:
C = ( − NDVI + 1 2 )

2.2.5. Conservation Practices Factor

The conservation practices factor was used to express the effect of land use and cover on soil erosion. The P factor describes the changes in potential erosion through the effect of conservation practices such as terraces, contour ditches, and others [28].
The maximum value of the P factor is usually set at 1, to signify that there are no conservation practices in the watershed for erosion control. Decreasing values of the P factor imply that there is evidence of conservation practices in the watershed soils, so that water flow is reduced in terms of volume and velocity, which favors soil conservation. It also means a lower intensity of sediment deposition on the surface.

2.2.6. Application of GIS and Remote Sensing Tools

Input data, such as precipitation, soil types, land use, topography, and cover properties were imported into the RUSLE model and calculated using the geospatial functions of QGIS 3.16.3. The 5 factors were analyzed according to their spatial resolution and the original coordinate system of the information. Satellite image processing was performed in Google Earth Engine and precipitation data were analyzed using the Hydro TSM and ggplot2 libraries in R studio.
The final results of soil erosion in the Mayo river basin were generated for a maximum grid of 30 m spatial resolution, based on the original data. The erosion rate was analyzed using the results of 2 types of erosion (potential erosion and actual erosion). The factors R, K, and LS were considered as potential erosion, whereas the factors R, K, LS, C, and P were examined as actual soil erosion.

2.2.7. Sediment Rate Estimation

Sediment calculation was performed using SWAT in the QGIS interface, for which 6 fundamental steps are required prior to sediment rate calculation. These are (i) delimitation of the basins and sub-basins contributing to the Mayo river; (ii) definition of the hydrological response units (RHU), which allows the model to reflect differences in runoff generation and erosion rates; (iii) incorporation of climatic data; (iv) editing of model input data; (v) simulation; and (vi) calibration and validation, where the similarity between simulated and observed variables is evaluated.
In the erosive phase, sediment production was modeled using the modified universal soil loss equation (MUSLE) [68], which is shown in Equation:
Sed = 11.8 × ( Q surf   ×   q peak   ×   area hru ) 0.56 ×   K   ×   C   ×   LS
where Sed is the sediment production, Q surf is the volume of surface runoff, qpeak is the peak flow, rhu area is the area of the hydrologic response unit, K is erosivity factor, C is vegetation cover factor, and LS is topographic factor.

3. Results

3.1. Soil Loss Factors

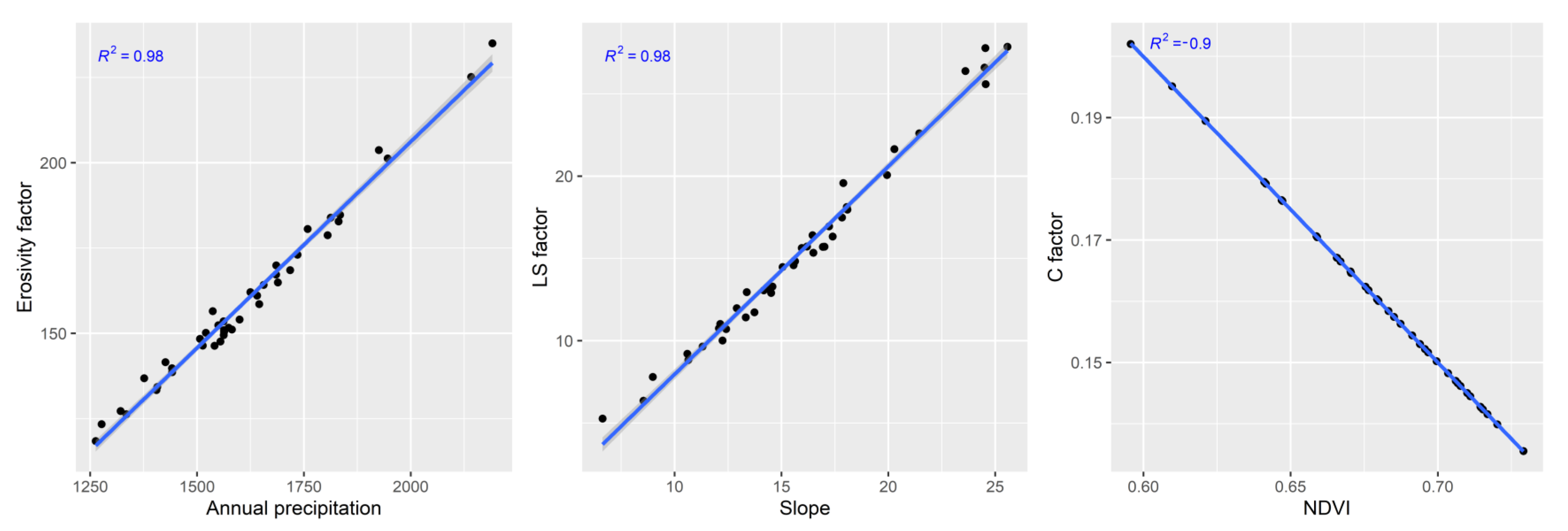
3.1.1. Rainfall Erosivity Factor

The R-factor values were analyzed using Equation (2) through 12 rain-gauge stations for the period 1981–2019. Figure 2a show mean multiannual precipitation. Figure 2b shows the spatial distribution of the mean multi-year R-factor for the Mayo river basin. The range of the R factor was 103.8 to 325.5 MJ.mm/(ha.hr.y) with an average of 170 MJ.mm/(ha.hr.y). The standard deviation was 42 MJ.mm/(ha.hr.y). The lowest R-factor pixel values were mostly distributed in the lower areas of the basin. Meanwhile, the highest R factor values were distributed primarily in the upper zones of the basin, which corresponds mostly to the upper Mayo tributaries, such as Serranoyacu, Yuracyacu, Naranjos, and Naranjillo. According to the results, the R factor increases from the lower part of the basin to the upper part of the basin; this scenario explains the influence of the orographic factor and the climatology of the Mayo river basin.
In this respect, the catchments with the highest average erosivity values were the following: Naranjos, Serranoyacu, Tonchima, Naranjillo, Yuracyacu, and Gera with 235 MJ.mm/(ha.hr.y), 225 MJ.mm/(ha.hr.y), 203 MJ.mm/(ha.hr.y), 201 MJ.mm/(ha.hr.y), 183.9 MJ.mm/(ha.hr.y), and 180.5 MJ.mm/(ha.hr.y), respectively. Otherwise, the lowest erosivity was observed in the Bajomayo, especially in catchments with relevant agriculture activities such as Cumbaza, Rumicallpa, Mamonaquihua, Risagonavi, and Zapatero at 126.3 MJ.mm/(ha.hr.y), 138.6 MJ.mm/(ha.hr.y), 136.8 MJ.mm/(ha.hr.y), 127.2 MJ.mm/(ha.hr.y), and 141.5 MJ.mm/(ha.hr.y), respectively.

3.1.2. Topographic Factor

The topographic factor had the greatest impact on water erosion due to precipitation and runoff water flows. The LS factor was considered from the elevation map of the Mayo basin (Figure 3a) and its calculations from Equation (9). The elevation range in the study area is from 180 m a.s.l. to 4000 m a.s.l., and the mean elevation is 1300 m a.s.l. The highest elevations in the basin are mostly located in the Altomayo part and the elevation gradually decreases in the center of the Mayo basin, where the cities of Rioja, Moyobamba, Tarapoto, etc. are located. More than 50% of the watershed area has a slope greater than 15%, and this is in the Altomayo, including the areas of Yuracyacu, Indoche, Naranjos, Naranjillo, Serranoyacu, among others. Then, the LS factor results were found in the range of 0 to 264 (Figure 3b), and its mean value was 14.65. Areas with high LS factor values were in the upper part of the Mayo river, while areas with low LS factor values were in the central part of the valley.
The highest mean values of the LS factor were obtained in the Serranoyacu, Naranjos, Naranjillo, and Yuracyacu basins, with 26.38, 27.78, 21.63, and 19.57, respectively, located in the upper basin. In the middle part, the watershed with the highest LS was Torochapana with 22.5. Finally, in the lower part, the Cumbaza, Zapatero, and Mamonaquihua watersheds had LS values of 10.74, 10.71, and 12.9, respectively.

3.1.3. Soil Erodibility Factor

Soil groups in the Mayo river watershed were determined using the SoilGrids database from the ISRIC-World Soil Information [69]. The K-factor was calculated with Equations (3)–(8). The range of the K-factor was 0.0147 to 0.0172 t/(hr.MJ.mm) (Figure 4), with an average of 0.016 t/(hr.MJ.mm). The standard deviation was 0.0004. The spatial distribution in Figure 4 indicates that the K-factor decreases towards the western parts of the Mayo basin, but in some areas of the Tonchima, Yuracyacu, Naranjillo, Tioyacu, and Serranoyacu rivers and in the lower part of the basin these values are higher. In the Altomayo, the highest areas, close to the mountain range, high K-factor values were identified. However, in the higher areas of the Mayo (in the Cumbaza area), lower K-factor values were identified, which may be due to the local soil types in those areas.

3.1.4. Crop Management Factor

The C factor was applied using the NDVI analysis (Figure 5a) of the SENTINEL 2A images and the calculation of Equation (11). The C factor varied from 0.06 to 0.64 (Figure 5b). The mean C and standard deviation were 0.15 and 0.057, respectively. The greatest cover in the study area is tropical forest in the upper Mayo area (Yuracyacu, Naranjos, and Naranjillo zones), where the Altomayo Protected Forest is located. In the lower Mayo, the most important zone is the Cordillera escalera (in the Cumbaza area), and these were represented by low values of factor C. On the other hand, high values of factor C were identified in the central zone of the Mayo basin and the zones near the Mayo river.

3.1.5. Conservation Practices Factor

A literature search was conducted in order to detect current conservation practices that have been applied in the Mayo river basin (both for the upper Mayo and lower Mayo); however, no conservation practices were found that would allow defining different values of the P factor. Therefore, according to Wischmeier [54], it was considered equal to 1.

3.2. Potential and Actual Erosion

Erosion was divided into 2 types: potential and actual erosion. Potential erosion (R, L, S, K) was defined as a natural erosion process without considering crop management activities (C) and practices (P) that have been developed in interest. If the potential erosion is combined with the C and P factors, then it is becomes the actual erosion. This was calculated using QGIS 3.16. and GIS techniques. The range of potential erosion (Figure 6a) was from 0–48,038.5 t/km2/year. The average potential erosion was 2738 t/km2/year. The results of the spatial distribution demonstrate a high potential for erosion in many areas of the Mayo river basin. When all RUSLE factors were considered to evaluate the actual erosion in the watershed, it was found to be in the range of 0–9237.05 t/km2/year (Figure 6b). The average erosion was 403 t/km2/year. Many of the areas that are more susceptible to water erosion are in the upper parts of the basin, where precipitation values and LS factor are higher; this corresponds to the Naranjillo, Yuracyacu, Naranjos, Serranoyacu, and Tonchima basins, located in the upper Mayo.

3.3. Risk of Erosion

The results of current erosion were classified into 4 categories according to FAO (1981) [52]. Several areas of soil loss in the Mayo river basin (45% of the total area) present moderate erosion. Thirty-five percent of the total area shows very high erosion, with an average erosion rate of 325 t/km2/year, which includes the highest parts of the basin. On the other hand, the lower parts show low and medium erosion (12% and 8%, respectively of the total area of the basin), corresponding to the valley areas of the cities of Rioja, Moyobamba, Tarapoto, San Antonio, and others.

3.4. Sediment Rate Estimation

The sediment rate was estimated using hydrological modeling via SWAT in the QGIS 3.16 environment. For this, it was necessary to discretize the hydrographic basins (Figure 7a) using the Alos DEM with a spatial resolution of 12.5 m. The hydrologic response units (RHU) were generated, using as inputs the land use classification using the NDVI from the Sentinel 2A image, the FAO soil types, and the DEM slope classification. In total, 953 RHUs were generated. Sediments were calculated using Equation (12).
Figure 7b shows the sediment concentration for the watershed delimited in SWAT. The results show that the watersheds that generate the most sediment are Huascayacu, Yuracyacu, and Tonchima with values of 2286.4 t/ha, 3461.7 t/ha, and 4458 t/ha, respectively (Table 3).
The following table shows the monthly results for each watershed delineated by the SWAT algorithm for the Mayo river watershed.

4. Discussion

This work consisted of the evaluation of soil loss and sediment rate in the Mayo river basin using the RUSLE model and GIS techniques.
In this study, we chose to use RUSLE instead of USLE. Although USLE is the standard soil loss prediction model [70] and some authors have reported on extensive use of USLE for large basins [71], it was derived with data from small agricultural plots. In addition, there are a number of implicit assumptions involved in runoff and sediment generation embedded in the USLE.
The basin as a research target had many limitations of information and access to input information on soil and sediment erosion. Currently, there are no stations in the basin that measure sediment rates. In addition, from the review of local literature, no information on sediment estimates in the Mayo river and erosion rates were available. In this sense, this work can be considered as a basis for further studies related to erosion and sediment rates in the basin.
This work utilized previous work on erosion in the Mayo river basin [28,72], since there is no other evidence and additional information on how much the soil erosion rate has changed in this watershed. Authors Gonzales and Llanos report that average erosion in the Altomayo ranges from 30,000 t/km2/year to 100,000 t/km2/year [72]. The results are in the mid-range of the mean values of the previous work.
The spatial pattern of soil erosion occurs in the northwestern part of the basin, especially in the higher elevations. This is consistent with the findings of the authors Camacho, Gomez, and Gallo, since high erosion rates occurred in the upper parts of the basin [28]. In addition, this may be influenced by the R factor (the main factor in soil erosion) which is influenced by differences in rainfall data. This is consistent with a study conducted in the Guayas basin in Ecuador, where the authors determined an important seasonal influence of rainfall on the calculation of erosivity, increasing preferably in high mountain areas [73]. Available rainfall information was developed from weather stations and the PISCO product [74]. Figure 8 and Figure 9 show the seasonality of precipitation for the period 1981–2019.
It is observed that, in the upper Mayo and lower Mayo ground stations, the highest precipitation occurs between the months of December–March and the lowest values between June–August. However, seasonality may be better defined in Altomayo.
In general, rainfall in the basin is high, which indicates higher erosivity values, especially in high mountain areas (e.g., Yuracyacu, Naranjillo, Naranjos). Although the R factor was developed with meteorological stations and a historical period, it can be further improved by adding gridded information to contrast the values in the middle and upper parts of the basin that lack measurements.
Most studies on soil erosion and sedimentation state that geographic features, precipitation, slopes, and cover types are directly affected by soil erosion in specific areas [31,75,76]. The results in the Mayo watershed indicate that the R, LS and C factors are directly related to (1) precipitation, (2) slope, and (3) vegetation cover in terms of NDVI, respectively (Figure 10).
However, these analytical results may not be entirely effective because, for example, precipitation in the Amazon basin is influenced not only by altitude, but also by latitude, longitude, and other factors. Authors Chuenchum, Xu, and Tang point out that geological and geomorphological characteristics and different altitudinal conditions directly affect RUSLE input factors [31].
LS factor values were categorized according to Ruthes [77], who adopted the classification by Fornelos and Neves [78]. In that sense, in the Altomayo, LS values were classified as very high for watersheds such as Naranjos, Naranjillo, Serranoyacu, and Yuracyacu; high in Tonchima, Gera, Cumbaza, Tabalosos, and Cachiyacu, among other inter-basins and unnamed streams. Finally, the LS factor was moderate in the Avisado, Tumbaro, Santa Isabel, and Soritor catchments.
Factor P represents management practices that contribute to erosion control. However, due to the difficulty in identifying such practices through satellite images, it was decided to adopt a value equal to 1, as seen in similar works, especially Garcia [29].
Additionally, the potential and actual erosion verifies the ability of the C and P factor to protect and reduce soil erosion. The upper Mayo watershed has tropical forests, such as the Alto Mayo protection forest, which can reduce soil erosion at a higher rate than in agricultural areas; therefore, the decrease in forest cover may increase the rate of soil erosion, especially in areas of the upper watershed [79].
Some main tributaries of the Mayo River in the lower areas are Risagonavi, Cumbaza, and Zapatero, where average potential erosion rates of 239.1 t/km2/y, 250.08 t/km2/y, and 263.2 t/km2/y were obtained. In these catchments, the C-factor was 0.16, 0.17, and 0.18. These values are low, which indicates that the vegetation cover contributes to lower erosion rates compared to the Altomayo basins.
Potential erosion values must be taken only as reference values, because the erosion process is complex, and its adequate representation depends on accurate information and estimation of the characteristics of the catchment [80].
The FAO provisional methodology for soil degradation assessment was applied in this study [52] to classify the soil erosion rate in the watershed. One of the reasons is that this area has not been evaluated using this classification. In addition, the same organization consider lower ranges and therefore do not correspond to the results of the present study [81].
Finally, regarding the estimation of the sediment rate, we can mention that soil erosion is the initial process for sedimentation along the Mayo riverbed. This important basin for the development of the San Martin region faces the great challenge of the lack of solid flow measurements, which can be important considering the hydroelectric potential that exists in the basin and could validate our results. Therefore, it is considered that the relevant organizations and regional and local governments should pay special attention to the instrumentation in the basin for sediment measurement. RUSLE allowed our estimation of the sediment production rate in the area, which was appropriate considering the limited information in the study area.

5. Conclusions

This study integrated the RUSLE model with GIS techniques to evaluate soil erosion and sediment production in the Mayo watershed. The results indicate that soil erosion occurs in all areas of the upper and middle Mayo river basin, with an erosion rate of 403 t/km2/year, or approximately 45% of the basin’s surface area. The northern part of the upper basin and some parts of the lower Mayo, such as Cumbaza, have higher terrain than other areas, and they have good vegetation cover. However, the LS factor shows that it exerts a strong influence in contributing to soil erosion in the study area.
The sediment capacity of each simulated input area in the Mayo river basin was determined using a DEM. The spatial distribution of sediment deposition and erosion indicates that there is high sedimentation when erosion occurs along the direction of flow downstream of the Mayo river basin, from the upper Mayo in the northern part to its confluence with the Huallaga river. The results of the sediment estimation derived from the RUSLE indicate that the watersheds with the greatest contribution are Yuracyacu, Tonchima, and Cumbaza.
The RUSLE model was successfully applied to evaluate the rate and spatial distribution of erosion and sediment in the Mayo river basin. The method can be applied not only in this river, but also in other important areas. Finally, the authors state that this work can contribute to decision making and relevant organizations to improve the actions to be applied in the basin, and provides valuable information on soil erosion and sedimentation in this region.

Author Contributions

Conceptualization, K.d.C.C.-Z., J.W.G.-L. and V.H.G.-R.; methodology, K.d.C.C.-Z. and J.W.G.-L.; software, V.H.G.-R.; validation, K.d.C.C.-Z. and J.W.G.-L.; formal analysis, K.d.C.C.-Z., J.W.G.-L. and J.C.M.; investigation, K.d.C.C.-Z. and V.G.D.; resources, J.C.M.; data curation, K.d.C.C.-Z., J.W.G.-L. and V.H.G.-R.; writing—original draft preparation, K.d.C.C.-Z. and V.H.G.-R.; writing— review and editing, K.d.C.C.-Z. and V.H.G.-R.; visualization, J.C.M. and V.G.D.; supervision, J.W.G.-L. and V.G.D.; project administration, J.C.M. and V.G.D.; funding acquisition, J.C.M. All authors have read and agreed to the published version of the manuscript.

Funding

This study was supported in a partial funding by Engineering Faculty of Universidad Católica Sedes Sapientiae—UCSS according to Extraordinary Funding Facility N° EXT 009-2023 and Confirmation of operation details N° EXT 013-2023.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Poesen, J. Soil erosion in the Anthropocene: Research needs. Earth Surf. Process. Landf. 2018, 43, 64–84. [Google Scholar] [CrossRef]
  2. Steinmetz, A.; Cassalho, F.; Caldeira, T.L.; Oliveira, V.A.; Beskow, S.; Timm, T.C. Assessment of soil loss vulnerability in data-scarce watersheds in southern Brazil. Agric. Sci. 2018, 6, 575–587. [Google Scholar] [CrossRef] [Green Version]
  3. Ebabu, K.; Taye, G.; Tsunekawa, A.; Haregeweyn, N.; Adgo, E.; Tsubo, M.; Fenta, A.A.; Meshesha, D.T.; Sultan, D.; Aklog, D.; et al. Land use, management and climate effects on runoff and soil loss responses in the highlands of Ethiopia. J. Environ. Manag. 2023, 326, 116707. [Google Scholar] [CrossRef] [PubMed]
  4. Eswaran, H.; Lal, R.; Reich, P.F. Land Degradation: An Overview. Responses to Land Degradation. In Proceedings of the 2nd International Conference on Land Degradation and Desertification, New Delhi, India, 15 March 2016; pp. 20–35. [Google Scholar]
  5. Alkharabsheh, M.; Alexandridis, T.; Bilas, G.; Misopolinos, N.; Silleos, N. Impact of Land Cover Change on Soil Erosion Hazard in Northern Jordan Using Remote Sensing and GIS. Procedia Environ. Sci. 2013, 19, 912–921. [Google Scholar] [CrossRef] [Green Version]
  6. Bahadur, K.C.K. Mapping soil erosion susceptibility using remote sensing and GIS: A case of the Upper Nam Wa Watershed, Nan Province, Thailand. Environ. Geol. 2009, 57, 695–705. [Google Scholar] [CrossRef]
  7. Xu, L.; Xu, X.; Meng, X. Risk assessment of soil erosion in different rainfall scenarios by RUSLE model coupled with Information Diffusion Model: A case study of Bohai Rim, China. Catena 2013, 100, 74–82. [Google Scholar] [CrossRef]
  8. Rawat, K.S.; Mishra, A.K.; Bhattacharyya, R. Soil erosion risk assessment and spatial mapping using LANDSAT-7 ETM+, RUSLE, and GIS—A case study. Arab. J. Geosci. 2016, 9, 288. [Google Scholar] [CrossRef]
  9. Samanta, S.; Koloa, C.; Pal, D.K.; Palsamanta, B. Estimation of potential soil erosion rate using RUSLE and E30 model. Model. Earth Syst. Environ. 2016, 2, 149. [Google Scholar] [CrossRef]
  10. Saha, A.; Ghosh, P.; Mitra, B. GIS Based Soil Erosion Estimation Using Rusle Model: A Case Study of Upper Kangsabati Watershed, West Bengal, India. Int. J. Environ. Sci. Nat. Resour. 2018, 13, 55871. [Google Scholar] [CrossRef]
  11. Tang, Q.; Xu, Y.; Bennett, S.J.; Li, Y. Assessment of soil erosion using RUSLE and GIS: A case study of the Yangou watershed in the Loess Plateau, China. Environ. Earth Sci. 2015, 73, 1715–1724. [Google Scholar] [CrossRef] [Green Version]
  12. Endalew, T.; Biru, D. Soil erosion risk and sediment yield assessment with Revised Universal Soil Loss Equation and GIS: The case of Nesha watershed, Southwestern Ethiopia. Results Geophys. Sci. 2022, 12, 100049. [Google Scholar] [CrossRef]
  13. Pimentel, D.; Burgess, M. Soil Erosion Threatens Food Production. Agriculture 2013, 3, 443–463. [Google Scholar] [CrossRef] [Green Version]
  14. Prashanth, M.; Kumar, A.; Dhar, S.; Verma, O.; Sharma, S. Morphometric characterization and prioritization of sub-watersheds for assessing soil erosion susceptibility in the Dehar watershed (Himachal Himalaya), Northern India. Himal. Geol. 2021, 42, 345–358. [Google Scholar]
  15. Prashanth, M.; Kumar, A.; Dhar, S.; Verma, O.; Gogoi, K. Hypsometric analysis for determining erosion proneness of Dehar watershed, Himachal Himalaya, North India. J. Geosci. 2022, 7, 86–94. [Google Scholar]
  16. Prashanth, M.; Kumar, A.; Dhar, S.; Verma, O.; Rai, S.K.; Kouser, B. Land use/land cover change and its implication on soil erosion in an ecologically sensitive Himachal Himalayan watershed, Northern India. Front. For. Glob. Chang. 2023, 6, 1–17. [Google Scholar] [CrossRef]
  17. Oliveira, M.L.; Saikia, B.K.; da Boit, K.; Pinto, D.; Tutikian, B.F.; Silva, L.F. River dynamics and nanopaticles formation: A comprehensive study on the nanoparticle geochemistry of suspended sediments in the Magdalena River, Caribbean Industrial Area. J. Clean. Prod. 2019, 213, 819–824. [Google Scholar] [CrossRef]
  18. Chelkeba, T. The Response of Sensitive LULC Changes to Runoff and Sediment Yield in a Semihumid Urban Watershed of the Upper Awash Subbasin Using the SWAT+ Model, Oromia, Ethiopia. Appl. Environ. Soil. Sci. 2023, 2023, 6856144. [Google Scholar] [CrossRef]
  19. Biggelaar, C.D.; Lal, R.; Wiebe, K.; Eswaran, H.; Breneman, V.; Reich, P. The global impact of soil erosion on productivity. II. Effects on crop yields and production over time. Adv. Agron. 2004, 81, 49. [Google Scholar] [CrossRef]
  20. Montanarella, L. Agricultural policy: Govern our soils. Nature 2015, 528, 32–33. [Google Scholar] [CrossRef] [Green Version]
  21. Borrelli, D.A.; Robinson, L.R.; Fleischer, E.; Lugato, C.; Ballabio, C.; Alewell, K.; Meusburger, S.; Modugno, S.; Schutt, B.; Ferro, V.; et al. An assessment of the global impact of 21st century land use change on soil erosion. Nat. Commun. 2017, 8, 2013. [Google Scholar] [CrossRef] [Green Version]
  22. Comisión Económica para América Latina y el Caribe [Cepal] y Patrimonio Natural. Amazonia Posible y Sostenible. Technical Report. 2013. Available online: https://repositorio.cepal.org/handle/11362/1506 (accessed on 18 October 2022).
  23. Silva, S.F.; Ocimar, A.; Cândido, L.A.; Nascimento, R.N.; Pauliquevis, T. Balanço de umidade na Amazônia e sua sensibilidade às mudanças na cobertura vegetal. Mudanças Clim. 2007, 59, 39–43. [Google Scholar]
  24. Tiria, F.; Bonilla, C.; Bonilla, C. Transformación de las coberturas vegetales y uso del suelo en la llanura amazónica colombiana: El caso de Puerto Leguízamo, Putumayo (Colombia). Rev. Colomb. Geogr. 2018, 27, 286–300. [Google Scholar]
  25. Ministerio del Ambiente [MINAM]. MINAM y MINAGRI Presentaron Datos Oficiales Sobre Cobertura y Pérdida de Bosques Húmedos Amazónicos al. 2016. Available online: https://www.minam.gob.pe/cambioclimatico/2017/09/08/minam-y-minagri-presentaron-datos-oficiales-sobre-cobertura-y-perdida-de-bosques-humedos-amazonicos-al-2016/ (accessed on 8 September 2021).
  26. Ministerio del Ambiente [MINAM]. Mapa Nacional de Cobertura Vegetal: Memoria Descriptiva. Technical Report. 2015. Dirección General de Evaluación, Valoración y Financiamiento del Patrimonio Natural. Available online: https://www.minam.gob.pe/patrimonio-natural/wp-content/uploads/sites/6/2013/10/MAPA-NACIONAL-DE-COBERTURA-VEGETAL-FINAL.compressed.pdf (accessed on 10 November 2021).
  27. Ministerio del Ambiente [MINAM]. Mapa de Deforestación de la Amazonía Peruana 2000—MINAM. In Capítulo 3: Resultados; Ministerio del Ambiente: Lima, Peru, 2000. [Google Scholar]
  28. Camacho-Zorogastúa, K.; Gómez-Lora, J.; Gallo-Ramos, V.; Camacho-Zorogastúa, P. Guía práctica de erosión hídrica. In Casos de Estudio: Subcuenca Cumbaza y Yuracyacu—Amazonía Peruana, 1st ed.; Environmental and Hydrologic Engineering S.A.C.: Lima, Peru, 2022; p. 21. [Google Scholar]
  29. García, L.; Veneros, J.; Pucha-Cofrep, F.; Chávez, S.; Bustamante, D.E.; Calderón, M.S.; Morales, E.; Oliva, M. Geospatial Analysis of Soil Erosion including Precipitation Scenarios in a Conservation Area of the Amazon Region in Peru. Appl. Environ. Soil Sci. 2021, 2021, 5753942. [Google Scholar] [CrossRef]
  30. Camacho, K.; Gomez, J.W. Erosión hídrica por lluvias máximas en diferentes periodos de retorno en la subcuenca Cumbaza. Catedra Villarreal. 2018, 6, 125–145. [Google Scholar]
  31. Chuenchum, P.; Xu, M.; Tang, W. Estimation of Soil Erosion and Sediment Yield in the Lancang–Mekong River Using the Modified Revised Universal Soil Loss Equation and GIS Techniques. Water 2020, 12, 135. [Google Scholar] [CrossRef] [Green Version]
  32. Montanarella, L.; Badraoui, M.; Chude, V.; Costa, I.; Mamo, T.; Yemefack, M.; McKenzie, N. Status o’ the World’s Soil Resources: Main Report. Technical Report. 2015. Available online: https://reliefweb.int/report/world/status-worlds-soil-resources?gclid=Cj0KCQiAx6ugBhCcARIsAGNmMbjLvYW6tjmFbykNOQzy7-ZFy8Cv6jzvjnkHqPYmVoIam1kU5l_srEEaAlUaEALw_wcB (accessed on 26 June 2020).
  33. Pimentel, D. Soil Erosion: A Food and Environmental Threat. Environ. Dev. Sustain. 2006, 8, 119–137. [Google Scholar] [CrossRef]
  34. Food and Agriculture Organization of the United Nations [FAO]. Soil Change: Impacts and Responses. Technical Report. 2015. Available online: https://www.fao.org/documents/card/en/c/c6814873-efc3-41db-b7d3-2081a10ede50/ (accessed on 2 July 2021).
  35. Sabri, E.; Spalevic, V.; Boukdir, A.; Karaoui, I.; Ouallali, A.; Mincato, R.L.; Sestras, P. Estimation of soil losses and reservoir sedimentation: A case study in tillouguite sub-basin (high atlas—Morocco). J. Agric. For. 2022, 68, 207–220. [Google Scholar] [CrossRef]
  36. Kumar, R.; Deshmukh, B.; Kumar, A. Using Google Earth Engine and GIS for basin scale soil erosion risk assessment: A case study of Chambal river basin, central India. J. Earth Syst. Sci. 2022, 131, 228. [Google Scholar] [CrossRef]
  37. Renard, K.; Foster, G.; Weesies, G.; McCool, D.; Yoder, D. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); Agricultural Handbook N° 703; United States Government: Washington, WA, USA, 1997; pp. 65–100.
  38. Nearing, M.A.; Foster, G.R.; Lane, L.J.; Finkner, S.C. A Process-Based Soil Erosion Model for USDA-Water Erosion Prediction Project Technology. Trans. ASAE 1989, 32, 1587–1593. [Google Scholar] [CrossRef]
  39. Morgan, R.P.C.; Quinton, J.N.; Smith, R.E.; Govers, G.; Poesen, J.W.A.; Auerswald, K. The European soil erosion model (EUROSEM): A dynamic approach for predicting sediment transport from fields and small catchments. Earth Surf Process Landf. 1998, 23, 527–544. [Google Scholar] [CrossRef]
  40. Viney, N.R.; Sivapalan, M. A conceptual model of sediment transport: Application to the Avon River Basin in Western Aus-tralia. Hydrol. Process. 1999, 13, 727–743. [Google Scholar] [CrossRef]
  41. Risse, L.M.; Nearing, M.A.; Laflen, J.M.; Nicks, A.D. Error Assessment in the Universal Soil Loss Equation. Soil Sci. Soc. Am. J. 1993, 57, 825–833. [Google Scholar] [CrossRef]
  42. Kumar, R.; Devrani, R.; Deshmukh, B. A Review of Remote Sensing and GIS -Based Soil Loss Models with a Comparative Study from the Upper and Marginal Ganga River Basin, 1st ed.; Wiley & Sons Ltd.: Hoboken, NJ, USA, 2023; p. 6. [Google Scholar]
  43. Vaezi, A.R.; Abbasi, M.; Keesstra, S.; Cerdà, A. Assessment of soil particle erodibility and sediment trapping using check dams in small semi-arid catchments. Catena 2017, 157, 227–240. [Google Scholar] [CrossRef] [Green Version]
  44. Gomez-Lora, J.W.; Gallo-Ramos, V.H. Guia de Hidrologia, 1st ed.; Environmental and Hydrologic Engineering S.A.C.: Lima, Peru, 2022. [Google Scholar]
  45. Poggio, L.; de Sousa, L.M.; Batjes, N.H.; Heuvelink, G.B.M.; Kempen, B.; Ribeiro, E.; Rossiter, D. SoilGrids 2.0: Producing soil information for the globe with quantified spatial uncertainty. Soil 2021, 7, 217–240. [Google Scholar] [CrossRef]
  46. Elkhrachy, I. Vertical accuracy assessment for SRTM and ASTER Digital Elevation Models: A case study of Najran city, Saudi Arabia. Ain Shams Eng. J. 2018, 9, 1807–1817. [Google Scholar] [CrossRef]
  47. Casas, S.; Mejía, J. Modelo autorregresivo de primer orden aplicado a la predicción anual de caudales en la Amazonía peruana: Cuenca del río Mayo. In Proceedings of the I International Congress on Water and Sustainability, Barcelona, Spain, 26–27 June 2017; pp. 1–9. [Google Scholar]
  48. Servicio Nacional de Meteorología e Hidrología del Perú [SENAMHI]. Escenarios Climáticos del río Mayo Para el Año 2030. Technical Report. 2009. Available online: https://repositorio.senamhi.gob.pe/handle/20.500.12542/122 (accessed on 10 July 2022).
  49. Autoridad Nacional del Agua [ANA]. Plan de Gestión de los Recursos Hídricos en la Cuenca del Río Mayo. Technical Report. 2020. Available online: https://crhc.ana.gob.pe/mayo/publicacion/plan-de-gestion-de-recursos-hidricos-en-la-cuenca-del-rio-mayo (accessed on 8 May 2022).
  50. Ozcan, A.; Erpul, G.; Basaran, M.; Erdogan, H. Use of USLE/GIS technology integrated with geostatistics to assess soil erosion risk in different land uses of Indagi Mountain Pass-Cankiri, Turkey. Envirom. Geol. 2008, 53, 1731–1741. [Google Scholar] [CrossRef]
  51. Zhou, Q.; Yang, S.; Zhao, C.; Cai, M.; Ya, L. A soil erosion assessment of the Upper Mekong River in Yunnnan Province, China. Mt. Res. Dev. 2014, 34, 36–47. [Google Scholar] [CrossRef]
  52. Food and Agriculture Organisation [FAO]; United Nations Environment Programme [PNUMA]; United Nations Educational, Scientific and Cultural Organization [UNESCO]. Metodología Provisional para la Evaluación de la Degradación de Los Suelos. Technical Report. 1981. Available online: https://catalogosiidca.csuca.org/Record/UCR.000142550/Description (accessed on 25 December 2022).
  53. Wang, Z.-Y.; Lee, J.H.W.; Melching, C.S. River Dynamics and Integrated River Management, 1st ed.; Tsinghua University Press: Beijing, China, 2014; pp. 13–16. [Google Scholar] [CrossRef]
  54. Wischmeier, W.; Smith, D.D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning; Agricultural Handbook N° 537; Science and Education Administration: Washington DC, USA, 1978; pp. 285–291.
  55. Arnoldus, H. An Approximation of the Rainfall Factor in the Universal Soil Loss Equation. In Assessment of Erosion; De Boodt, M., Gabriels, D., Eds.; John Wiley and Sons: New York, NY, USA, 1980; pp. 127–132. [Google Scholar]
  56. Neitsch, S.; Arnold, J.; Kiniry, J.; Williams, J. Soil and Water Assessment Tool Theoretical; Technical Report 2011; Texas Agricultural Experiment Station: College Station, TX, USA, 2011. [Google Scholar]
  57. Sharpley, A.N.; Williams, J.R. Epic “Erosion/Productivity Impact Calculator: 1. Model Documentation”. United Stated Deparment of Agriculture Technical Bulletin. Technical Report. 1990. Available online: https://naldc.nal.usda.gov/download/CAT10698097/pdf (accessed on 24 April 2022).
  58. Williams, J.R. The Epic model in computer models of watershed hydrology. In Chapter 25: Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Resources Publications: Littleton, CO, USA, 1995; pp. 909–1000. [Google Scholar]
  59. Panagos, P.; Borrelli, P.; Meusburger, K.; Yu, B.; Klik, A.; Lim, K.J.; Yang, J.E.; Ni, J.; Miao, C.; Chattopadhyay, N.; et al. Global rainfall erosivity assessment based on high-temporal resolution rainfall records. Sci. Rep. 2017, 7, 4175. [Google Scholar] [CrossRef] [Green Version]
  60. Desmet, P.; Govers, G. A GIS procedure for automatically calculating the USLE LS factor on topographically complex landscape units. J. Soil Water Conserv. 1996, 51, 427–433. [Google Scholar]
  61. Liu, H.; Fohrer, N.; Hörmann, G.; Kiesel, J. Suitability of S factor algorithms for soil loss estimation at gently sloped landscapes. Catena 2009, 77, 248–255. [Google Scholar] [CrossRef]
  62. Castro, I. Estimación de pérdida de suelo por erosión hídrica en microcuenca de presa Madín, México. Ing. Hidráulica Y Ambiental. 2013, 34, 3–16. [Google Scholar]
  63. Knijff, J.; Jones, R.; Montanarella, L. Soil Erosion Risk Assessment in Europe; Technical Report 2000; European Union, Joint Research Centre European Commission: Geel, Belgium, 2000; Available online: https://www.unisdr.org/files/1581_ereurnew2.pdf (accessed on 13 November 2022).
  64. Patil, R.; Sharma, S. Remote Sensing and GIS based modeling of crop/cover management factor (C) of USLE in Shakker river watershed. In Proceedings of the International Conference on Chemical, Agricultural and Medical Sciences (CAMS-2013), Kuala Lumpur, Malaysia, 29–30 December 2013; pp. 1–4. [Google Scholar]
  65. Pham, T.G.; Degener, J.; Kappas, M. Integrated universal soil loss equation (USLE) and Geographical Information System (GIS) for soil erosion estimation in A Sap basin: Central Vietnam. Int. Soil Water Conserv. Res. 2018, 6, 99–110. [Google Scholar] [CrossRef]
  66. Turkey, C. Red and Photographic Infrared Linear Combinations for Monitoring Vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar]
  67. Durigon, V.L.; de Carvalho, D.F.; Antunes, M.A.H.; Oliveira, P.T.; Fernandes, M.M. NDVI time series for monitoring RUSLE cover management factor in a tropical watershed. Int. J. Remote Sens. 2014, 35, 441–453. [Google Scholar] [CrossRef]
  68. Williams, J.R. Sediment-yield prediction with universal equation using runoff energy factor. In Present and Perspective Technology for Predicting Sediment Yield and Sources; US Department of Agriculture: Washington, DC, USA, 1975; pp. 244–252. [Google Scholar]
  69. Hengl, T.; de Jesus, J.M.; MacMillan, R.A.; Batjes, N.H.; Heuvelink, G.B.M.; Ribeiro, E.; Samuel-Rosa, A.; Kempen, B.; Leenaars, J.G.B.; Walsh, M.G.; et al. SoilGrids1km—Global Soil Information Based on Automated Mapping. PLoS ONE 2014, 9, e105992. [Google Scholar] [CrossRef] [Green Version]
  70. Chao-Yuan, L.; Wen-Tzu, L.; Wen-Chieh, C. Soil erosion prediction and sediment yield estimation: The Taiwan experience. Soil Tillage Res. 2002, 68, 143–152. [Google Scholar]
  71. Ahamed, T.N.; Rao, K.G.; Murthy, J. Fuzzy class membership approach to soil erosion modelling. Agric. Syst. 2000, 63, 97–110. [Google Scholar] [CrossRef]
  72. Gonzáles, C.; Llanos, R. Evaluación de los Efectos de la Deforestación en la Hidrología y Pérdida Lateral de Carbono Orgánico del Suelo de la Cuenca del Altomayo; Technical Report 2015; Infobosques: Lima, Peru, 2015. [Google Scholar]
  73. Ilbay-Yupa, M.; Zuvieta, R.; Lavado-Casimiro, W. Regionalización de la precipitación, su agresividad y concentración en la cuenca del río Guayas, Ecuador. La Granja 2019, 30, 57–80. [Google Scholar] [CrossRef] [Green Version]
  74. Aybar, C.; Fernández, C.; Huerta, A.; Lavado, W.; Vega, F.; Felipe-Obando, O. Construction of a high-resolution gridded rainfall dataset for Peru from 1981 to the present day. Hydrol. Sci. J. 2020, 65, 770–785. [Google Scholar] [CrossRef]
  75. Correa, S.W.; Mello, C.R.; Chou, S.C.; Curi, N.; Norton, L.D. Soil erosion risk associated with climate change at Mantaro River basin, Peruvian Andes. Catena 2016, 147, 110–124. [Google Scholar] [CrossRef]
  76. Khalil, U.; Aslam, B. Geospatial-based soil management analysis using novel technique for better soil conservation. Model. Earth Syst. Environ. 2021, 8, 259–275. [Google Scholar] [CrossRef]
  77. Ruthes, J.M.; Tomazoni, J.C.; Guimarães, E.; Gomes, T.C. Uso de sistema de informação geográfica na determinação do fator topográfico da Bacia do Rio Catorze, Sudoeste do PR. Rev. Bras. Geogr. Fís. 2012, 5, 1099–1109. [Google Scholar] [CrossRef] [Green Version]
  78. Fornelos, L.F.; Alves da Silva, S.M. Uso de modelos digitais de elevação (MDE) gerados a partir de imagens de radar interferométrico (SRTM) na estimativa de perdas de solo. Rev. Bras. Cartogr. 2007, 59, 25–33. [Google Scholar] [CrossRef]
  79. Gallo, V.H. Evolución de la Cobertura Boscosa en la Subcuenca Yuracyacu y su Influencia la Regulación Hídrica. Bachelor’s Thesis, Ingeniero Ambiental de la Universidad Nacional Federico Villarreal, Lima, Peru, 2018. [Google Scholar]
  80. Kinell, P.I.A. Geographic variation of USLE/RUSLE erosivity and erodibility factors. J. Hydrol. Eng. 2015, 20, C4014012. [Google Scholar] [CrossRef]
  81. Food and Agriculture Organization of the United Nations [FAO]. A Provisional Methodology for Soil Degradation Assessment. Technical Report. 1979. Available online: https://agris.fao.org/agris-search/search.do?recordID=XF8108785 (accessed on 28 November 2022).
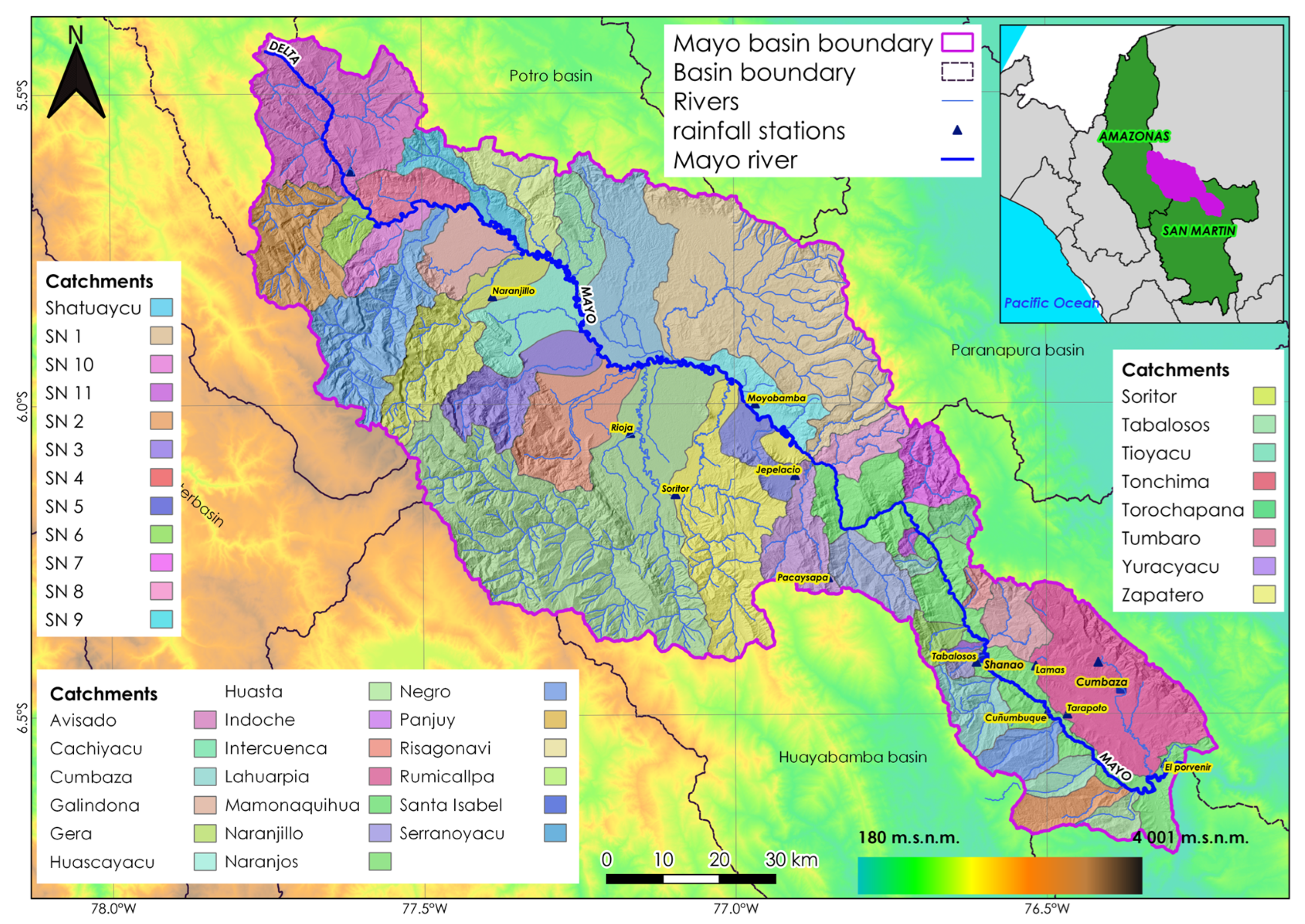
Sustainability 15 09059 g001 550
Figure 1. Location of the Mayo river basin.
Figure 1. Location of the Mayo river basin.
Sustainability 15 09059 g001
Sustainability 15 09059 g002 550
Figure 2. (a) Annual precipitation (1981–2019) and (b) mean R-factor.
Figure 2. (a) Annual precipitation (1981–2019) and (b) mean R-factor.
Sustainability 15 09059 g002
Sustainability 15 09059 g003 550
Figure 3. (a) Altitudinal variation and (b) LS factor.
Figure 3. (a) Altitudinal variation and (b) LS factor.
Sustainability 15 09059 g003
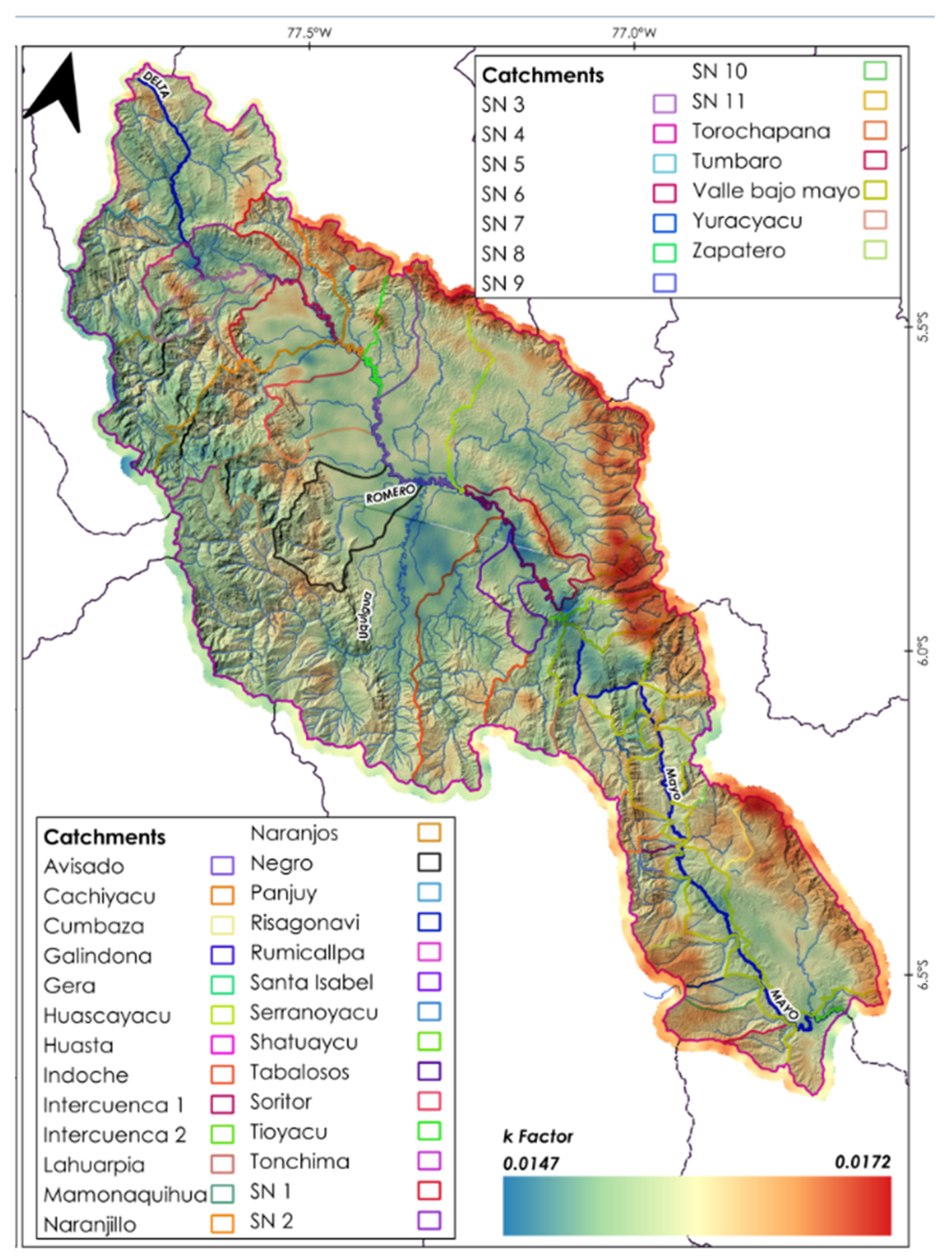
Sustainability 15 09059 g004 550
Figure 4. K-factor of the Mayo basin.
Figure 4. K-factor of the Mayo basin.
Sustainability 15 09059 g004
Sustainability 15 09059 g005 550
Figure 5. (a) NDVI and (b) C-factor.
Figure 5. (a) NDVI and (b) C-factor.
Sustainability 15 09059 g005
Sustainability 15 09059 g006 550
Figure 6. Potential (a) and actual (b) erosion of the Mayo basin.
Figure 6. Potential (a) and actual (b) erosion of the Mayo basin.
Sustainability 15 09059 g006
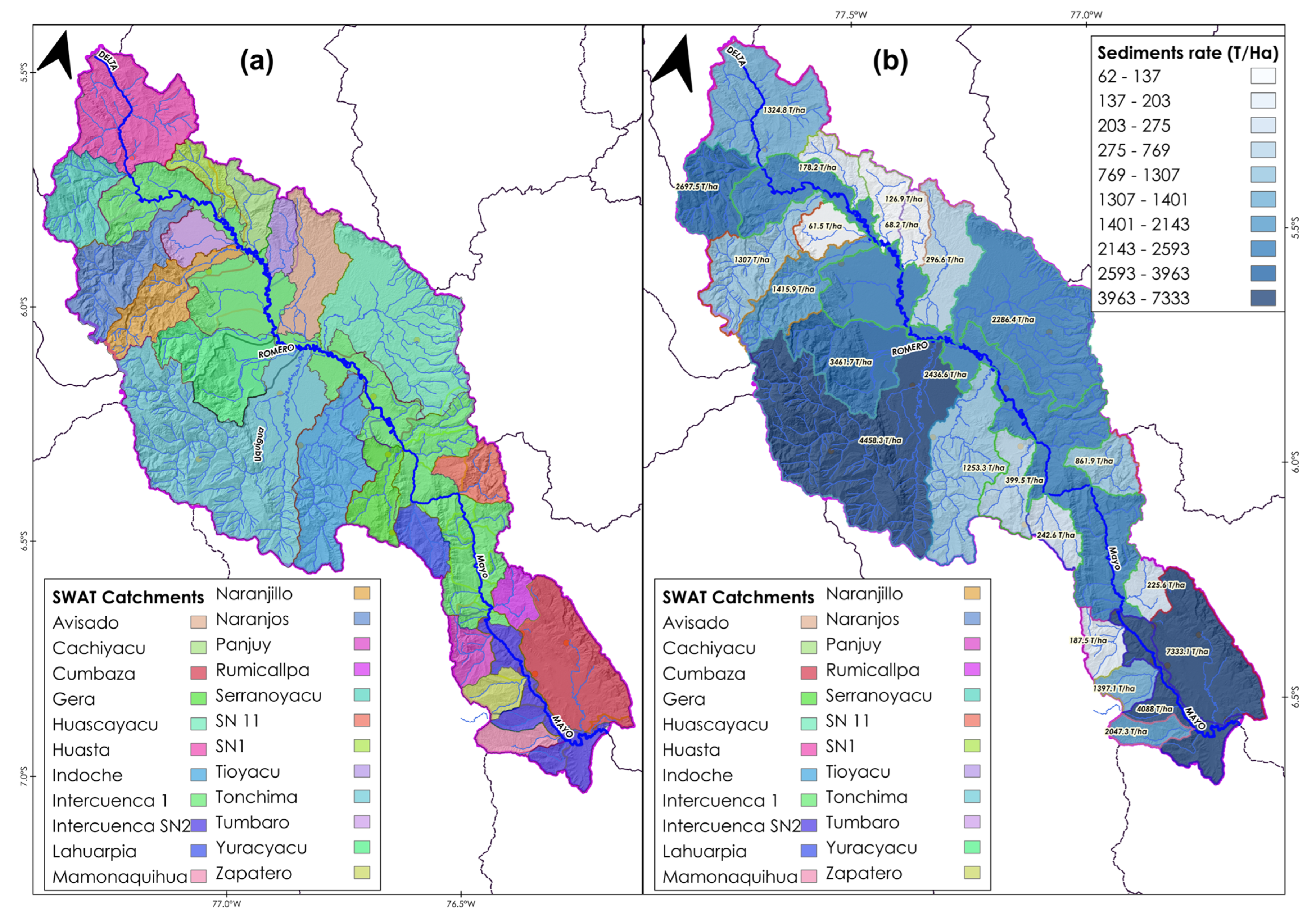
Sustainability 15 09059 g007 550
Figure 7. SWAT basins: (a) sediment rate, (b) (T/Ha).
Figure 7. SWAT basins: (a) sediment rate, (b) (T/Ha).
Sustainability 15 09059 g007
Sustainability 15 09059 g008 550
Figure 8. Seasonality of monthly precipitation in Altomayo area.
Figure 8. Seasonality of monthly precipitation in Altomayo area.
Sustainability 15 09059 g008
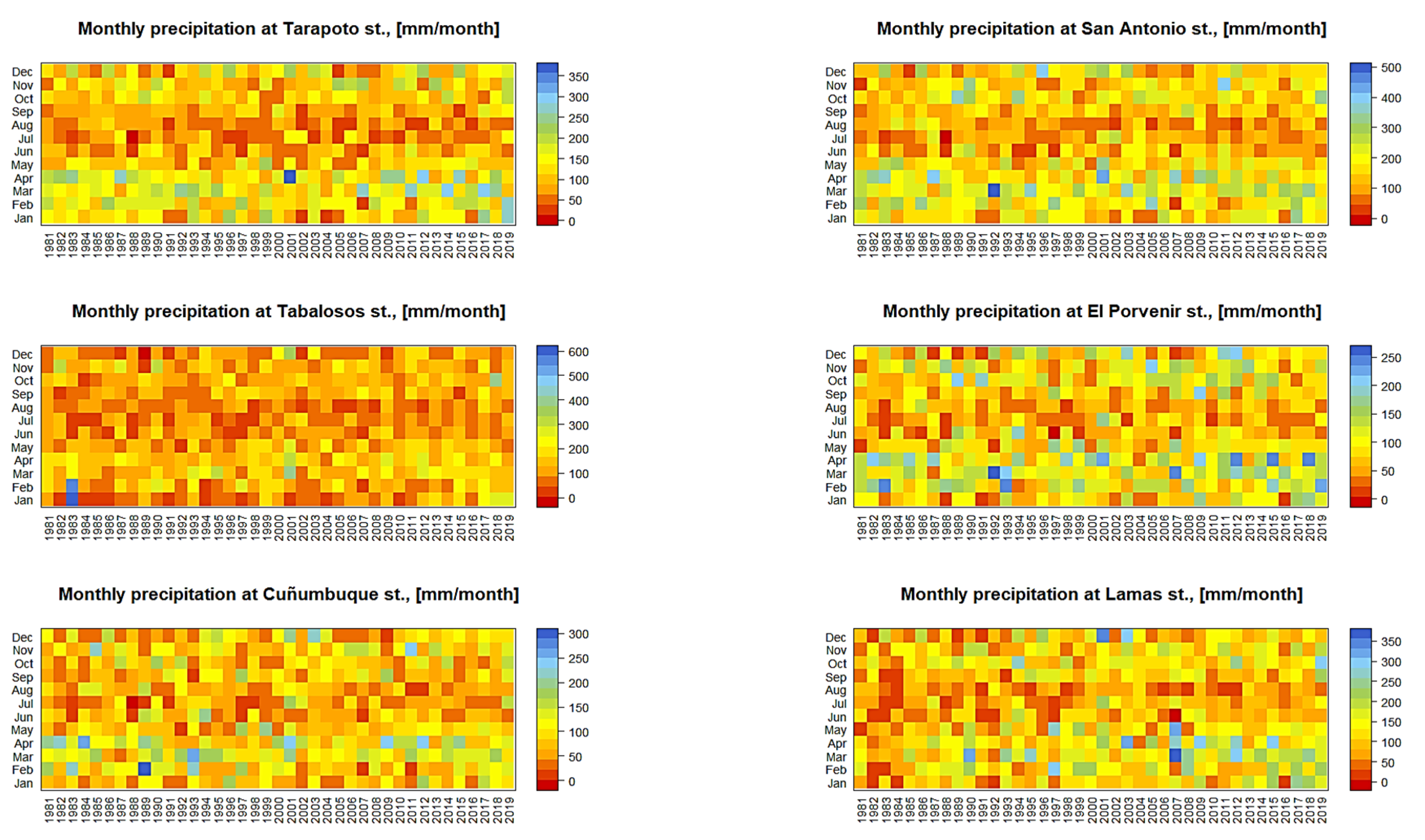
Sustainability 15 09059 g009 550
Figure 9. Seasonality of monthly precipitation in Bajomayo area.
Figure 9. Seasonality of monthly precipitation in Bajomayo area.
Sustainability 15 09059 g009
Sustainability 15 09059 g010 550
Figure 10. Correlation between different RUSLE input factors and physics characteristics in Mayo basin.
Figure 10. Correlation between different RUSLE input factors and physics characteristics in Mayo basin.
Sustainability 15 09059 g010
Table
Table 1. Details of the datasets used.
Table 1. Details of the datasets used.
Dataset UsedData SourceRemarks
Departmental and district boundariesInstituto Geográfico Nacional (IGN)National vector information for Peru.
Hydrography and National basin boundariesAutoridad Nacional del Agua (ANA)
RainfallServicio Nacional de Meteorología e Hidrología del Perú (SENAMHI)12 ground stations in the Mayo basin were used for the period 1981–2019.
Soil textureSoilGrids–250mMaps of soil properties for the entire globe at medium spatial resolution (250 m cell size) using state-of-the-art machine learning methods [45].
DEMSRTM–30m
(Google Earth Engine)		10 m spatial resolution multispectral data.
Remote sensing data for NDVI mapSentinel 2–level-2A
(Google Earth Engine)		Near global coverage of land elevation data at 1 arc-second generated through interferometric radar technique [46].
Table
Table 2. Physiographic characteristics of the Mayo river basins.
Table 2. Physiographic characteristics of the Mayo river basins.
NameAPKcH MeanH MinH MaxSLl
Huasta607.9127.21.41450.8938.02337.00.0351.911.7
Serranoyacu299.689.01.42153.9948.03444.00.0736.28.3
Naranjos401.9131.21.82297.7862.04001.00.0558.86.8
Tumbaro168.773.61.6948.2823.01755.00.0331.55.4
Cachiyacu179.383.41.71234.1819.01750.00.0336.84.9
Naranjillo350.3131.72.01823.2813.03819.00.0560.05.8
Tonchima1542.1265.71.91808.0320.03762.00.03120.012.8
Soritor215.488.41.7963.1805.02092.00.0338.65.6
Yuracyacu250.9101.31.81548.9805.03611.00.0645.15.6
Negro315.891.91.41159.7341.02831.00.0737.58.4
Tioyacu133.467.81.61017.6809.01690.00.0329.34.5
Avisado419.0141.11.9934.4801.01848.00.0264.06.5
Huascayacu962.2159.91.41066.0801.02266.00.0265.214.8
Indoche531.4144.11.71293.8800.02562.00.0363.78.3
Santa Isabel111.063.11.71012.3793.01632.00.0327.54.0
Huascayacu109.164.71.71438.0773.02224.00.0528.53.8
Panjuy128.655.11.41004.8267.01831.00.0721.66.0
Gera179.875.91.61414.2765.02136.00.0432.45.5
Lahuarpia144.655.81.31155.1680.01974.00.0621.16.9
Galindona102.953.91.51317.9745.01964.00.0522.34.6
Zapatero102.246.01.3788.9217.01560.00.0817.06.0
Risagonavi62.834.81.2623.6207.01366.00.0912.35.1
Mamonaquihua103.353.51.5726.4196.01362.00.0522.14.7
Shatuaycu27.137.42.0453.8180.01171.00.0617.11.6
Tabalosos16.221.41.5750.4283.01569.00.148.91.8
Rumicallpa114.251.51.3814.6277.01644.00.0720.05.7
Torochapana53.137.61.4935.8304.01642.00.0915.33.5
Cumbaza573.9120.91.4619.5193.01853.00.0348.711.8
Valle bajo mayo656.9337.63.7713.7180.01734.00.01164.84.0
Intercuenca1138.894.82.31042.5783.01685.00.0244.33.1
Intercuenca 233.532.51.6966.3767.01636.00.0613.82.4
SN 1135.190.22.21297.7823.02187.00.0341.93.2
SN 2130.765.41.61170.0851.01921.00.0428.04.7
SN 3100.563.31.81531.3868.03439.00.0928.03.6
SN 468.137.41.31533.1927.02794.00.1413.84.9
SN 513.115.81.21004.5442.01408.00.175.62.4
SN 653.338.01.5487.7197.0873.00.0415.63.4
SN 720.622.51.4972.5392.01605.00.148.92.3
SN 857.836.41.31129.8418.01770.00.1014.14.1
SN 919.921.31.3794.4276.01560.00.168.22.4
SN 1029.726.91.4917.6319.01687.00.1310.62.8
SN 11129.552.31.31276.8516.02505.00.1019.66.6
A: area (km2), P: perimeter (km), Kc: compactness index (dimensionless), H mean: mean altitude (m a.s.l.), H min: minimum altitude (m a.s.l.), H max: maximum altitude (m a.s.l.), S: average slope (m/m), L: equivalent major rectangle side (km), l: equivalent smaller side rectangle (km).
Table
Table 3. Sediment rate by watershed delineated using QSWAT (T/ha).
Table 3. Sediment rate by watershed delineated using QSWAT (T/ha).
BasinJanFebMarAprMayJunJulAugSepOctNovDecAverage
Huasta3162.02657.54589.11917.0611.4616.2237.6332.7136.1892.9483.4261.81324.8
SN1432.2381.3621.7250.778.282.632.042.315.6112.158.431.7178.2
Tumbaro167.727.1395.075.216.14.52.68.310.94.47.718.061.5
Serranoyacu6088.65381.38998.54562.11473.11581.5587.4809.5326.81542.6535.4482.72697.5
Cachiyacu306.551.3830.0164.633.78.24.216.322.413.027.344.9126.9
Tioyacu169.528.4432.784.618.74.92.59.813.68.117.228.568.2
Naranjos3451.6565.78798.61717.0322.371.439.2126.8168.665.2104.2253.91307.0
Avisado704.4113.81971.4394.280.118.49.036.849.027.759.195.5296.6
Huascayacu8065.17037.45169.41375.5627.1205.0313.4225.21838.9279.21187.71112.62286.4
Yuracyacu5114.59311.310,960.04564.91089.3250.6288.5364.3852.31907.42440.74396.13461.7
Naranjillo3653.1610.29257.41812.7379.593.053.3177.8253.9115.1181.5403.31415.9
Tonchima2534.85838.612,337.34485.53180.2960.7904.02318.58439.98990.02209.61301.04458.3
Indoche2916.73153.14241.41549.5437.952.9112.1134.0231.7575.0579.01056.51253.3
SN 112016.81767.93171.2959.7270.4142.393.274.1278.9385.3414.2768.8861.9
Gera504.8575.72244.4646.7204.963.940.748.5105.0100.3147.1112.2399.5
Lahuarpia297.2345.81350.8408.4107.245.425.331.173.864.992.668.8242.6
Rumicallpa278.61135.0525.0288.650.016.630.815.141.148.150.7227.0225.6
Intercuenca 13225.13671.86523.44057.52474.21226.4732.1572.01264.31687.91978.91826.02436.6
Panjuy262.5501.5587.5361.392.716.324.212.068.3118.759.9145.4187.5
Zapatero3109.95456.22730.41755.1514.0227.7201.2211.4207.7208.8342.01801.21397.1
Cumbaza14,883.127,722.214,517.58277.32538.71496.41421.51310.41315.01709.43634.49178.57333.7
Intercuenca SN25139.26314.810,271.96899.34290.82228.21409.11043.32025.62773.53444.53215.94088.0
Mamonaquihua4883.68794.73089.81654.7468.0241.8208.4221.9265.2362.71273.73103.12047.3
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Camacho-Zorogastúa, K.d.C.; Cesar Minga, J.; Gómez-Lora, J.W.; Gallo-Ramos, V.H.; Garcés Díaz, V. Evaluation of Soil Loss and Sediment Yield Based on GIS and Remote Sensing Techniques in a Complex Amazon Mountain Basin of Peru: Case Study Mayo River Basin, San Martin Region. Sustainability 2023, 15, 9059. https://doi.org/10.3390/su15119059

AMA Style

Camacho-Zorogastúa KdC, Cesar Minga J, Gómez-Lora JW, Gallo-Ramos VH, Garcés Díaz V. Evaluation of Soil Loss and Sediment Yield Based on GIS and Remote Sensing Techniques in a Complex Amazon Mountain Basin of Peru: Case Study Mayo River Basin, San Martin Region. Sustainability. 2023; 15(11):9059. https://doi.org/10.3390/su15119059

Chicago/Turabian Style

Camacho-Zorogastúa, Katherine del Carmen, Julio Cesar Minga, Jhon Walter Gómez-Lora, Víctor Hugo Gallo-Ramos, and Victor Garcés Díaz. 2023. "Evaluation of Soil Loss and Sediment Yield Based on GIS and Remote Sensing Techniques in a Complex Amazon Mountain Basin of Peru: Case Study Mayo River Basin, San Martin Region" Sustainability 15, no. 11: 9059. https://doi.org/10.3390/su15119059

APA Style

Camacho-Zorogastúa, K. d. C., Cesar Minga, J., Gómez-Lora, J. W., Gallo-Ramos, V. H., & Garcés Díaz, V. (2023). Evaluation of Soil Loss and Sediment Yield Based on GIS and Remote Sensing Techniques in a Complex Amazon Mountain Basin of Peru: Case Study Mayo River Basin, San Martin Region. Sustainability, 15(11), 9059. https://doi.org/10.3390/su15119059

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop