A Study of the Relevant Parameters for Converting Water Supply to Small Towns in the Province of Alicante to Systems Powered by Photovoltaic Solar Panels
Abstract
:1. Introduction
2. Materials and Methods
2.1. Input Data
- 1.
- Manometric head variation between June and December. This parameter has been adopted in aquifers (wells) where solar pumping has been installed;
- 2.
- Manometric head variation between May and December. Note that variables 1 and 2 are similar, but consider May or June the months with the highest and lowest (December) solar radiation;
- 3.
- Range of the manometric head;
- 4.
- Ratio of water volume consumed in June and December;
- 5.
- Ratio of water volume consumed in May and December;
- 6.
- Ratio of the maximum and minimum monthly water volume of the year. Because these months are different depending on the municipality;
- 7.
- Hydraulic efficiency;
- 8.
- Tank autonomy (capacity/volume consumed);
- 9.
- Average municipal consumption;
- 10.
- Average manometric head;
- 11.
- Maximum manometric head;
- 12.
- Energy cost per m3 of water.
2.1.1. Water Distribution Network Data
- ○
- Aquifer: The aquifer used for water abstraction is modeled as a reservoir, where the reservoir’s height represents the monthly average dynamic aquifer level (m). This level refers to the water height after the system has been lowered due to pump operation. To calculate this average depth, the maximum daily depths of the last five years (which correspond to the dynamic levels) are considered, as stated in [37];
- ○
- Piezometric head of the well. A reservoir is added to the hydraulic model to simulate the effect of the water level on the aquifer;
- ○
- Node downstream of the pump, necessary to include the pipeline from the aquifer to the reservoir supplying the town;
- ○
- Tanks. All features describe the tanks (elevation (m), diameter (m), volume (m3), maximum and minimum levels (m), etc.);
- ○
- Water distribution network. To speed up the simulation, the entire network can be simplified as a consumption node and with the municipal hourly consumption pattern;
- ○
- Characteristic curves of the pumping equipment: The model includes the relationship between flow rate and head (pressure) as well as the relationship between flow rate and efficiency.
- , : Nominal speed y when changing frequency (rpm);
- , : Flow rate at and at (m3/h);
- , : manometric head at and at (m);
- , : Power at and at (kW).
- ○
- Efficiency of a water supply network. This parameter has a direct impact on the variation in volume between June and December. Because leaks remain constant throughout the year, lower consumption leads to reduced injected flow. As a result, the supply network experiences higher pressure, which is directly linked to the volume of leakage. This means that the lower the performance of the supply network (greater leaks), the smaller the difference in volume consumed between June and December.
2.1.2. Data Measured in Every Municipality
- ○
- Base demand. The base demand corresponds to the average daily consumption for each month. This value results from the daily average of each month in the last five years and assumes that each month analyzed has different consumptions. The annual study results from 12 different models;
- ○
- Daily consumption patterns: the hourly pattern for each hour of the day of the simulated month shall be entered. To calculate the consumption patterns, the average of each hour of the day for each month over the last five years has been used;
- ○
- Water depth. The reservoir elevation in the model represents the aquifer. It is calculated as the average depth of the dynamic levels (depth with the pump running) for each month over the past five years.
- ○
- Average hourly solar radiation. This parameter has been calculated hourly. Each model incorporates these daily parameters for calculating the number of hours that pumping can work.
- Space requirements. Wherever possible, the best choice is to install solar panels on the tank’s roof. This will limit the available surface area. The greater the tilt angle, the greater the distance needed to avoid shading;
- Weight of the structure. To make sure a certain angle of inclination, a structure (which adds weight to the tank) is required. This will not always be due to overloading, which can sometimes lead to structural problems in the tank;
- Shading: To prevent voltage drops along the power line, it is recommended to position the solar PV installation near the pumping equipment. Because of the limited available land and sloping terrain in wooded areas or valleys, the wells are typically situated in such areas. Solar panels are often installed near each other to minimize the space required for the photovoltaic installation.
2.1.3. Municipalities Studied
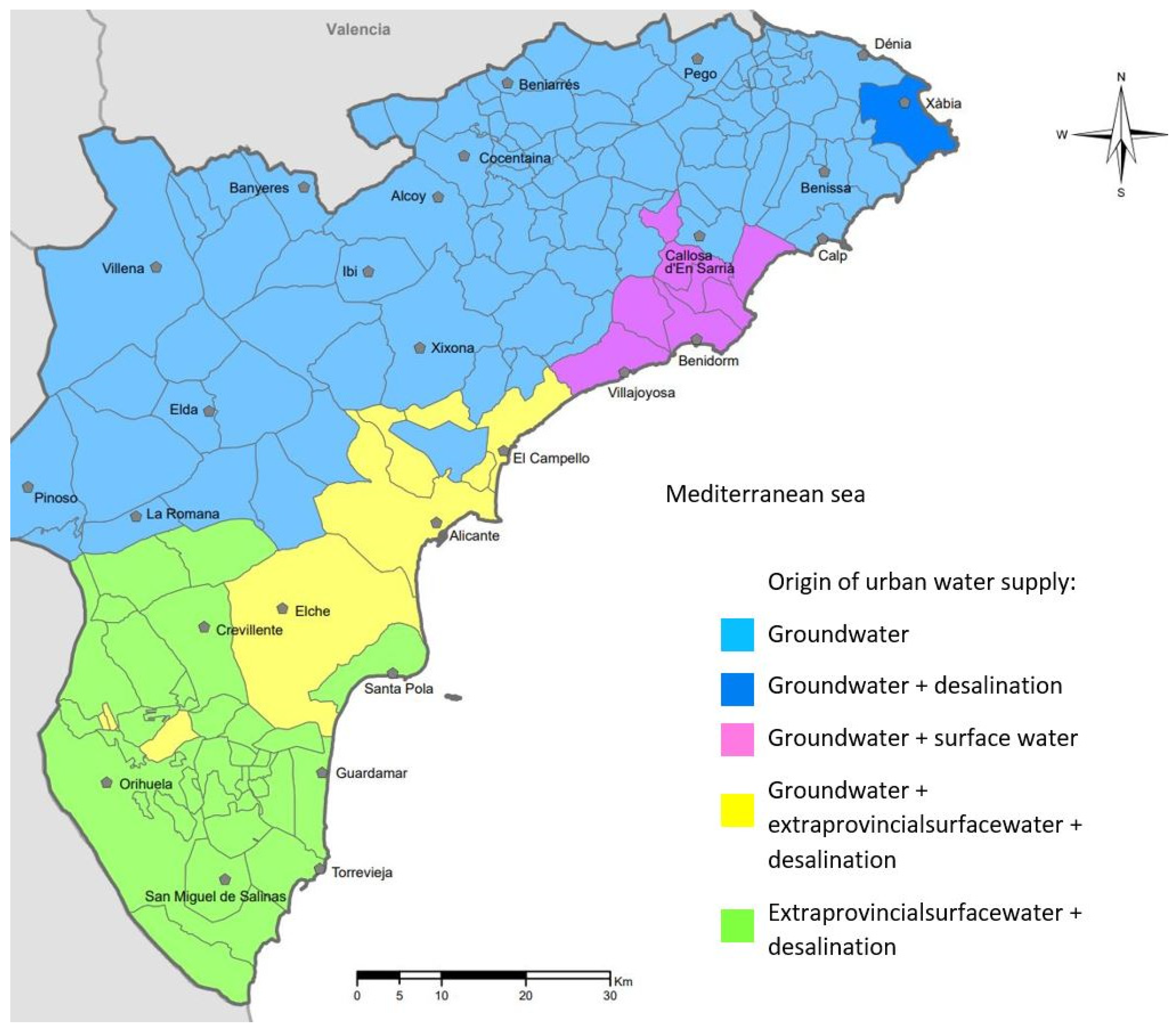
2.1.4. Municipalities Classified According to Drinking Water Origin
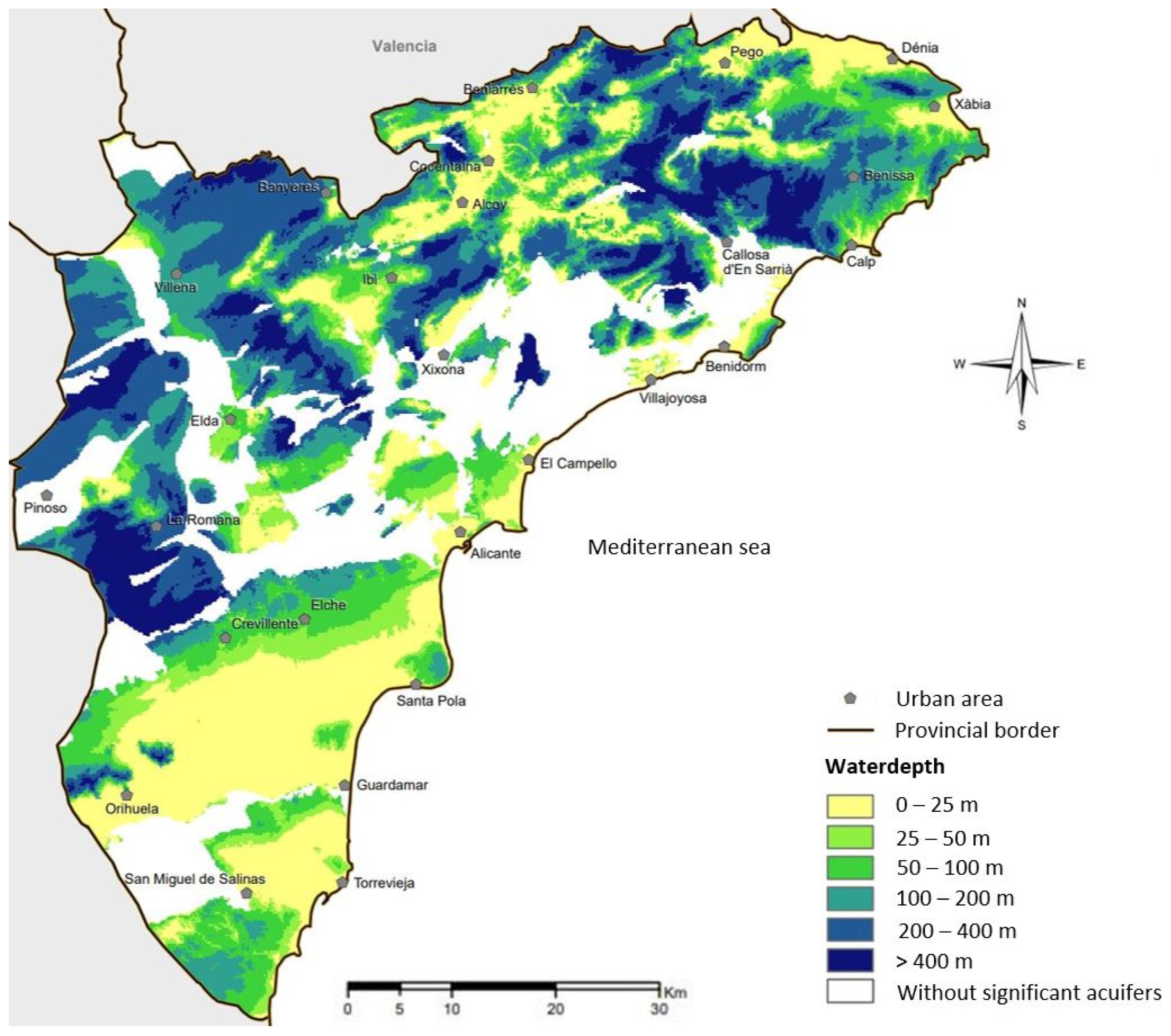
2.1.5. Classification of Municipalities According to the Height at Which Groundwater Is Found
2.2. Energy Consumption Calculation
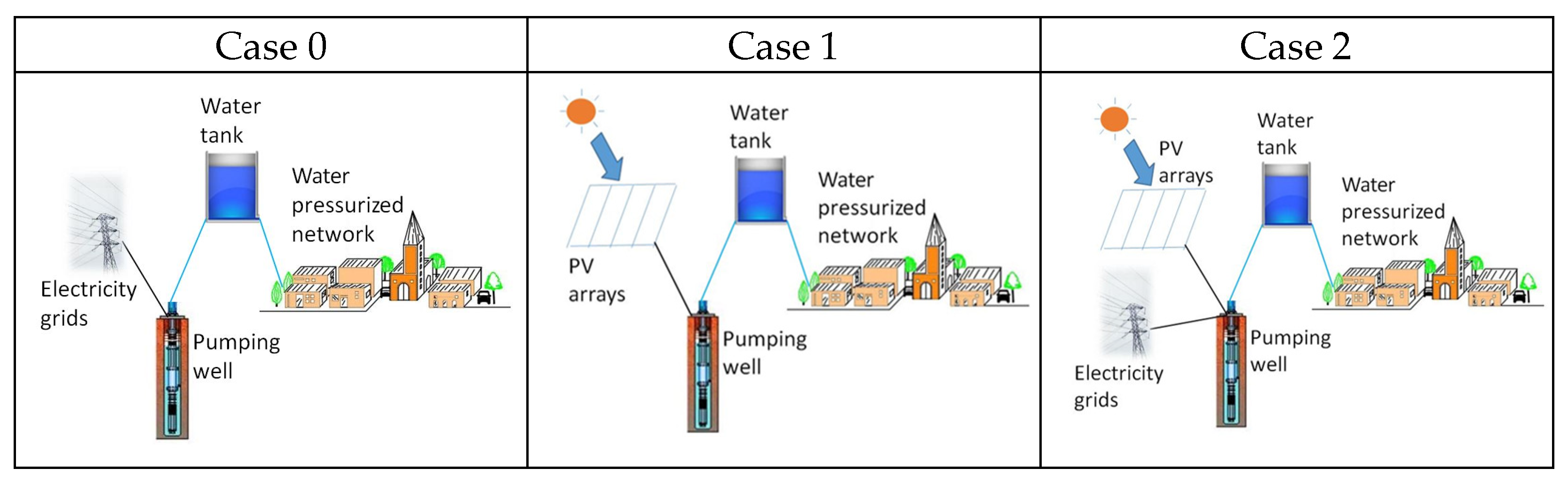
2.2.1. On-Grid Pumping (Case 0)
- A pump is selected with the capacity to pump the daily consumption of the population in 8 h (the number of off-peak hours of the electricity tariff). In most cases, the actual pump in the municipality meets these conditions. The pump must also be able to supply the greatest daily consumption of the year in 24 h, a need to be considered, especially in areas with high seasonality. This restriction was less restrictive than the earlier restriction, and all pumping stations met it;
- The hydraulic problem is solved. The pumps operate during off-peak hours (from 00:00 to 08:00). Peak hours (from 11:00 to 15:00 and from 19:00 to 23:00 in summer and winter) are avoided. The simulation period is equal to 744 h (31-day months); 720 h (30-day months), and 672 h in February (28 days);
- The operating hours are calculated and separated into off-peak, flat, and peak periods. In this way, the cost of the electrical energy consumed each month can be calculated by multiplying the hours by the costs in each period.
2.2.2. Off-Grid Pumping (Case 1)
- We choose the pumping equipment meeting the most unfavorable conditions (December in these latitudes). In situations where oversizing the photovoltaic installation would cause unaffordable investment costs, this condition is not taken into account. For this study, the limit has been set when the amortization period exceeds 30 years.
- 2.
- The hydraulic model is simulated (using a hydraulic solver such as EPAnet) [36]. Here, the pumping conditions will depend on the hours in which enough solar radiation is for the pump to work. If an inverter is available (increasing the cost-effectiveness of solar pumping), the power required at different pump frequencies is calculated to offer more pumping hours.
- 3.
- The number of pumping hours using solar energy must complete 100% of the water supply to the network; otherwise, the area of the solar park must be increased.
- 4.
- The cost of the investment in each scenario and the savings in the electricity bill (obtained by difference with the electricity bill for the case without solar panels) are shown. The point showing the best scenario is in the upper right corner of the graph. It corresponds to the scenario with the highest investment cost and the highest electricity bill savings, due to in this scenario, 100% of the electric bill is saved.
2.2.3. Hybrid Pumping (Case 2)
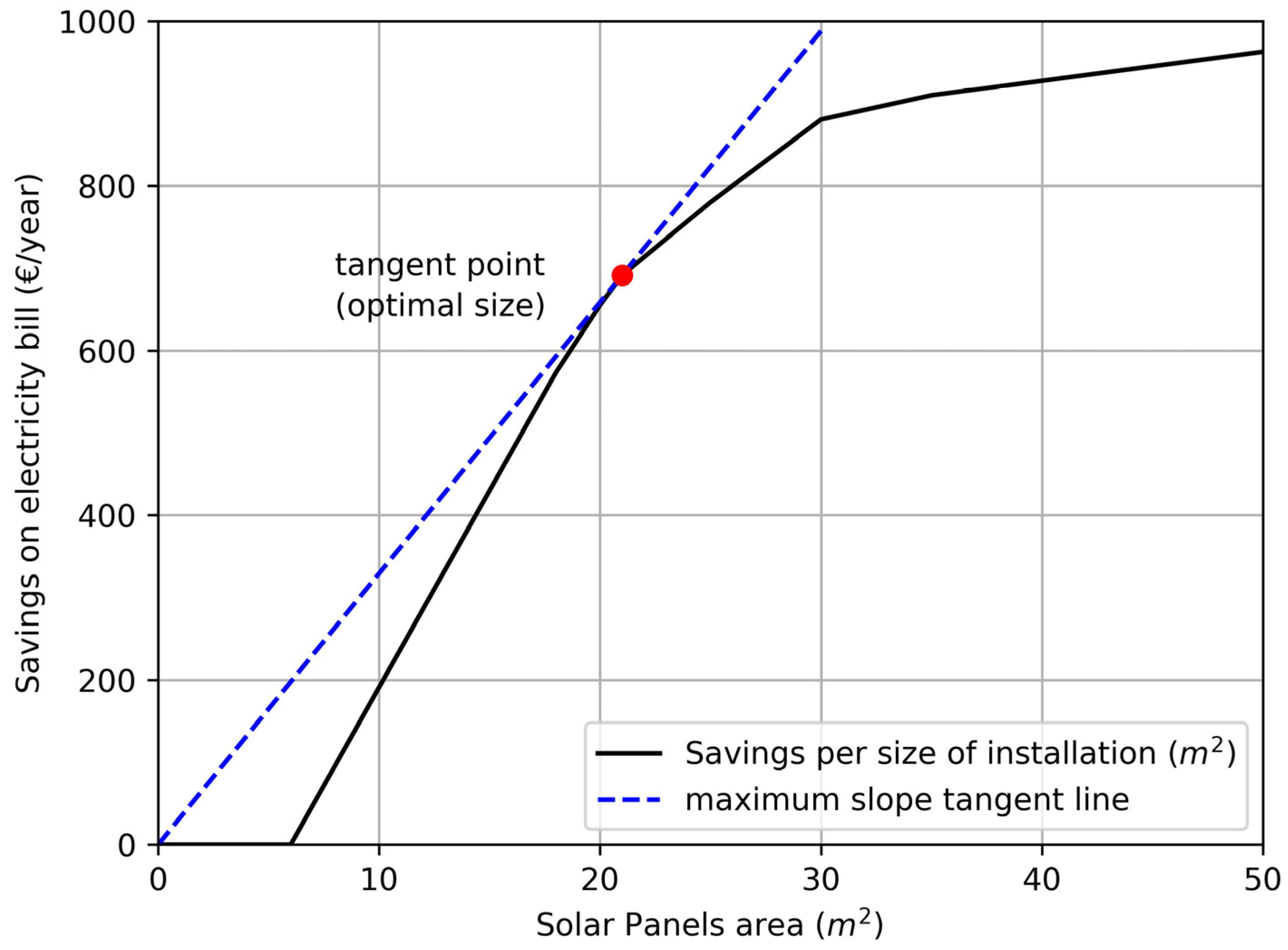
2.2.4. Optimal Point
- (0;0) Pumping without solar panels: Corresponds to the conventional scenario (Case 0), in which pumping is conducted with energy from the electricity grid, so neither investment nor savings;
- Largest area of solar PV modules with no savings: This is the scenario in which the dimensions of the solar park are 1 m2 smaller than the minimum area in which the solar park would supply the pump with enough power to lift water to the well and, therefore, produce savings in the electricity bill;
- 100% solar pumping (Case I): in this scenario, it will not be necessary to pump using energy from the electricity grid;
- The remaining scenarios necessary for the Savings/Area graph represent the point of least payback period with enough accuracy.
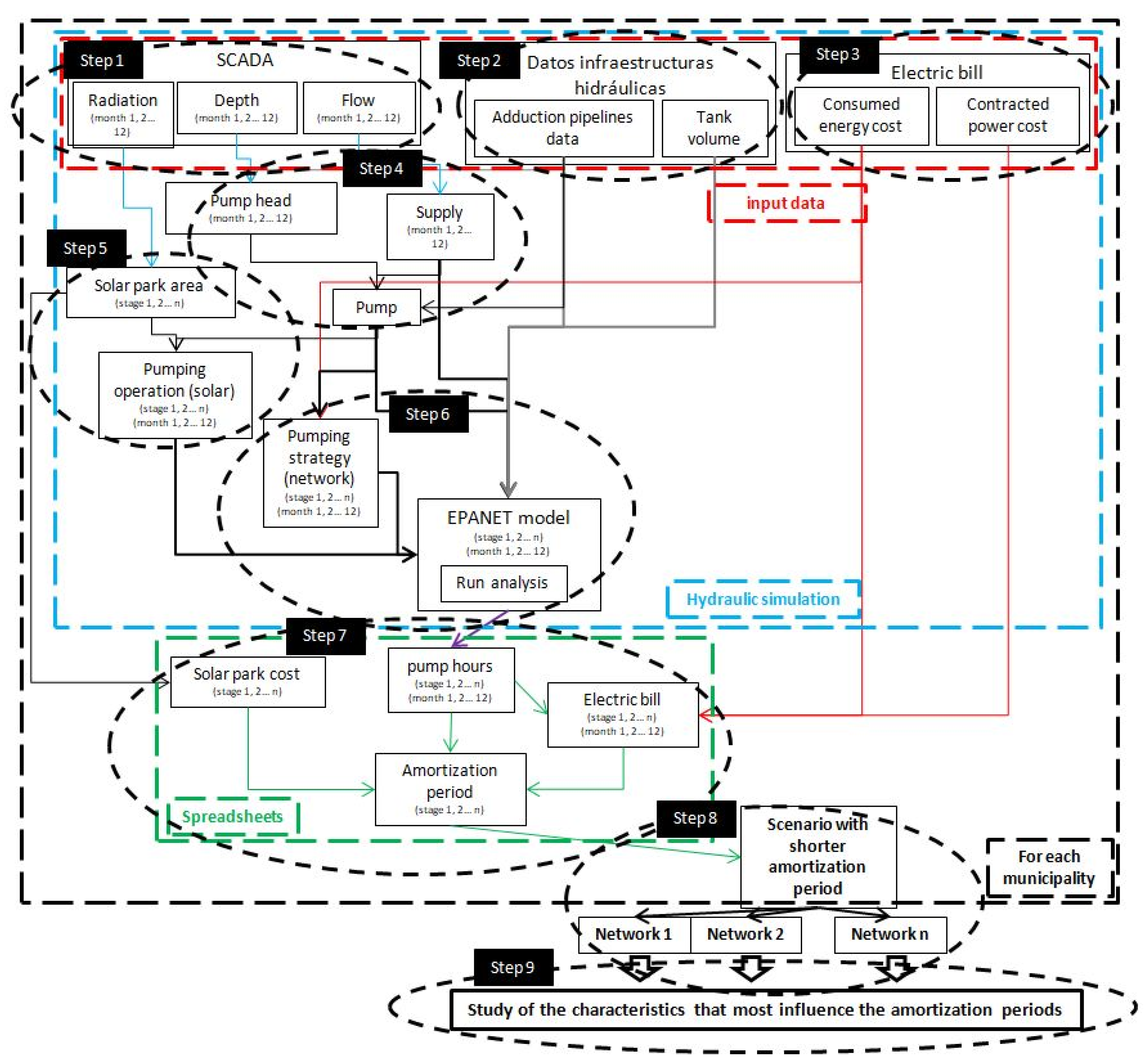
2.3. Method
- Radiation: Daily averages are collected for each month of the year; the ultimate aim is to have the average hourly irradiation for each month;
- Flow: On the one hand, the daily averages are obtained, and the monthly average values are calculated;
- Depth: The average value of the maximum daily depth is collected. These values correspond to the monthly dynamic level and represent the geometric head that the pump needs to overcome. They also account for head losses because of friction. In short, this geometric level difference is the minimum head of the pumping equipment.
2.4. Relevant Parameters
- Maximum, minimum, and annual average gauge head;
- Maximum, average, and minimum monthly consumption;
- Efficiency of the supply network;
- Storage volume of the reservoir(s);
- Maximum and minimum autonomy of the tank(s) (depending on seasonal consumptions);
- Length of supply network;
- Cost of water.
3. Case Study
3.1. Monthly Irradiation
3.2. Study of Energy Consumption by Month Analyzed
3.3. Principal Components Study
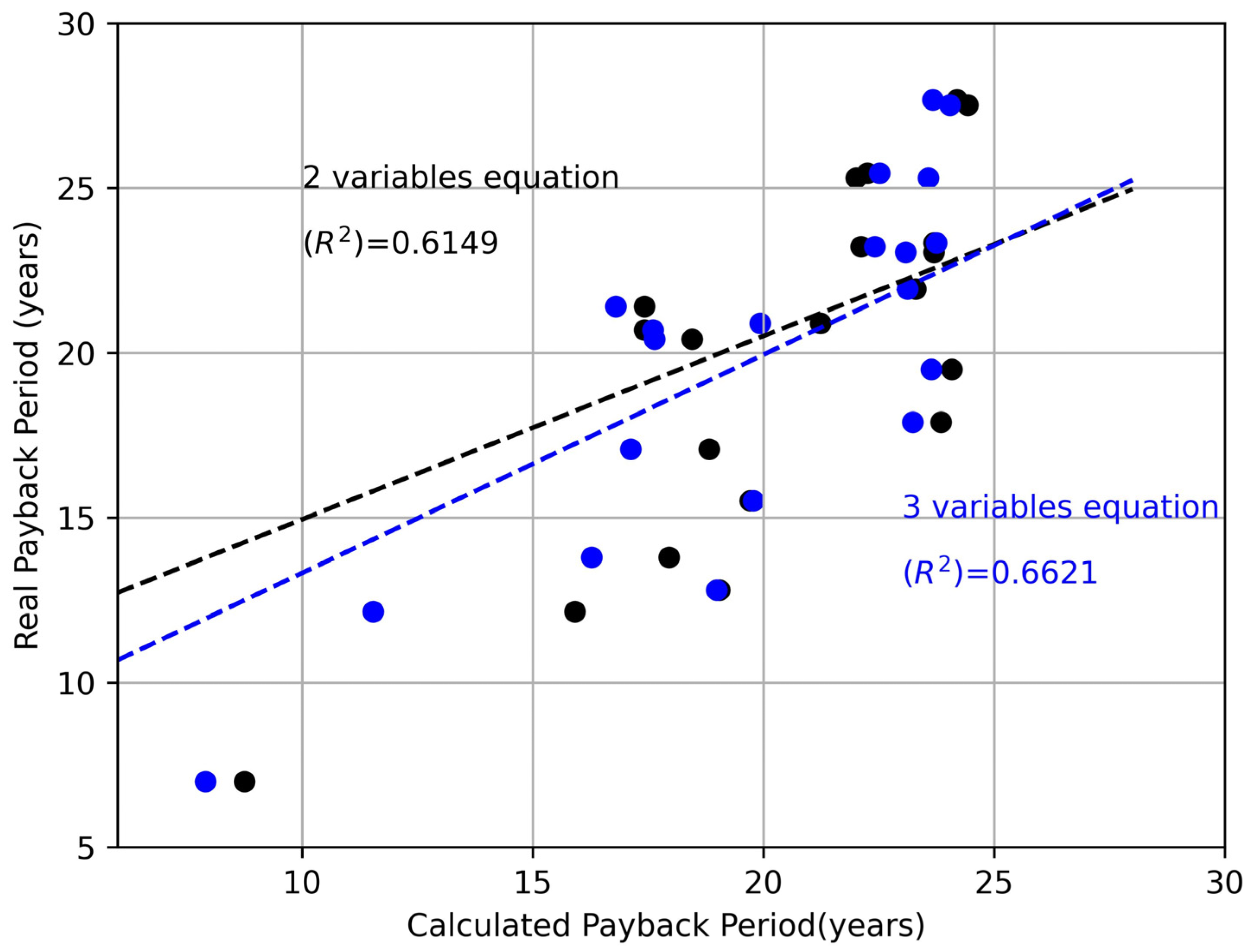
3.4. Calculation of the Amortization Period
3.5. Adjustment of the Amortization Period from the Representative Variables
- CAP: Calculated amortization period (years)
- C: Constant (dimensionless)
- A: Multiplier factor (dimensionless)
- α and β: Boosting factors (dimensionless)
- : Maximum manometric head/Minimum manometric head, annual (dimensionless).
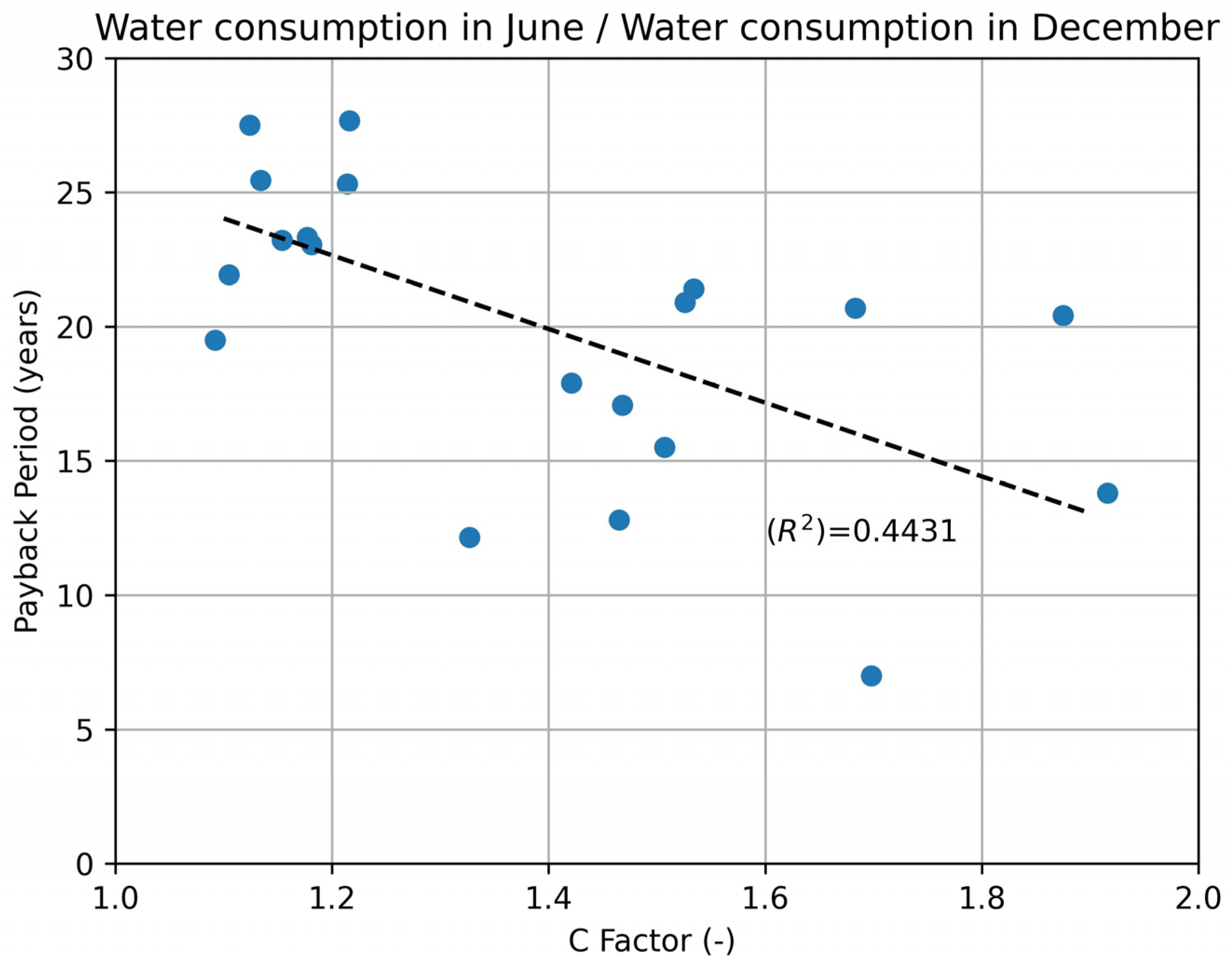
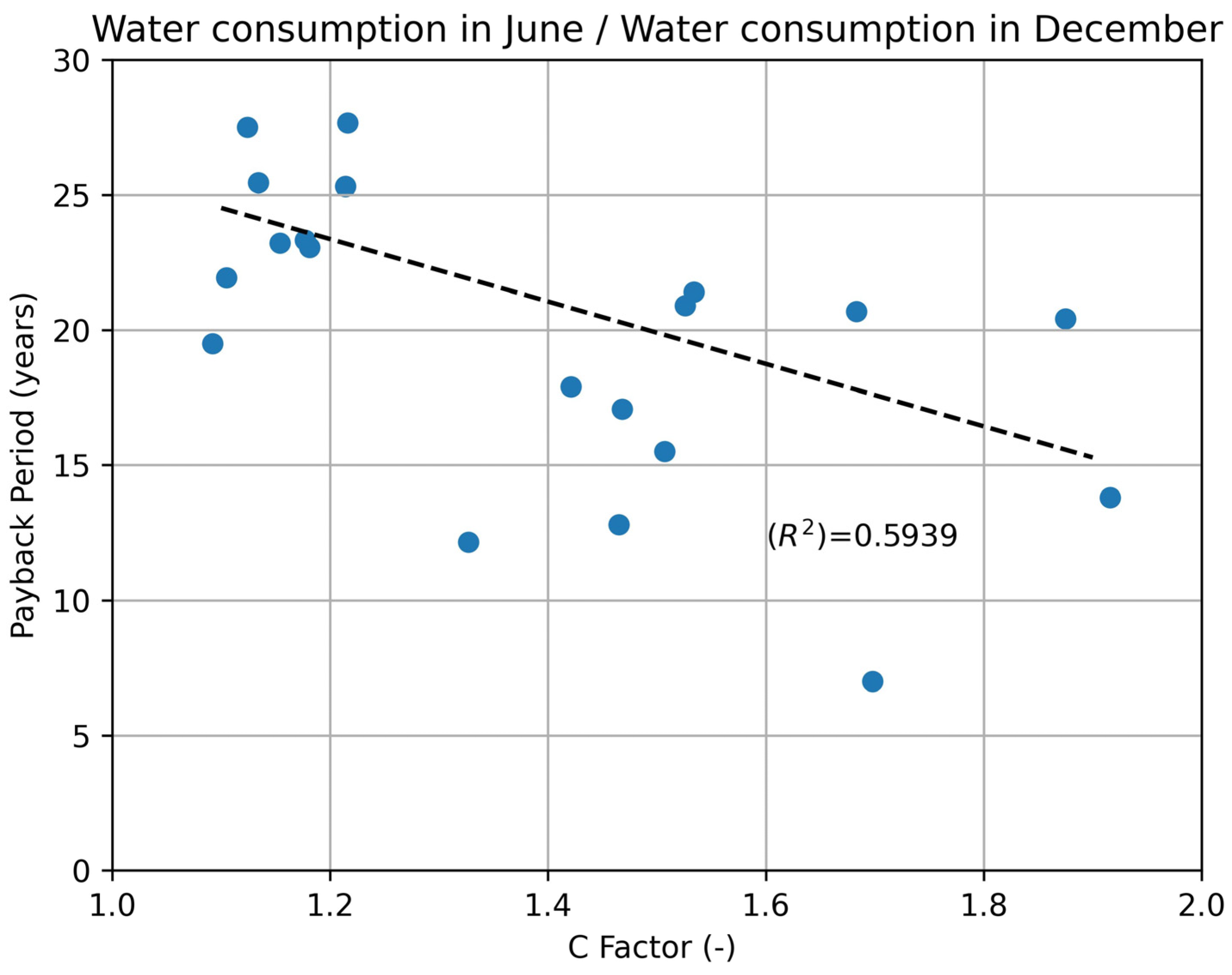
- : Volume consumed in June/Volume consumed in December (dimensionless).
- CAP: Calculated amortization period (years)
- C: Constant (dimensionless)
- A: Multiplier factor (dimensionless)
- α, β and Υ: Boosting factors (dimensionless)
- ((H.m.max.)/(H.m.min)): Maximum manometric head/Minimum manometric head, annual (dimensionless).
- ((Cons.June.)/(Cons.December)): Volume consumed in June/Volume consumed in December (dimensionless).
- ((H.m.June.)/(H.m.December)): Manometric head for June/Manometric head for December (dimensionless).
3.6. Influence of Piezometric Head Differences
4. Discussion
4.1. Future Developments
4.2. Recommendation for Practitioners
- Incorporating advanced solar panels with high conversion efficiency allows for optimal energy generation even in low-light conditions;
- Innovative storage systems enable efficient utilization of solar energy during non-daylight hours;
- Combination of solar panels and wind turbines, providing a hybrid renewable energy solution for continuous pump operation.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Cons. December | Volume supplied in December |
| Cons. June | Volume supplied in June |
| H.m.máx | Maximum manometric head of the year |
| H.m.mín | Minimum manometric head of the year |
| Hmn | Manometric head at 50 Hz of frequency |
| Hmx | Manometric head at x frequency |
| nn | Frequency (Hz) |
| nx | x frequency |
| Pn | Power rate at 50 Hz of frequency |
| PV | Photovoltaic |
| Px | Power rate at x frequency |
| Qn | Flow rate at 50 Hz of frequency |
| Qx | Flow rate at x frequency |
| Acronyms | |
| CAP | Calculated amortization period |
| CO2 | Carbon dioxide |
| PCA | Principal Components Study |
| SCADA | Supervisory Control And Data Acquisition |
References
- Palacios-Cabrera, T.A.; Valdés-Abellán, J.; Jódar-Abellán, A.; Rodrigo-Comino, J. Land-use changes and precipitation cycles to understand hydrodynamic responses in semiarid Mediterranean karstic watersheds. Sci. Total Environ. 2022, 819, 153182. [Google Scholar] [CrossRef] [PubMed]
- Ram, M.; Bogdanov, D.; Aghahosseini, A.; Gulagi, A.; Oyewo, A.; Child, M.; Caldera, U.; Sadovskaia, K.; Farfan Orozco, F.; Noel, L.; et al. Global Energy System based on 100% Renewable Energy: Energy Transition in Europe Across Power, Heat, Transport and Desalination Sectors. In Study by LUT University and Energy Watch Group; Research Reports 89; Lappeenranta University of Technology: Lappeenranta, Finland, 2018. [Google Scholar] [CrossRef]
- Kang, J.-N.; Wei, Y.-M.; Liu, L.-C.; Han, R.; Yu, B.-Y.; Wang, J.-W. Energy systems for climate change mitigation: A systematic review. Appl. Energy 2020, 263, 114602. [Google Scholar] [CrossRef]
- Liu, S.; Yuan, J.; Deng, W.; Luo, M.; Xie, Y.; Liang, Q.; Zou, Y.; He, Z.; Wu, H.; Cao, Y. High-efficiency organic solar cells with low non-radiative recombination loss and low energetic disorder. Nat. Photonics 2020, 14, 300–305. [Google Scholar] [CrossRef]
- IEA. World Energy Outlook 2019; IEA: Paris, France, 2019. Available online: https://www.iea.org/reports/world-energy-outlook-2019 (accessed on 1 November 2019).
- Saleh Yassien, H.; Alomar, O.; Mohamed Salih, M. Performance analysis of triple-pass solar air heater system: Effects of adding a net of tubes below absorber surface. Sol. Energy 2020, 207, 813–824. [Google Scholar] [CrossRef]
- Oishi, A.; Tanjim, M.; Ali, M.T. Loss Analysis of Market Available Solar Cells and Possible Solutions. Int. J. Sci. Eng. Res. 2019, 10, 210–216. [Google Scholar] [CrossRef]
- Halkos, G.; Gkampoura, E.-C. Reviewing Usage, Potentials, and Limitations of Renewable Energy Sources. Energies 2020, 13, 2906. [Google Scholar] [CrossRef]
- Sugianto, S. Comparative Analysis of Solar Cell Efficiency between Monocrystalline and Polycrystalline. INTEK J. Penelit. 2020, 7, 92. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, Y.; Jin, K.; Qin, J.; Xu, J.; Li, W.; Xiong, J.; Liu, J.; Xiao, Z.; Sun, K.; et al. 18% Efficiency organic solar cells. Sci. Bull. 2020, 65, 272–275. [Google Scholar] [CrossRef] [Green Version]
- Menke, S.M.; Ran, N.A.; Bazan, G.C.; Friend, R.H. Understanding Energy Loss in Organic Solar Cells: Toward a New Efficiency Regime. Joule 2018, 2, 25–35. [Google Scholar] [CrossRef] [Green Version]
- Kiprono, A.; Ibanez Llario, A. Solar Pumping for Water Supply; Practical Action Publishing: Rugby, UK, 2020. [Google Scholar] [CrossRef]
- Chandel, S.; Naik, M.; Chandel, R. Review of Solar Photovoltaic Water Pumping System Technology for Irrigation and Community Drinking Water Supplies. Renew. Sustain. Energy Rev. 2015, 49, 1084–1099. [Google Scholar] [CrossRef]
- Şenol, R. An analysis of solar energy and irrigation systems in Turkey. Energy Policy 2012, 47, 478–486. [Google Scholar] [CrossRef]
- Marques-Perez, I.; Guaita-Pradas, I.; Gallego, A.; Segura, B. Territorial planning for photovoltaic power plants using an outranking approach and GIS. J. Clean. Prod. 2020, 257, 120602. [Google Scholar] [CrossRef]
- Pardo, M.Á.; Jodar-Abellan, A.; Vélez, S.; Rodrigo-Comino, J. A method to estimate optimal renovation period of solar photovoltaic modules. Clean Technol. Environ. Policy 2022, 24, 2865–2880. [Google Scholar] [CrossRef]
- Pardo, M.; Fernández Rodríguez, H.; Jódar-Abellán, A. Converting a Water Pressurized Network in a Small Town into a Solar Power Water System. Energies 2020, 13, 4013. [Google Scholar] [CrossRef]
- García-López, M.; Montano, B.; Melgarejo, J. The financial competitiveness of photovoltaic installations in water utilities: The case of the Tagus-Segura water transfer system. Sol. Energy 2023, 249, 734–743. [Google Scholar] [CrossRef]
- Hamidat, A.; Benyoucef, B. Systematic procedures for sizing photovoltaic pumping system, using water tank storage. Energy Policy 2009, 37, 1489–1501. [Google Scholar] [CrossRef]
- Loaui, N.; Khaldi, F.; Aksas, M. Design of photo voltaic pumping system using water tank storage for a remote area in Algeria. In Proceedings of the IREC 2014—5th International Renewable Energy Congress, Hammamet, Tunisia, 25–27 March 2014. [Google Scholar] [CrossRef]
- Imjai, T.; Thinsurat, K.; Ditthakit, P.; Wipulanusat, W.; Setkit, M.; Garcia, R. Performance Study of Integrated Solar-Water Supply System for Isolated Agricultural Areas in Thailand: Two Case-Study Villages of The Royal Initiative Project. Water Sci. Technol. 2020. [CrossRef]
- Longwe, B.; Mganga, M.; Sinyiza, N. Review of sustainable solar powered water supply system design approach by Water Mission Malawi. Water Pract. Technol. 2019, 14, 749–763. [Google Scholar] [CrossRef]
- Sharma, E.; Khatiwada, N.R.; Ghimire, A. Design of Micro Water Supply System Using Solar Energy. Acad. Soc. Appropr. Technol. 2019, 5, 8–17. [Google Scholar] [CrossRef]
- Agbo, S.; Samuel, O.; Amosun, S.; Joel, O.; Fayomi, O.S.I.; Bamisaye, O.; Afolalu, A. Development of a solar energy-powered surface water pump. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1107, 012002. [Google Scholar] [CrossRef]
- Al Zyoud, A.; Othman, A.; Manasrah, A.; Abdelhafez, E.A. Investment Analysis of a Solar Water Pumping System in Rural Areas in Jordan. Int. J. Energy A Clean Environ. 2020, 21, 269–281. [Google Scholar] [CrossRef]
- Guno, C.S.; Agaton, C.B. Socio-Economic and Environmental Analyses of Solar Irrigation Systems for Sustainable Agricultural Production. Sustainability 2022, 14, 6834. [Google Scholar] [CrossRef]
- Mantri, S.; Kasibhatla, R.; Chennapragada, B. Grid-connected vs. off-grid solar water pumping systems for agriculture in India: A comparative study. Energy Sources Part A Recovery Util. Environ. Eff. 2020, 1–15. [Google Scholar] [CrossRef]
- de Souza Grilo, M.M.; Fortes, A.F.C.; de Souza, R.P.G.; Silva, J.A.M.; Carvalho, M. Carbon footprints for the supply of electricity to a heat pump: Solar energy vs. electric grid. J. Renew. Sustain. Energy 2018, 10, 023701. [Google Scholar] [CrossRef]
- Compain, P. Solar Energy for Water Desalination. Procedia Eng. 2012, 46, 220–227. [Google Scholar] [CrossRef] [Green Version]
- Boudjemaa, M.; Chenni, R. Water Pumping Using Solar Energy. Int. J. Adv. Appl. Sci. 2017, 6, 221. [Google Scholar] [CrossRef] [Green Version]
- Navarro-González, F.J.; Pardo, M.; Chabour, H.E.; Alskaif, T. An irrigation scheduling algorithm for sustainable energy consumption in pressurised irrigation networks supplied by photovoltaic modules. Clean Technol. Environ. Policy 2023, 1–16. [Google Scholar] [CrossRef]
- Viveros, P.; Wulff, F.; Kristjanpoller, F.; Nikulin, C.; Grubessich, T. Sizing of a Standalone PV System with Battery Storage for a Dairy: A Case Study from Chile. Complexity 2020, 2020, 5792782. [Google Scholar] [CrossRef]
- Pardo, M.Á.; Manzano, J.; Valdes-Abellan, J.; Cobacho, R. Standalone direct pumping photovoltaic system or energy storage in batteries for supplying irrigation networks. Cost analysis. Sci. Total Environ. 2019, 673, 821–830. [Google Scholar] [CrossRef] [Green Version]
- Jane, R.; Parker, G.; Vaucher, G.; Berman, M. Characterizing Meteorological Forecast Impact on Microgrid Optimization Performance and Design. Energies 2020, 13, 577. [Google Scholar] [CrossRef] [Green Version]
- Melgarejo Moreno, J.; Fernández Mejuto, M. (Eds.) El Agua en la Provincia de Alicante. Alicante: Diputación Provincial de Alicante; Universidad de Alicante: Alicante, Spain, 2020; 366p, ISBN 978-84-15327-92-9. [Google Scholar]
- Rossman, L. Epanet 2 Users Manual; Cincinnati US Environmental Protection Agency National Risk Management Research Laboratory: Cincinnati, OH, USA, 2000; Volume 38.
- Valdes-Abellán, J.; Pardo, M.A.; Jodar-Abellan, A.; Pla, C.; Fernandez-Mejuto, M. Climate change impact on karstic aquifer hydrodynamics in southern Europe semi-arid region using the KAGIS model. Sci. Total Environ. 2020, 723, 138110. [Google Scholar] [CrossRef] [PubMed]
- Campana, P.E.; Li, H.; Zhang, J.; Zhang, R.; Liu, J.; Yan, J. Economic optimization of photovoltaic water pumping systems for irrigation. Energy Convers. Manag. 2015, 95, 32–41. [Google Scholar] [CrossRef] [Green Version]
- Flowers, M.E.; Smith, M.K.; Parsekian, A.W.; Boyuk, D.S.; McGrath, J.K.; Yates, L. Climate impacts on the cost of solar energy. Energy Policy 2016, 94, 264–273. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Castillo, M.L.; Youssef, A.; Serdy, J.G.; Watts, A.; Schmid, C.; Kurtz, S.; Peters, I.M.; Buonassisi, T. Quantitative analysis of degradation mechanisms in 30-year-old PV modules. Sol. Energy Mater. Sol. Cells 2019, 200, 110019. [Google Scholar] [CrossRef]
- Cromratie Clemons, S.K.; Salloum, C.R.; Herdegen, K.G.; Kamens, R.M.; Gheewala, S.H. Life cycle assessment of a floating photovoltaic system and feasibility for application in Thailand. Renew. Energy 2021, 168, 448–462. [Google Scholar] [CrossRef]
- Chabour, H.E.; Pardo, M.A.; Riquelme, A. Economic assessment of converting a pressurised water distribution network into an off-grid system supplied with solar photovoltaic energy. Clean Technol. Environ. Policy 2022, 24, 1823–1835. [Google Scholar] [CrossRef]
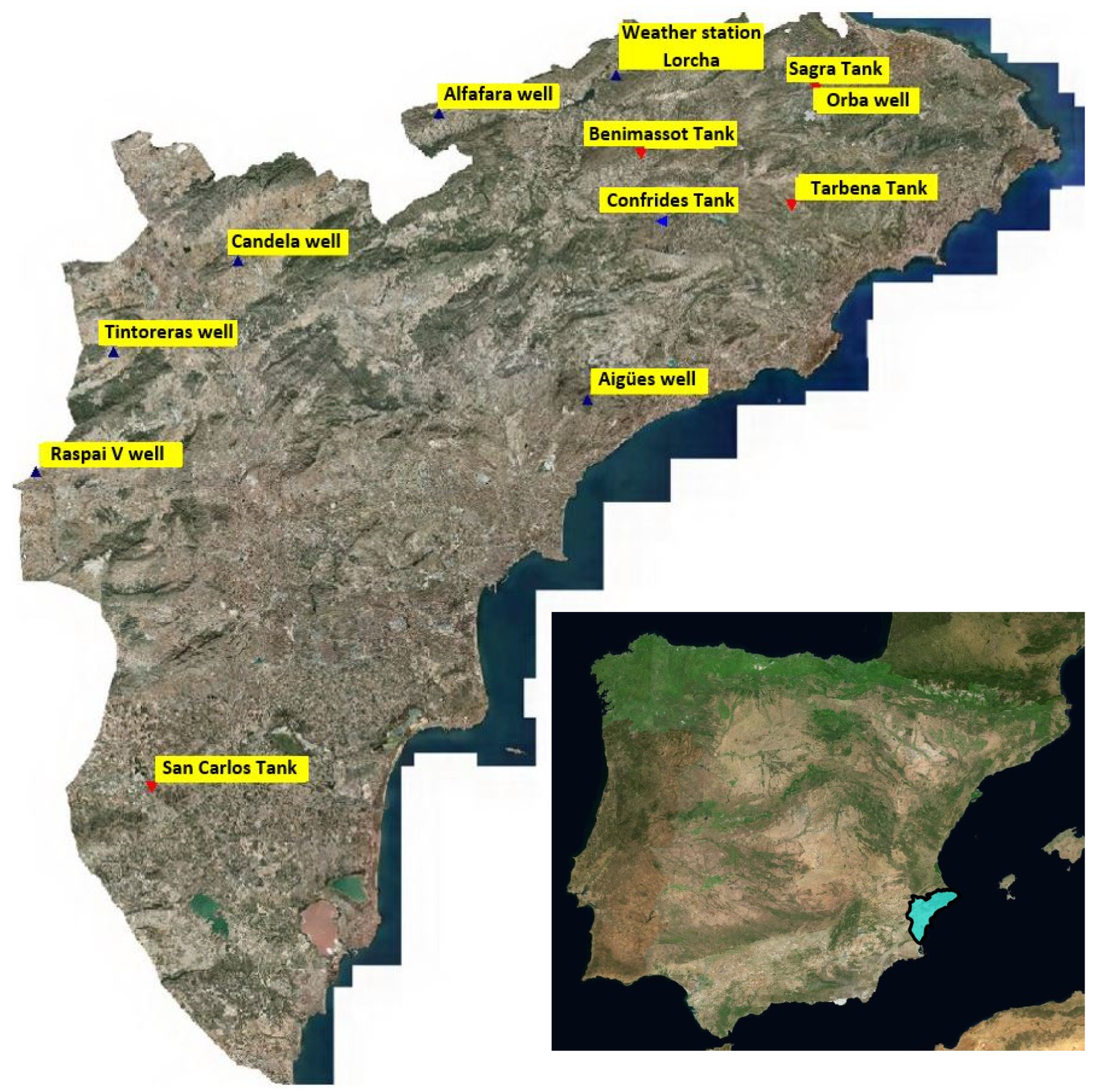


| Town | UTMX | UTMY | Town | UTMX | UTMY |
|---|---|---|---|---|---|
| Redován | 681,589 | 4,223,053 | Orba | 753,762 | 4,296,672 |
| Pinoso | 668,864 | 4,257,731 | Alfafara | 713,061 | 4,296,925 |
| Aigües | 729,290 | 4,265,542 | Cañada | 690,935 | 4,280,706 |
| Villena | 677,276 | 4,270,853 | Confrides | 737,504 | 4,285,055 |
| Tárbena | 751,781 | 4,286,809 | Sagra | 754,387 | 4,299,526 |
| Benimassot | 735,190 | 4,292,504 | Lorcha | 732,483 | 4,301,177 |
| Payback Period. (Years) | Variability | Payback Period. (Years) | Variability |
|---|---|---|---|
| H.m. minimum | 0.56 | May consumption | 0.28 |
| H.m. maximum | 0.56 | June consumption | 0.24 |
| H.m. Average | 0.568 | December consumption | 0.27 |
| H.m. May | 0.55 | average consumption | 0.27 |
| H.m. June | 0.53 | Cons. June/Cons. December | −0.56 |
| H.m. December | 0.53 | Storage autonomy (days) | −0.19 |
| H.m. max./H.m. min. | −0.65 | June/December | −0.77 |
| H.m. June/H.m. December | −0.53 | June/Dec (Hm squared) | −0.71 |
| H.m. May/H.m. December | 0.07 | June/Dec (consumption squared) | −0.71 |
| H.m. minimum | 0.56 | H.m. June | 0.53 |
| H.m. maximum | 0.56 | H.m. December | 0.53 |
| H.m. Average | 0.56 | H.m. max./H.m. min. | −0.65 |
| H.m. May | 0.54 | H.m. June/H.m. December | −0.53 |
| H.m. May/H.m. December | 0.07 |
| Town | Payback (Years) | Town | Payback (Years) | Town | Payback (Years) | Town | Payback (Years) |
|---|---|---|---|---|---|---|---|
| 1 | 7.00 | 6 | 17.08 | 11 | 20.90 | 16 | 23.33 |
| 2 | 12.15 | 7 | 17.90 | 12 | 21.41 | 17 | 25.31 |
| 3 | 12.80 | 8 | 19.50 | 13 | 21.93 | 18 | 25.45 |
| 4 | 13.80 | 9 | 20.41 | 14 | 23.05 | 19 | 27.51 |
| 5 | 15.51 | 10 | 20.69 | 15 | 23.22 | 20 | 27.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández Rodríguez, H.; Pardo, M.Á. A Study of the Relevant Parameters for Converting Water Supply to Small Towns in the Province of Alicante to Systems Powered by Photovoltaic Solar Panels. Sustainability 2023, 15, 9324. https://doi.org/10.3390/su15129324
Fernández Rodríguez H, Pardo MÁ. A Study of the Relevant Parameters for Converting Water Supply to Small Towns in the Province of Alicante to Systems Powered by Photovoltaic Solar Panels. Sustainability. 2023; 15(12):9324. https://doi.org/10.3390/su15129324
Chicago/Turabian StyleFernández Rodríguez, Héctor, and Miguel Ángel Pardo. 2023. "A Study of the Relevant Parameters for Converting Water Supply to Small Towns in the Province of Alicante to Systems Powered by Photovoltaic Solar Panels" Sustainability 15, no. 12: 9324. https://doi.org/10.3390/su15129324





