Review of Metaheuristic Optimization Algorithms for Power Systems Problems
Abstract
:1. Introduction
2. Metaheuristic Optimization
2.1. Overview
- The fundamental principles of these algorithms may be explained abstractly without reference to any specific situation, from simple local search techniques to complicated learning processes.
- Metaheuristic algorithms are ways of directing the search process to explore the search space efficiently. They often use updating coefficients that balance global and local search methods. These coefficients are initialized with large values, raising the global searching ability. At the end of the optimization process, this coefficient should be small to converge to the best solutions.
- Metaheuristic algorithms use domain-specific information in the form of heuristics regulated by a higher-level approach.
- The objective function in the metaheuristic algorithm formulation does not include the gradient or Hessian matrix. Therefore, they are no-deterministic algorithms, providing near-optimal solutions.
- These algorithms memorize the results of the previous searches and are used to guide the actual search process.
- These algorithms contain a number of parameters that must be adapted to the considered task, as well as techniques to prevent becoming stuck in local solutions in the search space. Considering the solved problem, these parameters are selected to provide better performance [32].
2.2. Basic Concepts
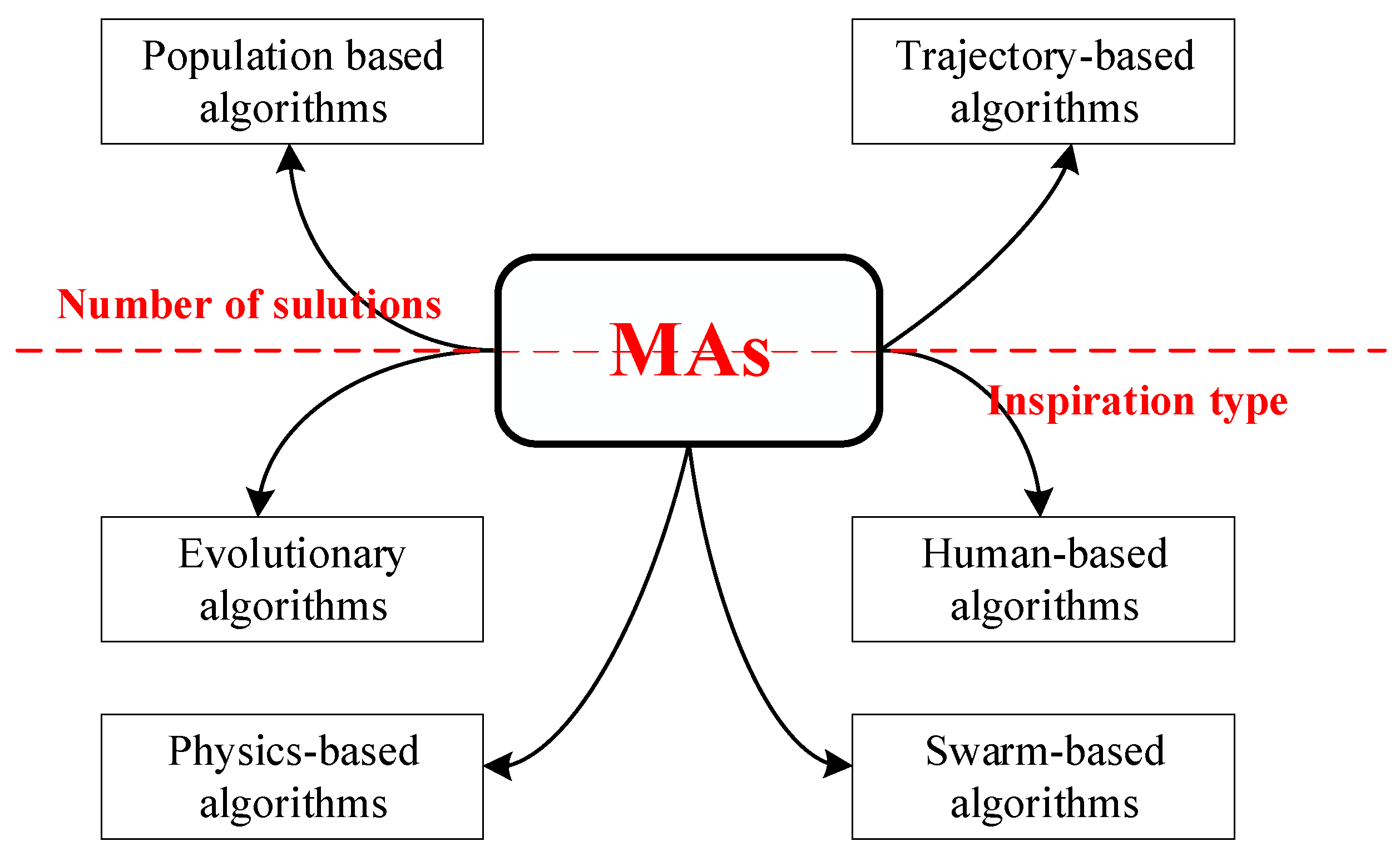
2.3. Classification
- Trajectory-based (single solution) algorithms, including tabu search (TS), hill climbing (HC), and simulated annealing (SA), start with a single solution and replace it with a better solution located nearby at each iteration.
- Population-based algorithms employ a group of possible solutions at the same task to address the same task. The population is randomly initialized, and an iterative method is used to improve it. After each iteration, a new generation is created based on the elitism strategy. The best-adapted individuals (representing the elite group) from the last generation are moved to the new generation. Meanwhile, the newly generated individuals have a relationship with this elite.
- Evolutionary algorithms are biological evolution-inspired algorithms, which include genetic recombination, mutation, and natural selection.
- Swarm-based algorithms use the collective behavior of multiple individuals. Each individual wants to engage with others to develop themselves based on the collective experience of the swarm.
- Physics-based algorithms are based on physical concepts, such as electromagnetism, momentum, and gravity.
- Human-based algorithms are algorithms based on human social acts.
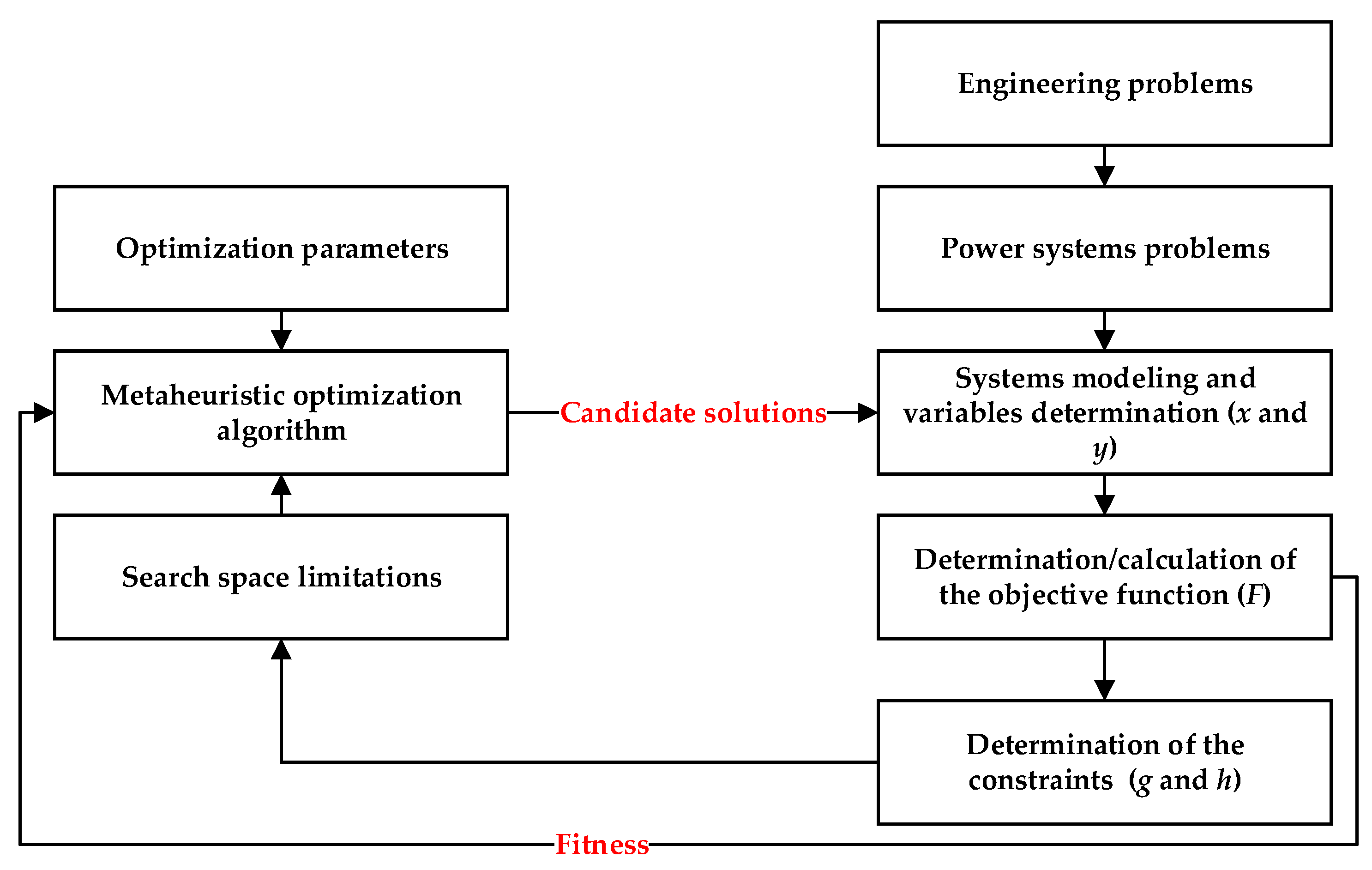
2.4. Formulation
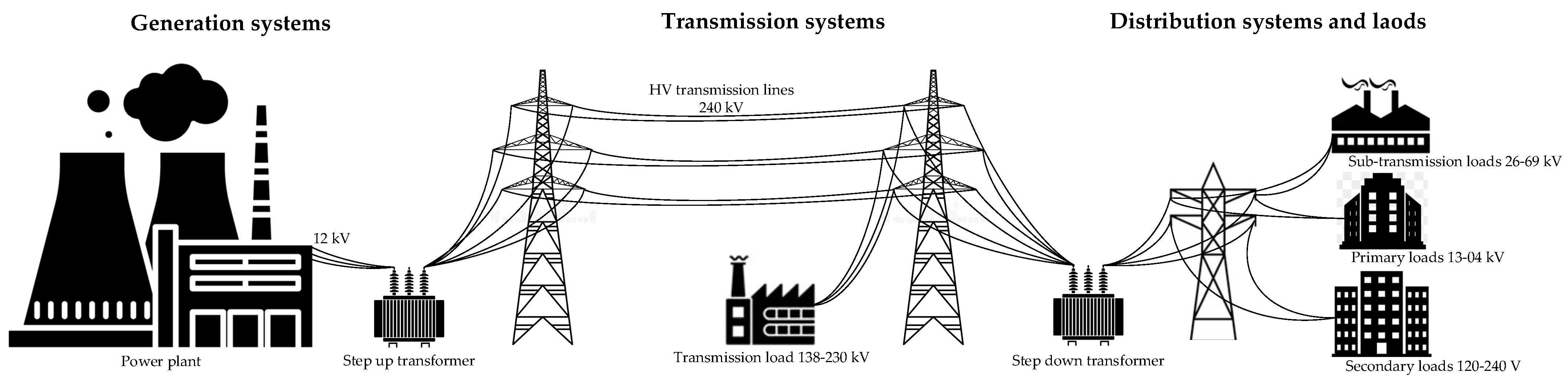
3. Metaheuristic Algorithms for Power System Applications
3.1. Optimal Power Flow for Transmission Power Systems
3.2. Optimal Reactive Power Dispatching
3.3. Optimal Combined Economic and Emission Dispatching
3.4. Optimal Power Flow in Distribution Networks
3.5. Optimal Volt/Var Controlling in the Distribution Power Network
- VRs, OVTCTs, and ULTCTs tap-changer settings;
- voltage magnitudes in PV buses;
- capacitors and SVCs’ reactive powers.
3.6. Optimizing the Size and Placement of DGs
3.7. Unit Commitment
- Start-up costs; these costs are described as an exponential (for cooling) or linear (for banking) function of the number of hours the machine has been down.
- Shut-clown costs; these expenses are specified as a set sum for each unit per shutdown.
- Fuel costs; however, using multiple fuels for flame stability while the machine is operating at low output levels might make this aspect more complicated.
- Power balance.
- System reserve requirements.
- Initial conditions.
- High and low production limits.
- Unit minimum-up and minimum-down times.
- Rate limits.
- Unit start-up and shut-down ramps.
- Flame stabilization using dual or alternate fuel.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Leon-Aldaco, S.E.; Calleja, H.; Aguayo Alquicira, J. Metaheuristic Optimization Methods Applied to Power Converters: A Review. IEEE Trans. Power Electron. 2015, 30, 6791–6803. [Google Scholar] [CrossRef]
- Dantzig, G.B. Linear Programming. Oper. Res. 2002, 50, 42–47. [Google Scholar] [CrossRef] [Green Version]
- Bertsekas, D.P. Nonlinear Programming. J. Oper. Res. Soc. 1997, 48, 334. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic Programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef]
- Fletcher, R. Practical Methods of Optimization; John Wiley & Sons, Ltd.: Chichester, UK, 2000; ISBN 9781118723203. [Google Scholar]
- Box, F. A Heuristic Technique for Assigning Frequencies to Mobile Radio Nets. IEEE Trans. Veh. Technol. 1978, 27, 57–64. [Google Scholar] [CrossRef]
- Devarapalli, R.; Bhattacharyya, B.; Sinha, N.K. An Intelligent EGWO-SCA-CS Algorithm for PSS Parameter Tuning under System Uncertainties. Int. J. Intell. Syst. 2020, 35, 1520–1569. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1995, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Tsai, C.-W.; Chiang, M.-C.; Ksentini, A.; Chen, M. Metaheuristic Algorithms for Healthcare: Open Issues and Challenges. Comput. Electr. Eng. 2016, 53, 421–434. [Google Scholar] [CrossRef]
- Shah, P.; Sekhar, R.; Kulkarni, A.J.; Siarry, P. Metaheuristic Algorithms in Industry 4.0; CRC Press: Boca Raton, FL, USA, 2021; ISBN 9781003143505. [Google Scholar]
- Dai, Y.; Zhou, X.; Chu, X.; Li, C.; Su, Z.; Zhu, Z.; Cui, P.; Qi, J.; Wang, Y. Effect of Entrainer Thermodynamic Properties on the Separation of Ternary Mixtures Containing Two Minimum Boiling Azeotropes by Extractive Distillation. Ind. Eng. Chem. Res. 2022, 61, 15273–15288. [Google Scholar] [CrossRef]
- Wang, Y.; Bu, G.; Wang, Y.; Zhao, T.; Zhang, Z.; Zhu, Z. Application of a Simulated Annealing Algorithm to Design and Optimize a Pressure-Swing Distillation Process. Comput. Chem. Eng. 2016, 95, 97–107. [Google Scholar] [CrossRef]
- Byles, D.; Mohagheghi, S. Sustainable Power Grid Expansion: Life Cycle Assessment, Modeling Approaches, Challenges, and Opportunities. Sustainability 2023, 15, 8788. [Google Scholar] [CrossRef]
- Massoud Amin, S.; Wollenberg, B.F. Toward a Smart Grid: Power Delivery for the 21st Century. IEEE Power Energy Mag. 2005, 3, 34–41. [Google Scholar] [CrossRef]
- Agustriyanto, R.; Zhang, J. Obtaining the Worst Case RGA and RDGA for Uncertain Systems via Optimization. Proc. Am. Control Conf. 2007, 5360–5365. [Google Scholar] [CrossRef]
- Han, Q.; Wen, M. An Uncertain Optimization Model for Repairable Inventory System. In Proceedings of the 2014 Prognostics and System Health Management Conference (PHM-2014 Hunan), Zhangjiajie, China, 24–27 August 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 378–382. [Google Scholar]
- Fu, X.; Guo, Q.; Sun, H. Statistical Machine Learning Model for Stochastic Optimal Planning of Distribution Networks Considering a Dynamic Correlation and Dimension Reduction. IEEE Trans. Smart Grid 2020, 11, 2904–2917. [Google Scholar] [CrossRef]
- Fu, X. Statistical Machine Learning Model for Capacitor Planning Considering Uncertainties in Photovoltaic Power. Prot. Control Mod. Power Syst. 2022, 7, 5. [Google Scholar] [CrossRef]
- Lee k, Y.; EI-Sharkawi, M. Modern Heuristic Optimization Techniques; Lee, K.Y., El-Sharkawi, M.A., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008; ISBN 9780470225868. [Google Scholar]
- Rezk, H.; Olabi, A.G.; Wilberforce, T.; Sayed, E.T. A Comprehensive Review and Application of Metaheuristics in Solving the Optimal Parameter Identification Problems. Sustainability 2023, 15, 5732. [Google Scholar] [CrossRef]
- Rezk, H.; Olabi, A.G.; Sayed, E.T.; Wilberforce, T. Role of Metaheuristics in Optimizing Microgrids Operating and Management Issues: A Comprehensive Review. Sustainability 2023, 15, 4982. [Google Scholar] [CrossRef]
- Ganesan, V.; Sobhana, M.; Anuradha, G.; Yellamma, P.; Devi, O.R.; Prakash, K.B.; Naren, J. Quantum Inspired Meta-Heuristic Approach for Optimization of Genetic Algorithm. Comput. Electr. Eng. 2021, 94, 107356. [Google Scholar] [CrossRef]
- Lazar, A. Heuristic Knowledge Discovery for Archaeological Data Using Genetic Algorithms and Rough Sets. In Heuristic and Optimization for Knowledge Discovery; IGI Global: Hershey, PA, USA, 2002; Volume 2, pp. 263–278. [Google Scholar]
- Yang, X. Nature-Inspired Metaheuristic Algorithms, 2nd ed.; Luniver Press: Bristol, UK, 2010; p. 115. [Google Scholar]
- Voß, S.; Martello, S.; Osman, I.H.; Roucairol, C. (Eds.) Meta-Heuristics: Advances and Trends in Local Search Paradigms for Optimization; Springer: Boston, MA, USA, 1998; ISBN 978-0-7923-8369-7. [Google Scholar]
- Vinod Chandra, S.S.; Anand, H.S. Nature Inspired Meta Heuristic Algorithms for Optimization Problems. Computing 2022, 104, 251–269. [Google Scholar] [CrossRef]
- Abdullah, H.M.; Park, S.; Seong, K.; Lee, S. Hybrid Renewable Energy System Design: A Machine Learning Approach for Optimal Sizing with Net-Metering Costs. Sustainability 2023, 15, 8538. [Google Scholar] [CrossRef]
- Justin, S.; Saleh, W.; Lashin, M.M.A.; Albalawi, H.M. Design of Metaheuristic Optimization with Deep-Learning-Assisted Solar-Operated On-Board Smart Charging Station for Mass Transport Passenger Vehicle. Sustainability 2023, 15, 7845. [Google Scholar] [CrossRef]
- Alshammari, A.; Chabaan, R.C. Metaheruistic Optimization Based Ensemble Machine Learning Model for Designing Detection Coil with Prediction of Electric Vehicle Charging Time. Sustainability 2023, 15, 6684. [Google Scholar] [CrossRef]
- Boussaïd, I.; Lepagnot, J.; Siarry, P. A Survey on Optimization Metaheuristics. Inf. Sci. 2013, 237, 82–117. [Google Scholar] [CrossRef]
- Dreo, J.; Petrowsdki, A.; Siarry, P.; Taillard, E.; Chatterjee, A. Metaheuristics for Hard Optimization: Methods and Case Studies; Springer: Cham, Switzerland, 2006; ISBN 978-3-540-30966-6. [Google Scholar]
- Knypiński, Ł. Adaptation of the Penalty Function Method to Genetic Algorithm in Electromagnetic Devices Designing. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2019, 38, 1285–1294. [Google Scholar] [CrossRef]
- Batrinu, F.; Carpaneto, E.; Chicco, G. A Unified Scheme for Testing Alternative Techniques for Distribution System Minimum Loss Reconfiguration. In Proceedings of the 2005 International Conference on Future Power Systems, Amsterdam, The Netherlands, 16–18 November 2005; IEEE: Piscataway, NJ, USA, 2005; Volume 2005, p. 6. [Google Scholar]
- Baretich, M.F. Electrical Power. In Clinical Engineering Handbook; Elsevier: Amsterdam, The Netherlands, 2020; pp. 667–669. [Google Scholar]
- Da Silva Filho, J.I.; Shozo, A.; Pompeo Ferrara, L.F.; Conceicao, M.; de Melo Camargo, J.; Vilanova, D.; dos Santos, M.R.; Rocco, A. Electric Power System Operation Decision Support by Expert System Built with Paraconsistent Annotated Logic. In Advances in Expert Systems; InTech: Rijeka, Croatia, 2012. [Google Scholar]
- Cain, M.; O’Neill, R.; Castillo, A. History of Optimal Power Flow and Formulations. Fed. Energy Regul. Comm. 2012, 1, 1–36. [Google Scholar]
- Kargarian, A.; Mohammadi, J.; Guo, J.; Chakrabarti, S.; Barati, M.; Hug, G.; Kar, S.; Baldick, R. Toward Distributed/Decentralized DC Optimal Power Flow Implementation in Future Electric Power Systems. IEEE Trans. Smart Grid 2018, 9, 2574–2594. [Google Scholar] [CrossRef]
- Dommel, H.W.; Tinney, W.F. Optimal Power Flow Solutions. IEEE Trans. Power Appar. Syst. 1968, PAS-87, 1866–1876. [Google Scholar] [CrossRef]
- Niu, M.; Wan, C.; Xu, Z. A Review on Applications of Heuristic Optimization Algorithms for Optimal Power Flow in Modern Power Systems. J. Mod. Power Syst. Clean Energy 2014, 2, 289–297. [Google Scholar] [CrossRef] [Green Version]
- Abou El Ela, A.A.; Abido, M.A.; Spea, S.R. Optimal Power Flow Using Differential Evolution Algorithm. Electr. Eng. 2009, 91, 69–78. [Google Scholar] [CrossRef]
- Abido, M.A. Optimal Power Flow Using Particle Swarm Optimization. Int. J. Electr. Power Energy Syst. 2002, 24, 563–571. [Google Scholar] [CrossRef]
- Lai, L.L.; Ma, J.T.; Yokoyama, R.; Zhao, M. Improved Genetic Algorithms for Optimal Power Flow under Both Normal and Contingent Operation States. Int. J. Electr. Power Energy Syst. 1997, 19, 287–292. [Google Scholar] [CrossRef]
- Bakirtzis, A.G.; Biskas, P.N.; Zoumas, C.E.; Petridis, V. Optimal Power Flow by Enhanced Genetic Algorithm. IEEE Trans. Power Syst. 2002, 17, 229–236. [Google Scholar] [CrossRef]
- Banu, R.N.; Devaraj, D. Genetic Algorithm Approach for Optimal Power Flow with FACTS Devices. In Proceedings of the 2008 4th International IEEE Conference Intelligent Systems, Varna, Bulgaria, 6–8 September 2008; IEEE: Piscataway, NJ, USA, 2008; Volume 2, pp. 23-11–23-16. [Google Scholar]
- Mahdad, B.; Bouktir, T.; Srairi, K.; EL Benbouzid, M. Dynamic Strategy Based Fast Decomposed GA Coordinated with FACTS Devices to Enhance the Optimal Power Flow. Energy Convers. Manag. 2010, 51, 1370–1380. [Google Scholar] [CrossRef] [Green Version]
- Attia, A.-F.; Al-Turki, Y.A.; Abusorrah, A.M. Optimal Power Flow Using Adapted Genetic Algorithm with Adjusting Population Size. Electr. Power Compon. Syst. 2012, 40, 1285–1299. [Google Scholar] [CrossRef]
- Saravanan, T.; Saritha, G.; Srinivasan, V. Optimal Power Flow Using Particle Swarm Optimization. Middle-East J. Sci. Res. 2014, 20, 1554–1560. [Google Scholar] [CrossRef]
- Vo, D.N.; Schegner, P. An Improved Particle Swarm Optimization for Optimal Power Flow. In Meta-Heuristics Optimization Algorithms in Engineering, Business, Economics, and Finance; IGI Global: Hershey, PA, USA, 2013; pp. 1–40. ISBN 9781466620865. [Google Scholar]
- Wang, C.-R.; Yuan, H.-J.; Huang, Z.-Q.; Zhang, J.-W.; Sun, C.-J. A Modified Particle Swarm Optimization Algorithm and Its Application in Optimal Power Flow Problem. In Proceedings of the 2005 International Conference on Machine Learning and Cybernetics, Guangzhou, China, 18–21 August 2005; IEEE: Piscataway, NJ, USA, 2005; Volume 5, pp. 2885–2889. [Google Scholar]
- Yumbla, P.E.O.; Ramirez, J.M.; Coello Coello, C.A. Optimal Power Flow Subject to Security Constraints Solved with a Particle Swarm Optimizer. IEEE Trans. Power Syst. 2008, 23, 33–40. [Google Scholar] [CrossRef]
- Swaroopan, N.M.J.; Somasundaram, P. Optimal Power Flow for Security Enhancement Using Fuzzified Particle Swarm Optimization. In Proceedings of the International Conference on Sustainable Energy and Intelligent Systems (SEISCON 2011), Chennai, India, 20–22 July 2011; IET: London, UK, 2011; Volume 2011, pp. 474–479. [Google Scholar]
- Niknam, T.; Narimani, M.R.; Aghaei, J.; Azizipanah-Abarghooee, R. Improved Particle Swarm Optimisation for Multi-Objective Optimal Power Flow Considering the Cost, Loss, Emission and Voltage Stability Index. IET Gener. Transm. Distrib. 2012, 6, 515–527. [Google Scholar] [CrossRef]
- Chang, Y.-C.; Lee, T.-Y.; Chen, C.-L.; Jan, R.-M. Optimal Power Flow of a Wind-Thermal Generation System. Int. J. Electr. Power Energy Syst. 2014, 55, 312–320. [Google Scholar] [CrossRef]
- Basu, M. Multi-Objective Optimal Power Flow with FACTS Devices. Energy Convers. Manag. 2011, 52, 903–910. [Google Scholar] [CrossRef]
- Basu, M. Optimal Power Flow with FACTS Devices Using Differential Evolution. Int. J. Electr. Power Energy Syst. 2008, 30, 150–156. [Google Scholar] [CrossRef]
- Varadarajan, M.; Swarup, K.S. Solving Multi-Objective Optimal Power Flow Using Differential Evolution. IET Gener. Transm. Distrib. 2008, 2, 720. [Google Scholar] [CrossRef]
- Amjady, N.; Sharifzadeh, H. Security Constrained Optimal Power Flow Considering Detailed Generator Model by a New Robust Differential Evolution Algorithm. Electr. Power Syst. Res. 2011, 81, 740–749. [Google Scholar] [CrossRef]
- Sayah, S.; Zehar, K. Modified Differential Evolution Algorithm for Optimal Power Flow with Non-Smooth Cost Functions. Energy Convers. Manag. 2008, 49, 3036–3042. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A.; Farrag, S.M. Solving Multi-objective Optimal Power Flow Problem via Forced Initialised Differential Evolution Algorithm. IET Gener. Transm. Distrib. 2016, 10, 1634–1647. [Google Scholar] [CrossRef]
- Duman, S.; Güvenç, U.; Sönmez, Y.; Yörükeren, N. Optimal Power Flow Using Gravitational Search Algorithm. Energy Convers. Manag. 2012, 59, 86–95. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Roy, P.K. Solution of Multi-Objective Optimal Power Flow Using Gravitational Search Algorithm. IET Gener. Transm. Distrib. 2012, 6, 751. [Google Scholar] [CrossRef]
- Jahan, M.S.; Amjady, N. Solution of Large-Scale Security Constrained Optimal Power Flow by a New Bi-Level Optimisation Approach Based on Enhanced Gravitational Search Algorithm. IET Gener. Transm. Distrib. 2013, 7, 1481–1491. [Google Scholar] [CrossRef]
- Allaoua, B.; Laoufi, A. Optimal Power Flow Solution Using Ant Manners for Electrical Network. Adv. Electr. Comput. Eng. 2009, 9, 34–40. [Google Scholar] [CrossRef]
- Allaoua, B.; Laoufi, A. Collective Intelligence for Optimal Power Flow Solution Using Ant Colony Optimization. Leonardo Electron. J. Pract. Technol. 2008, 7, 088–105. [Google Scholar]
- Gasbaoui, B.; Allaoua, B. Ant Colony Optimization Applied on Combinatorial Problem for Optimal Power Flow Solution. Leonardo J. Sci. 2009, 14, 1–17. [Google Scholar]
- Joshi, S.K.; Ghanchi, V.H. Solution of Optimal Power Flow Subject to Security Constraints by an Ant Colony Optimization. In Proceedings of the Third International Conference on Computational Intelligence and Information Technology (CIIT 2013), Mumbai, India, 18–19 October 2013; Institution of Engineering and Technology: London, UK, 2013; Volume 2013, pp. 590–597. [Google Scholar]
- Kılıç, U. Backtracking Search Algorithm-Based Optimal Power Flow with Valve Point Effect and Prohibited Zones. Electr. Eng. 2015, 97, 101–110. [Google Scholar] [CrossRef]
- Bouchekara, H.R.E.H.; Chaib, A.E.; Abido, M.A.; El-Sehiemy, R.A. Optimal Power Flow Using an Improved Colliding Bodies Optimization Algorithm. Appl. Soft Comput. 2016, 42, 119–131. [Google Scholar] [CrossRef]
- Bouchekara, H.R.E.H. Optimal Power Flow Using Black-Hole-Based Optimization Approach. Appl. Soft Comput. 2014, 24, 879–888. [Google Scholar] [CrossRef]
- Mahdad, B.; Srairi, K. Blackout Risk Prevention in a Smart Grid Based Flexible Optimal Strategy Using Grey Wolf-Pattern Search Algorithms. Energy Convers. Manag. 2015, 98, 411–429. [Google Scholar] [CrossRef]
- Herbadji, O. Optimal Power Flow Using Firefly Algorithm with Consideration of FACTS Devices “UPFC”. Int. J. Electr. Eng. Inform. 2015, 7, 12–28. [Google Scholar] [CrossRef]
- Balasubbareddy, M.; Sivanagaraju, S.; Suresh, C.V. Multi-Objective Optimization in the Presence of Practical Constraints Using Non-Dominated Sorting Hybrid Cuckoo Search Algorithm. Eng. Sci. Technol. Int. J. 2015, 18, 603–615. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, A.-A.A.A.A.; Mohamed, Y.S.; El-Gaafary, A.A.M.; Hemeida, A.M. Optimal Power Flow Using Moth Swarm Algorithm. Electr. Power Syst. Res. 2017, 142, 190–206. [Google Scholar] [CrossRef]
- Roy, P.K.; Paul, C. Optimal Power Flow Using Krill Herd Algorithm. Int. Trans. Electr. Energy Syst. 2015, 25, 1397–1419. [Google Scholar] [CrossRef]
- Mukherjee, A.; Mukherjee, V. Solution of Optimal Power Flow with FACTS Devices Using a Novel Oppositional Krill Herd Algorithm. Int. J. Electr. Power Energy Syst. 2016, 78, 700–714. [Google Scholar] [CrossRef]
- Mukherjee, A.; Roy, P.K.; Mukherjee, V. Transient Stability Constrained Optimal Power Flow Using Oppositional Krill Herd Algorithm. Int. J. Electr. Power Energy Syst. 2016, 83, 283–297. [Google Scholar] [CrossRef]
- Rahiminejad, A.; Alimardani, A.; Vahidi, B.; Hosseinian, S.H. Shuffled Frog Leaping Algorithm Optimization for AC--DC Optimal Power Flow Dispatch. TURKISH J. Electr. Eng. Comput. Sci. 2014, 22, 874–892. [Google Scholar] [CrossRef]
- Vahedi, H.; Hosseini, S.H.; Noroozian, R. Bacterial Foraging Algorithm for Security Constrained Optimal Power Flow. In Proceedings of the 2010 7th International Conference on the European Energy Market, Madrid, Spain, 23–25 June 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–6. [Google Scholar]
- Panda, A.; Tripathy, M. Security Constrained Optimal Power Flow Solution of Wind-Thermal Generation System Using Modified Bacteria Foraging Algorithm. Energy 2015, 93, 816–827. [Google Scholar] [CrossRef]
- Mahdad, B.; Srairi, K. A New Interactive Sine Cosine Algorithm for Loading Margin Stability Improvement under Contingency. Electr. Eng. 2018, 100, 913–933. [Google Scholar] [CrossRef]
- Warid, W.; Hizam, H.; Mariun, N.; Abdul-Wahab, N. Optimal Power Flow Using the Jaya Algorithm. Energies 2016, 9, 678. [Google Scholar] [CrossRef] [Green Version]
- Devarapalli, R.; Sinha, N.K.; Rao, B.V.; Knypinski, L.; Lakshmi, N.J.N.; Márquez, F.P.G. Allocation of Real Power Generation Based on Computing over All Generation Cost: An Approach of Salp Swarm Algorithm. Arch. Electr. Eng. 2021, 70, 337–349. [Google Scholar] [CrossRef]
- Khan, M.H.; Ulasyar, A.; Khattak, A.; Zad, H.S.; Alsharef, M.; Alahmadi, A.A.; Ullah, N. Optimal Sizing and Allocation of Distributed Generation in the Radial Power Distribution System Using Honey Badger Algorithm. Energies 2022, 15, 5891. [Google Scholar] [CrossRef]
- Truong, K.H.; Nallagownden, P.; Elamvazuthi, I.; Vo, D.N. A Quasi-Oppositional-Chaotic Symbiotic Organisms Search Algorithm for Optimal Allocation of DG in Radial Distribution Networks. Appl. Soft Comput. J. 2020, 88, 106067. [Google Scholar] [CrossRef]
- Radosavljević, J.; Jevtić, M.; Milovanović, M. A Solution to the ORPD Problem and Critical Analysis of the Results. Electr. Eng. 2018, 100, 253–265. [Google Scholar] [CrossRef]
- Radosavljevic, J.; Jevtic, M. Solution of Optimal Reactive Power Dispatch by a Hybrid GSA-SQP Algorithm. Elektron. Ir Elektrotechnika 2016, 22, 3–6. [Google Scholar] [CrossRef] [Green Version]
- Robbins, B.A.; Domínguez-García, A.D. Optimal Reactive Power Dispatch for Voltage Regulation in Unbalanced Distribution Systems. IEEE Trans. Power Syst. 2016, 31, 2903–2913. [Google Scholar] [CrossRef]
- Vlachogiannis, J.G.; Lee, K.Y. Quantum-Inspired Evolutionary Algorithm for Real and Reactive Power Dispatch. IEEE Trans. Power Syst. 2008, 23, 1627–1636. [Google Scholar] [CrossRef] [Green Version]
- Gangotri, K.M.; Bhimwal, M.K. Genetic Algorithm Based Reactive Power Dispatch for Voltage Stability Improvement. Int. J. Electr. Power Energy Syst. 2010, 32, 1151–1156. [Google Scholar]
- Muhammad, Y.; Khan, R.; Raja, M.A.Z.; Ullah, F.; Chaudhary, N.I.; He, Y. Solution of Optimal Reactive Power Dispatch with FACTS Devices: A Survey. Energy Rep. 2020, 6, 2211–2229. [Google Scholar] [CrossRef]
- Saddique, M.S.; Bhatti, A.R.; Haroon, S.S.; Sattar, M.K.; Amin, S.; Sajjad, I.A.; ul Haq, S.S.; Awan, A.B.; Rasheed, N. Solution to Optimal Reactive Power Dispatch in Transmission System Using Meta-Heuristic Techniques―Status and Technological Review. Electr. Power Syst. Res. 2020, 178, 106031. [Google Scholar] [CrossRef]
- Yoshida, H.; Kawata, K.; Fukuyama, Y.; Takayama, S.; Nakanishi, Y. A Particle Swarm Optimization for Reactive Power and Voltage Control Considering Voltage Security Assessment. IEEE Trans. Power Syst. 2000, 15, 1232–1239. [Google Scholar] [CrossRef] [Green Version]
- Zhao, B.; Guo, C.X.; Cao, Y.J. A Multiagent-Based Particle Swarm Optimization Approach for Optimal Reactive Power Dispatch. IEEE Trans. Power Syst. 2005, 20, 1070–1078. [Google Scholar] [CrossRef]
- Mahadevan, K.; Kannan, P.S. Comprehensive Learning Particle Swarm Optimization for Reactive Power Dispatch. Appl. Soft Comput. J. 2010, 10, 641–652. [Google Scholar] [CrossRef]
- El Ela, A.A.A.; Abido, M.A.; Spea, S.R. Differential Evolution Algorithm for Optimal Reactive Power Dispatch. Electr. Power Syst. Res. 2011, 81, 458–464. [Google Scholar] [CrossRef]
- Basu, M. Quasi-Oppositional Differential Evolution for Optimal Reactive Power Dispatch. Int. J. Electr. Power Energy Syst. 2016, 78, 29–40. [Google Scholar] [CrossRef]
- Sakr, W.S.; EL-Sehiemy, R.A.; Azmy, A.M. Adaptive Differential Evolution Algorithm for Efficient Reactive Power Management. Appl. Soft Comput. J. 2017, 53, 336–351. [Google Scholar] [CrossRef]
- Subbaraj, P.; Rajnarayanan, P.N. Optimal Reactive Power Dispatch Using Self-Adaptive Real Coded Genetic Algorithm. Electr. Power Syst. Res. 2009, 79, 374–381. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Chattopadhyay, P.K. Solution of Optimal Reactive Power Flow Using Biogeography-Based Optimization. World Acad. Sci. Eng. Technol. 2009, 39, 852–860. [Google Scholar]
- Duman, S.; Sönmez, Y.; Güvenç, U.; Yörükeren, N. Optimal Reactive Power Dispatch Using a Gravitational Search Algorithm. IET Gener. Transm. Distrib. 2012, 6, 563–576. [Google Scholar] [CrossRef]
- Shaw, B.; Mukherjee, V.; Ghoshal, S.P. Solution of Reactive Power Dispatch of Power Systems by an Opposition-Based Gravitational Search Algorithm. Int. J. Electr. Power Energy Syst. 2014, 55, 29–40. [Google Scholar] [CrossRef] [Green Version]
- Mukherjee, A.; Mukherjee, V. Solution of Optimal Reactive Power Dispatch by Chaotic Krill Herd Algorithm. IET Gener. Transm. Distrib. 2015, 9, 2351–2362. [Google Scholar] [CrossRef]
- Khazali, A.H.; Kalantar, M. Optimal Reactive Power Dispatch Based on Harmony Search Algorithm. Int. J. Electr. Power Energy Syst. 2011, 33, 684–692. [Google Scholar] [CrossRef]
- Mandal, B.; Roy, P.K. Optimal Reactive Power Dispatch Using Quasi-Oppositional Teaching Learning Based Optimization. Int. J. Electr. Power Energy Syst. 2013, 53, 123–134. [Google Scholar] [CrossRef]
- Abou El-Ela, A.A.; Kinawy, A.M.; El-Sehiemy, R.A.; Mouwafi, M.T. Optimal Reactive Power Dispatch Using Ant Colony Optimization Algorithm. Electr. Eng. 2011, 93, 103–116. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z.; Mohamed, M.R.; Aliman, O. Using the Gray Wolf Optimizer for Solving Optimal Reactive Power Dispatch Problem. Appl. Soft Comput. J. 2015, 32, 286–292. [Google Scholar] [CrossRef] [Green Version]
- Rajan, A.; Malakar, T. Exchange Market Algorithm Based Optimum Reactive Power Dispatch. Appl. Soft Comput. J. 2016, 43, 320–336. [Google Scholar] [CrossRef]
- Rajan, A.; Malakar, T. Optimal Reactive Power Dispatch Using Hybrid Nelder-Mead Simplex Based Firefly Algorithm. Int. J. Electr. Power Energy Syst. 2015, 66, 9–24. [Google Scholar] [CrossRef]
- Kulkarni, P.S.; Kothari, A.G.; Kothari, D.P. Combined Economic and Emission Dispatch Using Improved Backpropagation Neural Network. Electr. Mach. Power Syst. 2000, 28, 31–44. [Google Scholar] [CrossRef]
- Radosavljević, J. A Solution to the Combined Economic and Emission Dispatch Using Hybrid PSOGSA Algorithm. Appl. Artif. Intell. 2016, 30, 445–474. [Google Scholar] [CrossRef]
- Mahdi, F.P.; Vasant, P.; Kallimani, V.; Watada, J.; Fai, P.Y.S.; Abdullah-Al-Wadud, M. A Holistic Review on Optimization Strategies for Combined Economic Emission Dispatch Problem. Renew. Sustain. Energy Rev. 2018, 81, 3006–3020. [Google Scholar] [CrossRef]
- Radosavljevic, J. Metaheuristic Optimization in Power Engineering; Institution of Engineering and Technology: London, UK, 2018; ISBN 978-1-78561-547-4. [Google Scholar]
- Jacob Raglend, I.; Veeravalli, S.; Sailaja, K.; Sudheera, B.; Kothari, D.P. Comparison of AI Techniques to Solve Combined Economic Emission Dispatch Problem with Line Flow Constraints. Int. J. Electr. Power Energy Syst. 2010, 32, 592–598. [Google Scholar] [CrossRef]
- Abido, M.A. Multiobjective Evolutionary Algorithms for Electric Power Dispatch Problem. IEEE Trans. Evol. Comput. 2006, 10, 315–329. [Google Scholar] [CrossRef]
- Avvari, R.K.; DM, V.K. A New Hybrid Evolutionary Algorithm for Multi-Objective Optimal Power Flow in an Integrated WE, PV, and PEV Power System. Electr. Power Syst. Res. 2023, 214, 108870. [Google Scholar] [CrossRef]
- Park, J.B.; Jeong, Y.W.; Shin, J.R.; Lee, K.Y. An Improved Particle Swarm Optimization for Nonconvex Economic Dispatch Problems. IEEE Trans. Power Syst. 2010, 25, 156–166. [Google Scholar] [CrossRef]
- Ghorbani, N.; Vakili, S.; Babaei, E.; Sakhavati, A. Particle Swarm Optimization with Smart Inertia Factor for Solving Non-Convex Economic Load Dispatch Problems. Int. Trans. Electr. Energy Syst. 2014, 24, 1120–1133. [Google Scholar] [CrossRef]
- Sheng, W.; Li, R.; Yan, T.; Tseng, M.-L.; Lou, J.; Li, L. A Hybrid Dynamic Economics Emissions Dispatch Model: Distributed Renewable Power Systems Based on Improved COOT Optimization Algorithm. Renew. Energy 2023, 204, 493–506. [Google Scholar] [CrossRef]
- Nazir, M.S.; Almasoudi, F.M.; Abdalla, A.N.; Zhu, C.; Alatawi, K.S.S. Multi-Objective Optimal Dispatching of Combined Cooling, Heating and Power Using Hybrid Gravitational Search Algorithm and Random Forest Regression: Towards the Microgrid Orientation. Energy Rep. 2023, 9, 1926–1936. [Google Scholar] [CrossRef]
- Maharana, H.S.; Dash, S.K. Quantum Behaved Artificial Bee Colony Based Conventional Controller for Optimum Dispatch. Int. J. Electr. Comput. Eng. 2023, 13, 1260. [Google Scholar] [CrossRef]
- Pang, A.; Liang, H.; Lin, C.; Yao, L. A Surrogate-Assisted Adaptive Bat Algorithm for Large-Scale Economic Dispatch. Energies 2023, 16, 1011. [Google Scholar] [CrossRef]
- Hassan, M.H.; Kamel, S.; Salih, S.Q.; Khurshaid, T.; Ebeed, M. Developing Chaotic Artificial Ecosystem-Based Optimization Algorithm for Combined Economic Emission Dispatch. IEEE Access 2021, 9, 51146–51165. [Google Scholar] [CrossRef]
- Benasla, L.; Belmadani, A.; Rahli, M. Spiral Optimization Algorithm for Solving Combined Economic and Emission Dispatch. Int. J. Electr. Power Energy Syst. 2014, 62, 163–174. [Google Scholar] [CrossRef]
- Arunachalam, S.; AgnesBhomila, T.; Ramesh Babu, M. Hybrid Particle Swarm Optimization Algorithm and Firefly Algorithm Based Combined Economic and Emission Dispatch Including Valve Point Effect. In Proceedings of the Swarm, Evolutionary, and Memetic Computing: 5th International Conference, SEMCCO 2014, Bhubaneswar, India, 18–20 December 2014; Volume 8947, pp. 647–660. [Google Scholar] [CrossRef]
- Abdelaziz, A.Y.; Ali, E.S.; Abd Elazim, S.M. Implementation of Flower Pollination Algorithm for Solving Economic Load Dispatch and Combined Economic Emission Dispatch Problems in Power Systems. Energy 2016, 101, 506–518. [Google Scholar] [CrossRef]
- Acharya, S.; Sivarajan, G.; Kumar, D.V.; Srikrishna, S. Modeling Combined Economic Emission Dispatch for Renewable Energy System via Levy-Based Glowworm Swarm Optimization. Kybernetes 2022. [Google Scholar] [CrossRef]
- Safigianni, A.S.; Koutroumpezis, G.N.; Poulios, V.C. Mixed Distributed Generation Technologies in a Medium Voltage Network. Electr. Power Syst. Res. 2013, 96, 75–80. [Google Scholar] [CrossRef]
- Moghaddas-Tafreshi, S.M.; Mashhour, E. Distributed Generation Modeling for Power Flow Studies and a Three-Phase Unbalanced Power Flow Solution for Radial Distribution Systems Considering Distributed Generation. Electr. Power Syst. Res. 2009, 79, 680–686. [Google Scholar] [CrossRef]
- Neto, A.B.; Barbosa, M.B.; Mota, L.M.; Lavorato, M.; de Carvalho, M.F.H. Optimal Power Flow Technique for Distribution System Considering Distributed Energy Resources (DER). Energies 2022, 15, 8507. [Google Scholar] [CrossRef]
- Gabash, A.; Li, P. Active-Reactive Optimal Power Flow in Distribution Networks With Embedded Generation and Battery Storage. IEEE Trans. Power Syst. 2012, 27, 2026–2035. [Google Scholar] [CrossRef]
- Li, B.; Wan, C.; Li, Y.; Jiang, Y.; Yu, P. Generalized Linear-constrained Optimal Power Flow for Distribution Networks. IET Gener. Transm. Distrib. 2023, 17, 1298–1309. [Google Scholar] [CrossRef]
- Radosavljevic, J.; Jevtic, M.; Klimenta, D.; Arsic, N. Optimal Power Flow for Distribution Networks with Distributed Generation. Serbian J. Electr. Eng. 2015, 12, 145–170. [Google Scholar] [CrossRef]
- Shu, J.; Guan, R.; Wu, L. Optimal Power Flow in Distribution Network Considering Spatial Electro-Thermal Coupling Effect. IET Gener. Transm. Distrib. 2017, 11, 1162–1169. [Google Scholar] [CrossRef]
- Niknam, T. An Approach Based on Particle Swarm Optimization for Optimal Operation of Distribution Network Considering Distributed Generators. In Proceedings of the IECON 2006—32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 7–10 November 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 633–637. [Google Scholar]
- Radosavljević, J.; Jevtic, M.; Arsić, N.; Klimenta, D. Optimal Power Flow for Distribution Networks Using Gravitational Search Algorithm. Electr. Eng. 2014, 96, 335–345. [Google Scholar] [CrossRef]
- Wang, S.; Wang, N.; Wang, Q.; Yang, Y.; Huang, G. Reactive Power Optimization in Distribution Network by Using Improved Gravitational Search Algorithm. In Proceedings of the 2015 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Changsha, China, 26–29 November 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 178–182. [Google Scholar]
- Saha, A.; Dash, P.; Babu, N.R.; Chiranjeevi, T.; Dhananjaya, M.; Knypiński, Ł. Dynamic Stability Evaluation of an Integrated Biodiesel-Geothermal Power Plant-Based Power System with Spotted Hyena Optimized Cascade Controller. Sustainability 2022, 14, 14842. [Google Scholar] [CrossRef]
- Mahmud, M.A.; Hossain, M.J.; Pota, H.R. Voltage Variation on Distribution Networks with Distributed Generation: Worst Case Scenario. IEEE Syst. J. 2014, 8, 1096–1103. [Google Scholar] [CrossRef]
- Castro, J.R.; Saad, M.; Lefebvre, S.; Asber, D.; Lenoir, L. Optimal Voltage Control in Distribution Network in the Presence of DGs. Int. J. Electr. Power Energy Syst. 2016, 78, 239–247. [Google Scholar] [CrossRef]
- Viawan, F.A.; Sannino, A.; Daalder, J. Voltage Control with On-Load Tap Changers in Medium Voltage Feeders in Presence of Distributed Generation. Electr. Power Syst. Res. 2007, 77, 1314–1322. [Google Scholar] [CrossRef]
- Viawan, F.A.; Karlsson, D. Combined Local and Remote Voltage and Reactive Power Control in the Presence of Induction Machine Distributed Generation. IEEE Trans. Power Syst. 2007, 22, 2003–2012. [Google Scholar] [CrossRef]
- Hong, Y.Y.; Luo, Y.F. Optimal VAR Control Considering Wind Farms Using Probabilistic Load-Flow and Gray-Based Genetic Algorithms. IEEE Trans. Power Deliv. 2009, 24, 1441–1449. [Google Scholar] [CrossRef]
- Villacci, D.; Bontempi, G.; Vaccaro, A. An Adaptive Local Learning-Based Methodology for Voltage Regulation in Distribution Networks with Dispersed Generation. IEEE Trans. Power Syst. 2006, 21, 1131–1140. [Google Scholar] [CrossRef]
- Galdi, V.; Vaccaro, A.; Villacci, D. Voltage Regulation in MV Networks with Dispersed Generations by a Neural-Based Multiobjective Methodology. Electr. Power Syst. Res. 2008, 78, 785–793. [Google Scholar] [CrossRef]
- Niknam, T.; Firouzi, B.B.; Ostadi, A. A New Fuzzy Adaptive Particle Swarm Optimization for Daily Volt/Var Control in Distribution Networks Considering Distributed Generators. Appl. Energy 2010, 87, 1919–1928. [Google Scholar] [CrossRef]
- Chen, S.; Hu, W.; Su, C.; Zhang, X.; Chen, Z. Optimal Reactive Power and Voltage Control in Distribution Networks with Distributed Generators by Fuzzy Adaptive Hybrid Particle Swarm Optimisation Method. IET Gener. Transm. Distrib. 2015, 9, 1096–1103. [Google Scholar] [CrossRef]
- Cheng, S.; Chen, M.Y. Multi-Objective Reactive Power Optimization Strategy for Distribution System with Penetration of Distributed Generation. Int. J. Electr. Power Energy Syst. 2014, 62, 221–228. [Google Scholar] [CrossRef]
- Zhang, L.; Tang, W.; Liang, J.; Cong, P.; Cai, Y. Coordinated Day-Ahead Reactive Power Dispatch in Distribution Network Based on Real Power Forecast Errors. IEEE Trans. Power Syst. 2016, 31, 2472–2480. [Google Scholar] [CrossRef]
- Daratha, N.; Das, B.; Sharma, J. Robust Voltage Regulation in Unbalanced Radial Distribution System under Uncertainty of Distributed Generation and Loads. Int. J. Electr. Power Energy Syst. 2015, 73, 516–527. [Google Scholar] [CrossRef]
- Ulinuha, A.; Masoum, M.A.S.; Islam, S. Hybrid Genetic-Fuzzy Algorithm for Volt/Var/Total Harmonic Distortion Control of Distribution Systems with High Penetration of Non-Linear Loads. IET Gener. Transm. Distrib. 2011, 5, 425–439. [Google Scholar] [CrossRef]
- Jashfar, S.; Esmaeili, S. Volt/Var/THD Control in Distribution Networks Considering Reactive Power Capability of Solar Energy Conversion. Int. J. Electr. Power Energy Syst. 2014, 60, 221–233. [Google Scholar] [CrossRef]
- Jashfar, S.; Hosseini-Biyouki, M.M.; Esmaeili, S. A Stochastic Programming to Volt/VAR/Total Harmonic Distortion Control in Distribution Networks Including Wind Turbines. Electr. Power Components Syst. 2015, 43, 733–746. [Google Scholar] [CrossRef]
- Seelig, B.H.T.; de Souza, L.J.; Prada, R.B. Voltage Control in Heavily Loaded Networks. Int. Trans. Electr. Energy Syst. 2015, 25, 3275–3287. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, X.; Chen, H.; Taylor, G.A. Volt/VAr Control in Distribution Systems Using a Time-Interval Based Approach. IEEE Proc.-Gener. Transm. Distrib. 2003, 150, 548. [Google Scholar] [CrossRef]
- Park, J.Y.; Nam, S.R.; Park, J.K. Control of a ULTC Considering the Dispatch Schedule of Capacitors in a Distribution System. IEEE Trans. Power Syst. 2007, 22, 755–761. [Google Scholar] [CrossRef]
- Senjyu, T.; Miyazato, Y.; Yona, A.; Urasaki, N.; Funabashi, T. Optimal Distribution Voltage Control and Coordination with Distributed Generation. IEEE Trans. Power Deliv. 2008, 23, 1236–1242. [Google Scholar] [CrossRef]
- Madureira, A.G.; Peças Lopes, J.A. Coordinated Voltage Support in Distribution Networks with Distributed Generation and Microgrids. IET Renew. Power Gener. 2009, 3, 439–454. [Google Scholar] [CrossRef] [Green Version]
- Mokgonyana, L.; Zhang, J.; Zhang, L.; Xia, X. Coordinated Two-Stage Volt/Var Management in Distribution Networks. Electr. Power Syst. Res. 2016, 141, 157–164. [Google Scholar] [CrossRef] [Green Version]
- Niknam, T.; Zare, M.; Aghaei, J. Scenario-Based Multiobjective Volt/Var Control in Distribution Networks Including Renewable Energy Sources. IEEE Trans. Power Deliv. 2012, 27, 2004–2019. [Google Scholar] [CrossRef]
- Zare, M.; Niknam, T. A New Multi-Objective for Environmental and Economic Management of Volt/Var Control Considering Renewable Energy Resources. Energy 2013, 55, 236–252. [Google Scholar] [CrossRef]
- Mohamed Shuaib, Y.; Surya Kalavathi, M.; Christober Asir Rajan, C. Optimal Capacitor Placement in Radial Distribution System Using Gravitational Search Algorithm. Int. J. Electr. Power Energy Syst. 2015, 64, 384–397. [Google Scholar] [CrossRef]
- Abdul Kadir, A.F.; Mohamed, A.; Shareef, H.; Che Wanik, M.Z. Optimal Placement and Sizing of Distributed Generations in Distribution Systems for Minimizing Losses and THD$_{v}$ Using Evolutionary Programming. TURKISH J. Electr. Eng. Comput. Sci. 2013, 21, 2269–2282. [Google Scholar] [CrossRef]
- Khoa, T.Q.D.; Binh, P.T.T.; Tran, H.B. Optimizing Location and Sizing of Distributed Generation in Distribution Systems. In Proceedings of the 2006 IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 1 November 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 725–732. [Google Scholar]
- Elsaiah, S.; Benidris, M.; Mitra, J. Analytical Approach for Placement and Sizing of Distributed Generation on Distribution Systems. IET Gener. Transm. Distrib. 2014, 8, 1039–1049. [Google Scholar] [CrossRef] [Green Version]
- Gopiya Naik, S.N.; Khatod, D.K.; Sharma, M.P. Analytical Approach for Optimal Siting and Sizing of Distributed Generation in Radial Distribution Networks. IET Gener. Transm. Distrib. 2015, 9, 209–220. [Google Scholar] [CrossRef]
- Viral, R.; Khatod, D.K. An Analytical Approach for Sizing and Siting of DGs in Balanced Radial Distribution Networks for Loss Minimization. Int. J. Electr. Power Energy Syst. 2015, 67, 191–201. [Google Scholar] [CrossRef]
- Keane, A.; O’Malley, M. Optimal Allocation of Embedded Generation on Distribution Networks. IEEE Trans. Power Syst. 2005, 20, 1640–1646. [Google Scholar] [CrossRef]
- Le, A.D.T.; Kashem, M.A.; Negnevitsky, M.; Ledwich, G. Optimal Distributed Generation Parameters for Reducing Losses with Economic Consideration. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1–8. [Google Scholar]
- Prenc, R.; Škrlec, D.; Komen, V. Distributed Generation Allocation Based on Average Daily Load and Power Production Curves. Int. J. Electr. Power Energy Syst. 2013, 53, 612–622. [Google Scholar] [CrossRef]
- Savić, A.; Đurišić, Ž. Optimal Sizing and Location of SVC Devices for Improvement of Voltage Profile in Distribution Network with Dispersed Photovoltaic and Wind Power Plants. Appl. Energy 2014, 134, 114–124. [Google Scholar] [CrossRef]
- Mohammadi, M.; Nafar, M. Optimal Placement of Multitypes DG as Independent Private Sector under Pool/Hybrid Power Market Using GA-Based Tabu Search Method. Int. J. Electr. Power Energy Syst. 2013, 51, 43–53. [Google Scholar] [CrossRef]
- Dehghanian, P.; Hosseini, S.H.; Moeini-Aghtaie, M.; Arabali, A. Optimal Siting of DG Units in Power Systems from a Probabilistic Multi-Objective Optimization Perspective. Int. J. Electr. Power Energy Syst. 2013, 51, 14–26. [Google Scholar] [CrossRef]
- Vatani, M.; Alkaran, D.S.; Sanjari, M.J.; Gharehpetian, G.B. Multiple Distributed Generation Units Allocation in Distribution Network for Loss Reduction Based on a Combination of Analytical and Genetic Algorithm Methods. IET Gener. Transm. Distrib. 2016, 10, 66–72. [Google Scholar] [CrossRef]
- Gkaidatzis, P.A.; Bouhouras, A.S.; Doukas, D.I.; Sgouras, K.I.; Labridis, D.P. Load Variations Impact on Optimal DG Placement Problem Concerning Energy Loss Reduction. Electr. Power Syst. Res. 2017, 152, 36–47. [Google Scholar] [CrossRef]
- Zeinalzadeh, A.; Mohammadi, Y.; Moradi, M.H. Optimal Multi Objective Placement and Sizing of Multiple DGs and Shunt Capacitor Banks Simultaneously Considering Load Uncertainty via MOPSO Approach. Int. J. Electr. Power Energy Syst. 2015, 67, 336–349. [Google Scholar] [CrossRef]
- Cheng, S.; Chen, M.-Y.; Fleming, P.J. Improved Multi-Objective Particle Swarm Optimization with Preference Strategy for Optimal DG Integration into the Distribution System. Neurocomputing 2015, 148, 23–29. [Google Scholar] [CrossRef]
- Bohre, A.K.; Agnihotri, G.; Dubey, M. Optimal Sizing and Sitting of DG with Load Models Using Soft Computing Techniques in Practical Distribution System. IET Gener. Transm. Distrib. 2016, 10, 2606–2621. [Google Scholar] [CrossRef]
- Kumawat, M.; Gupta, N.; Jain, N.; Bansal, R.C. Swarm-Intelligence-Based Optimal Planning of Distributed Generators in Distribution Network for Minimizing Energy Loss. Electr. Power Components Syst. 2017, 45, 589–600. [Google Scholar] [CrossRef]
- Sharma, D.; Kumar Yadav, N.; Gunjan; Bala, A. Impact of Distributed Generation on Voltage Profile Using Different Optimization Techniques. In Proceedings of the 2016 International Conference on Control, Computing, Communication and Materials (ICCCCM), Allahabad, India, 21–22 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Fazliana Abdul Kadir, A.; Mohamed, A.; Shareef, H.; Asrul Ibrahim, A.; Khatib, T.; Elmenreich, W. An Improved Gravitational Search Algorithm for Optimal Placement and Sizing of Renewable Distributed Generation Units in a Distribution System for Power Quality Enhancement. J. Renew. Sustain. Energy 2014, 6, 033112. [Google Scholar] [CrossRef]
- Sarkar, B.K.; Chakrabarti, A. OPF Governed Determination of Location and Size of Distribution Generators Using Gravitational Search Algorithm. In Proceedings of the 2016 2nd International Conference on Control, Instrumentation, Energy & Communication (CIEC), Kolkata, India, 28–30 January 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 446–450. [Google Scholar]
- Fadel, W.; Kilic, U.; Taskin, S. Placement of Dg, Cb, and Tcsc in Radial Distribution System for Power Loss Minimization Using Back-Tracking Search Algorithm. Electr. Eng. 2017, 99, 791–802. [Google Scholar] [CrossRef]
- El-Fergany, A. Optimal Allocation of Multi-Type Distributed Generators Using Backtracking Search Optimization Algorithm. Int. J. Electr. Power Energy Syst. 2015, 64, 1197–1205. [Google Scholar] [CrossRef]
- Kefayat, M.; Lashkar Ara, A.; Nabavi Niaki, S.A. A Hybrid of Ant Colony Optimization and Artificial Bee Colony Algorithm for Probabilistic Optimal Placement and Sizing of Distributed Energy Resources. Energy Convers. Manag. 2015, 92, 149–161. [Google Scholar] [CrossRef]
- Sultana, U.; Khairuddin, A.B.; Mokhtar, A.S.; Zareen, N.; Sultana, B. Grey Wolf Optimizer Based Placement and Sizing of Multiple Distributed Generation in the Distribution System. Energy 2016, 111, 525–536. [Google Scholar] [CrossRef]
- Devi, S.; Geethanjali, M. Application of Modified Bacterial Foraging Optimization Algorithm for Optimal Placement and Sizing of Distributed Generation. Expert Syst. Appl. 2014, 41, 2772–2781. [Google Scholar] [CrossRef]
- Chicco, G.; Mazza, A. Metaheuristic Optimization of Power and Energy Systems: Underlying Principles and Main Issues of the “Rush to Heuristics”. Energies 2020, 13, 5097. [Google Scholar] [CrossRef]
- Zheng, Q.P.; Wang, J.; Liu, A.L. Stochastic Optimization for Unit Commitment—A Review. IEEE Trans. Power Syst. 2015, 30, 1913–1924. [Google Scholar] [CrossRef]
- Tejada-Arango, D.A.; Lumbreras, S.; Sanchez-Martin, P.; Ramos, A. Which Unit-Commitment Formulation Is Best? A Comparison Framework. IEEE Trans. Power Syst. 2020, 35, 2926–2936. [Google Scholar] [CrossRef]
- Kazarlis, S.A.; Bakirtzis, A.G.; Petridis, V. A Genetic Algorithm Solution to the Unit Commitment Problem. IEEE Trans. Power Syst. 1996, 11, 83–92. [Google Scholar] [CrossRef]
- Muralikrishnan, N.; Jebaraj, L.; Rajan, C.C.A. A Comprehensive Review on Evolutionary Optimization Techniques Applied for Unit Commitment Problem. IEEE Access 2020, 8, 132980–133014. [Google Scholar] [CrossRef]
- Logenthiran, T.; Srinivasan, D. Particle Swarm Optimization for Unit Commitment Problem. In Proceedings of the 2010 IEEE 11th International Conference on Probabilistic Methods Applied to Power Systems, Singapore, 14–17 June 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 642–647. [Google Scholar]
- Jang, S.H.; Roh, J.H.; Kim, W.; Sherpa, T.; Kim, J.H.; Park, J.B. A Novel Binary Ant Colony Optimization: Application to the Unit Commitment Problem of Power Systems. J. Electr. Eng. Technol. 2011, 6, 174–181. [Google Scholar] [CrossRef] [Green Version]
- Yuan-Kang, W.; Chih-Cheng, H.; Chun-Liang, L. Resolution of the Unit Commitment Problems by Using the Hybrid Taguchi-Ant Colony System Algorithm. Int. J. Electr. Power Energy Syst. 2013, 49, 188–198. [Google Scholar] [CrossRef]

| Concept | Description | |
|---|---|---|
| Parallelism (used for population-based algorithms) | A number of individuals are assigned simultaneously to perform a single function, and the results are compared. This idea affects the evolution of individuals inside the population or produces new ones. | |
| Acceptance | Case 1: Accept interim solutions that weaken objective function as a result of the expansion of the search space. | |
| Case 2: Management of the constraints of the objective function | Method 1: Any solution that includes any violation is rejected. When the initial conditions meet any conceivable solution, this procedure is used. | |
| Method 2: In this case, all solutions are automatically accepted, and the initial conditions could correspond to inconceivable solutions. If any solution can be assigned a numerical value, this approach is used. | ||
| Case 3: Adding constraints on approved solutions that improve the best solution by at least the restricting level. When comparing values produced from previous calculations, this strategy aids in avoiding numerical issues. | ||
| Elitism (for population-based algorithms) | The elitism concept is used to uphold the best-found solutions and utilize them as a reference for the following iteration or update them if other best solutions are identified. | |
| Selection | A probability-based approach for producing new random solutions from existing ones. | |
| Decay | Allows for more initial flexibility, followed by incremental flexibility constraints. | Each repetition includes a multiplicative factor of less than one. |
| Reinforcement | Each repetition includes a multiplicative factor greater than one. | |
| Immunity | Identifying characteristics of certain solutions that lead to appropriate setups. It promotes solutions with characteristics similar to those criteria. | |
| Self-Adaptation | A method that permits adjusting the algorithms’ parameters based on the optimization progression. | |
| Topology | This concept is involved if the examined problem must be subjected to special limitations. | |
| Refs. | Algorithm | Description and Objectives | |||||
|---|---|---|---|---|---|---|---|
| Fuel Cost | P/Q | VD | Transformer Tap Set | Transmission Losses | Emissions | ||
| [63,64] | Ant colony optimization (ACO) | x | x | x | x | x | |
| [65] | Ant colony optimization (ACO) | x | x | ||||
| [66] | Ant colony optimization (ACO) | x | x | x | |||
| [67] | Backtracking search algorithm (BSA) | x | x | x | |||
| [68] | Colliding bodies optimization (CBO) | x | x | x | |||
| [69] | Black-hole optimization (BHO) | x | x | x | x | ||
| [70] | Gray wolf optimizer (GWO) | x | x | x | |||
| [71] | Firefly algorithm (FFA) | x | x | ||||
| [72] | Cuckoo search (CS) | x | x | x | x | ||
| [73] | Moth swarm algorithm (MSA) | x | x | x | |||
| [74] | Krill herd algorithm (KHA) | x | x | ||||
| [75,76] | opposition-based Krill herd algorithm | x | |||||
| [77] | Shuffled frog leaping algorithm (SFLA) | x | |||||
| [78] | Bacterial foraging algorithm (BFA) | x | x | x | x | ||
| [79] | modified Bacterial foraging algorithm | x | x | x | |||
| [80] | Sine cosine algorithm (SCA) | x | x | x | x | ||
| [81] | Jaya algorithm (JA) | x | x | x | |||
| [82] | Salp swarm algorithm (SSA) | x | |||||
| [83] | Honey Badger Optimizer (HBO) | x | x | x | |||
| [84] | Quasi-Oppositional-Chaotic Symbiotic Organisms Search algorithm | x | x | x | |||
| Ref. | Algorithm | Objectives | |||||
|---|---|---|---|---|---|---|---|
| Voltage Profile | Voltage Stability | Power Losses | Transformer Tap set | Power Losses | VAR Compensation | ||
| [92] | Particle swarm optimization (PSO) | x | |||||
| [93] | Multi-agent and PSO | x | x | ||||
| [94] | Learning PSO | x | x | ||||
| [95] | Differential evolution (DE) | x | x | x | |||
| [96] | Quasi-oppositional DE | x | x | x | x | ||
| [97] | Adaptive DE | x | x | ||||
| [98] | Genetic algorithm (GA) | x | x | x | |||
| [99] | Biogeography-based optimization (BBO) | x | x | x | |||
| [100] | Gravitational search algorithm (GSA) | x | |||||
| [101] | Opposition-based GSA | x | x | ||||
| [102] | Chaotic krill herd algorithm (CKHA) | x | x | ||||
| [103] | Harmony search (HS) | x | x | x | |||
| [104] | Teaching learning-based optimization (TLBO) | x | x | x | |||
| [105] | Ant colony optimization (ACO) | x | x | ||||
| [106] | Gray wolf optimizer (GWO) | x | x | ||||
| [107] | Exchange market algorithm (EMA) | x | x | ||||
| [108] | Firefly Algorithm (FA) | x | x | ||||
| Ref | Algorithm | Description and Objectives |
|---|---|---|
| [113] | Genetic algorithm (GA) Evolutionary programming (EP) Particle swarm optimization (PSO) Differential evolution (DE) | Solve CEED for the IEEE 30-bus and 15-unit systems. |
| [114] | Pareto-based, multi-objective evolutionary algorithms (MOEA) | Solve CEED for the IEEE 30-bus and 6-unit systems. |
| [115] | Hybrid evolutionary algorithm (HEA) | Solve CEED problems for the IEEE 57 and 118-bus systems. |
| [116] | Improved particle swarm optimization (IPSO) | Used three ED problems applied to the large-scale power system in Korea. |
| [117] | PSO with smart inertia factor (PSO-SIF) | Used 6, 15, 20, and 40 units testing systems. |
| [118] | Improved COOT optimization Algorithm (iCOOT) | Reduce the generating cost, pollutant emissions, and satisfaction weight coefficient of the unit. |
| [119] | Hybrid gravitational search algorithm and random forest regression (GSA-RFR) | Solve the CEED for combined cooling, heating, and power (CCHP) and power-to-gas (P2G)-based microgrid. |
| [120] | Artificial bee colony (ABC) | Assess the combined cost and emission targets to decrease losses and raise transmission line efficiency. |
| [121] | Adaptive Bat Algorithm | Resolve large-scale ED with reduced execution time |
| [122] | Artificial ecosystem optimization (AEO) | Reduce the economic charges as well as the three harmful gas emissions of sulfur dioxide (SO2), nitrous oxide (N2O), and carbon dioxide (CO2). |
| [123] | Spiral optimization algorithm (SOA) | Reduce costs and emissions while meeting load requirements and operating restrictions. |
| [124] | Hybrid PSO-FA | Reduce costs and emissions while meeting load requirements and operating restrictions. |
| [125] | Flower pollination algorithm (FPA) | Solve the CEED problem while taking into account the environmental consequences of fossil-fueled power stations’ emissions of gaseous pollutants. |
| [126] | Levy-based glowworm swarm optimization (LGSO) Grey wolf optimization (GWO) Whale optimization algorithm (WOA) Dragonfly algorithm (DA) Glowworm swarm optimization (GSO) | The LGSO provided the best solution by choosing the generation of renewable energy sources. |
| Ref | Algorithm | Description and Objectives |
|---|---|---|
| [132] | Genetic algorithm (GA) | DG units include fuel cells (FCs), microturbines (MTs), diesel generators (DGs), photovoltaic systems (PVs), and wind turbines (WTs). |
| [133] | Genetic algorithm (GA) | Resolving the OPF considering the spatial electrothermal coupling effect. |
| [134] | Particle swarm optimization (PSO) | Use the PSO to determine each DG unit’s active and reactive power and the tap of tap-changer transformers to reduce the cost, considering various physical and technical restrictions. |
| [135] | Gravitational search algorithm (GSA) | The GSA successfully resolved the OPF problem on two distribution systems, and its results were compared to those obtained using the GA method. |
| [136] | Improved GSA | DGs with unpredictable power outputs are included in the distribution networks’ optimum reactive power flow issue-solving. |
| [137] | Spotted hyena optimizer (SHO) | Reducing the overshoot/undershoot peaks and time response of a power system with various DERs. |
| Ref | Algorithm | Description and Objectives |
|---|---|---|
| [154] | Genetic algorithm (GA) | Based on the day-ahead load projection, create optimal dispatch schedules for on-load tap changer (OLTC) settings at substations and all shunt capacitor switching to minimize the loss and enhance the voltage profile. |
| [155] | Genetic algorithm (GA) | Reduce the operation numbers of ULTC and switching capacitors to minimize the loss and enhance the voltage profile for 24 h. |
| [156] | Genetic algorithm (GA) | GA controls the load ratio of the transformer, the step voltage regulator (SVR), the shunt capacitor, the reactor, and the static Var compensator. |
| [148] | Genetic algorithm (GA) | Minimal power losses and capacitor banks’ switching are the goals of the proposed day-ahead coordinated reactive power dispatch technique while forecasting the DG errors to assess their reactive power capability. |
| [151] | Genetic algorithm (GA) | The PV solar reactive power is an additional control variable for substation capacitors, feeder capacitors, and OLTC tap positions. |
| [157] | Evolutionary programming (EP) | Microgeneration shedding is included to enhance the Volt/Var solving performance. |
| [158] | Particle swarm optimization (PSO) | The distribution networks are feeder capacitors, paired substation capacitors, and OLTC. |
| [145] | Fuzzy adaptive PSO (FAPSO) | Find the best active and reactive power distribution for the DG units, including the capacitor banks and the tap settings for the transformers, for 24 h. |
| [147] | Particle swarm optimization (PSO) | Eliminate the active power loss, the VD, and the reactive power compensation device’s capacity (or reduce its investment cost). |
| [146] | Fuzzy adaptive PSO (FAPSO) | Minimize operation cost of transformers and capacitors and power loss while meeting the system constraints. |
| [136] | Improved gravitational search algorithm (IGSA) | Active network loss minimization in the IEEE-33 node standard test system. |
| [159] | modified Teaching-Learning Algorithm (mTLA) | Solve the Volt/Var problem considering the loads and generated power uncertainties. |
| [160] | Bacterial Foraging Algorithm (BFA) | Solve the Volt/Var problem for several DGs as a weighted combination of a single objective, and then determine the best Pareto-front for different combinations of objective functions. |
| [161] | Gravitational Search Algorithm (GSA) | Optimal capacitor power control to reduce power losses and the reactive power cost generated by capacitors. |
| Ref | Algorithm | Description and Objectives |
|---|---|---|
| [169] | Genetic algorithm (GA) | The best allocation of several DG types is established using GA to minimize total mean daily active power losses. |
| [170] | Genetic algorithm (GA) | Optimal sizing and placement of DGs considering power quality improvement. |
| [171] | GA-based tabu search (GA-TS) | Determine the best position of DG units in a distribution system as the independent private sector. |
| [172] | Non-dominated sorting GA (NSGAII) | Solve this problem as a multi-objective probabilistic optimization problem that includes total costs, power losses, and investment charges. |
| [173] | An analytical method with GA | The objective function includes the minimization of the distribution network power loss. |
| [174] | Particle swarm optimization (PSO) | PSO is used to handle the problem of optimal DG unit placement while accounting for load changes in the distribution network. |
| [175] | Multiobjective PSO (MOPSO) | Determine the best position and size of DGs and shunt capacitor banks in distribution networks while considering load randomness. |
| [176] | Improved MOPSO (IMOPSO) | Determine the best location and size for DG units in the distribution network. |
| [177] | Multiobjective PSO (MOPSO) | Determine the best DG size and location by considering several metrics, such as active and reactive power losses, VD, and reliability. |
| [178] | Particle swarm optimization (PSO) | Consider the time-varying features of electrical load demand to calculate DGs’ appropriate size and position to minimize yearly power loss. |
| [179] | Particle swarm optimization (PSO) | Determine the appropriate position and size of various DG units by considering factors, such as total power losses, voltage profile enhancement, and greenhouse gas emissions. |
| [180] | Improved Gravitational Search Algorithm (IGSA) | Find DG’s appropriate location and sizing in a radial distribution network to reduce power losses, harmonic distortion, and VD. |
| [181] | Gravitational Search Algorithm (GSA) | Enhance nodal pricing and voltage profiles in the distribution network using the GSA. |
| [182] | Backtracking search algorithm (BSA) | In a radial distribution network, optimal sizing and location of DGs, capacitor banks, and a thyristor-controlled series compensator. |
| [183] | Fuzzy-BSA | Increasing operational performance, reducing the loss, and enhancing the voltage profile goals are included in the objective function. The combined power factor and network reactive power loss decrease are also included. |
| [184] | Hybrid ACO–ABC | Reducing electrical energy costs, power losses, and total emissions from substations and resources enhances voltage stability. |
| [185] | Gray wolf optimizer (GWO) | Reduce reactive power losses and enhance distribution system voltage profiles while remaining within power system restrictions. |
| [186] | Bacterial foraging optimization (BFO) | Reduce power loss and enhance voltage profile of radial distribution network on 12-bus, 34-bus, and 69-bus radial distribution systems with 11, 33, and 68 sections, respectively. |
| Ref | Algorithm | Description and Objectives |
|---|---|---|
| [190] | Genetic algorithm (GA) | Provide enhanced binary coding performance for each unit on/off switching states. |
| [191] | Evolutionary algorithm (EA) | A comprehensive review of the UC problem using evolutionary optimization algorithms |
| [192] | Particle swarm optimization (PSO) | Use three versions of PSO algorithms: Binary PSO, Improved binary PSO, and PSO with Lagrangian relaxation for unit commitment problems. |
| [193] | novel binary ant colony optimization (NBACO) | Consider all possible solution sets as well as drawbacks, such as large memory size and a long execution time while solving the UC problem. |
| [194] | Hybrid Taguchi-ant colony system (HTACS) | Better UC solutions are rapidly chosen to reflect possible UC schedules. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nassef, A.M.; Abdelkareem, M.A.; Maghrabie, H.M.; Baroutaji, A. Review of Metaheuristic Optimization Algorithms for Power Systems Problems. Sustainability 2023, 15, 9434. https://doi.org/10.3390/su15129434
Nassef AM, Abdelkareem MA, Maghrabie HM, Baroutaji A. Review of Metaheuristic Optimization Algorithms for Power Systems Problems. Sustainability. 2023; 15(12):9434. https://doi.org/10.3390/su15129434
Chicago/Turabian StyleNassef, Ahmed M., Mohammad Ali Abdelkareem, Hussein M. Maghrabie, and Ahmad Baroutaji. 2023. "Review of Metaheuristic Optimization Algorithms for Power Systems Problems" Sustainability 15, no. 12: 9434. https://doi.org/10.3390/su15129434
APA StyleNassef, A. M., Abdelkareem, M. A., Maghrabie, H. M., & Baroutaji, A. (2023). Review of Metaheuristic Optimization Algorithms for Power Systems Problems. Sustainability, 15(12), 9434. https://doi.org/10.3390/su15129434










