Study on the Fracture Evolution Characteristics of Existing Defect Lining under Unsymmetrical Load
Abstract
:1. Introduction
2. Model Test Design and Device
2.1. Model Test Device
2.2. Lining Model Preparation and Working Condition Design
2.3. Test Loading and Sensor Arrangement
3. Analysis of Lining Cracking Characteristics under Unsymmetrical Load
3.1. Analysis of Cracking Characteristics of Intact Lining
3.2. Influence of Different Positions of Existing Defects on Bearing Capacity and Deformation of Lining
4. Analysis of Fracture Evolution Characteristics of Unsymmetrical Lining Based on AE
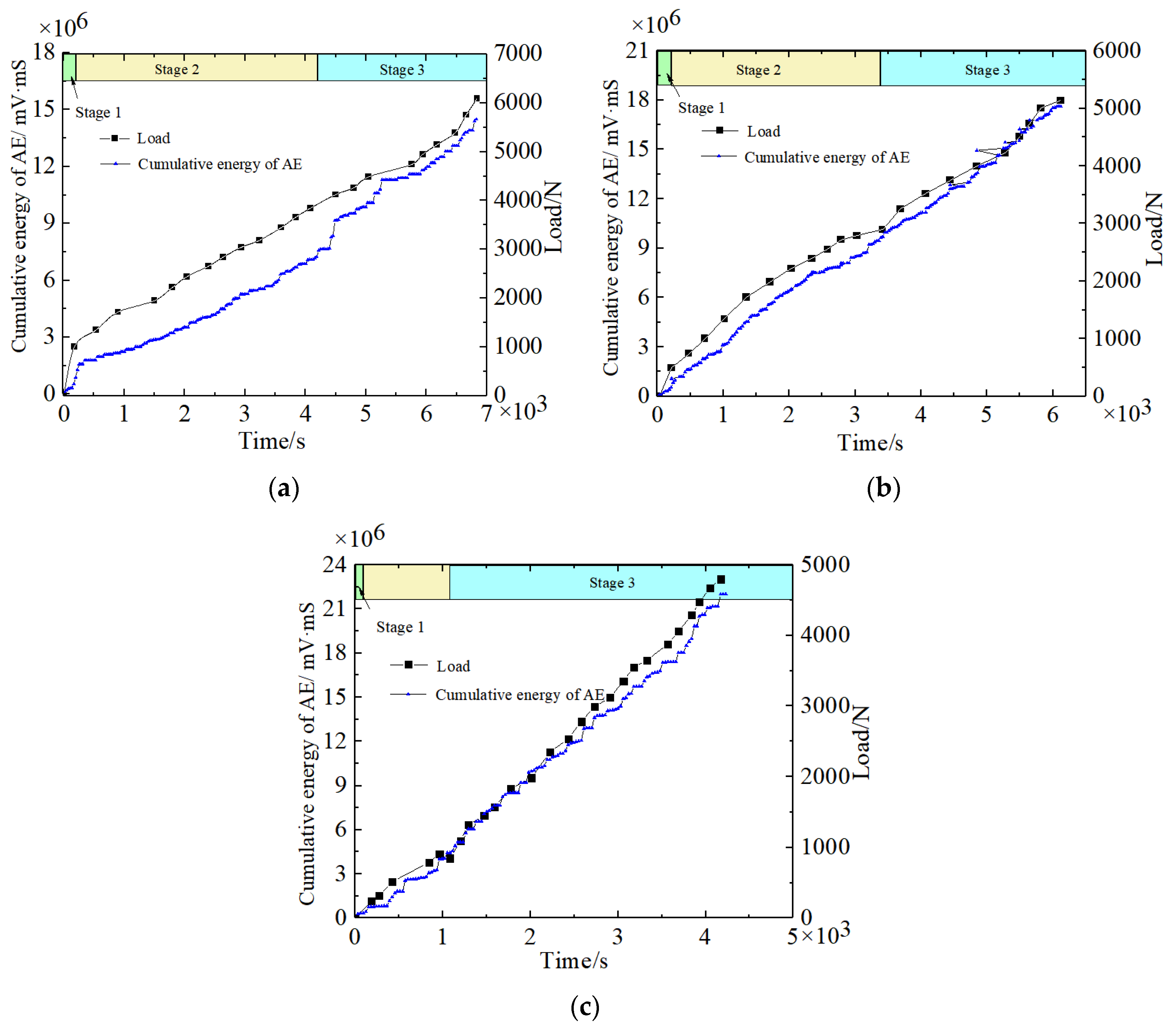
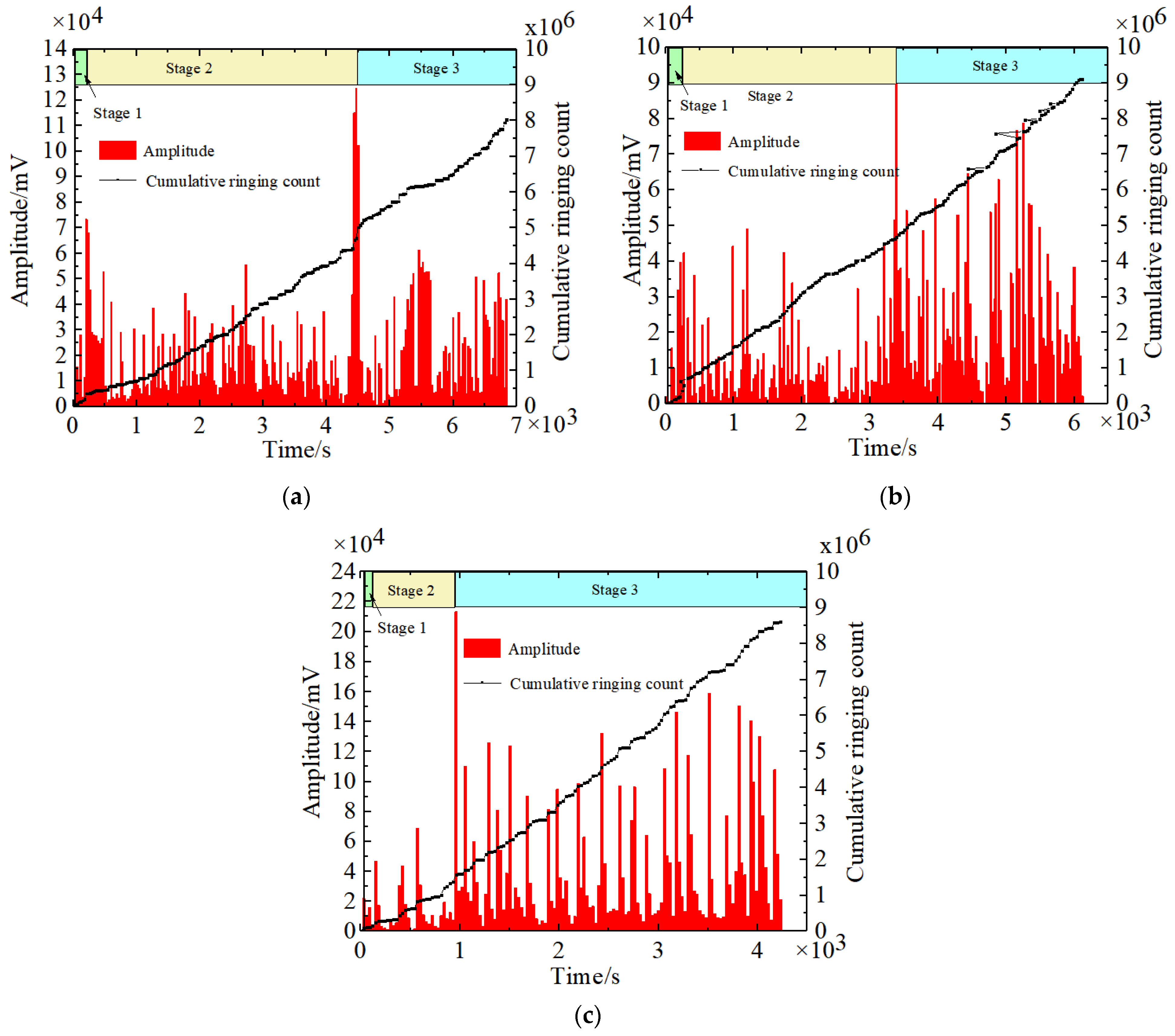
4.1. AE Test Results
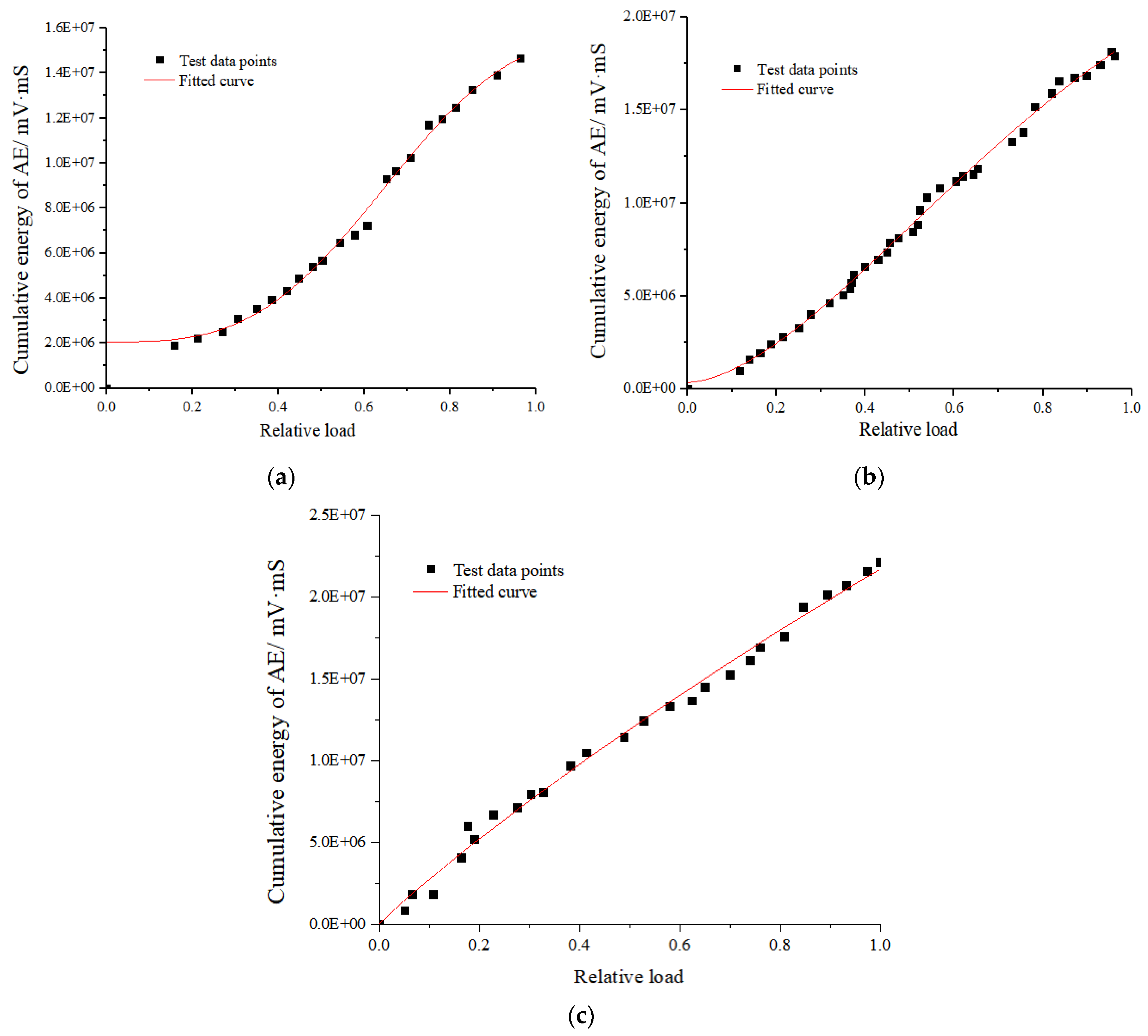
4.2. Fracture Evolution Model of Lining
5. Conclusions
- (1)
- The failure process of the intact lining under unsymmetrical load has three stages: “initial crack cracking at the unsymmetrical position → development and formation of main crack → specimen cracking failure”. The sequence of crack development is as follows: inside of the arch waist at the unsymmetrical load → the outside of the vault → the outside of the arch foot on the unsymmetrical side and the inside of the inverted arch. The load ratio of initial crack cracking is 16.5%, and the load ratio of main crack development and formation is 52.2%. Once the main crack is formed, the specimen enters a stage of rapid failure.
- (2)
- The initial cracking location of the lining under unsymmetrical load is independent of the location of existing defects, and all cracks occur at the unsymmetrical position. Other cracks are mainly distributed at the vault, inverted arch and arch foot.
- (3)
- The closer the existing defects are to the unsymmetrical position, the faster the initial cracking at the unsymmetrical position and faster the lining instability will be. Compared with intact lining, the ultimate bearing capacity of vault defect and arch waist defect decreased by 14.2% and 21.3%, respectively, and the maximum deformation decreased by 44.6% and 50.6%, respectively. The radial deformation degree in an unsymmetrical position at each stage is basically the same under unsymmetrical load and is not affected by the location of existing defects. The proportion of radial deformation in each stage is concentrated in 5%, 40% and 53%, respectively.
- (4)
- The AE technology can effectively reflect the three stage characteristics of lining fracture evolution under unsymmetrical load. The closer the existing defect is to the unsymmetrical position, the faster the initial cracking, the lower the degree of initial cracking damage, the shorter the main crack forming time, the higher the degree of damage during lining failure will be, but the less active a degree of damage occurs during the whole cracking process.
- (5)
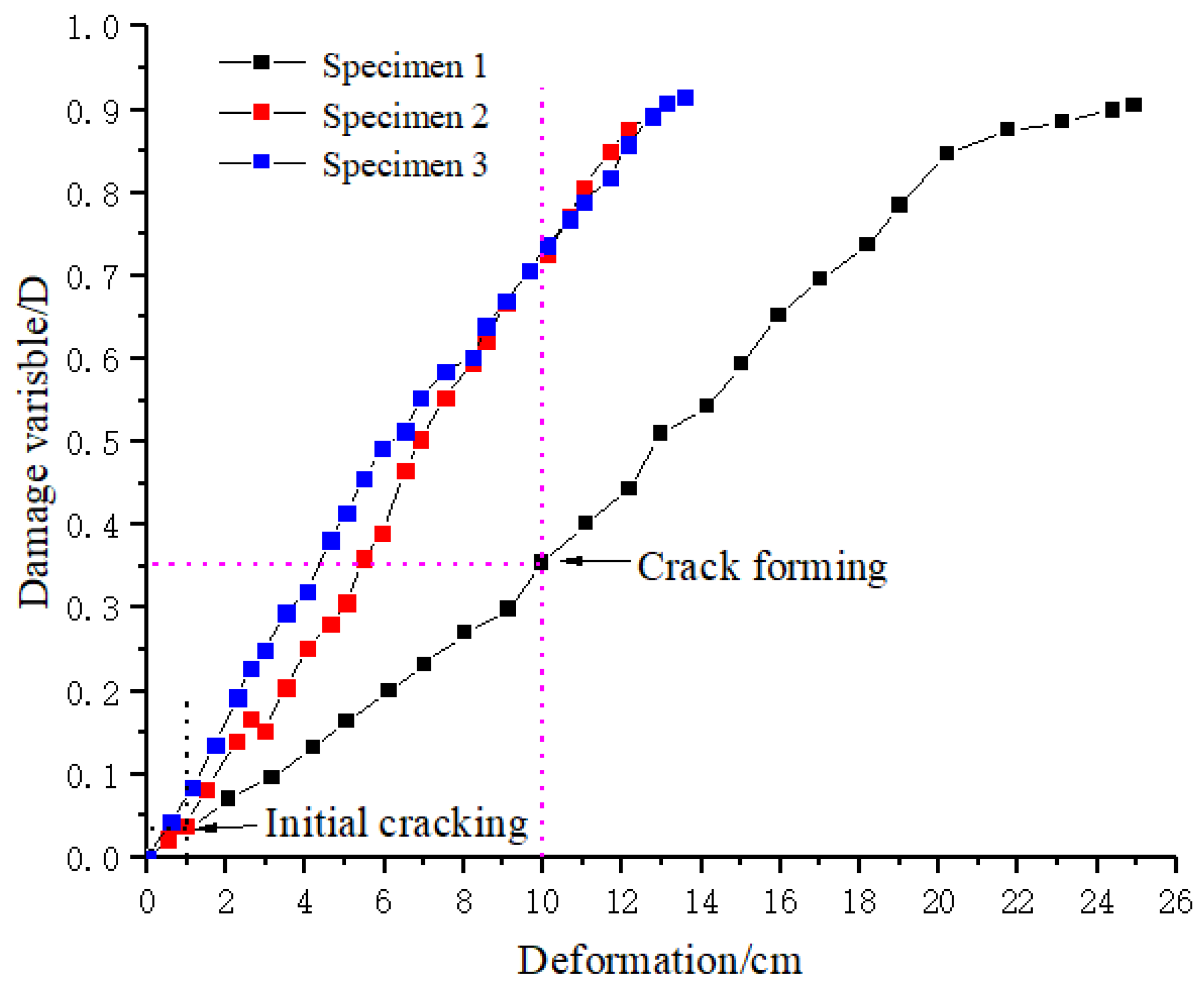
- The fracture evolution model of unsymmetrical lining was derived based on the cumulative energy of AE, and the quantitative relationship between the damage variables of unsymmetrical lining and the deformation of lining was established. Compared with the intact lining, the location of existing defects only affects the damage evolution rate during crack cracking and development but does not affect the damage rate of the structure after crack propagation.
- (6)
- Under the unsymmetrical load, when the radial deformation in unsymmetrical position of the complete lining reaches 1.21 cm and 9.96 cm, the fracture degree of the lining reaches 0.04 and 0.35. At this time, the tunnel lining should be reinforced in time to ensure the normal use of the tunnel. However, when the vault defect lining and arch waist defect lining reach the fracture degree, the deformation is 58.3%, 75.0% 40.2%, and 50.6% earlier than that of the complete lining. The results provide guidance for determining the damage degree of a biased tunnel with existing defects in real engineering and when to adopt reinforcement.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lei, M.F.; Peng, L.M.; Shi, C.H. Damage mechanism and evolution law of mechanical property of tunnel structure suffering sulfate ambient. J. Cent. South Univ. 2012, 43, 4865–4872. [Google Scholar]
- Zheng, X.Y.; Wang, Y.R.; Zhang, S.Q.; Xu, F.; Zhu, X.P.; Jiang, X.; Zhou, L.; Shen, Y.; Chen, Q.; Yan, Z.G.; et al. Research progress of the thermophysical and mechanical properties of concrete subjected to freeze-thaw cycles. Constr. Build. Mater. 2022, 330, 127254. [Google Scholar] [CrossRef]
- Tan, Z.S.; Zeng, C.; Li, J.; Du, C.W.; Zhang, P. Model test investigation on the mechanical characteristics of support structure of subsea tunnels. China Civ. Eng. J. 2011, 44, 99–105. [Google Scholar]
- Zhao, L.H.; Huang, F.; Sun, Q.H.; Xu, Z.M.; Luo, W. Rock pressure of unsymmetrical shallow rectangular tunnel based on upper bound limit analysis method. J. Cent. South Univ. 2014, 45, 3093–3103. [Google Scholar]
- Du, J.M.; Fang, Q.; Hai, L.; Mai, H.Y.; Wang, G. Calculation method for surrounding rock pressure of shallow tunnel with asymmetrical pressure of variable slopes. J. Cent. South Univ. 2021, 52, 4088–4098. [Google Scholar]
- Liu, X.R.; Chen, H.J.; Liu, K.; He, C.M. Model test and stress distribution law of unsymmetrical loading tunnel in bedding rock mass. Arab. J. Geosci. 2017, 10, 184. [Google Scholar] [CrossRef]
- She, J.; He, C.; Wang, B.; Wang, Y. Study on Effect of Cavities behind Linings on Bearing Capacity of Tunnel Structure by Model Test. J. Highw. Transp. Res. Dev. 2008, 1, 104–110. [Google Scholar]
- He, C.; Tang, Z.C.; Wang, B.; She, J. Research on effect of inner surface reinforcing on structure bearing capacity by model test in defective tunnel. Rock Soil Mech. 2009, 30, 406–412. [Google Scholar]
- Liu, X.Z.; Liu, W.Y.; Sang, Y.L.; Gu, Y.C. Experiment on the influence of cracking characteristics under unsymmetrical load on stresses or forces in tunnel lining. China Civ. Eng. J. 2015, 48, 119–128. [Google Scholar]
- Liu, X.Z.; Duan, J.M.; Guo, Q.K. Analysis on Damage Evolution of Highway Tunnel Lining under Lateral Load. Chin. J. Undergr. Space Eng. 2021, 17, 1529–1536. [Google Scholar]
- Lei, M.F.; Peng, L.M.; Shi, C.H.; Wang, L.C.; Liu, Z.C. Calculation of the surrounding rock pressure on a shallow buried tunnel using linear and nonlinear failure criteria. Autom. Constr. 2014, 37, 191–195. [Google Scholar] [CrossRef]
- Lei, M.F.; Peng, L.M.; Shi, C.H. Model test to investigate the failure mechanisms and lining stress characteristics of shallow buried tunnels under unsymmetrical loading. Tunn. Undergr. Space Technol. 2015, 46, 64–75. [Google Scholar] [CrossRef]
- Zhang, Z.G.; Jiang, Y.J.; Liu, M.; Dong, J.F. Rock pressure of shallow unsymmetrical-loading tunnels considering the cohesion and earthquake action. J. China Univ. Min. Technol. 2018, 47, 780–790. [Google Scholar]
- Li, J.W.; Xu, F.; Wang, T.M.; Shi, S.T. Research on the Evolution of Shield Segment Cracks Based on Acoustic Emission and CMOD. Materials 2022, 15, 5829. [Google Scholar] [CrossRef] [PubMed]
- Amedeo, M.; Gianni, N.; Alberto, C. AE monitoring of a concrete arch road tunnel: Damage evolution and localization. Eng. Fract. Mech. 2019, 210, 279–287. [Google Scholar]
- Triantis, D.; Loukidis, A.; Stavrakas, I.; Pasiou, E.D.; Kourkoulis, S.K. Attenuation of the Acoustic Activity in Cement Beams under Constant Bending Load Closely Approaching the Fracture Load. Foundations 2022, 2, 590–606. [Google Scholar] [CrossRef]
- Efe, S.; Amir, G.; Ninel, A. Study of fracture evolution in FRP-strengthened reinforced concrete beam under cyclic load by acoustic emission technique: An integrated mechanical-acoustic energy approach. Constr. Build. Mater. 2015, 95, 832–841. [Google Scholar]
- Yu, J. Study on the influence of stress distribution law by lining crack in highway tunnel. China Civ. Eng. J. 2017, 50, 70–75. [Google Scholar]
- Liu, X.Z.; Wang, X.L.; He, B.G.; Sang, Y.L. Model Test of Cracked Tunnel Lining Reinforced with Umbrella Arch Based on Secondary Loading. J. Sichuan Univ. 2015, 47, 21–28. [Google Scholar]
- Li, J.W.; Xu, F.; Wang, B.; Gao, Y. Influence of concrete aggregate particle size on acoustic emission detection. J. Shangdong Univ. 2021, 51, 7. [Google Scholar]

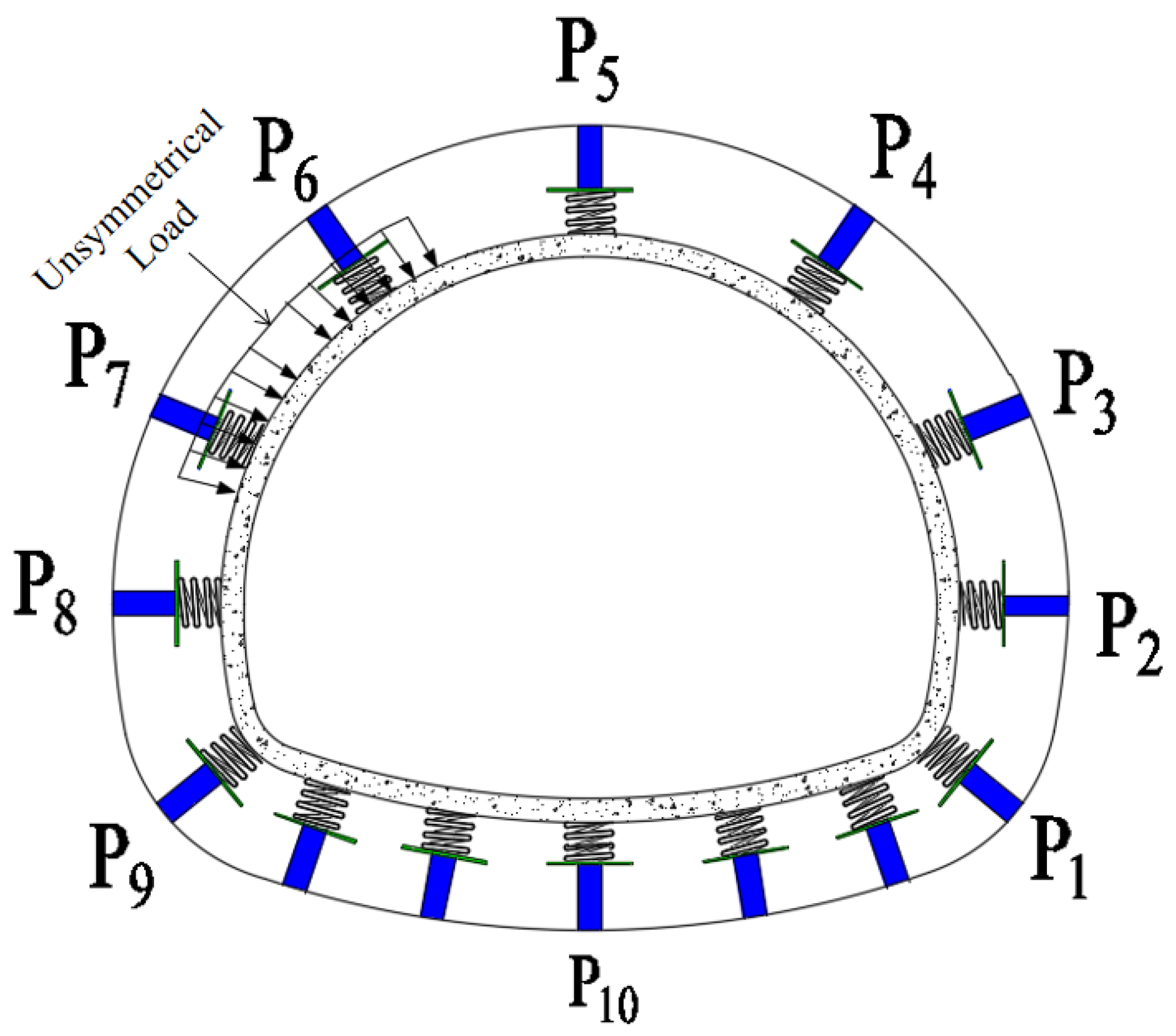

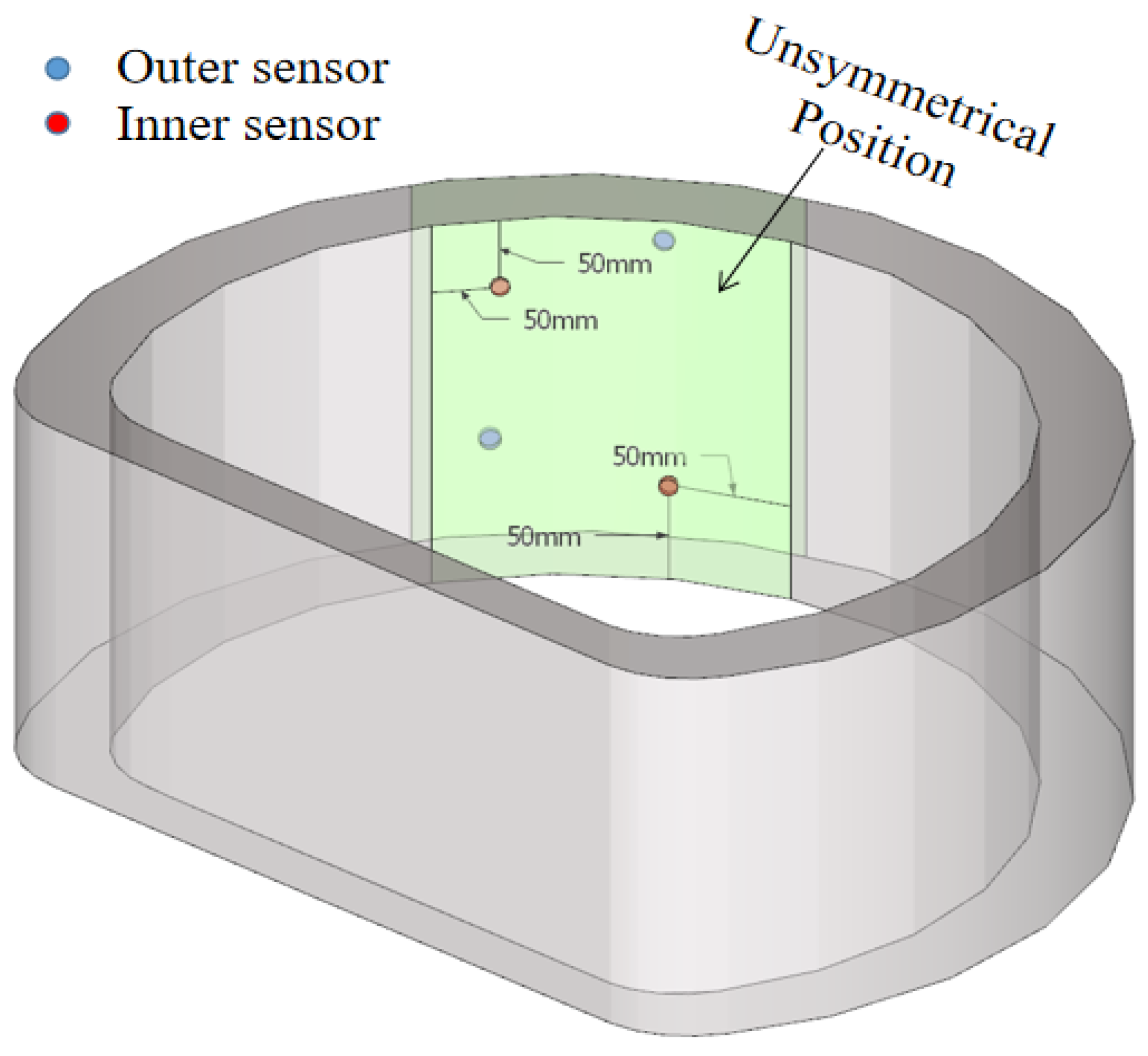
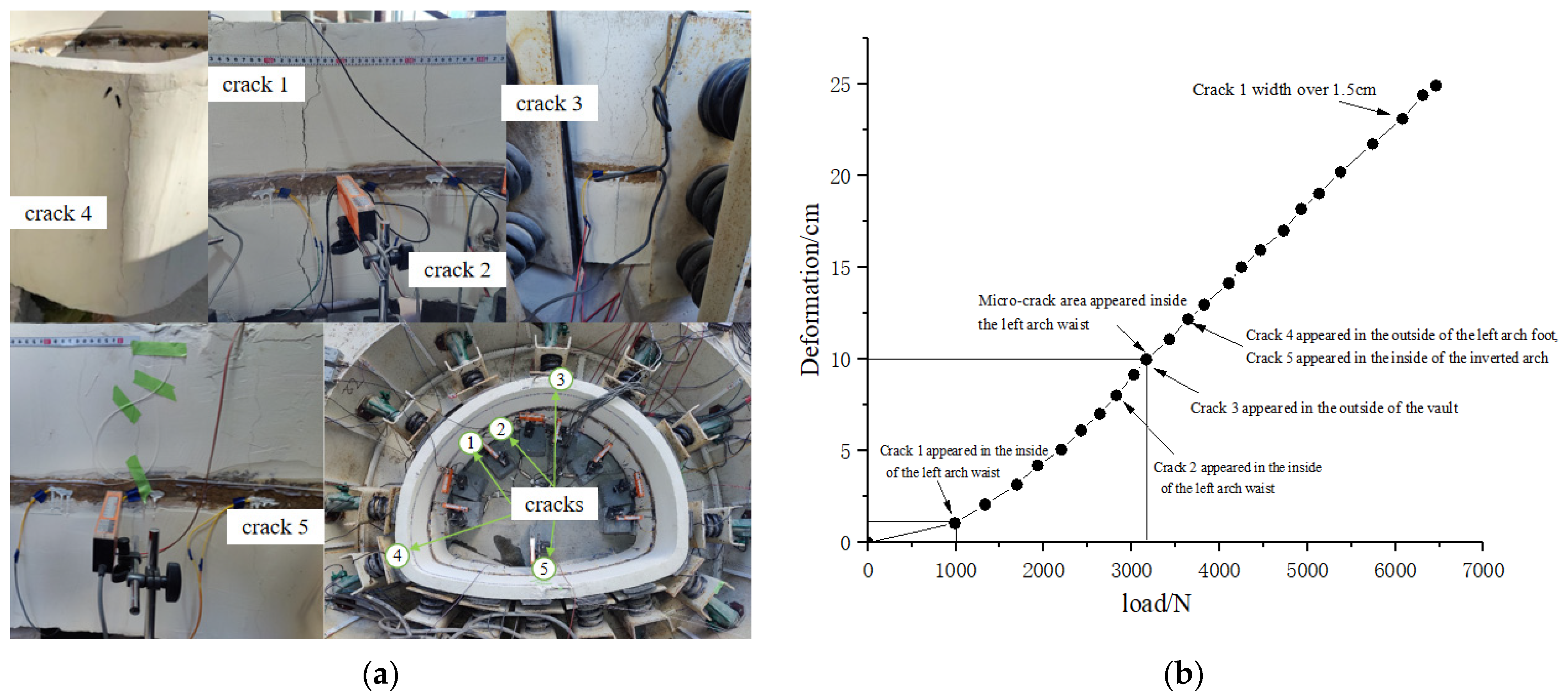


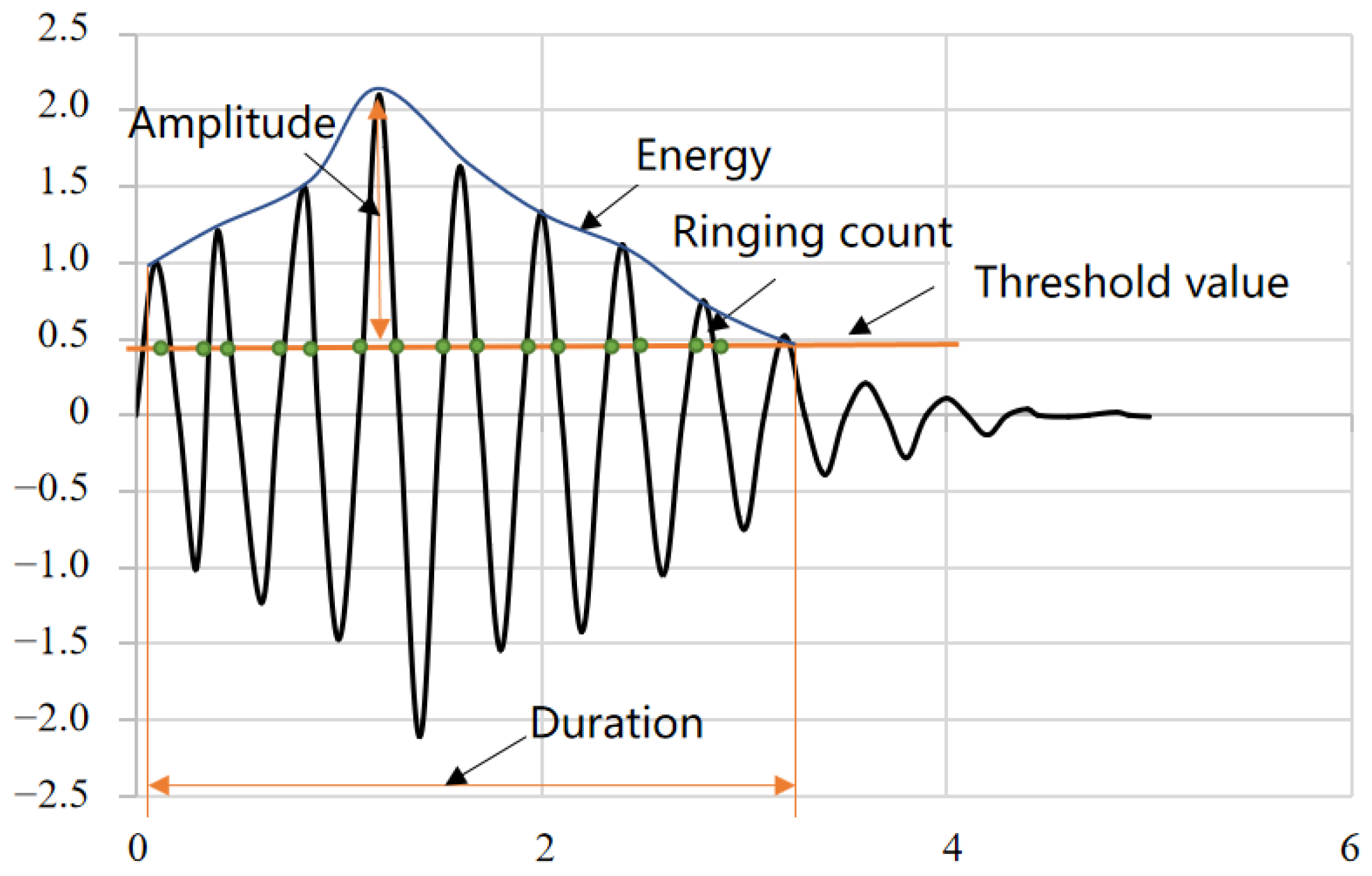
| Related Parameters | Similarity Ratio |
|---|---|
| Geometric Dimensioning L (m) | 1:10 |
| Load N (N) | 1:1820 |
| Formation Resistance Coefficient K (MPa/m) | 1:1.82 |
| Stress (MPa) | 1:18.2 |
| Elasticity Modulus E (MPa) | 1:18.2 |
| Strain | 1:1 |
| Poisson Ratio | 1:1 |
| Displacement (cm) | 1:10 |
| Required Materials | Cement | River Sand | Limestone | Water |
|---|---|---|---|---|
| Mix Ratio | 1 | 7.7 | 0.6 | 1.75 |
| Test Conditions | Defects | ||
|---|---|---|---|
| Location | Depth | ||
| Specimen 1 | Intact Lining | - | - |
| Specimen 2 | Defective Lining | Vault | h/3 |
| Specimen 3 | Arch Waist | h/3 | |
| Schematic Diagram | 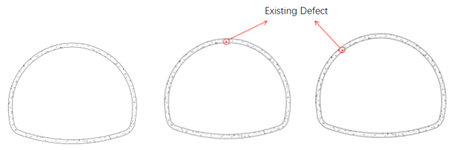 Specimen 1 Specimen 2 Specimen 3 | ||
| Initial Cracking | Fracture Development | Late Fracture | Ultimate Load (N) | Ultimate Deformation (cm) | ||
|---|---|---|---|---|---|---|
| Specimen 1 | Location | Inside of the the left arch waist | Inside of the left arch waist and outside of the vault | Outside of the left arch foot, inside of the inverted arch | 6093 | 24.9 |
| Load (N) | 1008 | 3182 | 3746 | |||
| Load Ratio | 16.5% | 52.2% | 61.4% | |||
| Deformation (cm) | 1.21 | 9.96 | 13.08 | |||
| Deformation Ratio | 4.8% | 40.0% | 52.5% | |||
| Specimen 2 | Location | Inside of the the left arch waist | Outside of the vault, inside of the inverted arch and outside of the the left arch foot | Inside of the right arch foot | 5230 | 13.8 |
| Load (N) | 674 | 2698 | 3079 | |||
| Load Ratio | 12.9% | 51.6% | 58.9% | |||
| Deformation (cm) | 0.62 | 5.54 | 7.23 | |||
| Deformation Ratio | 4.5% | 40.1% | 52.4% | |||
| Specimen 3 | Location | Inside of the the left arch waist | Inside of the the left arch waist, outside of the the right spandrel | Outside of the the left arch foot, inside of the inverted arch | 4797 | 12.3 |
| Load (N) | 272 | 1471 | 2267 | |||
| Load Ratio | 5.6% | 30.7% | 47.3% | |||
| Deformation (cm) | 0.58 | 4.95 | 6.62 | |||
| Deformation Ratio | 4.7% | 40.2% | 53.8% | |||
| Specimen | a | b | d | k | R2 |
|---|---|---|---|---|---|
| 1 | 1.59 × 107 | 2.06 × 106 | 3.18 | 1.37 | 0.99 |
| 2 | 2.62 × 107 | 0.76 × 106 | 1.67 | 1.14 | 0.99 |
| 3 | 1.02 × 107 | 0.55 × 106 | 0.95 | 0.22 | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Xu, F.; Zheng, X.; Liu, B.; Bai, T.; Tang, Q. Study on the Fracture Evolution Characteristics of Existing Defect Lining under Unsymmetrical Load. Sustainability 2023, 15, 9531. https://doi.org/10.3390/su15129531
Li J, Xu F, Zheng X, Liu B, Bai T, Tang Q. Study on the Fracture Evolution Characteristics of Existing Defect Lining under Unsymmetrical Load. Sustainability. 2023; 15(12):9531. https://doi.org/10.3390/su15129531
Chicago/Turabian StyleLi, Junwei, Fei Xu, Xinyu Zheng, Bo Liu, Tao Bai, and Qingjingyi Tang. 2023. "Study on the Fracture Evolution Characteristics of Existing Defect Lining under Unsymmetrical Load" Sustainability 15, no. 12: 9531. https://doi.org/10.3390/su15129531
APA StyleLi, J., Xu, F., Zheng, X., Liu, B., Bai, T., & Tang, Q. (2023). Study on the Fracture Evolution Characteristics of Existing Defect Lining under Unsymmetrical Load. Sustainability, 15(12), 9531. https://doi.org/10.3390/su15129531





