Pavement Roughness Prediction Using Explainable and Supervised Machine Learning Technique for Long-Term Performance
Abstract
1. Introduction
2. Background Study
2.1. IRI Prediction Models
2.2. Use of Machine Learning Approach for Predicting IRI
3. Materials and Methods
3.1. Study Area
3.2. Data Processing
3.3. Machine Learning Models
3.3.1. Extreme Gradient Boosting
3.3.2. Decision Tree
3.3.3. K-Nearest Neighbor
3.3.4. Random Forest
3.3.5. Support Vector Machine
3.4. Explainable Artificial Intelligence
SHAP (SHapley Additive exPlanations)
4. Results
4.1. Multiple Regression Analysis
4.2. Machine Learning Models
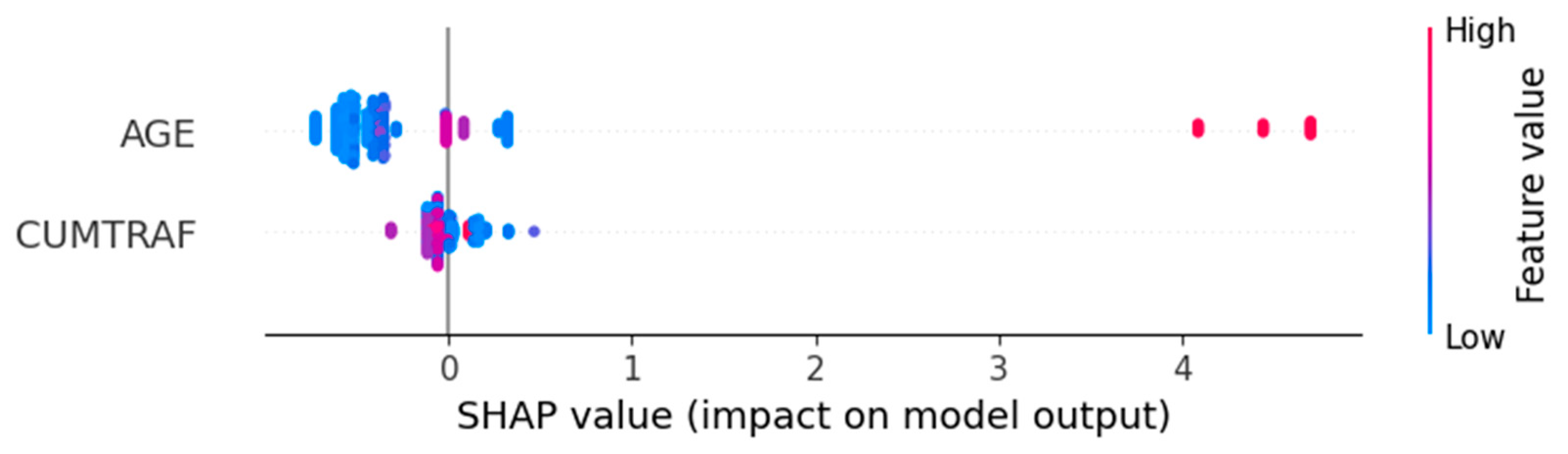
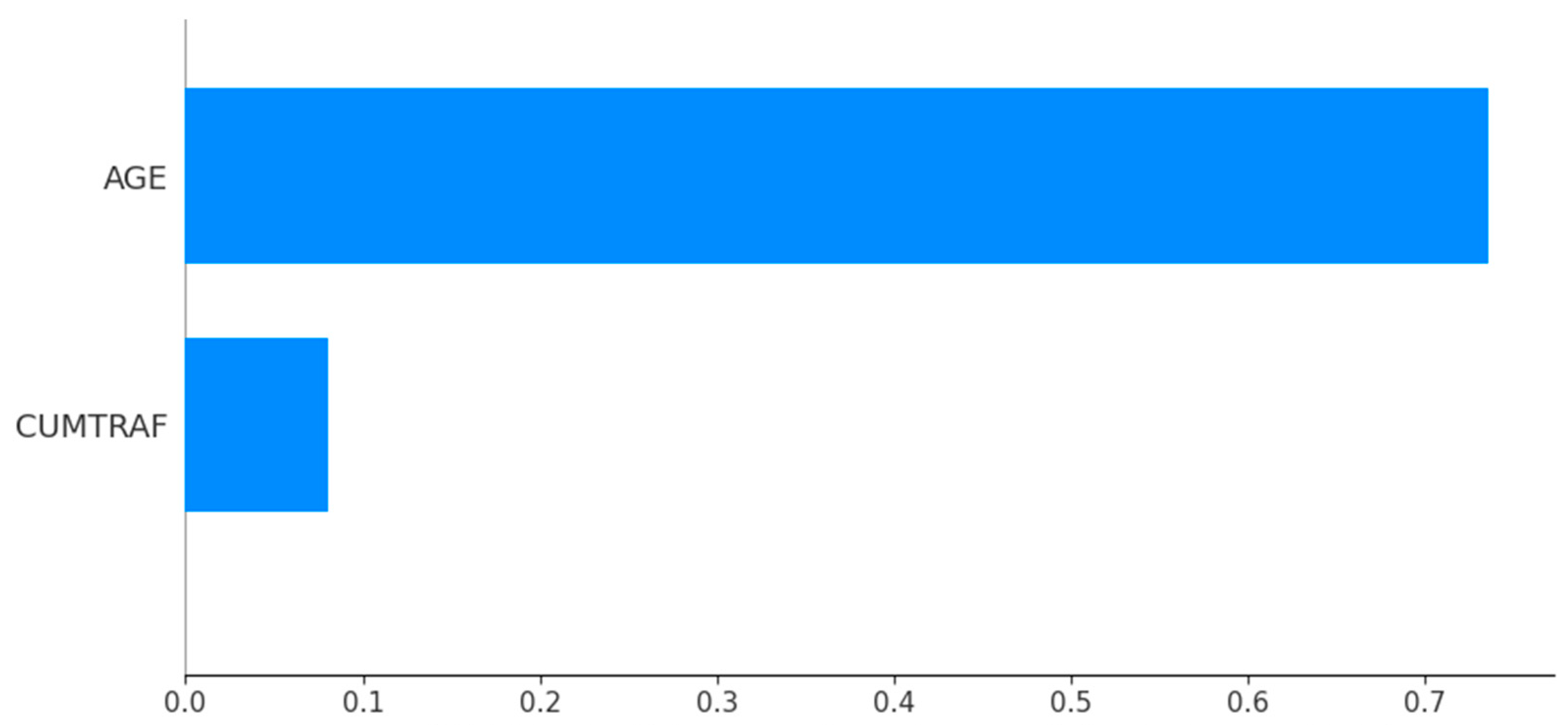
4.3. Machine Learning Global Explanation
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Golova, E.; Evtyukova, S.; Protsuto, M.; Evtyukov, S.; Sorokina, E. Influence of the road surface roughness (according to the International Roughness Index) on road safety. Transp. Res. Procedia 2022, 63, 999–1006. [Google Scholar] [CrossRef]
- Abdelaziz, N.; Abd El-Hakim, R.T.; El-Badawy, S.M.; Afify, H.A. International Roughness Index prediction model for flexible pavements. Int. J. Pavement Eng. 2020, 21, 88–99. [Google Scholar] [CrossRef]
- ASTM International. Standard Test Method for Measuring Road Roughness by Static Level Method; ASTM International: West Conshohocken, PA, USA, 2007. [Google Scholar]
- Perera, M.Y.I.; Pasindu, H.R.; Sandamal, R.M.K. Pavement Management System for Low Volume Roads in Sri Lanka. In Proceedings of the Moratuwa Engineering Research Conference (MERCon), Moratuwa, Sri Lanka, 3–5 July 2019; pp. 250–255. [Google Scholar] [CrossRef]
- Sidess, A.; Ravina, A.; Oged, E. A model for predicting the deterioration of the international roughness index. Int. J. Pavement Eng. 2020, 23, 1393–1403. [Google Scholar] [CrossRef]
- Salas, M.Á.; Pérez-Acebo, H.; Calderón, V.; Gonzalo-Orden, H. Bitumen modified with recycled polyurethane foam for employment in hot mix asphalt. Ing. Investig. 2018, 38, 60–66. [Google Scholar] [CrossRef]
- Wen, T.; Ding, S.; Lang, H.; Lu, J.J.; Yuan, Y.; Peng, Y.; Chen, J.; Wang, A. Automated pavement distress segmentation on asphalt surfaces using a deep learning network. Int. J. Pavement Eng. 2022. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, J.; Li, Q.; Fang, N.; Wang, P.; Ding, L.; Li, S. A hybrid model for prediction in asphalt pavement performance based on support vector machine and grey relation analysis. J. Adv. Transp. 2020, 2020, 7534970. [Google Scholar] [CrossRef]
- Zeiada, W.; Dabous, S.A.; Hamad, K.; Al-Ruzouq, R.; Khalil, M.A. Machine Learning for Pavement Performance Modelling in Warm Climate Regions. Arab. J. Sci. Eng. 2020, 45, 4091–4109. [Google Scholar] [CrossRef]
- Gong, H.; Sun, Y.; Shu, X.; Huang, B. Use of random forests regression for predicting IRI of asphalt pavements. Constr. Build. Mater. 2018, 189, 890–897. [Google Scholar] [CrossRef]
- Mazari, M.; Rodriguez, D.D. Prediction of pavement roughness using a hybrid gene expression programming-neural network technique. J. Traffic Transp. Eng. 2016, 3, 448–455. [Google Scholar] [CrossRef]
- Barros, R. Roughness Modeling for Composite Pavements using Machine Learning. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1203, 032035. [Google Scholar] [CrossRef]
- Sandamal, R.M.K.; Pasindu, H.R. Development of Pavement Roughness Prediction Model for National Highways in Sri Lanka. J. Inst. Eng. 2020, 53, 81–91. [Google Scholar] [CrossRef]
- Sollazzo, G.; Fwa, T.F.; Bosurgi, G. An ANN model to correlate roughness and structural performance in asphalt pavements. Constr. Build. Mater. 2017, 134, 684–693. [Google Scholar] [CrossRef]
- Chandra, S.; Sekhar, C.R.; Bharti, A.K.; Kangadurai, B. Relationship between Pavement Roughness and Distress Parameters for Indian Highways. J. Transp. Eng. 2013, 139, 467–475. [Google Scholar] [CrossRef]
- García de Soto, B.; Bumbacher, A.; Deublein, M.; Adey, B.T. Predicting road traffic accidents using artificial neural network models. Infrastruct. Asset Manag. 2018, 5, 132–144. [Google Scholar] [CrossRef]
- Sayers, M.W.; Gillespie, T.D.; Queiroz, C.A.V. The International Road Roughness Experiment Establishing Correlation and a Calibration Standard for Measurements; Technical Paper Number 45; The World Bank: Washington, DC, USA, 1986. [Google Scholar]
- Sayers, M.W. On the Calculation of International Roughness Index from Longitudinal Road Profile; Transportation Research Board: Washington, DC, USA, 1995; Volume 1051, pp. 1–12. [Google Scholar]
- Zang, K.; Shen, J.; Huang, H.; Wan, M.; Shi, J. Assessing and Mapping of Road Surface Roughness based on GPS and Accelerometer Sensors on Bicycle-Mounted Smartphones. Sensors 2018, 18, 914. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Hou, J.; Duan, Z.; Jankowski, Ł.; Hu, X. Road Roughness Estimation Based on the Vehicle Frequency Response Function. Actuators 2021, 10, 89. [Google Scholar] [CrossRef]
- Loprencipe, G.; Zoccali, P.; Cantisani, G. Effects of Vehicular Speed on the Assessment of Pavement Road Roughness. Appl. Sci. 2019, 9, 1783. [Google Scholar] [CrossRef]
- Pérez-Acebo, H.; Linares-Unamunzaga, A.; Rojí, E.; Gonzalo-Orden, H. IRI performance models for flexible pavements in two-lane roads until first maintenance and/or rehabilitation work. Coatings 2020, 10, 97. [Google Scholar] [CrossRef]
- Abaza, K.A. Empirical-Markovian approach for estimating the flexible pavement structural capacity: Caltrans method as a case study. Int. J. Transp. Sci. Technol. 2021, 10, 156–166. [Google Scholar] [CrossRef]
- Ali, A.A.; Heneash, U.; Hussein, A.; Khan, S. Application of Artificial neural network technique for prediction of pavement roughness as a performance indicator. J. King Saud Univ. Eng. Sci. 2023; in press. [Google Scholar] [CrossRef]
- Sigdel, T.; Pradhananga, R. Development of IRI Prediction Model for National Highways of Nepal. In Proceedings of the 10th IOE Graduate Conference, Tribhuvan University, Nepal, October 2021; Available online: https://conference.ioe.edu.np/ioegc10/papers/ioegc-10-046-10065.pdf (accessed on 17 May 2023).
- Qian, J.; Jin, C.; Zhang, J.; Ling, J.; Sun, C. International Roughness Index Prediction Model for Thin Hot Mix Asphalt Overlay Treatment of Flexible Pavements. Transp. Res. Rec. 2018, 8, 87–99. [Google Scholar] [CrossRef]
- Soncim, S.P.; de Oliveira, I.C.S.; Santos, F.B.; Oliveira, C.A.D.S. Development of probabilistic models for predicting roughness in asphalt pavement. Road Mater. Pavement Des. 2018, 19, 1448–1457. [Google Scholar] [CrossRef]
- Albuquerque, F.S.; Núñez, W.C. Development of Roughness Prediction Models for Low-Volume Road Networks in Northeast Brazil. Transp. Res. Rec. 2011, 2205, 198–205. [Google Scholar] [CrossRef]
- Pérez-Acebo, H.; Gonzalo-Orden, H.; Findley, D.J.; Rojí, E. Modeling the international roughness index performance on semi-rigid pavements in single carriageway roads. Constr. Build Mater. 2021, 272, 121665. [Google Scholar] [CrossRef]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; The MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Li, W.; Huyan, J.; Xiao, L.; Tighe, S.; Pei, L. International roughness index prediction based on multigranularity fuzzy time series and particle swarm optimization. Expert Syst. 2019, 2, 100006. [Google Scholar] [CrossRef]
- Kaloop, M.R.; El-Badawy, S.M.; Ahn, J.; Sim, H.B.; Hu, J.W.; Abd El-Hakim, R.T. A hybrid wavelet-optimally-pruned extreme learning machine model for the estimation of international roughness index of rigid pavements. Int. J. Pavement Eng. 2020, 23, 3346–3356. [Google Scholar] [CrossRef]
- Breiman, L. Statistical Modeling: The Two Cultures (with comments and a rejoinder by the author). Statist. Sci. 2021, 16, 199–231. [Google Scholar] [CrossRef]
- Luo, Z.; Wang, H.; Li, S. Prediction of International Roughness Index Based on Stacking Fusion Model. Sustainability 2022, 14, 6949. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, M.; Sabri, M.M.S.; Huang, J.A. Comparative Study of AI-Based International Roughness Index (IRI) Prediction Models for Jointed Plain Concrete Pavement (JPCP). Materials 2022, 15, 5605. [Google Scholar] [CrossRef]
- Guo, R.; Fu, D.; Sollazzo, G. An ensemble learning model for asphalt pavement performance prediction based on gradient. Int. J. Pavement Eng. 2021, 23, 3633–3646. [Google Scholar] [CrossRef]
- Damirchilo, F.; Hosseini, A.; Parast, M.; Fini, E. Machine Learning Approach to Predict International Roughness Index using Long-Term Pavement Performance Data. J. Transp. Eng. Part B Pavements. 2021, 147, 4. [Google Scholar] [CrossRef]
- Bajic, M.; Pour, S.M.; Skar, A.; Pettinari, M.; Levenberg, E.; Alstrom, T.S. Road Roughness Estimation Using Machine Learning. arXiv 2021. [Google Scholar] [CrossRef]
- Marcelino, P.; Antunes, M.D.L.; Fortunato, E.; Gomes, M.C. Machine learning approach for pavement performance prediction. Int. J. Pavement Eng. 2019, 22, 341–354. [Google Scholar] [CrossRef]
- Ostadi, N.M.; Stoffels, S.M. Framework for Development and Comprehensive Comparison of Empirical Pavement Performance Models. J. Transp. Eng. 2015, 141, 8. [Google Scholar] [CrossRef]
- Ziari, H.; Sobhani, J.; Ayoubinejad, J.; Hartmann, T. Prediction of IRI in short and long terms for flexible pavements: ANN and GMDH methods. Int. J. Pavement Eng. 2016, 17, 776–788. [Google Scholar] [CrossRef]
- Maga Engineering, “MAGA”, 2023. Available online: https://www.maga.lk/portfolio/completed-projects/highways-roads/# (accessed on 17 May 2023).
- International Construction Consortium, 2022. Available online: https://icc-construct.com/completed-road-bridges/ (accessed on 17 May 2023).
- Ziari, H.; Sobhani, J.; Ayoubinejad, J.; Hartmann, T. Analysing the accuracy of pavement performance models in the short and long terms: GMDH and ANFIS methods. Road Mater. Pavement Des. 2015, 17, 619–637. [Google Scholar] [CrossRef]
- Ziari, H.; Maghrebi, M.; Ayoubinejad, J.; Waller, S.T. Prediction of Pavement Performance: Application of Support Vector Regression with Different Kernels. Transp. Res. Rec. 2016, 2589, 135–145. [Google Scholar] [CrossRef]
- Choi, S.; Do, M. Development of the Road Pavement Deterioration Model Based on the Deep Learning Method. Electronics 2020, 9, 3. [Google Scholar] [CrossRef]
- Scikit-Learn, Machine Learning in Python, 2023. Available online: https://scikit-learn.org/stable/ (accessed on 10 April 2023).
- Blessy, A.; Kumar, A.; Prabagaran, A.; Md, A.Q.; Alharbi, A.I.; Almusharraf, A.; Khan, S.B. Sustainable Irrigation Requirement Prediction Using Internet of Things and Transfer Learning. Sustainability 2023, 15, 8260. [Google Scholar] [CrossRef]
- Ramón, A.; Torres, A.M.; Milara, J.; Cascón, J.; Blasco, P.; Mateo, J. eXtreme Gradient Boosting-based method to classify patients with COVID-19. J. Investig. Med. 2022, 70, 1472–1480. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. arXiv 2016, arXiv:1603.02754. [Google Scholar]
- Lussier, P.; Deslauriers-Varin, N.; Collin-Santerre, J.; Bélanger, R. Using decision tree algorithms to screen individuals at risk of entry into sexual recidivism. J. Crim. Justice 2019, 63, 12–24. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, Z.; Yeom, D.S. Decision Tree Algorithm-Based Model and Computer Simulation for Evaluating the Effectiveness of Physical Education in Universities. Complexity 2020, 2020, 8868793. [Google Scholar] [CrossRef]
- Matzavela, V.; Alepis, E. Decision tree learning through a Predictive Model for Student Academic Performance in Intelligent M-Learning environments. Comput. Educ. AI 2021, 2, 100035. [Google Scholar] [CrossRef]
- Zhang, S.; Li, X.; Zong, M.; Zhu, X.; Cheng, D. Learning k for kNN Classification. ACM Trans. Intell. Syst. Technol. 2017, 8, 1–19. [Google Scholar] [CrossRef]
- Saha, D.; Basso, B.; Robertson, G.P. Machine learning improves predictions of agricultural nitrous oxide (N2O) emissions from intensively managed cropping systems. Environ. Lett. Res. 2021, 16, 2. [Google Scholar] [CrossRef]
- Fong, R.C.; Vedaldi, A. Interpretable Explanations of Black Boxes by Meaningful Perturbation. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 3449–3457. [Google Scholar] [CrossRef]
- Liang, Y.; Li, S.; Yan, C.Y.; Li, M.; Jiang, C. Explaining the black-box model: A survey of local interpretation methods for deep neural networks. Neurocomputing 2021, 419, 168–182. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Why Should I Trust You? Explaining the Predictions of Any Classifier. In Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Demonstrations, San Diego, CA, USA, 12–17 June 2016. [Google Scholar] [CrossRef]
- Petsiuk, V.; Das, A.; Saenko, K. RISE: Randomized Input Sampling for Explanation of Black-box Models. arXiv 2018, arXiv:1806.07421. [Google Scholar] [CrossRef]
- Lundburg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4768–4777. [Google Scholar] [CrossRef]
- Kumar, I.E.; Venkatasubramanian, S.; Scheidegger, C.; Friedler, S.A. Problems with Shapley-value-based explanations as feature importance measures. In Proceedings of the 37th International Conference on Machine Learning, Vienna, Austria, 13–18 July 2020; Available online: https://arxiv.org/pdf/2002.11097.pdf (accessed on 10 May 2023).

| Reference | Factors Used | IRI Prediction Model |
|---|---|---|
| Pérez-Acebo et al. [22] | Age, Total thickness of Bituminous layers (TotBit), Accumulated Total number of Heavy Vehicles (TotH.Veh) | IRI = 5.353 + 0.68 × e (0.026.R.Age) − 1.411 LnTotBit + 7.941 × 10−8 TotH.Veh2 |
| Ali et al. [24] | Age, Distress (X1,…, X7) | IRI = 0.365Age + a1 × 1 + b1 × 2 + … + a7 × 7 |
| Sigdel and Pradhananga [25] | Commercial Vehicles (CV), Rainfall (RF), Accumulated low-temperature days (TDl), Accumulated high-temperature days (TDh), Initial IRI (IRI0) | IRI = β0 + β1IRI0 + β2CV + β3RF + β4TDl + β5TDh |
| Qian et al. [26] | Equivalent Single Axle Loads (ESAL), Deflection, Overlay Thickness, Climate | Several models developed based on different level of each factor |
| Soncim et al. [27] | Traffic Density, Climate | Probability Matrix: Pij(t) = ∑k = 0, mPik(v). Pjk(t-v) |
| Albuquerque and Núñez [28] | Modified Structural Number (S), ESAL (N), Climate (C) | IRI(HMA) = −173.4 + e (5.177 + 0.001C − 0.002S + 0.005N) |
| Pérez-Acebo et al. [29] | Age (R.Age), Accumulated Vehicles (TotVeh), Total thickness of Bituminous layers (TotBit), Accumulated Total number of Heavy Vehicles (TotH.Veh), Coefficient that considers the combinations of materials (BASE), Thickness of the treated base layer (Bthick) | IRI = 2.223 + 0.221LnR.Age − 1.162 10−6 TotVeh TotBit + 1.87 10−4 TotH.Veh + BASE Bthick |
| Reference | Data Source | Predictor Variables | Machine Learning Model | R2 (Testing) | ||
|---|---|---|---|---|---|---|
| Age | Traffic | Other | ||||
| Gong et al. [10] | LTPP | √ | √ | √ | RF | 0.95 |
| Ali et al. [30] | - | √ | - | √ | RF | 0.99 |
| SVM | 0.97 | |||||
| Luo et al. [34] | LTPP | - | √ | √ | XGBoost | 0.93 |
| SVM | 0.16 | |||||
| Wang et al. [35] | LTPP | √ | - | √ | RF | 0.84 |
| DT | 0.53 | |||||
| SVM | 0.41 | |||||
| Guo et al. [36] | LTPP | √ | √ | √ | RF | 0.88 |
| XGBoost | 0.90 | |||||
| Damirchilo et al. [37] | LTPP | √ | √ | √ | RF | 0.66 |
| SVM | 0.44 | |||||
| XGBoost | 0.70 | |||||
| Bajic et al. [38] | Denmark | √ | - | - | RF | 0.58 |
| KNN | 0.59 | |||||
| SVM | 0.63 | |||||
| Marcelino et al. [39] | LTPP | - | √ | √ | RF | 0.93 |
| Kargah-Ostadi and Stoffels [40] | LTPP | √ | √ | - | SVM | 0.90 |
| Ziari et al. [41] | LTPP | √ | √ | √ | SVM | 0.83 |
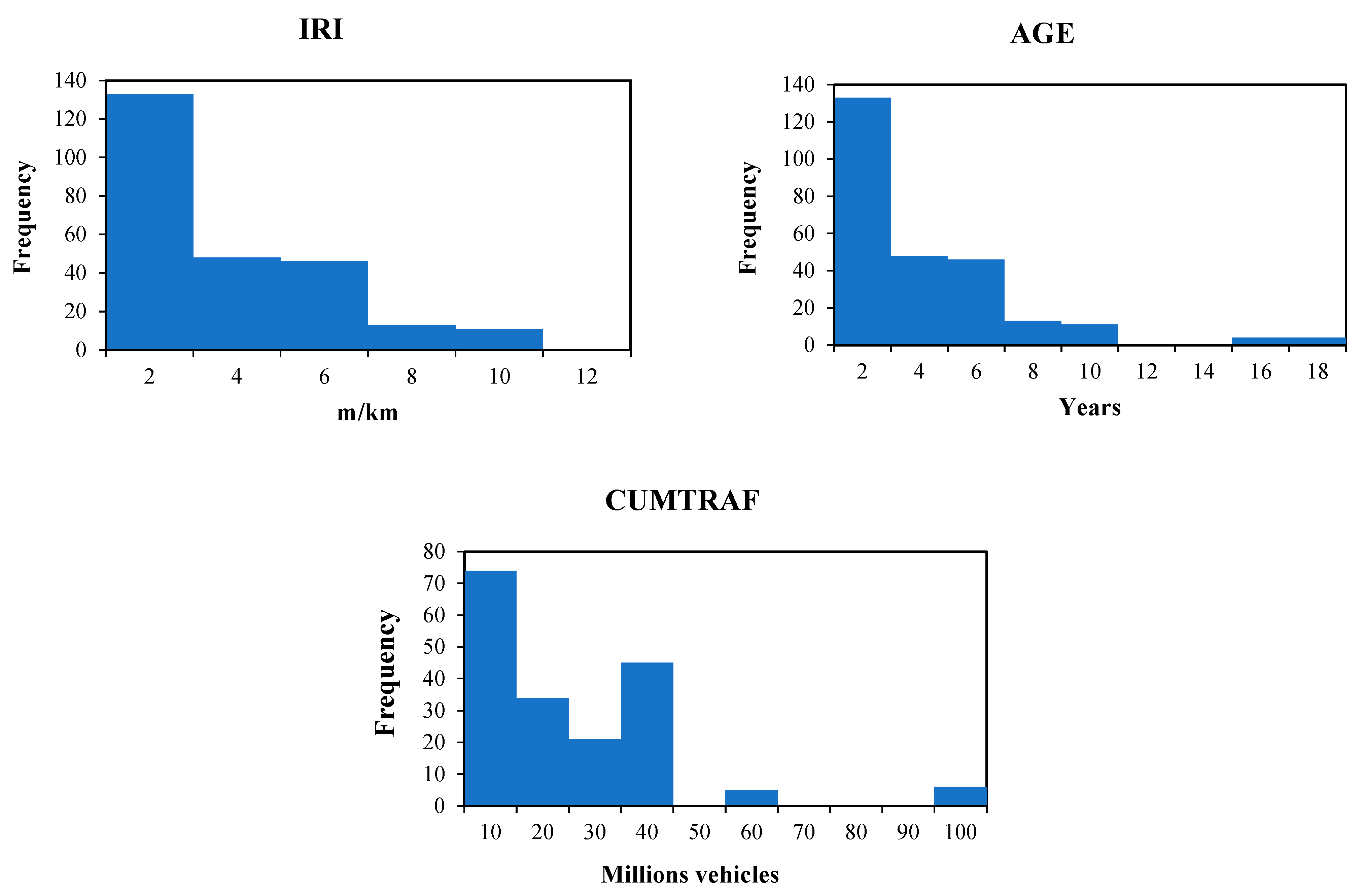
| Variable | Description | Mean | Standard Deviation | Minimum | Maximum |
|---|---|---|---|---|---|
| IRI | Average IRI value in a road per direction (m/km) | 2.59 | 1.37 | 1.51 | 9.09 |
| AGE | Time since the latest rehabilitation/reconstruction activity (years) e.g., 0.5 refers to half of a year (six months). | 2.75 | 3.37 | 0.5 | 16.5 |
| CUMTRAF | Cumulative number of vehicles that travelled on the road segment since latest rehabilitation/reconstruction activity (number of vehicles in millions) | 20.04 | 18.89 | 1.28 | 97.95 |
| Independent Variable | Correlation with IRI | Significance (p-Value) |
|---|---|---|
| AGE | 0.83 | <0.001 |
| CUMTRAF | 0.58 | <0.001 |
| Independent Variable | Type of Equation | Model Accuracy | Parameter Estimates | |||||
|---|---|---|---|---|---|---|---|---|
| R2 | F Value | Significance | Intercept | Coefficient b1 | Coefficient b2 | Coefficient b3 | ||
| AGE | Cubic | 0.76 | 193.92 | <0.001 | 2.525 | −0.506 | 0.147 | −0.006 |
| AGE | Quadratic | 0.69 | 205.17 | <0.001 | 1.856 | 0.206 | 0.009 | - |
| AGE | Linear | 0.67 | 392.78 | <0.001 | 1.668 | 0.336 | - | - |
| AGE | Exponential | 0.63 | 309.89 | <0.001 | 1.890 | 0.085 | - | - |
| AGE | Logistic | 0.63 | 309.89 | <0.001 | 0.529 | 0.919 | - | - |
| AGE | Logarithm | 0.42 | 134.46 | <0.001 | 2.038 | 1.001 | - | - |
| CUMTRAF | Cubic | 0.44 | 47.34 | <0.001 | 1.662 | 0.103 | −0.003 | <0.001 |
| CUMTRAF | Quadratic | 0.41 | 62.37 | <0.001 | 2.234 | −0.002 | 0.001 | - |
| CUMTRAF | Linear | 0.34 | 92.75 | <0.001 | 1.752 | 0.042 | - | - |
| CUMTRAF | Exponential | 0.29 | 74.38 | <0.001 | 1.945 | 0.010 | - | - |
| CUMTRAF | Logistic | 0.29 | 74.38 | <0.001 | 0.514 | 0.990 | - | - |
| CUMTRAF | Logarithm | 0.16 | 35.53 | <0.001 | 1.085 | 0.582 | - | - |
| Parameter | Coefficient | Standard Error | p-Value | 95% CI |
|---|---|---|---|---|
| Intercept | 1.569 | 0.083 | <0.001 | [1.410, 1.733] |
| Pavement age | 0.305 | 0.021 | <0.001 | [0.263, 0.346] |
| Cumulative traffic | 0.010 | 0.003 | 0.013 | [0.002, 0.017] |
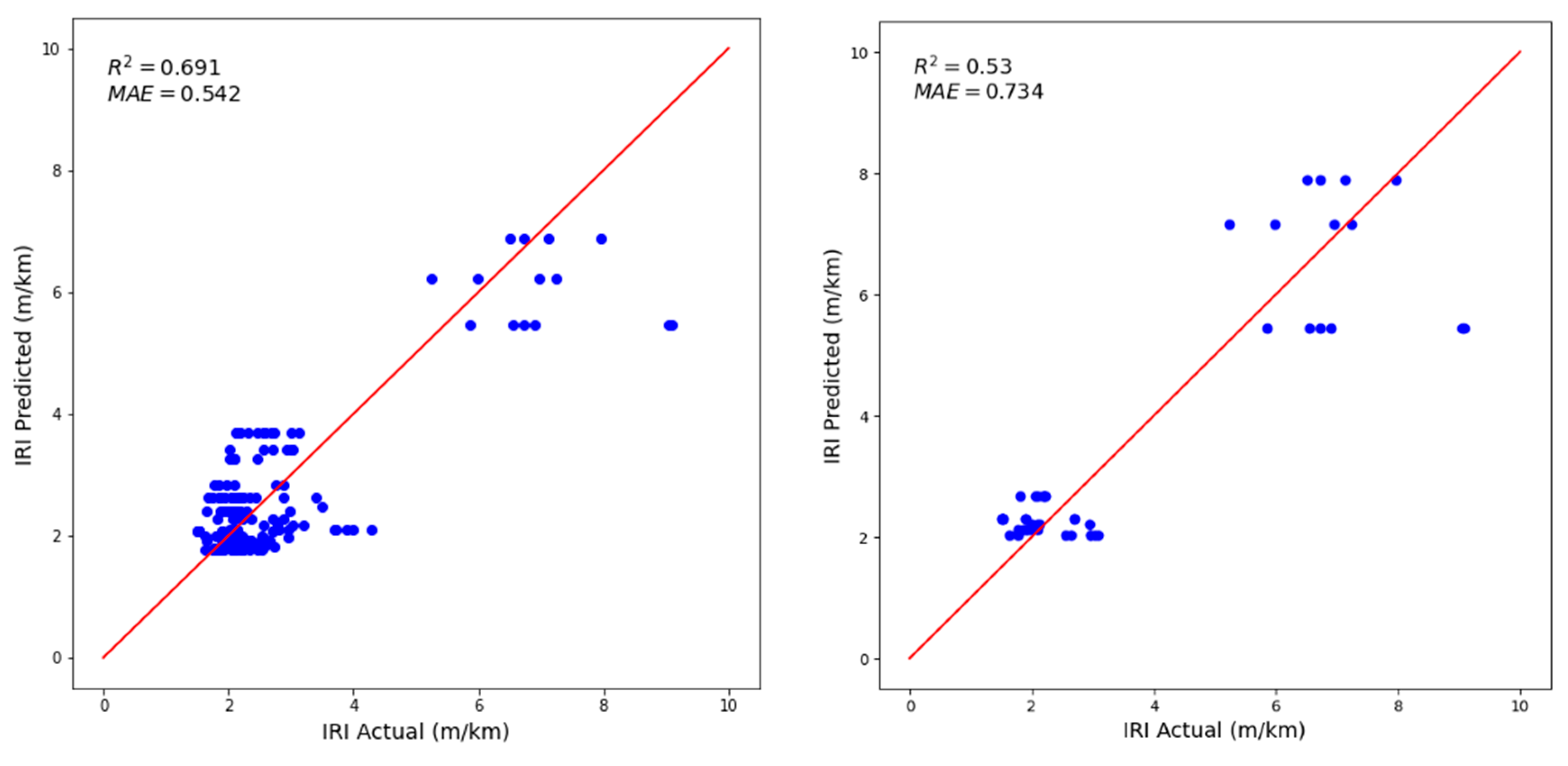
| Proposed Model | R2 | Standard Error | F Value | Comments |
|---|---|---|---|---|
| IRI = Intercept + AGE + CUMTRAF2 | 0.75 | 0.69 | 271.83 | All variables significant (p < 0.001) |
| IRI = Intercept + AGE + CUMTRAF + CUMTRAF2 | 0.83 | 0.57 | 294.80 | All variables significant (p < 0.001) |
| IRI = Intercept + AGE + AGE2 + CUMTRAF | 0.76 | 0.69 | 186.64 | All variables significant (p < 0.006) |
| IRI = Intercept + AGE2 + CUMTRAF2 | 0.81 | 0.60 | 400.34 | All variables significant (p < 0.001) |
| IRI = Intercept + AGE + AGE2 + CUMTRAF2 | 0.82 | 0.58 | 284.68 | All variables significant (p < 0.002) |
| IRI = Intercept + AGE + AGE2 + CUMTRAF + CUMTRAF2 | 0.84 | 0.55 | 243.19 | Low significance of AGE (p = 0.379) |
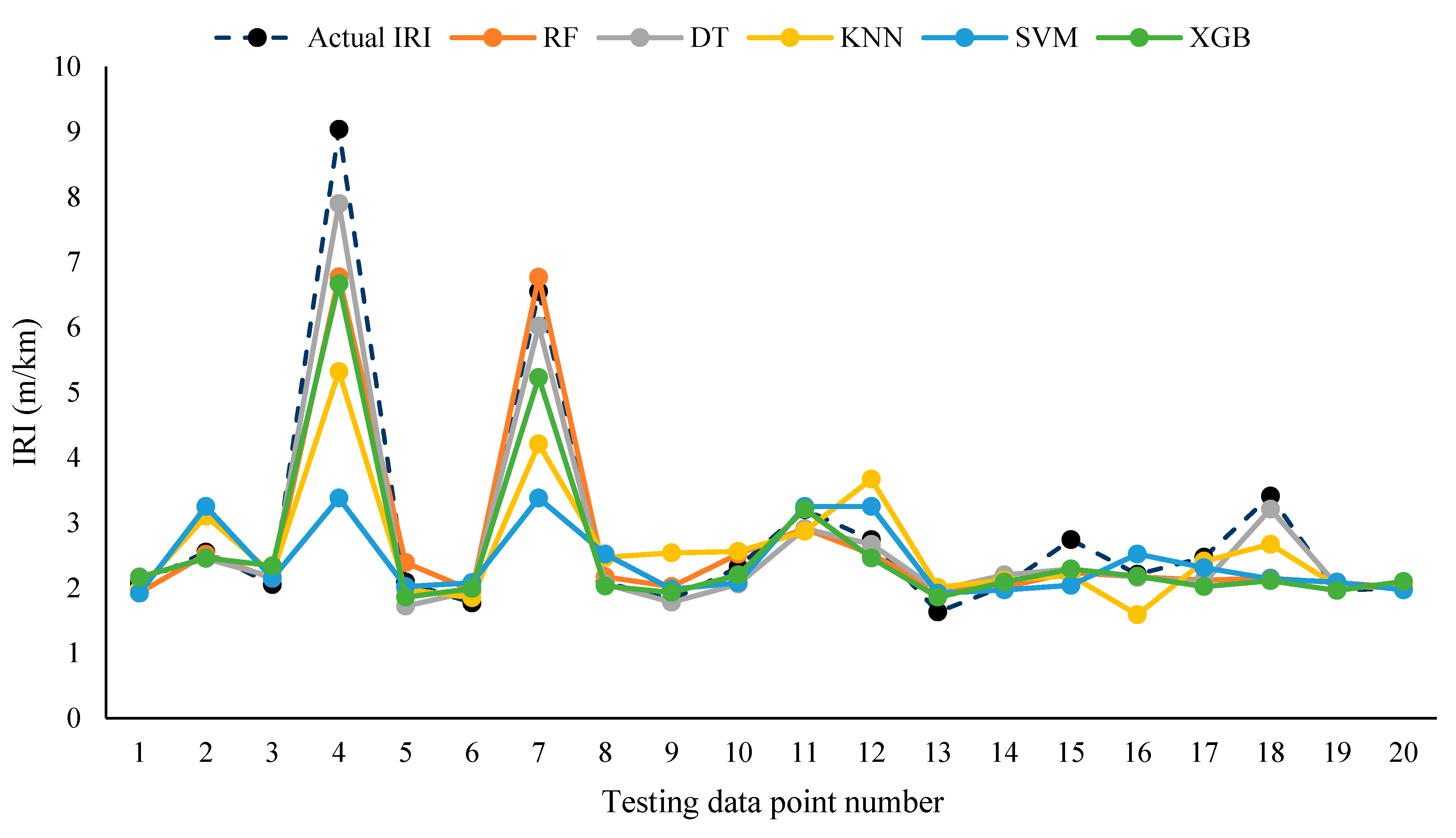
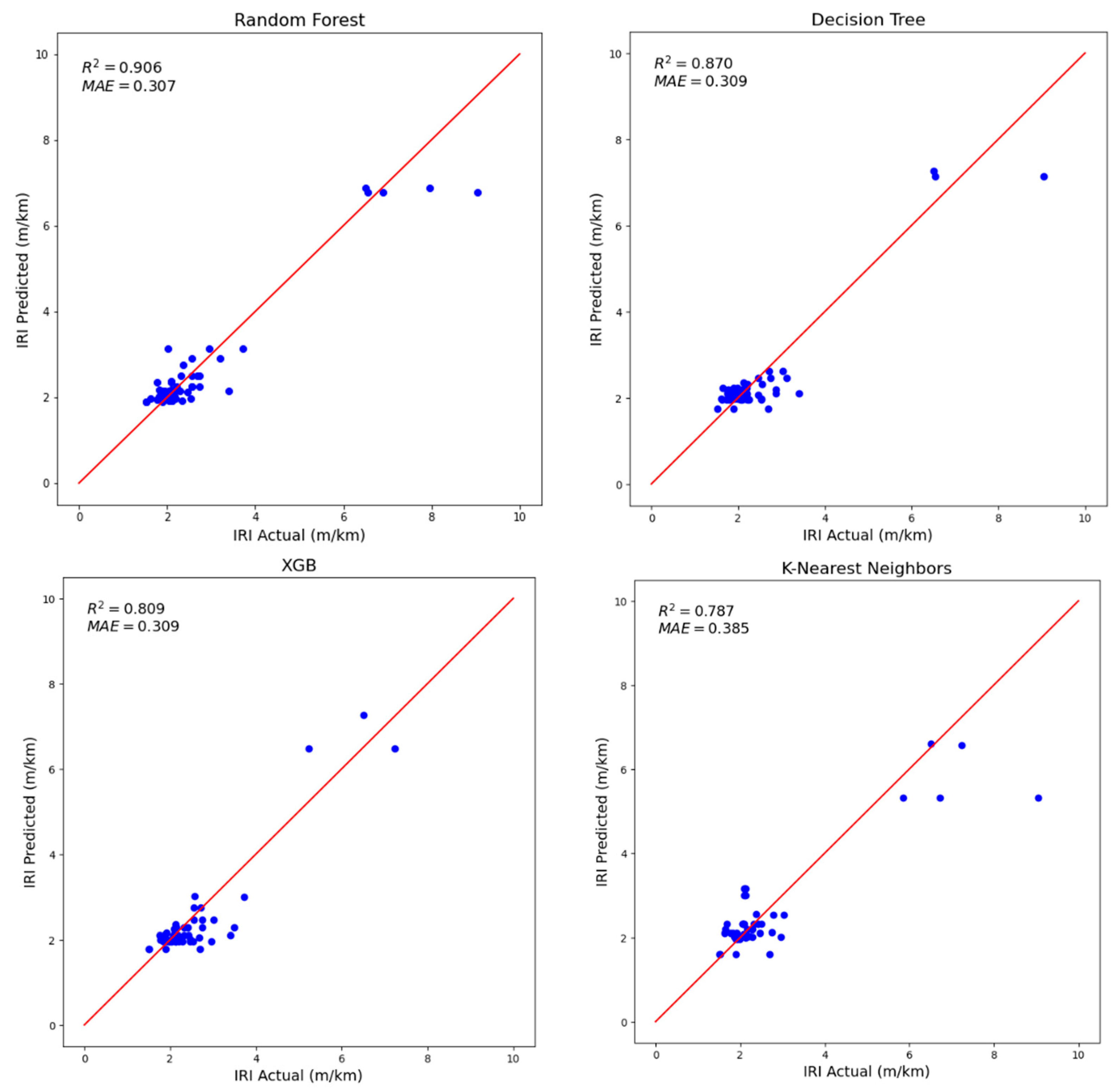
| Machine Learning Model | R2 | MAE |
|---|---|---|
| Random Forest (RF) | 0.906 | 0.310 |
| Decision Tree (DT) | 0.870 | 0.309 |
| Extreme Gradient Boosting (XGB) | 0.809 | 0.309 |
| K-Nearest Neighbor (KNN) | 0.787 | 0.385 |
| Support Vector Machine (SVM) | 0.503 | 0.579 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sandamal, K.; Shashiprabha, S.; Muttil, N.; Rathnayake, U. Pavement Roughness Prediction Using Explainable and Supervised Machine Learning Technique for Long-Term Performance. Sustainability 2023, 15, 9617. https://doi.org/10.3390/su15129617
Sandamal K, Shashiprabha S, Muttil N, Rathnayake U. Pavement Roughness Prediction Using Explainable and Supervised Machine Learning Technique for Long-Term Performance. Sustainability. 2023; 15(12):9617. https://doi.org/10.3390/su15129617
Chicago/Turabian StyleSandamal, Kelum, Sachini Shashiprabha, Nitin Muttil, and Upaka Rathnayake. 2023. "Pavement Roughness Prediction Using Explainable and Supervised Machine Learning Technique for Long-Term Performance" Sustainability 15, no. 12: 9617. https://doi.org/10.3390/su15129617
APA StyleSandamal, K., Shashiprabha, S., Muttil, N., & Rathnayake, U. (2023). Pavement Roughness Prediction Using Explainable and Supervised Machine Learning Technique for Long-Term Performance. Sustainability, 15(12), 9617. https://doi.org/10.3390/su15129617









