TMR-Array-Based Pipeline Location Method and Its Realization
Abstract
:1. Introduction
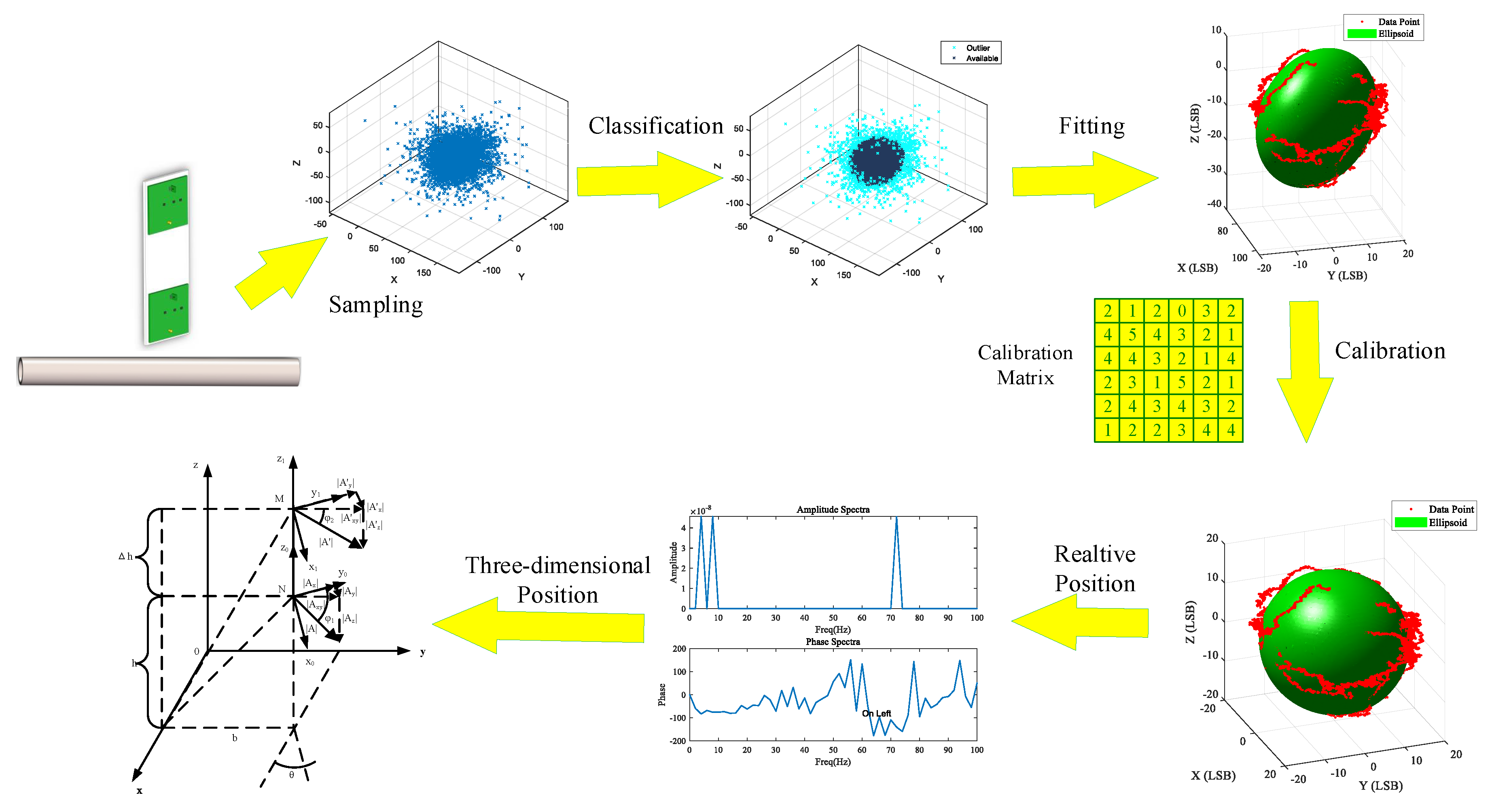
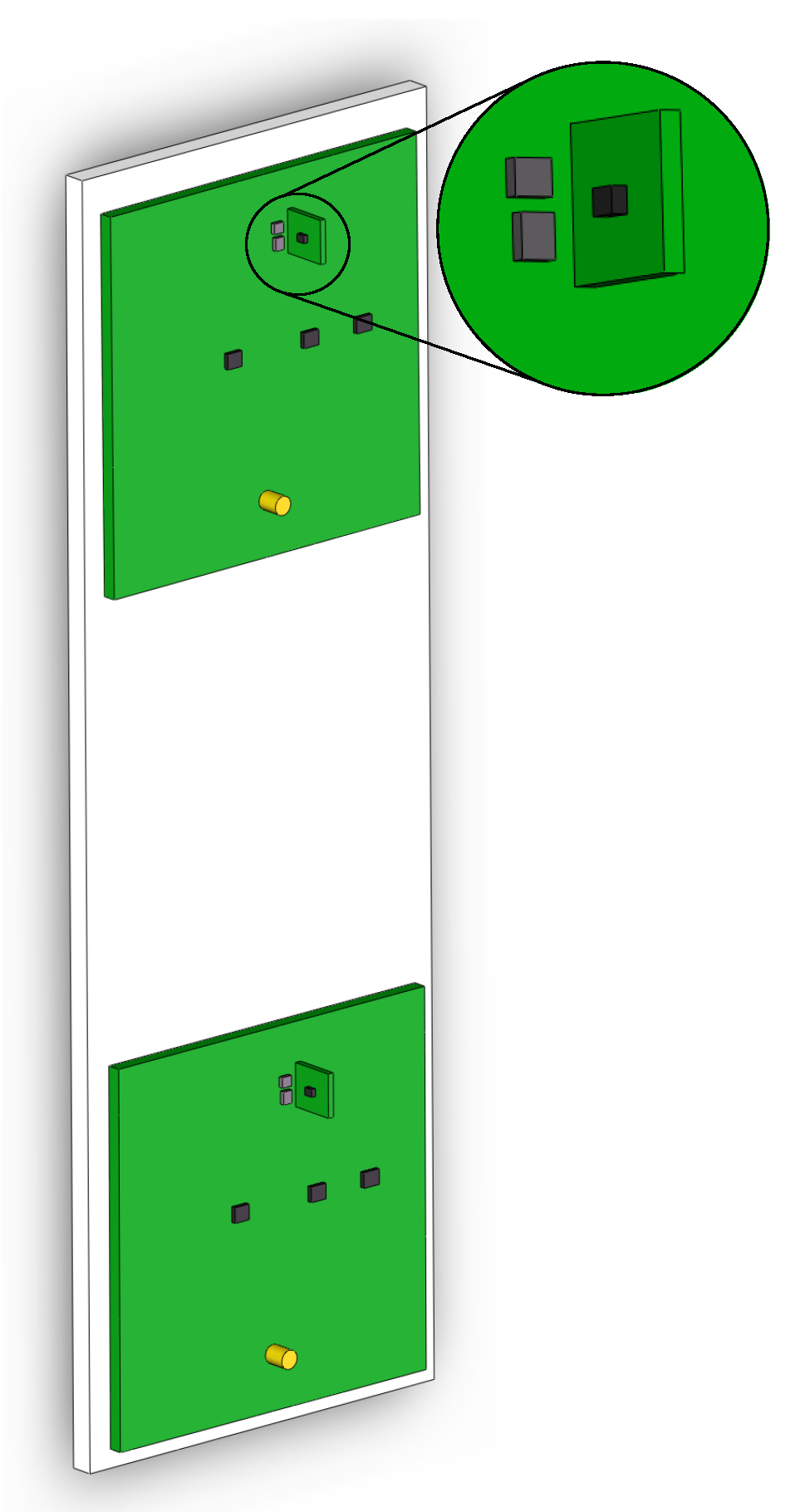
- The detection probe is redesigned to locate pipelines accurately. By adopting TMR sensors as linear magnetic sensors, magnetic fields surrounding pipelines can be detected accurately, and the difficulties of traditional PCM receiving equipment are conquered.
- An improved ellipsoid fitting method is proposed to calibrate the TMR array. The Gaussian mixture model (GMM) binary classification method is adopted to eliminate the invalid data collected by the TMR array and generated by the ADC jitter. The ellipsoid fitting method is adopted to calibrate the TMR array and acquire data without invalidations. It improves the calibration effect, eliminates non-orthogonal and sensitivity errors, and improves accuracy when detecting magnetic induction intensity.
- A relative pipeline position location method is proposed. Based on the relationships of the lag times of different frequency signals generated around pipelines, this method is adopted to locate the detection probe’s left or right side relative to the pipeline. Compared with the PCM, which locates the pipeline by the amplitude of signals from different detection coils, our method improves the reliability of position detection.
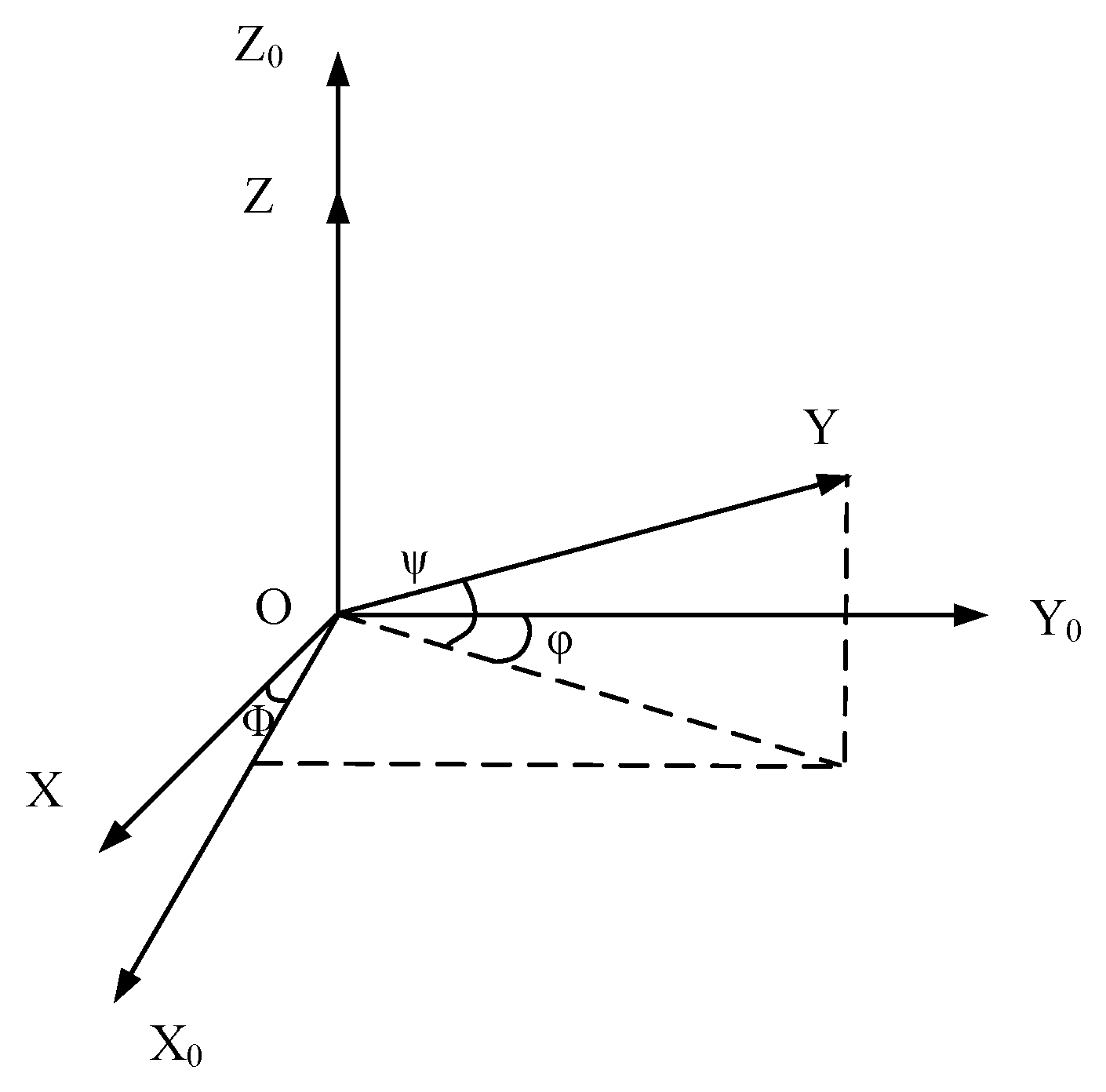
- A three-dimensional pipeline location method is proposed. Based on the relationships of the amplitudes of the three-dimensional components of the magnetic induction intensity in different directions and positions around the pipeline, this method is proposed to calculate the three-dimensional position of pipelines, including the horizontal angle, vertical distance, and horizontal distance between the sensor and the pipeline, respectively. Compared with the PCM, which can only locate the rough direction of the pipeline, our method improves the accuracy and efficiency of the location process.
- A TMR array calibration experiment and three-dimensional location experiment are conducted to evaluate the proposed methods. The experimental results illustrate that the three-dimensional pipeline location method adopting the redesigned detection probe can locate the pipeline in three dimensions with satisfactory linearity and a low average error.
2. The Principle of PCM
3. Materials and Methods
- The error sources of the TMR array are analyzed, the calibration model of the sensors is established, and the accurate measurement of the magnetic induction intensity is realized.
- A relative pipeline position location method is proposed to detect whether the pipeline is positioned left or right relative to the detection probe.
- A three-dimensional pipeline location method is proposed to ocate the three-dimensional position of pipelines.
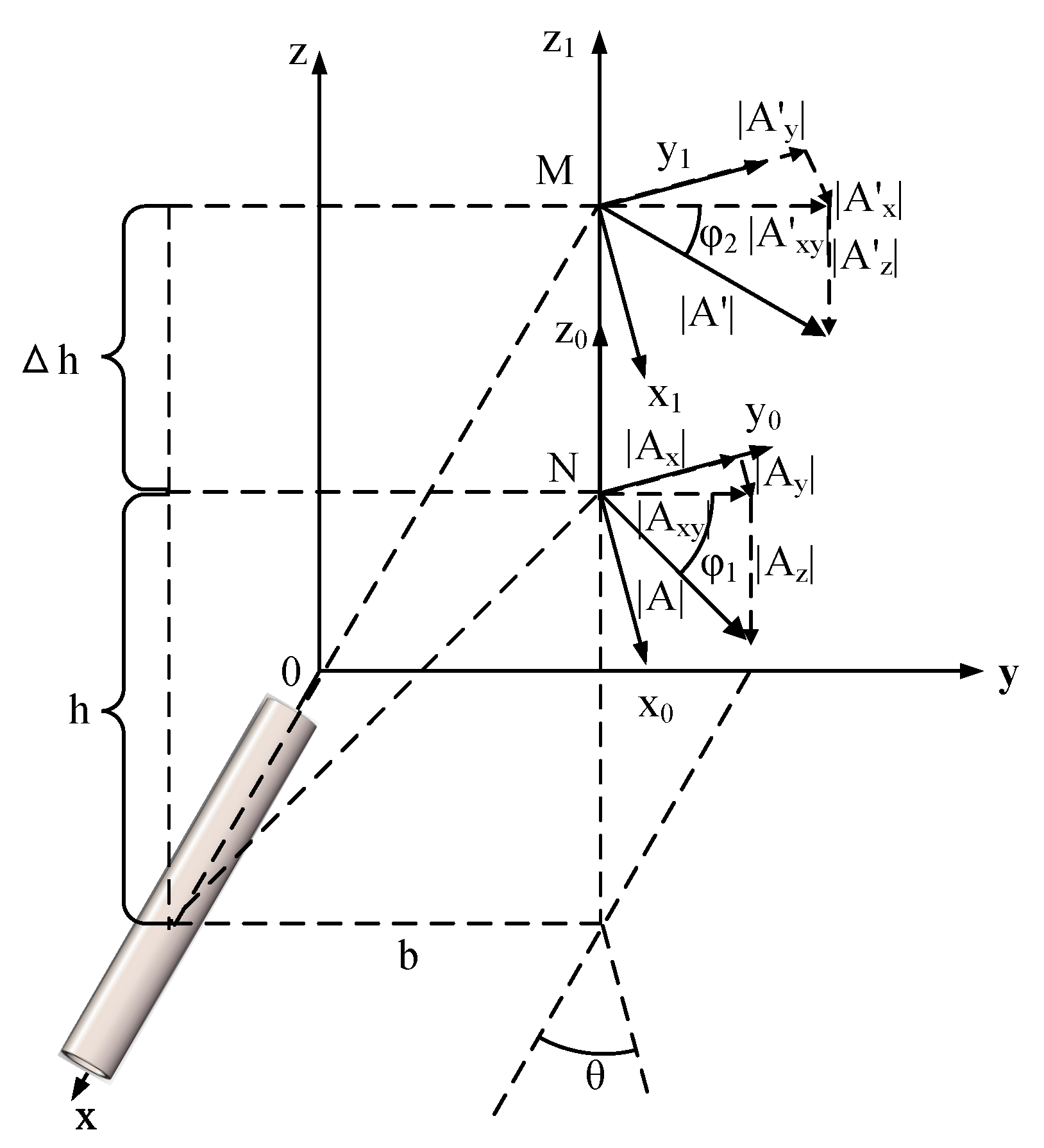
3.1. Calibration of TMR Array
3.2. Pipeline Location and Calculation Model
3.2.1. Redesigned Detection Probe
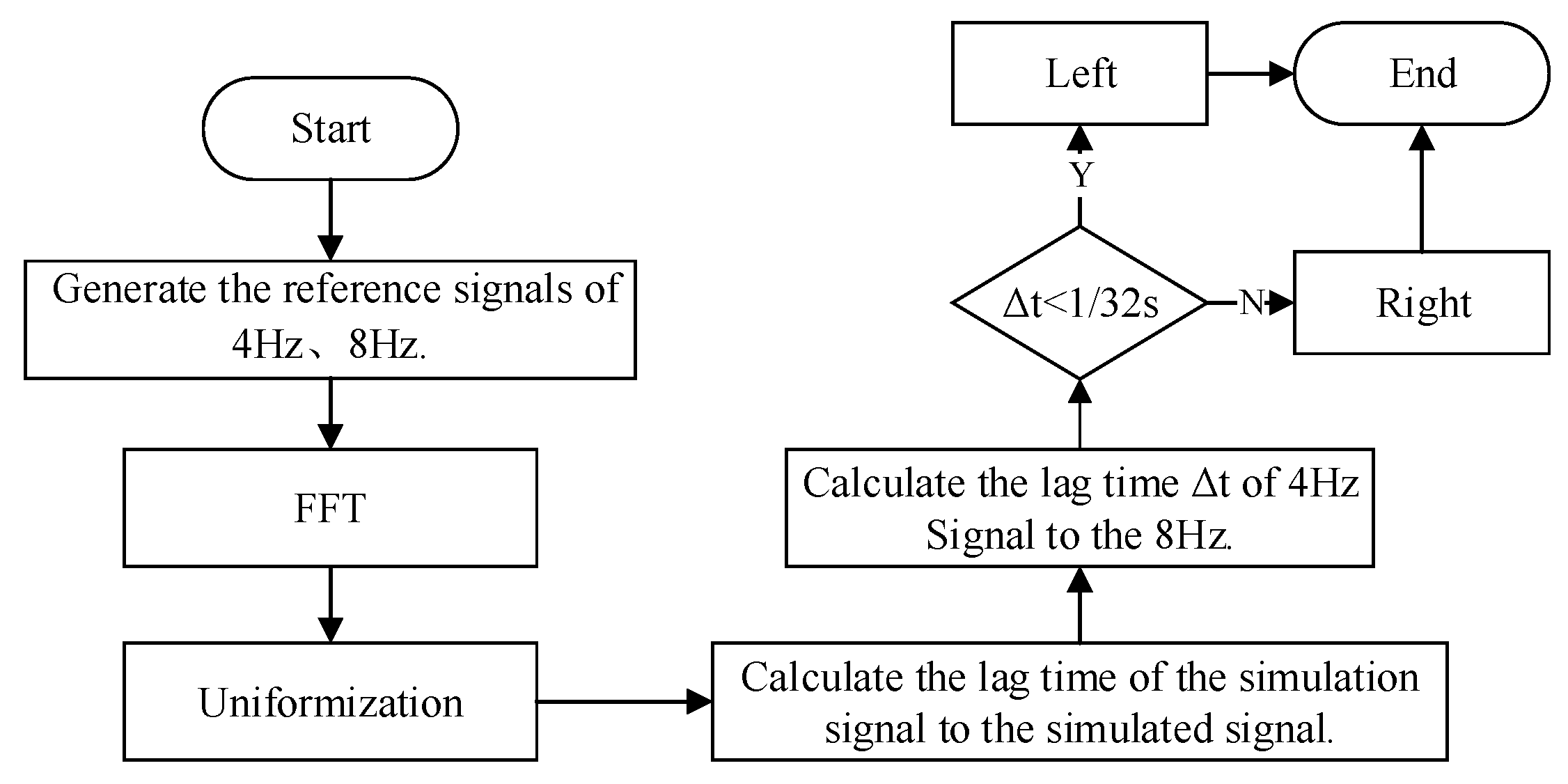
3.2.2. Relative Pipeline Position Location Method
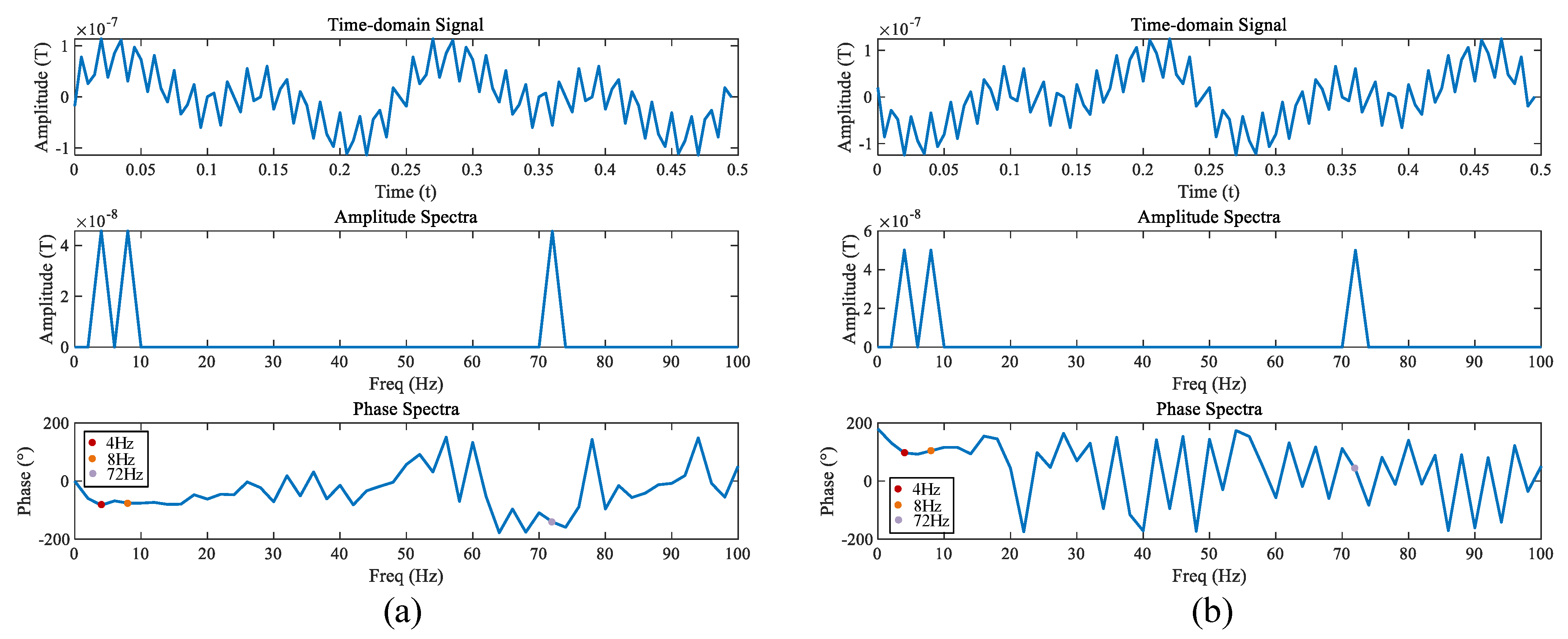
- Transform the signal by FFT and extract the phase and amplitude information. The amplitudes and and phase angles and are obtained for 4 Hz and 8 Hz signals, respectively, along the Y-axis.
- Supposing that data are obtained on the left side of the pipeline, the lag time of the signal’s phase at the detected location relative to the probe at the emitted position can be represented by Equation (9),
- The lag time of the signal’s phase at the detected location relative to the probe at the emitted position can be represented by Equation (10),
- The time difference between and is expressed in Equation (11),
- The lag time of the signal’s phase at the detected location relative to the probe at the emitted position can be represented by Equation (14),
- Since the phases of the 4 Hz and 8 Hz are the same at the position of signal emission, the current lag times of the 4 Hz and 8 Hz signals are the same for transmissions over identical distances. This can be expressed as , as shown in Equation (15),
- The lag times of the 4 Hz and 8 Hz signal compared to the reference signal are the same, as shown in Equation (16).
- The position of the pipeline relative to the probe can be located. The threshold is assigned. When , the probe is on the left side of the pipeline. Otherwise, the probe is on the right side of the pipeline.
3.2.3. Three-Dimensional Pipeline Location Method
4. Results and Discussion
4.1. Calibration Experiment of Three-Axis TMR Array
- Rotate the TMR array in space uniformly and connect the output terminals of the TMR sensors to the ADC channels of STM32F103.
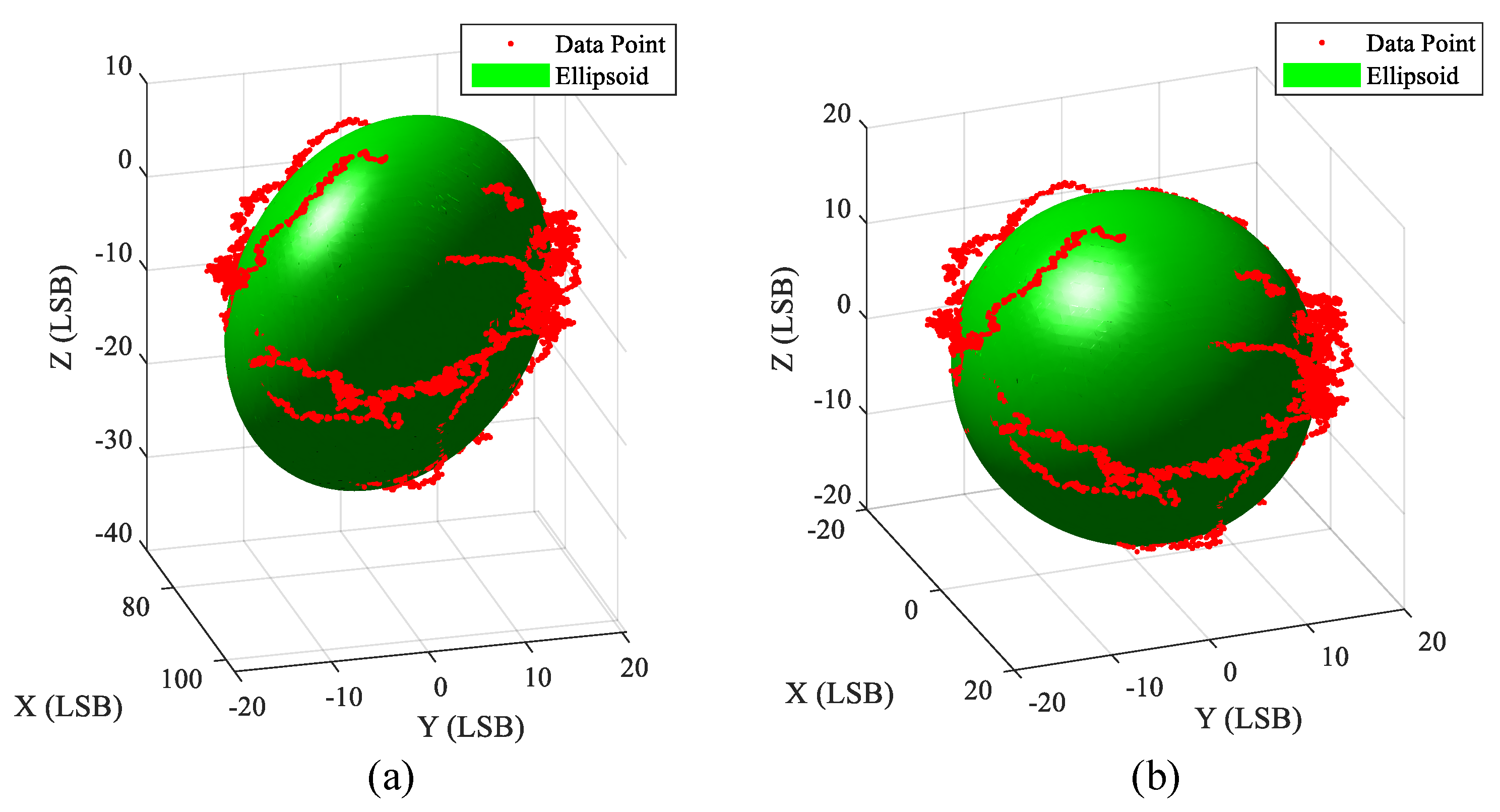
- Import the collected data into the computer and detect the outliers by adopting the GMM binary classification method, as shown in Figure 8a. The data points are divided into two classes, and the class dissociated from the center is labeled the outlier class.
- Adpot a sliding mean filter using MATLAB to reduce the error caused by ADC sampling jitter, as shown in Figure 8b.
- Calculate all parameters of the compensation matrix according to Equation (8) to calibrate the three-axis magnetic sensor.
- Calculate the original data points through the compensation matrix to obtain calibrated data. Use the least squares method to fit the ellipsoid and calculate the ellipsoid’s parameters, as shown in Figure 9b.
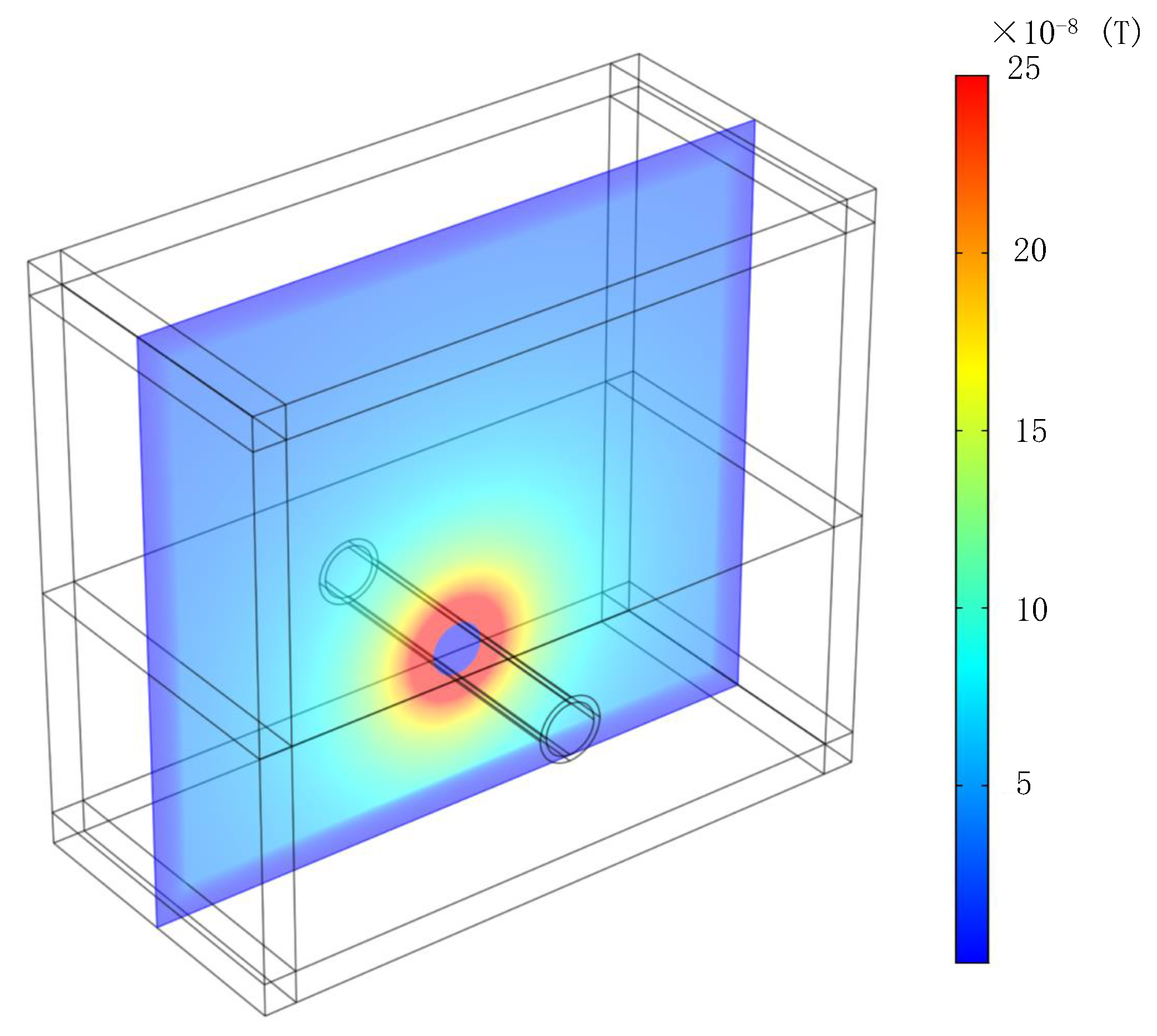
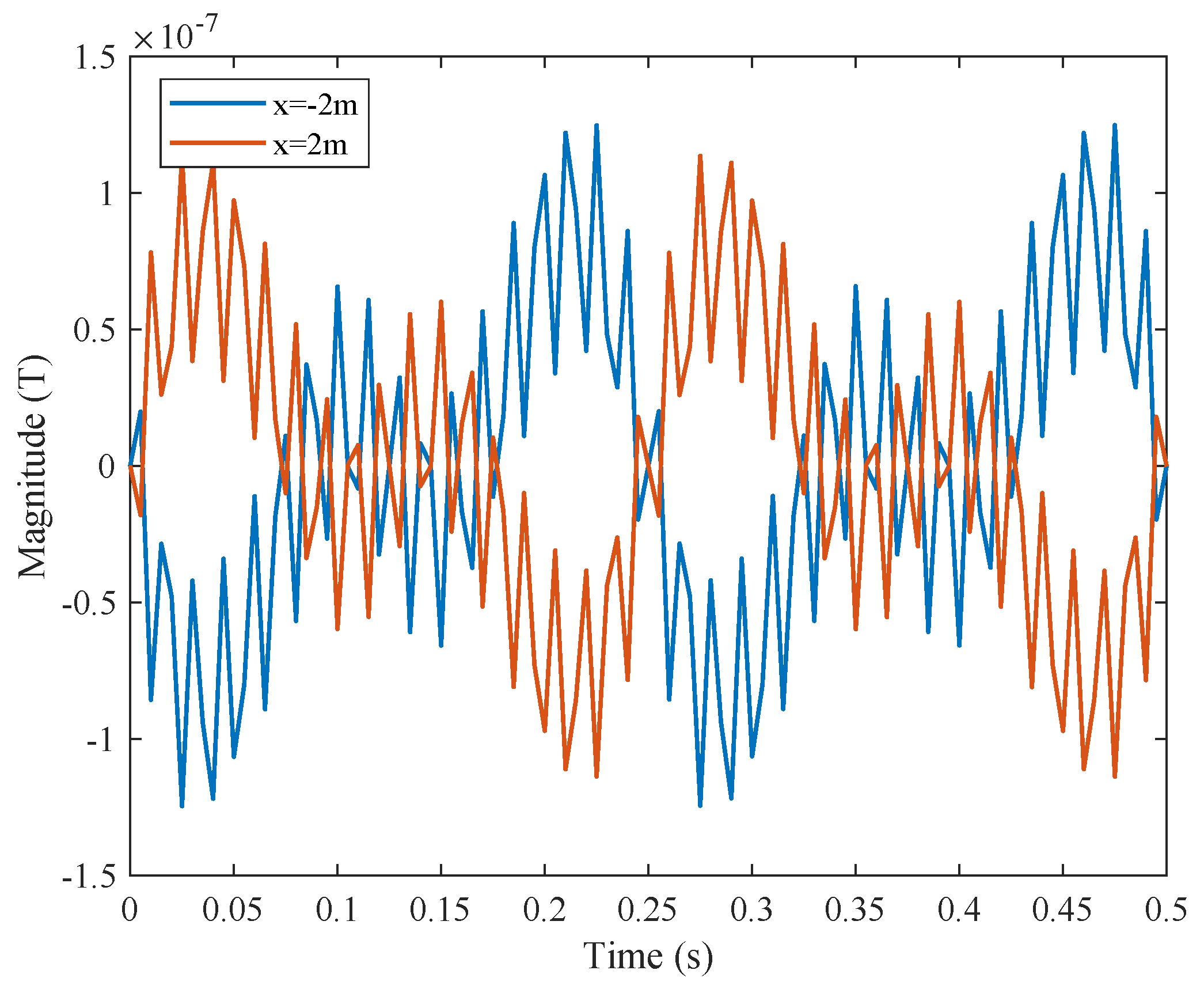
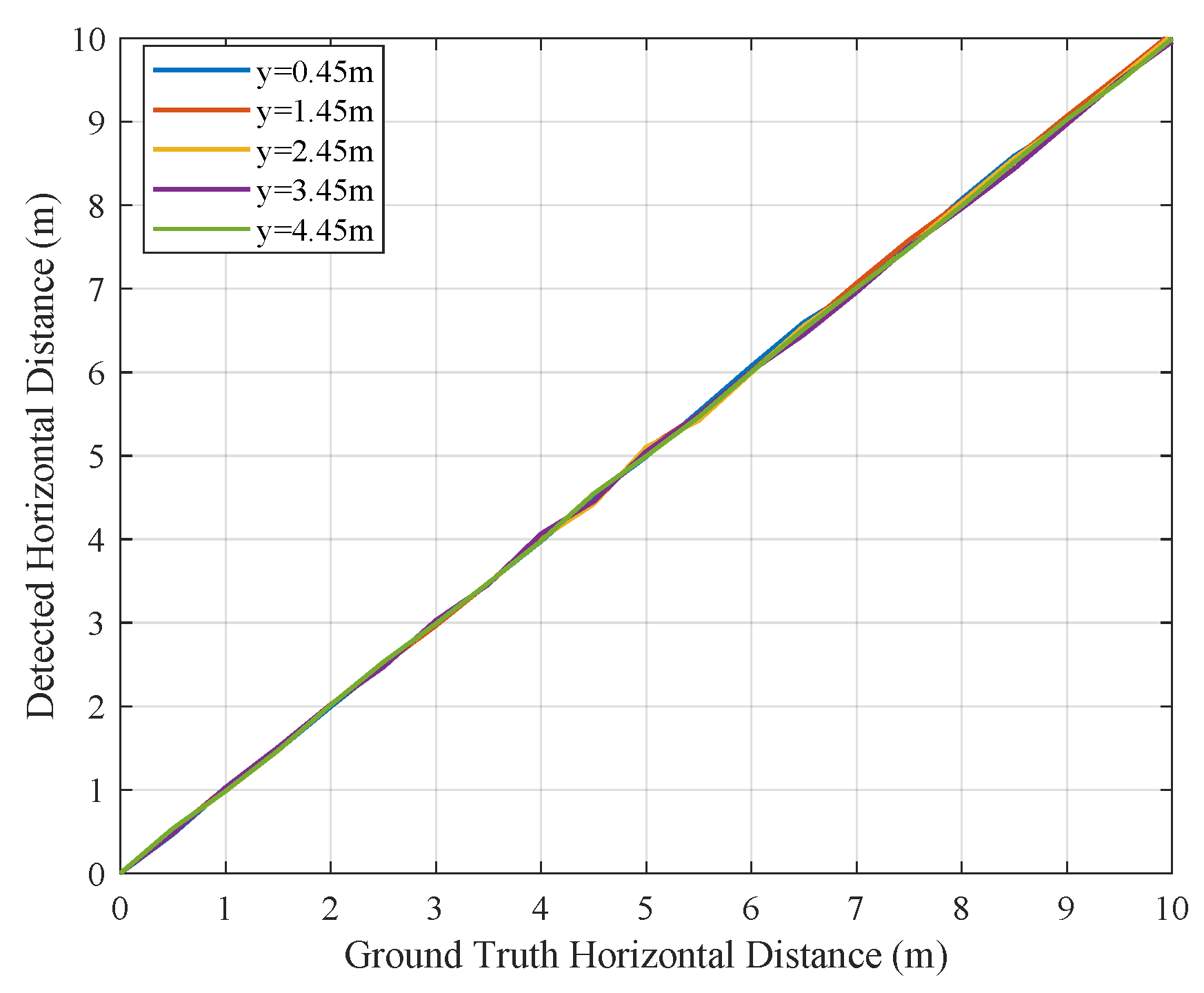
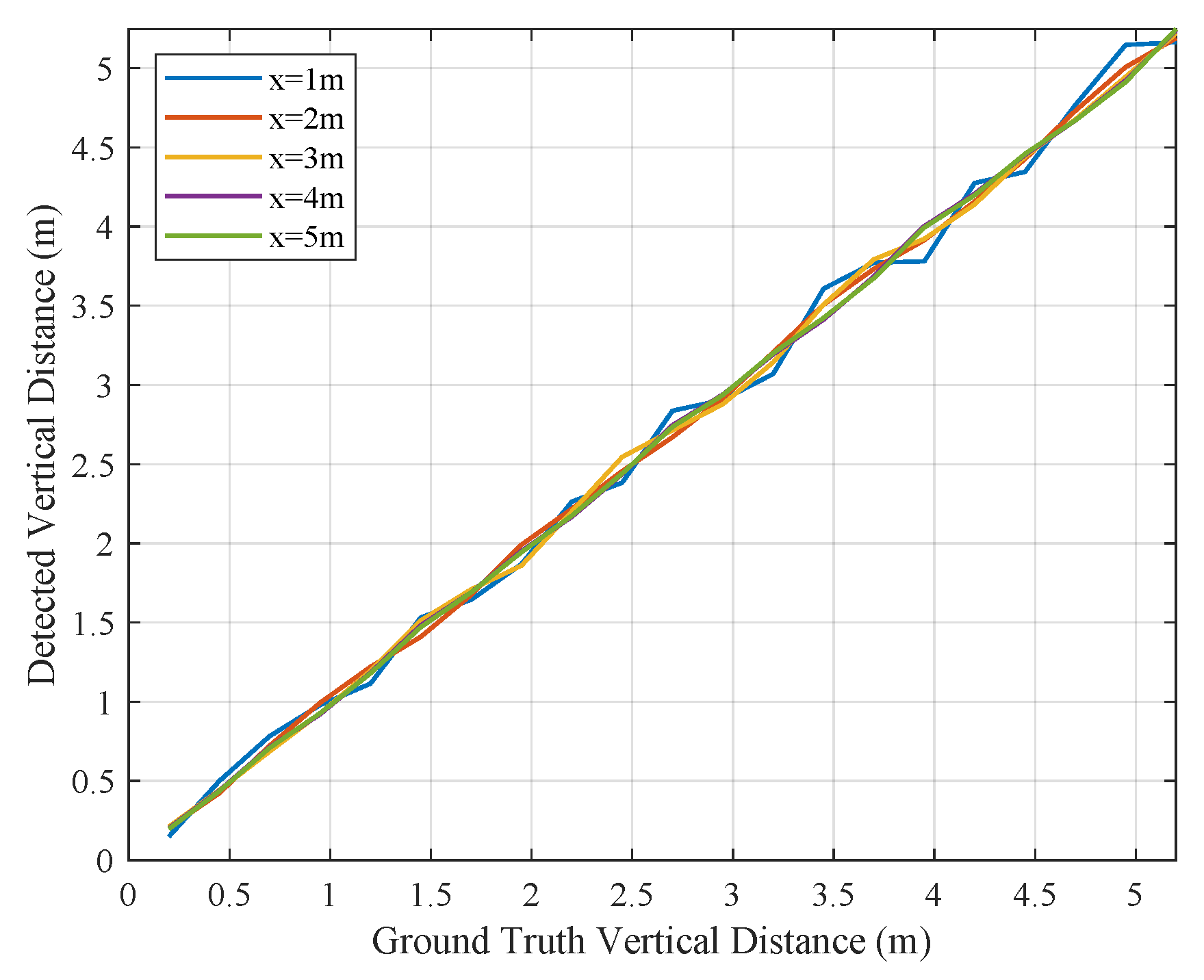
4.2. Three-Dimensional Pipeline Location Simulation
4.3. Experiment
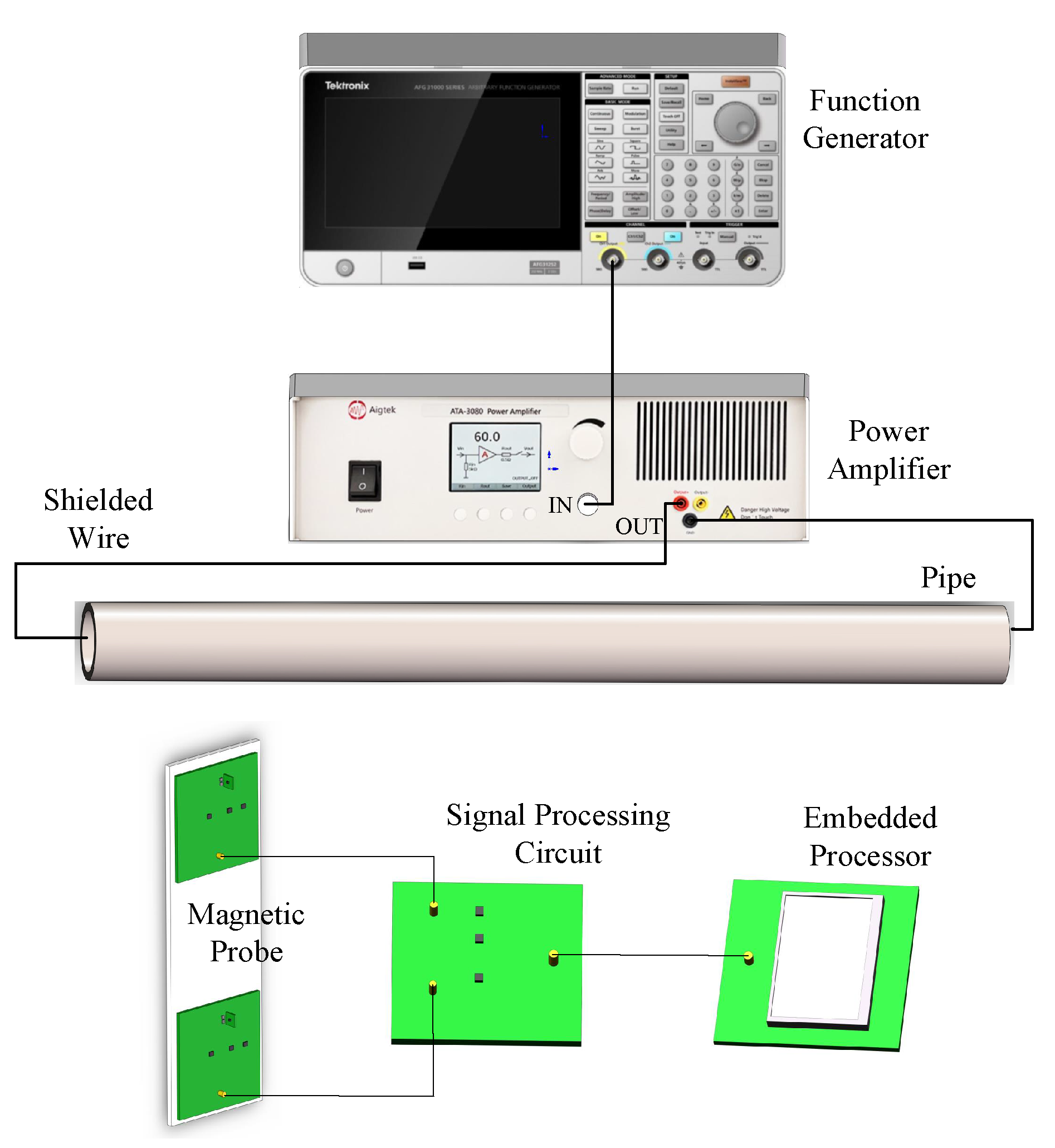
4.3.1. Experiment Design
4.3.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PCM | Pipeline current mapper |
| TMR | Tunnel magnetoresistance |
| PCB | Printed circuit board |
| ADC | Analog-to-digital converter |
| RMS | Root-mean-square |
| FFT | Fast Fourier transform |
| GMM | Gaussian mixture model |
| NDT | Non-destructive testing |
References
- Jacobi, M.; Karimanzira, D. Underwater pipeline and cable inspection using autonomous underwater vehicles. In Proceedings of the 2013 MTS/IEEE OCEANS—Bergen, Bergen, Norway, 10–14 June 2013. [Google Scholar]
- Kandroodi, M.R.; Araabi, B.N.; Ahmadabadi, M.N.; Shirani, F.; Bassiri, M.M. Detection of natural gas pipeline defects using magnetic flux leakage measurements. In Proceedings of the 2013 21st Iranian Conference on Electrical Engineering (ICEE), Mashhad, Iran, 14–16 May 2013. [Google Scholar]
- Lu, S.; Yue, Y.; Liu, X.; Wu, J.; Wang, Y. A novel unbalanced weighted KNN based on SVM method for pipeline defect detection using eddy current measurements. Meas. Sci. Technol. 2022, 34, 014001. [Google Scholar] [CrossRef]
- Wang, Y.; Su, C.; Xie, M. Optimal inspection and maintenance plans for corroded pipelines. In Proceedings of the 2021 Global Reliability and Prognostics and Health Management (PHM-Nanjing), Nanjing, China, 15–17 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, X.; Zheng, J.; Fu, J.; Nie, Z.; Chen, G. Optimal inspection planning of corroded pipelines using BN and GA. J. Pet. Sci. Eng. 2018, 163, 546–555. [Google Scholar] [CrossRef]
- Liu, B.; Lian, Z.; Liu, T.; Wu, Z.; Ge, Q. Study of MFL signal identification in pipelines based on non-uniform magnetic charge distribution patterns. Meas. Sci. Technol. 2023, 34, 044003. [Google Scholar] [CrossRef]
- Pasha, M.A.; Khan, T.M. A pipeline inspection gauge based on low cost magnetic flux leakage sensing magnetometers for non-destructive testing of pipelines. In Proceedings of the 2016 International Conference on Emerging Technologies (ICET), Islamabad, Pakistan, 18–19 October 2016. [Google Scholar]
- Chen, W.; Ma, F. The application of the risk-based inspection technique in the failure possibility analysis of the buried gas pipeline. In Proceedings of the 2009 16th International Conference on Industrial Engineering and Engineering Management, Beijing, China, 21–23 October 2009; pp. 1308–1311. [Google Scholar]
- Liu, X.; Hu, C.; Peng, P.; Li, R.; Zheng, D.Z. In-pipe Detection System Based on Magnetic Flux Leakage and Eddy Current Detection. In Proceedings of the 2020 International Conference on Sensing, Measurement & Data Analytics in the Era of Artificial Intelligence (ICSMD), Xi’an, China, 15–17 October 2020. [Google Scholar]
- Li, S.; Huang, R.; Xu, W.; Zuo, Z.; Liang, S. Unsupervised leak detection of natural gas pipe based on leak-free flow data and deep auto-encoder. In Proceedings of the 2022 China Automation Congress (CAC), Xiamen, China, 25–27 November 2022; pp. 678–683. [Google Scholar] [CrossRef]
- Li, X.; Ma, L.; Liu, L.; Dai, J.; Zhang, H.; Liang, J.; Liang, S. A Leak Detection Algorithm for Natural Gas Pipeline Based on Bhattacharyya Distance. In Proceedings of the 2021 International Conference on Advanced Mechatronic Systems (ICAMechS), Tokyo, Japan, 9–12 December 2021; pp. 33–36. [Google Scholar] [CrossRef]
- Akinsete, O.; Oshingbesan, A. Leak Detection in Natural Gas Pipelines Using Intelligent Models. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, Lagos, Nigeria, 5–7 August 2019. [Google Scholar]
- Sheltami, T.R.; Bala, A.; Shakshuki, E.M. Wireless sensor networks for leak detection in pipelines: A survey. J. Ambient. Intell. Humaniz. Comput. 2016, 7, 347–356. [Google Scholar] [CrossRef]
- Extended Abstract for Presenting the Pipeline Current Mapper Solution at NACE, Vol. All Days. In Proceedings of the AMPP Annual Conference + Expo, AMPP-2022-17617, San Antonio, TX, USA, March 2022.
- Li, R. Urban Underground Pipeline Measurement and Automatic Mapping. Master’s Thesis, North China University of Science and Technology, Qinhuangdao, China, 2019. [Google Scholar]
- Technology of Detecting Deep Underground Metal Pipeline by Magnetic Gradient Method. IOP Conf. Ser. Earth Environ. Sci. 2021, 7, 390–393.
- Zhao, Y.; Wang, X.; Sun, T.; Chen, Y.; Yang, L.; Zhang, T.; Ju, H. Non-contact harmonic magnetic field detection for parallel steel pipeline localization and defects recognition. Measurement 2021, 180, 109534. [Google Scholar] [CrossRef]
- Velázquez, J.C.; Hernández-Sánchez, E.; Terán, G.; Capula-Colindres, S.; Diaz-Cruz, M.; Cervantes-Tobón, A. Probabilistic and Statistical Techniques to Study the Impact of Localized Corrosion Defects in Oil and Gas Pipelines: A Review. Metals 2022, 12, 576. [Google Scholar] [CrossRef]
- Velázquez, J.C.; Caleyo, F.; Valor, A. Predictive Model for Pitting Corrosion in Buried Oil and Gas Pipelines. Corros. J. Sci. Eng. 2009, 65, 332–342. [Google Scholar] [CrossRef]
- Fang, X.; Deng, J. Detection of Deep Pipeline. In Proceedings of the 20th Annual of the Chinese Geophysical Society, Xi’an, China, 16–20 October 2003. [Google Scholar]
- Tian, W.M. Integrated method for the detection and location of underwater pipelines. Appl. Acoust. 2008, 69, 387–398. [Google Scholar] [CrossRef]
- Hongzhi, W.; Jinghe, C.; Kaifeng, L.; Xin, G.; Zidong, Z. Improved Correction Method of Signal Values Based on One-pass System. In Proceedings of the CORROSION, San Antonio, TX, USA, 9–13 March 2014. [Google Scholar]
- Nadimi, N.; Javidan, R.; Layeghi, K. Efficient Detection of Underwater Natural Gas Pipeline Leak Based on Synthetic Aperture Sonar (SAS) Systems. J. Mar. Sci. Eng. 2021, 9, 1273. [Google Scholar] [CrossRef]
- Jinnah Sheik Mohamed, A.B.; Venusamy, K.; Sangeetha, S.; Abdullah Al Rawahi, A.S.; Said Mahmood Al Balushi, A. Leak Detection and Corrosion Identification in Water Tubes, Gas Pipes by Mobile Robot. In Proceedings of the 2021 2nd International Conference on Smart Electronics and Communication (ICOSEC), Trichy, India, 7–9 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Roskosz, M. Metal magnetic memory testing of welded joints of ferritic and austenitic steels. NDT & E Int. 2011, 44, 305–310. [Google Scholar]
- Chen, Z.; Dang, R.; Xie, R. Research on electromagnetic Detection Technology of underground metal pipeline. Electron. Test 2017, 15, 50–51. [Google Scholar]
- Yang, Q.; Yang, J.; Liu, W. Application of current method in multi—Frequency tube in buried pipeline detection. Chem. Mach. 2017, 44, 6. [Google Scholar]
- Liu, S.; Ren, X.; Qiao, H. Design of constant current transmitter for underground pipeline detection system based on PCM. Int. Electron. Elem. 2023, 31, 8. [Google Scholar]
- Tuo, Y. Research and Design of Intelligent Cable Path Detector. Master’s Thesis, Xidian University, Xi’an, China, 2009. [Google Scholar]
- Li, Q.; Li, Z.; Zhang, Y.; Fan, H.; Yin, G. Integrated Compensation and Rotation Alignment for Three-Axis Magnetic Sensors Array. IEEE Trans. Magn. 2018, 54, 4001011. [Google Scholar] [CrossRef]
- Xueyuan, L.; Yulin, C.; Min, Z. Error Analysis and Compensation of Three-axis Strap-down Magnetometers. In Proceedings of the 2007 8th International Conference on Electronic Measurement and Instruments, Xi’an, China, 16–18 August 2007; pp. 1-294–1-297. [Google Scholar] [CrossRef]
- Hu, F.; Wu, Y.; Yu, Y.; Nie, J.; Li, W.; Gao, Q. An Improved Method for the Magnetometer Calibration Based on Ellipsoid Fitting. In Proceedings of the 2019 12th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Suzhou, China, 19–21 October 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Fang, J.; Sun, H.; Cao, J.; Xiao, Z.; Ye, T. A Novel Calibration Method of Magnetic Compass Based on Ellipsoid Fitting. IEEE Trans. Instrum. Meas. 2011, 60, 2053–2061. [Google Scholar] [CrossRef]

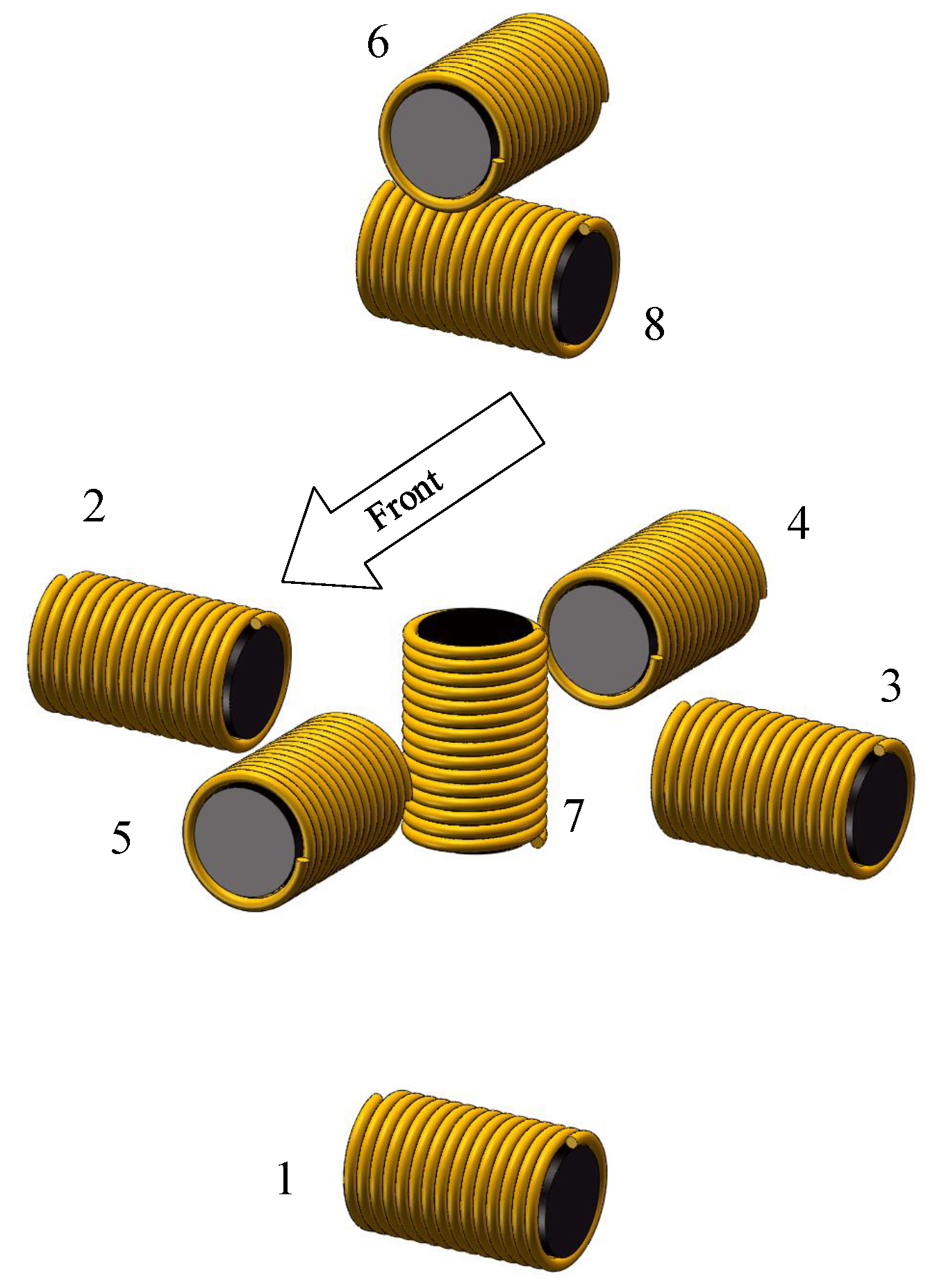









| Signal Intensity | Pipeline Position |
|---|---|
| , | Left |
| , | Front left |
| , | Front |
| , | Front right |
| , | Right |
| , | Rear right |
| , | Rear |
| , | Rear left |
| Material | Relative Magnetic Conductivity | Relative Dielectric Constant | Specific Conductance (S/m) |
|---|---|---|---|
| Air | 1 | 1 | 0 |
| Iron | 1 | 1 | × |
| Soil | 0.975 | 2.6 | × |
| Object | Variable (m) | Average Error | |
|---|---|---|---|
| Angle (°) | 0.5 | 0.9953 | 1.85° |
| 1 | 0.9822 | 3.67° | |
| 1.5 | 0.9935 | 2.51° | |
| Horizontal Distance (cm) | 0.5 | 0.9937 | 2.39 (cm) |
| 1 | 0.9975 | 2.19 (cm) | |
| 1.5 | 0.9953 | 3.14 (cm) | |
| Vertical Distance (cm) | 0.5 | 0.9966 | 3.12 (cm) |
| 1 | 0.9977 | 2.01 (cm) | |
| 1.5 | 0.996 | 3.17 (cm) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Huang, H.; Zhao, G.; Liu, J. TMR-Array-Based Pipeline Location Method and Its Realization. Sustainability 2023, 15, 9816. https://doi.org/10.3390/su15129816
Wu Z, Huang H, Zhao G, Liu J. TMR-Array-Based Pipeline Location Method and Its Realization. Sustainability. 2023; 15(12):9816. https://doi.org/10.3390/su15129816
Chicago/Turabian StyleWu, Zhenning, Hanyang Huang, Guangdong Zhao, and Jinhai Liu. 2023. "TMR-Array-Based Pipeline Location Method and Its Realization" Sustainability 15, no. 12: 9816. https://doi.org/10.3390/su15129816
APA StyleWu, Z., Huang, H., Zhao, G., & Liu, J. (2023). TMR-Array-Based Pipeline Location Method and Its Realization. Sustainability, 15(12), 9816. https://doi.org/10.3390/su15129816






