Using Energy Conservation-Based Demand-Side Management to Optimize an Off-Grid Integrated Renewable Energy System Using Different Battery Technologies
Abstract
1. Introduction
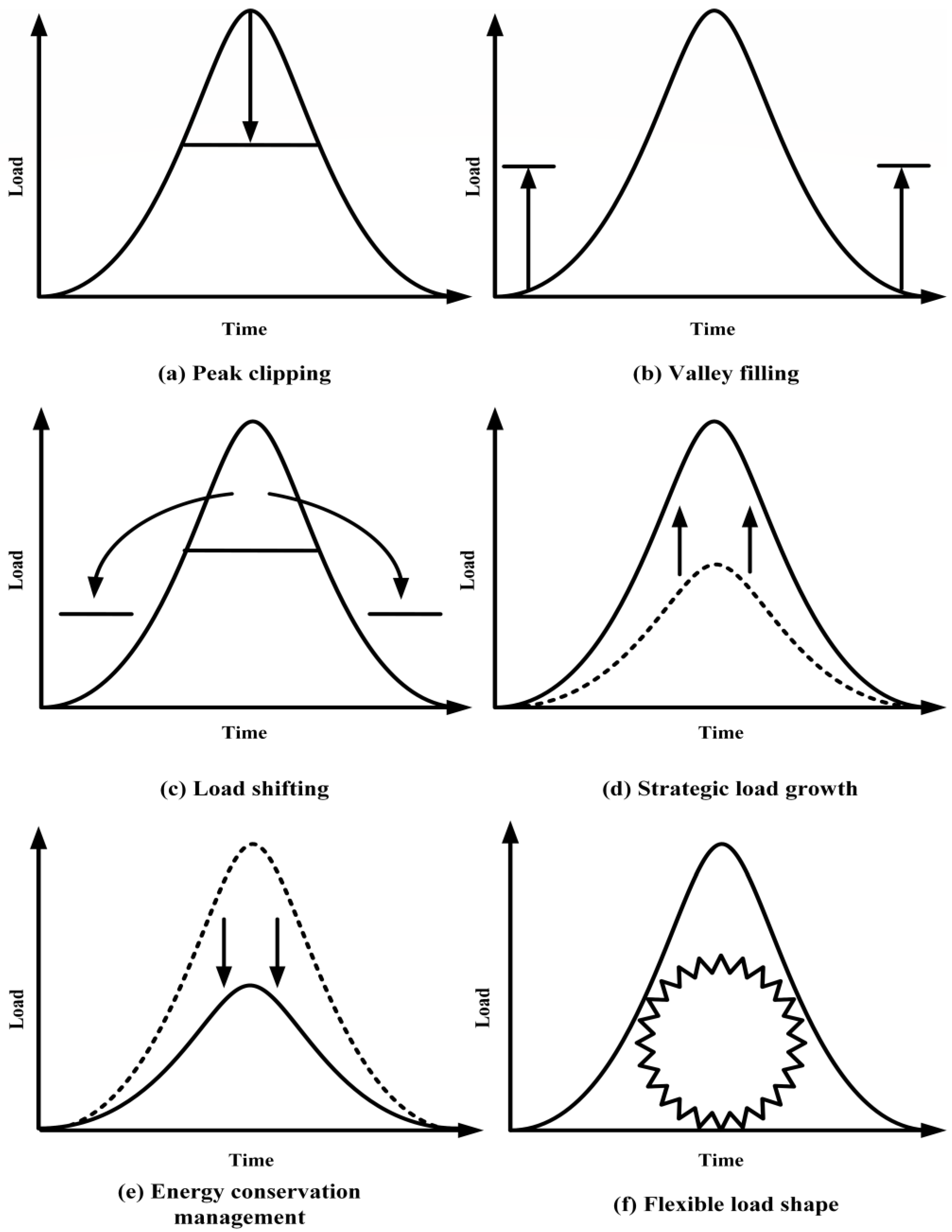
- i.
- Peak clipping: Its purpose is to reduce the strain on energy systems during peak demand periods. This is typically achieved by limiting the use of appliances during peak hours or by offering customers incentives to shift their energy consumption away from peak times;
- ii.
- Valley filling: The aim of valley filling is to maximize the utilization of facilities by promoting energy consumption during off-peak hours. To achieve this, governments can incentivize customers to schedule such activities as charging and loading during off-peak times. By doing this, customers will be able to take full advantage of available resources, resulting in more efficient use of energy;
- iii.
- Load shifting: To reduce overall energy consumption, load shifting from peak to off-peak times is recommended. Customers can store thermal heat during the off-peak hours, which can then be used to maintain a comfortable temperature throughout the day. Furthermore, household chores, such as laundry and dishwashing, can be completed at night to avoid peak loading;
- iv.
- Energy conservation: Its goal is to reduce energy consumption by investing in more energy-efficient devices. This can help lower load demand, thus leading to more efficient energy use overall;
- v.
- Load building: Smart grids enable the use of load building and flexible loads through the improved network connection. This, in turn, increases the grid’s responsiveness through improved load sharing and the application of energy storage systems;
- vi.
- Flexible load shape: By adjusting the flexible load demand, the reliability conditions necessary for system reliability can be determined, thus improving the system’s reliability.
1.1. The Literature Review
- Alpesh and Sunil [1] utilized a combination of PV/Wind Turbine WT)/Biomass Generator (BMG)/Biogas Generator (BGG)/LA battery technology to electrify hamlets with 123 households located on the border of India’s Gujarat and Rajasthan states and analyzed the optimal component selection using multi-variable linear regression technique along with the gradient descent (MVLRT-GD) algorithm and particle swarm optimization (PSO) to determine the optimal results;
- Ramesh and Saini [8] conducted a study that assessed the feasibility of PV/WT/Micro Hydro Power Plant (MHP)/Diesel Generator (DG)/Battery (BAT) configurations with LA and Li-Ion battery technologies for off-grid un-electrified villages in Chikmagalur district in India. They used HOMER Pro® software to evaluate three different dispatch strategies and found that the Li-Ion-battery-based system with a combined dispatch strategy provided the lowest net present cost (NPC) and cost of energy (COE) compared to the cycle charging and load-following strategy-based systems using the LA battery technology;
- Haein and Tae [9] studied the most cost-effective way to electrify an off-grid rural area in Myanmar by using PV/DG/BAT configuration with both LA and Li-Ion battery technologies. They used the HOMER Pro® software tool to minimize the NPC of the system and determined that using the LA battery technology provided the most optimal results;
- Kaabeche and Bakelli [10] evaluated the PV/WT/BAT system with LA, Li-Ion, and nickel–cadmium battery technologies in Adrarin province, Algeria. They applied various optimization algorithms, such as GWO, ALO, Krill Herd, and JAYA, to minimize the electricity cost of the system and concluded that LA battery-based configuration with the JAYA algorithm was the most optimal solution, followed by the Li-Ion and Ni-Cd batteries;
- Sarah et al. [11] examined the PV/WT/DG/BAT system for Dodoma, Tanzania, with both LA and Li-Ion battery technologies to identify the most cost-efficient configuration. These researchers found that Li-Ion battery configuration with a genetic algorithm provided the lowest cost of energy (COE);
- Chong Li et al. [12] conducted a study of the WT/DG/BAT system for 280 off-grid households in Gansu province, China, with LA, Li-Ion, and Zinc–Bromine (ZB) battery technologies. They used the HOMER Pro® software tool to determine the optimal option and found that the ZB battery technology provided the optimal results;
- Muhammad Fahad Zia et al. [7] examined the use of a microgrid for remote area applications, such as oceanic islands, specifically in the context of Ouessant Island in Brittany, France. The microgrid consists of a PV system, tidal turbine, diesel generator, and Li-Ion battery, and the economic operation of the system is achieved by taking into account various factors, such as battery degradation cost, levelized costs of energy, operating and emission costs of the diesel generator, and network constraints;
- George Κ. Farinis and Fotios D. Kanellos [13] proposed an energy management system for microgrids and building prosumers using a multi-agent system, particle swarm optimization, and thermal and electrical models. It allows for optimal operation scheduling in grid-connected and autonomous operational modes and can result in cost savings of around 11%. Simulation results demonstrate its effectiveness in meeting a large number of operation and technical constraints;
- Vasileios Boglou et al. [14] used a decentralized energy management system based on multi-agent systems, which was developed for the efficient charging of electric vehicles. This approach leads to a significant reduction in investment costs, peak load, and load variances. Furthermore, it increases the total amount of chargeable EVs. This novel charging management system offers an intelligent approach to the islanding of distribution grids with high penetration of electric vehicles by offering operational and financial benefits;
- Eliseo Zarate-Perez et al. [15] used a systematic and bibliometric approach to evaluate the performance and challenges of integrating battery energy-storage systems into microgrids. This review finds that optimization methods and cost-benefit analysis are key elements for developing an optimal battery energy-storage system. Other considerations include factors, such as reliability, battery technology, power quality, frequency variations, and environmental conditions. Overall, economic factors are the biggest challenges for battery energy-storage systems;
- Vasileios Boglou et al. [16] proposed a distributed optimal small-scale PV energy-system-sizing strategy for residential distribution grids that takes into account individual energy needs and EV charging. Fuzzy cognitive maps theory is used to address the correlation between individual energy parameters and RES characteristics. The optimization results showcase that the adopted hybrid approach can reduce energy costs significantly, with no need for expansion of the utility network. Thus, EV charging through residential RES can become a viable option;
- Dimitrios Rimpas et al. [17] reviewed various motor technologies available for use in electric vehicles, such as brushless motors, synchronous reluctance, and induction motors. By taking into account eleven criteria, such as power density and regenerative braking efficiency, the motors are classified in terms of their ability to function in hybrid energy-storage systems to maximize efficiency and sizing. It is concluded that permanent magnet motors and induction motors are the most suitable for such applications, with the synchronous reluctance motor offering superior performance when it comes to the key factors impacting the system;
- Shih-Chieh Huang et al. [18] integrated a structural equation model (SEM) and fuzzy cognitive map (FCM) to analyze the mutual relationship between the various elements influencing the development of wind power. Results suggest that “policy” is the main obstacle to development, and management strategies should focus on the “technology” and “environment” in the short term and consider “social” factors in the mid-term, with a focus on “policy” in the long-term;
- Christos-Spyridon Karavas et al. [19] proposed a decentralized energy management system for an autonomous polygeneration microgrid topology. A decentralized architecture offers advantages, such as greater chances of partial operation in cases of malfunctions, in comparison with a centralized system. The multi-agent system based on fuzzy cognitive maps was explored for their implementation and compared to an existing centralized energy management system in terms of technical performance, financial efficiency, and operational simplicity. The results showed similar technical performance between the two systems, along with advantages in financial and operational terms for the decentralized system;
- Konstantinos Kokkinos et al. [20] proposed a semi-quantitative assessment of biowaste-based energy transition by engaging stakeholders. To achieve this, a decision support system (DSS) and a fuzzy cognitive map (FCM) are proposed to evaluate the interplay of local and sectoral low-carbon actions. A use case study of a Greek region is potentially employed to analyze the effect of energy provision on urbanization and the influence of actors on decision-making related to low-carbon policies. The proposed decision-making tool utilizes analytics, optimization algorithms, and surveys to guide competent authorities to sustainable energy transitioning toward decarbonization;
- Lucchi E.’s design policy-related requirements that protect existing history and cultural values are essential for the successful integration of such renewable energy sources as photovoltaics into the built environment. As part of this process, he conferred with heritage authorities to learn about the most up-to-date standards, as well as the benefits and cons of the potential integration of solar energy and other renewable sources into the cultural heritage sites. Proper implementation of this strategy can improve clean and integrated energy production, which, in turn, can help mitigate climate change and fulfil today’s energy demands;
- Lucchi, E., Baiani, S., and Altamura, P. studied to aid in the design and construction of historically significant buildings that incorporate active solar technology, such as photovoltaic and solar thermal systems, by providing a classification system for international norms. By analyzing and comparing recurring criteria and recommendations from 44 international guidelines, it develops and identifies shared-design requirements for the integration of various active solar technologies and works to create a shared vocabulary to promote their adoption. They also look at how incorporating active solar technologies can increase a building’s market value, improve occupants’ quality of life, and reduce energy consumption while also positively supporting energy transition and climate change mitigation;
- Lucchi E.’s study shows that applied to historic buildings, they can cause significant conservation problems that endanger the buildings’ cultural significance, biodiversity, traditional appearance, and even the materials themselves. Based on a survey of the literature from 2020 to 2023, this study provides an up-to-date summary of the use of such renewable energy sources as solar, wind, geothermal, and bioenergy to preserve historic buildings. Acceptability, design requirements, and cutting-edge technologies are discussed, with examples from real-world applications. The compatibility of wind turbines with their natural and cultural surroundings and municipal rules is crucial to the widespread adoption of wind energy in historical sites. Heating and cooling systems, among other geothermal energy uses, have been effectively incorporated in both old and new buildings.
1.2. Research Gaps Identified
- From the research in the Indian context, using lithium-lon (Li-Ion), lead–acid (LA), and nickel–iron (Ni–Fe) batteries for the off-grid microgrids has not been thoroughly explored. To gain an understanding of the advantages of these technologies in off-grid microgrids, further research is necessary. This should include an analysis of cost-effectiveness, reliability, long-term performance, environmental impact, and a cost-benefit assessment. Additionally, safety, usability, scalability, and potential integration with other energy sources should also be considered;
- Further, the majority of studies carried out a techno-economic feasibility analysis with one or two types of battery technologies to provide a continuous power supply. This often fails to take into account the unique requirements and characteristics of different battery technologies. Given that lithium-ion (Li-Ion), lead–acid (LA), and nickel–iron (Ni–Fe) each have distinct advantages and disadvantages, it is important to explore the potential for utilizing these technologies for the off-grid microgrids in order to create an optimal balance between cost, performance, and reliability. Furthermore, there is a need for further research into the design of these combinations and their potential for scalability and integration with other energy sources;
- Further research can be conducted to compare the proposed algorithm with other algorithms in terms of robustness, efficiency, and scalability. Such studies would help identify the best algorithms for different conditions, such as complexity, grid constraints, load profiles, and cost considerations. Additionally, other approaches, such as meta-heuristics and optimization techniques, could also be applied to the off-grid microgrid-sizing problem. This would enable a more comprehensive comparison between various algorithms in terms of performance and implementation;
- Demand side management (DSM) strategies have the potential to play a major role in achieving better energy balance and overall efficiency of the off-grid microgrids. However, there is still a need for more studies to explore the potential benefits of different DSM approaches for off-grid microgrids. Research should focus on the assessment of individual DSM techniques, such as time-of-use pricing, demand–response programs, dynamic pricing, and the potential for their combinations with other distributed energy resources, such as solar PV, storage, and wind turbines. Further, there is an urgent need to investigate the potential of energy-conservation DSM strategies for off-grid microgrids, such as energy-efficiency measures, demand management, and load shifting. Such research could help to identify cost-effective approaches that can improve the operational efficiency and overall economic viability of the off-grid microgrids.
1.3. Novelties of This Article
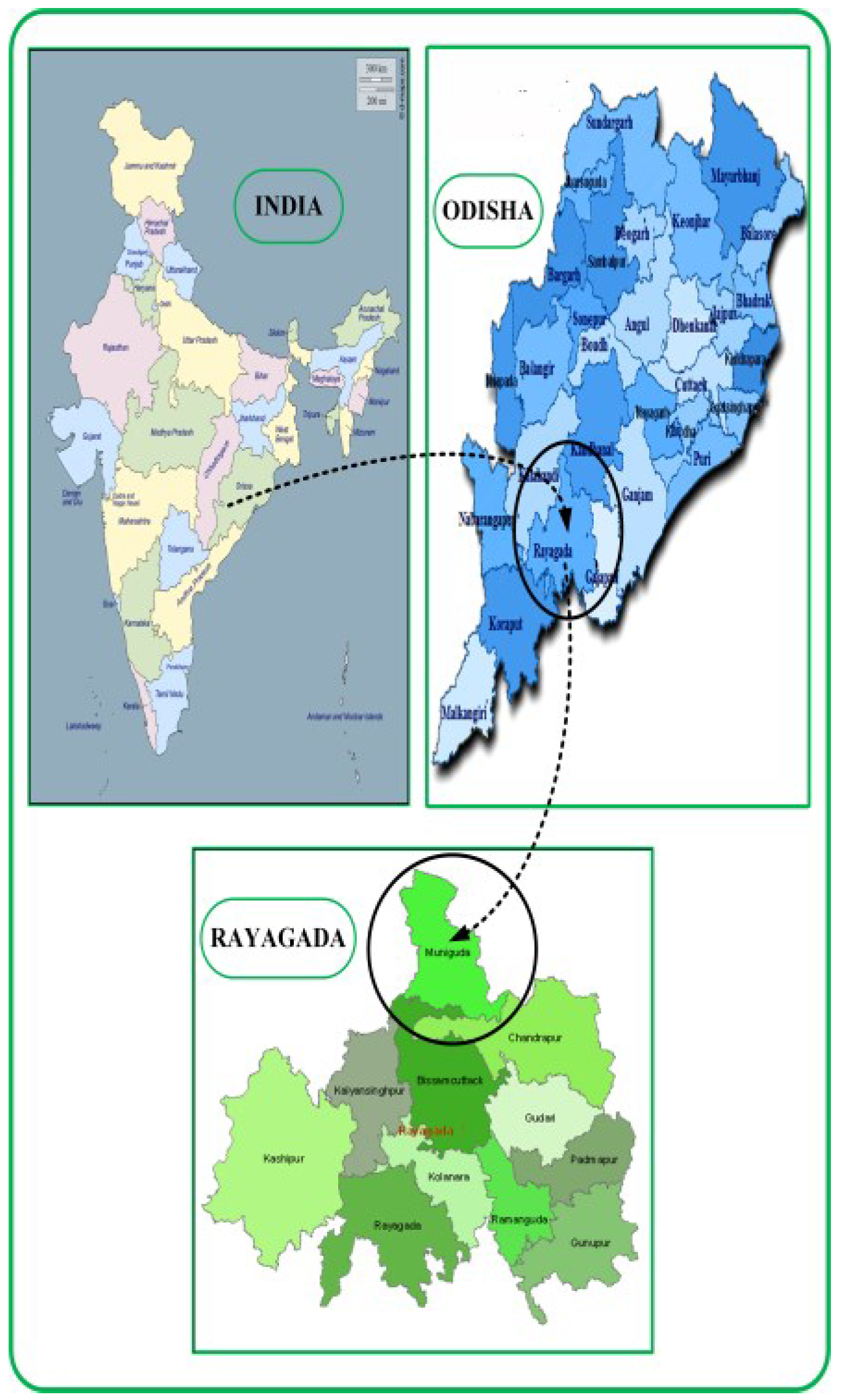
- The techno-economic reliability of providing energy to five off-grid communities in the Rayagada region of Odisha state in India was studied, leveraging existing renewable energy sources in the area, such as solar and biomass. Furthermore, a novel method of combining these two energy sources was proposed to create a reliable energy system that optimizes cost-effectiveness and maximizes sustainability. This new approach could be applied to other off-grid communities to provide secure and affordable energy access;
- Six specific configurations are modeled by the available RE sources and suggested batteries “PV/BMG/LA@70% DOD, PV/BMG/LA@80% DOD, PV/BMG/Li-Ion@50% DOD, PV/BMG/Li-Ion@70% DOD, PV/BMG/Li-Ion@80% DOD, and PV/BMG/Ni–Fe@80% DOD” with their varying depths of discharge to figure out which configuration will provide the most reliable power supply;
- To identify the most reliable power supply, six specific configurations of renewable energy sources and suggested batteries have been modeled, with varying depths of discharge. The configurations are PV/BMG/LA@70% DOD, PV/BMG/LA@80% DOD, PV/BMG/Li-Ion@50% DOD, PV/BMG/Li-Ion@70% DOD, PV/BMG/Li-Ion@80% DOD; and PV/BMG/Ni–Fe@80% DOD;
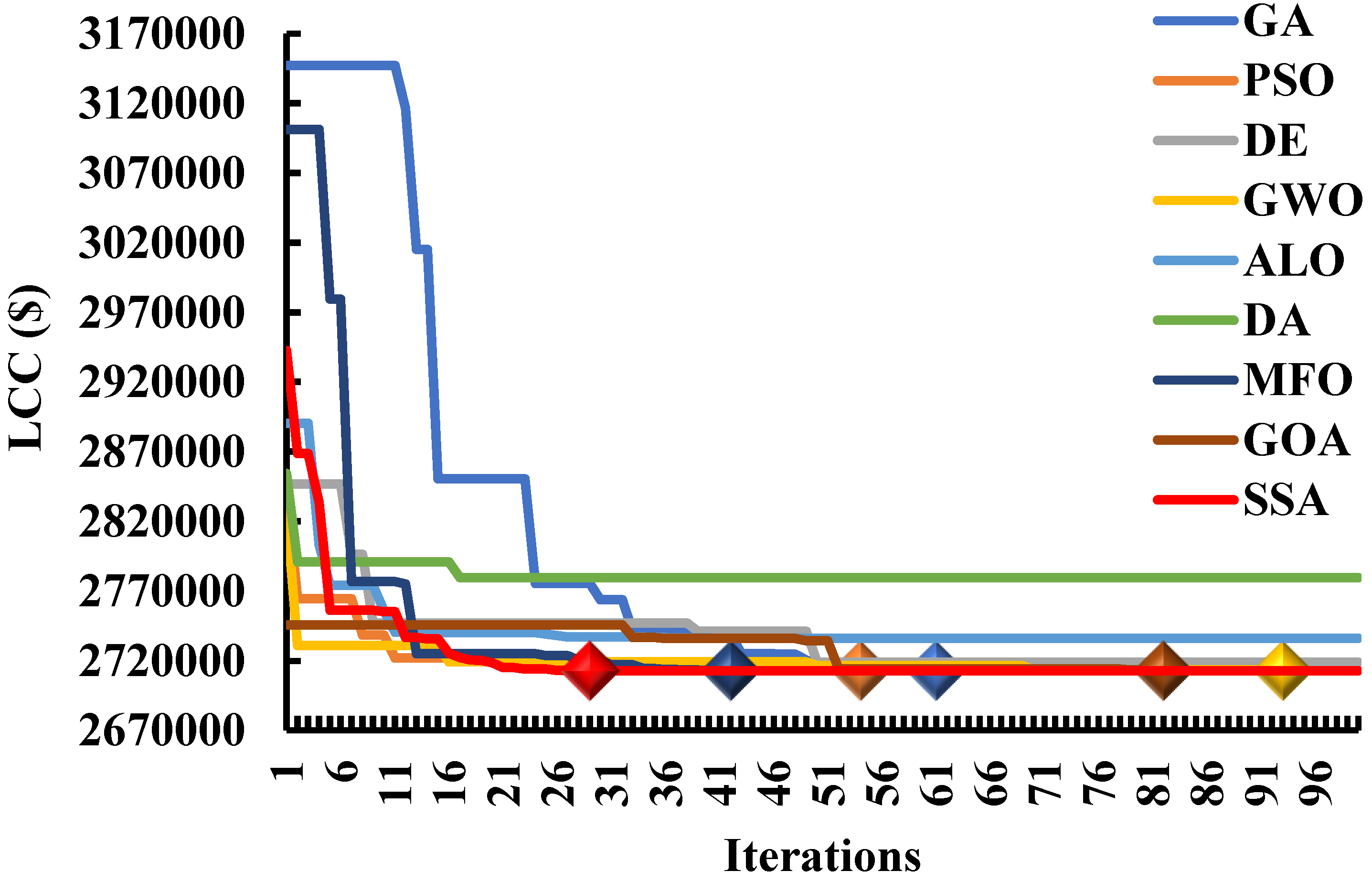
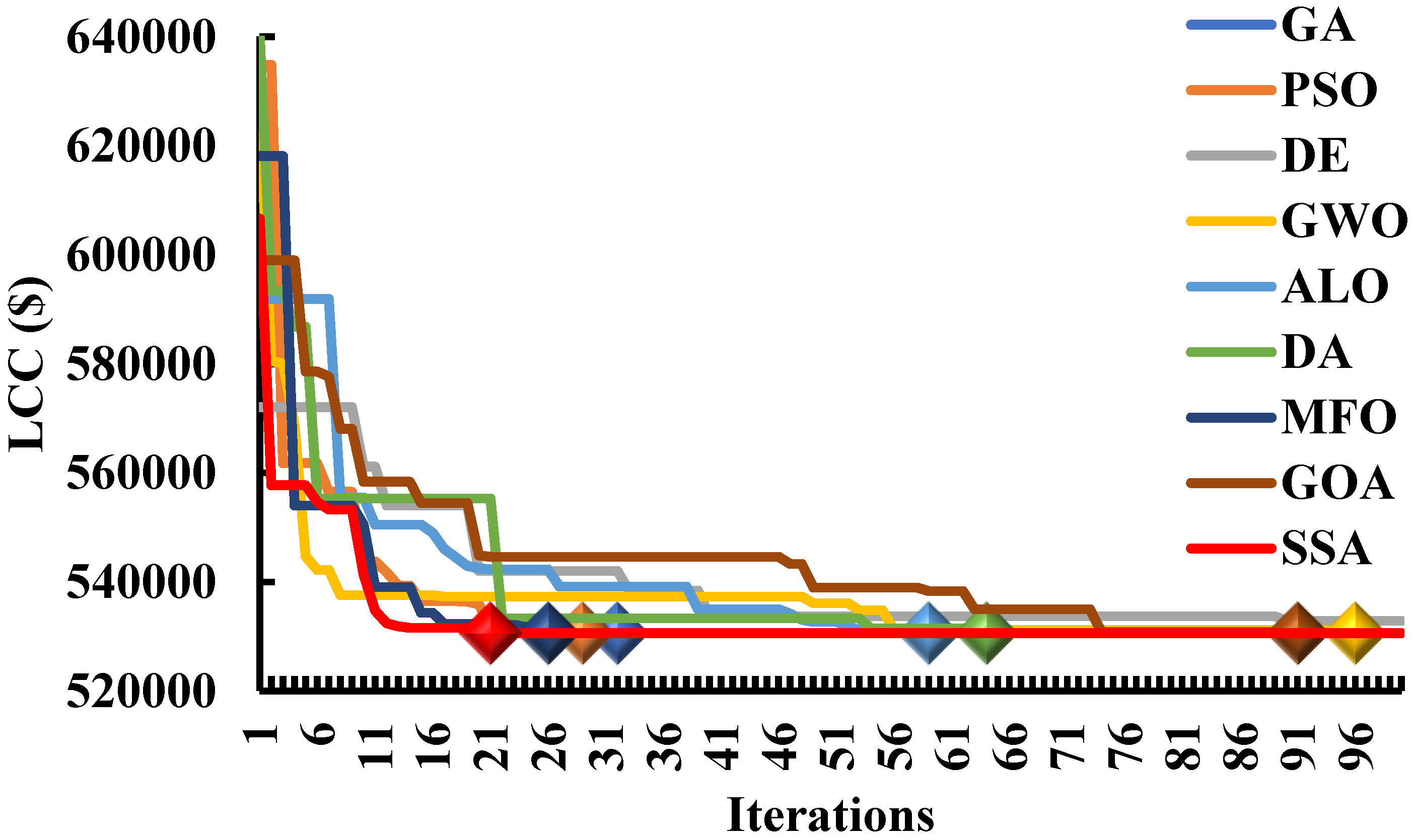
- This research has presented a unique solution for solving optimization problems—the salp swarm algorithm. This algorithm is a novel metaheuristic algorithmic approach that does not rely on predetermined parameters. Furthermore, the results obtained from testing this algorithm demonstrate superior performance to existing optimization algorithms across various metrics. This algorithm shows a high degree of robustness and convergence efficiency compared to eight other algorithms, including the particle swarm optimization (PSO) [21], differential evolutionary algorithm (DE) [22], genetic algorithm (GA) [23], ant lion optimization (ALO) [24], grasshopper optimization algorithms (GOA) [25], grey wolf optimization (GWO) [26], moth flame optimization (MFO) [27], and dragonfly algorithm (DA) [28]. It is clear that the salp swarm algorithm is a reliable and effective algorithm for solving optimization problems and can be used to significantly improve the performance of optimization solutions;
- This research not only explored various demand-side management techniques but also implemented energy-conservation-based demand-side management for the current study area. The results were impressive, as it effectively reduced peak-load demands and improved customer satisfaction while providing a reliable and cost-effective power system. Furthermore, with these successes in mind, this strategy can be applied to other areas in need of a demand-side management technique, allowing for a larger-scale approach to energy conservation and security. As such, this method proves to be an innovative, effective, and much-needed solution for meeting the growing energy requirements.
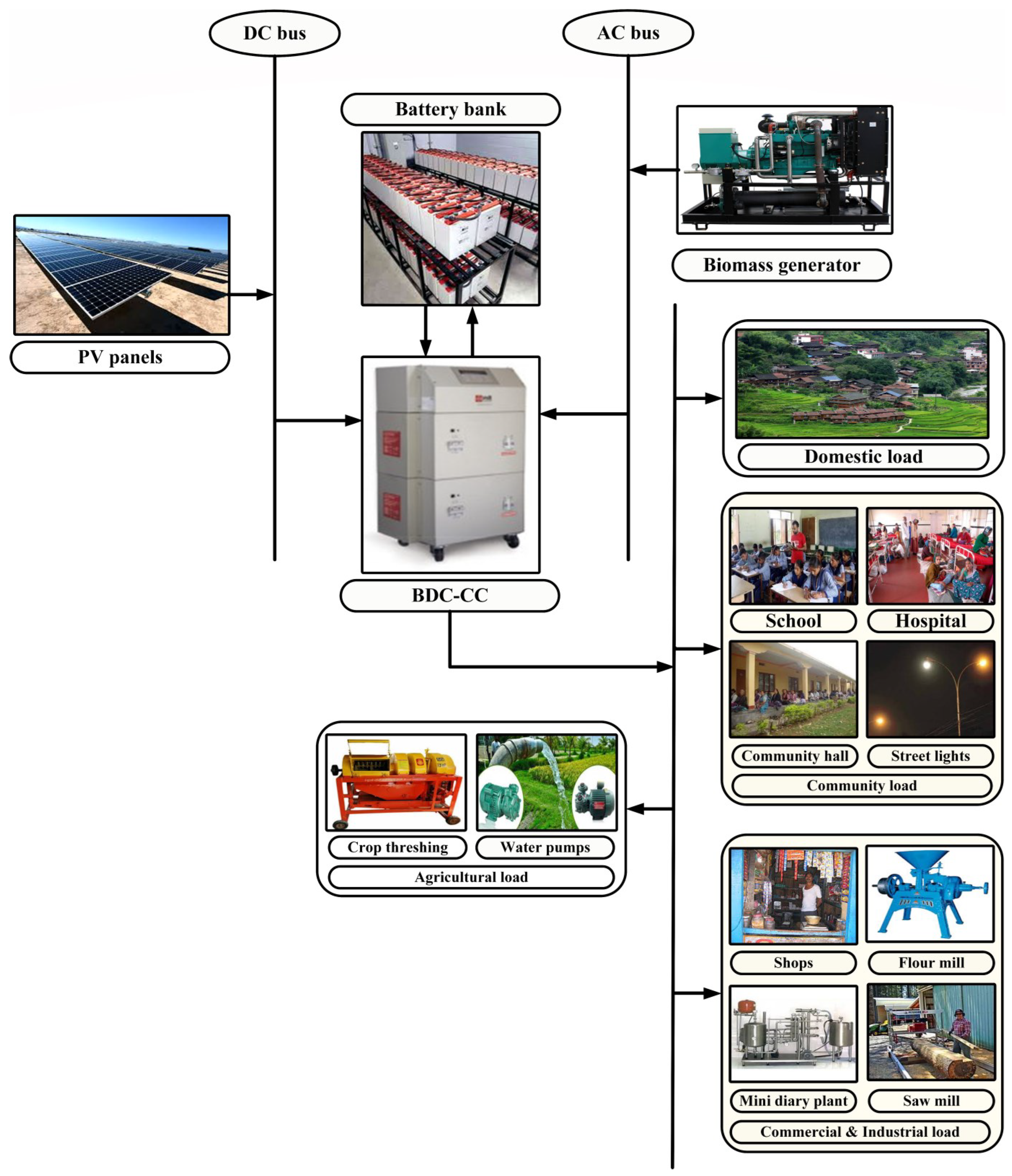
2. Development of the Integrated Renewable Energy System
- Step 1—Study-area identification
- Step 2—Estimation of electrical energy demand
- Step 3—Resource assessment
3. The IRES Component’s Mathematical Modeling
3.1. Solar Energy
3.2. Biomass Generator
3.3. Battery Bank
4. Economic Analysis of the IRES
5. The Objective Function and Its Constraints
5.1. Life-Cycle Cost
5.2. Upper and Lower Bounds
5.3. Battery Bank Energy Storage Limits
5.4. Power Reliability Index
6. Methodology
7. Results and Discussions
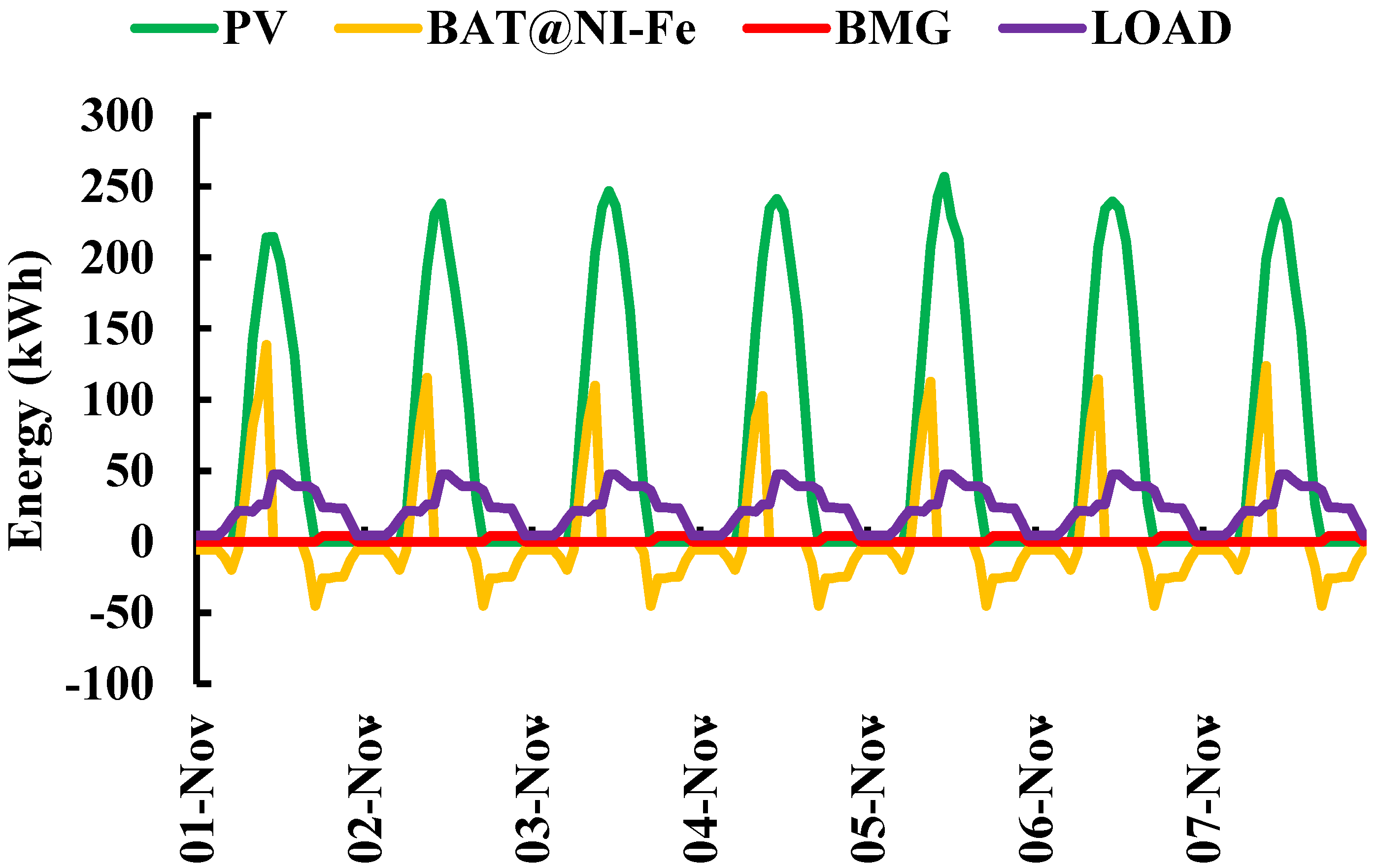
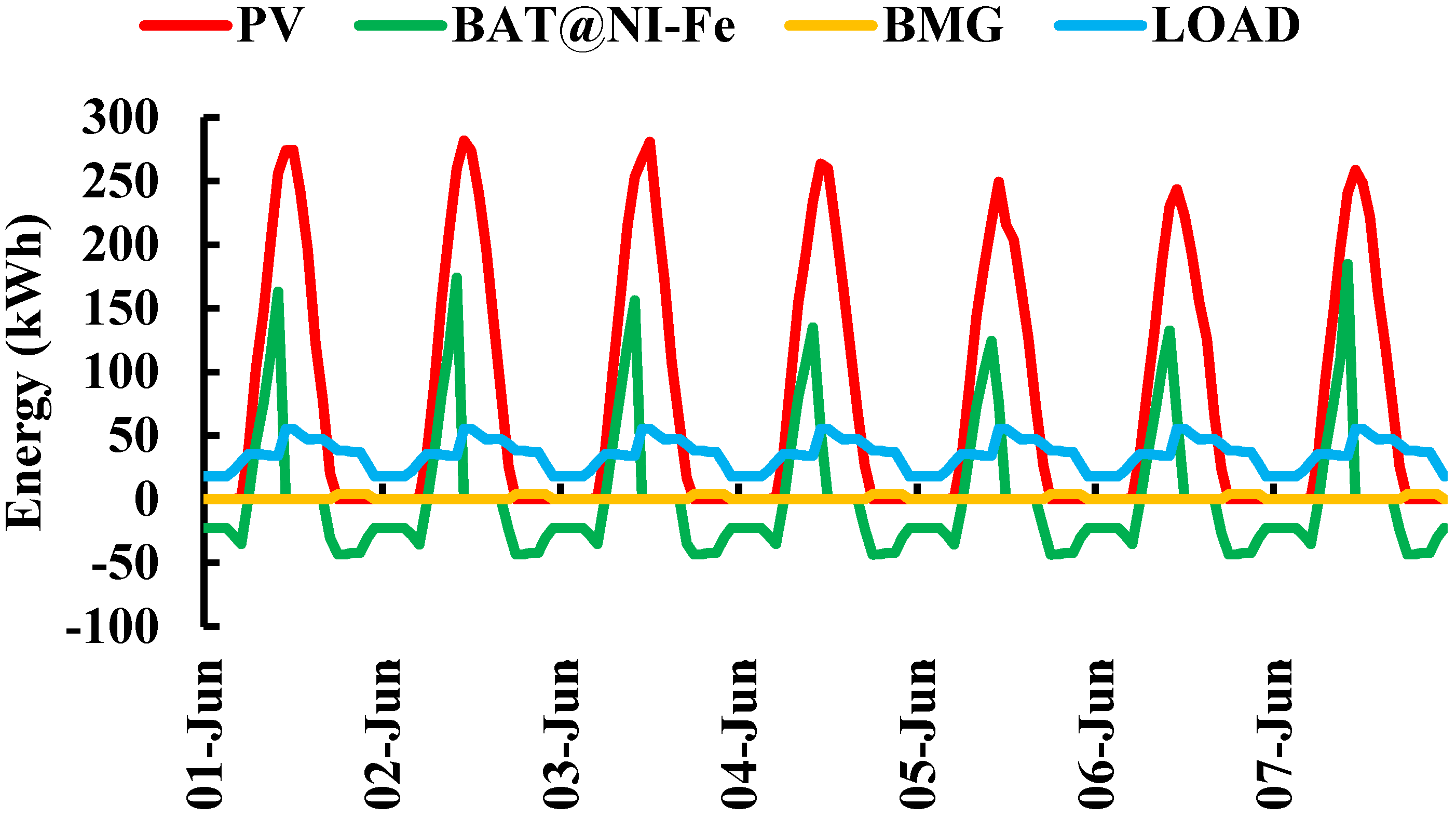
7.1. Various Configurations Using Battery Technologies and Renewable Energy Sources
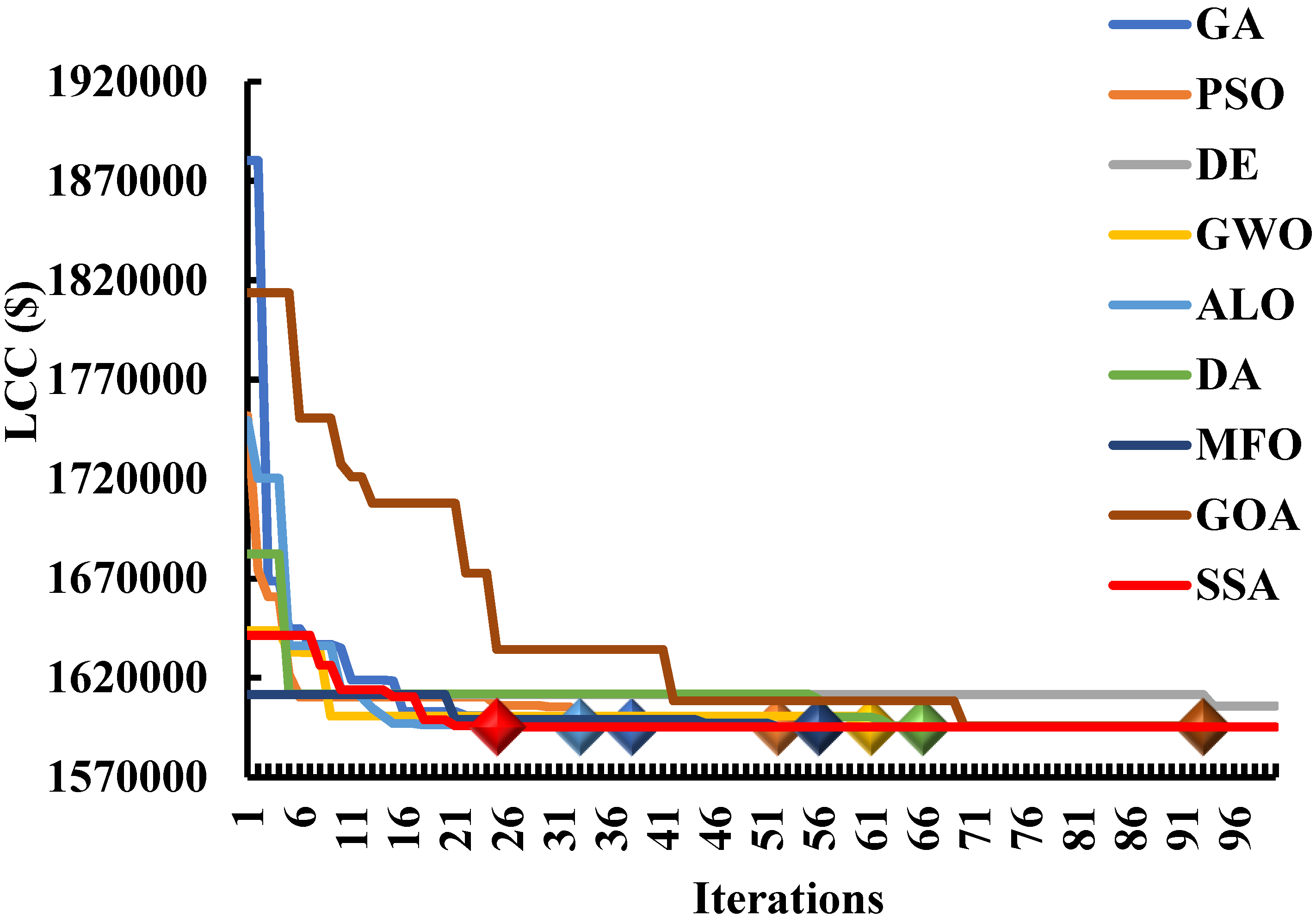
7.2. The Optimal Configuration from the Lead–Acid Battery Technology
7.3. The Optimal Configuration from the Lithium-Ion Battery Technology
7.4. The Optimal Configuration from the Nickel–Iron Battery Technology
7.5. Optimal Configuration from the HPRALC, MPRAMC, and LPRAHC-Based Configurations
7.5.1. The HPRALC-Based Scenario (without DSM)
7.5.2. Medium Efficiency Appliances Usage-Based Scenario (MPRAMC) (with DSM)
7.5.3. High-Efficiency Appliances Usage-Based Scenario (LPRAHC) (with DSM)
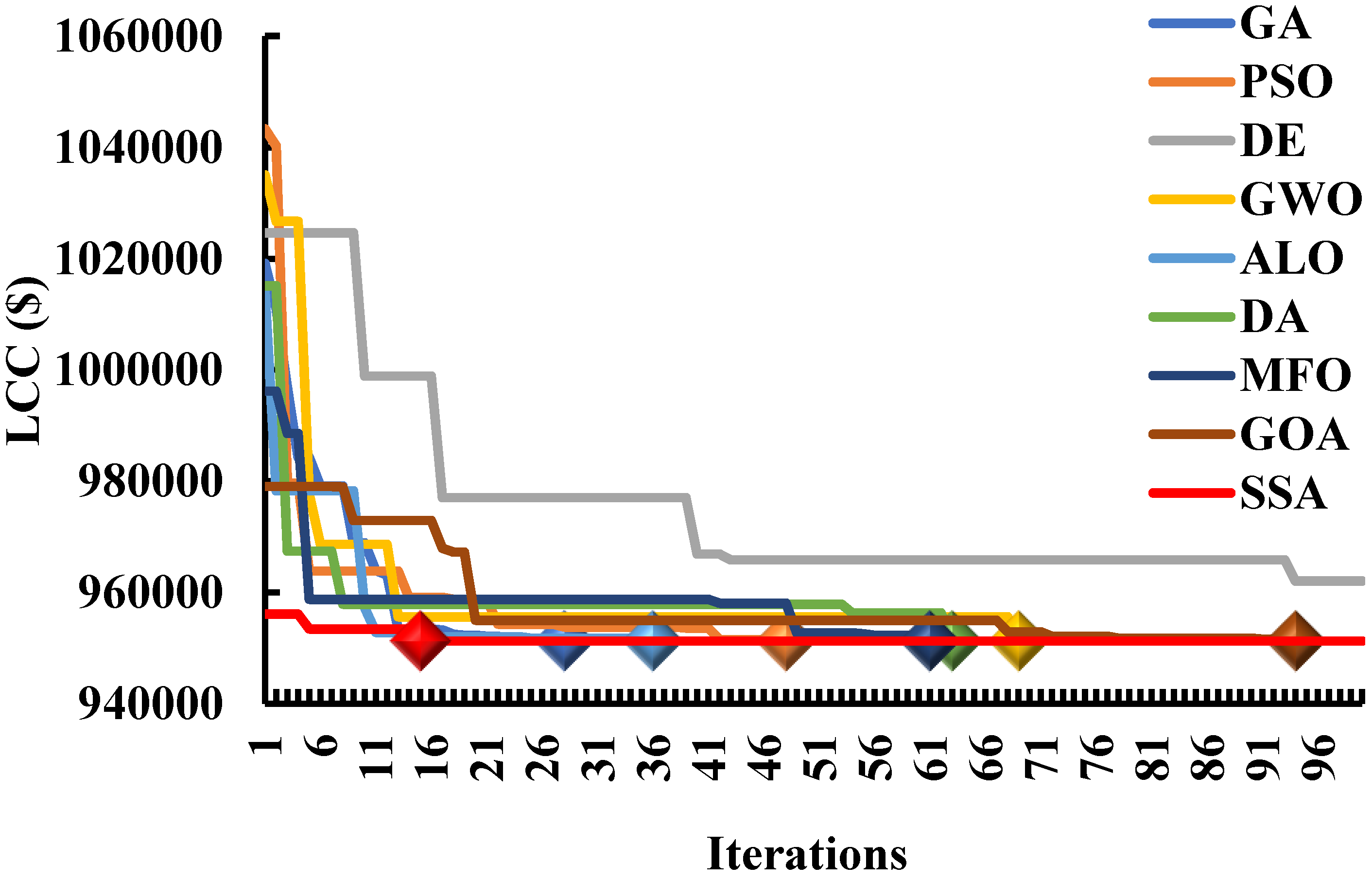
7.6. The Algorithm’s Ability to Find the Global Best Optimal Solutions
7.7. The Algorithms’ Effectiveness in Achieving the Global Best Optimal Solutions
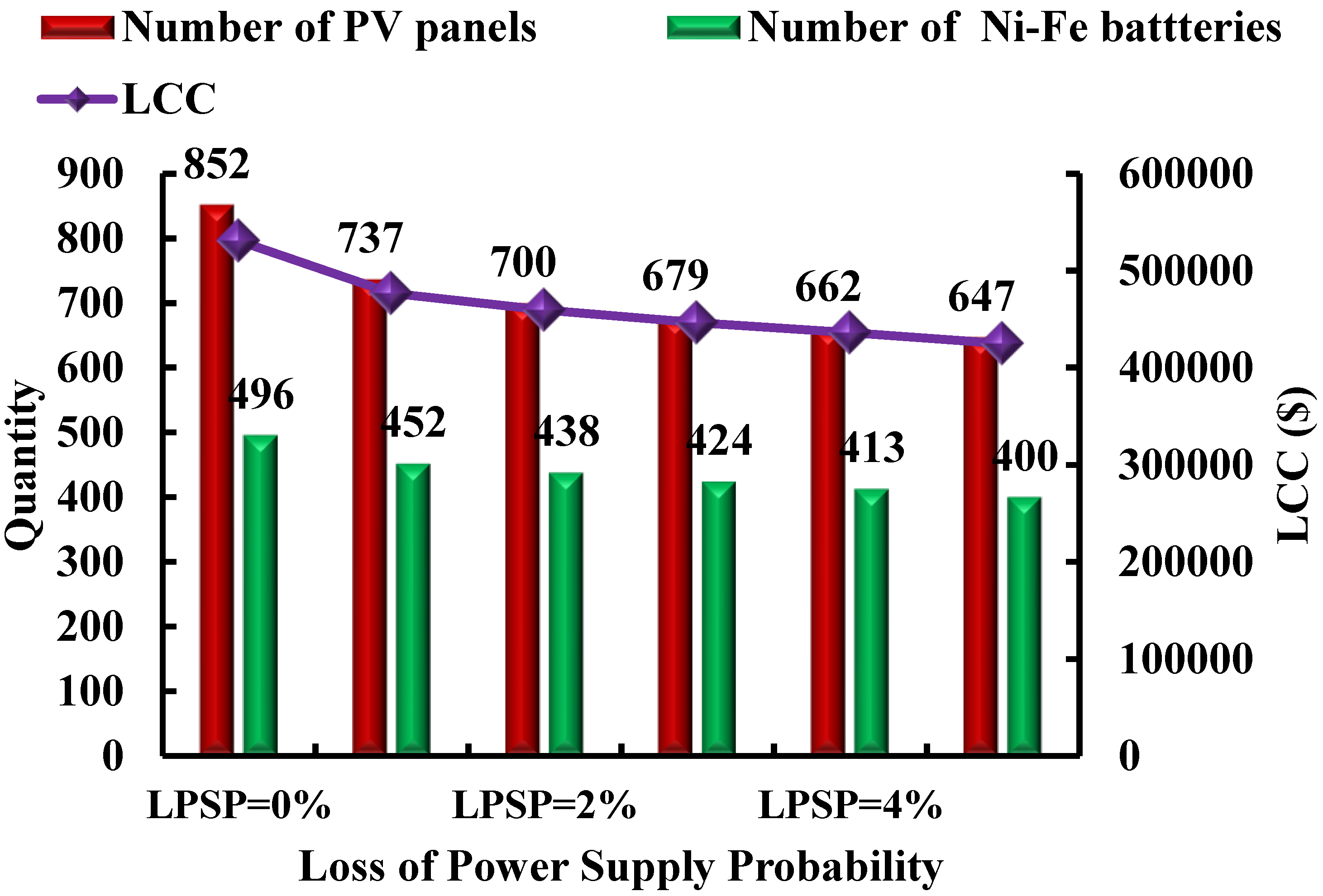
7.8. The Impact of LPSP on the System Efficiency
8. Conclusions
- The Ni–Fe-battery-based IRES with low-efficiency-appliance usage-based scenario obtained a life-cycle cost (LCC) of $951,257, which was 40% and 65% lower than the LA (@80% DOD) and lithium-ion (@50% DOD) battery-based IRESs LCCs, respectively;
- The Ni–Fe-battery-based IRES with medium-efficiency appliance usage-based scenario, i.e., with demand side management (DSM), yielded an LCC of $635,271, which was 33% lower than its LCC when using the low-efficiency appliance usage-based scenario;
- The Ni–Fe-battery-based IRES system with the integration of high-efficiency appliance usage-based scenario, i.e., with DSM, led to a significant decrease in the LCC by 44% and 17% when compared to the scenarios based on low and medium-efficiency appliance usage-based scenarios, respectively, to $530,603;
- This study determined that the Ni–Fe-battery-based IRES with DSM was the most cost-effective and efficient system for the study area. Future research should explore other renewable energy sources, control strategies, and innovative energy storage technologies in order to optimize the design of renewable energy-based systems.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Patel, A.M.; Singal, S.K. Optimal component selection of integrated renewable energy system for power generation in stand-alone applications. Energy 2019, 175, 481–504. [Google Scholar] [CrossRef]
- Bukar, A.L.; Tan, C.W.; Lau, K.Y. Optimal sizing of an autonomous photovoltaic/wind/battery/diesel generator microgrid using grasshopper optimization algorithm. Sol. Energy 2019, 188, 685–696. [Google Scholar] [CrossRef]
- Kumar, P.P.; Saini, R.P. Optimization of an off-grid integrated hybrid renewable energy system with different battery technologies for rural electrification in India. J. Energy Storage 2020, 32, 101912. [Google Scholar] [CrossRef]
- Bukar, A.L.; Tan, C.W. A review on stand-alone photovoltaic-wind energy system with fuel cell: System optimization and energy management strategy. J. Clean. Prod. 2019, 221, 73–88. [Google Scholar] [CrossRef]
- Sinha, S.; Chandel, S. Review of software tools for hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2014, 32, 192–205. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Zia, M.F.; Elbouchikhi, E.; Benbouzid, M.; Guerrero, J.M. Energy Management System for an Islanded Microgrid with Convex Relaxation. IEEE Trans. Ind. Appl. 2019, 55, 7175–7185. [Google Scholar] [CrossRef]
- Ramesh, M.; Saini, R.P. Dispatch strategies based performance analysis of a hybrid renewable energy system for a remote rural area in India. J. Clean. Prod. 2020, 259, 120697. [Google Scholar] [CrossRef]
- Kim, H.; Jung, T.Y. Independent solar photovoltaic with Energy Storage Systems (ESS) for rural electrification in Myanmar. Renew. Sustain. Energy Rev. 2018, 82, 1187–1194. [Google Scholar] [CrossRef]
- Kaabeche, A.; Bakelli, Y. Renewable hybrid system size optimization considering various electrochemical energy storage technologies. Energy Convers. Manag. 2019, 193, 162–175. [Google Scholar] [CrossRef]
- Ayeng’O, S.P.; Schirmer, T.; Kairies, K.-P.; Axelsen, H.; Sauer, D.U. Comparison of off-grid power supply systems using lead-acid and lithium-ion batteries. Sol. Energy 2018, 162, 140–152. [Google Scholar] [CrossRef]
- Li, C.; Zhou, D.; Wang, H.; Lu, Y.; Li, D. Techno-economic performance study of stand-alone wind/diesel/battery hybrid system with different battery technologies in the cold region of China. Energy 2020, 192, 116702. [Google Scholar] [CrossRef]
- Farinis, G.; Kanellos, F.D. Integrated energy management system for Microgrids of building prosumers. Electr. Power Syst. Res. 2021, 198, 107357. [Google Scholar] [CrossRef]
- Boglou, V.; Karavas, C.; Karlis, A.; Arvanitis, K. An intelligent decentralized energy management strategy for the optimal electric vehicles’ charging in low-voltage islanded microgrids. Int. J. Energy Res. 2022, 46, 2988–3016. [Google Scholar] [CrossRef]
- Zarate-Perez, E.; Rosales-Asensio, E.; González-Martínez, A.; de Simón-Martín, M.; Colmenar-Santos, A. Battery energy storage performance in microgrids: A scientific mapping perspective. Energy Rep. 2022, 8, 259–268. [Google Scholar] [CrossRef]
- Boglou, V.; Karavas, C.-S.; Karlis, A.; Arvanitis, K.G.; Palaiologou, I. An Optimal Distributed RES Sizing Strategy in Hybrid Low Voltage Networks Focused on EVs’ Integration. IEEE Access 2023, 11, 16250–16270. [Google Scholar] [CrossRef]
- Rimpas, D.; Kaminaris, S.D.; Piromalis, D.D.; Vokas, G.; Arvanitis, K.G.; Karavas, C.-S. Comparative Review of Motor Technologies for Electric Vehicles Powered by a Hybrid Energy Storage System Based on Multi-Criteria Analysis. Energies 2023, 16, 2555. [Google Scholar] [CrossRef]
- Huang, S.-C.; Lo, S.-L.; Lin, Y.-C. Application of a fuzzy cognitive map based on a structural equation model for the identification of limitations to the development of wind power. Energy Policy 2013, 63, 851–861. [Google Scholar] [CrossRef]
- Karavas, C.-S.; Kyriakarakos, G.; Arvanitis, K.G.; Papadakis, G. A multi-agent decentralized energy management system based on distributed intelligence for the design and control of autonomous polygeneration microgrids. Energy Convers. Manag. 2015, 103, 166–179. [Google Scholar] [CrossRef]
- Kokkinos, K.; Karayannis, V.; Moustakas, K. Circular bio-economy via energy transition supported by Fuzzy Cognitive Map modeling towards sustainable low-carbon environment. Sci. Total Environ. 2020, 721, 137754. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Man, K.F.; Tang, K.S.; Kwong, S. Genetic algorithms: Concepts and applications [in engineering design]. IEEE Trans. Ind. Electron. 1996, 43, 519–534. [Google Scholar] [CrossRef]
- Mirjalili, S. The Ant Lion Optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Chauhan, A.; Saini, R. Discrete harmony search based size optimization of Integrated Renewable Energy System for remote rural areas of Uttarakhand state in India. Renew. Energy 2016, 94, 587–604. [Google Scholar] [CrossRef]
- Lucchi, E. Integration between photovoltaic systems and cultural heritage: A socio-technical comparison of international policies, design criteria, applications, and innovation developments. Energy Policy 2022, 171, 113303. [Google Scholar] [CrossRef]
- Lucchi, E.; Baiani, S.; Altamura, P. Design criteria for the integration of active solar technologies in the historic built environment: Taxonomy of international recommendations. Energy Build. 2023, 278, 112651. [Google Scholar] [CrossRef]
- Lucchi, E. Renewable Energies and Architectural Heritage: Advanced Solutions and Future Perspectives. Buildings 2023, 13, 631. [Google Scholar] [CrossRef]
- Maleki, A. Design and optimization of autonomous solar-wind-reverse osmosis desalination systems coupling battery and hydrogen energy storage by an improved bee algorithm. Desalination 2018, 435, 221–234. [Google Scholar] [CrossRef]



| Configuration | Q&C | GA | PSO | DE | GWO | ALO | DA | MFO | GOA | SSA |
|---|---|---|---|---|---|---|---|---|---|---|
| PV/ BMG/ Ni–Fe @DOD = 80% | NPV | 1469 | 1469 | 1485 | 1469 | 1469 | 1469 | 1469 | 1469 | 1469 |
| NBAT | 950 | 950 | 962 | 950 | 950 | 950 | 950 | 950 | 950 | |
| LCC ($) | 951,257 | 951,257 | 962,065 | 951,257 | 951,257 | 951,257 | 951,257 | 951,257 | 951,257 | |
| PV/ BMG/ LA @DOD = 70% | NPV | 1364 | 1364 | 1364 | 1422 | 1364 | 1364 | 1364 | 1364 | 1364 |
| NBAT | 420 | 420 | 420 | 422 | 420 | 420 | 420 | 420 | 420 | |
| LCC ($) | 1,620,231 | 1,620,231 | 1,620,231 | 1,640,650 | 1,620,231 | 1,620,231 | 1,620,231 | 1,620,231 | 1,620,231 | |
| PV/ BMG/ LA @DOD = 80% | NPV | 1367 | 1367 | 1383 | 1367 | 1367 | 1367 | 1367 | 1367 | 1367 |
| NBAT | 367 | 367 | 369 | 367 | 367 | 367 | 367 | 367 | 367 | |
| LCC ($) | 1,595,267 | 1,595,267 | 1,605,861 | 1,595,267 | 1,595,267 | 1,595,267 | 1,595,267 | 1,595,267 | 1,595,267 | |
| PV/ BMG/ Li-Ion @DOD = 50% | NPV | 1264 | 1264 | 1266 | 1264 | 1536 | 2000 | 1264 | 1264 | 1264 |
| NBAT | 419 | 419 | 420 | 419 | 411 | 398 | 419 | 419 | 419 | |
| LCC ($) | 2,712,794 | 2,712,794 | 2,718,907 | 2,712,794 | 2,736,122 | 2,779,547 | 2,712,794 | 2,712,794 | 2,712,794 | |
| PV/ BMG/ Li-Ion @DOD = 70% | NPV | 1649 | 1268 | 1268 | 1268 | 1364 | 1730 | 1272 | 1242 | 1268 |
| NBAT | 291 | 299 | 299 | 299 | 297 | 290 | 300 | 300 | 299 | |
| LCC ($) | 2,804,117 | 2,773,053 | 2,773,053 | 2,773,053 | 2,781,007 | 2,816,370 | 2,782,117 | 2,774,594 | 2,773,053 | |
| PV/ BMG/ Li-Ion @DOD = 80% | NPV | 1245 | 1354 | 1408 | 1245 | 1953 | 2000 | 1245 | 1245 | 1245 |
| NBAT | 262 | 260 | 259 | 262 | 249 | 249 | 262 | 262 | 262 | |
| LCC ($) | 3,025,532 | 3,032,498 | 3,035,855 | 3,025,532 | 3,070,686 | 3,082,473 | 3,025,532 | 3,025,532 | 3,025,532 |
| Configuration | Q&C | GA | PSO | DE | GWO | ALO | DA | MFO | GOA | SSA |
|---|---|---|---|---|---|---|---|---|---|---|
| PV/ BMG/ Ni–Fe @DOD = 80% | NPV | 1005 | 1005 | 1008 | 1005 | 1005 | 1005 | 1005 | 1005 | 1005 |
| NBAT | 612 | 612 | 625 | 612 | 612 | 612 | 612 | 612 | 612 | |
| LCC ($) | 635,271 | 635,271 | 643,385 | 635,271 | 635,271 | 635,271 | 635,271 | 635,271 | 635,271 |
| Configuration | Q&C | GA | PSO | DE | GWO | ALO | DA | MFO | GOA | SSA |
|---|---|---|---|---|---|---|---|---|---|---|
| PV/ BMG/ Ni–Fe @DOD = 80% | NPV | 852 | 852 | 852 | 852 | 852 | 852 | 852 | 852 | 852 |
| NBAT | 496 | 496 | 500 | 496 | 496 | 496 | 496 | 496 | 496 | |
| LCC ($) | 530,603 | 530,603 | 532,868 | 530,603 | 530,603 | 530,603 | 530,603 | 530,603 | 530,603 |
| Configuration | Quantity and Cost | LPSP (0%) | LPSP (1%) | LPSP (2%) | LPSP (3%) | LPSP (4%) | LPSP (5%) |
|---|---|---|---|---|---|---|---|
| PV/ BMG/ Ni–Fe @DOD = 80% | NPV | 852 | 737 | 700 | 679 | 662 | 647 |
| NBAT | 496 | 452 | 438 | 424 | 413 | 400 | |
| LCC ($) | 530,603 | 476,846 | 459,639 | 446,445 | 435,953 | 424,829 | |
| LPSH | 0 | 173 | 310 | 467 | 579 | 649 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, P.P.; Rahman, A.; Nuvvula, R.S.S.; Colak, I.; Muyeen, S.M.; Shezan, S.A.; Shafiullah, G.M.; Ishraque, M.F.; Hossain, M.A.; Alsaif, F.; et al. Using Energy Conservation-Based Demand-Side Management to Optimize an Off-Grid Integrated Renewable Energy System Using Different Battery Technologies. Sustainability 2023, 15, 10137. https://doi.org/10.3390/su151310137
Kumar PP, Rahman A, Nuvvula RSS, Colak I, Muyeen SM, Shezan SA, Shafiullah GM, Ishraque MF, Hossain MA, Alsaif F, et al. Using Energy Conservation-Based Demand-Side Management to Optimize an Off-Grid Integrated Renewable Energy System Using Different Battery Technologies. Sustainability. 2023; 15(13):10137. https://doi.org/10.3390/su151310137
Chicago/Turabian StyleKumar, Polamarasetty P, Akhlaqur Rahman, Ramakrishna S. S. Nuvvula, Ilhami Colak, S. M. Muyeen, Sk. A. Shezan, G. M. Shafiullah, Md. Fatin Ishraque, Md. Alamgir Hossain, Faisal Alsaif, and et al. 2023. "Using Energy Conservation-Based Demand-Side Management to Optimize an Off-Grid Integrated Renewable Energy System Using Different Battery Technologies" Sustainability 15, no. 13: 10137. https://doi.org/10.3390/su151310137
APA StyleKumar, P. P., Rahman, A., Nuvvula, R. S. S., Colak, I., Muyeen, S. M., Shezan, S. A., Shafiullah, G. M., Ishraque, M. F., Hossain, M. A., Alsaif, F., & Elavarasan, R. M. (2023). Using Energy Conservation-Based Demand-Side Management to Optimize an Off-Grid Integrated Renewable Energy System Using Different Battery Technologies. Sustainability, 15(13), 10137. https://doi.org/10.3390/su151310137













