Crop Cultivation Efficiency and GHG Emission: SBM-DEA Model with Undesirable Output Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Data and Data Curation
2.2. Carbon Footprint Evaluation
2.3. Efficiency Measurement Using SBM-DEA Model with Undesirable Output
2.4. Explaining Efficiency
3. Results
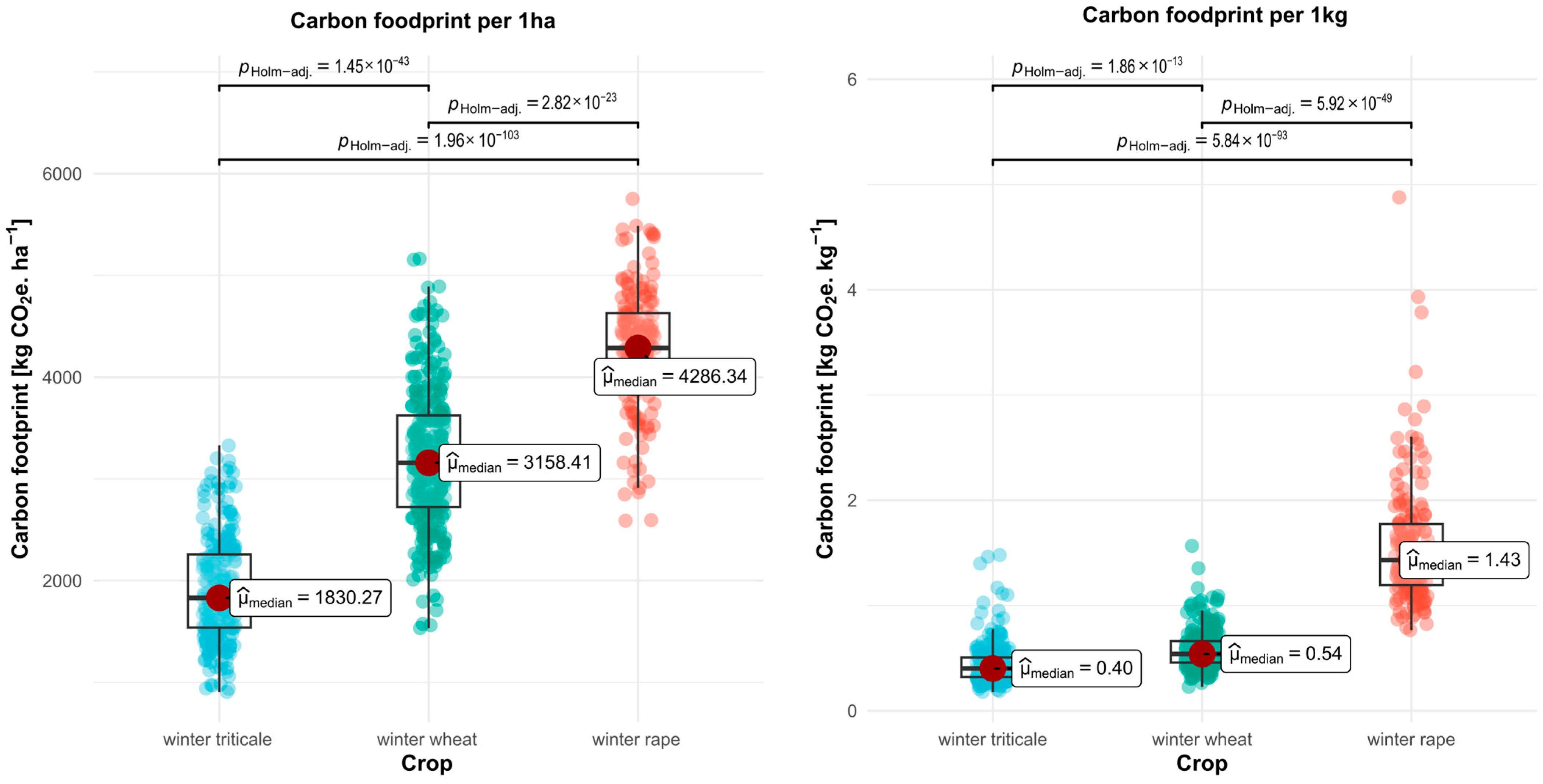
3.1. Carbon Footprint
3.2. SBM-DEA Efficient vs. Non-Efficient Farms
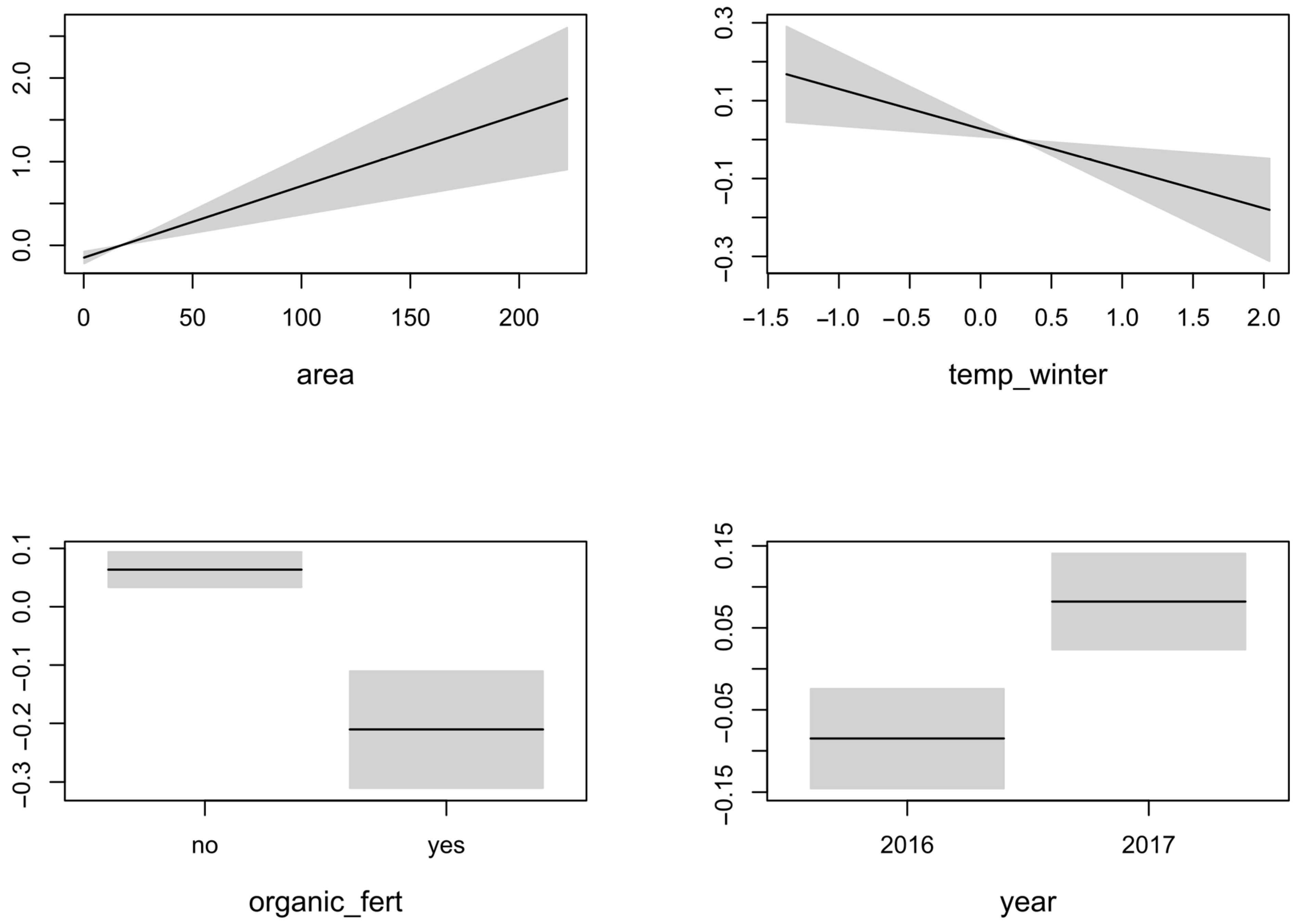
3.3. Factors That Influence Eco-Efficiency
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Food and Agriculture Organization of the United Nations. Energy-Smart Food at FAO: An Overview; Food and Agriculture Organization of the United Nations: Rome, Italy, 2012. [Google Scholar]
- European Comission. CAP Strategic Plans. Available online: https://agriculture.ec.europa.eu/cap-my-country/cap-strategic-plans_en (accessed on 9 November 2022).
- European Comission. A European Green Deal: Striving to Be the First Climate-Neutral Continent. Available online: https://commission.europa.eu/strategy-and-policy/priorities-2019-2024/european-green-deal_en (accessed on 9 November 2022).
- World Business Council for Sustainable Development. Eco-Efficiency, Creating More Value with Less Impact; World Business Council for Sustainable Development: Geneva, Switzerland, 2000. [Google Scholar]
- Streimikis, J.; Saraji, M.K. Green Productivity and Undesirable Outputs in Agriculture: A Systematic Review of DEA Approach and Policy Recommendations. Econ. Res. Ekon. Istraživanja 2022, 35, 819–853. [Google Scholar] [CrossRef]
- Kuosmanen, T.; Kortelainen, M. Measuring Eco-Efficiency of Production with Data Envelopment Analysis. J. Ind. Ecol. 2005, 9, 59–72. [Google Scholar] [CrossRef]
- Moradi, M.; Nematollahi, M.A.; Mousavi Khaneghah, A.; Pishgar-Komleh, S.H.; Rajabi, M.R. Comparison of Energy Consumption of Wheat Production in Conservation and Conventional Agriculture Using DEA. Environ. Sci. Pollut. Res. 2018, 25, 35200–35209. [Google Scholar] [CrossRef] [PubMed]
- Nabavi-Pelesaraei, A.; Rafiee, S.; Mohtasebi, S.S.; Hosseinzadeh-Bandbafha, H.; Chau, K. Energy Consumption Enhancement and Environmental Life Cycle Assessment in Paddy Production Using Optimization Techniques. J. Clean. Prod. 2017, 162, 571–586. [Google Scholar] [CrossRef]
- Khoshnevisan, B.; Rafiee, S.; Omid, M.; Mousazadeh, H. Reduction of CO2 Emission by Improving Energy Use Efficiency of Greenhouse Cucumber Production Using DEA Approach. Energy 2013, 55, 676–682. [Google Scholar] [CrossRef]
- Dong, G.; Wang, Z.; Mao, X. Production Efficiency and GHG Emissions Reduction Potential Evaluation in the Crop Production System Based on Emergy Synthesis and Nonseparable Undesirable Output DEA: A Case Study in Zhejiang Province, China. PLoS ONE 2018, 13, e0206680. [Google Scholar] [CrossRef]
- Oukil, A.; Zekri, S. A Three-Stage Analytical Framework for the Evaluation of Farming Efficiency. In Proceedings of the 12th International Conference on Data Envelopment Analysis, Kuala Lumpur, Malaysia, 14–17 April 2014. [Google Scholar]
- Pishgar-Komleh, S.H.; Zylowski, T.; Rozakis, S.; Kozyra, J. Efficiency under Different Methods for Incorporating Undesirable Outputs in an LCA+DEA Framework: A Case Study of Winter Wheat Production in Poland. J. Environ. Manag. 2020, 260, 110138. [Google Scholar] [CrossRef]
- Tone, K. Dealing with Undesirable Outputs in DEA: A Slacks-Based Measure (SBM) Approach. GRIPS Res. Rep. Ser. 2003, 6, 67–74. [Google Scholar]
- Mohammadi, A.; Venkatesh, G.; Eskandari, S.; Rafiee, S. Eco-Efficiency Analysis to Improve Environmental Performance of Wheat Production. Agriculture 2022, 12, 1031. [Google Scholar] [CrossRef]
- Ramalho, E.A.; Ramalho, J.J.S.; Henriques, P.D. Fractional Regression Models for Second Stage DEA Efficiency Analyses. J. Product. Anal. 2010, 34, 239–255. [Google Scholar] [CrossRef]
- Simar, L.; Wilson, P.W. Estimation and Inference in Two-Stage, Semi-Parametric Models of Production Processes. J. Econ. 2007, 136, 31–64. [Google Scholar] [CrossRef]
- Balcombe, K.; Fraser, I.; Latruffe, L.; Rahman, M.; Smith, L. An Application of the DEA Double Bootstrap to Examine Sources of Efficiency in Bangladesh Rice Farming. Appl. Econ. 2008, 40, 1919–1925. [Google Scholar] [CrossRef]
- Picazo-Tadeo, A.J.; Gómez-Limón, J.A.; Reig-Martínez, E. Assessing Farming Eco-Efficiency: A Data Envelopment Analysis Approach. J. Environ. Manag. 2011, 92, 1154–1164. [Google Scholar] [CrossRef]
- Chidmi, B.; Solis, D.; Funtanilla; Cabrera, V. Analyzing the Determinants of Technical Efficiency among Traditional Dairy Farms in Wisconsin: A Quantile Regression Approach. In Proceedings of the Agricultural and Applied Economics Association (AAEA) Conferences 2010 Annual Meeting, Denver, CO, USA, 25–27 July 2010; p. 22. [Google Scholar]
- Darmawan, A.S.; Anggraeni, D.; Tirta, I.M. Application of Generalized Additive Model Location, Scale and Shape (GAMLSS) for Rice Production in Banyuwangi Regency. J. Phys. Conf. Ser. 2019, 1211, 012025. [Google Scholar] [CrossRef]
- Schaak, H.; Musshoff, O. The Distribution of the Rent–Price Relationship of Agricultural Land in Germany. Eur. Rev. Agric. Econ. 2021, 49, 696–718. [Google Scholar] [CrossRef]
- Łączyński, A. Rocznik Statystyczny Rolnictwa; Główny Urząd Statystyczny: Warsaw, Poland, 2017; p. 495. [Google Scholar]
- Kopiński, J.; Witorożec, A. Resources of main macronutrients in natural fertilizers in Poland. Ann. Pol. Assoc. Agric. Agribus. Econ. 2021, 23, 64–74. [Google Scholar] [CrossRef]
- The Journal of Laws of the Republic of Poland, 2020, Item 243, Page 107, Table 11. Available online: https://isap.sejm.gov.pl/isap.nsf/download.xsp/WDU20200000243/O/D20200243.pdf (accessed on 17 December 2022).
- Ester, M.; Kriegel, H.-P.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; p. 6. [Google Scholar]
- Hahsler, M.; Piekenbrock, M.; Doran, D. Dbscan: Fast Density-Based Clustering with R. J. Stat. Softw. 2019, 91, 28. [Google Scholar] [CrossRef]
- Cornes, R.C.; van der Schrier, G.; van den Besselaar, E.J.M.; Jones, P.D. An Ensemble Version of the E-OBS Temperature and Precipitation Data Sets. J. Geophys. Res. Atmos. 2018, 123, 9391–9409. [Google Scholar] [CrossRef]
- Schulzweida, U.; Kornblueh, L.; Quast, R. CDO User’s Guide; Climate Data Operators Version; MPI for Meteorology: Hamburg, Germany, 2006; p. 1. [Google Scholar]
- Wiedmann, T.; Minx, J. A Definition of ‘Carbon Footprint’. In Ecological Economics Research Trends; Nova Science Publishers: Hauppauge, NY, USA, 2008; Volume 1, pp. 1–11. [Google Scholar]
- Intergovernmental Panel on Climate Change. N2O Emissions from Managed Soils, and CO2 Emissions from Lime and Urea Application. In Proceedings of the 2019 Refinement to the 2006 IPCC Guidelines for National Greenhouse Gas Inventories, Kyoto, Japan, 12 May 2019. [Google Scholar]
- National Centre for Emission Management (KOBiZE). Poland’s National Inventory Report 2020. Greenhouse Gas Inventory for 1998–2018; Institute of Environmental Protection–National Research Institute: Warsaw, Poland, 2020.
- Stocker, T.F.; Qin, D.; Plattner, G.-K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, B.; Midgley, B.M. IPCC, 2013: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Biograce–Complete List of Standard Values to Harmonise European GHG Calculations, Version 4, Public. 2011. Available online: https://www.biograce.net/content/ghgcalculationtools/standardvalues (accessed on 17 December 2022).
- Wernet, G.; Bauer, C.; Steubing, B.; Reinhard, J.; Moreno-Ruiz, E.; Weidema, B. The Ecoinvent Database Version 3 (Part I): Overview and Methodology. Int. J. Life Cycle Assess. 2016, 21, 1218–1230. [Google Scholar] [CrossRef]
- Nemecek, T.; Kägi, T. Life Cycle Inventories of Agricultural Production Systems; Ecoinvent: Zurich, Switzerland, 2007; p. 360. [Google Scholar]
- Muzalewski, A. Zasady Doboru Maszyn Rolniczych w Ramach PROW na Lata 2014–2020; ITP: Warsaw, Poland, 2015; p. 125. [Google Scholar]
- Koch, P.; Salou, T.; Colomb, V.; Payen, S.; Perret, S.R.; Tailleur, A.; Willmann, S. Agribalyse: Methodology; Version 1.2; ADEME: Angers, France, 2015. [Google Scholar]
- Emrouznejad, A.; Yang, G. A Survey and Analysis of the First 40 Years of Scholarly Literature in DEA: 1978–2016. Socio-Econ. Plan. Sci. 2018, 61, 4–8. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the Efficiency of Decision Making Units. Eur. J. Oper. Res. 1978, 26, 429–444. [Google Scholar] [CrossRef]
- Cooper, W.W.; Seiford, L.M.; Tone, K. Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software, 2nd ed.; Springer: New York, NY, USA, 2007; ISBN 978-0-387-45281-4. [Google Scholar]
- Cooper, W.W. International series in operations research & management science. In Handbook on Data Envelopment Analysis, 2nd ed.; Springer: New York, NY, USA, 2011; ISBN 978-1-4419-6150-1. [Google Scholar]
- Tone, K. A Slacks-Based Measure of Effciency in Data Envelopment Analysis. Eur. J. Oper. Res. 2001, 12, 498–509. [Google Scholar] [CrossRef]
- Liu, W.B.; Meng, W.; Li, X.X.; Zhang, D.Q. DEA Models with Undesirable Inputs and Outputs. Ann. Oper. Res. 2010, 173, 177–194. [Google Scholar] [CrossRef]
- Coll, V.; Benítez, R.; Bolós, V.J. Data Envelopment Analysis with DeaR; School of Economics, University of Valencia: Valencia, Spain, 2018. [Google Scholar]
- Woods, J.; Williams, A.; Hughes, J.K.; Black, M.; Murphy, R. Energy and the Food System. Philos. Trans. R. Soc. B Biol. Sci. 2010, 365, 2991–3006. [Google Scholar] [CrossRef] [PubMed]
- Rigby, B.; Stasinopoulos, M. A FLexible Regression Approach Using GAMLSS in R; London Metropolitan University: London, UK, 2009; p. 282. [Google Scholar]
- Stasinopoulos, D.M.; Rigby, R.A. Generalized Additive Models for Location Scale and Shape (GAMLSS) in R. J. Stat. Softw. 2007, 23, 1–46. [Google Scholar] [CrossRef]
- Kaditi, E.A.; Nitsi, E.I. Applying Regression Quantiles to Farm Efficiency Estimation. In Proceedings of the Agricultural and Applied Economics Association (AAEA) Conferences 2010 Annual Meeting, Denver, CO, USA, 25–27 July 2010; p. 15. [Google Scholar]
- Clune, S.; Crossin, E.; Verghese, K. Systematic Review of Greenhouse Gas Emissions for Different Fresh Food Categories. J. Clean. Prod. 2017, 140, 766–783. [Google Scholar] [CrossRef]
- Hillier, J.; Hawes, C.; Squire, G.; Hilton, A.; Wale, S.; Smith, P. The Carbon Footprints of Food Crop Production. Int. J. Agric. Sustain. 2009, 7, 107–118. [Google Scholar] [CrossRef]
- Bieńkowski, J.; Holka, M. Cost and Environmental Efficiency in Measuring the Eco-Efficiency Performance of Winter Triticale Production. In Proceedings of the X International Agriculture Symposium, Agrosym 2019, Jahorina, East Sarajevo, Bosnia and Herzegovina, 3–6 October 2019; pp. 1325–1330. [Google Scholar]
- Zhang, W.; Qian, C.; Carlson, K.M.; Ge, X.; Wang, X.; Chen, X. Increasing Farm Size to Improve Energy Use Efficiency and Sustainability in Maize Production. Food Energy Secur. 2021, 10, e271. [Google Scholar] [CrossRef]
- Ricciardi, V.; Mehrabi, Z.; Wittman, H.; James, D.; Ramankutty, N. Higher Yields and More Biodiversity on Smaller Farms. Nat. Sustain. 2021, 4, 651–657. [Google Scholar] [CrossRef]
- Galushko, V.; Gamtessa, S. Impact of Climate Change on Productivity and Technical Efficiency in Canadian Crop Production. Sustainability 2022, 14, 4241. [Google Scholar] [CrossRef]
- Raza, A.; Razzaq, A.; Mehmood, S.; Zou, X.; Zhang, X.; Lv, Y.; Xu, J. Impact of Climate Change on Crops Adaptation and Strategies to Tackle Its Outcome: A Review. Plants 2019, 8, 34. [Google Scholar] [CrossRef] [PubMed]
- Olesen, J.E.; Trnka, M.; Kersebaum, K.C.; Skjelvåg, A.O.; Seguin, B.; Peltonen-Sainio, P.; Rossi, F.; Kozyra, J.; Micale, F. Impacts and Adaptation of European Crop Production Systems to Climate Change. Eur. J. Agron. 2011, 34, 96–112. [Google Scholar] [CrossRef]
- Rebouh, N.Y.; Latati, M.; Polityko, P.M.; Kucher, D.E.; Hezla, L.; Norezzine, A.; Kalisa, L.; Vvedenskiy, V.; Gadzhikurbanov, A.S.; Ivanov, N.; et al. Influence of Three Cultivation Technologies to Control Fusarium Spp. in Winter Wheat (Triticum Aestivum L.) Production under Moscow Conditions. Res. Crops 2020, 21, 17–25. [Google Scholar] [CrossRef]
- Rebouh, N.Y.; Aliat, T.; Polityko, P.M.; Kherchouche, D.; Boulelouah, N.; Temirbekova, S.K.; Afanasyeva, Y.V.; Kucher, D.E.; Plushikov, V.G.; Parakhina, E.A.; et al. Environmentally Friendly Wheat Farming: Biological and Economic Efficiency of Three Treatments to Control Fungal Diseases in Winter Wheat (Triticum Aestivum L.) under Field Conditions. Plants 2022, 11, 1566. [Google Scholar] [CrossRef]
- Zemmouri, B.; Lammoglia, S.-K.; Bouras, F.-Z.; Seghouani, M.; Rebouh, N.Y.; Latati, M. Modelling Human Health Risks from Pesticide Use in Innovative Legume-Cereal Intercropping Systems in Mediterranean Conditions. Ecotoxicol. Environ. Saf. 2022, 238, 113590. [Google Scholar] [CrossRef]



| Input/Output | Unit | Winter Wheat | Winter Triticale | Winter Oilseed Rape |
|---|---|---|---|---|
| Number of farms | 293 | 230 | 174 | |
| Inputs | ||||
| 1. Seed | kg | 200.2 (±32.1) | 199.9 (±30.9) | 3.3 (±0.8) |
| 2. Diesel fuel | l | 109.1 (±37.6) | 96.9 (±36.8) | 111.0 (±35.1) |
| 3. Machinery | h | 9.5 (±3.3) | 9.5 (±3.4) | 8.8 (±2.9) |
| 4. Total NPK Mineral N Mineral P2O5 Mineral K2O Natural N Natural P2O5 Natural K2O | kg kg kg kg kg kg kg | 238.9 (±107.4) 124.7 (±61.9) 27.1 (±31.3) 44.7 (±45.4) 11.0 (±22.8) 9.3 (±20.4) 20.4 (±48.2) | 262.1 (±131.1) 96.6 (±46.7) 30.0 (±24.8) 46.6 (± 22.0) 22.0 (±27.3) 17.1 (±22.8) 49.9 (±67.0) | 308.3 (±121.7) 172.4 (±55.1) 43.6 (±44.1) 63.6 (±43.6) 7.9 (±20.8) 7.1 (±19.4) 13.8 (±38.9) |
| 5. Pesticides | kg a.i. | 3.4 (±1.8) | 2.6 (±1.8) | 4.3 (±1.6) |
| Output (grain) | t | 5.8 (±1.4) | 4.6 (±1.2) | 3.0 (±0.8) |
| Variable Name | Description | Range |
|---|---|---|
| area | Size of arable field [ha] | [0.2; 50] |
| temp_autumn | Mean of autumn air temperature (IX-XI) [°C] | [9.22; 12.97] |
| prec_autumn | Sum of autumn precipitation [mm] | [62.90; 215.6] |
| temp_winter | Mean of winter air temperature (XII-II) [°C] | [−1.37; 2.17] |
| prec_winter | Sum of winter precipitation [mm] | [80.30; 236.2] |
| temp_spring | Mean of spring air temperature (III-V) [°C] | [7.49; 10.43] |
| prec_spring | Sum of spring precipitation [mm] | [72.50; 261.8] |
| temp_summer | Mean of summer air temperature (VI-VII) [°C] | [16.01; 19.44] |
| prec_summer | Sum of summer precipitation [mm] | [66.00; 292.1] |
| soil | Soil class | {good *, medium, poor} |
| type | The main type of production (FADN) | {crop *, dairy, pig} |
| econ_class | Economic size of farm (FADN) | {big *, medium, small} |
| organic_fert | Use of natural fertilizers (manure/slurry) in a given season | {no *, yes} |
| year | Season of cultivation (2015/2016 or 2016/2017) | {2016 *, 2017} |
| fadn | Belongs to Polish FADN region | {A *, B, C, D} |
| residue_collected | Is residue collected? | {no *, yes} |
| Emissions Related to Agricultural Inputs | Unit | kg CO2e/Unit | Source | Comments/Details |
|---|---|---|---|---|
| Inputs | ||||
| Urea-based fertilizer | kg N | 3.17 | [33] | |
| Ammonium based | kg N | 1.62 | [33] | Ammonium sulphate |
| Nitrate based | kg N | 6.34 | [33] | CAN |
| Ammonium nitrate | kg N | 6.21 | [33] | |
| P2O | kg P2O5 | 1.01 | [33] | |
| K2O5 | kg K2O | 0.58 | [33] | |
| CaO | kg CaO | 0.13 | [33] | |
| Pesticides | kg | 10.97 | [33] | |
| Diesel fuel | l | 3.15 | [33] | |
| Machinery | ||||
| Tractor | kg | 7.78 | [34] | Tractor, 4-wheel, agricultural {RoW}|production|APOS, U |
| Equipment | kg | 5.56 | [34] | Agricultural machinery, unspecified {RoW}|production|APOS|U |
| Harvester | kg | 6.66 | [34] | Harvester{RoW}|production|APOS|U |
| Seeds | ||||
| winter wheat/triticale | kg | 0.87 | [34] | Wheat seed, for sowing {GLO}|market for|APOS, U |
| winter oilseed rape | kg | 1.23 | [34] | Rape seed, for sowing {RoW}|market for rape seed, for sowing|APOS, U |
| Manure/Slurry | t/m3 | 0.00 | [33] |
| Crop/ Variable | Econ_Class | Area [ha] | Yield [t ha−1] | NPK_Total [kg ha−1] | Fuel [kg ha−1] | Machinery [h ha−1] | CF_ha [kg CO2e ha−1] | CF_kg [kg CO2e kg−1] |
|---|---|---|---|---|---|---|---|---|
| big | 25.9 a | 3.03 a | 317 a | 116 a | 8.23 a | 4315 a | 1.51 a | |
| winter rape | medium | 14.3 b | 2.98 a | 297 a | 106 a | 9.09 ab | 4203 a | 1.57 a |
| small | 6.29 c | 2.56 a | 323 a | 110 a | 10.4 b | 4401 a | 1.95 a | |
| big | 11.9 a | 5.11 a | 301 a | 114 a | 9.25 a | 2121 a | 0.428 a | |
| winter triticale | medium | 6.2 b | 4.51 b | 257 b | 90.4 b | 9.44 a | 1849 b | 0.458 a |
| small | 3.12 c | 4.09 b | 202 c | 83.1 c | 10.1 a | 1717 b | 0.447 a | |
| big | 30.4 a | 6.07 a | 278 a | 125 a | 8.54 a | 3424 a | 0.586 a | |
| winter wheat | medium | 12 b | 5.85 ab | 226 b | 103 b | 9.85 b | 3131 b | 0.562 a |
| small | 4.86 c | 5.08 b | 190 b | 94.9 b | 11 c | 2850 c | 0.623 a |
| Crop/ Variable | Type | Area [ha] | Yield [t ha−1] | NPK_Total [kg ha−1] | Fuel [kg ha−1] | Machinery [h ha−1] | CF_ha [kg CO2e ha−1] | CF_kg [kg CO2e kg−1] |
|---|---|---|---|---|---|---|---|---|
| crop | 23.7 a | 2.91 a | 287 a | 106 a | 8.54 a | 4231 a | 1.6 a | |
| winter rape | dairy | 7.9 b | 3.04 a | 331 ab | 126 a | 8.8 a | 4420 a | 1.56 a |
| pig | 8.53 b | 3.11 a | 363 b | 122 a | 9.5 a | 4350 a | 1.51 a | |
| crop | 9.44 a | 4.35 a | 200 a | 82.2 a | 7.51 a | 1918 a b | 0.472 a | |
| winter triticale | dairy | 4.34 b | 4.47 a | 264 b | 93.1 a | 9.73 b | 1809 a | 0.444 a |
| pig | 9.21 a | 4.93 b | 295 b | 108 b | 10.4 b | 2005 b | 0.434 a | |
| crop | 28 a | 6.02 a | 223 a | 106 a | 8.97 a | 3297 a | 0.584 a | |
| winter wheat | dairy | 4.27 b | 5.3 b | 205 a | 103 a | 10.2 b | 2909 b | 0.574 a |
| pig | 7.21 c | 5.9 a | 291 b | 120 a | 10.2 a b | 3220 a | 0.565 a |
| Item | Winter Rape | Winter Triticale | Winter Wheat |
|---|---|---|---|
| Total number of farms | 174 | 230 | 293 |
| TE = 1 | 12 (6.9%) | 20 (8.7%) | 20 (6.8%) |
| PTE = 1 | 25 (14.4%) | 35 (15.2%) | 34 (11.6%) |
| TE score | 0.49 (±0.20) | 0.47(±0.20) | 0.50 (±0.18) |
| PTE score | 0.56 (±0.22) | 0.53 (±0.23) | 0.56 (±0.21) |
| SE score | 0.88 (±0.13) | 0.90 (±0.13) | 0.90 (±0.12) |
| Type of scale efficiency | |||
| Increasing Return to Scale (IRS) | 80 (46.0%) | 66 (28.7%) | 184 (62.8%) |
| Constant Return to Scale (CRS) | 12 (6.9%) | 20 (8.7%) | 20 (6.8%) |
| Decreasing Return to Scale (DRS) | 82 (47.1%) | 144 (62.6%) | 89 (30.4%) |
| Crop/ Variable | VRS | Area [ha] | Yield [t ha−1] | N_min [kg ha−1] | N_org [kg ha−1] | CF_ha [kg CO2e ha−1] | CF_kg [kg CO2e kg−1] |
|---|---|---|---|---|---|---|---|
| Constant | 17.6 a | 3.8 a | 107.8 a | 0.6 a b | 3535.0 a | 1.13 a | |
| winter rape | Decreasing | 31.4 b | 3.1 b | 178.0 b | 4.4 a | 4346.2 b | 1.50 b |
| Increasing | 6.6 c | 2.8 c | 176.3 b | 12.4 b | 4304.5 b | 1.71 c | |
| Constant | 8.2 a | 5.5 a | 80.5 a | 13.4 a b | 1596.4 a | 0.30 a | |
| winter triticale | Decreasing | 9.4 a | 4.7 b | 101.6 b | 26.7 a | 2009.4 b | 0.45 b |
| Increasing | 3.2 b | 4.2 c | 90.5 a b | 14.2 b | 1805.4 c | 0.49 b | |
| Constant | 16.4 a | 7.1 a | 89.0 a | 5.5 a b | 2705.6 a | 0.40 a | |
| winter wheat | Decreasing | 41.7 b | 6.5 a | 151.6 b | 2.4 a | 3476.0 b | 0.55 b |
| Increasing | 5.5 c | 5.4 b | 115.6 a | 15.7 b | 3114.7 c | 0.61 c |
| Item | Oilseed Rape | Triticale | Wheat | ||||||
|---|---|---|---|---|---|---|---|---|---|
| PTE = 1 | PTE < 1 | Diff | PTE = 1 | PTE < 1 | Diff | PTE = 1 | PTE < 1 | Diff | |
| NPK total [kg] | 249.0 | 318.3 | 21.8% * | 274.4 | 194.0 | 29.3% * | 209.6 | 242.6 | 13.6% * |
| Diesel [L] | 89.0 | 114.7 | 22.4% * | 99.4 | 82.9 | 16.6% * | 84.1 | 112.6 | 25.3% * |
| Machinery [hours] | 7.5 | 9.0 | 17.1% * | 9.8 | 7.7 | 21.4% * | 7.2 | 9.8 | 26.6% * |
| Seeds [kg] | 3.3 | 3.4 | 3.0% | 199.9 | 199.6 | 0.2% | 189 | 201.8 | 6.3% * |
| Pesticides [kg a.i.] | 3.0 | 4.5 | 33.2% * | 2.9 | 1.4 | 51.7% * | 3 | 3.4 | 12.5% |
| CF_ha [kg CO2e] | 3809.3 | 4348.6 | 12.4% * | 1619.6 | 1968.0 | 17.7% * | 2887.7 | 3237.1 | 10.8% * |
| Yield [kg] | 3540.8 | 2874 | −23.2% * | 4532.7 | 5184.6 | −14.4% * | 6891.2 | 5704.2 | −20.8% * |
| Item | Winter Rape | Winter Triticale | Winter Wheat |
|---|---|---|---|
| area | ↑ * | ↑ | ↑ * |
| temp_autumn | ↓ * | ||
| temp_winter | ↓ * | ||
| prec_winter | ↑ * | ||
| temp_spring | ↑ * | ||
| prec_spring | ↑ * | ↑ | |
| temp_summer | ↓ | ||
| prec_summer | ↓ * | ||
| soil = medium | ↓ | ||
| soil = poor | ↓ * | ||
| organic_fert = yes | ↓ * | ↓ * | |
| year = 2017 | ↑ * | ↑ * | |
| residue_collected = yes | ↑ | ||
| intercrop = yes | ↑ * |
| Winter Triticale Final Model: PTE~f(μ, σ, ν) | |||||
|---|---|---|---|---|---|
| logit (μ) | |||||
| Estimate | Std. Error | t-value | Pr(>|t|) | ||
| Intercept | 0.955174 | 1.097768 | 0.87 | 0.3853 | |
| area | 0.006279 | 0.006082 | 1.032 | 0.3032 | |
| temp_autumn | −0.19332 | 0.082152 | −2.353 | 0.0196 | * |
| temp_spring | 0.45148 | 0.207186 | 2.179 | 0.0305 | * |
| temp_summer | −0.16958 | 0.135658 | −1.25 | 0.2127 | |
| prec_spring | 0.001588 | 0.001425 | 1.115 | 0.2663 | |
| soil_class = medium | −0.1749 | 0.112606 | −1.553 | 0.1219 | |
| soil_class = poor | −0.29521 | 0.137317 | −2.15 | 0.0327 | * |
| intercrop = yes | 0.208173 | 0.104801 | 1.986 | 0.0483 | * |
| organic_fert = yes | −0.150683 | 0.064945 | −2.32 | 0.0213 | * |
| logit (σ) | |||||
| Intercept | −2.736911 | 0.534855 | −5.117 | 7.12 × 10−7 | *** |
| area | 1.51 × 10−2 | 1.51 × 10−2 | 1.356 | 0.1766 | |
| prec_summer | 3.75 × 10−3 | 1.53 × 10−3 | 2.451 | 0.0151 | * |
| prec_spring | 4.40 × 10−3 | 2.35 × 10−3 | 1.875 | 0.0622 | ˙ |
| econ_class = medium | 2.72 × 10−1 | 1.52 × 10−1 | 1.791 | 0.0748 | ˙ |
| econ_classs = small | −1.30 × 10−1 | 2.06 × 10−1 | −0.632 | 0.5284 | |
| type = dairy | 3.43 × 10−1 | 1.94 × 10−1 | 1.767 | 0.0787 | ˙ |
| type = pig | 4.07 × 10−2 | 1.88 × 10−1 | 0.217 | 0.8284 | |
| organic_fert = yes | 2.38 × 10−1 | 1.40 × 10−1 | 1.702 | 0.0903 | ˙ |
| year = 2017 | −4.30 × 10−1 | 2.78 × 10−1 | 15463.1 | <2 × 10−16 | *** |
| log (ν) | |||||
| Intercept | −1.32892 | 0.53396 | −2.489 | 0.01361 | * |
| area | 0.06408 | 0.01944 | 3.297 | 0.00115 | ** |
| soil_class = medium | −0.87209 | 0.58519 | −1.49 | 0.13769 | |
| soil_class = poor | 0.08487 | 0.66581 | 0.127 | 0.89869 | |
| organic_fert = yes | −1.01697 | 0.43303 | −2.349 | 0.0198 | * |
| Winter Wheat Final Model: PTE~f(μ, σ, ν) | |||||
|---|---|---|---|---|---|
| logit (μ) | |||||
| Estimate | Std. Error | t-value | Pr(>|t|) | ||
| (Intercept) | −0.085217 | 0.057847 | −1.473 | 0.14186 | |
| area | 0.00856 | 0.002137 | 4.006 | 7.96 × 10−5 | *** |
| temp_winter | −0.102088 | 0.038769 | −2.633 | 0.00894 | ** |
| organic_fert = yes | −0.274073 | 0.065262 | −4.2 | 3.62 × 10−5 | *** |
| year = 2017 | 0.16694 | 0.062716 | 2.662 | 0.00823 | ** |
| logit (σ) | |||||
| Intercept | 3.63557 | 1.365483 | 2.662 | 0.00822 | ** |
| area | 0.005196 | 0.003506 | 1.482 | 0.13943 | |
| temp_summer | −0.26405 | 0.075841 | −3.482 | 0.00058 | *** |
| econ_class = medium | −0.03608 | 0.129021 | −0.28 | 0.77994 | |
| econ_classs = small | 0.44972 | 0.210833 | 2.133 | 0.03381 | * |
| organic_fert = yes | −0.22761 | 0.13114 | −1.736 | 0.08376 | ˙ |
| log (ν) | |||||
| (Intercept) | −4.3938 | 1.266181 | −3.47 | 0.000604 | *** |
| area | 0.048616 | 0.011791 | 4.123 | 4.96 × 10−5 | *** |
| prec_spring | 0.013238 | 0.006016 | 2.201 | 0.028595 | * |
| prec_autumn | −0.01913 | 0.008191 | −2.335 | 0.020267 | * |
| type = dairy | 1.593927 | 0.606189 | 2.629 | 0.009036 | ** |
| type = pig | 1.328754 | 0.658671 | 2.017 | 0.044636 | * |
| econ_class = medium | 1.253814 | 0.62203 | 2.016 | 0.044809 | * |
| econ_class = small | 1.40318 | 0.94883 | 1.479 | 0.140328 | |
| Winter Oilseed Rape Final Model: PTE~f(μ, σ, ν) | |||||
|---|---|---|---|---|---|
| logit (μ) | |||||
| Estimate | Std. Error | t-value | Pr(>|t|) | ||
| Intercept | −0.61884 | 0.270816 | −2.285 | 0.023662 | * |
| area | 0.005752 | 0.002054 | 2.8 | 0.005758 | ** |
| prec_winter | 0.00387 | 0.001345 | 2.877 | 0.004586 | ** |
| prec_spring | 0.002801 | 0.000734 | 3.818 | 0.000194 | *** |
| prec_summer | −0.00326 | 0.000946 | −3.448 | 0.000726 | *** |
| residue_colected = yes | 0.161078 | 0.135882 | 1.185 | 0.237665 | |
| year = 2017 | 0.200319 | 0.076398 | 2.622 | 0.009612 | ** |
| logit (σ) | |||||
| Intercept | −3.60193 | 2.625933 | −1.372 | 0.1721 | |
| temp_summer | 0.287265 | 0.139291 | 2.062 | 0.0408 | * |
| prec_spring | −0.00559 | 0.002846 | −1.963 | 0.0515 | ˙ |
| prec_summer | −0.00488 | 0.002401 | −2.032 | 0.0439 | * |
| fadn = B | −0.44165 | 0.266573 | −1.657 | 0.0996 | ˙ |
| fadn = C | −0.09261 | 0.327823 | −0.283 | 0.7779 | |
| fadn = D | −0.80073 | 0.426971 | −1.875 | 0.0626 | ˙ |
| year = 2017 | −0.28932 | 0.156327 | −1.851 | 0.0661 | ˙ |
| log (ν) | |||||
| Intercept | −1.5919 | 0.2288 | −6.959 | 9.08× 10−11 | *** |
| residue_colected = yes | −12.5212 | 435.7352 | −0.029 | 0.977 | |
| intercrop = yes | −1.0108 | 0.7677 | −1.317 | 0.19 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Żyłowski, T.; Kozyra, J. Crop Cultivation Efficiency and GHG Emission: SBM-DEA Model with Undesirable Output Approach. Sustainability 2023, 15, 10557. https://doi.org/10.3390/su151310557
Żyłowski T, Kozyra J. Crop Cultivation Efficiency and GHG Emission: SBM-DEA Model with Undesirable Output Approach. Sustainability. 2023; 15(13):10557. https://doi.org/10.3390/su151310557
Chicago/Turabian StyleŻyłowski, Tomasz, and Jerzy Kozyra. 2023. "Crop Cultivation Efficiency and GHG Emission: SBM-DEA Model with Undesirable Output Approach" Sustainability 15, no. 13: 10557. https://doi.org/10.3390/su151310557
APA StyleŻyłowski, T., & Kozyra, J. (2023). Crop Cultivation Efficiency and GHG Emission: SBM-DEA Model with Undesirable Output Approach. Sustainability, 15(13), 10557. https://doi.org/10.3390/su151310557







