Dynamic Tensile Failure Characteristics and Energy Dissipation of Red Sandstone under Dry–Wet Cycles
Abstract
:1. Introduction
2. Materials and Methods
2.1. Preparation of Red-Sandstone Specimen
2.2. Experimental Methods and Procedures
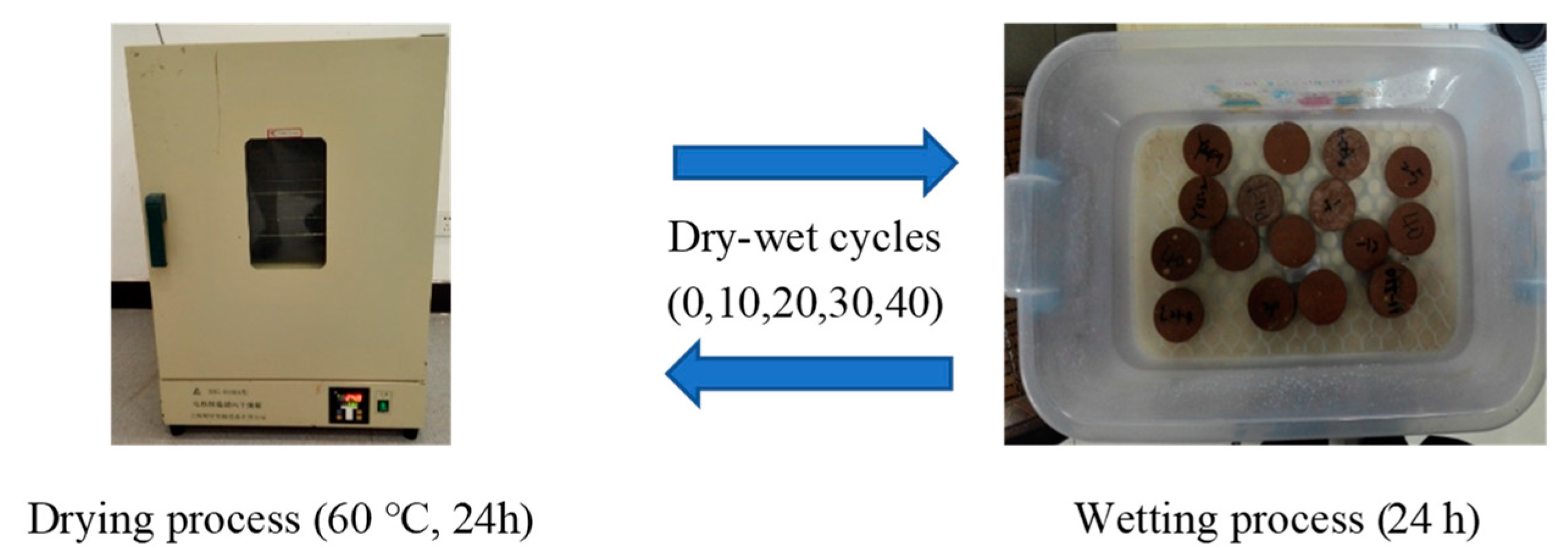
2.2.1. Dry–Wet Cycle Design
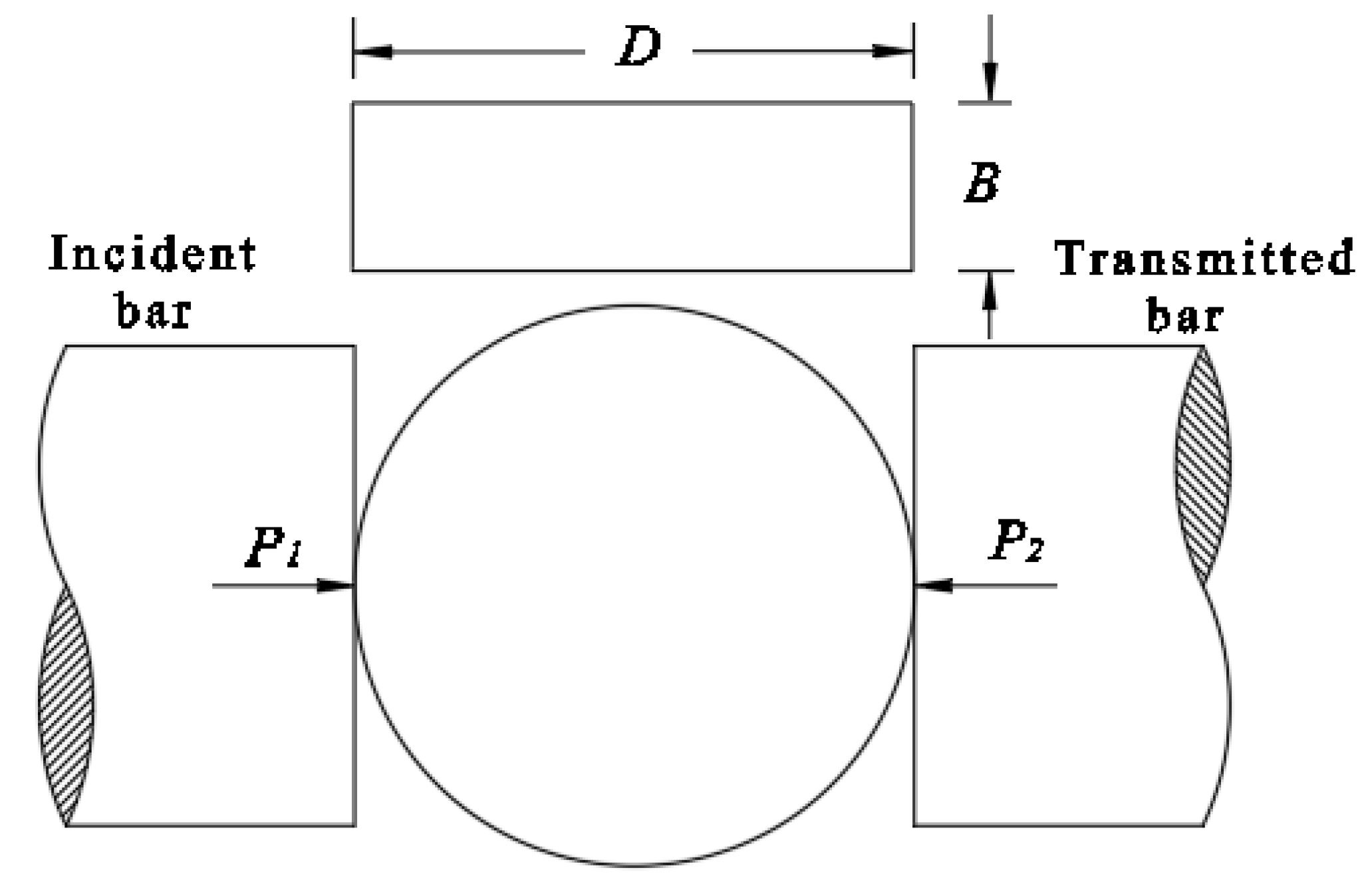
2.2.2. SHPB Test Device
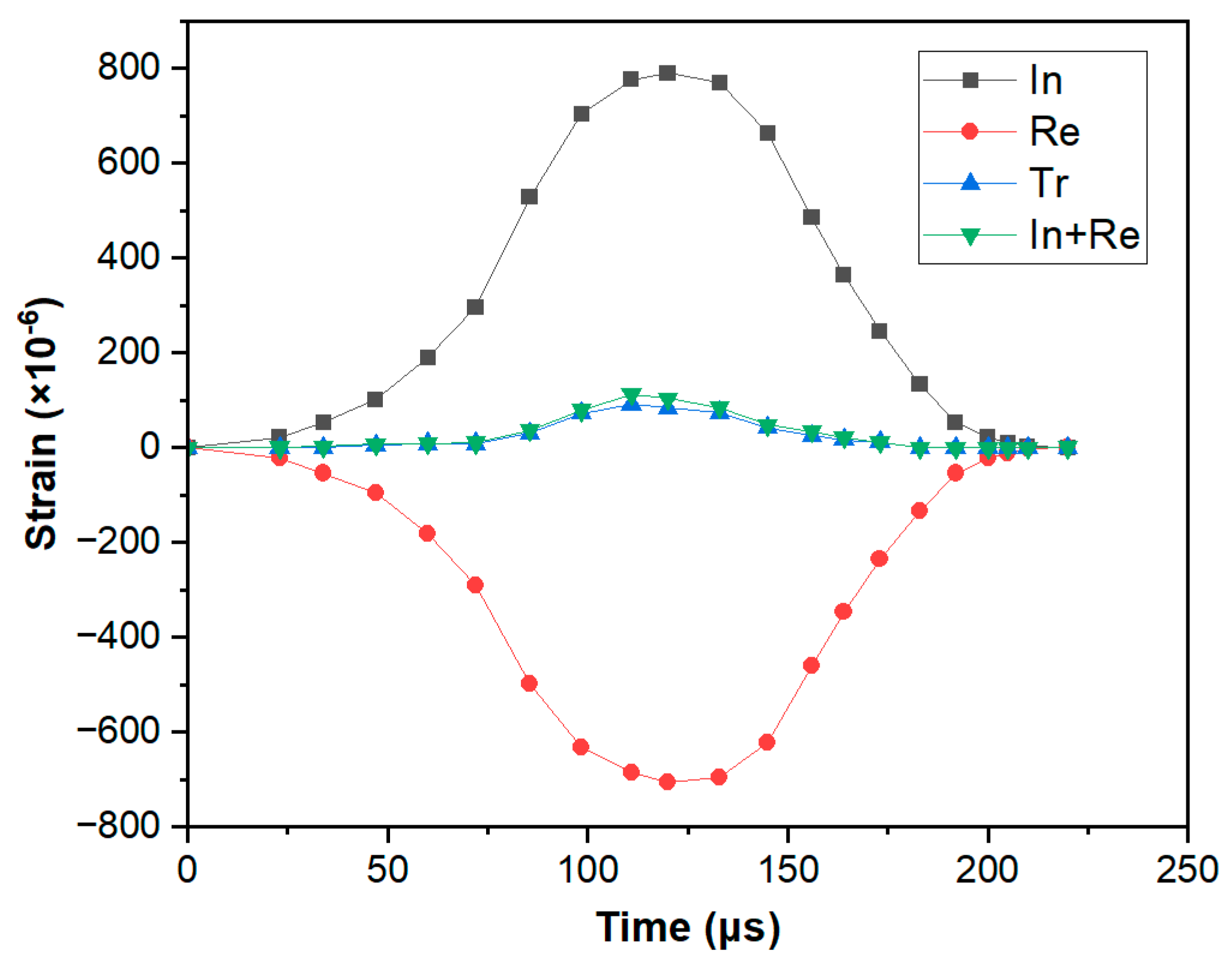
2.2.3. Test Verification
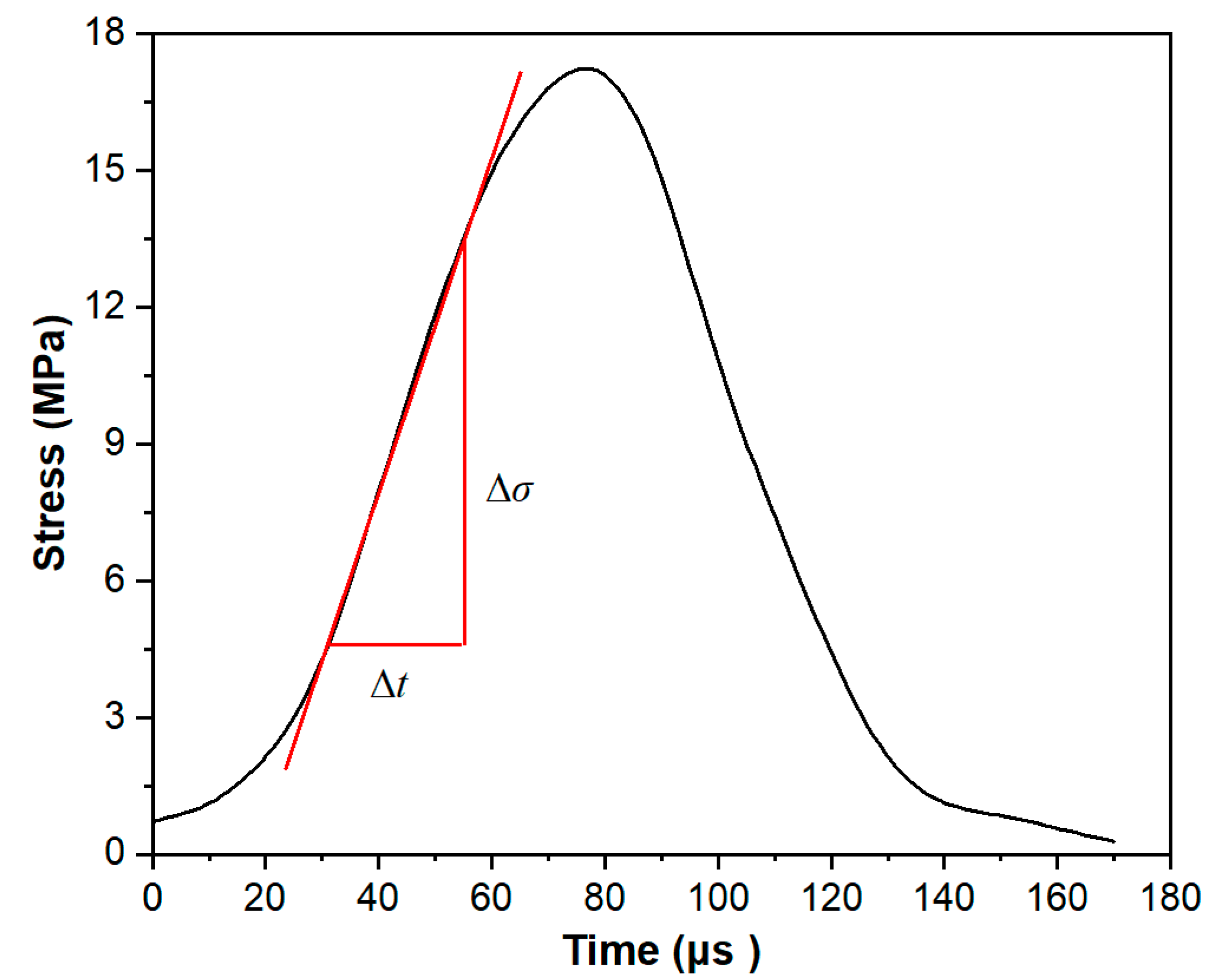
2.2.4. Determination of Loading Rate
3. Test Results and Analysis
3.1. Analysis of Dynamic Tensile Failure Characteristics
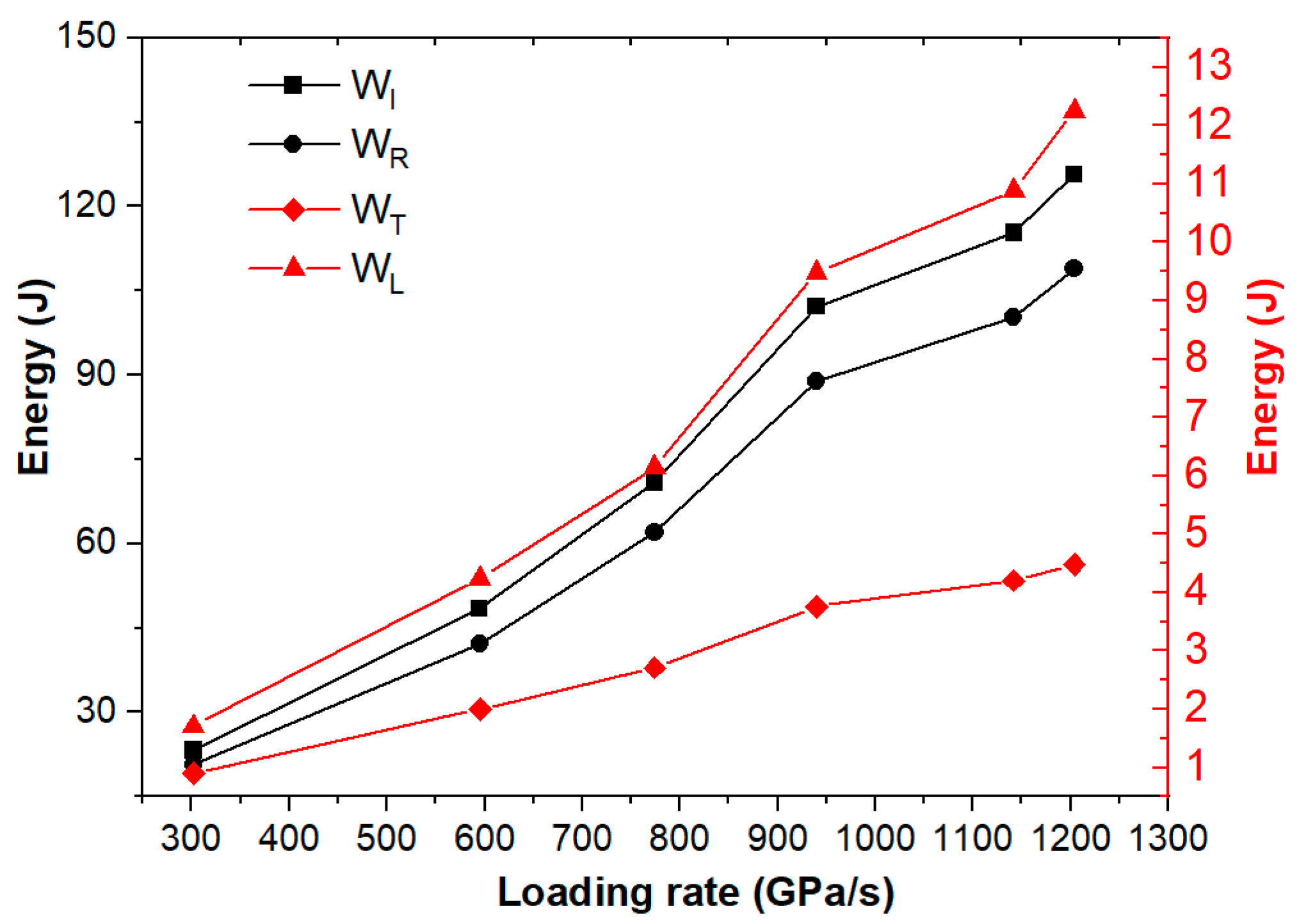
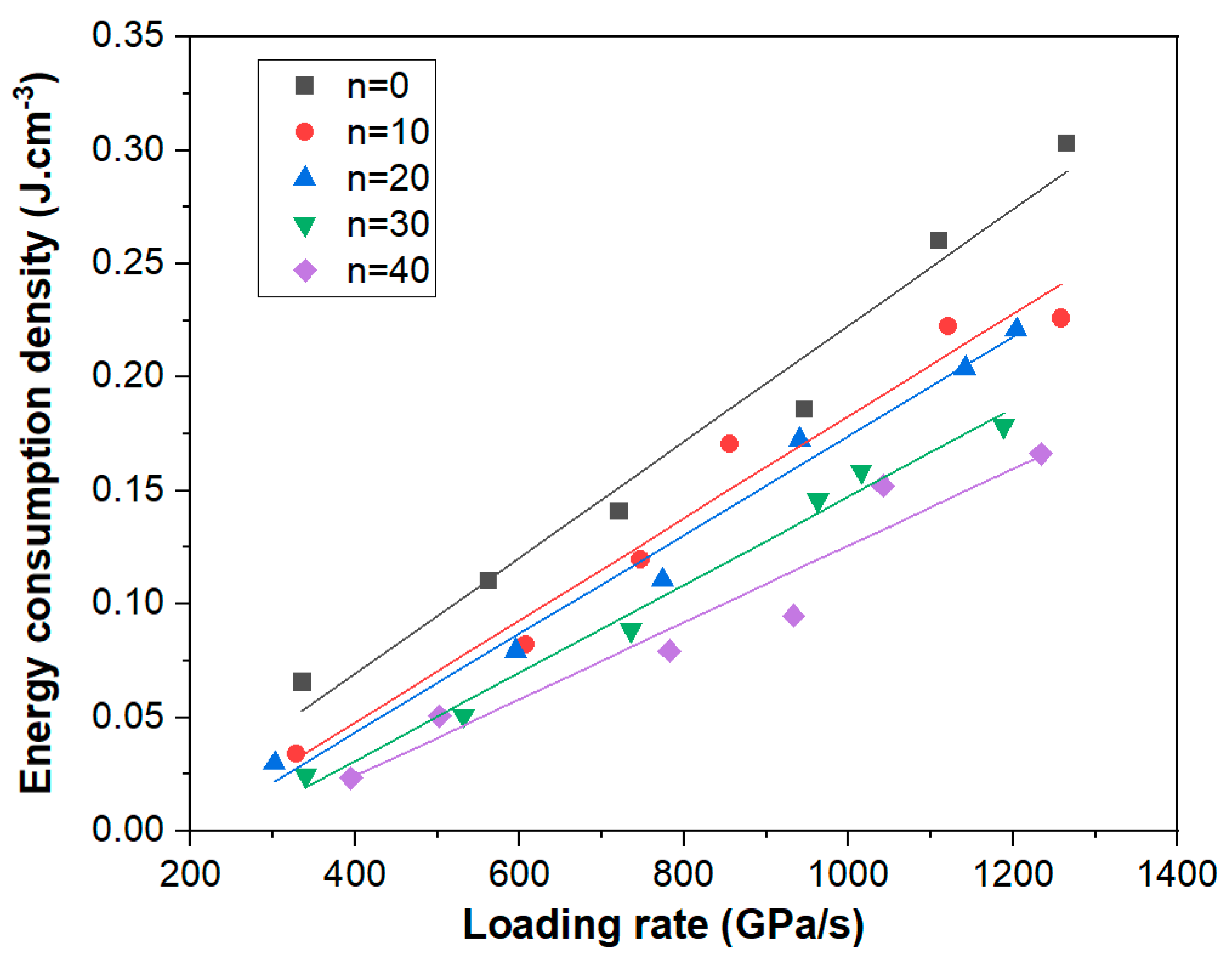
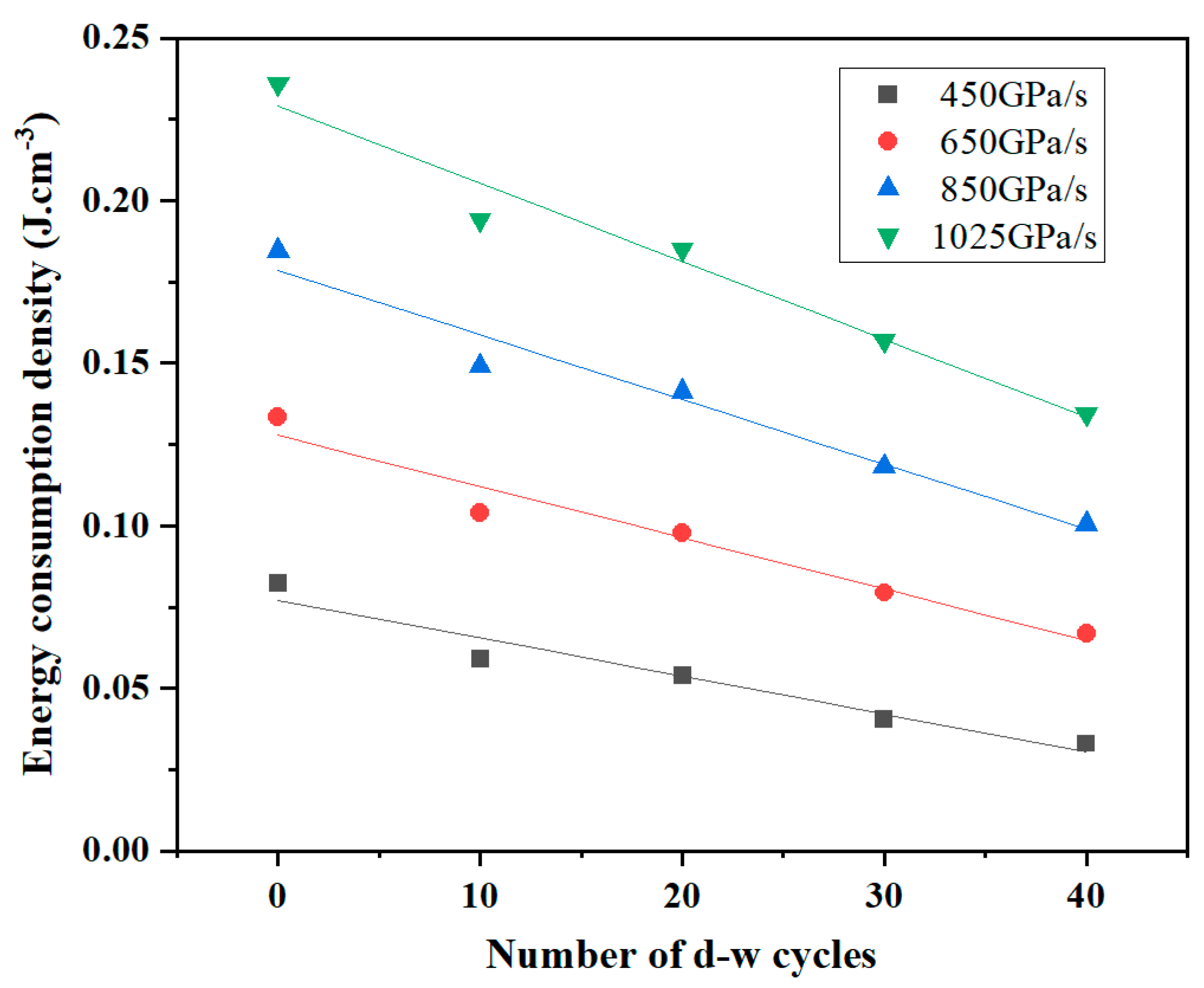
3.2. Analysis of Dynamic Tensile Energy Dissipation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, D.; Duan, H.; Zhang, J.; Liu, X.; Li, Z. Numerical simulation of water-silt inrush hazard of fault rock: A three-phase flow model. Rock Mech. Rock Eng. 2022, 55, 5163–5182. [Google Scholar] [CrossRef]
- Ma, D.; Duan, H.; Zhang, J. Solid grain migration on hydraulic properties of fault rocks in underground mining tunnel: Radial seepage experiments and verification of permeability prediction. Tunn. Undergr. Space Technol. 2022, 126, 104525. [Google Scholar] [CrossRef]
- Momeni, A.; Hashemi, S.S.; Khanlari, G.R.; Heidari, M. The effect of weathering on durability and deformability properties of granitoid rocks. Bull. Eng. Geol. Environ 2017, 76, 1037–1049. [Google Scholar] [CrossRef]
- Ma, D.; Duan, H.; Zhang, J.; Bai, H. A state-of-the-art review on rock seepage mechanism of water inrush disaster in coal mines. Int. J. Coal Sci. Technol. 2022, 9, 50. [Google Scholar] [CrossRef]
- Cai, X.; Zhou, Z.; Zang, H.; Song, Z. Water saturation effects on dynamic behavior and microstructure damage of sandstone: Phenomena and mechanisms. Eng. Geol. 2020, 276, 105760. [Google Scholar] [CrossRef]
- Özbek, A. Investigation of the effects of wetting-drying and freezing-thawing cycles on some physical and mechanical properties of selected ignimbrites. Bull. Eng. Geol. Environ. 2014, 73, 595–609. [Google Scholar] [CrossRef]
- Zhou, Z.; Cai, X.; Chen, L.; Cao, W.; Zhao, Y.; Xiong, C. Influence of cyclic wetting and drying on physical and dynamic compressive properties of sandstone. Eng. Geol. 2017, 220, 1–12. [Google Scholar] [CrossRef]
- Khanlari, G.; Abdilor, Y. Influence of wet-dry, freeze-thaw, and heat-cool cycles on the physical and mechanical properties of Upper Red sandstones in central Iran. Bull. Eng. Geol. Environ. 2015, 74, 1287–1300. [Google Scholar] [CrossRef]
- Hale, P.A.; Shakoor, A. A laboratory investigation of the effects of cyclic heating and cooling, wetting and drying, and freezing and thawing on the compressive strength of selected sandstones. Environ. Eng. Geosci. 2003, 9, 117–130. [Google Scholar] [CrossRef]
- Zhao, Z.; Yang, J.; Zhang, D.; Peng, H. Effects of wetting and cyclic wetting-drying on tensile strength of sandstone with a low clay mineral content. Rock Mech. Rock Eng. 2017, 50, 485–491. [Google Scholar] [CrossRef]
- Hua, W.; Dong, S.; Li, Y.; Xu, J.; Wang, Q. The influence of cyclic wetting and drying on the fracture toughness of sandstone. Int. J. Rock Mech. Min. Sci. 2015, 78, 331–335. [Google Scholar] [CrossRef]
- Hua, W.; Dong, S.; Li, Y.; Wang, Q. Effect of cyclic wetting and drying on the pure mode II fracture toughness of sandstone. Eng. Fract. Mech. 2016, 153, 143–150. [Google Scholar] [CrossRef]
- Hua, W.; Dong, S.; Peng, F.; Li, K.; Wang, Q. Experimental investigation on the effect of wetting-drying cycles on mixed mode fracture toughness of sandstone. Int. J. Rock Mech. Min. Sci. 2017, 93, 242–249. [Google Scholar] [CrossRef]
- Ma, D.; Duan, H.Y.; Zhang, Q.; Zhang, J.X.; Li, W.X.; Zhou, Z.L.; Liu, W.T. A numerical gas fracturing model of coupled thermal, flowing and mechanical effects. Comput. Mater. Contin. 2020, 65, 2123–2141. [Google Scholar] [CrossRef]
- Xia, K.; Yao, W. Dynamic rock tests using split Hopkinson (Kolsky) bar system—A review. J. Rock Mech. Geotech. Eng. 2015, 7, 27–59. [Google Scholar] [CrossRef] [Green Version]
- Li, X.B.; Lok, T.S.; Zhao, J. Dynamic characteristics of granite subjected to intermediate loading rate. Rock Mech. Rock Eng. 2005, 38, 21–39. [Google Scholar] [CrossRef]
- Liu, S.; Xu, J. Mechanical properties of qinling biotite granite after high temperature treatment. Int. J. Rock Mech. Min. Sci. 2014, 71, 188–193. [Google Scholar] [CrossRef]
- Cai, X.; Zhou, Z.; Tan, L.; Zang, H.; Song, Z. Fracture behavior and damage mechanisms of sandstone subjected to wetting-drying cycles. Eng. Fract. Mech. 2020, 234, 107109. [Google Scholar] [CrossRef]
- Wang, P.; Xu, J.; Liu, S.; Liu, S.; Wang, H. A prediction model for the dynamic mechanical degradation of sedimentary rock after a long-term freeze-thaw weathering: Considering the strain-rate effect. Cold Reg. Sci. Technol. 2016, 131, 16–23. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Xu, J.; Fang, X.; Wen, M.; Zheng, G.; Wang, P. Dynamic splitting tensile behaviors of red-sandstone subjected to repeated thermal shocks: Deterioration and micro-mechanism. Eng. Geol. 2017, 223, 1–10. [Google Scholar] [CrossRef]
- Zhou, Z.; Cai, X.; Cao, W.; Li, X.; Xiong, C. Influence of Water Content on Mechanical Properties of Rock in Both Saturation and Drying Processes. Rock Mech. Rock Eng. 2016, 49, 3009–3025. [Google Scholar] [CrossRef]
- Du, B.; Bai, H.; Zhai, M.; He, S. Experimental Study on Dynamic Compression Characteristics of Red Sandstone under Wetting-Drying Cycles. Adv. Civ. Eng. 2020, 2020, 6688202. [Google Scholar] [CrossRef]
- Du, B.; Bai, H. A Damage Constitutive Model of Red Sandstone under Coupling of Wet-Dry Cycles and Impact Load. Shock. Vib. 2019, 2019, 7692424. [Google Scholar] [CrossRef] [Green Version]
- Yin, T.; Li, X.; Cao, W.; Xia, K. Effects of thermal treatment on tensile strength of Laurentian granite using Brazilian test. Rock Mech. Rock Eng. 2015, 48, 2213–2223. [Google Scholar] [CrossRef]
- Zhou, Z.; Cai, X.; Li, X.; Cao, W.; Du, X. Dynamic Response and Energy Evolution of Sandstone Under Coupled Static–Dynamic Compression: Insights from Experimental Study into Deep Rock Engineering Applications. Rock Mech. Rock Eng. 2019, 53, 1305–1331. [Google Scholar] [CrossRef]
- Zhou, Z.; Cai, X.; Ma, D.; Chen, L.; Wang, S.; Tan, L. Dynamic tensile properties of sandstone subjected to wetting and drying cycles. Constr. Build. Mater. 2018, 182, 215–232. [Google Scholar] [CrossRef]
- Gong, F.; Jia, H.; Zhang, Z.; Hu, J.; Luo, S. Energy Dissipation and Particle Size Distribution of Granite under Different Incident Energies in SHPB Compression Tests. Shock. Vib. 2020, 2020, 8899355. [Google Scholar] [CrossRef]
- YZhou, X.; Xia, K.; Li, X.B.; Li, H.B.; Ma, G.W.; Zhao, J.; Zhou, Z.L.; Dai, F. Suggested methods for determining the dynamic strength parameters and mode-I fracture toughness of rock materials. Int. J. Rock Mech. Min. Sci. 2012, 49, 105–112. [Google Scholar]
- Dai, F.; Xia, K.; Luo, S.N. Semicircular bend testing with split Hopkinson pressure bar for measuring dynamic tensile strength of brittle solids. Rev. Sci. Instrum. 2008, 79, 123903. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Wong, L.N.Y. The Brazilian disc test for rock mechanics applications: Review and new insights. Rock Mech. Rock Eng. 2013, 46, 269–287. [Google Scholar] [CrossRef]
- Gong, F.Q.; Luo, S.; Yan, J.Y. Energy Storage and Dissipation Evolution Process and Characteristics of Marble in Three Tension-Type Failure Tests. Rock Mech. Rock Eng. 2018, 51, 3613–3624. [Google Scholar] [CrossRef]
- Luo, S.; Gong, F. Linear energy storage and dissipation laws during rock fracture under three-point flexural loading. Eng. Fract. Mech. 2020, 234, 107102. [Google Scholar] [CrossRef]
- Ma, D.; Zhang, J.X.; Duan, H.Y.; Huang, Y.L.; Li, M.; Sun, Q.; Zhou, N. Reutilization of gangue wastes in underground backfilling mining: Overburden aquifer protection. Chemosphere 2021, 264, 128400. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Sun, H.; Cui, Y.; Fei, D.; Lan, H.; Yan, C.; Bao, H.; Wu, F. Study on Dynamic Characteristics of Diorite Under Dry–Wet Cycle. Rock Mech. Rock Eng. 2021, 54, 6339–6349. [Google Scholar] [CrossRef]







| Parameters | Bulk Density (kg/m3) | P-Wave Velocity (m/s) | Uniaxial Compressive Strength (MPa) | Tensile Strength (MPa) | Poisson’s Ratio |
|---|---|---|---|---|---|
| Value | 2268 | 2467 | 65.8 | 3.52 | 0.26 |
| Number of Dry–Wet Cycles | Loading Rate (GPa/s) | WI (J) | WR (J) | WT (J) | Ws (J) | (J·cm−3) |
|---|---|---|---|---|---|---|
| 0 | 336 | 33.93 | 28.13 | 2.12 | 3.68 | 0.07 |
| 0 | 562 | 48.24 | 39.49 | 2.86 | 5.90 | 0.11 |
| 0 | 721 | 66.33 | 54.33 | 3.98 | 8.02 | 0.14 |
| 0 | 946 | 87.90 | 72.28 | 5.04 | 10.59 | 0.19 |
| 0 | 1110 | 112.28 | 91.34 | 6.52 | 14.42 | 0.26 |
| 0 | 1265 | 139.47 | 113.95 | 8.17 | 17.34 | 0.30 |
| 10 | 329 | 25.45 | 22.51 | 1.07 | 1.87 | 0.03 |
| 10 | 608 | 53.79 | 46.94 | 2.21 | 4.64 | 0.08 |
| 10 | 747 | 72.81 | 63.07 | 3.03 | 6.71 | 0.12 |
| 10 | 856 | 92.22 | 79.26 | 3.78 | 9.18 | 0.17 |
| 10 | 1121 | 119.12 | 102.16 | 4.90 | 12.05 | 0.22 |
| 10 | 1258 | 124.21 | 106.36 | 5.30 | 12.55 | 0.23 |
| 20 | 302 | 23.31 | 20.70 | 0.90 | 1.71 | 0.03 |
| 20 | 595 | 48.50 | 42.26 | 2.00 | 4.24 | 0.08 |
| 20 | 774 | 70.86 | 61.99 | 2.71 | 6.15 | 0.11 |
| 20 | 940 | 102.21 | 88.97 | 3.76 | 9.48 | 0.17 |
| 20 | 1142 | 115.33 | 100.25 | 4.20 | 10.89 | 0.20 |
| 20 | 1204 | 125.77 | 109.04 | 4.48 | 12.25 | 0.22 |
| 30 | 340 | 20.86 | 18.73 | 0.77 | 1.36 | 0.02 |
| 30 | 531 | 39.93 | 35.86 | 1.24 | 2.82 | 0.05 |
| 30 | 735 | 69.91 | 62.78 | 2.08 | 5.04 | 0.09 |
| 30 | 963 | 98.63 | 87.19 | 3.27 | 8.17 | 0.15 |
| 30 | 1015 | 111.79 | 99.22 | 3.59 | 8.97 | 0.16 |
| 30 | 1189 | 124.83 | 110.80 | 3.95 | 10.08 | 0.18 |
| 40 | 395 | 27.31 | 25.49 | 0.56 | 1.26 | 0.02 |
| 40 | 502 | 43.62 | 39.74 | 1.11 | 2.77 | 0.05 |
| 40 | 782 | 74.62 | 68.11 | 1.87 | 4.64 | 0.08 |
| 40 | 933 | 91.10 | 83.54 | 2.06 | 5.50 | 0.09 |
| 40 | 1042 | 115.69 | 104.93 | 2.64 | 8.12 | 0.15 |
| 40 | 1234 | 124.83 | 112.16 | 3.39 | 9.28 | 0.17 |
| Number of Dry–Wet Cycles | Fitting Curve | R2 |
|---|---|---|
| 0 | 0.9748 | |
| 10 | 0.9675 | |
| 20 | 0.9843 | |
| 30 | 0.9879 | |
| 40 | 0.9401 |
| Number of Dry–Wet Cycles | Parameters | |||
|---|---|---|---|---|
| (MPa) | R2 | |||
| 0 | 16.915 | −20.762 | −15.73 | 0.998 |
| 10 | 14.36 | −8.39 | −7.726 | 0.958 |
| 20 | 11.251 | −7.884 | −14.52 | 0.949 |
| 30 | 10.284 | −6.91 | −12.27 | 0.990 |
| 40 | 8.173 | −6.575 | −23.79 | 0.965 |
| Loading Rate (GPa/s) | Fitting Curve | R2 |
|---|---|---|
| 450 | 0.969 | |
| 650 | 0.960 | |
| 850 | 0.980 | |
| 1050 | 0.985 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Du, B.; Cheng, Q. Dynamic Tensile Failure Characteristics and Energy Dissipation of Red Sandstone under Dry–Wet Cycles. Sustainability 2023, 15, 10566. https://doi.org/10.3390/su151310566
Sun W, Du B, Cheng Q. Dynamic Tensile Failure Characteristics and Energy Dissipation of Red Sandstone under Dry–Wet Cycles. Sustainability. 2023; 15(13):10566. https://doi.org/10.3390/su151310566
Chicago/Turabian StyleSun, Wu, Bin Du, and Qiangqiang Cheng. 2023. "Dynamic Tensile Failure Characteristics and Energy Dissipation of Red Sandstone under Dry–Wet Cycles" Sustainability 15, no. 13: 10566. https://doi.org/10.3390/su151310566
APA StyleSun, W., Du, B., & Cheng, Q. (2023). Dynamic Tensile Failure Characteristics and Energy Dissipation of Red Sandstone under Dry–Wet Cycles. Sustainability, 15(13), 10566. https://doi.org/10.3390/su151310566





