Impact of Agricultural Industrial Agglomeration on Agricultural Environmental Efficiency in China: A Spatial Econometric Analysis
Abstract
:1. Introduction
2. Literature Review and Research Hypothesis
2.1. Methods for Measuring AEE
2.2. Relationship between AIA and AEE
3. Methodology and Data
3.1. Estimation of AEE
3.1.1. Traditional Stochastic Frontier Model
3.1.2. Fixed-Effects Stochastic Frontier Model
3.2. Empirical Models
3.2.1. Spatial Autocorrelation Test
3.2.2. Spatial Econometric Models
3.2.3. Spatial Weight Matrix
3.3. Variables and Data
3.3.1. Data Source
3.3.2. Explained Variable: AEE
3.3.3. Explanatory Variable: AIA
3.3.4. Control Variables
4. Empirical Results
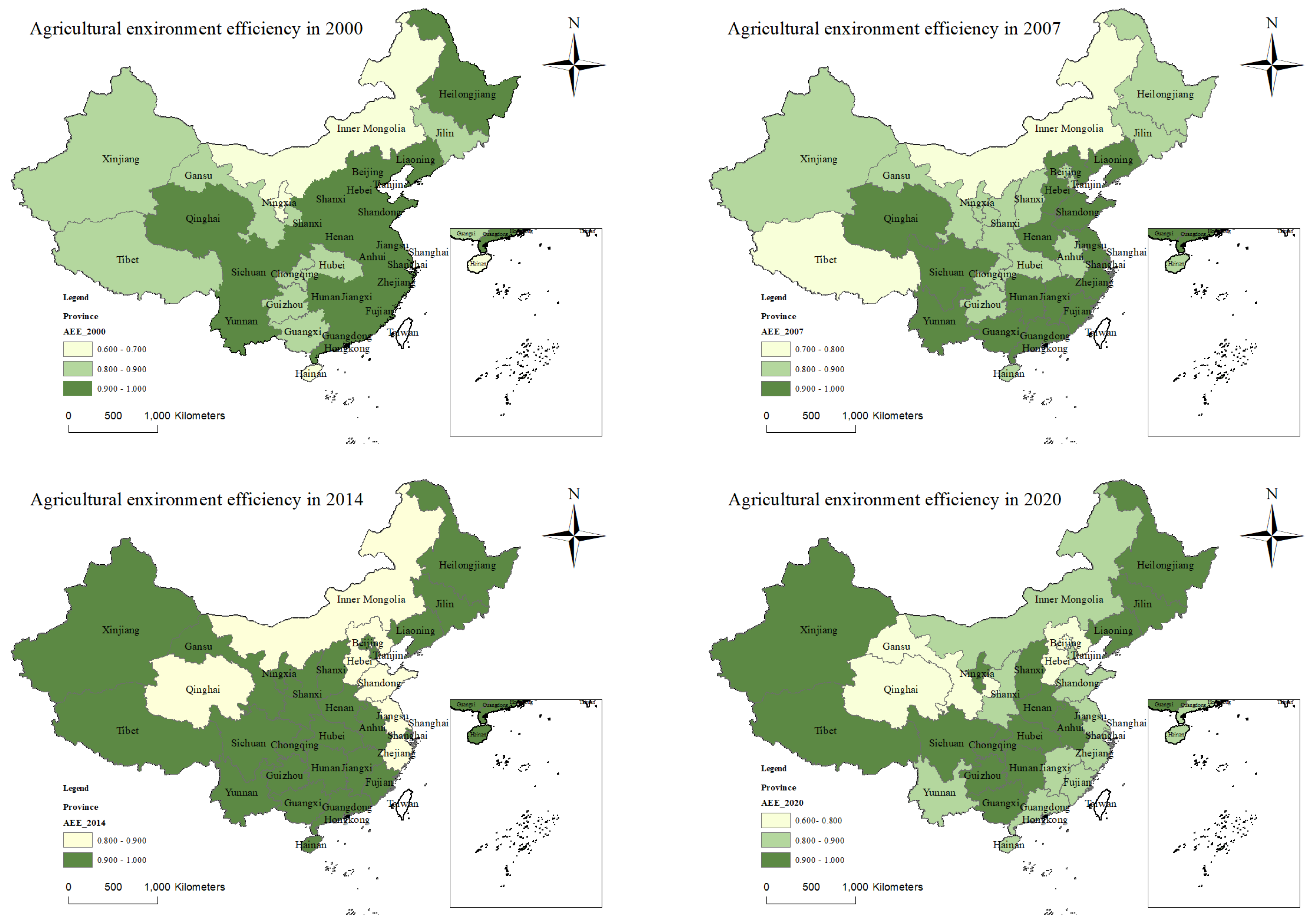
4.1. Estimation of AEE
4.2. Spatial Autocorrelation of AEE
4.3. Estimation Results of Spatial Panel Data Model
4.4. Robust Analysis
5. Discussion and Conclusions
5.1. Conclusions
5.2. Policy Recommendations
5.3. Limitations and Prospects of the Study
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shukla, P.R.; Skea, J.; Calvo Buendia, E.; Masson-Delmotte, V.; Portner, H.O.; Roberts, D.C.; Zhai, P.; Slade, R.; Connors, S.; van Diemen, R.; et al. IPCC: Climate Change and Land: An IPCC Special Report on Climate Change, Desertification, Land Degradation, Sustainable Land Management, Food Security, and Greenhouse Gas Fluxes in Terrestrial Ecosystems; IPCC: Geneva, Switzerland, 2019. [Google Scholar]
- Cohen, J.P.; Paul, C.J.M. Agglomeration economies and industry location decisions: The impacts of spatial and industrial spillovers. Reg. Sci. Urban. Econ. 2005, 35, 215–237. [Google Scholar] [CrossRef]
- Han, F.; Xie, R.; Fang, J. Urban agglomeration economies and industrial energy efficiency. Energy 2018, 162, 45–59. [Google Scholar] [CrossRef]
- Zheng, S.; Kahn, M.E. Understanding China’s urban pollution dynamics. J. Econ. Lit. 2013, 51, 731–772. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Fang, C.; Wang, Y.; Huang, Y.; Ma, H. Quantifying the relationship between urban development intensity and carbon dioxide emissions using a panel data analysis. Ecol. Indic. 2015, 49, 121–131. [Google Scholar] [CrossRef]
- Shen, N.; Peng, H. Can industrial agglomeration achieve the emission-reduction effect? Socio-Econ. Plan. Sci. 2021, 75, 100867. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, H.; Zhang, K.; Zhao, L.; Fan, F. Can innovation agglomeration reduce carbon emissions? Evidence from China. Int. J. Environ. Res. 2021, 18, 382. [Google Scholar] [CrossRef]
- Wu, J.; Xu, H.; Tang, K. Industrial agglomeration, CO2 emissions and regional development programs: A decomposition analysis based on 286 Chinese cities. Energy 2021, 225, 120239. [Google Scholar] [CrossRef]
- Li, X.; Xu, Y.; Yao, X. Effects of industrial agglomeration on haze pollution: A Chinese city-level study. Energy Policy 2021, 148, 111928. [Google Scholar] [CrossRef]
- Xu, J.; Wang, J.; Wang, T.; Li, C. Impact of industrial agglomeration on carbon emissions from dairy farming—Empirical analysis based on life cycle assessment method and spatial Durbin model. J. Clean. Prod. 2023, 406, 137081. [Google Scholar] [CrossRef]
- Odum, H.T.; Odum, E.P. The energetic basis for valuation of ecosystem services. Ecosystems 2000, 3, 21–23. [Google Scholar] [CrossRef]
- Amigues, J.P.; Moreaux, M. Competing land uses and fossil fuel, and optimal energy conversion rates during the transition toward a green economy under a pollution stock constraint. J. Environ. Manag. 2019, 97, 92–115. [Google Scholar] [CrossRef]
- Song, M.; An, Q.; Zhang, W.; Wang, Z.; Wu, J. Environmental efficiency evaluation based on data envelopment analysis: A review. Renew. Sustain. Energy Rev. 2012, 16, 4465–4469. [Google Scholar] [CrossRef]
- Chen, L.; Jia, G. Environmental efficiency analysis of China’s regional industry: A data envelopment analysis (DEA) based approach. J. Clean. Prod. 2017, 142, 846–853. [Google Scholar] [CrossRef]
- Vlontzos, G.; Niavis, S.; Manos, B.A. DEA approach for estimating the agricultural energy and environmental efficiency of EU countries. Renew. Sustain. Energy Rev. 2014, 40, 91–96. [Google Scholar] [CrossRef]
- Li, H.; Fang, K.; Yang, W.; Wang, D.; Hong, X. Regional environmental efficiency evaluation in China: Analysis based on the Super-SBM model with undesirable outputs. Math. Comput. Model. 2013, 58, 1018–1031. [Google Scholar] [CrossRef]
- Yuan, H.; Feng, Y.; Lee, C.C.; Cen, Y. How does manufacturing agglomeration affect green economic efficiency? Energy Econ. 2020, 92, 104944. [Google Scholar] [CrossRef]
- Shang, H.; Jiang, L.; Pan, X.; Pan, X. Green technology innovation spillover effect and urban eco-efficiency convergence: Evidence from Chinese cities. Energy Econ. 2022, 114, 106307. [Google Scholar] [CrossRef]
- Headey, D.; Alauddin, M.; Rao, D.P. Explaining agricultural productivity growth: An international perspective. Agric. Econ. 2010, 41, 1–14. [Google Scholar] [CrossRef]
- Honma, S.; Hu, J.L. A panel data parametric frontier technique for measuring total-factor energy efficiency: An application to Japanese regions. Energy 2014, 78, 732–739. [Google Scholar] [CrossRef]
- Cullinane, K.; Wang, T.F.; Song, D.W.; Ji, P. The technical efficiency of container ports: Comparing data envelopment analysis and stochastic frontier analysis. Transp. Res. Part A Policy Pract. 2006, 40, 354–374. [Google Scholar] [CrossRef]
- Cuesta, R.A.; Lovell, C.K.; Zofío, J.L. Environmental efficiency measurement with translog distance functions: A parametric approach. Ecol. Econ. 2009, 68, 2232–2242. [Google Scholar] [CrossRef]
- Reinhard, S.; Knox Lovell, C.A.; Thijssen, G.J. Environmental efficiency with multiple environmentally detrimental variables; Estimated with SFA and DEA. Eur. J. Oper. Res. 2000, 121, 287–303. [Google Scholar] [CrossRef]
- Kumbhakar, S.C. Production frontiers, panel data, and time-varying technical inefficiency. J. Econom. 1990, 46, 201–211. [Google Scholar] [CrossRef]
- Battese, G.E.; Coelli, T.J. Frontier production functions, technical efficiency and panel data: With application to paddy farmers in India. J. Product. Anal. 1992, 3, 153–169. [Google Scholar] [CrossRef]
- Lee, Y.H.; Schmidt, P. A Production Frontier Model with Flexible Temporal Variation in Technical Efficiency. In The Measurement of Productive Efficiency Techniques and Applications; Oxford Academic Press: Oxford, UK, 1993; pp. 237–255. [Google Scholar]
- Greene, W. Reconsidering heterogeneity in panel data estimators of the stochastic frontier model. J. Econom. 2005, 126, 269–303. [Google Scholar] [CrossRef]
- Neyman, J.; Scott, E.L. Consistent estimates based on partially consistent observations. Econometrica 1948, 16, 1–32. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Schmidt, P.; Wang, H.J. Consistent estimation of the fixed effects stochastic frontier model. J. Econom. 2014, 181, 65–76. [Google Scholar] [CrossRef]
- Belotti, F.; Ilardi, G. Consistent inference in fixed-effects stochastic frontier models. J. Econom. 2018, 202, 161–177. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.J.; Hu, M.J.; Zhou, M.X. The spatial pattern and influencing factors of industrial eco-efficiency in Chinese prefecture-level cities. Econ. Geogr. 2018, 38, 126–134. (In Chinese) [Google Scholar]
- Zhang, F. Evaluating public organization performance under extreme weather events: Does organizational adaptive capacity matter? J. Environ. Manag. 2021, 296, 113388. [Google Scholar] [CrossRef]
- Zou, G.; Chen, L.; Liu, W.; Hong, X.; Zhang, G.; Zhang, Z. Measurement and evaluation of Chinese regional energy efficiency based on provincial panel data. Math. Comput. Model. 2013, 58, 1000–1009. [Google Scholar] [CrossRef]
- Li, L.; Shan, Y.; Lei, Y.; Wu, S.; Yu, X.; Lin, X.; Chen, Y. Decoupling of economic growth and emissions in China’s cities: A case study of the central plains urban agglomeration. Appl. Energy 2019, 244, 36–45. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Bai, Y.; Quan, T.; Ran, R.; Hua, L. Influence and effect of industrial agglomeration on urban green total factor productivity—On the regulatory role of innovation agglomeration and institutional distance. Econ. Anal. Policy 2023, 78, 1158–1173. [Google Scholar] [CrossRef]
- Kevane, M. Agrarian structure and agricultural practice: Typology and application to Western Sudan. Am. J. Agric. Econ. 1996, 78, 236–245. [Google Scholar] [CrossRef]
- Du, J.J.; Xie, J.P.; Liu, B.M. Agricultural industry agglomeration and agricultural labor productivity in China: An empirical study based on data from 275 cities. J. Financ. Econ. 2020, 46, 49–63. (In Chinese) [Google Scholar]
- Dong, B.; Gong, J.; Zhao, X. FDI and environmental regulation: Pollution haven or a race to the top? J. Regul. Econ. 2012, 41, 216–237. [Google Scholar] [CrossRef]
- Hanson, G.H. Scale economies and the geographic concentration of industry. J. Econ. Geogr. 2001, 1, 255–276. [Google Scholar] [CrossRef]
- Andersson, M.; Lööf, H. Agglomeration and productivity: Evidence from firm-level data. Ann. Reg. Sci. 2011, 46, 601–620. [Google Scholar] [CrossRef] [Green Version]
- Henderson, J.V. Efficiency of resource usage and city size. J. Urban Econ. 1986, 19, 47–70. [Google Scholar] [CrossRef]
- Zhang, J.; Chang, Y.; Zhang, L.; Li, D. Do technological innovations promote urban green development?—A spatial econometric analysis of 105 cities in China. J. Clean. Prod. 2018, 182, 395–403. [Google Scholar] [CrossRef]
- Wang, H.; Liu, C.; Xiong, L.; Wang, F. The spatial spillover effect and impact paths of agricultural industry agglomeration on agricultural non-point source pollution: A case study in Yangtze River Delta, China. J. Clean. Prod. 2023, 401, 136600. [Google Scholar] [CrossRef]
- Aigner, D.; Lovell, C.K.; Schmidt, P. Formulation and estimation of stochastic frontier production function models. J. Econom. 1977, 6, 21–37. [Google Scholar] [CrossRef]
- Meeusen, W.; van Den Broeck, J. Efficiency estimation from Cobb-Douglas production functions with composed error. Int. Econ. Rev. 1977, 18, 435–444. [Google Scholar] [CrossRef]
- Stevenson, R.E. Likelihood functions for generalized stochastic frontier estimation. J. Econom. 1980, 13, 57–66. [Google Scholar] [CrossRef]
- Greene, W.H. A gamma-distributed stochastic frontier model. J. Econom. 1990, 46, 141–163. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, P.; Sickles, R.C. Production frontiers and panel data. J. Bus. Econ. Stat. 1984, 2, 367–374. [Google Scholar]
- González-Farıías, G.; Domıínguez-Molina, A.; Gupta, A.K. Additive properties of skew normal random vectors. J. Stat. Plan. Inference 2004, 126, 521–534. [Google Scholar] [CrossRef]
- National Bureau of Statistics of China. China Statistical Yearbook; China Statistical Press: Beijing, China, 2000–2020.
- Department of Rural Socio-Economic Survey, National Bureau of Statistics of China. China Rural Statistical Yearbook; China Statistical Press: Beijing, China, 2000–2020.
- China Agricultural Yearbook Committee. China Agricultural Yearbook; China Agriculture Press: Beijing, China, 2000–2020. [Google Scholar]
- Li, B.; Zhang, J.P.; Li, H. Research on spatial-temporal characteristics and affecting factors decomposition of agricultural carbon emission in China. Chin. J. Popul. Resour. Environ. 2011, 21, 80–86. (In Chinese) [Google Scholar]
- Gong, B. Agricultural reforms and production in China: Changes in provincial production function and productivity in 1978–2015. J. Dev. Econ. 2018, 132, 18–31. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, S.; He, X.; Li, J. Efficiency change in North-East China agricultural sector: A DEA approach. Agric. Econ. 2015, 61, 522–532. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.D.; Tu, X.W. Manufacturing agglomeration, technological progress and enterprise total factor energy efficiency. China Ind. Econ. 2022, 412, 103–121. [Google Scholar]
- Elhorst, J.P. Spatial Panel Data Models. In Spatial Econometrics: From Cross-Sectional Data to Spatial Panels; Springer: Berlin/Heidelberg, Germany, 2014; pp. 37–93. [Google Scholar]
- Zhang, H.; Zhang, J.; Song, J. Analysis of the threshold effect of agricultural industrial agglomeration and industrial structure upgrading on sustainable agricultural development in China. J. Clean. Prod. 2022, 341, 130818. [Google Scholar] [CrossRef]
- Luo, J.; Huang, M.; Hu, M.; Bai, Y. How does agricultural production agglomeration affect green total factor productivity? Empirical evidence from China. Environ. Sci. Pollut. Res. 2023, 30, 67865–67879. [Google Scholar] [CrossRef] [PubMed]
| Carbon Source | Carbon Emission Coefficient | Reference |
|---|---|---|
| Fertilizer | 0.8956 kg·kg | Oak Ridge National Laboratory, ORNL |
| Pesticides | 4.9341 kg·kg | Oak Ridge National Laboratory, ORNL |
| Agricultural plastic sheeting | 5.18 kg·kg | Nanjing Agricultural University |
| Agricultural diesel | 0.5927 kg·kg | IPCC |
| Agricultural ploughing | 312.6 kg·km | Institute of Agriculture and Biotechnology of China |
| Agricultural irrigation | 20.476 kg/hm | Dubey |
| Variable Type | Variables | Unit | Obs | Mean | Std. Dev. | Min | Max |
|---|---|---|---|---|---|---|---|
| Output variables | GVAO | billion CNY | 651 | 2366.430 | 2168.945 | 51.220 | 10,190.600 |
| million tons | 651 | 301.299 | 227.189 | 7.282 | 995.753 | ||
| Input variables | LAB | million people | 651 | 893.618 | 698.079 | 27.000 | 3558.550 |
| LAND | million hectares | 651 | 5168.415 | 3675.812 | 88.600 | 14,910.100 | |
| FERT | million tons | 651 | 169.616 | 138.495 | 2.500 | 716.090 | |
| MAC | million kilowatts | 651 | 2763.119 | 2687.327 | 94.000 | 13,353.000 | |
| Explanatory variable | AIA | % | 651 | 1.015 | 0.406 | 0.083 | 2.123 |
| Control variables | INC | % | 651 | 2.857 | 0.595 | 1.845 | 5.525 |
| IND | % | 651 | 0.422 | 0.083 | 0.160 | 0.619 | |
| EDU | year | 651 | 8.466 | 1.291 | 2.998 | 12.782 | |
| lnRGDP | yuan | 651 | 9.161 | 0.522 | 7.887 | 10.760 | |
| lnTRANS | kilometer | 651 | 11.347 | 0.904 | 8.372 | 12.885 | |
| ENV | % | 651 | 0.005 | 0.004 | 0.000 | 0.309 |
| Parameter | Coefficient | t-Value | Parameter | Coefficient | t-Value |
|---|---|---|---|---|---|
| 0.043 | 0.889 | −0.179 *** | −2.760 | ||
| −0.281 *** | −3.200 | −0.019 *** | −3.860 | ||
| −0.108 *** | −3.200 | −0.003 | −0.628 | ||
| −0.295 *** | −5.050 | 0.011 *** | 3.230 | ||
| −0.055 *** | −22.900 | 0.017 *** | 3.760 | ||
| −0.136 | −1.260 | −0.387 *** | −14.100 | ||
| 0.016 | 0.132 | 0.150 *** | 7.620 | ||
| −0.096 | −1.520 | 0.098 *** | 3.090 | ||
| −0.164 * | −1.750 | −0.089 *** | −2.620 | ||
| 0.002 *** | 4.560 | −0.011 | −0.521 | ||
| −0.224 ** | −2.560 | −0.074 ** | −2.060 | ||
| 0.155 *** | 2.640 | −0.007 *** | −3.790 | ||
| 0.115 | 1.580 | 6.164 *** | 14.300 | ||
| 0.093 | 1.350 | 4.486 *** | 15.900 | ||
| 0.217 *** | 2.840 | ||||
| log-likelihood | 759.027 |
| Year | Year | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Moran’s I | Z Value | Moran’s I | Z Value | Moran’s I | Z Value | Moran’s I | Z Value | ||
| 2000 | 0.436 *** | 3.942 | 0.240 *** | 7.498 | 2011 | 0.541 *** | 4.830 | 0.288 *** | 8.588 |
| 2001 | 0.441 *** | 3.988 | 0.239 *** | 7.481 | 2012 | 0.539 *** | 4.808 | 0.293 *** | 8.709 |
| 2002 | 0.473 *** | 4.252 | 0.227 *** | 7.138 | 2013 | 0.543 *** | 4.842 | 0.303 *** | 8.964 |
| 2003 | 0.469 *** | 4.229 | 0.245 *** | 7.556 | 2014 | 0.544 *** | 4.852 | 0.309 *** | 9.114 |
| 2004 | 0.512 *** | 4.589 | 0.263 *** | 8.097 | 2015 | 0.544 *** | 4.851 | 0.306 *** | 9.042 |
| 2005 | 0.526 *** | 4.706 | 0.269 *** | 8.231 | 2016 | 0.522 *** | 4.665 | 0.295 *** | 8.698 |
| 2006 | 0.542 *** | 4.842 | 0.274 *** | 8.318 | 2017 | 0.516 *** | 4.612 | 0.290 *** | 8.569 |
| 2007 | 0.551 *** | 4.915 | 0.283 *** | 8.533 | 2018 | 0.519 *** | 4.640 | 0.294 *** | 8.661 |
| 2008 | 0.549 *** | 4.894 | 0.285 *** | 8.558 | 2019 | 0.536 *** | 4.786 | 0.301 *** | 8.835 |
| 2009 | 0.535 *** | 4.777 | 0.283 *** | 8.497 | 2020 | 0.582 *** | 5.167 | 0.317 *** | 9.218 |
| 2010 | 0.544 *** | 4.850 | 0.288 *** | 8.609 | |||||
| Variables | OLS with Fixed Effects | SAR | SDM | ||
|---|---|---|---|---|---|
| AIA | 0.246 *** (3.931) | 0.190 *** (3.156) | 0.226 *** (3.774) | 0.128 ** (2.051) | 0.219 *** (3.774) |
| −0.056 ** (−2.254) | −0.042 * (−1.779) | −0.053 ** (−2.637) | −0.020 (−0.818) | −0.060 *** (−2.637) | |
| INC | −0.027 *** (−3.242) | −0.031 *** (−3.011) | −0.035 *** (−3.461) | −0.038 *** (−3.162) | −0.036 *** (−3.420) |
| IND | 0.235 *** (4.141) | 0.141 ** (2.060) | 0.126 * (1.842) | 0.152 ** (2.325) | 0.209 *** (3.098) |
| EDU | −0.006 (−0.812) | −0.004 (−0.353) | −0.005 (−0.477) | −0.001 (−0.108) | −0.003 (−0.270) |
| lnRGDP | 0.080 *** (3.142) | 0.025 (0.945) | 0.027 (1.016) | 0.064 ** (2.323) | 0.022 (0.808) |
| lnTRANS | −0.020 * (−1.960) | −0.018 (−1.234) | −0.017 (−1.165) | −0.012 (−0.734) | −0.013 (−0.955) |
| ENV | 0.671 (0.861) | 0.235 (0.294) | 0.286 (0.356) | 0.634 (0.836) | 1.544 ** (1.988) |
| 0.319 *** (3.074) | 1.888 *** (4.922) | ||||
| −0.083 * (−1.951) | −0.688 *** (−4.614) | ||||
| 0.023 (0.993) | −0.195 ** (−2.552) | ||||
| −0.264 * (−1.849) | 0.315 (0.719) | ||||
| 0.015 (0.663) | −0.183 ** (−2.359) | ||||
| −0.014 (−0.292) | 0.005 (0.033) | ||||
| −0.04 (−1.077) | −0.422 *** (−3.486) | ||||
| 4.241 ** (2.473) | 24.617 *** (4.306) | ||||
| 1.139 *** (2.723) | 0.079 (0.708) | 0.002 (0.036) | −0.412 *** (−2.865) | ||
| Regional control effect | Yes | Yes | Yes | Yes | |
| Time control effect | Yes | Yes | Yes | Yes | |
| R-squared | 0.103 | 0.37 | 0.365 | 0.403 | 0.43 |
| log-likelihood | 1020.556 | 1020.404 | 1038.715 | 1051.049 | |
| LM test no spatial lag | 5.204 ** | 3.166 * | |||
| LM test no spatial error | 3.785 * | 4.188 ** | |||
| Wald_spatial_lag | 14.159 * | 31.424 *** | |||
| Wald_spatial_error | 14.704 * | 30.920 *** | |||
| Variables | ||||||
|---|---|---|---|---|---|---|
| Direct | Indirect | Total | Direct | Indirect | Total | |
| AIA | 0.129 ** (2.054) | 0.319 *** (3.175) | 0.448 *** (4.540) | 0.189 *** (3.147) | 1.328 *** (4.207) | 1.517 *** (4.923) |
| −0.020 (−0.833) | −0.083 ** (−2.003) | −0.103 ** (−2.492) | −0.049 ** (−2.118) | −0.489 *** (−3.993) | −0.538 *** (−4.436) | |
| INC | −0.038 *** (−3.153) | 0.022 (0.971) | −0.016 (−0.761) | −0.033 *** (−3.002) | −0.136 ** (−2.260) | −0.169 *** (−2.899) |
| IND | 0.148 ** (2.204) | −0.270 * (−1.842) | −0.121 (−0.728) | 0.206 *** (3.110) | 0.163 (0.514) | 0.368 (1.107) |
| EDU | −0.001 (−0.098) | 0.015 ** (0.663) | 0.014 (0.551) | −0.001 (−0.047) | −0.136 ** (−2.358) | −0.137 ** (−2.319) |
| lnRGDP | 0.063 ** (2.287) | −0.013 (−0.275) | 0.050 (1.072) | 0.020 (0.716) | 0.003 (0.031) | 0.023 (0.237) |
| lnTRANS | −0.011 (−0.660) | −0.039 (−1.036) | −0.050 (−1.523) | −0.007 (−0.507) | −0.305 *** (−3.169) | −0.313 *** (−3.352) |
| ENV | 0.633 (0.817) | 4.200 *** (2.456) | 4.834 ** (2.566) | 1.178 (1.554) | 17.481 *** (3.897) | 18.659 *** (4.028) |
| Variables | SDM | SEM | ||
|---|---|---|---|---|
| AIA | 0.280 (1.579) | 0.038 ** (2.324) | 0.198 *** (3.245) | 0.245 *** (4.118) |
| −0.002 * (1.834) | −0.003 *** (−2.742) | −0.044 * (−1.835) | −0.060 *** (−2.565) | |
| INC | −0.020 * (−1.704) | −0.027 *** (−2.606) | −0.035 *** (−3.381) | −0.037 *** (−3.635) |
| IND | 0.065 0.915) | 0.164 ** (2.267) | 0.142 ** (2.083) | 0.121 * (1.750) |
| EDU | −0.000 (−0.027) | −0.002 (−0.177) | −0.004 (−0.389) | −0.007 (−0.624) |
| lnRGDP | 0.065 ** (2.281) | 0.042 (1.473) | 0.027 (1.001) | 0.029 (1.112) |
| lnTRANS | −0.008 (−0.504) | −0.001 (−0.067) | −0.164 (−1.072) | −0.020 (−1.367) |
| ENV | 0.573 (0.751) | 1.267 (1.644) | 0.152 (0.190) | 0.435 (0.539) |
| 0.267 *** (7.250) | 0.694 *** (6.473) | |||
| −0.018 *** (−7.112) | −0.050 *** (−7.068) | |||
| 0.007 (0.291) | −0.108 (−1.473) | |||
| −0.013 (−0.086) | 0.834 * (1.757) | |||
| 0.016 (0.691) | −0.225 *** (−2.865) | |||
| 0.082 (1.560) | 0.331 ** (2.191) | |||
| −0.029 (−0.775) | −0.518 *** (−4.193) | |||
| 4.717 *** (2.698) | 23.225 *** (4.066) | |||
| / | 0.117 ** (2.261) | −0.356 ** (−2.536) | 0.130 ** (2.482) | −0.027 (−0.217) |
| Regional control effect | Yes | Yes | Yes | Yes |
| Time control effect | Yes | Yes | Yes | Yes |
| R-squared | 0.396 | 0.415 | 0.403 | 0.366 |
| log-likelihood | 1033.993 | 1043.418 | 1038.715 | 1021.538 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, R.; Qi, Y.; Zhu, W. Impact of Agricultural Industrial Agglomeration on Agricultural Environmental Efficiency in China: A Spatial Econometric Analysis. Sustainability 2023, 15, 10799. https://doi.org/10.3390/su151410799
Ye R, Qi Y, Zhu W. Impact of Agricultural Industrial Agglomeration on Agricultural Environmental Efficiency in China: A Spatial Econometric Analysis. Sustainability. 2023; 15(14):10799. https://doi.org/10.3390/su151410799
Chicago/Turabian StyleYe, Rendao, Yue Qi, and Wenyan Zhu. 2023. "Impact of Agricultural Industrial Agglomeration on Agricultural Environmental Efficiency in China: A Spatial Econometric Analysis" Sustainability 15, no. 14: 10799. https://doi.org/10.3390/su151410799
APA StyleYe, R., Qi, Y., & Zhu, W. (2023). Impact of Agricultural Industrial Agglomeration on Agricultural Environmental Efficiency in China: A Spatial Econometric Analysis. Sustainability, 15(14), 10799. https://doi.org/10.3390/su151410799





