Synthesis of Biomass Corridor in Peninsular Malaysia via Hybrid Mathematical and Graphical Framework
Abstract
:1. Introduction
- Identify the optimal location in which to establish processing hubs (sinks) in Peninsular Malaysia;
- Evaluate the optimum allocation of various types of biomasses for valorisation;
- Evaluate the impact of the key parameters on the economic feasibility of the supply chain.
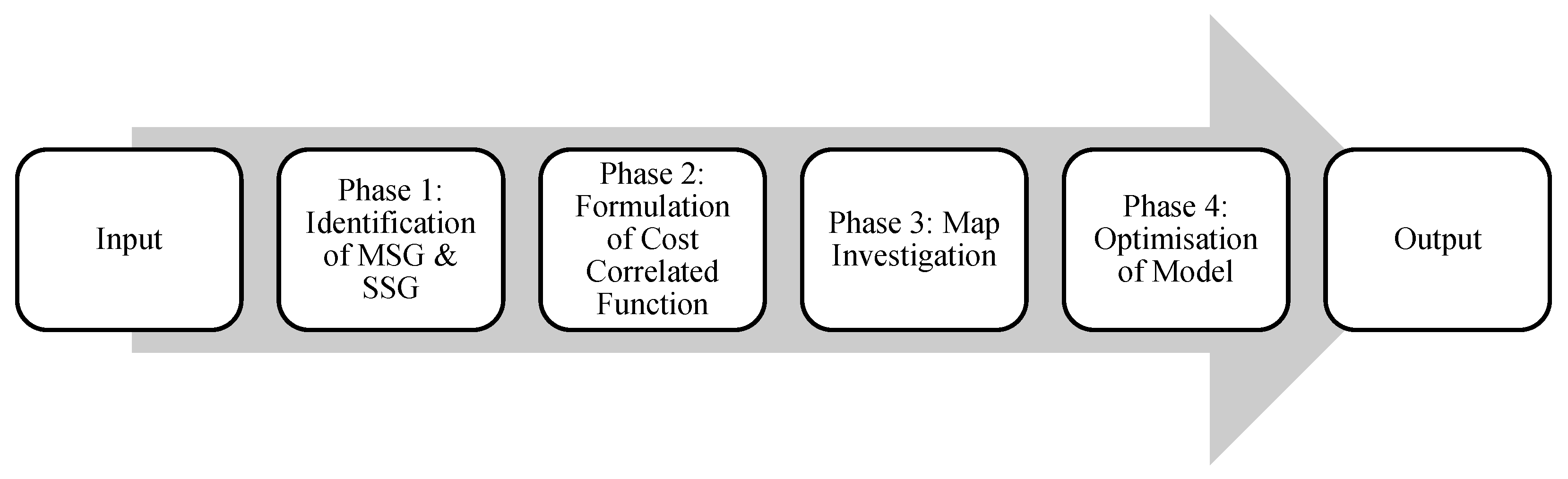
2. Methods
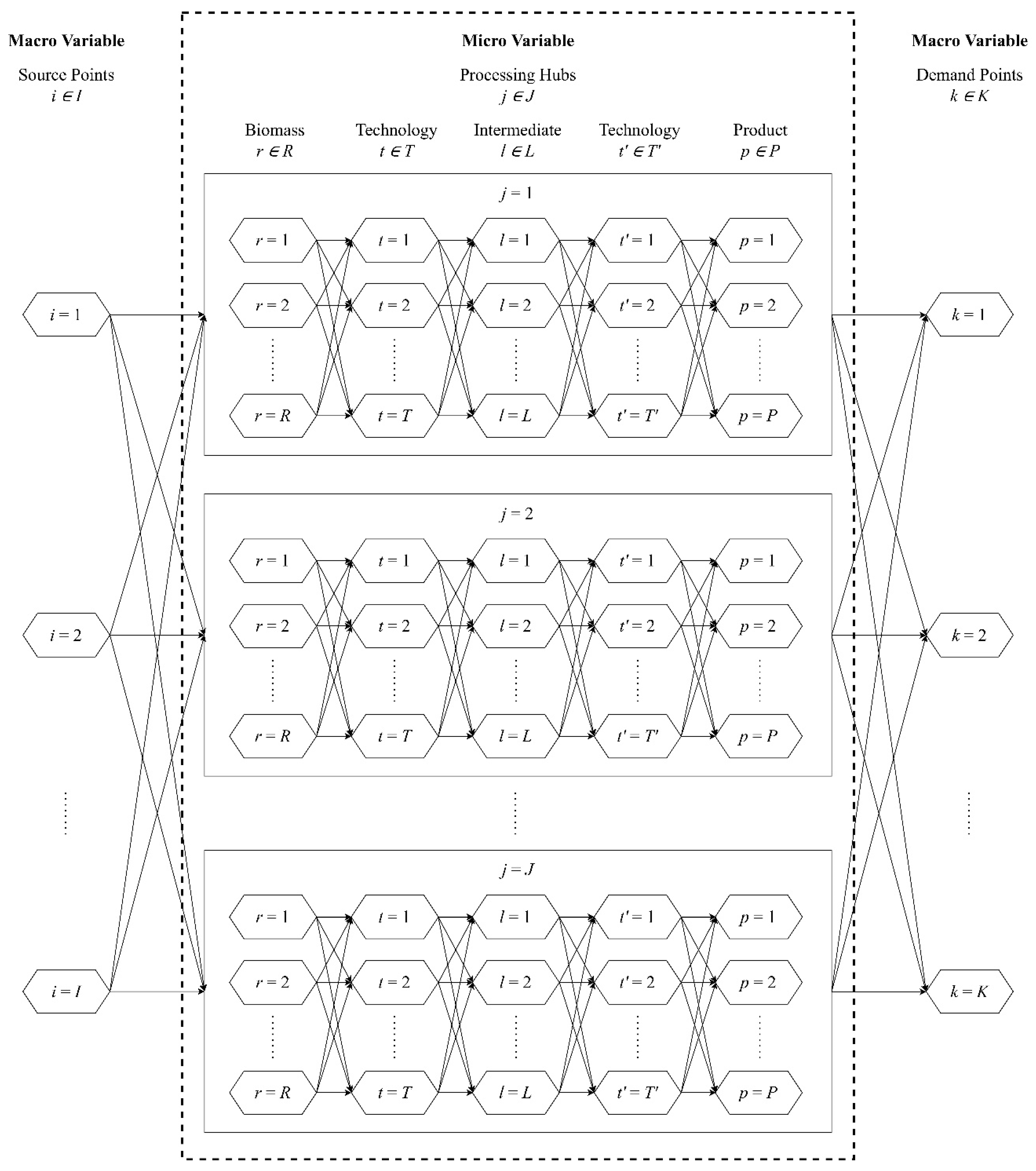
2.1. Phase I: Generation of MSG and SSG of Processing Hub
2.2. Phase II: Formulation of Cost-Correlated Function
2.3. Phase III: Map Investigation
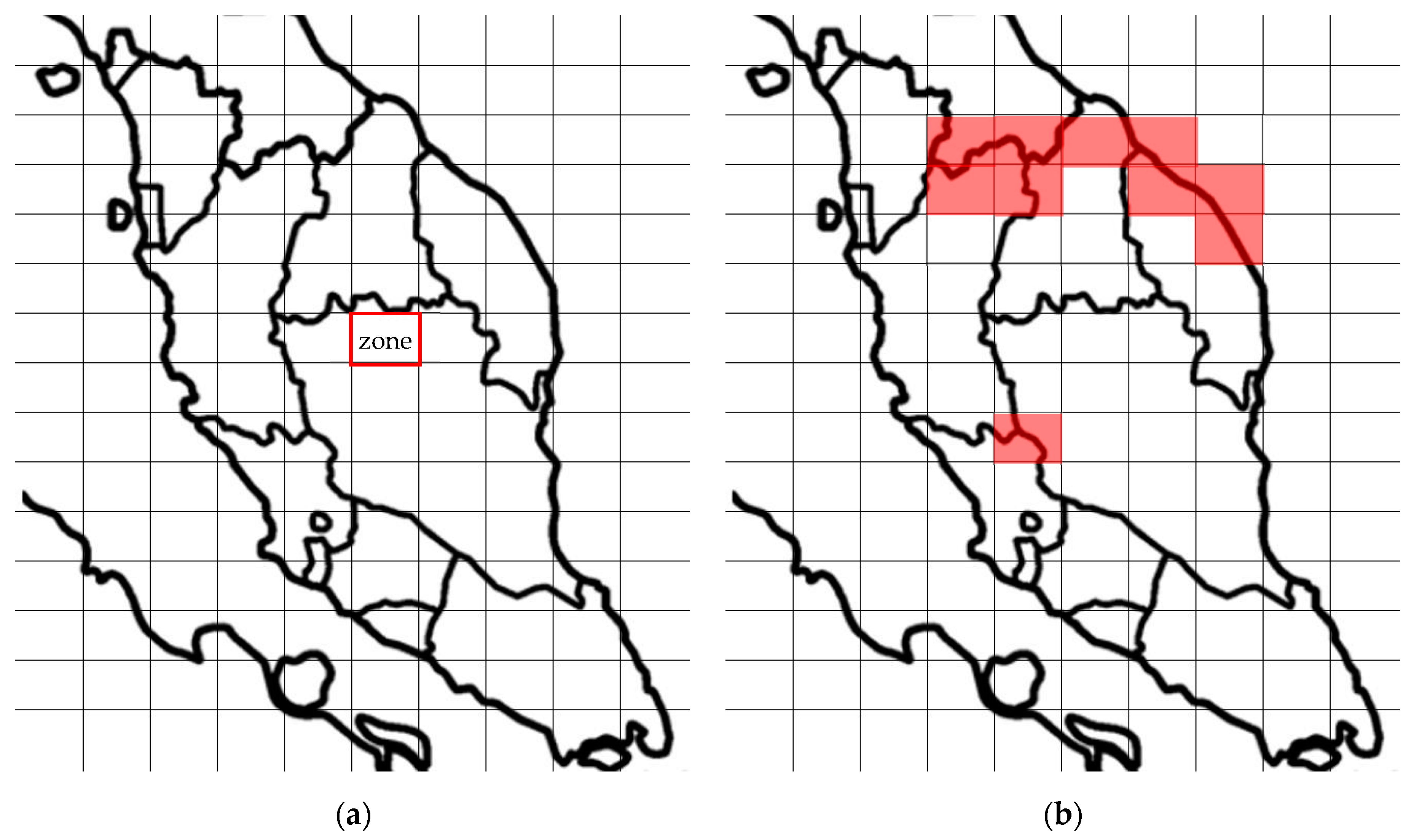
2.3.1. Regional Division
2.3.2. Elimination of Infeasible Zones
2.3.3. Connectivity Detachment
2.4. Phase IV: Optimisation of Model
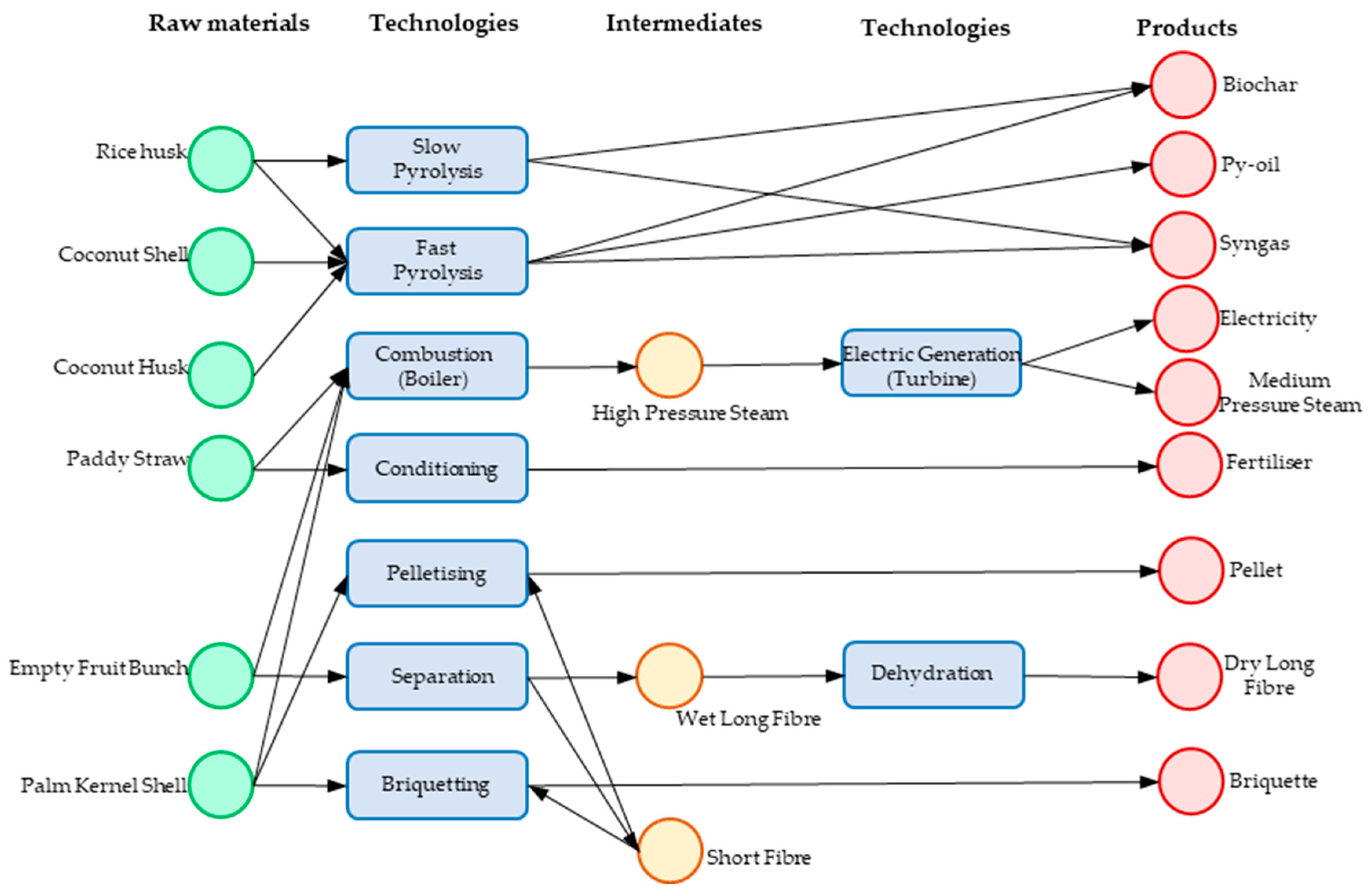
3. Case Study
4. Results and Discussions
4.1. Cost Correlated Function
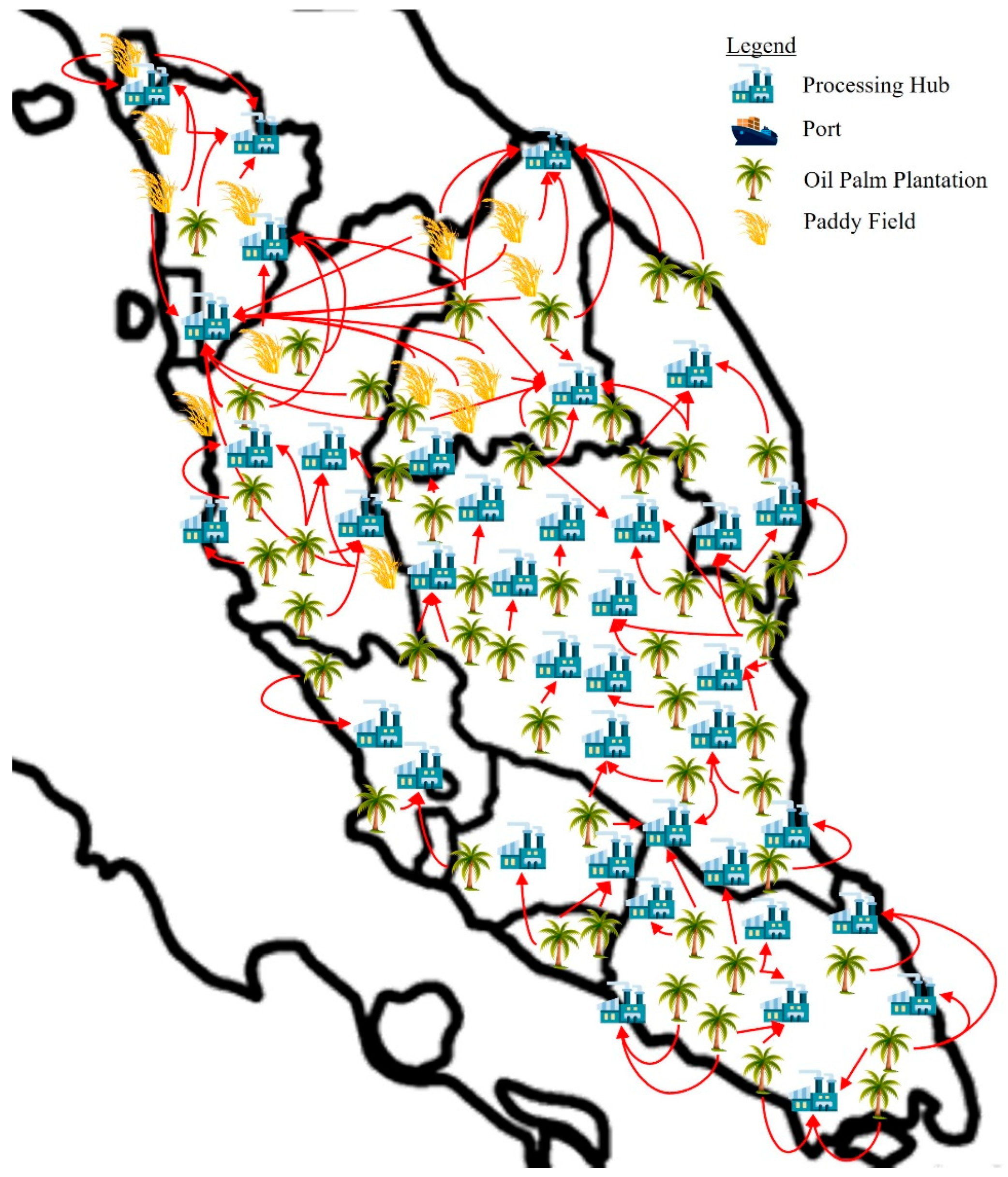
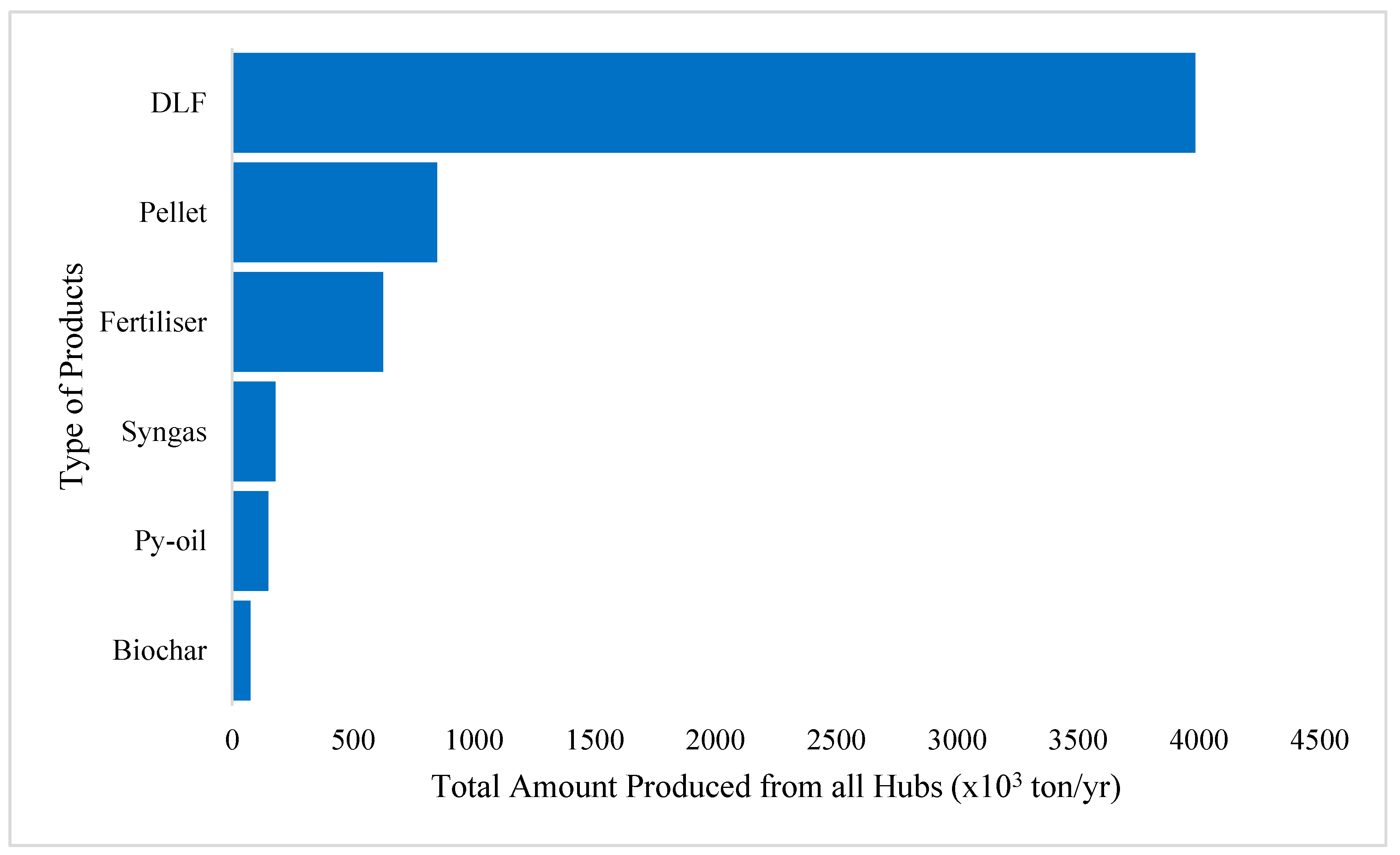
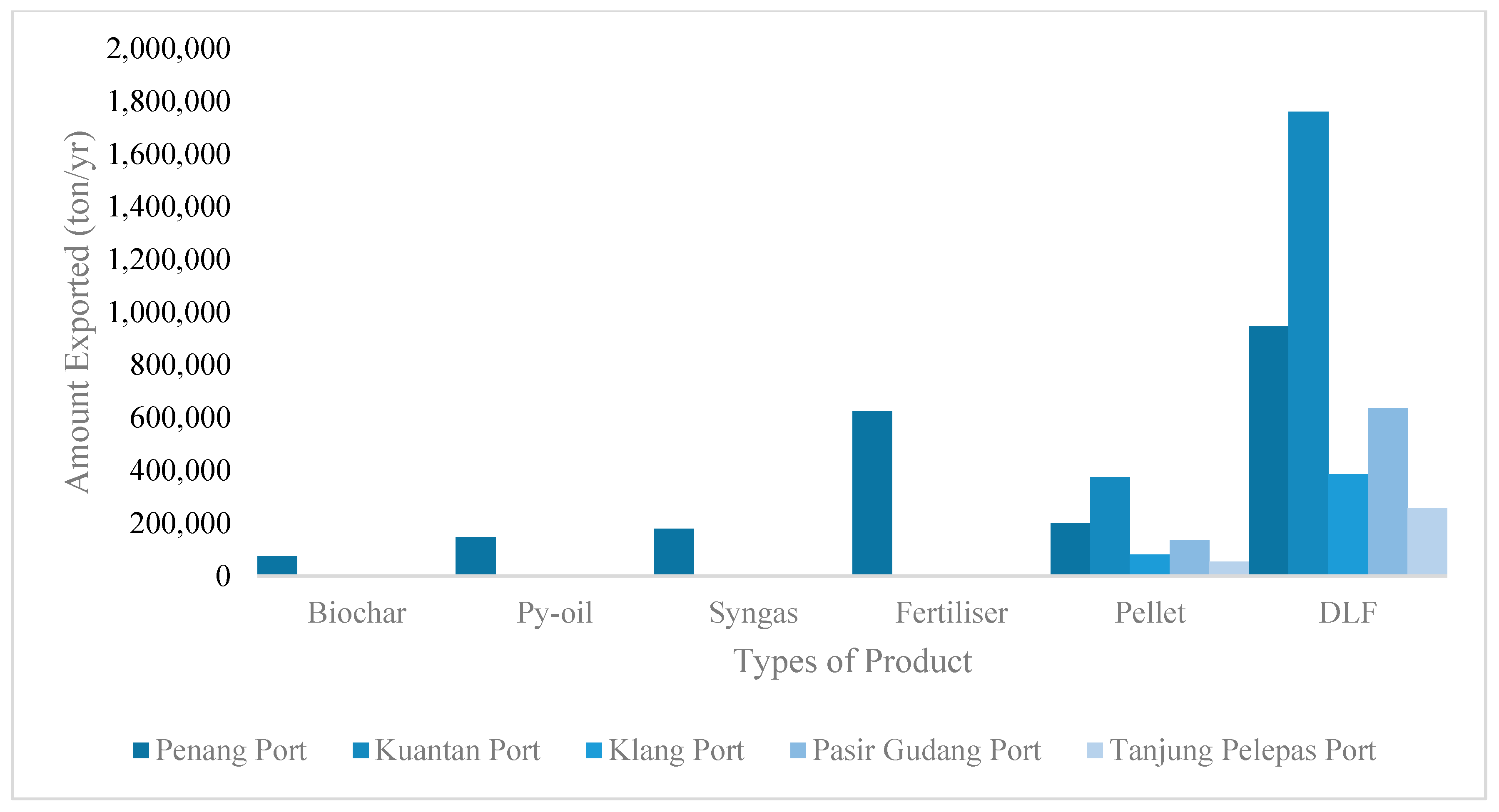
4.2. Optimal Biomass Allocation Design
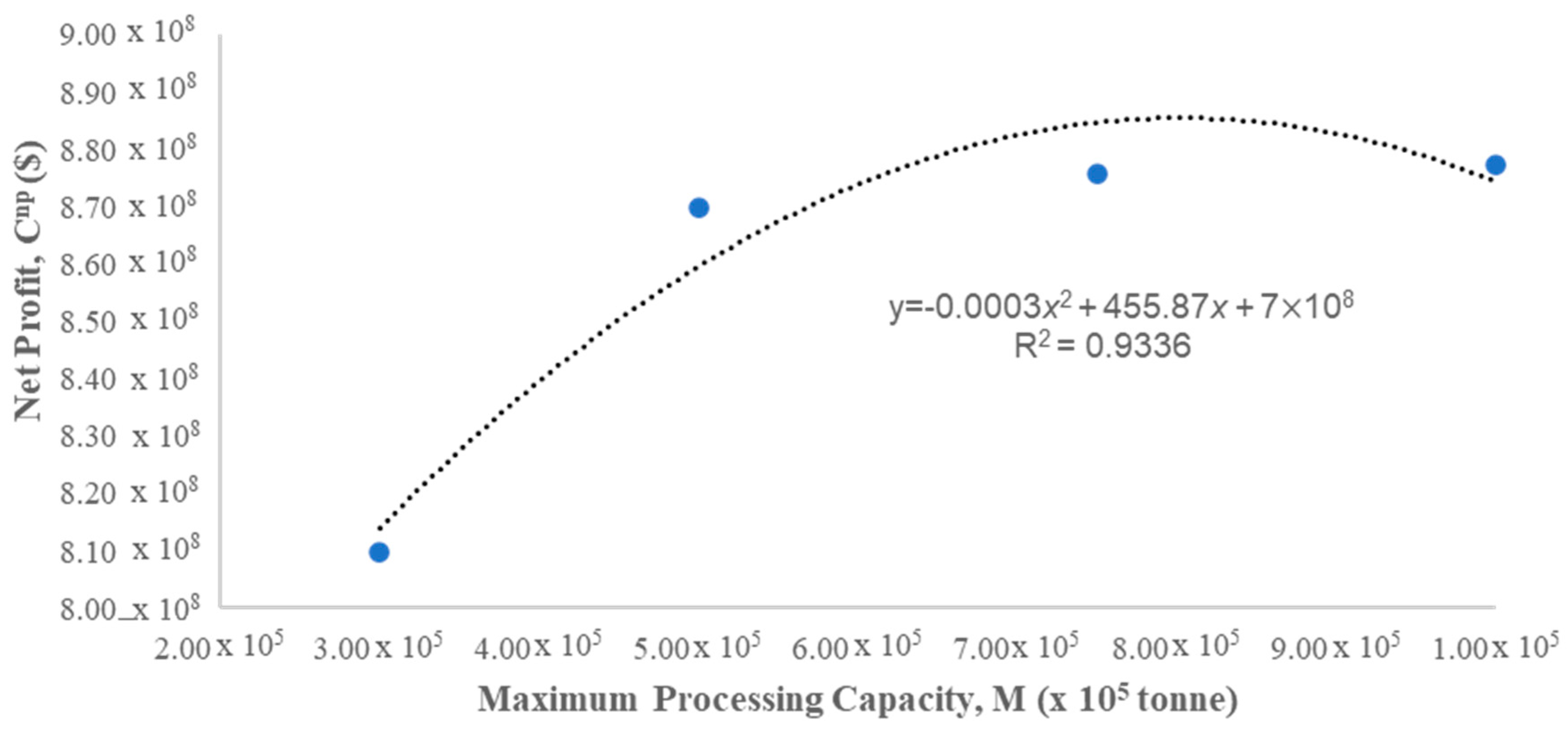
4.3. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Source, i | Xi | Yi | Area (ha) | Availability (t/y) |
|---|---|---|---|---|
| i1 | 135.55 | 714.83 | 23,075.00 | 131,989.00 |
| i2 | 166.00 | 624.80 | 25,417.00 | 145,385.24 |
| i3 | 154.40 | 578.33 | 31,165.00 | 178,263.80 |
| i4 | 218.19 | 572.52 | 29,477.00 | 168,608.44 |
| i5 | 165.27 | 505.72 | 47,813.00 | 273,490.36 |
| i6 | 221.09 | 503.79 | 49,706.00 | 284,318.32 |
| i7 | 175.42 | 454.41 | 47,650.00 | 272,558.00 |
| i8 | 204.42 | 466.03 | 64,413.00 | 368,442.36 |
| i9 | 199.34 | 441.83 | 6649.00 | 25,801.44 |
| i10 | 221.82 | 415.69 | 47,650.00 | 272,558.00 |
| i11 | 339.97 | 766.14 | 5750.00 | 22,312.88 |
| i12 | 279.81 | 626.73 | 24,895.00 | 142,399.40 |
| i13 | 334.17 | 624.80 | 24,895.00 | 142,399.40 |
| i14 | 265.31 | 568.65 | 24,895.00 | 142,399.40 |
| i15 | 333.45 | 579.30 | 24,895.00 | 142,399.40 |
| i16 | 377.67 | 578.33 | 24,895.00 | 142,399.40 |
| i17 | 403.04 | 679.01 | 24,948.00 | 142,702.56 |
| i18 | 432.03 | 678.04 | 20,794.00 | 118,941.68 |
| i19 | 406.66 | 573.49 | 35,150.00 | 201,058.00 |
| i20 | 453.78 | 505.72 | 36,169.00 | 206,886.68 |
| i21 | 461.75 | 462.16 | 36,169.00 | 206,886.68 |
| i22 | 276.91 | 502.82 | 14,333.75 | 81,989.05 |
| i23 | 333.45 | 505.72 | 14,333.75 | 81,989.05 |
| i24 | 390.72 | 504.76 | 26,381.00 | 150,899.32 |
| i25 | 288.51 | 446.67 | 14,333.75 | 81,989.05 |
| i26 | 334.90 | 444.73 | 14,333.75 | 81,989.05 |
| i27 | 393.62 | 441.83 | 26,381.00 | 150,899.32 |
| i28 | 445.81 | 437.96 | 90,324.00 | 516,653.28 |
| i29 | 293.58 | 394.39 | 21,141.00 | 120,926.52 |
| i30 | 334.90 | 384.71 | 38,456.00 | 219,968.32 |
| i31 | 394.34 | 382.78 | 32,945.00 | 188,445.40 |
| i32 | 453.78 | 382.78 | 102,010.00 | 583,497.20 |
| i33 | 334.17 | 324.69 | 26,793.00 | 153,255.96 |
| i34 | 392.89 | 324.69 | 32,945.00 | 188,445.40 |
| i35 | 451.61 | 322.75 | 68,636.00 | 392,597.92 |
| i36 | 403.04 | 268.54 | 95,287.00 | 545,041.64 |
| i37 | 452.33 | 261.76 | 68,636.00 | 392,597.92 |
| i38 | 452.33 | 218.20 | 68,636.00 | 392,597.92 |
| i39 | 210.94 | 384.71 | 5047.00 | 19,584.88 |
| i40 | 220.37 | 345.02 | 28,150.00 | 161,018.00 |
| i41 | 263.14 | 379.87 | 23,255.00 | 133,018.60 |
| i42 | 239.21 | 261.76 | 27,110.00 | 155,069.20 |
| i43 | 293.58 | 216.26 | 29,049.00 | 166,160.28 |
| i44 | 376.22 | 260.80 | 73,493.00 | 420,379.96 |
| i45 | 372.59 | 205.61 | 29,262.00 | 167,378.64 |
| i46 | 351.57 | 170.76 | 54,131.00 | 309,629.32 |
| i47 | 406.66 | 194.97 | 108,043.00 | 618,005.96 |
| i48 | 508.15 | 156.24 | 62,814.00 | 359,296.08 |
| i49 | 466.10 | 141.72 | 181,738.00 | 1,039,541.36 |
| i50 | 396.51 | 116.55 | 46,639.00 | 266,775.08 |
| i51 | 437.11 | 90.41 | 58,695.00 | 335,735.40 |
| i52 | 457.41 | 90.41 | 8624.00 | 33,465.43 |
| i53 | 476.25 | 53.62 | 22,073.00 | 126,257.56 |
| i54 | 535.69 | 92.35 | 146,250.00 | 836,550.00 |
| i55 | 515.40 | 41.04 | 47,341.00 | 270,790.52 |
| i56 | 93.41 | 853.40 | 50,326.50 | 185,571.92 |
| i57 | 114.17 | 791.99 | 50,326.50 | 185,571.92 |
| i58 | 115.11 | 746.60 | 50,326.50 | 185,571.92 |
| i59 | 149.08 | 758.57 | 50,326.50 | 185,571.92 |
| i60 | 347.22 | 738.21 | 17,591.06 | 64,864.57 |
| i61 | 290.61 | 690.52 | 5552.06 | 20,472.44 |
| i62 | 334.01 | 695.09 | 9510.77 | 35,069.63 |
| i63 | 264.19 | 618.16 | 6692.85 | 24,678.95 |
| i64 | 318.92 | 622.93 | 6398.98 | 23,595.34 |
| i65 | 294.38 | 584.65 | 1211.45 | 4467.05 |
| i66 | 151.91 | 619.90 | 20,949.00 | 77,246.50 |
| i67 | 149.08 | 555.53 | 20,949.00 | 77,246.50 |
| i68 | 231.17 | 464.96 | 27,735.00 | 102,268.93 |
| Sink, j | Xj | Yj |
|---|---|---|
| j1 | 150.55 | 588.98 |
| j2 | 138.55 | 538.78 |
| j3 | 154.91 | 491.02 |
| j4 | 214.91 | 484.90 |
| j5 | 163.64 | 437.14 |
| j6 | 210.55 | 427.35 |
| j7 | 163.64 | 384.49 |
| j8 | 207.27 | 379.59 |
| j9 | 266.18 | 487.35 |
| j10 | 414.55 | 486.12 |
| j11 | 457.09 | 439.59 |
| j12 | 459.27 | 399.18 |
| j13 | 276.00 | 433.47 |
| j14 | 337.09 | 432.24 |
| j15 | 391.64 | 435.92 |
| j16 | 280.36 | 383.27 |
| j17 | 333.82 | 382.04 |
| j18 | 401.45 | 383.27 |
| j19 | 341.45 | 335.51 |
| j20 | 393.82 | 335.51 |
| j21 | 447.27 | 324.49 |
| j22 | 333.82 | 286.53 |
| j23 | 390.55 | 282.86 |
| j24 | 450.55 | 280.41 |
| j25 | 402.55 | 242.45 |
| j26 | 452.73 | 236.33 |
| j27 | 456.00 | 194.69 |
| j28 | 258.55 | 322.04 |
| j29 | 225.82 | 293.88 |
| j30 | 258.55 | 240.00 |
| j31 | 225.82 | 219.18 |
| j32 | 328.36 | 231.43 |
| j33 | 288.00 | 187.35 |
| j34 | 330.55 | 184.90 |
| j35 | 370.91 | 184.90 |
| j36 | 346.91 | 140.82 |
| j37 | 409.09 | 172.65 |
| j38 | 452.73 | 143.27 |
| j39 | 519.27 | 143.27 |
| j40 | 408.00 | 94.29 |
| j41 | 447.27 | 77.14 |
| j42 | 555.27 | 90.61 |
| j43 | 507.27 | 41.63 |
| j44 | 94.74 | 748.09 |
| j45 | 140.00 | 699.57 |
| j46 | 328.42 | 670.21 |
| j47 | 331.58 | 557.87 |
| i/j | j1 | j2 | j3 | j4 | j5 | j6 | j7 | j8 | j9 | j10 | j11 | j12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i2 | 145,385 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i3 | 170,451 | 7813 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i4 | 0 | 168,608 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i5 | 0 | 0 | 273,490 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i6 | 0 | 0 | 0 | 284,318 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i7 | 0 | 0 | 0 | 0 | 272,558 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i8 | 0 | 0 | 226,510 | 137,868 | 0 | 4064 | 0 | 0 | 0 | 0 | 0 | 0 |
| i9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i10 | 0 | 0 | 0 | 0 | 0 | 272,558 | 0 | 0 | 0 | 0 | 0 | 0 |
| i11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i12 | 106,917 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i14 | 0 | 113,920 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 142,214 | 0 | 0 |
| i20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 206,887 | 0 | 0 |
| i21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 206,887 | 0 |
| i22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 81,989 | 0 | 0 | 0 |
| i23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i24 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 150,899 | 0 | 0 |
| i25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i26 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i27 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i28 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 293,113 | 120,209 |
| i29 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i30 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i31 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i32 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 379,791 |
| i33 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i34 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i35 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i37 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i38 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i39 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i40 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i41 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i42 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i43 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i44 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i45 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i46 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i47 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i48 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i49 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i50 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i51 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i52 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i53 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i54 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i55 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i56 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i57 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i58 | 0 | 44,376 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i59 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i60 | 0 | 15,511 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i61 | 0 | 4896 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i62 | 0 | 8386 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i63 | 0 | 24,679 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i64 | 0 | 5642 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i65 | 0 | 4467 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i66 | 77,247 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i67 | 0 | 77,247 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i68 | 0 | 24,456 | 0 | 77,813 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sum | 500,000 | 500,000 | 500,000 | 500,000 | 272,558 | 276,622 | 0 | 0 | 81,989 | 500,000 | 500,000 | 500,000 |
| i/j | j13 | j14 | j15 | j16 | j17 | j18 | j19 | j20 | j21 | j22 | j23 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| i1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i23 | 0 | 0 | 65,591 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i24 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i25 | 81,989 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i26 | 0 | 81,989 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i27 | 0 | 0 | 150,899 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i28 | 0 | 0 | 103,331 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i29 | 0 | 0 | 0 | 120,927 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i30 | 0 | 0 | 0 | 0 | 219,968 | 0 | 0 | 0 | 0 | 0 | 0 |
| i31 | 0 | 0 | 0 | 0 | 0 | 188,445 | 0 | 0 | 0 | 0 | 0 |
| i32 | 0 | 0 | 0 | 0 | 0 | 96,304 | 0 | 0 | 107,402 | 0 | 0 |
| i33 | 0 | 0 | 0 | 0 | 0 | 0 | 153,256 | 0 | 0 | 0 | 0 |
| i34 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 188,445 | 0 | 0 | 0 |
| i35 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 392,598 | 0 | 0 |
| i36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 328,631 |
| i37 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i38 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i39 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i40 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i41 | 0 | 0 | 0 | 133,019 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i42 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i43 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i44 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 171,369 |
| i45 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i46 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i47 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i48 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i49 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i50 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i51 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i52 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i53 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i54 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i55 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i56 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i57 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i58 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i59 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i60 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i61 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i62 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i63 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i64 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i65 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i66 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i67 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i68 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sum | 81,989 | 81,989 | 319,821 | 253,945 | 219,968 | 284,750 | 153,256 | 188,445 | 500,000 | 0 | 500,000 |
| i/j | j24 | j25 | j26 | j27 | j28 | j29 | j30 | j31 | j32 | j33 | j34 | j35 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i24 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i26 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i27 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i28 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i29 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i30 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i31 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i32 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i33 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i34 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i35 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i36 | 107,402 | 109,008 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i37 | 392,598 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i38 | 0 | 0 | 392,598 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i39 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i40 | 0 | 0 | 0 | 0 | 0 | 161,018 | 0 | 0 | 0 | 0 | 0 | 0 |
| i41 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i42 | 0 | 0 | 0 | 0 | 0 | 0 | 155,069 | 0 | 0 | 0 | 0 | 0 |
| i43 | 0 | 0 | 0 | 0 | 0 | 0 | 166,160 | 0 | 0 | 0 | 0 | 0 |
| i44 | 0 | 249,011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i45 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 167,379 |
| i46 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 247,703 | 61,926 |
| i47 | 0 | 141,980 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i48 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i49 | 0 | 0 | 0 | 401,024 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i50 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i51 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i52 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i53 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i54 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i55 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i56 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i57 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i58 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i59 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i60 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i61 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i62 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i63 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i64 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i65 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i66 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i67 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i68 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sum | 500,000 | 500,000 | 392,598 | 401,024 | 0 | 161,018 | 321,229 | 0 | 0 | 0 | 247,703 | 229,305 |
| i/j | j36 | j37 | j38 | j39 | j40 | j41 | j42 | j43 | j44 | j45 | j46 | j47 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 131,989 | 0 | 0 |
| i2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 28,480 | 7002 |
| i13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 118,262 | 24,137 |
| i14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 28,480 |
| i15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 142,399 |
| i16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 142,399 |
| i17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 142,703 | 0 |
| i18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 118,942 | 0 |
| i19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 58,844 |
| i20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 16,398 |
| i24 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i26 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i27 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i28 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i29 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i30 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i31 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i32 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i33 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i34 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i35 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i37 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i38 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i39 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i40 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i41 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i42 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i43 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i44 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i45 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i46 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i47 | 0 | 476,025 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i48 | 0 | 0 | 0 | 359,296 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i49 | 0 | 0 | 500,000 | 0 | 0 | 138,518 | 0 | 0 | 0 | 0 | 0 | 0 |
| i50 | 0 | 0 | 0 | 0 | 266,775 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i51 | 0 | 0 | 0 | 0 | 67,147 | 268,588 | 0 | 0 | 0 | 0 | 0 | 0 |
| i52 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i53 | 0 | 0 | 0 | 0 | 0 | 92,894 | 0 | 33,363 | 0 | 0 | 0 | 0 |
| i54 | 0 | 0 | 0 | 140,704 | 0 | 0 | 500,000 | 195,846 | 0 | 0 | 0 | 0 |
| i55 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 270,791 | 0 | 0 | 0 | 0 |
| i56 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 141,196 | 44,376 | 0 | 0 |
| i57 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 141,196 | 44,376 | 0 | 0 |
| i58 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 141,196 | 0 | 0 | 0 |
| i59 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 185,572 | 0 | 0 |
| i60 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 49,353 | 0 |
| i61 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15,577 | 0 |
| i62 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 26,683 | 0 |
| i63 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i64 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 17,953 |
| i65 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i66 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i67 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i68 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sum | 0 | 476,025 | 500,000 | 500,000 | 333,922 | 500,000 | 500,000 | 500,000 | 423,588 | 406,313 | 500,000 | 437,613 |
References
- EIA. EIA Projects Nearly 50% Increase in World Energy Usage by 2050, Led by Growth in Asia. 2019. Available online: https://www.eia.gov/todayinenergy/detail.php?id=41433 (accessed on 17 April 2022).
- Jin, C.; Lv, Z.; Li, Z.; Sun, K. Green finance, renewable energy and carbon neutrality in OECD countries. Renew. Energy 2023, 211, 279–284. [Google Scholar] [CrossRef]
- Raihan, A.; Tuspekova, A. Toward a sustainable environment: Nexus between economic growth, renewable energy use, forested area, and carbon emissions in Malaysia. Resour. Conserv. Recycl. Adv. 2022, 15, 200096. [Google Scholar] [CrossRef]
- Idris, M.N.M.; Hashim, H.; Leduc, S.; Yowargana, P.; Kraxner, F.; Woon, K.S. Deploying bioenergy for decarbonizing Malaysian energy sectors and alleviating renewable energy poverty. Energy 2021, 232, 120967. [Google Scholar] [CrossRef]
- MPOC. Malaysian Palm Oil Industry. 2021. Available online: https://mpoc.org.my/malaysian-palm-oil-industry/ (accessed on 17 April 2022).
- MPOB. Overview of the Malaysian Oil Palm Industry 2021. 2021. Available online: https://bepi.mpob.gov.my/images/overview/Overview2021.pdf (accessed on 17 April 2022).
- AIM. National Biomass Strategy 2020: New Wealth Creation for Malaysia’s Biomass Industry; AIM: Selangor, Malaysia, 2013. [Google Scholar]
- Derman, E.; Abdulla, R.; Marbawi, H.; Sabullah, M.K. Oil palm empty fruit bunches as a promising feedstock for bioethanol production in Malaysia. Renew. Energy 2018, 129, 285–298. [Google Scholar] [CrossRef]
- Rashidi, N.A.; Yusup, S. Production of palm kernel shell-based activated carbon by direct physical activation for carbon dioxide adsorption. Environ. Sci. Pollut. Res. 2018, 26, 33732–33746. [Google Scholar] [CrossRef]
- Chin, M.J.; Poh, P.E.; Tey, B.T.; Chan, E.S.; Chin, K.L. Biogas from palm oil mill effluent (POME): Opportunities and challenges from Malaysia’s perspective. Renew. Sustain. Energy Rev. 2013, 26, 717–726. [Google Scholar] [CrossRef]
- Grimm, A.M.; Dorsch, L.Y.; Kloess, G.H.; Enke, D.; Roppertz, A. Transition metal promoted combustion of rice husk and rice straw towards an energy optimized synthesis of biogenic silica. Biomass Bioenergy 2021, 155, 106282. [Google Scholar] [CrossRef]
- DOA. Plantation Statistics 2021. 2021. Available online: http://www.doa.gov.my/index/resources/aktiviti_sumber/sumber_awam/maklumat_pertanian/perangkaan_tanaman/booklet_statistik_tanaman_2021.pdf (accessed on 17 April 2022).
- Yerrayya, A.; Vishnu, A.K.S.; Shreyas, S.; Chakravarthy, S.R.; Vinu, R. Hydrothermal Liquefaction of Rice Straw Using Methanol as Co-Solvent. Energies 2020, 13, 2618. [Google Scholar] [CrossRef]
- Hu, Q.; Shao, J.; Yang, H.; Yao, D.; Wang, X.; Chen, H. Effects of binders on the properties of bio-char pellets. Appl. Energy 2015, 157, 508–516. [Google Scholar] [CrossRef]
- Kaniapan, S.; Pasupuleti, J.; Nesan, K.P.; Abubackar, H.N.; Umar, H.A.; Oladosu, T.L.; Bello, S.R.; Rene, E.R. A Review of the Sustainable Utilization of Rice Residues for Bioenergy Conversion Using Different Valorization Techniques, Their Challenges, and Techno-Economic Assessment. Int. J. Environ. Res. Public Health 2022, 19, 3427. [Google Scholar] [CrossRef] [PubMed]
- Kamthan, R.; Tiwari, I. Agricultural Wastes- Potential Substrates For Mushroom Cultivation. Eur. J. Exp. Biol. 2017, 7, 31. [Google Scholar] [CrossRef]
- Goodman, B.A. Utilization of waste straw and husks from rice production: A review. J. Bioresour. Bioprod. 2020, 5, 143–162. [Google Scholar] [CrossRef]
- Shamsollahi, Z.; Partovinia, A. Recent advances on pollutants removal by rice husk as a bio-based adsorbent: A critical review. J. Environ. Manag. 2019, 246, 314–323. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, R.K.; Sulaiman, S.A.; Yusup, S.; Dol, S.S.; Inayat, M.; Umar, H.A. Exploring the potential of coconut shell biomass for charcoal production. Ain Shams Eng. J. 2021, 13, 101499. [Google Scholar] [CrossRef]
- Curia, A.C.; Souza, A.R.D.; Zaro, J.R.; Barbieri, M.R.R.; Kappler, G.; Moraes, C.A.M. Waste Management and Application of Coconut Biomass and Fibre. In Vegetable Fiber Composites and their Technological Applications; Springer: Singapore, 2021; pp. 215–237. [Google Scholar] [CrossRef]
- Ng, W.P.Q.; Ng, R.T.L.; Lam, H.L.; Kamal, M.; Ng, E.H.; Ng, D.K.S. Biomass corridor synthesis for malaysia green energy supply chain. Chem. Eng. Trans. 2012, 29, 703–708. [Google Scholar] [CrossRef]
- Xu, X.; Liu, G.; Mola-Yudego, B. Barriers and opportunities for bioenergy expansion in Chinese rural areas. Energy Sustain. Dev. 2022, 70, 181–193. [Google Scholar] [CrossRef]
- Maier, S.; Narodoslawsky, M. Optimal Renewable Energy Systems for Smart Cities. Comput. Aided Chem. Eng. 2014, 33, 1849–1854. [Google Scholar]
- How, B.S.; Hong, B.H.; Lam, H.L.; Friedler, F. Synthesis of multiple biomass corridor via decomposition approach: A P-graph application. J. Clean. Prod. 2016, 130, 45–57. [Google Scholar] [CrossRef]
- Lee, Y.H.; Golinska-Dawson, P.; Wu, J.-Z. Mathematical Models for Supply Chain Management. Math. Probl. Eng. 2016, 2016, 1–4. [Google Scholar] [CrossRef]
- Foo, D.C.Y. Automated targeting model for aggregate planning in production and energy supply chains. Clean Technol. Environ. Policy 2015, 18, 1405–1414. [Google Scholar] [CrossRef]
- Leong, H.; Foo, D.C.; Ng, L.Y.; Andiappan, V. Hybrid approach for carbon-constrained planning of bioenergy supply chain network. Sustain. Prod. Consum. 2019, 18, 250–267. [Google Scholar] [CrossRef]
- Leitão, F.O.; Lacerda, M.S.; Thomé, K.M.; Rodrigues, E.C.C. The reverse logistics costs for the reuse of green coconut residues. Custos E Agronegocio 2021, 17, 156–187. [Google Scholar]
- Ishii, K.; Furuichi, T.; Fujiyama, A.; Watanabe, S. Logistics cost analysis of rice straw pellets for feasible production capacity and spatial scale in heat utilization systems: A case study in Nanporo town, Hokkaido, Japan. Biomass Bioenergy 2016, 94, 155–166. [Google Scholar] [CrossRef]
- Friedler, F.; Aviso, K.B.; Bertok, B.; Foo, D.C.; Tan, R.R. Prospects and challenges for chemical process synthesis with P-graph. Curr. Opin. Chem. Eng. 2019, 26, 58–64. [Google Scholar] [CrossRef]
- Chin, H.H.; Foo, D.C.; Lam, H.L. Simultaneous water and energy integration with isothermal and non-isothermal mixing—A P-graph approach. Resour. Conserv. Recycl. 2019, 149, 687–713. [Google Scholar] [CrossRef]
- Ondruška, V.; How, B.S.; Netolický, M.; Máša, V.; Teng, S.Y. Resource optimisation in aquaponics facility via process monitoring and graph-theoretical approach. Carbon Resour. Convers. 2022, 5, 255–270. [Google Scholar] [CrossRef]
- Pimentel, J.; Orosz, Á.; Aviso, K.B.; Tan, R.R.; Friedler, F. Conceptual Design of a Negative Emissions Polygeneration Plant for Multiperiod Operations Using P-Graph. Processes 2021, 9, 233. [Google Scholar] [CrossRef]
- Lo, S.L.Y.; Lim, C.H.; Benjamin, M.F.D.; Lam, H.L.; Sunarso, J.; How, B.S. Addressing supply uncertainties using multi-period stochastic economic evaluation: A graph-theoretic aided element targeting approach. Clean. Eng. Technol. 2022. [Google Scholar] [CrossRef]
- Friedler, F.; Tarján, K.; Huang, Y.; Fan, L. Graph-theoretic approach to process synthesis: Axioms and theorems. Chem. Eng. Sci. 1992, 47, 1973–1988. [Google Scholar] [CrossRef]
- Friedler, F.; Orosz, A.; Losada, J.P. P-Graphs for Process Systems Engineering: Mathematical Models and Algorithms, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- How, B.S.; Yeoh, T.T.; Tan, T.K.; Chong, K.H.; Ganga, D.; Lam, H.L. Debottlenecking of sustainability performance for integrated biomass supply chain: P-graph approach. J. Clean. Prod. 2018, 193, 720–733. [Google Scholar] [CrossRef]
- Les, A.; Heckl, I.; Cabezas, H. Modeling Renewable Energy Systems in Rural Areas with Flexible Operating Units. Chem. Eng. Trans. 2021, 88, 643–648. [Google Scholar] [CrossRef]
- Holló, C.; Imreh, B.; Imreh, C. Reduction techniques for the PNS problems: A novel technique and a review. Optim. Eng. 2008, 10, 351–361. [Google Scholar] [CrossRef]
- Tuncer, Y.; Tanik, M.M.; Allison, D.B. An overview of statistical decomposition techniques applied to complex systems. Comput. Stat. Data Anal. 2008, 52, 2292–2310. [Google Scholar] [CrossRef] [Green Version]
- Friedler, F.; Tarjan, K.; Huang, Y.; Fan, L. Graph-theoretic approach to process synthesis: Polynomial algorithm for maximal structure generation. Comput. Chem. Eng. 1993, 17, 929–942. [Google Scholar] [CrossRef]
- Cao, J.; He, Y.-L.; Zhu, Q.-X. Maximal structure generation of superstructure for semantic triple generated by DEVS ontology in the process industry. Chemom. Intell. Lab. Syst. 2020, 205, 104119. [Google Scholar] [CrossRef]
- Cohen, J. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences, 3rd ed.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 2003. [Google Scholar]
- Thiangchanta, S.; Chaichana, C. The multiple linear regression models of heat load for air-conditioned room. Energy Rep. 2020, 6, 972–977. [Google Scholar] [CrossRef]
- Rath, S.; Tripathy, A.; Tripathy, A.R. Prediction of new active cases of coronavirus disease (COVID-19) pandemic using multiple linear regression model. Diabetes Metab. Syndr. Clin. Res. Rev. 2020, 14, 1467–1474. [Google Scholar] [CrossRef]
- Gowda, C.R.; Dutta, R.; Pasha, A.T.; Ravi, L. Use of multiple linear regression to compensate for diametrical deviations in machined components due to thermal errors. Mater. Today Proc. 2021, 56, 2630–2639. [Google Scholar] [CrossRef]
- Ottaviani, F.M.; De Marco, A. Multiple Linear Regression Model for Improved Project Cost Forecasting. Procedia Comput. Sci. 2022, 196, 808–815. [Google Scholar] [CrossRef]
- Microsoft Load the Analysis ToolPak in Excel. 2022. Available online: https://support.microsoft.com/en-au/office/load-the-analysis-toolpak-in-excel-6a63e598-cd6d-42e3-9317-6b40ba1a66b4 (accessed on 6 June 2023).
- Lam, H.L.; Klemeš, J.J.; Kravanja, Z. Model-size reduction techniques for large-scale biomass production and supply networks. Energy 2011, 36, 4599–4608. [Google Scholar] [CrossRef]
- Yeo, S.Z.; How, B.S.; Ngan, S.L.; Ng, W.P.; Leong, W.D.; Lim, C.H.; Lam, H.L. An integrated approach to prioritise parameters for multi-objective optimisation: A case study of biomass network. J. Clean. Prod. 2020, 274, 123053. [Google Scholar] [CrossRef]
- Samsudin, M.H.; Hassan, M.A.; Idris, J.; Ramli, N.; Yusoff, M.Z.M.; Ibrahim, I.; Othman, M.R.; Ali, A.A.M.; Shirai, Y. A one-step self-sustained low temperature carbonization of coconut shell biomass produced a high specific surface area biochar-derived nano-adsorbent. Waste Manag. Res. J. 2019, 37, 551–555. [Google Scholar] [CrossRef] [PubMed]
- Tsai, W.; Lee, M.; Chang, Y. Fast pyrolysis of rice husk: Product yields and compositions. Bioresour. Technol. 2007, 98, 22–28. [Google Scholar] [CrossRef]
- Azeta, O.; Ayeni, A.O.; Agboola, O.; Elehinafe, F.B. A review on the sustainable energy generation from the pyrolysis of coconut biomass. Sci. Afr. 2021, 13, e00909. [Google Scholar] [CrossRef]
- Wang, Q.; Sarkar, J. Pyrolysis behaviors of waste coconut shell and husk biomasses. Int. J. Energy Prod. Manag. 2018, 3, 111. [Google Scholar] [CrossRef] [Green Version]
- MPOB. The Malaysian Oil Palm Industry Performance. 2021. Available online: https://prestasisawit.mpob.gov.my/en/plantations-planted (accessed on 19 April 2022).
- Booneimsri, P.; Kubaha, K.; Chullabodhi, C. Increasing power generation with enhanced cogeneration using waste energy in palm oil mills. Energy Sci. Eng. 2018, 6, 154–173. [Google Scholar] [CrossRef]
- International Rice Research Institute (IRRI). The value of sustainable rice straw management. 2018. Available online: https://www.irri.org/rice-straw-management#:~:text=Ratio%20of%20straw%20to%20paddy,per%20year%20produced%20in%20Asia (accessed on 1 June 2023).
- Yin, M.; Li, X.; Liu, Q.; Tang, F. Rice husk ash addition to acid red soil improves the soil property and cotton seedling growth. Sci. Rep. 2022, 12, 1–9. [Google Scholar] [CrossRef] [PubMed]
- DP CleanTech. Understanding Coconut as a Biomass Fuel. 2021. Available online: https://www.dpcleantech.com/medias/downloads/download/1520/521/22 (accessed on 1 June 2023).
- Zhu, A.; Han, Y.; Liu, H. Effects of adaptive cooperation among heterogeneous manufacturers on supply chain viability under fluctuating demand in post-COVID-19 era: An agent-based simulation. Int. J. Prod. Res. 2023, 1–27. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, K.; Zhao, Y.; Zheng, H.; Dong, Z. Hub-and-Spoke Logistics Network Considering Pricing and Co-Opetition. Sustainability 2021, 13, 9979. [Google Scholar] [CrossRef]
- Lo, S.L.Y.; How, B.S.; Teng, S.Y.; Lam, H.L.; Lim, C.H.; Rhamdhani, M.A.; Sunarso, J. Stochastic techno-economic evaluation model for biomass supply chain: A biomass gasification case study with supply chain uncertainties. Renew. Sustain. Energy Rev. 2021, 152, 111644. [Google Scholar] [CrossRef]
- Marousi, A.; Charitopoulos, V.M. Game theoretic optimisation in process and energy systems engineering: A review. Front. Chem. Eng. 2023, 5, 1130568. [Google Scholar] [CrossRef]




| Item | Cost (USD) | References |
|---|---|---|
| EFB | 3/ton | [50] |
| PKS | 35/ton | [50] |
| Coconut Husk | 150/ton | [51] |
| Coconut Shell | 150/ton | [51] |
| Paddy Straw | 16.25/ton | [50] |
| Rice Husk | 25/ton | [50] |
| Fertiliser | 260/ton | [50] |
| Pellet | 140/ton | [50] |
| DLF | 160/ton | [50] |
| Briquette | 120/ton | [50] |
| Py-oil | 100/ton | [24] |
| Biochar | 350/ton | [50] |
| Syngas | 0.12/L | [50] |
| MPS | 22.6/ton | [50] |
| Electricity | 0.14/kWh | [50] |
| Biomass | Technology | Conversion | References |
|---|---|---|---|
| Palm Oil | Separation and Sieving | 0.67 ton WLF/ton EFB 0.24 ton SF/ton EFB | [50] |
| Drying and Sieving | 0.56 ton DLF/ton WLF | ||
| Pelletising | 0.33 ton Pellet/ton Biomass | ||
| Briquetting | 0.33 ton Briquette/ton Biomass | ||
| Combustion | 2.59 ton HPS/ton EFB 3.96 ton HPS/ton PKS | ||
| Paddy | Fast Pyrolysis | 0.53 ton Py-oil/ton Rice Husk 0.27 ton Biochar/ton Rice Husk 0.64 L Syngas/ton Rice Husk | [50] |
| Slow Pyrolysis | 0.36 ton Biochar/ton Rice Husk 0.21 L Syngas/ton Rice Husk | ||
| Conditioning | 0.7 ton Fertiliser/ton Paddy Straw | ||
| Combustion (steam generation) | 4.79 ton HPS/ton Paddy Straw | ||
| Coconut | Fast Pyrolysis | 0.346 ton Biochar/ton Coconut Husk 0.173 ton Py-oil/ton Coconut Husk 0.269 L Syngas/ton Coconut Husk | [54] |
| 0.243 ton Biochar/ton Coconut Shell 0.255 ton Py-oil/ton Coconut Shell 0.263 L Syngas/ton Coconut Shell | |||
| All | Electricity Generation | 0.91 ton MPS/ton HPS 0.58 kW/ton HPS | [50] |
| Technology | Cap Cost (USD) | Operating Cost (USD) |
|---|---|---|
| DLF Production | 9/ton/h | 18.5/ton/h |
| Pelletising | 5/ton/h | 22/ton/h |
| Briquetting | 4.5/ton/h | 27/ton/h * |
| Slow Pyrolysis | 48/ton | 30/ton |
| Fast Pyrolysis | 39.18/ton | 47.6/ton |
| Boiler | 2.6/ton HPS/h | - |
| Turbine | 0.05/kW | 0.05/kW |
| Parameter | Value |
|---|---|
| Processing Hub’s Capacity (M) | 5.00 × 105 ton |
| Investment Cost () | USD 1 million |
| Transportation Cost Constant () & | USD 0.1/ton/km |
| Discounted Rate (Dr) # | 6% |
| Lifespan | 20 years |
| Maximum Processing Capacity, (ton) | Net Profit, (USD) | No. of Biomass Sources Utilised, | No. of Processing Hubs Utilised, | Amount of Biomass Utilised, (ton) |
|---|---|---|---|---|
| 3.00 × 105 | 8.10 × 108 | 64 | 47 | 1.41 × 107 |
| 5.00 × 105 | 8.70 × 108 | 64 | 39 | 1.45 × 107 |
| 7.50 × 105 | 8.76 × 108 | 64 | 39 | 1.45 × 107 |
| 1.00 × 106 | 8.77 × 108 | 64 | 38 | 1.45 × 107 |
| 5.00 × 106 | 8.77 × 108 | 64 | 38 | 1.45 × 107 |
| 1.00 × 107 | 8.77 × 108 | 64 | 38 | 1.45 × 107 |
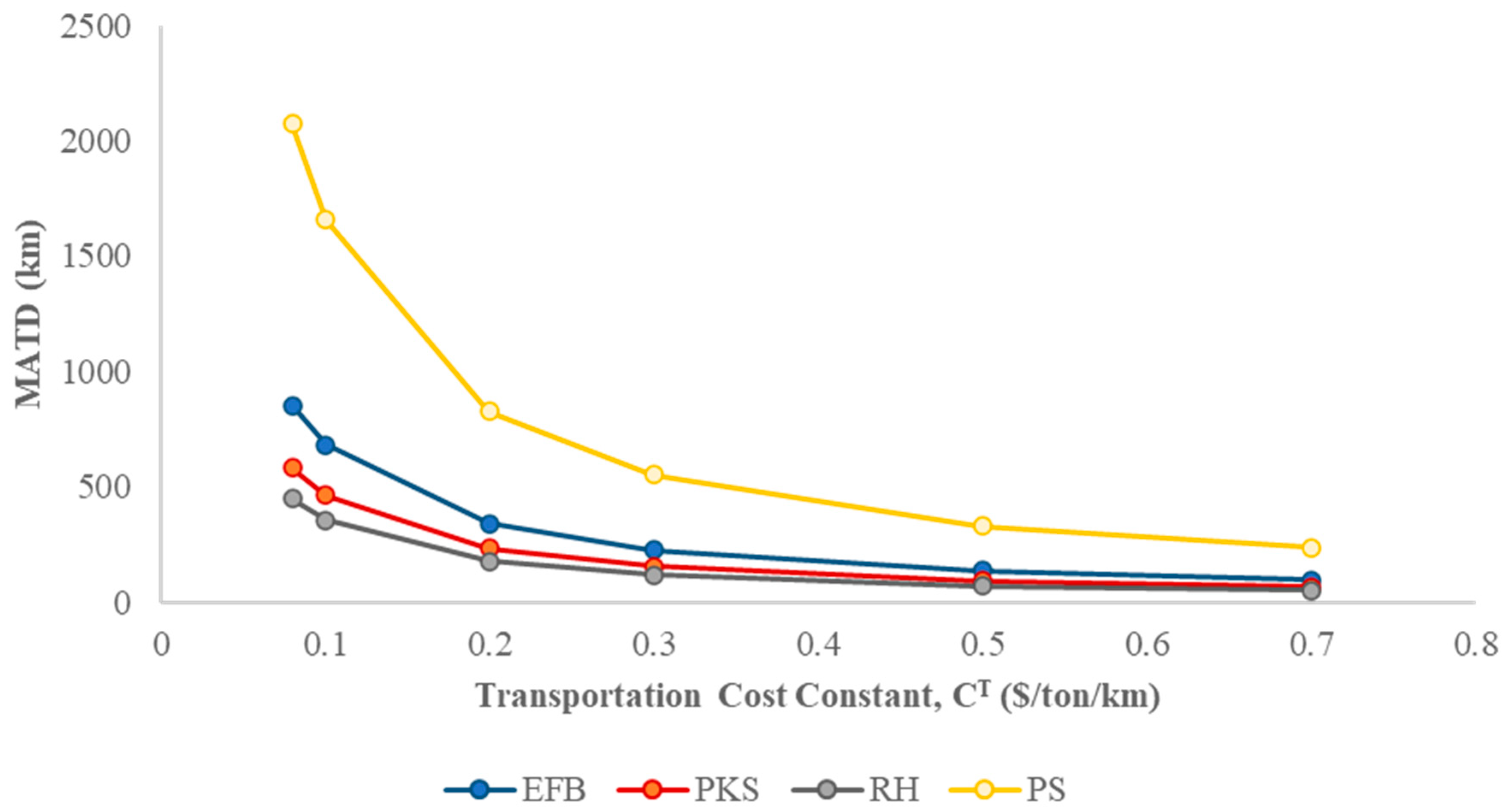
| Transportation Cost Constant, (USD/ton/km) | Net Profit, (USD) | No. of Biomass Sources Utilised, | No. of Processing Hubs Utilised, | Amount of Biomass Utilised, (ton) |
|---|---|---|---|---|
| 0.08 | 8.97 × 108 | 64 | 39 | 1.45 × 107 |
| 0.1 | 8.70 × 108 | 64 | 39 | 1.45 × 107 |
| 0.2 | 7.32 × 108 | 64 | 41 | 1.45 × 107 |
| 0.3 | 5.94 × 108 | 64 | 41 | 1.45 × 107 |
| 0.5 | 3.19 × 108 | 63 | 41 | 1.44 × 107 |
| 0.7 | 5.02 × 107 | 63 | 41 | 1.41 × 107 |
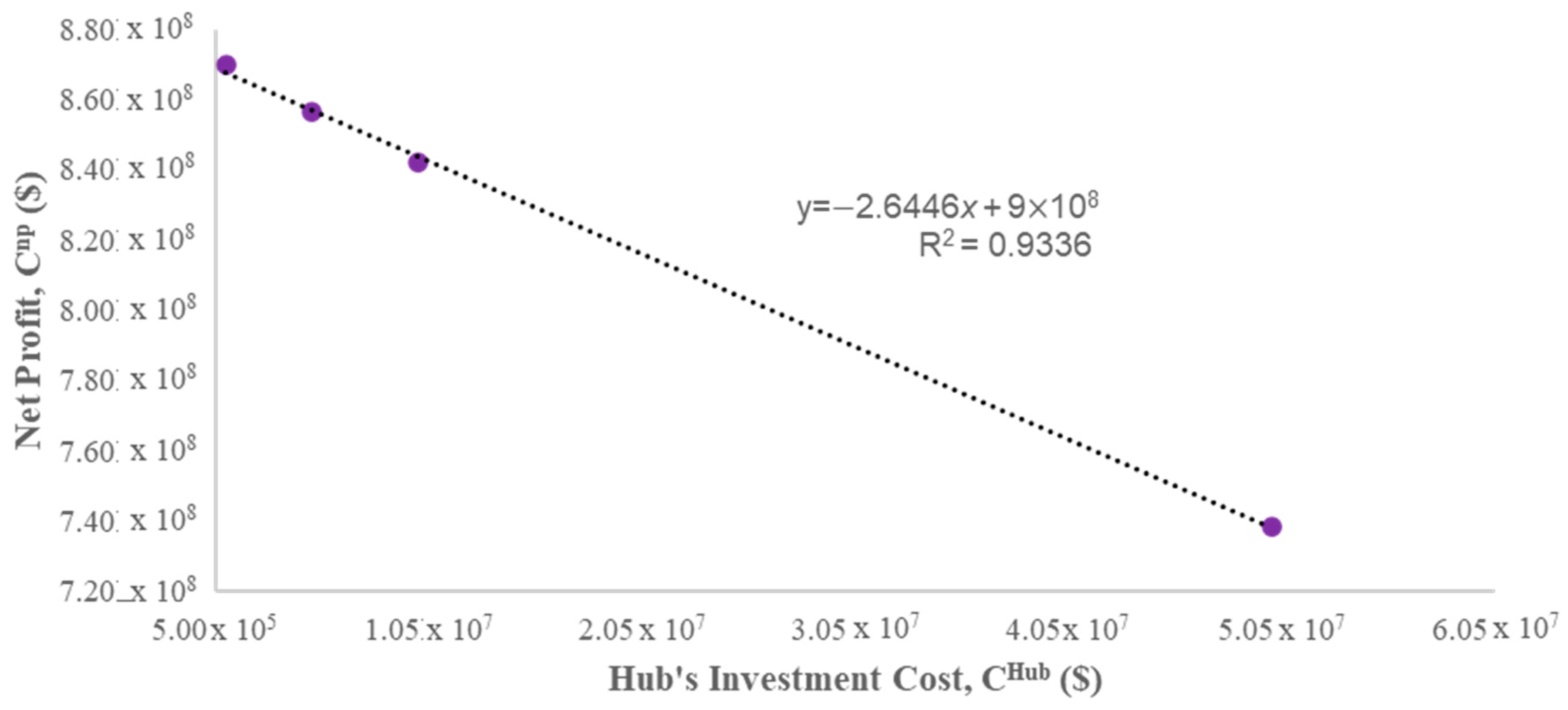
| Hub’s Investment Cost, (USD) | Net Profit, (USD) | No. of Biomass Sources Utilised, | No. of Processing Hubs Utilised, | Amount of Biomass Utilised, (ton) |
|---|---|---|---|---|
| 1.00 × 106 | 8.70 × 108 | 64 | 39 | 1.45 × 107 |
| 5.00 × 106 | 8.57 × 108 | 64 | 35 | 1.45 × 107 |
| 1.00 × 107 | 8.42 × 108 | 64 | 31 | 1.45 × 107 |
| 5.00 × 107 | 7.39 × 108 | 64 | 29 | 1.45 × 107 |
| Parameter | Unit | Dual Price Value |
|---|---|---|
| Processing Hub’s Capacity ( | ton | 49.190 |
| Transportation Cost Constant | USD/ton/km | −0.138 × 1010 |
| Processing hub’s investment cost | USD | −3.393 |
| Biomass | Targeted Technology | Threshold Unit Price (USD/ton) |
|---|---|---|
| EFB | DLF and pellet production | 37.14 |
| PKS | Power generation | 71.28 |
| Paddy Straw | Fertiliser production | 182.00 |
| Rice Husk | Fast pyrolysis | 60.80 |
| Coconut Husk | Fast pyrolysis | 51.65 |
| Coconut Shell | Fast pyrolysis | 23.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lam, H.L.; Ang, J.C.; Heng, Y.P.; Lee, H.Y.; Loy, A.C.M.; How, B.S. Synthesis of Biomass Corridor in Peninsular Malaysia via Hybrid Mathematical and Graphical Framework. Sustainability 2023, 15, 10980. https://doi.org/10.3390/su151410980
Lam HL, Ang JC, Heng YP, Lee HY, Loy ACM, How BS. Synthesis of Biomass Corridor in Peninsular Malaysia via Hybrid Mathematical and Graphical Framework. Sustainability. 2023; 15(14):10980. https://doi.org/10.3390/su151410980
Chicago/Turabian StyleLam, Hon Loong, Jia Chun Ang, Yi Peng Heng, Ho Yan Lee, Adrian Chun Minh Loy, and Bing Shen How. 2023. "Synthesis of Biomass Corridor in Peninsular Malaysia via Hybrid Mathematical and Graphical Framework" Sustainability 15, no. 14: 10980. https://doi.org/10.3390/su151410980





