Proton Exchange Membrane Fuel Cell Power Prediction Based on Ridge Regression and Convolutional Neural Network Data-Driven Model

Abstract

Research on the power prediction of proton exchange membrane fuel cells (PEMFCs) has garnered considerable attention. Because mainstream computational-fluid-dynamics-based methods are time-consuming, this study aimed to design a data-driven method based on Ridge regression (Ridge) and convolutional neural network (CNN) algorithms that can efficiently predict PEMFC power under uncertain conditions in real-world scenarios and reduce the time consumption. The measured data from a PEMFC test bench (3 kW) were collected as the data source for the model. First, we adopted Ridge to eliminate abnormal samples. Second, we analyzed and selected the variables that have a significant effect on PEMFC power. Moreover, we optimized the model using batch normalization, dropout, Nadam, Swish, and Huber techniques. Finally, the performance of the model was evaluated by combining real datasets and real polarization curves. The experimental results demonstrate that the polarization curves predicted by the CNN-based model agree with the real curves, with a prediction accuracy of approximately 0.96, a prediction time of 1 μs, and an iteration period of less than 1 s per cycle. A comparative analysis shows that the CNN-based model prediction precision was superior to that of other mainstream machine learning algorithms. In real scenarios, the CNN-based model accurately predicts the power of PEMFC.

1. Introduction

Proton exchange membrane fuel cells (PEMFCs) are energy conversion devices that transform chemical energy into electrical energy [1]. Currently, China is vigorously developing hydrogen energy owing to its characteristics of zero pollution, zero noise, high operating efficiency, high power density, and low-temperature operation [1,2,3,4,5], with PEMFCs being an important development direction in fuel cells. PEMFCs use polymer electrolyte membranes (particularly Nafion212) to conduct protons and separate gaseous reactants on both sides of the cathode and anode, making them best suited to replace automotive internal combustion engines. Free from the constraints of the Carnot cycle, the PEMFC, with a power generation efficiency as high as 40–60%, has become one of the main power generation options for distributed generation, portable power sources, and hybrid electric vehicles [6,7,8,9,10]. To improve PEMFC performance, it is essential to develop an accurate model to predict its overall performance and adjust it to improve its operating efficiency.

The performance of a PEMFC is represented by an I–V curve, which is affected by many factors, including operating conditions, material properties, fuel cell dimensions, and physical and electrochemical processes [11,12,13,14,15]. Numerous physical models and techniques have been developed to predict or measure polarization curves [15,16,17,18,19]. PEMFC performance prediction is mainly categorized into two approaches: data- and model-driven [20].

Model-driven approaches include empirical or semi-empirical models that are used to predict PEMFC performance [21,22,23,24,25,26] and include analytical, mechanical, and computational fluid dynamics (CFD) models, which are three-dimensional (3D) physical models. Three-dimensional physical models comprehensively consider the effects of chemical reactions, such as the reaction of kinetics and physical and chemical parameters [27]. To date, numerous approaches based on 3D physical models have been developed to predict PEMFC performance and study the influence of operating conditions [16,17,18,19,28]. Zhang et al. [29] established a 3D non-isothermal dynamic PEMFC model, studied the start-up strategy, and investigated the start-up time and temperature distribution during the start-up process. Xie et al. [30] established a 3D agglomerate PEMFC sub-model of the catalyst layer (CL) by investigating the effect on PEMFC performance through platinum loading and ionophore resistance. An optimal model can render more accurate predictions; however, designing a high-precision physical model for the PEMFC operating environment is a demanding task. This is because, as a problem in conventional CFD modeling, the membrane electrode assembly (MEA) contains complicated transport and electrochemical phases during PEMFC operation [27]. If traditional PEMFC model-driven methods are used, a deep understanding of the process parameters and physicochemical phenomena of the PEMFC is required [8,31], but these vary for different types of fuel cells, making them unsuitable for wide application in other types of fuel cells with different parameters [20]. Researchers should conduct several experiments to improve PEMFC performance and obtain the I–V curve, which is time-consuming and entails significant costs. Despite their capabilities for overall and local PEMFC performance prediction, 3D methods are time-consuming and require massively parallel computing to research microstructural constituents [32,33,34], industrial-scale fuel cells [28,35], and PEMFC stacks [36], as summarized in

Table 1. PEMFC performance prediction based on physical models.

	PEMFC Parameters	Simulations	Equipment Parameters	Operation Time
[33,37]	Two-phase flow of the GDL.	4 million hexahedral mesh grid points	28 Intel Xeon 2.93 GHz processors, VOF simulation	48 h
[35,37]	A single 200 cm2 PEMFC having a cooling-channel plate.	23 million fine mesh grid points	2.8 GHz Intel Pentium 4 CPU, 1.0 GB DDR RAM	A point in the I–V polarization curve took a 32-node cluster 20 h
[36,37]	A PEMFC having a metal foam flow field with size of 3 × 0.4 × 8 mm.	24 million grid points, captured the geometry of the PEMFC and the 3D microstructure of the metal foam	20 processors of 2.20 GHz Intel Xeon Silver 4114 CPU, Ansys Fluent	A point in the I–V polarization curve took over 168 h
[37,38]	The flow field of metal foam porous media with size of 2 × 0.5 × 4.8 mm.	10 million grid points reconstructed its digital 3D microstructure	112 processors of 2.80 GHz Intel Xeon CPU E5-2680 v2, Open FOAM VOF	Each case consumed about 100 h
[37,39]	A 5-cell stack having 50.4 cm2 MEA per cell.	3.14 million coarse mesh grid points	8 processors of 2.40 GHz Intel Xeon CPU E5- 2620 v3, 32 GB DDR RAM	Each case consumed about 24 h

Note: volume of fluids (VOF).

.

Computational and time costs are typically high in traditional 3D-physical-model-based methods, while predictions using simplified physical models lead to low accuracy [15]. Even for small-scale stacks consisting of 5–10 cells, 3D simulations based on physical models typically require 100–1000 million grid points and days or weeks to predict a steady-state operation [16,17,39]. Wang et al. [40] created a 3D PEMFC model with a CL agglomerate sub-model and constructed a performance database of PEMFCs with various CL compositions. The database was then used to train a data-driven model based on support vector machines (SVMs); the model had a predictive accuracy similar to or higher than that of conventional physical models and was more computationally efficient by several orders of magnitude. Predicting I–V curves takes only a second in a data-driven model but hundreds of hours of processing with a processor in a 3D-physical-model-based approach [15].

In contrast to model-driven approaches, data-driven methods do not require an understanding of the physical–chemical mechanisms and predict the performance based on the measured data obtained during PEMFC operation [20]. Data-driven models, including machine learning (ML) models, do not require prior knowledge and understanding of the complicated transport and electrochemical phases that occur during PEMFC operation, which significantly decreases the difficulty of modeling. Furthermore, ML-based methods excel in computational efficiency, and a data-driven approach can be applied to all aspects of PEMFCs. It has been documented that ML-based methods are effective in predicting aspects of PEMFCs, such as the PEMFC time-series voltage, PEMFC temperature, hydrogen flow, oxygen flow, the lifetime of the PEMFC, the material selection and optimization of membrane electrodes, the degradation of membrane electrodes, the design and optimization of flow channels, PEMFC fault diagnosis, PEMFC system control strategy and optimization, and PEMFC health status management and monitoring. The prediction speed and accuracy of ML-based methods are high, which shows the significant application potential of data-driven methods in PEMFCs. To study PEMFCs, multiple attempts have been made to propose ML-based methods for the replacement of complex 3D physical models. As summarized in

Table 2. ML-based PEMFC modeling.

Index	Output Predictions	Algorithms	Input	System Operating Conditions
[40]	Optimization of CL component, maximum power density of PEMFC	SVM, GA	Pt loading, Pt percentage, IC ratio	Data from CFD modeling.
[41]	Voltage degradation of PEMFC	BILSTM-AT	Current, inlet/outlet temperatures of H2 and air, cooling water, air pressure, flow rates of gas and cooling water, inlet hygrometry	Data from the literature, 1 kW test bench, 5 cells.
[42]	The performance of cathode CL	ANN	Ionomer film covering the agglomerate, agglomerate radius, platinum and carbon loadings, membrane content, GDL penetration content, CL thickness	Data from 1D model.
[43]	Optimization of the geometry of porous media flow field (current density)	SVM	Fiber diameter and distance, voltage	Data from 3D model.
[44]	Local current values	MLP	Current, temperature, pressure, stoichiometric ratio, and RH	Assembled experimental setups, 25 cm2 MEA, 100% RH, current density 1 A cm−2
[45]	PEMFC hydrogen consumption	ANN, MLR	Total energy, slope, peak power	600 W power, 46 cells, maximum ratings 46 V/70 A.
[46]	PEMFC RUL	MIMO-ESN	Voltage, current, stack temperature, reactant pressures	Data from the IEEE PHM 2014 Data Challenge, 1 kW test bench, five 100 cm2 cells, current density 0.7 A cm−2
[47]	PEMFC degradation	PSO, GNNM	Current, inlet temperature, hydrogen pressure, RH	5 cells, current 70 A, in FCLAB
[48]	Voltage, current	ANN	Air flow, stack temperature	1.2 kW test bench, maximum current 45 A
[49]	PEMFC RUL	SW-ELM	Stack aging time; voltage, current; temperature of air, H2, and cooling water	Data from 10 kW test bench at FCLAB
[50]	PEMFC lifetime	ESN	Inlet/outlet temperatures of H2, air, water, pressure of H2 and air	1 kW test bench, 220 cm2 8 cells, temperature 80 °C, current density 0.5 A cm−2

Notes: Bi-directional long short-term memory recurrent neural network with an attention mechanism (BILSTM-AT), genetic algorithm (GA), multivariable linear regression (MLR), artificial neural network (ANN), Multi-Layer Perceptron (MLP), Gray Neural Network Model (GNNM), Particle Swarm Optimization (PSO), Remaining Useful Life (RUL), ESN with multiple inputs and multiple outputs (MIMO-ESN), Summation Wavelet Extreme Learning Machine (SW-ELM), Echo State Network (ESN), Federation for Fuel Cell Research (FCLAB), relative humidity (RH).

, various ML-based methods have been applied for PEMFC modeling.

ML-based models have relatively few parameters and are suitable for small datasets; however, they do not perform well on large datasets, whereas deep learning (DL)-based methods are suitable for large datasets. Although several ML-based models have been proposed to predict the performance of PEMFCs, few DL-based methods have been applied to predict the power of PEMFCs, and the data sources are mostly based on CFD modeling, as summarized in

Table 3. PEMFC power prediction based on DL methods.

Index	Prediction	Algorithms	Input	Data Sources
[8]	The current density of a PEMFC.	DBN	Operating pressure, O2 mass flow rate, voltage, GDL thickness, and porosity	3D model
[27]	The performance of a PEMFC.	RF, CNN	BET surface area, N and S contents, mesopore ratio, cathodic loading amount, hot-press time, micropore ratio, backpressure, Fe	64 papers from 2010 to 2020
[37]	The performance of a PEMFC.	ANN, GA	Cell temperature, cathode and anode RH, voltage	3D model
[51]	The polarization curves of a PEMFC with a membrane area of 11.46 cm2.	GMDH NN	H2 and O2 pressure, flow rate	Assembled device
[52]	The effects of RH, stoichiometry, and temperature on the polarization curves of a PEMFC with MPL.	ANN	Current, temperature, RH, anode and cathode stoichiometry	1D model
[53]	The oxygen distribution uniformity on cathode CL, system efficiency, and power density.	ANN, NSGA-II	Operating pressure and temperature, anode stoichiometric ratio, GDL/membrane thickness, and channel width	3D model

Notes: Neural network (NN); one-dimensional (1D).

. It only takes a fraction of a second to predict the power of a PEMFC by applying DL-based methods, and the accuracy is higher. Introducing DL-based methods into PEMFC research can solve complex mechanical problems in traditional physical model methods and significantly improve the efficiency of PEMFC operation, system analysis, and optimization, which reflects their broad research prospects in PEMFCs. Therefore, this study investigated the PEMFC power and optimal model for PEMFC power prediction using DL-based methods.

The PEMFC instantaneous power prediction model aims to achieve the best operational performance, optimizing performance on the basis of the power predicted by the model. Transient characteristic variables, such as hydrogen and air flow transients, are input to a model that can predict the transient power of the PEMFC. This research applies to the design and development phase of fuel cells, where the researcher predicts the corresponding power by adjusting the values of any or several different PEMFC characteristic variables. The predicted power is then used to adjust the characteristic variables (i.e., parameters) and eventually adjust the PEMFC parameters within the desired range. This research helps designers to reduce the time cost and iteratively optimize the PEMFC design solution.

This study provides a PEMFC power prediction model based on Ridge and CNN data-driven models, reducing the cost of extensive experiments. The I–V polarization curve was selected as the target for power prediction Further, the influence of 20 characteristic variables on the PEMFC power was analyzed, and 10 characteristic variables with significant influence on the power were selected by using the methods of kernel density estimation (KDE) and heat mapping. Furthermore, DL technologies (including batch normalization and dropout layers) were used to increase the accuracy and generalization capacity of the model, and the model was optimized through the Nadam optimization algorithm, Swish activation function, Huber loss function, etc. There is a lack of actual data on PEMFCs in the previous literature, as most of the data were obtained using methods based on CFD modeling. This study applied measured data from a PEMFC system test bench (3 kW) in the laboratory, which includes 20 PEMFC characteristic variables, such as cell temperature, hydrogen and air flow, and hydrogen and air backpressure, to demonstrate the reliability and applicability of the model in real-world scenarios. In the previous literature, only two or three algorithms were compared for the determination of the optimal model for PEMFC power prediction, and the conclusions were not sufficiently comprehensive. Therefore, we complement the previous literature by comparing and optimizing more than ten mainstream conventional ML, ensemble learning (EL), and DL methods to propose an optimal model for PEMFC power prediction, providing a strong basis for the selection and optimization of the model. It takes days or weeks to predict a point on a polarization curve using mainstream CFD-based methods. Data-driven modeling methods can predict power within 1 μs to reduce the time cost. Trained with real data samples, the model is more suitable for PEMFC power prediction in real scenarios. In this study, the instantaneous power values and performance, represented by the polarization curves of the phenomenon at any point in time and in any spatial state, can be predicted with high speed and accuracy. This study can help designers to reduce the time and cost, and iteratively optimize the PEMFC design solution. The obtained power can also be used for the parameter tuning of fuel cells within the desired range. This study contributes to solving the problem of the difficulty in predicting the instantaneous energy consumption of the fuel and power cell side of PEMFCs.

2. Materials and Methods

2.1. Experimental Data Source

The data in this study are the actual measured data obtained with a PEMFC system test bench (RG220-3 kW, Dalian Rigor New Technology Co., LTD., Dalian, China), as shown in Figure 1a. The power range of the RG220 was 1.5~5 kW. The main purpose of the test bench was performance evaluation, activation, lifetime testing, and quality inspection of PEMFCs. The real-time monitoring interface of the PEMFC system test bench monitors the temperature, gas pressure, and gas flow of the PEMFC in real time. This experiment was conducted on a 3 kW PEMFC system test bench to feed hydrogen and air into the control system of the test bench to adjust the pressure, temperature, backpressure, stoichiometric ratio, flow rates of hydrogen and air, PEMFC temperature, and the real-time stack power obtained from the magnitude of the current. The test bench collected data every second. The operating parameters of the test bench were as follows: the relative humidity was 100%, the operating temperature was room temperature, the time interval of sampling was 1 s, and the stack power was 3 kW. Figure 1b shows the PEMFC test bench system structure. The PEMFC parameters are listed in

Table 4. PEMFC material composition.

Component	Parameter
BP material	Carbon
Channel shape	Serpentine
Source cell area	191 cm2
Cell number	10

.

The precision and accuracy of the dispensed liquid volume has a vital role in the overall efficiency of industrial processes. Meera et al. [54] proposed an automated accurate liquid transfer system that can replace the traditional unstable flow meters and expensive flow sensors used in the industry. This non-contact system improved the overall efficiency of the liquid transfer process in a remarkably cost-effective manner and has applicability in PEMFC systems.

This study used Python programming language to operate MXNet in the DL framework in the environment configuration of RTX2060. The datasets obtained by the experimental methods of this system test bench include physical and chemical parameters influencing the PEMFC and operational parameters during the test. Because the polarization curves can represent the power of the PEMFC, we employed the polarization curve as the main performance index. All datasets were randomly divided into training and test sets in a ratio of 8:2.

Table 5. Statistical information of the training set data.

Parameter	Count	Mean	Std	Min	25%	50%	75%	Max
V0 (A)	10,988	204.606	134.718	9.1	75.302	188.178	357.788	495.45
V1	10,988	1.997	0.726	0.875	1.777	1.793	1.823	5
V2	10,988	2.6	0.253	1	2.583	2.6	2.612	5
V3 (MPa)	10,988	0.792	0.087	0.36	0.77	0.79	0.83	0.98
V4 (MPa)	10,988	0.625	0.044	0.3	0.6	0.6	0.682	0.78
V5 (MPa)	10,988	1.035	0.2	0.506	0.907	1.004	1.228	1.482
V6 (MPa)	10,988	0.952	0.263	0.345	0.712	0.866	1.262	1.511
V7 (°C)	10,988	65.25	1.603	55.6	64.7	65.1	65.4	79.1
V8 (°C)	10,988	68.691	2.974	55.1	66.6	68.1	70.6	80.9
V9 (S m−1)	10,988	8.802	0.42	7.65	8.375	9.006	9.056	9.206
V10 (°C)	10,988	49.686	8.218	25.8	48.4	53.1	54.6	61.5
V11 (°C)	10,988	56.981	10.127	26.2	56.775	61.3	63.7	66.1
V12 (°C)	10,988	61.991	5.311	43.6	63	63.6	63.7	68.5
V13 (°C)	10,988	59.114	10.482	20.5	61.6	62.5	63.3	67.2
V14 (°C)	10,988	64.277	7.604	39.3	65	67.8	68.1	70.3
V15 (°C)	10,988	63.371	10.128	27.6	64.9	67.7	68.1	70.5
V16 (°C)	10,988	60.785	5.012	42.7	61	62.7	63.5	66.3
V17 (°C)	10,988	59.473	9.808	23.6	61.8	62.9	64.1	66.5
V18 (L min−1)	10,988	30.973	19.526	6	14	25	52	80
V19 (L min−1)	10,988	99.257	59.778	10	38	88	166	200
Target (W)	10,988	1380.402	810.798	80.058	606.462	1382.648	2297.894	2617.38

lists the statistical information of the training dataset, including the number of samples (Count), mean values (Mean), standard deviations (Std), minimum (Min), maximum (Max), lower quartile (25%), median (50%), and upper quartile of the data (75%). The training set had 10,988 samples and 20 characteristic variables (V0–V19) that affect the power of the PEMFC stack, with stack power set as Target, that is, the target variable predicted by the model, where the variable types were all numerical.

Table 6. Statistical information of the test set data.

Parameter	Count	Mean	Std	Min	25%	50%	75%	Max
V0 (A)	2748	208.795499	136.713295	9.661	75.26975	188.367	357.89925	475.628
V1	2748	2.01016	0.741688	1.5	1.777778	1.793103	1.823529	5
V2	2748	2.596528	0.257271	1	2.571429	2.6	2.612903	5
V3 (MPa)	2748	0.791754	0.089887	0.37	0.77	0.79	0.83	0.98
V4 (MPa)	2748	0.626496	0.045906	0.3	0.6	0.6	0.7	0.76
V5 (MPa)	2748	1.041037	0.203696	0.517	0.90775	1.0175	1.240125	1.47825
V6 (MPa)	2748	0.960963	0.2665	0.3475	0.7115	0.88275	1.2745	1.5115
V7 (°C)	2748	65.27409	1.619952	55.8	64.7	65.1	65.4	78.9
V8 (°C)	2748	68.775764	3.068836	55.3	66.6	68.2	70.7	80.9
V9 (S m−1)	2748	8.781393	0.436989	7.6375	8.35	9.00625	9.05625	9.18125
V10 (°C)	2748	49.422926	8.541383	25.8	48.375	53.1	54.6	61.5
V11 (°C)	2748	56.904512	10.20925	26.3	57.1	61.2	63.7	66.1
V12 (°C)	2748	61.7619	5.632606	43.6	63	63.6	63.7	68.5
V13 (°C)	2748	59.18599	10.224721	20.5	61.4	62.5	63.2	67.2
V14 (°C)	2748	64.306805	7.484603	39.3	65	67.8	68.1	70.3
V15 (°C)	2748	63.409279	9.957952	27.7	64.9	67.7	68.1	70.5
V16 (°C)	2748	60.629294	5.143232	42.7	60.7	62.7	63.4	66.3
V17 (°C)	2748	59.526965	9.620598	23.6	61.8	62.9	64	66.5
V18 (L min−1)	2748	31.69869	19.80041	6	14	29	52	80
V19 (L min−1)	2748	101.021106	60.284898	10	38	92.5	166	200
Target (W)	2748	1402.477	821.853	80.175	606.059	1401.004	2309.518	2617.380

lists the statistical information of the test dataset. Similarly, the test set had 2748 samples with 20 characteristic variables (V0–V19), which were all numerical. None of these characteristic variables required a control variable. There was no need to fix one characteristic variable and adjust the rest. The corresponding power was obtained by randomly adjusting the values of the characteristic variables and inputting them into the model, implying the wide applicability of the model. Only 20 characteristic variables are mentioned here, and details about the analysis of the effects of more characteristic variables on the PEMFC are given in the Feature Transformation section (2).

2.2. Experimental Algorithms

Because each algorithm has its own characteristics, we compared a variety of mainstream ML algorithms to make the optimal model more convincing. We used mainstream algorithms, including traditional ML, EL, and DL. Among them, the ML algorithms include linear regression (LR), K-Nearest Neighbor Regression (KNN), Decision Tree (DT), Elastic Net Regression (Elastic Net), Support Vector Regression (SVR), Lasso regression (Lasso), and Ridge; EL algorithms include Random Forest regression (RF), Extreme Gradient Boosting Regression (XGB), Gradient Boosting Regression (GBR), and AdaBoost regressor (AdaBoost); and DL algorithms include CNN and feedforward neural network (FFN).

In deep learning, ANN is one of the most basic neural networks and other neural networks are improvements of ANN structure. ANN consists of a number of interconnected nodes, each node represents the output function of the activation function and the connection between two nodes represents the weights. The output of the networks depends on the connections, weights and activation functions [55]. ANN inspired by information processing in the human brain are also an advanced technique. Salp Swarm Algorithm (SSA) is a metaheuristic algorithm on nature that solves optimization problems by simulating their behavior in nature. Soleimani, S. et al [56] chose the SSA embedded ANN (ANN-SSA) to obtain the least squares sum of errors and investigated its application in predicting the dissolution rate.

Among the mainstream DL algorithms, improved recurrent neural network (RNN)-based algorithms, such as Gated Recurrent Unit (GRU) and long short-term memory (LSTM), have evident advantages for application in predicting time series; however, the iteration speed per cycle is slow. Conversely, the iteration speed of CNN- and FFN-based algorithms is faster than that of RNN-based algorithms; hence, FFN- and CNN-based algorithms were chosen for comparison among DL algorithms.

CNN is one of the mainstream DL algorithms with a strong performance in the fields of image recognition and text data prediction. It decreases the complexity of the neural network through three strategies: local receptive field, weight sharing, and down-sampling. Owing to the parameter sharing and sparse connections of the weight-sharing network structure, fewer weight and bias parameters are present in the convolutional layer, reducing the model complexity. The local connection of CNN ensures that the acquired convolution kernel is the most responsive to the local spatial pattern of the input. CNN can learn corresponding features from several input samples, which avoids the complicated feature extraction process. Because FFN is a fully connected layer structure with more parameters, it requires a considerable amount of storage and computational space. The redundancy problem of parameters makes fully connected neural networks less likely to be applied in complex scenarios. Compared with FFN, CNNs are sparsely connected structures, which reduce the complexity of the model and allow it to iterate faster. One-dimensional CNN can also predict time-series data. Compared with one-dimensional CNN, the model structure of 2D CNN accelerates the training speed. Therefore, we adopted a 2D CNN, whose structure is shown in Figure 2a, and the convolution process can be expressed by Formula (1):

$$y_{l,j}^{conv}={\sum }_{i=1}^k{w}_{i,j}^l\otimes y_{l-1,i}^{activate}+b_j^l$$

(1)

where $y_{l,j}^{conv}$ represents the output features of the v-th channel in the convolutional layer l, $w_{i,j}^l$ denotes the weight parameters of the convolutional layer l, and $b_j^l$ is the bias value. Activation functions were used to implement nonlinear projections of neuron inputs. In this study, the application process of the Swish activation function can be represented as in (2), in which $y_{l,j}^{Swish}$ represents the output features of the j-th channel in the convolutional layer l.

$$y_{l,j}^{Swish}=f \left(y_{l,j}^{conv}\right)$$

(2)

2.3. Model Evaluation Index

To validate the reliability of the experimental results, six commonly used indicators were chosen to assess the performance of the prediction model: MSE, RMSE, MAE, MAPE, RAE and R². In the formulas below, $\widehat{y_i}$ denotes the predicted value, $y_i$ denotes the actual value, and $\overline{y_i}$ represents the average actual value. The value of R² ranges from 0 to 1, where 0 indicates no correlation, and 1 indicates a perfect positive correlation. RMSE represents the error between the actual and predicted values. The smaller the values of MSE, RMSE, MAE, MAPE, and RAE, and the closer the value of R² is to one, the better the performance of the model.

$$\mathrm{M}\mathrm{S}\mathrm{E}=\frac{1}{n}{\sum }_{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2,\in [0,+\infty )$$

(3)

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{1}{n}{\sum }_{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2},\in [0,+\infty )$$

(4)

$$\mathrm{M}\mathrm{A}\mathrm{E}=\frac{1}{n}{\sum }_{i=1}^n|y_i-\widehat{y_i}|,\in [0,+\mathrm{\infty })$$

(5)

$$\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}=\frac{100\%}{n}{\sum }_{i=1}^n\left|\frac{y_i-\widehat{y_i}}{y_i}\right|,\in [0,+\mathrm{\infty })$$

(6)

$$\mathrm{R}\mathrm{A}\mathrm{E}=\frac{{\sum }_{i=1}^n|y_i-\widehat{y_i}|}{{\sum }_{i=1}^n|y_i-\overline{y_i}|},\in [0, 1]$$

(7)

$${\mathrm{R}}^2=1-\frac{{\sum }_{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}{{\sum }_{i=1}^n{\left(y_i-\overline{y_i}\right)}^2},\in [0, 1]$$

(8)

3. Theory and Calculations

3.1. Development of the Prediction Model

This section illustrates the PEMFC power prediction model. The flow chart of the development of the CNN-based prediction model is illustrated in Figure 2b, which contains the following stages: feature engineering, model training, and model prediction. Feature engineering was performed on the sample datasets for higher prediction precision and a faster convergence speed of model training. Feature engineering includes the processing of abnormal samples in data cleaning, feature selection, feature transformation, and the provision of optimized training samples for prediction models. Thereafter, the training process of the model was performed. With the dropout layer and BN techniques, the generalization ability of the model was improved, and the model was optimized with the Huber loss function, Swish activation function, and Nadam optimization algorithm. Finally, the prediction model was assessed on actual datasets with six commonly used evaluation indicators: Mean Absolute Percent Error (MAPE), Determination Coefficient (R²), Mean Absolute Error (MAE), Root Mean Square Error (RMSE), Relative Absolute Error (RAE), and Mean Square Error (MSE).

3.1.1. Feature Engineering

This section analyzes the critical characteristic variables that influence the PEMFC power. Before training the model, feature engineering was performed for the dataset input to the prediction model. This helps to accelerate the training speed of the model and enhance the accuracy and generalization ability of the model.

Data Cleaning

Missing values affect the performance and accuracy of a model. It is observed from Table 5 that there were no missing values in the training set; hence, no missing value processing was required. We applied the measured data from the PEMFC test bench, which collects data once per second. PEMFC power is affected by 20 characteristic variables. Once the current or pressure is adjusted, the PEMFC control system equipment cannot respond quickly, and the unstable power at the beginning will cause the power to generate abnormal samples. The samples required in this study were steady-state power; hence, these abnormal samples did not need to be detected. If these abnormal samples are not removed, most algorithms cannot identify or avoid the influence of these samples on model parameters. All training data samples, including a few abnormal samples, have the same degree of impact on the final model parameters; hence, the impact of abnormal samples on the model cannot be identified during training, leading to the low prediction accuracy of the model (prediction results will be biased toward abnormal samples). Therefore, it is necessary to remove abnormal samples.

Because Ridge is significantly affected by abnormal samples in the datasets, abnormal samples were excluded from the data used for Ridge predictions, and the remaining samples were input into the model, which effectively reduced the time cost in the presence of a large amount of data. Ridge adds a regularization item to the loss function in the model iteration process and reduces the impact of abnormal samples on model parameters by setting the regularization strength. The greater the regularization strength, the stronger the generalization ability, which limits the matching of model parameters to abnormal samples and biases the prediction results toward normal samples, thereby improving the fitting precision of the model for most normal samples. To avoid the impact of outliers on the prediction results, Ridge reduces the weight of abnormal samples in the calculation.

Figure 3 shows the Ridge model on the training set, in which “Outlier” indicates an abnormal value of power, and “Accepted” represents normal power. The parameter of the Ridge model was set to sigma = 3. Figure 3a is the scatterplot representing the actual power (P) and predicted power (P_pred). Figure 3b shows the residual of the actual power (P) versus the predicted and actual power (P-P_pred). Figure 3c presents the residuals of the predicted and actual power of the model and the frequency (vertical axis: Frequency) falling in the intervals on the Z axis (Z = (resid-mean_resid)/(std_resid). On the horizontal axis Z, resid represents the residual of the predicted power and actual power, mean_resid is the mean value of the residuals of the predicted power and actual power, and std_resid denotes the variance of the residuals of the predicted and actual power. Setting the Ridge model parameter sigma = 3 indicates that samples with absolute values of residuals of predicted and actual power exceeding 3 (absolute value of Z exceeding 3) are considered abnormal samples.

R², MSE, RMSE, MAE, MAPE, and RAE of the Ridge model on the training set were 0.9968, 2076.3202, 45.5666, 33.4631, 0.0617, and 0.0461, respectively. Seventy-three groups of abnormal samples were removed, and the remaining samples were input into the model for training. Similarly, for the Ridge model on the test set, R², RMSE, MSE, MAE, MAPE, and RAE were 0.9963, 49.3830, 2438.6881, 37.9738, 0.0670, and 0.0514, respectively. Twelve groups of abnormal samples were removed.

Feature Selection

This section analyzes the impact of important characteristic variables on the PEMFC and the reasons for selecting the characteristic variables. The objective of this analysis is to choose the features that are necessary for the prediction model to attain high performance (accuracy).

(1)

KDE Distribution

Based on the distributions of all characteristic variables in the training and test sets in the KDE distribution graph, those with inconsistent distributions between the two datasets were removed to improve the prediction accuracy of the model. Figure S1 (in Supplementary Material) shows that because there was a large quantity of data samples in the two sets and their distributions in the two datasets were relatively consistent, it was unnecessary to exclude any characteristic variables.

(2)

PEMFC Characteristic Variable Analysis

The main influencing factors of the PEMFC are categorized into two types: operating and physicochemical parameters. In this study, the physicochemical parameters were kept constant, as summarized in Table 4. Among them, the backpressure of oxygen is an important operating parameter, which, together with the oxygen flow rate, is related to the stack power density, voltage–current characteristic, and voltage [57]. Raising the backpressure facilitates a rise in the partial pressure of the reactant gases and the electrical potential of the PEMFC, which is conducive to improving the performance of the PEMFC. The cell temperature is another important operating parameter that significantly impacts PEMFC performance. As the temperature rises, the cell performance improves within a certain range. The ohmic resistance of the electrolyte drops as the temperature rises, resulting in a lower internal resistance of the cell and a higher mass transfer rate. However, the PEMFC’s working temperature is limited by the water vapor pressure in the proton exchange membrane. If the temperature is high, the dehydration of the membrane leads to compromised ion conductivity.

The method in this study predicts the transient power of the PEMFC and polarization curves instead of the dynamically varying power. Therefore, transient data of the characteristic variables should be collected when the test bench reaches a steady state. Because the reactants are consumed along the length of the gas flow channels, which results in a change in the potential from the inlet to the outlet, the current density is not uniform. However, it does not influence the results predicted by the model. Because the test bench collects data once per second, when it is adjusted to a steady state, the data of the current density are also steady and remain almost unchanged. The inlet flow rate is variable and should not be controlled to match the consumption of the reactants because no matter how much the inlet flow rate changes or how much of a reactant is consumed, the data of these variables are input to the model, which predicts the results based on these available data. These are the advantages of AI-based models. In this study, the influence of critical characteristics on the PEMFC was adequately analyzed, for example, liquid condensation and critical limits for liquid water slug formation and movement, the variation in membrane resistance with local water activity and temperature, and the effect of gravity on liquid slug formation in the fuel cell flow channels. However, these characteristics have significantly little influence on the PEMFC power, and their performance influences certain critical characteristic variables (V0–V19). We selected the critical characteristic variables connected with the PEMFC stack: these variables have a significant influence on the stack. We simply considered the precision and training speed of the model in a real situation. Inputting too many characteristic variables into the model is not conducive to the training of the model; hence, they have minimal influence on the prediction results, and therefore, only the more significant characteristic variables (V0–V19) were analyzed.

We investigated the impact of the 20 operating parameters in Table 5 on the target variable. If too many characteristic variables are input, the model will become complicated, and its performance will decrease. Therefore, the heat map method was adopted to analyze the correlations between characteristic variables V0–V19 and the correlations between these variables and the target variable. The characteristic variables that significantly impact the power of the PEMFC were screened out based on their correlation coefficients. It is observed in Figure 4 that the characteristic variables with a correlation coefficient greater than 0.3 with the target variable were V0, V3, V4, V5, V6, V8, V18, and V19. V8 indicates the cell temperature.

The current was adjusted from small to large for each run on the test bench to enable the PEMFC to reach its maximum power when it was stable. Therefore, most of the data samples were concentrated below 75 °C, that is, in the range where the current density was low, leading to small correlation coefficients of V1 and V2 with the Target. This is because there are three types of polarization in the PEMFC: concentration, ohmic, and activation polarization. Activation polarization plays a major role, while the stoichiometric ratio has a limited influence on the stack performance at low current densities [58]. Concentration polarization plays a central role, and the stoichiometric ratio has a greater impact on the stack performance at high current densities. The larger the stoichiometric ratio, the higher the voltage. In actual reactions, it is necessary to add excess air to overcome the limitation of mass transport on the cathode side. The stoichiometric ratio is an important PEMFC parameter. A larger stoichiometric ratio increases the reaction rate of air and hydrogen within a certain range. Large amounts of unreacted air and hydrogen in the flow channel have a satisfactory purging effect on liquid water, and the speed of the reaction to generate water is fast, thereby making the PEMFC’s performance preferable. The stacks should work at a higher stoichiometric ratio at high currents. In consideration of the future applicability of the model, the characteristic variables V1 and V2 were added. Finally, 10 characteristic variables related to the Target were selected, namely, V0, V1, V2, V3, V4, V5, V6, V8, V18, and V19, while the other characteristic variables that were less relevant to the Target were excluded.

Feature Transformation

The objective of the process described in this section is to transform necessary features, reduce the complexity of the model, and increase the performance of the prediction model.

(1)

Z-Score Standardization

The data need to be normalized before being fed into the model to scale the data to the specified interval. As the model presumes a corresponding data distribution, it eliminates the influence of dimensions or values on the calculation results. Additionally, it can accelerate the gradient descent to obtain the optimal solution during model training, which improves the precision of the prediction results. Because the current range in the datasets in this study was 0–500 A, the backpressure range was 0–1 MPa, the maximum difference between the current and back pressure was vast, and the dataset was complicated by plenty of outliers and noise in the data, Z-score standardization was preferable to avoid the indirect influence of outliers and extreme values through centralization. The formula is as follows:

$$x^{\prime }=\frac{x-\overline{X}}{S}$$

(9)

where $x$ represents the sample, $S$ denotes the standard deviation of the sample, $\overline{X}$ denotes the mean of the sample, and $x^{\prime }$ denotes the sample after normalization.

(2)

Yeo–Johnson Transformation

Owing to the influence of the uneven distribution of variable values on the model’s performance, there were samples with zero or negative values in the data after normalization. Therefore, the Yeo–Johnson transformation was used to convert the value range of variables, reduce the heteroskedasticity of random variables, and amplify their normality, which mitigates the correlation between unobservable errors and predictive variables to a certain extent, such that the shape of the probability density function is approximated to a normal distribution. Consequently, the model satisfies linearity, normality, independence, and homogeneity of variance, which facilitates the fitting of linear models and feature correlation analysis, increasing the training speed of the model.

Histograms of the characteristic variable V3 are given in Figure S2a,b to evaluate the conformity of the original and transformed data to a normal distribution. Figure S2(a1–a3) show the histograms before the Yeo–Johnson transformation. Figure S2(a1) shows the probability density distribution of the original data of V3, which is used to evaluate the conformity of the variable to a normal distribution. It can be observed in the figure that the original data of V3 did not follow a normal distribution. Figure S2(a2) is a Q-Q diagram, that is, a graph comparing the quantiles of the original data and those of a normal distribution. If the original data fit a normal distribution, all the points would fall on a straight diagonal line. If the data distribution did not follow a diagonal line, the data were subsequently converted using the Yeo–Johnson transformation. The closer the blue points are to the red line, the better the fit. The skew represents the asymmetry of the data distribution, and the closer the skew is to zero, the better the fit. The skew of V3 was −1.7805. Figure S2(a3) shows the correlation coefficient diagram, where Corr is the correlation coefficient used to describe the degree of correlation between the two-dimensional random variable V3 and the two components of the Target. The correlation coefficient is within [−1, 1], and the closer Corr is to ±1, the stronger the correlation; the closer it is to zero, the weaker the correlation. Among them, the initial Corr of V3 was 0.62.

Figure S2(b1–b3) illustrate the probability density distribution diagram, Q-Q diagram, and correlation coefficient diagram of the characteristic variable V3 after the Yeo–Johnson transformation, respectively. The probability density of the original feature data approximated a normal distribution after the Yeo–Johnson transformation. The asymmetry was reduced from −1.7805 to 0.1876, and the correlation coefficient increased from 0.62 to 0.66. Similarly,

Table 7. Yeo–Johnson transformation of all variables.

		V0	V1	V2	V3	V4	V5	V6	V8	V18	V19
Original	Skew	0.0824	3.512	3.0689	−1.7805	0.8356	−0.1013	0.3384	0.3557	0.4634	0.1575
	Corr	0.99	−0.19	−0.13	0.62	0.38	0.88	0.96	0.88	0.91	0.98
Transformed	Skew	−0.1083	−3.8829	0.7481	0.1876	−0.7548	−0.0425	−0.0298	0.0167	−0.0245	−0.0753
	Corr	1	−0.02	−0.11	0.66	0.37	0.88	0.98	0.88	0.94	0.99

lists the coefficients of all characteristic variables before and after the Yeo–Johnson transformation. After the Yeo–Johnson transformation, the asymmetry of all characteristic variables was lower, whereas the correlation coefficients were higher.

(3)

Feature Dimension Reduction

In the training dataset, because of the large correlation coefficients between each characteristic variable and other characteristic variables, the possible severe effects of collinearity may lead to inaccurate prediction results from the model. The variance inflation factor (VIF), a measurement of the severity of multicollinearity in multiple linear regression models, expresses the ratio of the variance of the regression coefficients to that when the independent variables are assumed to be nonlinearly correlated. Multicollinearity analysis was performed on 10 characteristic variables in the VIF matrix. Table S1 (in Supplementary Material) indicates that the correlation coefficients between V0, V6, V19, and other variables were relatively large. Principal component analysis (PCA) was conducted to eliminate multicollinearity and reduce dimensionality.

Feature dimension reduction can reduce errors caused by redundant information, thereby enhancing the precision of model recognition. PCA maps high-dimensional data to a low-dimensional space through a linear projection and expects the largest variance of data in the projected dimension to retain more original data point features with fewer data dimensions. After PCA dimension reduction, the number of principal components remained 10. The VIF of each characteristic variable was within one after dimensionality reduction.

3.1.2. Prediction Model

Structure of the Prediction Model

Figure 5b depicts the structure of the 2D-CNN model used in this study, which incorporated DL techniques, including dropout and BN. Additionally, the model was optimized with the Huber loss function, Nadam optimization algorithm, and Swish activation function, which improved the computing performance.

In this study, data reconstruction was conducted to convert the training dataset into a standard input format for a CNN-based prediction model. As shown in Figure 5a, the data of 10 characteristic variables were input into the model to convert these sequence data into an image format.

(1)

Activation Function

The activation function is an important part of the DL model because it has a significant effect on the precision of the prediction results and the computational efficiency of the training process. Different activation functions and initialization methods significantly influence the convergence speed of model training. In the previous literature, the ReLU function was used as the CNN activation function, but it has some shortcomings. For instance, when the input is negative, the gradient of the ReLU function is zero, whereby the neuron output can only be zero. To overcome such shortcomings, the Swish function was used as the activation function. In this study, FFN and CNN employed the He initialization method and Swish activation function.

(2)

Loss Functions

The presence of power outliers in the training set has a significant effect on the prediction results of the model in this study. The more the outliers, the lower the accuracy of the model. Hence, the Huber loss function was adopted to impose smaller penalty terms on the outliers.

The MSE function is highly sensitive to outliers. Models significantly affected by outliers are more inclined to accept bigger penalty terms and give them greater weights while ignoring the role of smaller terms. The problem of a possible gradient explosion caused by outliers is unavoidable owing to the predictive effect of other normal data, leading to the compromised overall performance of the model. Compared to MSE, the MAE function is not sensitive to outliers, and its robustness is better. The gradient in MAE training is often large and equal in most cases. Furthermore, it is continuous at point zero but not derivable. Basically, the gradient is large even for small loss values, reducing the learning rate of the model. Meanwhile, it also causes a missed global minimum value at the end of the gradient descent, which is not beneficial to the convergence of the function and model learning.

The Huber function combines the advantages of the MSE and MAE functions. The function is smooth in [−1, 1], which solves the problem of the roughness of the MAE function, realizes constant derivation, and has a faster convergence speed than that of MAE. In the [−∞, 1) (1, +∞] interval, the problem of the gradient explosion of outliers that may arise in the MSE function is solved, the oversensitivity to outliers is weakened, and the gradient variation is relatively small. When |$y_i-\widehat{y_i}$| > $rho$, the gradient is always approximated to $rho$, ensuring that the model updates parameters at a faster speed. When |$y_i-\widehat{y_i}$| ≤ $rho$, the gradient gradually declines, which also guarantees that the model can obtain the global optimal value more accurately. When $rho$ = 5, the power fluctuates with the influence of various control system parameters and operating parameters within the range of 5 W. Here, $y_i$ is the real value, and $\widehat{y_i}$ is the predicted value.

$$Huber=\sum _i\left\{\begin{array}{c}\frac{1}{2rho}{\left(y_i-\widehat{y_i}\right)}^2, if \left|y_i-\widehat{y_i}\right|<rho \\ \left|y_i-\widehat{y_i}\right|-\frac{rho}{2}, otherwise\end{array}\right.$$

(10)

Optimization Model

(1)

Optimization Algorithms

Nesterov-accelerated adaptive moment estimation (Nadam) is an improvement based on adaptive moment estimation (Adam). With stronger constraints on the learning rate, it can improve the performance of the optimization algorithm. The formula for Nadam is as follows:

$${\widehat{g}}_t=\frac{g_t}{1-{\prod }_{i=1}^t{\mu }_i}$$

(11)

$$m_t={\mu }_t\ast m_{t-1}+(1-{\mu }_t){\ast g}_t$$

(12)

$${\widehat{m}}_t=\frac{m_t}{1-{\prod }_{i=1}^{t+1}{\mu }_i}$$

(13)

$$n_t=\nu \ast n_{t-1}+\left(1-\nu \right)\ast g_t^2$$

(14)

$${\widehat{n}}_t=\frac{n_t}{1-{\nu }^t}$$

(15)

$${\overline{m}}_t=\left(1-{\mu }_t\right)\ast {\widehat{g}}_t+{\mu }_{t+1}\ast {\widehat{m}}_t$$

(16)

$$∆{\theta }_t=-\eta \ast \frac{{\overline{m}}_t}{\sqrt{{\widehat{n}}_t}+\epsilon }$$

(17)

where $m_t$ and $n_t$ are the first- and second-order moment estimations of the gradient, respectively, which can be regarded as the estimation of the expectations $E\left|g_t\right|, E\left|g_t^2\right|$. ${\widehat{m}}_t$ and ${\widehat{n}}_t$ are corrections of $m_t$ and $n_t$, respectively, which can be approximated as an unbiased estimation of the expectations. $v_t$ represents the exponential decay average of historical squared gradients, and history $m_t$ denotes the exponential decay average of gradients.

(2)

Dropout layer

The purpose of the dropout layer is to prevent the model from overfitting. It was only applied in the training process of the model. During the training process of the model, some neurons’ activation values were randomly allowed to be zero; that is, these neurons were dropped. During the testing phase of the model, all neurons were kept in a working state, while the dropout layer was no longer applied in this process. The value of dropout can be determined from the validation set.

(3)

Batch Normalization

Batch normalization (BN) is conducive to accelerating the training process of DL prediction models [59]. Following the BN of the input samples, the output data of each layer were transformed into a normal distribution, such that the subsequent network layers could adapt to the data characteristics with different distributions without learning the data distribution of the previous layer. The process after BN is equivalent to the application of the linear part of the S-type activation function, which can alleviate the problem of the vanishing gradient in the backpropagation of the S-type activation function. BN accelerates the convergence of the model with a high learning rate for initialization and a fast learning rate decay to enhance the training speed of the model and the generalization ability of the network. BN can be expressed as follows:

$${\mu }_B\leftarrow \frac{1}{m}{\sum }_{i=1}^m{x}_i$$

(18)

$${\sigma }_B^2\leftarrow \frac{1}{m}{\sum }_{i=1}^m(x_i-{\mu }_B)$$

(19)

$$\widehat{x_i}\leftarrow \frac{x-{\mu }_B}{\sqrt{{\sigma }_B^2+\epsilon }}$$

(20)

$$y_i\leftarrow \gamma {\widehat{x_i}+\beta \equiv BN}_{\gamma ,\beta }\left(x_i\right)$$

(21)

In this case, y represents the output features, m represents the number of samples in the batch, and $\epsilon$ is a small constant. ${\mu }_B$ and ${\sigma }_B^2$ denote the mean value and the standard deviation of all samples in this batch, respectively. $\beta$ and $\gamma$ denote shift and scale parameters, respectively, which are obtained by model learning.

(4)

Computing Performance Improvement

MXNet integrates the advantages of both imperative and symbolic programming in hybrid programming. In this study, the neural network model constructed in the HybridSequential class was used to call the hybridize function to convert the imperative program into a symbolic program to maximize efficiency and performance. MXNet improved the computing performance of the model through asynchronous computing and automatic parallel computing on the CPU and GPU.

3.1.3. Model Training Process

Figure 5c shows the training flow chart based on the CNN model. The weight parameters of this model were optimized using Nadam (see the Optimization Model section for details). The weight parameters on the training dataset were continuously updated in gradient descent. The loss function values of the error between the actual target value and the predicted output of the model were calculated with the minimum error using the Huber loss function (see the Structure of the Prediction Model section for details). According to the values of the loss function, the Nadam optimizer constantly updated the weight parameters of the model. The purpose of this research is to accurately predict data with CNN-based models. To evaluate the generality of the model, the data were categorized into training and validation sets. During the training process, the training errors were measured based on the training dataset. The model performance was evaluated based on the validation errors computed on the validation dataset, where the dropout method was chosen to avoid model overfitting.

4. Results and Discussion

4.1. Model Parameters

Taking a part of the data in the training set as the cross-validation set, the optimal parameters of each model were found with 5-fold cross-validation and a grid search algorithm. Figure 6 represents the process of tuning parameters for traditional ML and EL. The prediction results of traditional ML models (Lasso) are shown in Figure 6a. As shown in Figure 6(a1), Lasso is the scatter plot of actual power (P) and predicted power (P_pred), where Corr is the correlation, and the closer it is to one, the better. The Corr of the model in this study was one, indicating a strong correlation. Figure 6(a2) shows the scatter plot of the residuals of the actual power, the predicted power (P- P_pred), and the real value (P), in which Std_resid represents the variance; the smaller it is, the more stable the model. There was a big deviation from the predicted value around P = 2500. In addition, the variance was 22.596, indicating that the model was unstable. Figure 6(a3) shows the residuals of the predicted and actual power of the model and the frequency falling in the intervals on the axis Z (Z = (Resid-Mean_Resid)/Std_Resid). On the horizontal axis Z, Resid represents the residual of predicted and actual power, Mean_Resid denotes the average residual of predicted and actual power, and Std_Resid denotes their variance. A total of 212 samples with Z > 3 indicate that the residual error between P_pred and P is greater than three times the standard deviation. The smaller the value, the better, whereas a larger value indicates that some samples in the prediction have a large deviation. Z = 212 means that this model does not have a good tolerance for data with severe deviations. Figure 6(a4) is the error bar diagram of the Lasso model parameters (alpha) and the evaluation indicator MSE (vertical axis: Score). With the increase in alpha, the value of the evaluation indicator score initially decreased and subsequently increased, and the variance of the model gradually increased. Similarly, the prediction results of EL models (XGB) are shown in Figure 6b. Because the EL models have multiple parameters, the error bar graph is not displayed. Tables S2 and S3 summarize the prediction results of traditional ML and EL models, respectively. “Score” represents the model score, where the model scoring standard is the evaluation indicator MSE, with CV_Mean representing the MSE average error of the 5-fold cross-validation set and CV_Std denoting the average variance of the 5-fold cross-validation set. Tables S2 and S3 show that models based on traditional ML have poor stability, while the stability and inclusiveness of EL models are generally better than those of traditional ML. The model stability of XGB and AdaBoost is better. Thus, Tables S4 and S5 are provided to represent the main parameters of the traditional ML and EL models in the cross-validation model, respectively. Similarly, Table S6 shows the optimal parameters of DL models.

4.2. Model Evaluation

After being adjusted to the optimal parameters, the model was tested for its generalization ability on the test set.

Table 8. Prediction results of traditional ML models.

	LR	Ridge	Lasso	Elastic Net	KNN	SVR	DT
MSE	547.58304	547.51989	548.53706	547.97498	186.81037	673.23565	6.28507
RMSE	23.40049	23.39914	23.42086	23.40886	13.66785	25.94678	2.50700
MAE	15.60335	15.63665	15.62929	15.64703	2.29899	18.27464	0.56811
MAPE	0.01895	0.01927	0.01916	0.01947	0.0024	0.03851	0.00050
RAE	0.02115	0.02120	0.02119	0.02121	0.00311	0.02477	0.00077
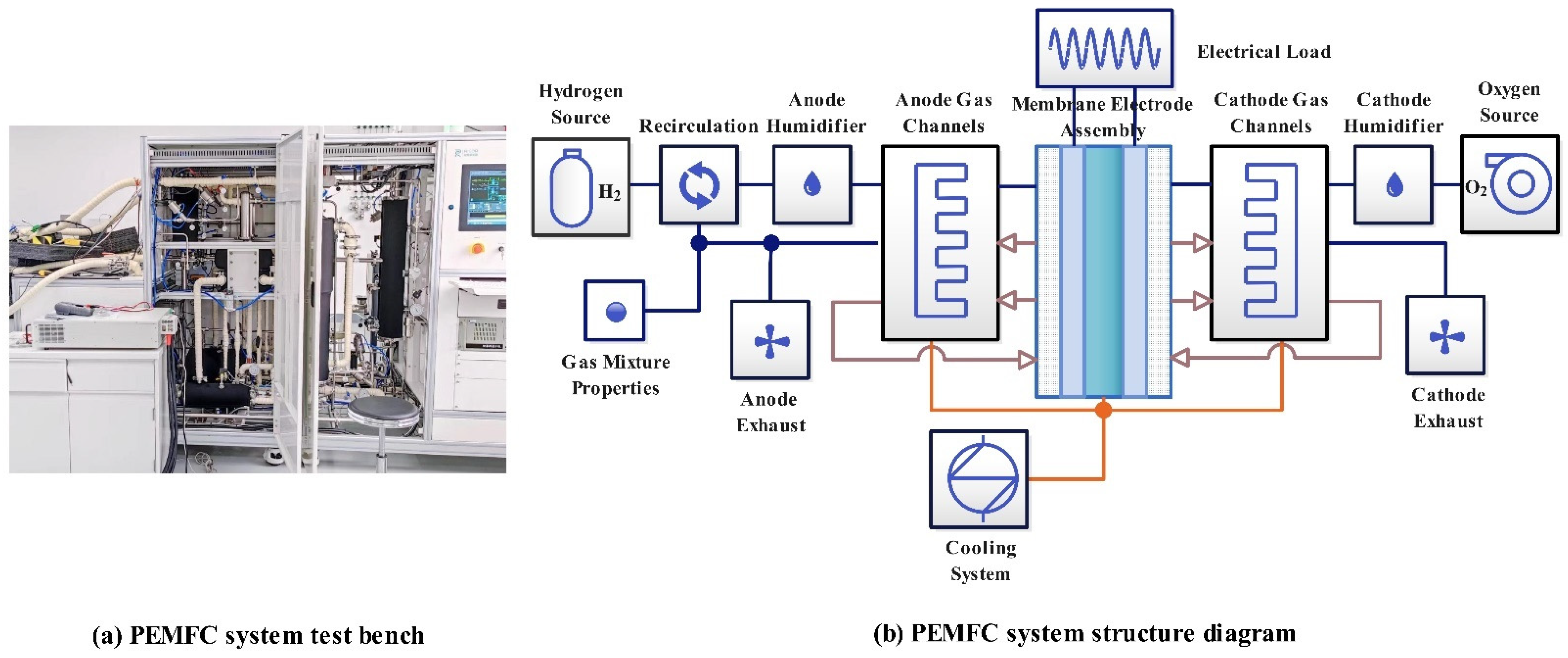
R2	0.99918	0.99918	0.99918	0.99918	0.99972	0.99899	0.99999

summarizes the prediction results of traditional ML methods. The large values of the six evaluation indicators do not mean that the performance of the model is unsatisfactory, as it should be analyzed in the actual situation. Because we applied the measured data from the PEMFC system test bench in the laboratory, as shown in Figure 1a, the power fluctuates with the influence of various control systems and operating parameters within the range of 5 W. Therefore, the error between the predicted and actual power is normal in this range. Clearly, traditional ML models have low prediction accuracy and are unsuitable for PEMFC power prediction. This is because traditional ML models are simple and have few parameters, which are unsuitable for predicting large sample sizes and thus not suitable for predicting PEMFC power in this study.

Table 9. Prediction results of EL models.

	RF	GBR	XGB	AdaBoost
MSE	4.18423	3.61780	2.15623	3.57858
RMSE	2.04554	1.90205	1.46841	1.89171
MAE	0.55385	0.69752	0.58897	0.36959
MAPE	0.00048	0.00063	0.00044	0.00024
RAE	0.00075	0.00094	0.00079	0.00050
R2	0.999993	0.999994	0.999996	0.999995

summarizes the prediction results of EL models, among which the performance of XGB, an improved GBDT-based algorithm, is better.

Table 10. Prediction results of DL models.

	FFN	CNN
MSE	2.16197	0.93717
RMSE	1.47036	0.96808
MAE	0.73705	0.52634
MAPE	0.00051	0.00040
RAE	0.00099	0.00071
R2	0.999997	0.999999

also summarizes the prediction results of DL models. Among them, the CNN model has the highest accuracy, where the six evaluation indicators are optimal, with the shortest training time being only 0.7 s for one iteration. Therefore, the CNN model better predicts the power of the PEMFC.

Figure 7a–c show the error curve predicted based on the CNN model, where “Epoch” represents the iteration cycle, “Loss function value” denotes the prediction error of the Huber loss function, “Test” is the test set error, and “Train” denotes the training set error. Applying the parameters in Tables S4–S6, the error curve of the model prediction is divided into three stages. In the first stage, if a small learning rate is used, the gradient decreases slowly and requires many iterations, which is significantly time-consuming. Therefore, we first set a larger learning rate for iteration such that the model gradient decreases rapidly. In the second stage, the error of the model was reduced to a certain range, using a slightly smaller learning rate than in the first stage to prevent the model from skipping the global optimal solution and falling into a local optimal solution. In the third stage, if a larger learning rate is used, the error curve fluctuates a lot. The prediction results are likely to fluctuate around the global optimum, resulting in inaccurate prediction results. Therefore, a smaller learning rate should be used to obtain more accurate results. Figure 7a shows the error curve of the first stage. The model parameters for this stage were set to learning_rate1 = 0.001, epochs1 = 1200, and weight_decay1 = 0.000000001. Figure 7b shows the error curve of the second stage. The model parameters for this stage were set to learning_rate2 = 0.0006, epochs2 = 1200, and weight_decay2 = 0.0000000001. Figure 7c shows the error curve of the third stage. The model parameters for this stage were set to learning_rate3 = 0.00006, epochs3 = 1500, and weight_decay3 = 0.0000000001. It is observed in the figure that the error of the Huber loss function was minimized at approximately 3900 cycles with the increase in the iteration cycle of the model, reaching final errors of Train = 0.31 and Test = 0.56.

Figure 7d shows the error between the power predicted by the CNN model and the actual power in the test set after the CNN training of the model was completed. It shows that the error between the power predicted by the CNN model and the actual power is low, indicating high fitting accuracy.

4.3. Model Results Discussion

This section presents discussions of the parameters, prediction results, and the applicability of models. Figure 6a–k show the tuning parameter process for ML and EL. The effects of the tuning process correspond to Tables S2 and S3 (in Supplementary Material). Figure 7a–c show the CNN-based parameter-tuning process. The final optimal parameters of all algorithms are presented in Tables S4–S6. From the model evaluation index in Section 2.3, the smaller the values of MSE, RMSE, RAE, MAE, and MAPE, and the closer the value of R² to one, the better the performance of the model.

(1)

ML-based model discussion

Ridge uses L₂ regularization and Lasso uses L₁ regularization to mitigate overfitting. Elastic Net is a weighted average of Ridge and Lasso regression. LR, Ridge, and Lasso are essentially linear regression methods and are only applicable to linear relationships between data. This study used nonlinear data, so these algorithms were not effective in separating signals from noise and had low prediction precision for the data; therefore, they were not suitable for modeling.

SVR does not overfit on high-dimensional datasets and is suitable for the case of the multiple characteristic variables in this study. It is suitable for small datasets and not for large datasets. Owing to more noise in the dataset in this study, SVR did not perform well in this case. Moreover, it is not easy to update the model when new data are added. Therefore, it was not suitable for modeling in this study.

KNN is computationally intensive, performs well on small datasets, and is not suitable for large datasets. It was not suitable for handling the high-dimensional data in this study. Moreover, the amount of data in this study was quite large, and KNN was not ideal for separating signals from noise.

DT is fast in training and predicting, good at obtaining nonlinear relationships, and also good at handling abnormal samples in our dataset. It is not suitable for small datasets, and when new data are added, it is not easy to update the model, which may be overfitted. DT could not separate signals from noise in this study, and the prediction accuracy was average.

(2)

EL-based model discussion

The structure of AdaBoost is simple, and we used the DT model to construct a weak learner. It is fast to train, has higher accuracy, and is not prone to overfitting. It is sensitive to abnormal samples. In this study, there were abnormal samples, which may be given higher weights in the iterations and affect the prediction accuracy of the final strong learner.

RF is the integration of multiple DT trees. The model is random, noise-resistant, and fast to train in parallel. There were 10 features in this study, and the features that took more value divisions tended to have a significant impact on the decisions of RF. There was a relatively noisy dataset; RF cannot correctly handle data samples that are extremely difficult, and its performance was average.

GBR is computationally fast in the prediction phase and can be computed in parallel from tree to tree. We used DT as a weak learner to make GBR more robust and automatically discover higher-order relationships between features. This model uses a robust Huber loss function, which is robust to outliers, and GBR generalizes relatively well to the densely distributed dataset. Owing to the dependency between the weak learner of GBR, it is difficult to train data in parallel, and the model does not perform as well as neural networks on high-dimensional sparse datasets (when handling numerical features).

XGB is an improved algorithm based on GBR. Improvements are made in the following three aspects: optimization of the algorithm, optimization of the algorithm operation efficiency, and optimization of the algorithm robustness. Clearly, from Table 9 and Table S5, XGB outperformed GBR, and it is the best algorithm for the prediction in EL.

(3)

DL-based model discussion

The greater the number of layers and parameters in the neural network, the longer the training time. FFN is a fully connected neural network with more weight parameters. Compared with FFN, the sparse connection and weight-sharing strategy of the CNN network can reduce the complexity of the model and make the training and prediction speed fast. The final prediction accuracy was 0.96, and the correlation coefficient was 0.999999, which are both higher than those obtained by FFN, and the prediction accuracy is the highest among all algorithms.

(4)

Performance comparison with previous methods

Table 11. Performance comparison with previous methods.

Index	Prediction	Data Sources	Comparison Algorithms	Activation Function	Optimization Algorithm	Loss Function	Prevent Overfitting	MAPE	R2
[51]	Polarization curves	Assembled device	GMDHNN, FFBPNN	\	BPLM	MSE	Hold-out cross-validation	\	0.9942
[27]	Polarization curves	64 papers from 2010 to 2020	CNN, DBN	ReLU	Adam	MSE	Dropout layer	\	0.9923
[52]	Polarization curves	1D model	ANN	Tanh	GA	\	None	\	0.987
[8]	Current density	3D model	DBN, BP, Bagging	Sigmoid	Adam	MSE	None	4.15	0.9976
[53]	Power density	3D model	ANN	Sigmoid	NSGA-II	\	None	\	0.9802
[37]	Maximum power	3D model	ANN	Tanh	GA	\	None	0.0088	\
This study	Power, polarization curves	Measured data from PEMFC test bench	13 ML algorithms	Swish	Nadam	Huber	Dropout Layer	0.0004	0.9999

Notes: Group method of data handling neural network (GMDHNN), one-dimensional (1D), backpropagation learning algorithm (BPLM), genetic algorithm (GA), deep neural network (DNN), feedforward backpropagation neural network (FFBPNN), backpropagation (BP).

shows a performance comparison of the algorithm in this paper with state-of-the-art methods. There has been less literature related to the prediction of PEMFC power using DL-based methods in recent years, and Table 11 compares the use of DL-based methods to predict PEMFC power with the method developed in this study.

In terms of the source of the data, there was a lack of actual data on PEMFC in most of the literature, as most of the data were obtained using methods based on 3D modeling. This study applied the measured data from the PEMFC system test bench (3 kW) in the laboratory, which included 20 PEMFC characteristic variables, such as cell temperature, hydrogen and air flow, and hydrogen and air backpressure, to demonstrate the model’s reliability and applicability in real-world scenarios.

According to the comparison of algorithms, in most of the literature, only two or three algorithms were compared for the determination of the optimal model for PEMFC power prediction, and the conclusions were not comprehensive enough. Given these circumstances, this paper complements previous work by comparing and optimizing more than ten mainstream conventional ML, EL, and DL methods to propose an optimal model for PEMFC power prediction, providing a strong basis for the selection and optimization of the model.

Comparing the optimization of algorithms, most of the literature did not use techniques to prevent overfitting. In this study, a dropout layer was used to prevent overfitting. This study used the Nadam optimization algorithm. As mentioned in the Optimization Model section, Nadam is an improvement based on Adam. Stronger constraints on the learning rate can improve the performance of the optimization algorithm.

Most of the literature used the MSE loss function. This work used the Huber loss function. From the Structure of the Prediction Model section, it can be seen that Huber is very robust to abnormal samples and solves the problem of MSE’s sensitivity to abnormal samples. In this work, the Swish activation function was chosen. As can be seen from the Optimization Model section, the Swish function solves the drawback that the negative gradient of the ReLU function is 0. Most of the literature used the Tanh or Sigmoid activation function, which lead to premature gradient disappearance in regions with large values, resulting in the slow convergence of the model. The Swish function solves these drawbacks.

The CNN-based model in this paper has an R² of 0.9999 and a MAPE of 0.0004, which makes it the best-performing model in the current literature.

4.4. I–V Polarization Curves

To further demonstrate the authenticity of the CNN-based model, the I–V polarization curves of the measured data from the PEMFC system test bench were fitted with the curves predicted by the model. The polarization curves can represent the performance of the PEMFC, including power. As mentioned in the Feature Selection section (2), the cell temperature (V8) and stoichiometric ratio are important features affecting PEMFC power. Therefore, the polarization curves of PEMFC were predicted with the CNN model based on different cell temperatures and stoichiometric ratios. The polarization curves of the cell temperatures T = 70–T = 80 are shown in Figure 8, where “Predict” represents the results predicted by the model. “Experiment” denotes the actual power, T = 80 denotes the polarization curves of the cell at a temperature of 75 to 80 °C, and R is the stoichiometric ratio (hydrogen stoichiometric ratio (V1)/air stoichiometric ratio (V2)). Similarly, T = 75 represents the data when the cell temperature is between 70 and 75 °C. It is observed in the figure that the predicted results of the model exhibit a satisfactory fitting ability with the actual polarization curves, and the prediction accuracy is high, indicating that the model can predict PEMFC power in the real world. The remaining polarization curves are shown in Figure S3.

5. Conclusions

This study shifted from traditional CFD-based PEMFC power prediction methods to the development of DL-based methods to efficiently and accurately predict the power of PEMFCs in real-world scenarios. It proposed a prediction method based on Ridge and CNN. The Ridge regression algorithm was used to eliminate abnormal samples of stack power. By comparing mainstream, traditional ML, EL, and DL algorithms, this study designed an optimal model based on CNN to predict PEMFC power in real scenarios, achieving high accuracy and fast prediction speed. Moreover, BN and dropout techniques were adopted to enhance the generalization capability of the model, and the model was optimized with the Swish activation function, Huber function, and Nadam optimization algorithm. The performance of the CNN-based prediction model was verified on actual datasets. The experimental results demonstrate that the I–V polarization curves predicted by the model fit well with the actual I–V polarization curves, and its prediction accuracy was 0.96, which is higher than those of other algorithms.

Compared with traditional CFD-based prediction methods, which consume a lot of time, the CNN-based prediction model can predict PEMFC power within a mere 1 μs, and the iteration speed when training the model is less than 1 s per cycle to reduce the time cost. Trained with real data samples, the model is more suitable than other methods for PEMFC power prediction in real scenarios. These results have proven that the CNN-based model accurately and efficiently predicts the PEMFC power, which can help improve prediction accuracy and speed, and may facilitate further applications of DL-based methods in PEMFC systems.

In this study, the instantaneous power values and performance represented by the polarization curves of the phenomenon at any point in time and in any spatial state can be predicted with high speed and accuracy. This research helps designers to reduce time and cost by iteratively optimizing the PEMFC design solution. The obtained power can also be used for fuel cell parameter tuning, and the fuel cell parameters can be tuned within the desired range. This study contributes to solving the problem of the difficulty in predicting the instantaneous energy consumption of the fuel cell and power cell side of the PEMFC, and it can provide a useful reference for the engineering application of PEMFC power parameter prediction.

After the ideal power is obtained through the predictions of the model, the best combination of characteristics for the maximum power of the fuel cell can also be obtained using a meta-heuristic algorithm. The evaluation of hydrogen-fuel-cell-driven vehicles, also energy-consuming vehicles, such as a comparison of their cost, is significantly influenced by energy consumption data; that is, the level of energy consumption directly affects the operating cost of the tool. This model can be applied to hydrogen fuel cell vehicles in the future with instrument storage to achieve the function of an intelligent power consumption display, providing customers with real-time vehicle power consumption reminders and increasing the power perception dimension of customers. Similarly, it can be applied to predict the instantaneous hydrogen consumption of vehicles. This model applied the data of 10 single cells to predict their power. Migration learning can be applied later to extend the model to predict the PEMFC power of N (N = 5, 20, 25…) single cells or other important characteristic variables, such as the cell temperature and current. In the future, it will be possible to Perform a techno-economic analysis of the hydrogen fuel cell system by the techno-economic analysis method proposed by Roushan Kumar et al [60], i.e., propose a minimum cost prediction based on data processing and analysis. The economic cost of the fuel cell system is reduced and the system efficiency is improved by neural network optimization.