Short-Term Power Load Forecasting in Three Stages Based on CEEMDAN-TGA Model
Abstract
1. Introduction
2. Proposed Approach
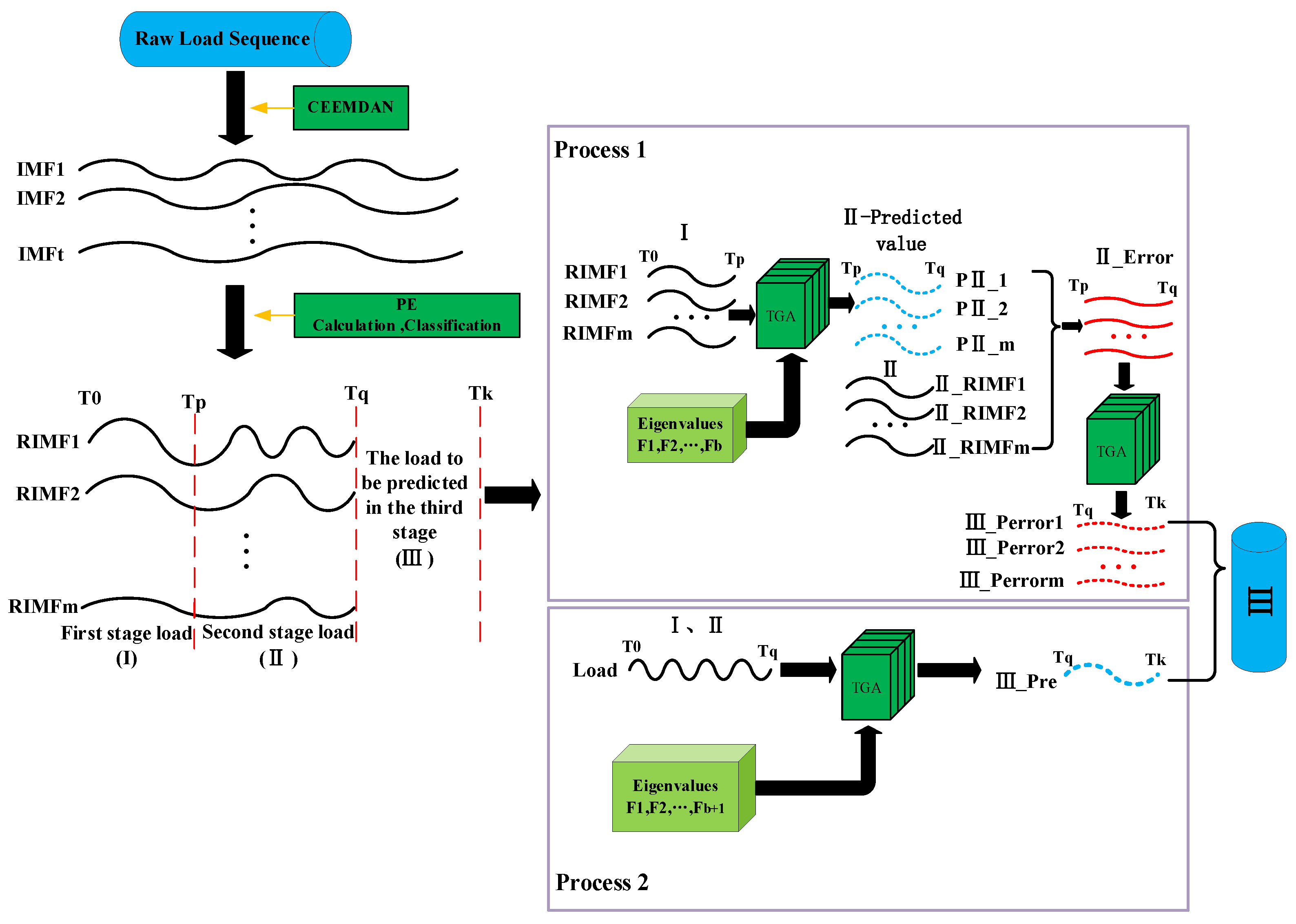
- Part 1 (green region): The original power load sequence is divided into three stages. Firstly, the data of the first and second stages are decomposed using the CEEMDAN algorithm into several intrinsic mode functions (IMFs). The permutation entropy values are calculated for each IMF, and the IMFs with similar permutation entropy values and similar trends of decomposition curves are grouped together. The grouped IMFs are summed to obtain several recombined IMFs. The TCN, GRU, and attention mechanism form the TGA model, which is used to process and predict the load sequence. Next, the first-stage load sequence and factors such as weather and economy are input into the TGA model for training in order to predict the load values of the second stage. The difference between the real values and the predicted values of the second stage is calculated as the error sequence. Finally, the error sequence is input into the pre-trained TGA model in order to predict the error values of the third stage.
- Part 2 (yellow region): Firstly, the first- and second-stage load sequences are decomposed using the seasonal and trend decomposition using Loess (STL) algorithm to obtain their trend features. Then, the average load sequence of the historical four years during the same period as the third stage is calculated. The STL algorithm is applied to the historical load sequence of the third stage using the same procedure to obtain its trend features. Next, the trend feature sequences are merged with the original weather and economic factors in order to form a new feature matrix. Finally, the first- and second-stage load data, along with the feature matrix, are input into the TGA model in order to predict the load sequence of the third stage.
- Part 3 (blue region): The predicted error sequence of the third stage is combined with the predicted load sequence of the third stage to obtain the final target sequence.
3. Applied Methodologies
3.1. Trend Feature Extraction
- Subtract the previous trend value from the time series value xv at time V: ;
- Fit the subsequence using Loess and extend it forward and backward by one period, denoted as ;
- The composed signal , which consists of z(p) groups, should undergo the application of a low-pass filter, and perform a slide smoothing of length z(p), z(p), and 3 sequentially. Perform Loess regression with d = 1 and q = z(l), resulting in ;
- Detrend: ;
- Decycle: ;
- Perform regressions to obtain .
3.2. CEEMDAN Algorithm
- The L(t), augmented with noise, is decomposed by EMD, yielding the first-order intrinsic mode function C1: , where q = 1, 2;
- The first intrinsic component is obtained by the mean value of all of the modal components taken together: ;
- The calculation of residuals: ;
- The r1(t) signal is subjected to EMD decomposition after the addition of positively and negatively paired white noise, resulting in the first-order modal component D1, and thus obtaining the second intrinsic mode component: ;
- The second residual is computed: ;
- By repeating these steps, a total of K intrinsic mode components is obtained, where the power load data are: .
3.3. Principle of TGA Model
- Input Layer: Merge and normalize the power load sequence and feature sequence to obtain the sequence as input.
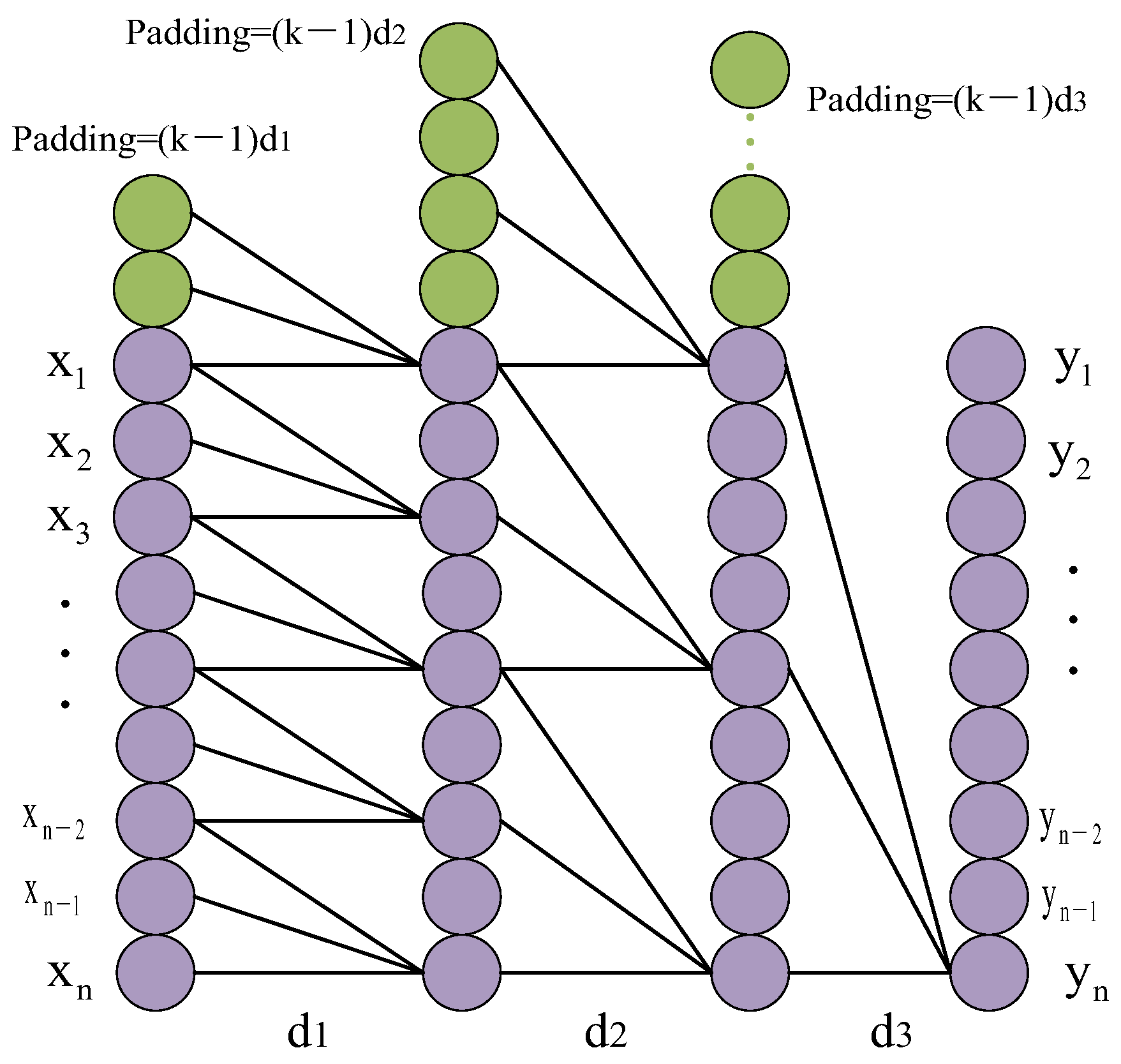
- TCN Layer: Use a single layer of residual units. Configure a single residual unit with two convolutional units and one non-linear mapping layer. To reduce dimensionality, add a 1 × 1 convolution layer into the residual mapping layer. The operation of one-dimensional dilated causal convolution is expressed as follows, where is the output result of the TCN layer:where x is the input sequence, f is the filter, d is the dilation factor, k is the kernel size, and s − di ensures that only past inputs are convolved.
- GRU Layer: Feed the output Ct from the TCN layer into a single-layer GRU model, which learns the extracted feature information. The output of the kth step of the GRU is denoted as hk, which is obtained using Equation (15):
- Attention Layer: Equations (16)–(18) represent the calculation process of weight coefficients. Compute the probabilities associated with various feature information by applying the weight allocation rules and derive the weight parameter matrix through iterative updating.where ek represents the attention probability distribution value at time k; u and w are weight coefficients; and b is the bias coefficient. The output of the attention mechanism layer at time k is denoted as sk.
- Output Layer: Equation (19) represents the predicted result of denormalization.where yk represents the predicted value at time step k; wq is the weight matrix; and bq is the bias.
3.4. Principle of Three-Stage Load Forecasting
3.5. Model Evaluation Indicators
4. Purpose of Experiment
5. Results
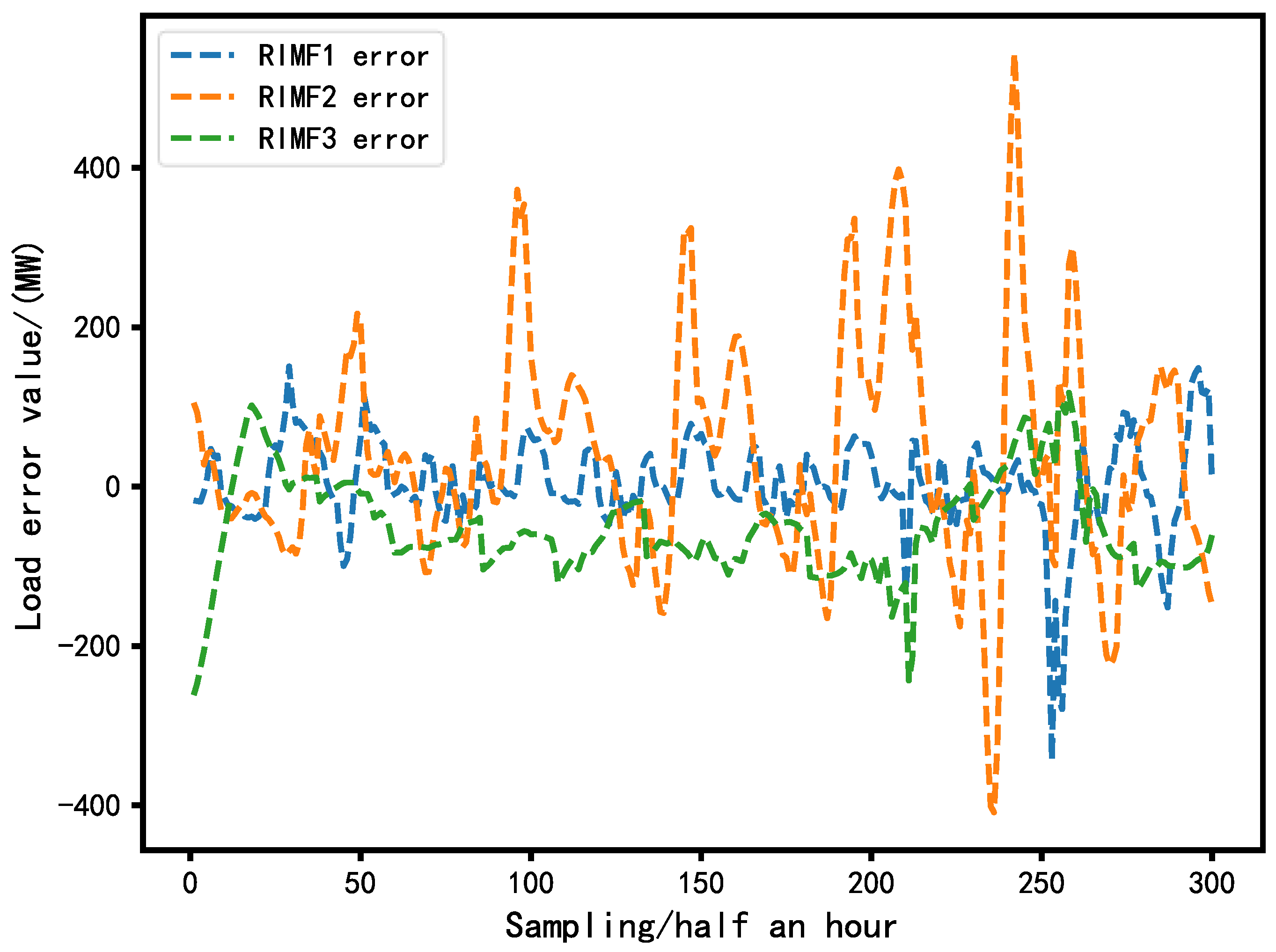
5.1. Decomposition of Power Load Sequence
5.2. Extracting Historical Data Features
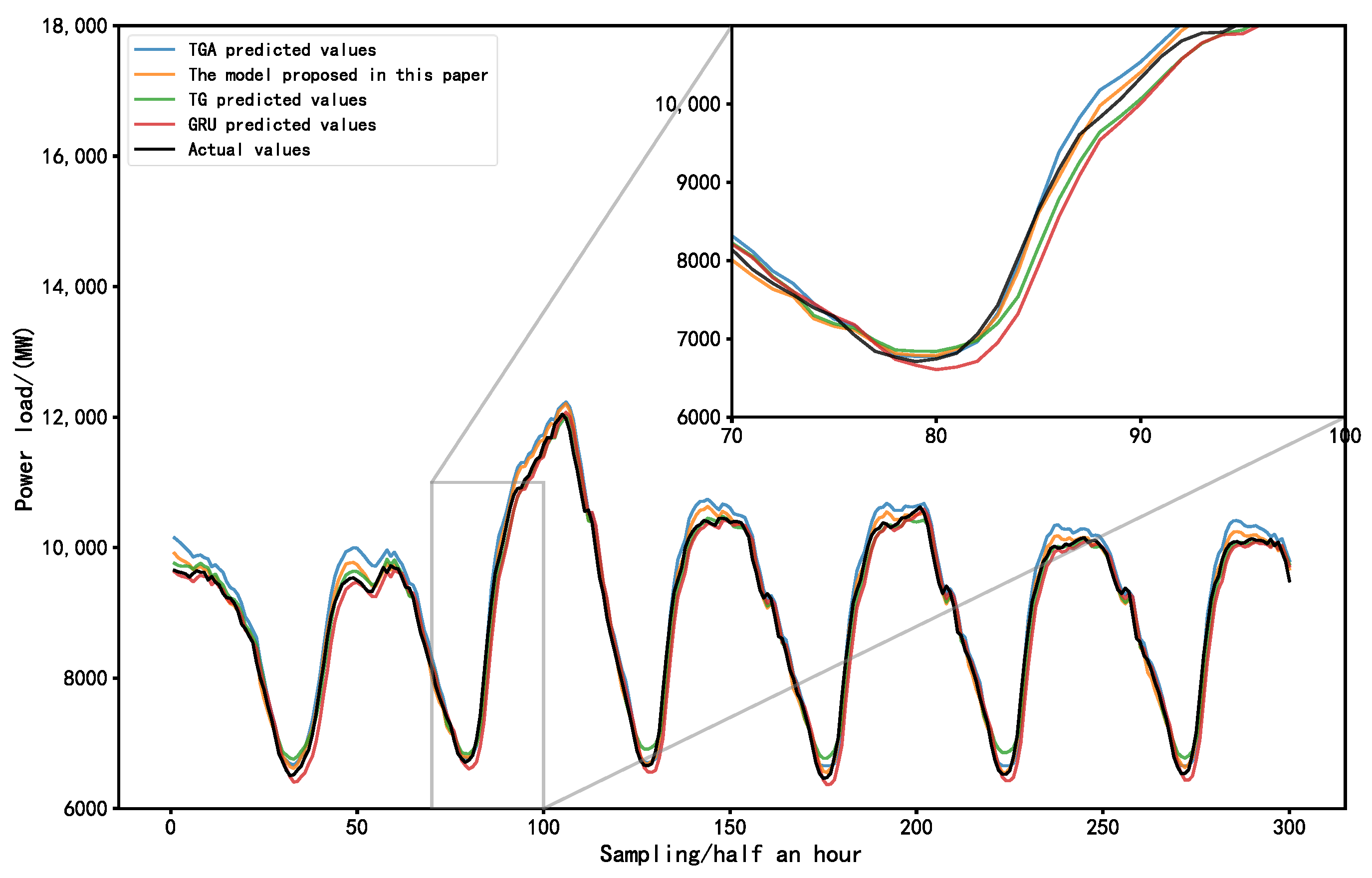
5.3. Model Prediction Results Analysis
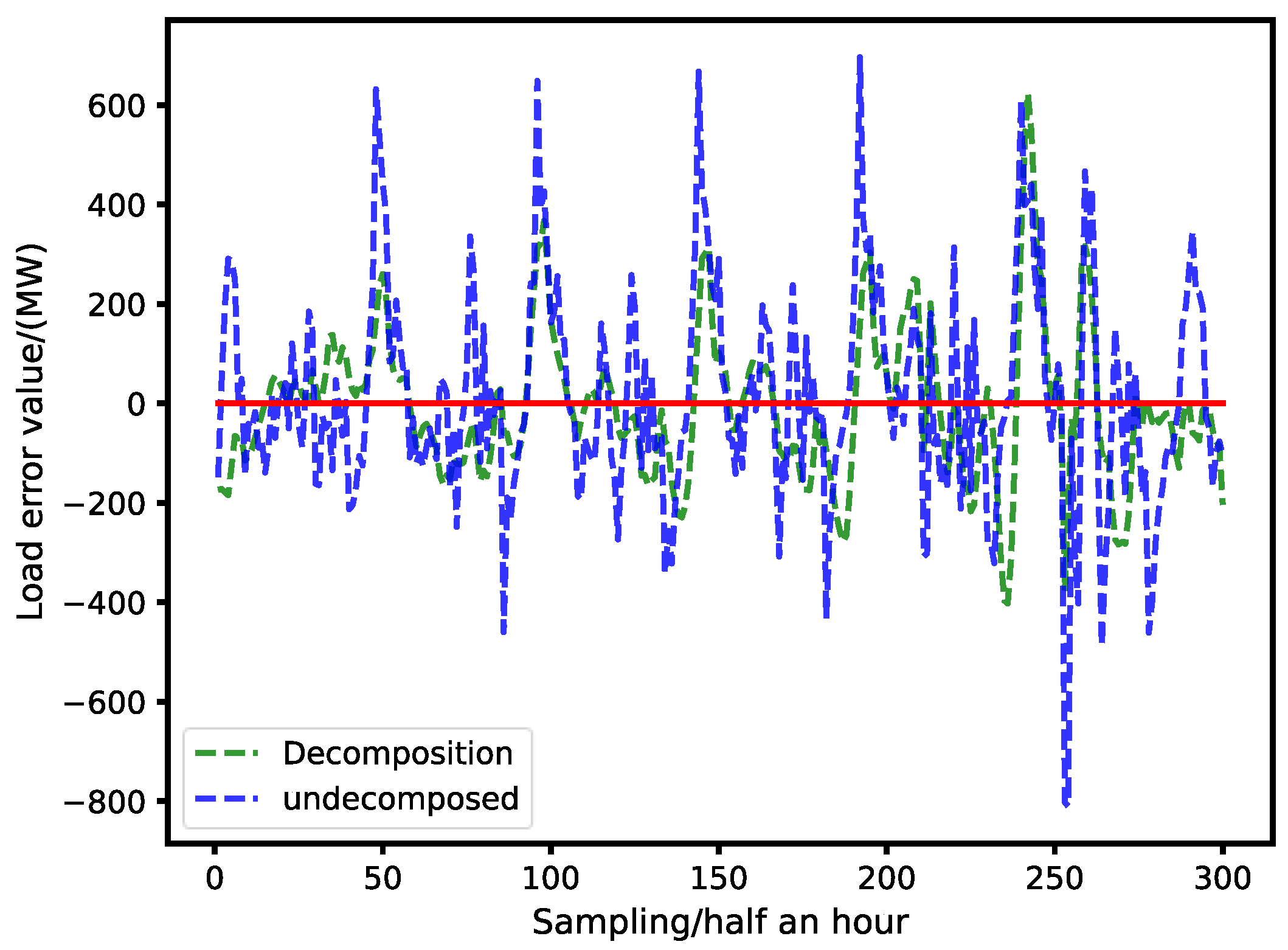
5.4. Decomposed and Undecomposed Results
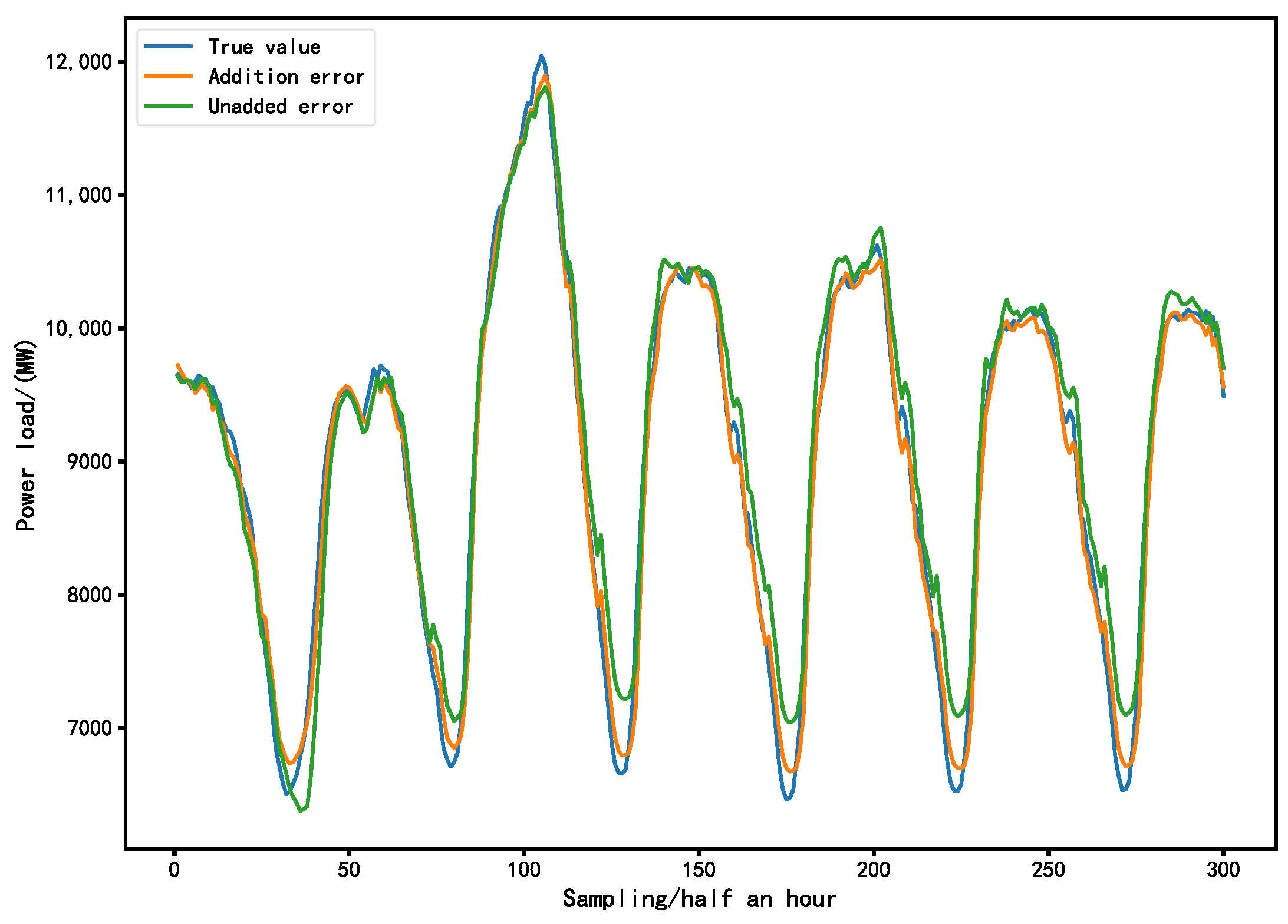
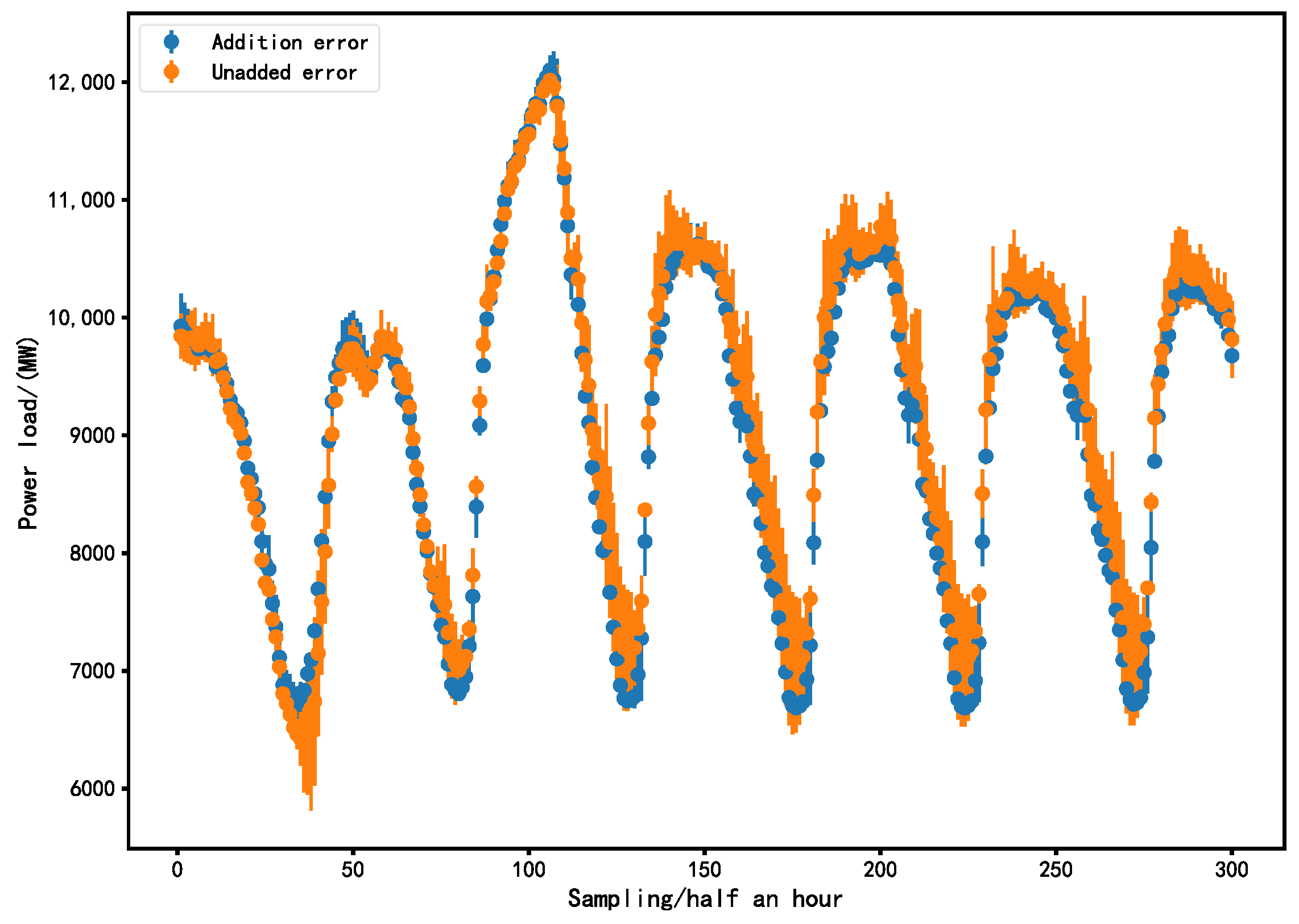
5.5. Target Sequence Prediction
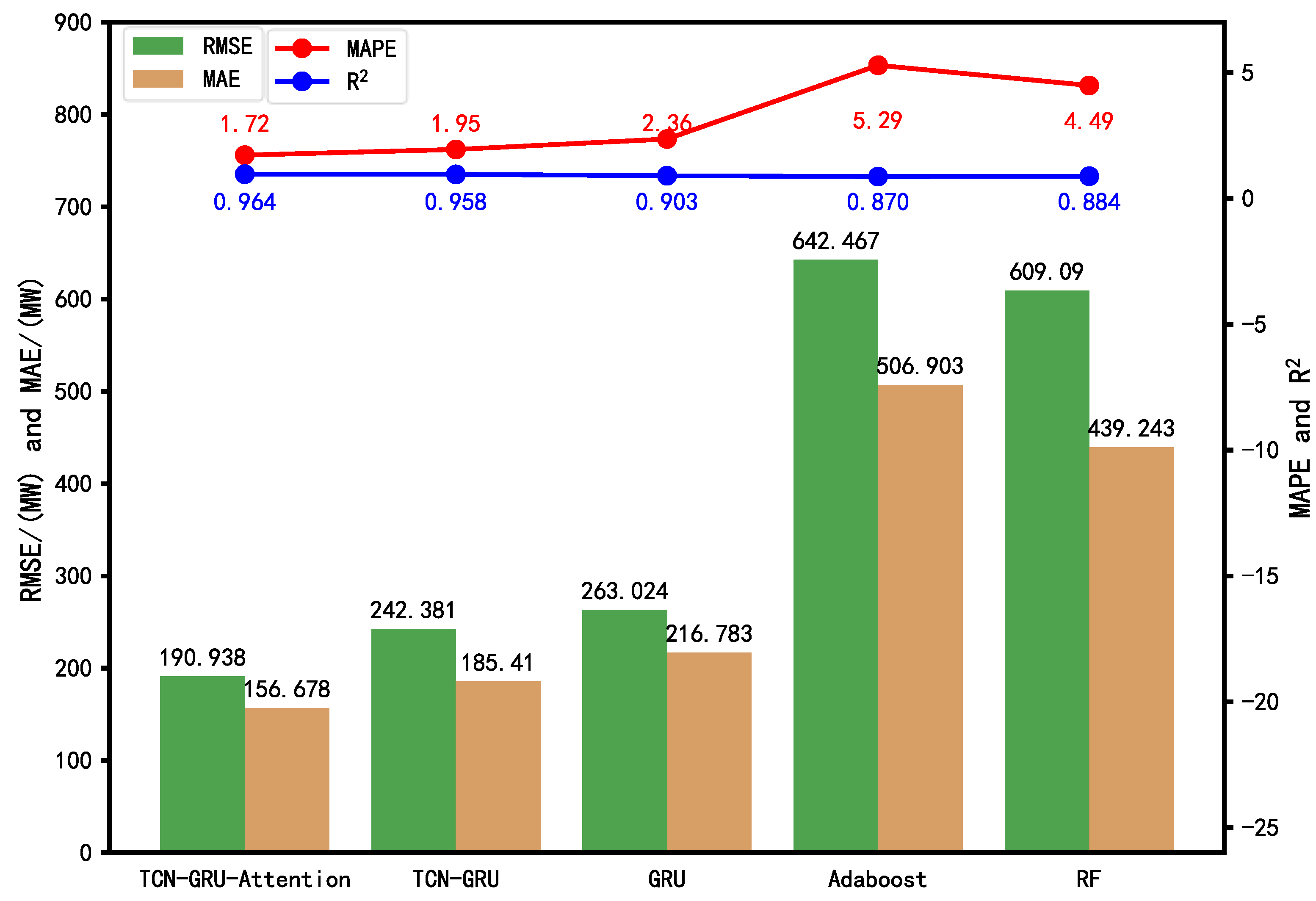
- The TCN-GRU model shows a decrease of 22.75% in MAE, 28.2% in RMSE, and 23.18% in MAPE compared to the GRU model, while the R2 value increases by 4.78%. These data results indicate that combining the one-dimensional feature capability of the temporal convolutional network (TCN) with GRU improves the accuracy compared to using GRU alone;
- The TCN-GRU-Attention model demonstrates a decrease of 17.5% in MAE, 22.3% in RMSE, and 22.6% in MAPE compared to the TCN-GRU model, while the R2 value increases to 0.971. These data results suggest that incorporating the attention mechanism into the TCN-GRU model can alleviate the progressive decrease in information importance and assign higher weights to important feature information outputs by GRU, thereby improving the prediction accuracy;
- The three-stage load prediction based on the CEEMDAN-TGA model proposed in this paper exhibits the lowest MAE, RMSE, and MAPE compared to the TGA, TG, and GRU models, with an R2 value of 0.982. This indicates that the combination of CEEMDAN decomposition and permutation entropy-based recombination of sub-modal features performs well in reducing the volatility of load sequences. Additionally, extracting historical trend features and employing a three-stage data processing approach reduces model errors and enhances the prediction accuracy.
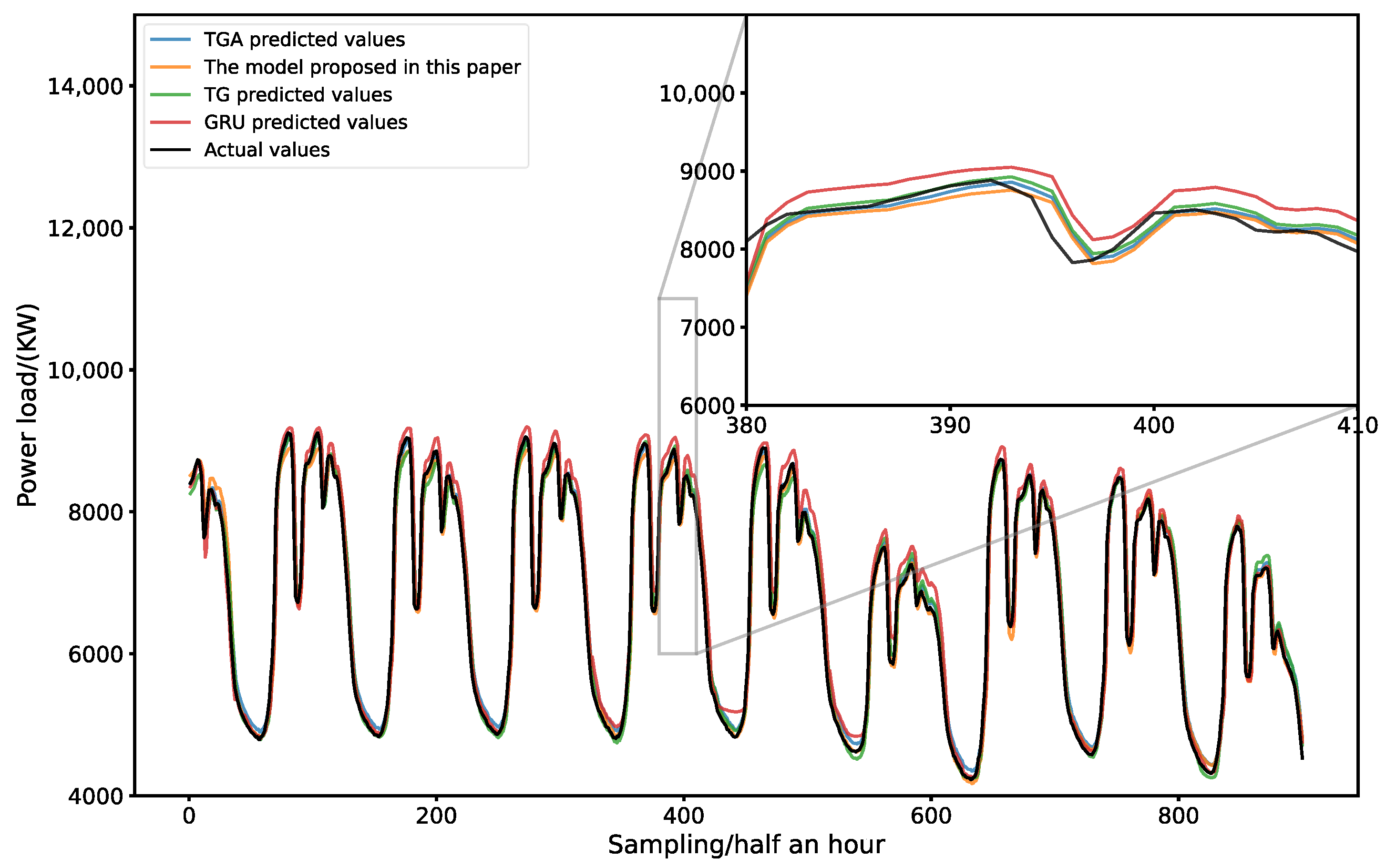
5.6. Data Verification in Quanzhou
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| CEEMDAN | Complete ensemble empirical mode decomposition with adaptive noise |
| EEMD | Ensemble empirical mode decomposition |
| EMD | Empirical mode decomposition |
| TCN | Temporal convolutional network |
| CNN | Convolution neural network |
| GRU | Gated recurrent unit |
| LSTM | Long Short-Term Memory |
| PE | Permutation entropy |
| IMF | Intrinsic mode function |
| RIMF | Reconstructed intrinsic mode function |
| STL | Seasonal and trend decomposition using Loess |
| CEEMDAN-TGA | TGA algorithm after CEEMDAN decomposition |
| RF | Random Forest algorithm |
| TCN-GRU | GRU after TCN algorithm |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| RMSE | Root mean square error |
| R2 | Determination coefficient |
| Tv | Trend value |
| Sv | Cycle value |
| Rv | Residual value |
| W(u) | The weight of the qth point near x |
| λt(x) | The maximum removing between xi and x |
| W(o) | The robustness weight |
| Xmean | The averaged sequence of Xn×m sequence |
| Xtrend | Trending section of Tv |
| Xnormal | The desired trend feature |
| L(t) | The original power load sequence |
| F | The filter |
| X | The time series |
| rt | The reset gate |
| zt | The update gate |
| σ | The sigmoid function |
| tanh | Activation function |
| Wr, Wz | Weight matrices |
| hn | Input data |
| ek | The attention probability distribution value at time k |
| yk | Predicted value at time step k |
| wq | The weight matrix |
| bq | The bias |
| T0 | Time 0 |
| Tp | Time p |
| Tq | Time q |
| Tk | Time k |
| PⅡ_m | The predicted value of the mth reconstructed eigenvalue in the second stage |
| Ⅱ_RIMFm | The mth reconstructed eigenvalue in the second stage |
| Ⅱ_Error | The error sequence of the second stage |
| Ⅲ_Perrorm | The mth prediction error sequence of the third stage |
| Ⅲ_Pre | Forecast Load Sequence of the third stage |
References
- Hernández, J.C.; Ruiz-Rodriguez, F.J.; Jurado, F. Modelling and assessment of the combined technical impact of electric vehicles and photovoltaic generation in radial distribution systems. Energy 2017, 141, 316–332. [Google Scholar] [CrossRef]
- Sanchez-Sutil, F.; Cano-Ortega, A.; Hernandez, J.C.; Rus-Casas, C. Development and calibration of an open source, low-cost power smart meter prototype for PV household-prosumers. Electronics 2019, 8, 878. [Google Scholar] [CrossRef]
- Fallah, S.N.; Ganjkhani, M.; Shamshirband, S.; Chau, K.W. Computational intelligence on short-term load forecasting: A methodological overview. Energies 2019, 12, 393. [Google Scholar] [CrossRef]
- Zhang, Z.; Hong, W.C. Electric load forecasting by complete ensemble empirical mode decomposition adaptive noise and support vector regression with quantum-based dragonfly algorithm. Nonlinear Dyn. 2019, 98, 1107–1136. [Google Scholar] [CrossRef]
- Sun, T.; Zhang, T.; Teng, Y.; Chen, Z.; Fang, J. Monthly electricity consumption forecasting method based on X12 and STL decomposition model in an integrated energy system. Math. Probl. Eng. 2019, 8, 9012543. [Google Scholar] [CrossRef]
- Malik, H.; Alotaibi, M.A.; Almutairi, A. A new hybrid model combining EMD and neural network for multi-step ahead load forecasting. J. Intell. Fuzzy Syst. 2022, 42, 1099–1114. [Google Scholar] [CrossRef]
- Song, C.; Chen, X.; Xia, W.; Ding, X.; Xu, C. Application of a novel signal decomposition prediction model in minute sea level prediction. Ocean Eng. 2022, 260, 111961. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. IEEE Int. Conf. Acoust. Speech Signal Process. IEEE 2011, 2011, 4144–4147. [Google Scholar]
- Sanabria-Villamizar, M.; Bueno-López, M.; Hernández, J.C.; Vera, D. Characterization of household-consumption load profiles in the time and frequency domain. Int. J. Electr. Power Energy Syst. 2022, 137, 107756. [Google Scholar] [CrossRef]
- Li, K.; Huang, W.; Hu, G.; Li, J. Ultra-short term power load forecasting based on CEEMDAN-SE and LSTM neural network. Energy Build. 2023, 279, 112666. [Google Scholar] [CrossRef]
- Chen, T.; Huang, W.; Wu, R.; Ouyang, H. Short Term Load Forecasting Based on SBiGRU and CEEMDAN-SBiGRU Combined Model. IEEE Access 2020, 9, 89311–89324. [Google Scholar] [CrossRef]
- Lv, L.; Wu, Z.; Zhang, J.; Zhang, L.; Tan, Z.; Tian, Z. A VMD and LSTM based hybrid model of load forecasting for power grid security. IEEE Trans. Ind. Inform. 2021, 18, 6474–6482. [Google Scholar] [CrossRef]
- Wang, N.; Li, Z. Short term power load forecasting based on BES-VMD and CNN-Bi-LSTM method with error correction. Front. Energy Res. 2023, 10, 2022. [Google Scholar] [CrossRef]
- Shen, Z.; Wu, X.; Guerrero, J.M.; Song, Y. Model-independent approach for short-term electric load forecasting with guaranteed error convergence. IET Control. Theory Appl. 2016, 10, 1365–1373. [Google Scholar] [CrossRef]
- Asrari, A.; Javan, D.S.; Javidi, M.H.; Monfared, M. Application of Gray-fuzzy-Markov chain method for day-ahead electric load forecasting. Prz. Elektrotechniczny 2012, 88, 228–237. [Google Scholar]
- Sheikh, S.; Rabiee, M.; Nasir, M.; Oztekin, A. An integrated decision support system for multi-target forecasting: A case study of energy load prediction for a solar-powered residential house. Comput. Ind. Eng. 2022, 166, 107966. [Google Scholar] [CrossRef]
- Xiao, L.; Li, M.; Zhang, S. Short-term power load interval forecasting based on nonparametric Bootstrap errors sampling. Energy Rep. 2022, 8, 6672–6686. [Google Scholar] [CrossRef]
- Dang, S.; Peng, L.; Zhao, J.; Li, J.; Kong, Z. A quantile regression random forest-based short-term load probabilistic forecasting method. Energies 2022, 15, 663. [Google Scholar] [CrossRef]
- Fan, G.F.; Zhang, L.Z.; Yu, M.; Hong, W.C.; Dong, S.Q. Applications of random forest in multivariable response surface for short-term load forecasting. Int. J. Electr. Power Energy Syst. 2022, 139, 108073. [Google Scholar] [CrossRef]
- Rodrigues, F.; Pereira, F.C. Beyond expectation: Deep joint mean and quantile regression for spatiotemporal problems. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 5377–5389. [Google Scholar] [CrossRef]
- Machado, E.; Pinto, T.; Guedes, V.; Morais, H. Electrical Load Demand Forecasting Using Feed-Forward Neural Networks. Energies 2021, 14, 7644. [Google Scholar] [CrossRef]
- Sajjad, M.; Khan, Z.A.; Ullah, A.; Hussain, T.; Ullah, W.; Lee, M.; Baik, S.W. A Novel CNN-GRU based Hybrid Approach for Short-term Residential Load Forecasting. IEEE Access 2020, 8, 143759–143768. [Google Scholar] [CrossRef]
- Huang, Y.; Gao, Y.; Gan, Y.; Ye, M. A new financial data forecasting model using genetic algorithm and long short-term memory network. Neurocomputing 2021, 425, 207–218. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, D.; Jiang, H.; Wang, L.; Chen, Y.; Xiao, Y.; Li, M. Load forecasting based on LSTM neural network and applicable to loads of “replacement of coal with electricity”. J. Electr. Eng. Technol. 2021, 16, 2333–2342. [Google Scholar] [CrossRef]
- Hong, Y.Y.; Chan, Y.H.; Cheng, Y.H.; Lee, Y.D.; Jiang, J.L.; Wang, S.S. Week-ahead daily peak load forecasting using genetic algorithm-based hybrid convolutional neural network. IET Gener. Transm. Distrib. 2022, 16, 2416–2424. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.; Zhu, T.; Li, C. Construction of perfect dispatch learning model based on adaptive GRU. Energy Rep. 2022, 8, 668–677. [Google Scholar] [CrossRef]
- Cai, C.; Li, Y.; Su, Z.; Zhu, T.; He, Y. Short-Term Electrical Load Forecasting Based on VMD and GRU-TCN Hybrid Network. Appl. Sci. 2022, 12, 6647. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, Q.; Yang, Z.; Tu, M.; Lu, J.; Peng, H. Short-term load forecasting method based on CNN-LSTM hybrid neural network model. Autom. Electr. Power Syst. 2019, 43, 131–137. [Google Scholar]
- Yu, E.; Xu, G.; Han, Y.; Li, Y. An efficient short-term wind speed prediction model based on cross-channel data integration and attention mechanisms. Energy 2022, 256, 124569. [Google Scholar] [CrossRef]
- Lang, K.; Zhang, M.; Yuan, Y.; Yue, X. Short-term load forecasting based on multivariate time series prediction and weighted neural network with random weights and kernels. Clust. Comput. 2019, 22, 12589–12597. [Google Scholar] [CrossRef]
- Liu, Y.; Lei, S.; Sun, C.; Zhou, Q.; Ren, H. A multivariate forecasting method for short-term load using chaotic features and RBF neural network. Eur. Trans. Electr. Power 2011, 21, 1376–1391. [Google Scholar] [CrossRef]
- Park, J.; Park, C.; Choi, J.; Park, S. DeepGate: Global-local decomposition for multivariate time series modeling. Inf. Sci. 2022, 590, 158–178. [Google Scholar] [CrossRef]
- Liang, H.; Wu, J.; Zhang, H.; Yang, J. Two-Stage Short-Term Power Load Forecasting Based on RFECV Feature Selection Algorithm and a TCN–ECA–LSTM Neural Network. Energies 2023, 16, 1925. [Google Scholar] [CrossRef]
- Kong, X.; Wang, Z.; Xiao, F.; Bai, L. Power load forecasting method based on demand response deviation correction. Int. J. Electr. Power Energy Syst. 2023, 148, 109013. [Google Scholar] [CrossRef]
- Li, J.; Zhang, C.; Sun, B. Two-Stage Hybrid Deep Learning With Strong Adaptability for Detailed Day-Ahead Photovoltaic Power Forecasting. IEEE Trans. Sustain. Energy 2022, 14, 193–205. [Google Scholar] [CrossRef]
- Çevik, H.H.; Çunkaş, M.; Polat, K. A new multistage short-term wind power forecast model using decomposition and artificial intelligence methods. Phys. A Stat. Mech. Its Appl. 2019, 534, 122177. [Google Scholar] [CrossRef]
- Li, W.; Shi, Q.; Sibtain, M.; Li, D.; Mbanze, D.E. A hybrid forecasting model for short-term power load based on sample entropy, two-phase decomposition and whale algorithm optimized support vector regression. IEEE Access 2020, 8, 166907–166921. [Google Scholar] [CrossRef]
- Wang, S.; Sun, Y.; Zhou, Y.; Jamil Mahfoud, R.; Hou, D. A new hybrid short-term interval forecasting of PV output power based on EEMD-SE-RVM. Energies 2019, 13, 87. [Google Scholar] [CrossRef]
- Trull, O.; García-Díaz, J.C.; Peiró-Signes, A. Multiple seasonal STL decomposition with discrete-interval moving seasonalities. Appl. Math. Comput. 2022, 433, 127398. [Google Scholar] [CrossRef]
- Zhang, X.; Li, R. A novel decomposition and combination technique for forecasting monthly electricity consumption. Front. Energy Res. 2021, 773, 792358. [Google Scholar] [CrossRef]
- Jaiswal, R.; Choudhary, K.; Kumar, R.R. STL-ELM: A Decomposition-Based Hybrid Model for Price Forecasting of Agricultural Commodities. Natl. Acad. Sci. Lett. 2022, 45, 477–480. [Google Scholar] [CrossRef]
- He, H.; Gao, S.; Jin, T.; Sato, S.; Zhang, X. A seasonal-trend decomposition-based dendritic neuron model for financial time series prediction. Appl. Soft Comput. 2021, 108, 107488. [Google Scholar] [CrossRef]
- Zhou, J.; Liang, Z.; Liu, Y.; Guo, H.; He, D.; Zhao, L. Six-decade temporal change and seasonal decomposition of climate variables in Lake Dianchi watershed (China): Stable trend or abrupt shift? Theor. Appl. Climatol. 2015, 119, 181–191. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L. Drought prediction method based on an improved CEEMDAN-QR-BL model. IEEE Access 2021, 9, 6050–6062. [Google Scholar] [CrossRef]
- Lea, C.; Vidal, R.; Reiter, A.; Hager, G.D. Temporal convolutional networks: A unified approach to action segmentation. Springer Int. Publ. 2016, 14, 47–54. [Google Scholar]
- Wang, Y.; Chen, J.; Chen, X.; Zeng, X.; Kong, Y.; Sun, S.; Liu, Y. Short-term load forecasting for industrial customers based on TCN-LightGBM. IEEE Trans. Power Syst. 2020, 36, 1984–1997. [Google Scholar] [CrossRef]
- Jiang, W. Deep learning based short-term load forecasting incorporating calendar and weather information. Internet Technol. Lett. 2022, 5, e383. [Google Scholar] [CrossRef]
- Bashari, M.; Rahimi-Kian, A. Forecasting electric load by aggregating meteorological and history-based deep learning modules. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; pp. 1–5. [Google Scholar]
- Son, H.; Kim, C. Short-term forecasting of electricity demand for the residential sector using weather and social variables. Resour. Conserv. Recycl. 2017, 123, 200–207. [Google Scholar] [CrossRef]













| Dry Bulb Temperature (°C) | Dew Point Temperature (°C) | Wet Bulb Temperature (°C) | Humidity | Electricity Price (AUD/GJ) | Load (MW) |
|---|---|---|---|---|---|
| 24.5 | 19.7 | 21.4 | 75 | 21.33 | 8531.56 |
| 24.95 | 19.85 | 21.65 | 73.5 | 21.71 | 9068.78 |
| 25.4 | 20 | 21.9 | 72 | 22.6 | 9756.34 |
| 26.2 | 19.7 | 22 | 67.5 | 23.26 | 10,338.65 |
| 27 | 19.4 | 22.1 | 63 | 23.71 | 10,742.79 |
| 26.7 | 19.85 | 22.25 | 66 | 28.02 | 11,178.09 |
| 26.4 | 20.3 | 22.4 | 69 | 30.73 | 11,455.07 |
| 26.6 | 20.25 | 22.45 | 68 | 34.35 | 11,659.23 |
| 26.8 | 20.2 | 22.5 | 67 | 35.16 | 11,808.46 |
| 26.9 | 20.35 | 22.6 | 67.5 | 40.95 | 11,903.07 |
| 27 | 20.5 | 22.7 | 68 | 39.28 | 12,073.69 |
| 27.05 | 20.3 | 22.6 | 67 | 36.94 | 12,145.38 |
| 27.1 | 20.1 | 22.5 | 66 | 33.31 | 12,177.38 |
| 26.5 | 19.9 | 22.2 | 67.5 | 32.79 | 12,199.36 |
| 25.9 | 19.7 | 21.9 | 69 | 34.05 | 12,157.97 |
| RIMF1 | RIMF2 | RIMF3 | Load | |
|---|---|---|---|---|
| RIMF1 | 1 | 0.177 | 0.027 | 0.332 |
| RIMF2 | 0.177 | 1 | −0.050 | 0.863 |
| RIMF3 | 0.027 | −0.050 | 1 | 0.434 |
| Load | 0.332 | 0.863 | 0.434 | 1 |
| MAE/(MW) | R2 | RMSE/(MW) | MAPE | |
|---|---|---|---|---|
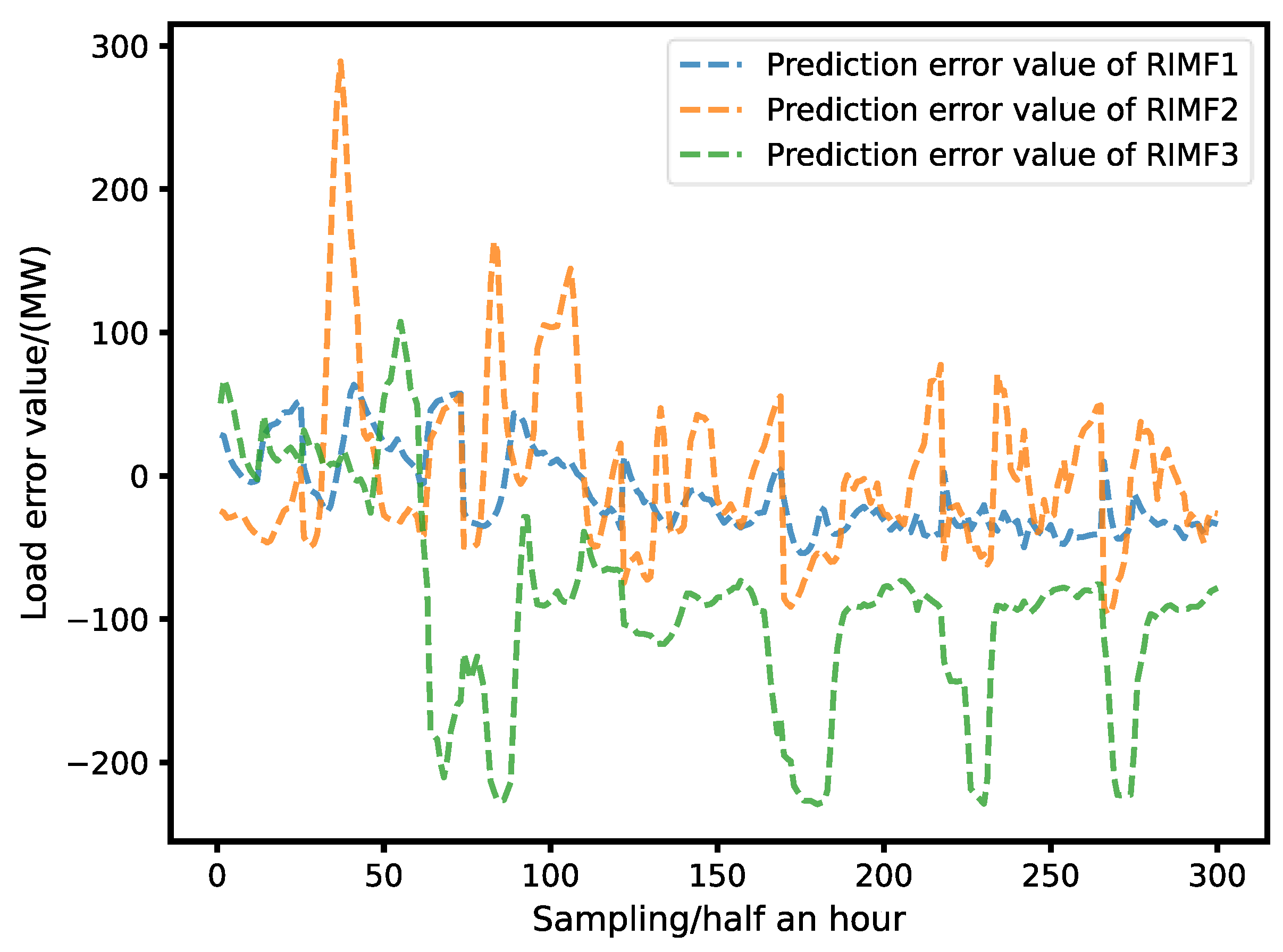
| RIMF1 | 100.126 | 0.870 | 133.224 | 260.420 |
| RIMF2 | 127.304 | 0.978 | 174.986 | 22.544 |
| RIMF3 | 47.520 | 0.981 | 63.799 | 6.520 |
| Sum of Absolute Values (MW) | Average Value (MW) | Maximum Value (MW) | |
|---|---|---|---|
| Decomposition | 33611.9 | 112.0 | 623.6 |
| Undecomposed | 46996.2 | 156.7 | 810.0 |
| MAE/(MW) | R2 | RMSE/(MW) | MAPE | |
|---|---|---|---|---|
| Decomposition | 103.62 | 0.976 | 127.15 | 1.157 |
| Undecomposed | 109.75 | 0.970 | 157.313 | 1.307 |
| MAE/(MW) | R2 | RMSE/(MW) | MAPE | |
|---|---|---|---|---|
| Three-stage load prediction based on the CEEMDAN-TGA | 95.581 | 0.982 | 125.23 | 1.099 |
| TCN-GRU-Attention | 106.433 | 0.971 | 130.17 | 1.187 |
| TCN-GRU | 129.001 | 0.965 | 167.58 | 1.534 |
| GRU | 167.001 | 0.921 | 233.492 | 1.997 |
| Maximum Temperature (°C) | Minimum Temperature (°C) | Average Temperature (°C) | Humidity | Precipitation | Load (KW) |
|---|---|---|---|---|---|
| 15.1 | 11.2 | 12.1 | 87 | 0.5 | 2938.256 |
| 11.9 | 9.1 | 10.8 | 93 | 15.4 | 3221.17 |
| 9.2 | 6.4 | 7.4 | 69 | 2.9 | 3264.545 |
| 7.4 | 4.8 | 5.9 | 56 | 0 | 3880.76 |
| 6.2 | 3.9 | 5.5 | 78 | 1.5 | 4094.79 |
| 7.3 | 5.1 | 6.1 | 88 | 8.2 | 4261.09 |
| 13.5 | 5.7 | 8.6 | 59 | 0 | 4477.83 |
| 19.1 | 8.8 | 15.1 | 92 | 1.2 | 4634.49 |
| 9.7 | 6.5 | 8.2 | 77 | 11.7 | 4716.54 |
| 14.6 | 10.8 | 12.9 | 70 | 0.5 | 5055.586 |
| 21.9 | 11.7 | 15.3 | 74 | 1 | 4866.71 |
| 22.5 | 17.3 | 19.5 | 79 | 0.8 | 5150.04 |
| 18.4 | 15.6 | 16.4 | 85 | 0.7 | 5179.52 |
| 18.7 | 14.2 | 16.3 | 80 | 0.6 | 5329.51 |
| 16.8 | 13.7 | 14.6 | 94 | 3.6 | 5316.71 |
| MAE/(KW) | R2 | RMSE/(KW) | MAPE | |
|---|---|---|---|---|
| Three-stage load prediction based on the CEEMDAN-TGA | 137.45 | 0.95 | 211.85 | 1.98 |
| TCN-GRU-Attention | 167.75 | 0.926 | 238.59 | 2.55 |
| TCN-GRU | 175.51 | 0.911 | 246.99 | 2.48 |
| GRU | 212.14 | 0.908 | 293.63 | 3.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, Y.; Wang, D.; Su, J.; Ren, M.; Xu, W.; Wei, Y.; Yang, Z. Short-Term Power Load Forecasting in Three Stages Based on CEEMDAN-TGA Model. Sustainability 2023, 15, 11123. https://doi.org/10.3390/su151411123
Hong Y, Wang D, Su J, Ren M, Xu W, Wei Y, Yang Z. Short-Term Power Load Forecasting in Three Stages Based on CEEMDAN-TGA Model. Sustainability. 2023; 15(14):11123. https://doi.org/10.3390/su151411123
Chicago/Turabian StyleHong, Yan, Ding Wang, Jingming Su, Maowei Ren, Wanqiu Xu, Yuhao Wei, and Zhen Yang. 2023. "Short-Term Power Load Forecasting in Three Stages Based on CEEMDAN-TGA Model" Sustainability 15, no. 14: 11123. https://doi.org/10.3390/su151411123
APA StyleHong, Y., Wang, D., Su, J., Ren, M., Xu, W., Wei, Y., & Yang, Z. (2023). Short-Term Power Load Forecasting in Three Stages Based on CEEMDAN-TGA Model. Sustainability, 15(14), 11123. https://doi.org/10.3390/su151411123






