Fusion of Remotely-Sensed Fire-Related Indices for Wildfire Prediction through the Contribution of Artificial Intelligence
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Region
2.2. Data Preprocessing
2.3. Primary Indices Estimation
2.3.1. Normalized Difference Vegetation Index (NDVI)
2.3.2. Normalized Difference Moisture Index (NDMI)
2.3.3. Fosberg Fire Weather Index (FFWI)
2.3.4. Fire Weather Index (FWI)
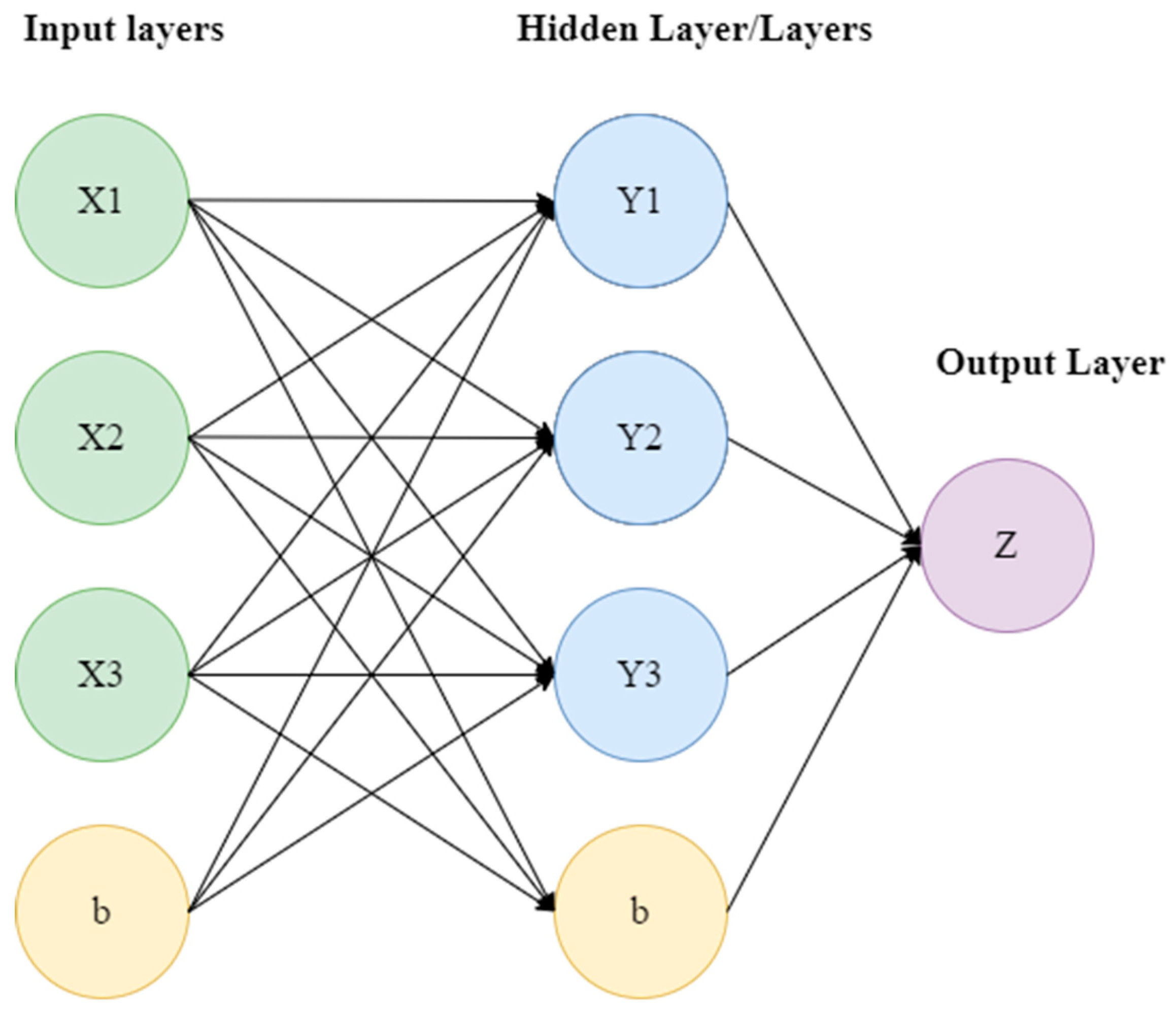
2.4. Implementation of Neural Networks
2.4.1. Implementation of Artificial Neural Network (ANN)
2.4.2. Implementation of Radial Basis Network (RBF)
[0, 1] => no fire.
2.5. General Assessment of Neural Networks, Applying the ROC (Relative Operating Characteristic) Method
- True Positive (TP): Each time the neural network correctly predicts ignition.
- False Positive (FP): Each time the neural network incorrectly predicts ignition.
- True Negative (TN): Each time the neural network correctly predicts non-ignition.
- False Negative (FN): Each time the neural network incorrectly predicts non-ignition.
2.6. Vegetation Enhanced Fire Weather Index
2.7. Validation—The Fire in Mati as a Pilot Case Study
3. Results
3.1. ANN Results
3.2. RBF Results
3.3. Results of the ROC Method
3.4. Results of the Vegetation-Enhanced FWI (FWIveg)
3.5. Validation of Results—The Fire in Mati as a Pilot Case Study
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Algorithm 1 Generation 1 | |
|---|---|
| 1. | If x − y > 0.7: |
| 2. | x’ = x |
| 3. | y’ = ey |
| 4. | Else if y − x > 0.7 AND x < 0.5: |
| 5. | x’ = x2 |
| 6. | y’ = y2 |
| 7. | Else: |
| 8. | x’= ex |
| 9. | y’ = y |
| 10. | Z = x’ + y’ |
| Algorithm 1 Generation 5 | |
|---|---|
| 1. | If y − x > 0.7: |
| 2. | x’ = 0.5 × x |
| 3. | y’ = 0.5 × y |
| 4. | Else if y − x > 0.7 OR y < 0.5: |
| 5. | x’ = x2 |
| 6. | y’ = y |
| 7. | Else: |
| 8. | x’= x2 |
| 9. | y’ = y2 |
| 10. | Z = x’ + y’ |
| Algorithm 2 Generation 5 | |
|---|---|
| 1. | If x − y > 0.7: |
| 2. | x’ = x2 |
| 3. | y’ = y2 |
| 4. | Else if x < 0.5 AND y < 0.5: |
| 5. | x’ = x |
| 6. | y’ = y2 |
| 7. | Else: |
| 8. | x’ = 0.5 × x |
| 9. | y’ = 0.5 × y |
| 10. | Z = x’ + y’ |
| Algorithm 3 Generation 5 | |
|---|---|
| 1. | If x < 0.5 AND y < 0.5: |
| 2. | x’ = x2 |
| 3. | y’ = y2 |
| 4. | Else: |
| 5. | x’ = x2 |
| 6. | y’ = y2 |
| 7. | Z = x’ + y’ |
| Algorithm 4 Generation 5 | |
|---|---|
| 1. | If x < 0.5 OR y < 0.5: |
| 2. | x’ = x2 |
| 3. | y’ = y |
| 4. | Else: |
| 5. | x’ = 0.5 × x |
| 6. | y’ = 0.5 y |
| 7. | Z = x’ + y’ |
References
- Tavakkoli Piralilou, S.; Einali, G.; Ghorbanzadeh, O.; Nachappa, T.G.; Gholamnia, K.; Blaschke, T.; Ghamisi, P. A Google Earth Engine Approach for Wildfire Susceptibility Prediction Fusion with Remote Sensing Data of Different Spatial Resolutions. Remote Sens. 2022, 14, 672. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Aryal, J. Forest Fire Susceptibility and Risk Mapping Using Social/Infrastructural Vulnerability and Environmental Variables. Fire 2019, 2, 50. [Google Scholar] [CrossRef] [Green Version]
- Lü, A.; Tian, H.; Liu, M.; Liu, J.; Melillo, J.M. Spatial and Temporal Patterns of Carbon Emissions from Forest Fires in China from 1950 to 2000. J. Geophys. Res. Atmos. 2006, 111, D05313. [Google Scholar] [CrossRef] [Green Version]
- Moayedi, H.; Mehrabi, M.; Bui, D.T.; Pradhan, B.; Foong, L.K. Fuzzy-Metaheuristic Ensembles for Spatial Assessment of Forest Fire Susceptibility. J. Environ. Manag. 2020, 260, 109867. [Google Scholar] [CrossRef]
- Sayad, Y.O.; Mousannif, H.; Al Moatassime, H. Predictive Modeling of Wildfires: A New Dataset and Machine Learning Approach. Fire Saf. J. 2019, 104, 130–146. [Google Scholar] [CrossRef]
- Boer, M.M.; Nolan, R.H.; Resco De Dios, V.; Clarke, H.; Price, O.F.; Bradstock, R.A. Changing Weather Extremes Call for Early Warning of Potential for Catastrophic Fire. Earth’s Future 2017, 5, 1196–1202. [Google Scholar] [CrossRef]
- Haynes, K.; Short, K.; Xanthopoulos, G.; Viegas, D.; Ribeiro, L.M.; Blanchi, R. Wildfires and WUI Fire Fatalities. In Encyclopedia of Wildfires and Wildland-Urban Interface (WUI) Fires; Manzello, S.L., Ed.; Springer: Cham, Switzerland, 2020; pp. 1–16. [Google Scholar] [CrossRef]
- Sfougaris, A.; Plexida, S.; Solomou, A. Assessing the Effects of Environmental Factors on the Presence and Density of Three Shrike Species in a Continental and a Coastal Area of Central Greece. North-West. J. Zool. 2014, 10, 101–109. [Google Scholar]
- Sulova, A.; Jokar Arsanjani, J. Exploratory Analysis of Driving Force of Wildfires in Australia: An Application of Machine Learning within Google Earth Engine. Remote Sens. 2021, 13, 10. [Google Scholar] [CrossRef]
- Vardoulakis, S.; Marks, G.; Abramson, M.J. Lessons Learned from the Australian Bushfires: Climate Change, Air Pollution, and Public Health. JAMA Intern. Med. 2020, 180, 635–636. [Google Scholar] [CrossRef]
- Wang, X.; Thompson, D.K.; Marshall, G.A.; Tymstra, C.; Carr, R.J.; Flannigan, M.D. Increasing Frequency of Extreme Fire Weather in Canada with Climate Change. Clim. Chang. 2015, 130, 573–586. [Google Scholar] [CrossRef]
- Abatzoglou, J.; Kolden, C. Relationships between Climate and Macroscale Area Burned in the Western United States. Int. J. Wildland Fire 2013, 22, 1003. [Google Scholar] [CrossRef]
- Vasiliades, L.; Loukas, A. Hydrological Response to Meteorological Drought Using the Palmer Drought Indices in Thessaly, Greece. Desalination 2009, 237, 3–21. [Google Scholar] [CrossRef]
- Sakellariou, S.; Sfougaris, A.; Christopoulou, O.; Tampekis, S. Integrated Wildfire Risk Assessment of Natural and Anthropogenic Ecosystems Based on Simulation Modeling and Remotely Sensed Data Fusion. Int. J. Disaster Risk Reduct. 2022, 78, 103129. [Google Scholar] [CrossRef]
- Sakellariou, S.; Sfougaris, A.; Christopoulou, O.; Tampekis, S. Spatial Resilience to Wildfires through the Optimal Deployment of Firefighting Resources: Impact of Topography on Initial Attack Effectiveness. Int. J. Disaster Risk Sci. 2023, 14, 98–112. [Google Scholar] [CrossRef]
- Resco de Dios, V.; Cunill Camprubí, À.; Pérez-Zanón, N.; Peña, J.C.; Martínez del Castillo, E.; Rodrigues, M.; Yao, Y.; Yebra, M.; Vega-García, C.; Boer, M.M. Convergence in Critical Fuel Moisture and Fire Weather Thresholds Associated with Fire Activity in the Pyroregions of Mediterranean Europe. Sci. Total Environ. 2022, 806, 151462. [Google Scholar] [CrossRef]
- Leidner, A.K.; Buchanan, G.M. (Eds.) Satellite Remote Sensing for Conservation Action: Case Studies from Aquatic and Terrestrial Ecosystems; Cambridge University Press: Cambridge, UK, 2018; ISBN 978-1-316-51386-6. [Google Scholar]
- Tien Bui, D.; Le, K.-T.T.; Nguyen, V.C.; Le, H.D.; Revhaug, I. Tropical Forest Fire Susceptibility Mapping at the Cat Ba National Park Area, Hai Phong City, Vietnam, Using GIS-Based Kernel Logistic Regression. Remote Sens. 2016, 8, 347. [Google Scholar] [CrossRef] [Green Version]
- Vilar del Hoyo, L.; Martín Isabel, M.P.; Martínez Vega, F.J. Logistic Regression Models for Human-Caused Wildfire Risk Estimation: Analysing the Effect of the Spatial Accuracy in Fire Occurrence Data. Eur. J. For. Res. 2011, 130, 983–996. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Valizadeh Kamran, K.; Blaschke, T.; Aryal, J.; Naboureh, A.; Einali, J.; Bian, J. Spatial Prediction of Wildfire Susceptibility Using Field Survey GPS Data and Machine Learning Approaches. Fire 2019, 2, 43. [Google Scholar] [CrossRef] [Green Version]
- Sakellariou, S.; Cabral, P.; Caetano, M.; Pla, F.; Painho, M.; Christopoulou, O.; Sfougaris, A.; Dalezios, N.; Vasilakos, C. Remotely Sensed Data Fusion for Spatiotemporal Geostatistical Analysis of Forest Fire Hazard. Sensors 2020, 20, 5014. [Google Scholar] [CrossRef]
- Sakellariou, S.; Tampekis, S.; Samara, F.; Flannigan, M.; Jaeger, D.; Christopoulou, O.; Sfougaris, A. Determination of Fire Risk to Assist Fire Management for Insular Areas: The Case of a Small Greek Island. J. For. Res. 2019, 30, 589–601. [Google Scholar] [CrossRef]
- Bedia, J.; Golding, N.; Casanueva, A.; Iturbide, M.; Buontempo, C.; Gutiérrez, J.M. Seasonal Predictions of Fire Weather Index: Paving the Way for Their Operational Applicability in Mediterranean Europe. Clim. Serv. 2018, 9, 101–110. [Google Scholar] [CrossRef]
- Karali, A.; Hatzaki, M.; Giannakopoulos, C.; Roussos, A.; Xanthopoulos, G.; Tenentes, V. Sensitivity and Evaluation of Current Fire Risk and Future Projections Due to Climate Change: The Case Study of Greece. Nat. Hazards Earth Syst. Sci. 2014, 14, 143–153. [Google Scholar] [CrossRef] [Green Version]
- Haines, D.A.; Main, W.A.; Frost, J.S.; Simard, A.J. Fire-Danger Rating and Wildfire Occurrence in the Northeastern United States. For. Sci. 1983, 29, 679–696. [Google Scholar] [CrossRef]
- Preisler, H.K.; Chen, S.-C.; Fujioka, F.; Benoit, J.W.; Westerling, A.L. Wildland Fire Probabilities Estimated from Weather Model-Deduced Monthly Mean Fire Danger Indices. Int. J. Wildland Fire 2008, 17, 305–316. [Google Scholar] [CrossRef] [Green Version]
- Matthews, S. A Comparison of Fire Danger Rating Systems for Use in Forests. Aust. Meteorol. Oceanogr. J. 2009, 58, 41–48. [Google Scholar] [CrossRef]
- Safi, Y.; Bouroumi, A. Prediction of Forest Fires Using Artificial Neural Networks. Appl. Math. Sci. 2013, 7, 271–286. [Google Scholar] [CrossRef]
- Zhang, Q.; Lin, G.; Zhang, Y.; Xu, G.; Wang, J. Wildland Forest Fire Smoke Detection Based on Faster R-CNN Using Synthetic Smoke Images. Procedia Eng. 2018, 211, 441–446. [Google Scholar] [CrossRef]
- Jeong, M.; Park, M.; Nam, J.; Ko, B.C. Light-Weight Student LSTM for Real-Time Wildfire Smoke Detection. Sensors 2020, 20, 5508. [Google Scholar] [CrossRef]
- Srinivas, K.; Dua, M. Fog Computing and Deep CNN Based Efficient Approach to Early Forest Fire Detection with Unmanned Aerial Vehicles. In Inventive Computation Technologies, Proceedings of the ICICT 2019 Conference, Coimbatore, India, 29–30 August 2019; Springer: Cham, Switzerland, 2020; Volume 98, pp. 646–652. [Google Scholar] [CrossRef]
- Alexandrov, D.; Pertseva, E.; Berman, I.; Pantiukhin, I.; Kapitonov, A. Analysis of Machine Learning Methods for Wildfire Security Monitoring with an Unmanned Aerial Vehicles. In Proceedings of the 2019 24th Conference of Open Innovations Association (FRUCT), Moscow, Russia, 8–12 April 2019; pp. 3–9. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, J.; Xu, L.; Guo, H. Forest Fire Smoke Recognition Based on Convolutional Neural Network; Atlantis Press: Amsterdam, The Netherlands, 2016; pp. 568–575. [Google Scholar]
- Jiao, Z.; Zhang, Y.; Xin, J.; Mu, L.; Yi, Y.; Liu, H.; Liu, D. A Deep Learning Based Forest Fire Detection Approach Using UAV and YOLOv3. In Proceedings of the 2019 1st International Conference on Industrial Artificial Intelligence (IAI), Shenyang, China, 23–27 July 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Cao, Y.; Yang, F.; Tang, Q.; Lu, X. An Attention Enhanced Bidirectional LSTM for Early Forest Fire Smoke Recognition. IEEE Access 2019, 7, 154732–154742. [Google Scholar] [CrossRef]
- Govil, K.; Welch, M.L.; Ball, J.T.; Pennypacker, C.R. Preliminary Results from a Wildfire Detection System Using Deep Learning on Remote Camera Images. Remote Sens. 2020, 12, 166. [Google Scholar] [CrossRef] [Green Version]
- Lai, C.; Zeng, S.; Guo, W.; Liu, X.; Li, Y.; Liao, B. Forest Fire Prediction with Imbalanced Data Using a Deep Neural Network Method. Forests 2022, 13, 1129. [Google Scholar] [CrossRef]
- Zheng, S.; Gao, P.; Wang, W.; Zou, X. A Highly Accurate Forest Fire Prediction Model Based on an Improved Dynamic Convolutional Neural Network. Appl. Sci. 2022, 12, 6721. [Google Scholar] [CrossRef]
- Bisquert, M.; Caselles, E.; Sánchez-Tomás, J.; Caselles, V. Application of Artificial Neural Networks and Logistic Regression to the Prediction of Forest Fire Danger in Galicia Using MODIS Data. Int. J. Wildland Fire 2012, 21, 1025–1029. [Google Scholar] [CrossRef]
- Joshi, J.; Sukumar, R. Improving Prediction and Assessment of Global Fires Using Multilayer Neural Networks. Sci. Rep. 2021, 11, 3295. [Google Scholar] [CrossRef] [PubMed]
- Kucuk, O.; Sevinc, V. Fire Behavior Prediction with Artificial Intelligence in Thinned Black Pine (Pinus Nigra Arnold) Stand. For. Ecol. Manag. 2023, 529, 120707. [Google Scholar] [CrossRef]
- Pais, C.; Miranda, A.; Carrasco, J.; Shen, Z.-J.M. Deep Fire Topology: Understanding the Role of Landscape Spatial Patterns in Wildfire Occurrence Using Artificial Intelligence. Environ. Model. Softw. 2021, 143, 105122. [Google Scholar] [CrossRef]
- Abdollahi, A.; Pradhan, B. Explainable Artificial Intelligence (XAI) for Interpreting the Contributing Factors Feed into the Wildfire Susceptibility Prediction Model. Sci. Total Environ. 2023, 879, 163004. [Google Scholar] [CrossRef]
- Saha, S.; Bera, B.; Shit, P.K.; Bhattacharjee, S.; Sengupta, N. Prediction of Forest Fire Susceptibility Applying Machine and Deep Learning Algorithms for Conservation Priorities of Forest Resources. Remote Sens. Appl. Soc. Environ. 2023, 29, 100917. [Google Scholar] [CrossRef]
- Permana, S.D.H.; Saputra, G.; Arifitama, B.; Yaddarabullah; Caesarendra, W.; Rahim, R. Classification of Bird Sounds as an Early Warning Method of Forest Fires Using Convolutional Neural Network (CNN) Algorithm. J. King Saud Univ.—Comput. Inf. Sci. 2022, 34, 4345–4357. [Google Scholar] [CrossRef]
- Bartzokas, A.; Lolis, C.; Metaxas, D. A Study on the Intra-annual Variation and the Spatial Distribution of Precipitation Amount and Duration over Greece on a 10 Day Basis. Int. J. Climatol. 2003, 23, 207–222. [Google Scholar] [CrossRef]
- Spiliotopoulos, M.; Holden, N.M.; Loukas, A. Mapping Evapotranspiration Coefficients in a Temperate Maritime Climate Using the METRIC Model and Landsat TM. Water 2017, 9, 23. [Google Scholar] [CrossRef] [Green Version]
- Pausas, J.G.; Ribeiro, E. The Global Fire–Productivity Relationship. Glob. Ecol. Biogeogr. 2013, 22, 728–736. [Google Scholar] [CrossRef]
- Mandal, A.; Nykiel, G.; Strzyżewski, T.; Kochanski, A.; Wrońska, W.; Gruszczynska, M.; Mariusz, F. High-Resolution Fire Danger Forecast for Poland Based on the Weather Research and Forecasting Model. Int. J. Wildland Fire 2021, 31, 149–162. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Pan, H.-L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP Climate Forecast System Reanalysis. Bull. Am. Meteorol. Soc. 2010, 91, 1015–1058. [Google Scholar] [CrossRef] [Green Version]
- Caraballo-Vega, J.A.; Carroll, M.L.; Neigh, C.S.R.; Wooten, M.; Lee, B.; Weis, A.; Aronne, M.; Alemu, W.G.; Williams, Z. Optimizing WorldView-2, -3 Cloud Masking Using Machine Learning Approaches. Remote Sens. Environ. 2023, 284, 113332. [Google Scholar] [CrossRef]
- Tarpley, J.D.; Schneider, S.R.; Money, L.R. Global Vegetation Indices from the NOAA-7 Meteorological Satellite. J. Appl. Meteorol. Climatol. 1984, 23, 491–494. [Google Scholar] [CrossRef]
- Kogan, F.N. Droughts of the Late 1980s in the United States as Derived from NOAA Polar-Orbiting Satellite Data. Bull. Am. Meteorol. Soc. 1995, 76, 655–668. [Google Scholar] [CrossRef]
- Kogan, F.N. Application of Vegetation Index and Brightness Temperature for Drought Detection. Adv. Space Res. 1995, 15, 91–100. [Google Scholar] [CrossRef]
- McFeeters, S.K. The Use of the Normalized Difference Water Index (NDWI) in the Delineation of Open Water Features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Kambezidis, H.D.; Kalliampakos, G.K. Fire-Risk Assessment in Northern Greece Using a Modified Fosberg Fire-Weather Index That Includes Forest Coverage. Int. J. Atmos. Sci. 2016, 2016, 8108691. [Google Scholar] [CrossRef]
- Van Wagner, C.E. Development and Structure of the Canadian Forest Fire Weather Index System; Canadian Forestry Service: Ottawa, ON, Canada, 1987; Volume 35, ISBN 978-0-662-15198-2. [Google Scholar]
- Ntinopoulos, N.; Spiliotopoulos, M.; Vasiliades, L.; Mylopoulos, N. Contribution to the Study of Forest Fires in Semi-Arid Regions with the Use of Canadian Fire Weather Index Application in Greece. Climate 2022, 10, 143. [Google Scholar] [CrossRef]
- Karouni, A.; Daya, B.; Bahak, S. Forest Fire Prediction: A Comparative Study of Applicability of Fire Weather Indices for Lebanon Allowing to Predict a Forest Fire. J. Commun. Comput. 2013, 11, 1403–1409. [Google Scholar]
- Kogan, F.N. Operational Space Technology for Global Vegetation Assessment. Bull. Am. Meteorol. Soc. 2001, 82, 1949–1964. [Google Scholar] [CrossRef]
- Domenikiotis, C.; Spiliotopoulos, M.; Tsiros, E.; Dalezios, N.R. Early Cotton Yield Assessment by the Use of the NOAA/AVHRR Derived Vegetation Condition Index (VCI) in Greece. Int. J. Remote Sens. 2004, 25, 2807–2819. [Google Scholar] [CrossRef]
- Kogan, F.N. Remote Sensing of Weather Impacts on Vegetation in Non-Homogeneous Areas. Int. J. Remote Sens. 1990, 11, 1405–1419. [Google Scholar] [CrossRef]
- Masitoh, F.; Rusydi, A.N. Vegetation Health Index (VHI) Analysis during Drought Season in Brantas Watershed. IOP Conf. Ser. Earth Environ. Sci. 2019, 389, 012033. [Google Scholar] [CrossRef]
- Yadav, R.; Tripathi, S.; Gogumalla, P.; Dubey, S. Trend Analysis by Mann-Kendall Test for Precipitation and Temperature for Thirteen Districts of Uttarakhand. J. Agrometeorol. 2014, 16, 164. [Google Scholar] [CrossRef]
- Kartsios, S.; Karacostas, T.; Pytharoulis, I.; Dimitrakopoulos, A.P. Numerical Investigation of Atmosphere-Fire Interactions during High-Impact Wildland Fire Events in Greece. Atmos. Res. 2021, 247, 105253. [Google Scholar] [CrossRef]
- Edwards, J.; Hakobyan, M.; Lin, A.; Golden, C. Predicting Forest Fires in Madagascar. Available online: https://projects.iq.harvard.edu/files/cs288/files/madagascar_fires.pdf (accessed on 15 December 2022).
- Al-Kahlout, M.M.; Ghaly, A.M.A.; Mudawah, D.Z.; Abu-Naser, S.S. Neural Network Approach to Predict Forest Fires Using Meteorological Data. Int. J. Eng. Inf. Syst. (IJEAIS) 2020, 4, 68–72. [Google Scholar]
- Wu, Z.; Wang, B.; Li, M.; Tian, Y.; Quan, Y.; Liu, J. Simulation of Forest Fire Spread Based on Artificial Intelligence. Ecol. Indic. 2022, 136, 108653. [Google Scholar] [CrossRef]
- Pinto, M.M.; DaCamara, C.C.; Hurduc, A.; Trigo, R.M.; Trigo, I.F. Enhancing the Fire Weather Index with Atmospheric Instability Information. Environ. Res. Lett. 2020, 15, 0940b7. [Google Scholar] [CrossRef]
- Velizarova, E.; Nedkov, R.; Molla, I.; Zaharinova, M. Application of aerospace data for forest fire risk assessment and prognoses. A case study for Vitosha mountain. Ecol. Eng. Environ. Prot. 2017, VIII, 38–45. [Google Scholar] [CrossRef]
- Gabban, A.; San-Miguel-Ayanz, J.; Viegas, D. A Comparative Analysis of the Use of NOAA-AVHRR NDVI and FWI Data for Forest Fire Risk Assessment. Int. J. Remote Sens. 2008, 29, 5677–5687. [Google Scholar] [CrossRef]
- Bugalho, L.; Camara, N.; Kogan, F. Study of Wildfire Environmental Conditions in Portugal with NOAA/NESDIS Satellite-Based Vegetation Health Index. J. Agric. Sci. Technol. B 2019, 9, 165–174. [Google Scholar] [CrossRef]
- Chéret, V.; Denux, J.-P. Analysis of MODIS NDVI Time Series to Calculate Indicators of Mediterranean Forest Fire Susceptibility. GISci. Remote Sens. 2011, 48, 171–194. [Google Scholar] [CrossRef]
- Talucci, A.C.; Meigs, G.W.; Knudby, A.; Krawchuk, M.A. Fire Severity and the Legacy of Mountain Pine Beetle Outbreak: High-Severity Fire Peaks with Mixed Live and Dead Vegetation. Environ. Res. Lett. 2022, 17, 124010. [Google Scholar] [CrossRef]
- Abdollahi, M.; Islam, T.; Gupta, A.; Hassan, Q. An Advanced Forest Fire Danger Forecasting System: Integration of Remote Sensing and Historical Sources of Ignition Data. Remote Sens. 2018, 10, 923. [Google Scholar] [CrossRef] [Green Version]
- Leblon, B.; Alexander, M.; Chen, J.; White, S. Monitoring Fire Danger of Northern Boreal Forests with NOAA-AVHRR NDVI Images. Int. J. Remote Sens. 2001, 22, 2839–2846. [Google Scholar] [CrossRef]
- Chen, M.; Tan, Y. SF-FWA: A Self-Adaptive Fast Fireworks Algorithm for Effective Large-Scale Optimization. Swarm Evol. Comput. 2023, 80, 101314. [Google Scholar] [CrossRef]
- Dulebenets, M.A. An Adaptive Polyploid Memetic Algorithm for Scheduling Trucks at a Cross-Docking Terminal. Inf. Sci. 2021, 565, 390–421. [Google Scholar] [CrossRef]
- Pasha, J.; Nwodu, A.L.; Fathollahi-Fard, A.M.; Tian, G.; Li, Z.; Wang, H.; Dulebenets, M.A. Exact and Metaheuristic Algorithms for the Vehicle Routing Problem with a Factory-in-a-Box in Multi-Objective Settings. Adv. Eng. Inform. 2022, 52, 101623. [Google Scholar] [CrossRef]
- Gholizadeh, H.; Fazlollahtabar, H.; Fathollahi-Fard, A.M.; Dulebenets, M.A. Preventive Maintenance for the Flexible Flowshop Scheduling under Uncertainty: A Waste-to-Energy System. Environ. Sci. Pollut. Res. 2021. [Google Scholar] [CrossRef] [PubMed]
- Dulebenets, M.A. A Diffused Memetic Optimizer for Reactive Berth Allocation and Scheduling at Marine Container Terminals in Response to Disruptions. Swarm Evol. Comput. 2023, 80, 101334. [Google Scholar] [CrossRef]
- Singh, E.; Pillay, N. A Study of Ant-Based Pheromone Spaces for Generation Constructive Hyper-Heuristics. Swarm Evol. Comput. 2022, 72, 101095. [Google Scholar] [CrossRef]
- Shtovba, S. Ant Algorithms: Theory and Applications. Program. Comput. Softw. 2005, 31, 167–178. [Google Scholar] [CrossRef]





| Joint Functions | Conditions | Mathematical Expressions |
|---|---|---|
| OR | x − y > 0.7 | 0.4 × x +0.6 × y |
| AND | x < 0.5 | 0 × (x + y) |
| y < 0.5 | 0.5 × (x + y) | |
| y − x < 0.5 | 0.7 × x + 0.3 × y | |
| 0.8 × x + 0.2 × y | ||
| Location | Date |
|---|---|
| Kinneta | 23 July 2018 |
| Istiaia Agios Stefanos | 10 August 2021 6 August 2021 |
| Palaiokoundoura Mandras | 20 May 2021 |
| Styra Psaxna | 8 August 2021 13 August 2019 |
| Mati | 23 July 2018 |
| Count | Min | Mean | Max | 25th Percentile | 50th Percentile | 75th Percentile | |
|---|---|---|---|---|---|---|---|
| FWI median | 100 | 10.289 | 11.246 | 11.049 | 11.252 | 11.455 | 11.951 |
| FFWI median | 100 | 4.955 | 4.095 | 4.563 | 4.829 | 5.125 | 6.219 |
| NDVI median | 100 | 0.154 | 0.423 | 0.728 | 0.318 | 0.420 | 0.522 |
| NDMI median | 100 | −0.976 | −0.468 | −0.380 | −0.533 | −0.476 | −0.409 |
| Ignitions | 100 | 0 | 0 | 0 | 0 | 1 | 5 |
| Training Batch | CAE | Tot. Predicted Ignitions | Tot. Actual Ignitions | Absolute Difference |
|---|---|---|---|---|
| 0 | 1.238 | 8 | 8 | 0 |
| 1 | 1.766 | 10 | 8 | 2 |
| 2 | 1.471 | 8 | 8 | 0 |
| 3 | 0.948 | 6 | 8 | 2 |
| 4 | 1.206 | 6 | 8 | 2 |
| 5 | 1.319 | 10 | 8 | 2 |
| 6 | 0.962 | 7 | 8 | 1 |
| 7 | 1.672 | 6 | 8 | 2 |
| 8 | 1.243 | 17 | 8 | 11 |
| Row Index | Predictions RBF (2nd Batch) | Actual Ignitions | Predictions AΝΝ (4th Batch) | Actual Ignitions | Absolute Difference RBF, ANN |
|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | [0, 0] |
| 1 | 1 | 1 | 4 | 3 | [0, 1] |
| 2 | 0 | 0 | 0 | 0 | [0, 0] |
| 3 | 1 | 0 | 0 | 0 | [1, 0] |
| 4 | 0 | 1 | 0 | 0 | [1, 0] |
| 5 | 0 | 0 | 0 | 1 | [0, 1] |
| 6 | 0 | 0 | 0 | 1 | [0, 1] |
| 7 | 1 | 1 | 1 | 0 | [0, 1] |
| 8 | 1 | 1 | 0 | 1 | [0, 1] |
| 9 | 1 | 1 | 0 | 1 | [0, 1] |
| Summary | 6 | 6 | 6 | 8 |
| RBF | ANN | |
|---|---|---|
| TP | 5 | 2 |
| FP | 1 | 1 |
| TN | 3 | 3 |
| FN | 1 | 4 |
| TPR% | 83.33 | 66.67 |
| FPR% | 18.18 | 18.18 |
| FPR/TPR | 0.218 | 0.272 |
| Generations | Slope | Trend | τ | z-Score | p-Value | S |
|---|---|---|---|---|---|---|
| 0 | −4.712 | 0.843 | −0.710 | −2.187 | 0.116 | −14.9 |
| 1 | −5.685 | 1 | −0.801 | −2.405 | 0.020 | −16.8 |
| 2 | −5.905 | 1 | −0.762 | −2.279 | 0.024 | −16.0 |
| 3 | −5.72 | 1 | −0.833 | −2.507 | 0.018 | −17.5 |
| 4 | −5.85 | 1 | −0.786 | −2.355 | 0.027 | −16.5 |
| 5 | −5.72 | 1 | −0.833 | −2.507 | 0.018 | −17.5 |
| Algorithm 4 Generation 5 | |
|---|---|
| 1. | If x < 0.5 OR y < 0.5: |
| 2. | x’ = x2 |
| 3. | y’ = y |
| 4. | Else: |
| 5. | x’ = 0.5 × x |
| 6. | y’ = 0.5 × y |
| 7. | Z = x’ + y’ |
| Date | Predicted State | Probability of Ignition | Actual State |
|---|---|---|---|
| 18 July 2018 | 0.0 | 0.0 | 0 |
| 19 July 2018 | 0.0 | 0.0 | 0 |
| 20 July 2018 | 2 × 10−193 | 2 × 10−193 | 0 |
| 21 July 2018 | 1.1 × 10−295 | 1.1 × 10−295 | 0 |
| 22 July 2018 | 0.0 | 0.0 | 0 |
| 23 July 2018 | 0.999925 | 1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ntinopoulos, N.; Sakellariou, S.; Christopoulou, O.; Sfougaris, A. Fusion of Remotely-Sensed Fire-Related Indices for Wildfire Prediction through the Contribution of Artificial Intelligence. Sustainability 2023, 15, 11527. https://doi.org/10.3390/su151511527
Ntinopoulos N, Sakellariou S, Christopoulou O, Sfougaris A. Fusion of Remotely-Sensed Fire-Related Indices for Wildfire Prediction through the Contribution of Artificial Intelligence. Sustainability. 2023; 15(15):11527. https://doi.org/10.3390/su151511527
Chicago/Turabian StyleNtinopoulos, Nikolaos, Stavros Sakellariou, Olga Christopoulou, and Athanasios Sfougaris. 2023. "Fusion of Remotely-Sensed Fire-Related Indices for Wildfire Prediction through the Contribution of Artificial Intelligence" Sustainability 15, no. 15: 11527. https://doi.org/10.3390/su151511527
APA StyleNtinopoulos, N., Sakellariou, S., Christopoulou, O., & Sfougaris, A. (2023). Fusion of Remotely-Sensed Fire-Related Indices for Wildfire Prediction through the Contribution of Artificial Intelligence. Sustainability, 15(15), 11527. https://doi.org/10.3390/su151511527








