Precursor Signal Identification and Acoustic Emission Characteristics of Coal Fracture Process Subjected to Uniaxial Loading
Abstract
:1. Introduction
2. Experiment
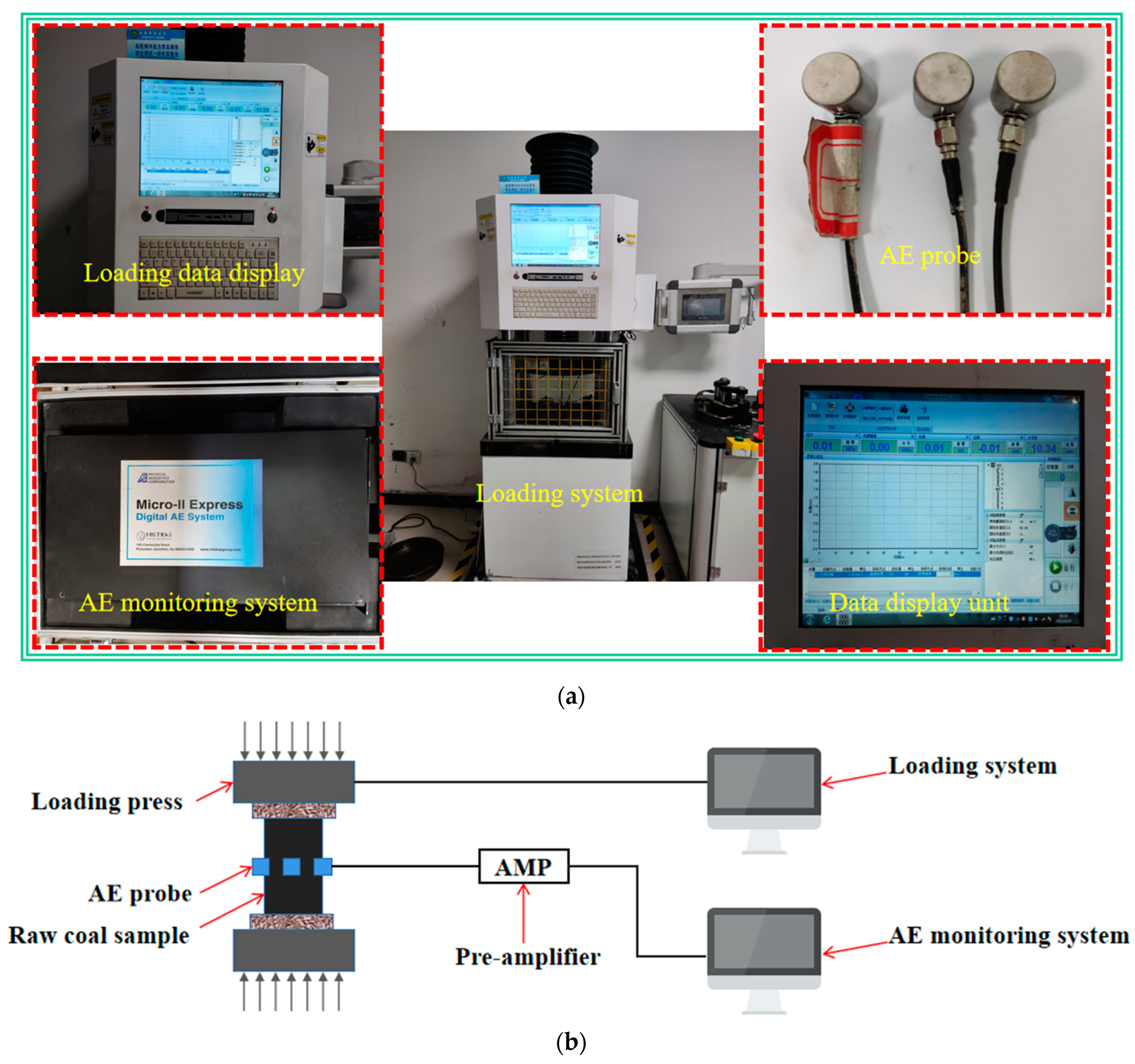
2.1. Experimental System
2.2. Experimental Method
2.3. Experimental Material
3. Results
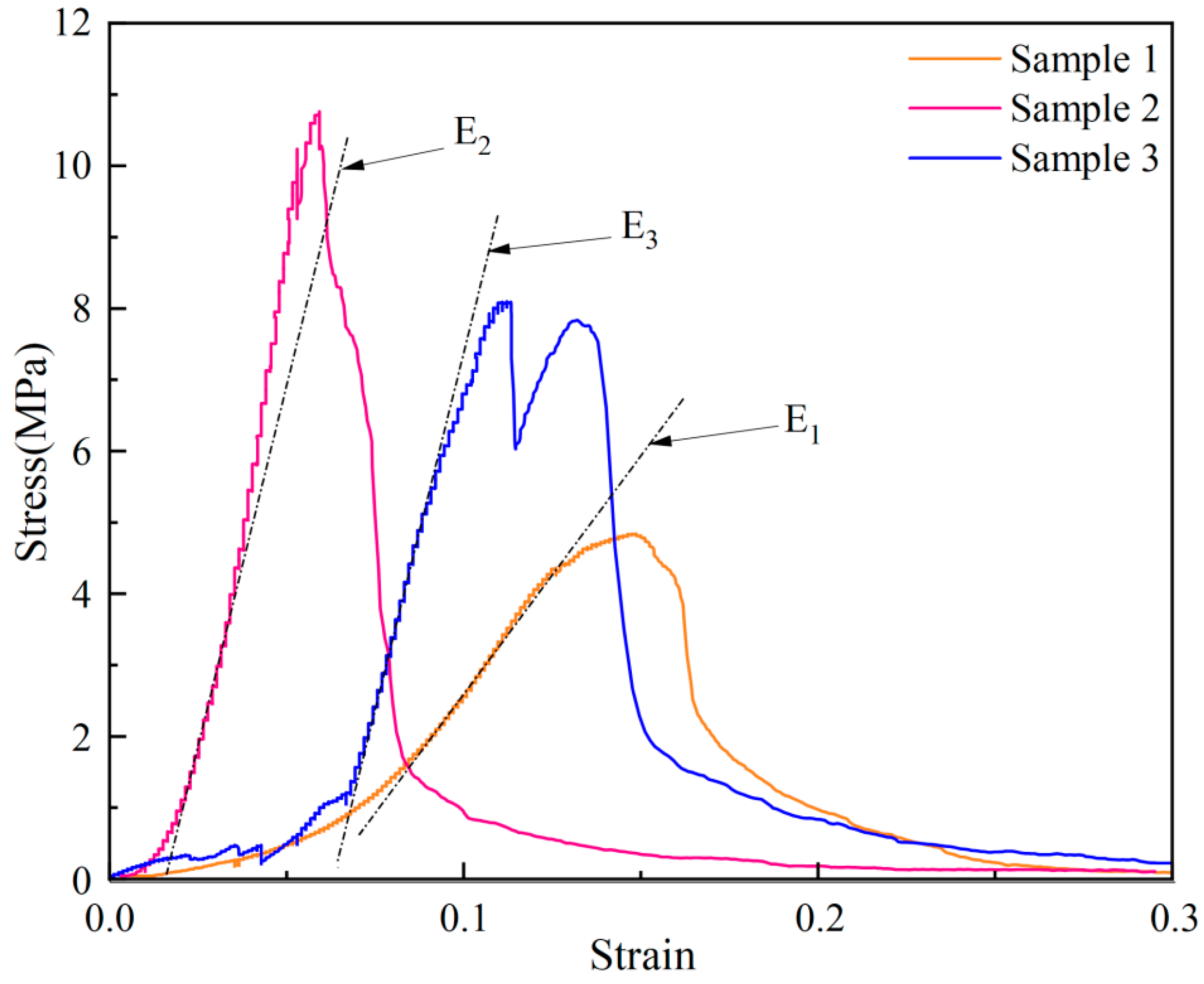
3.1. Mechanical Properties of Coal in Loading Process
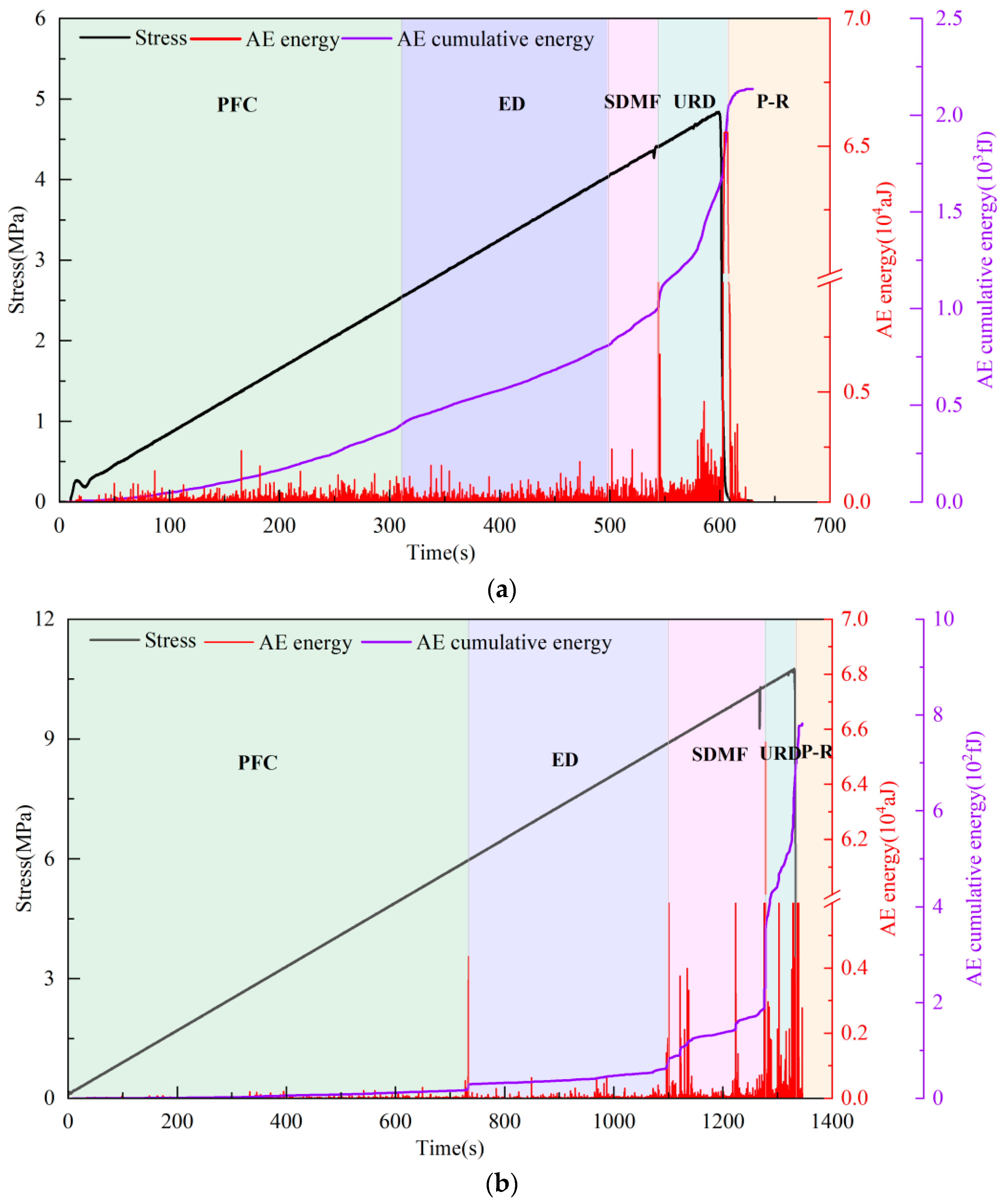
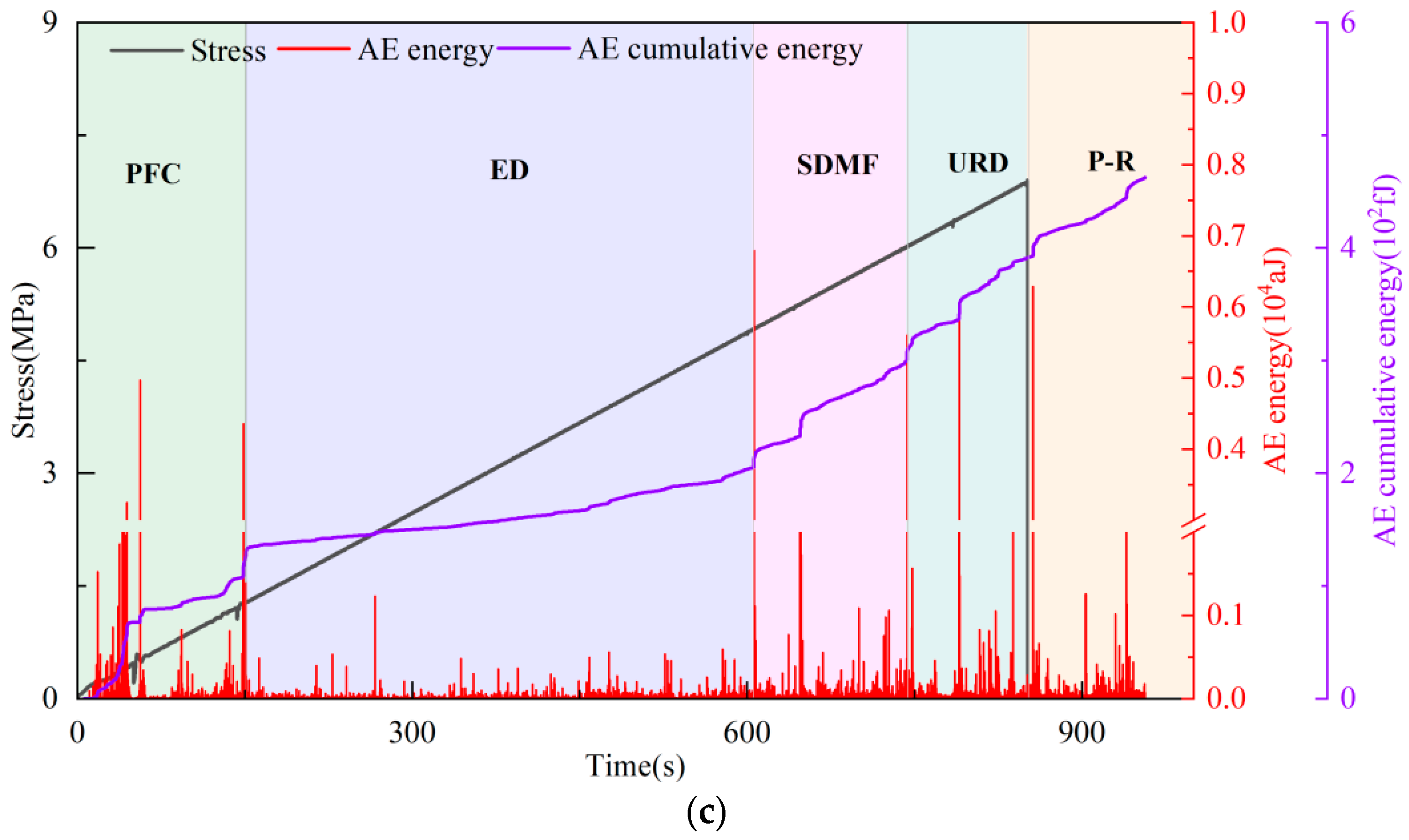
3.2. Evolution Laws of AE Energy
3.3. Cumulative Acoustic Emission Energy Risk Index
4. Discussion
4.1. Critical Slowing down Theory
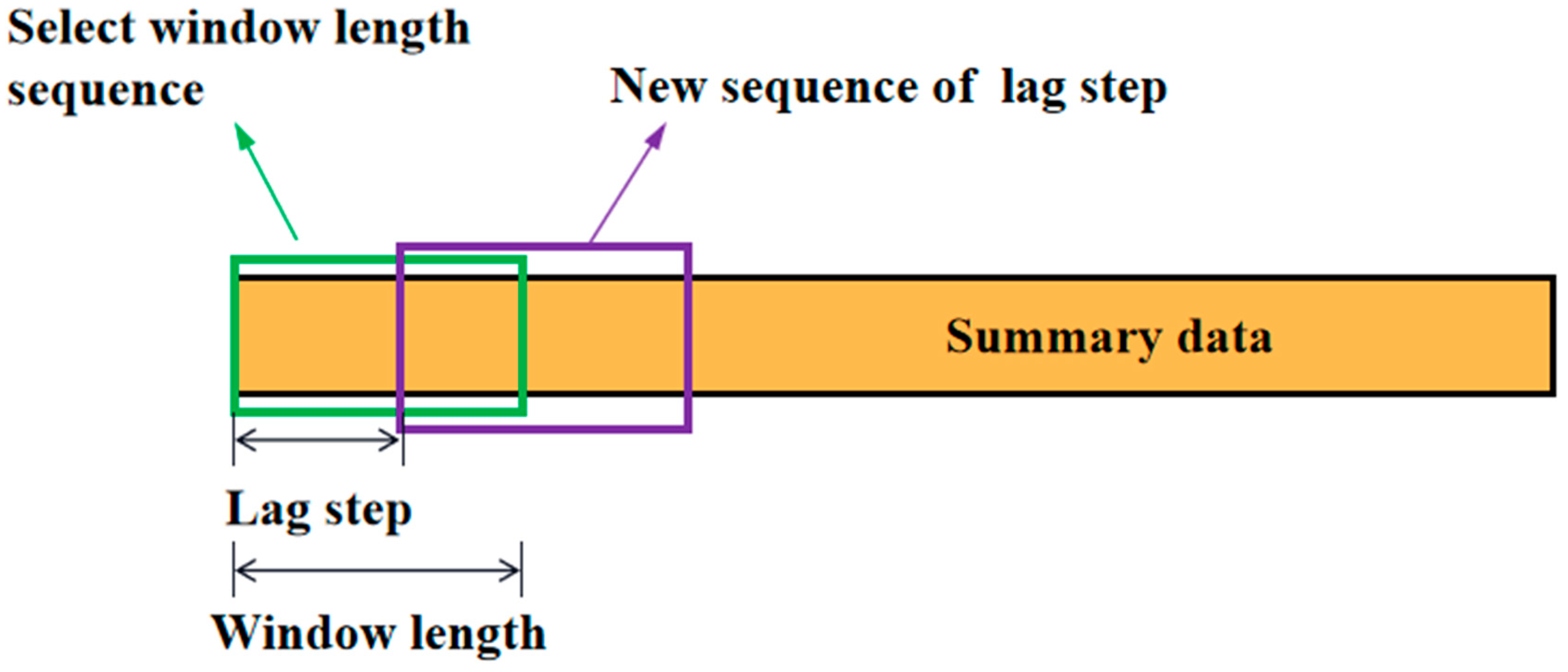
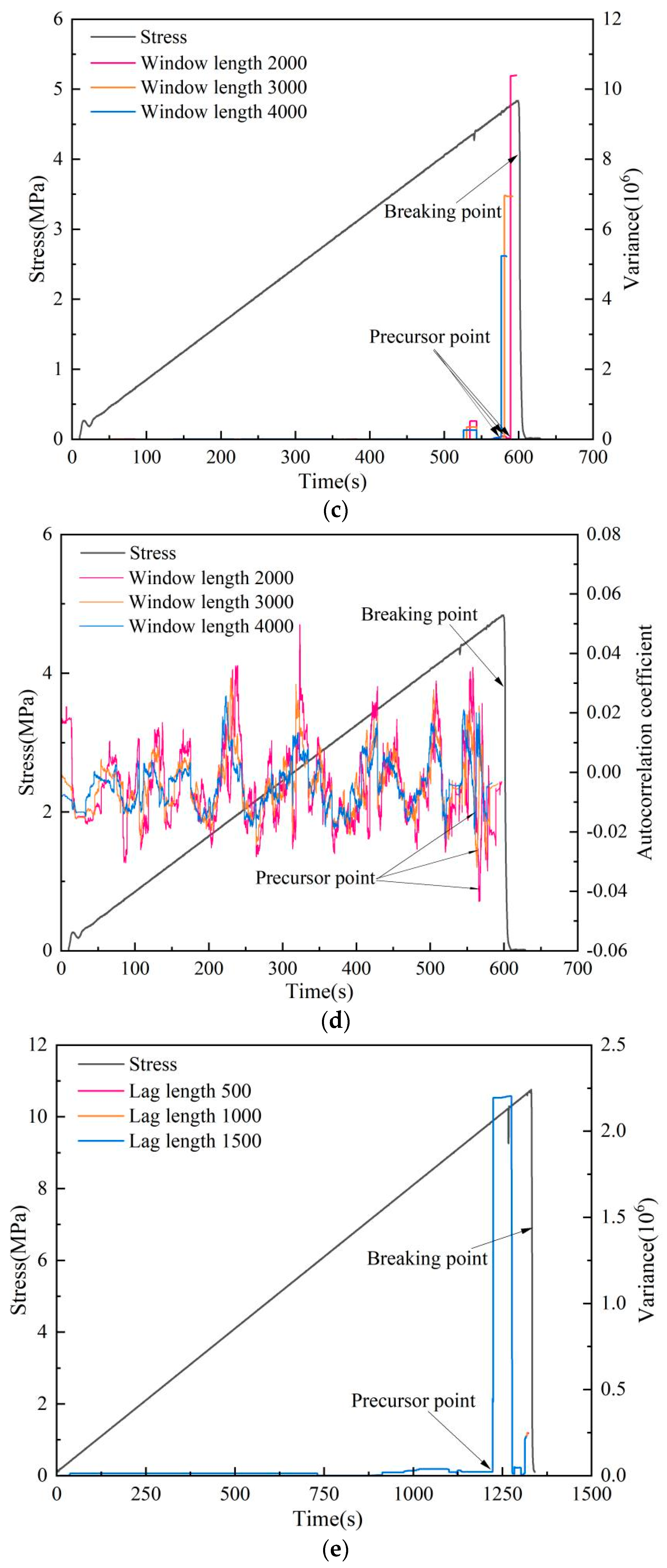
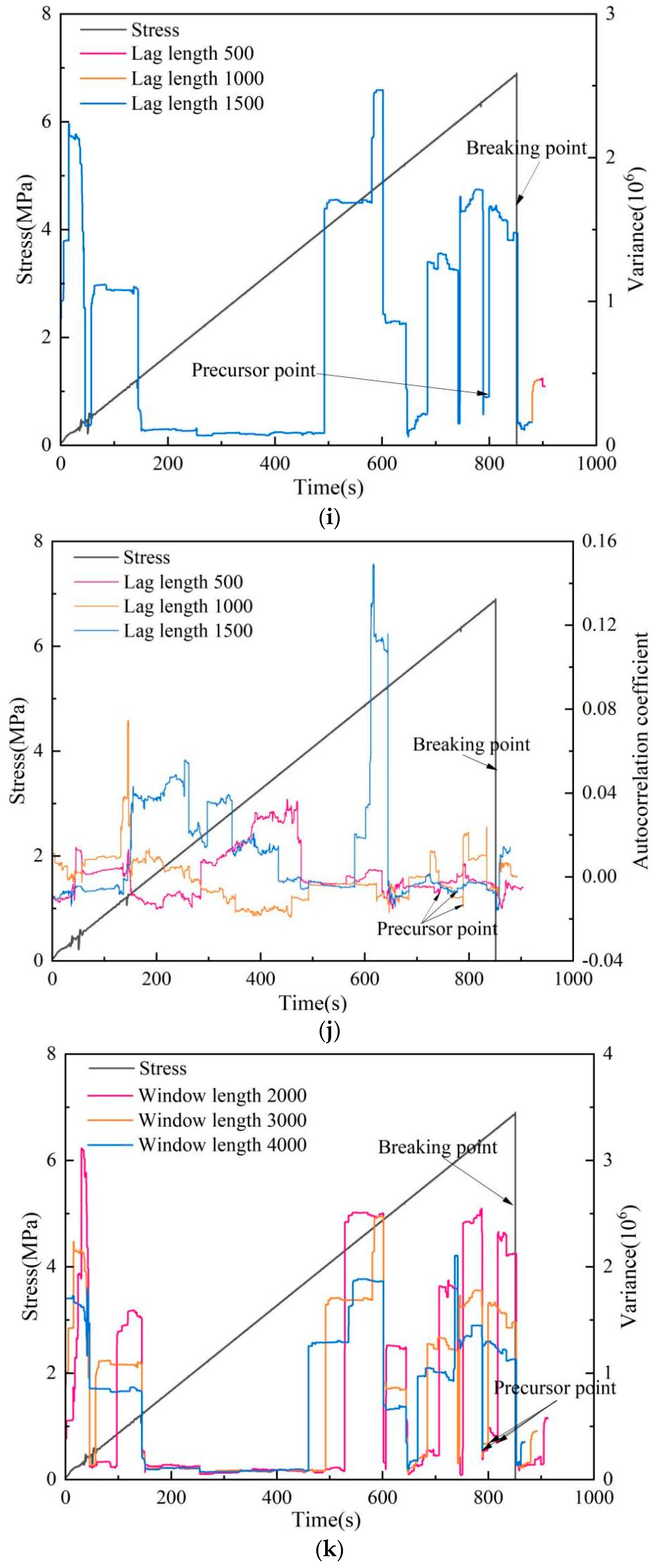
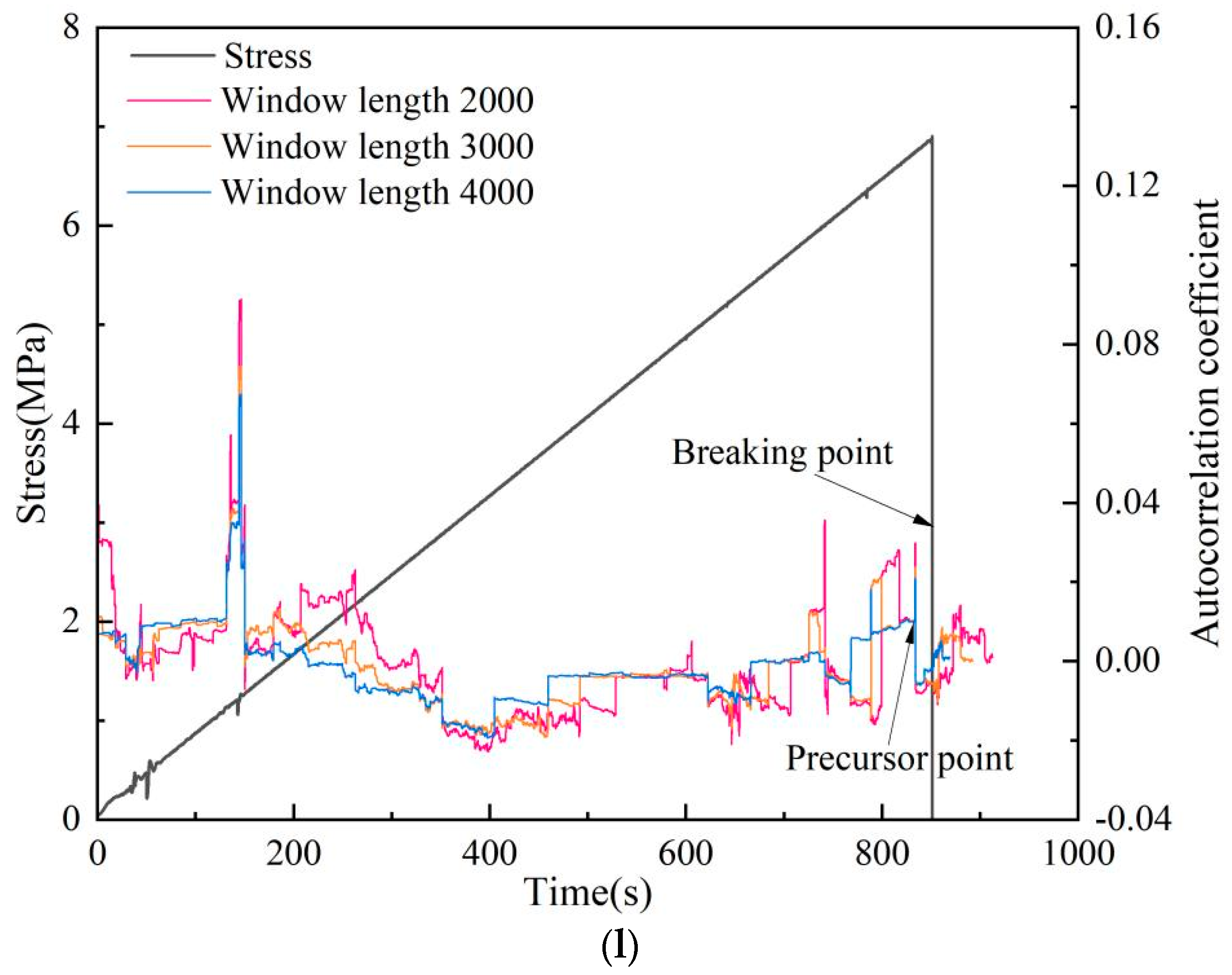
4.2. The Effect on Different Window or Lag Length on Critical Slowing Down
4.3. Compare the Precursor Characteristics of Each Index
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, X.L.; Cao, Z.Y.; Xu, Y.L. Characteristics and trends of coal mine safety development. Energy Sources Part A Recovery Util. Environ. Eff. 2021, 1–19. [Google Scholar] [CrossRef]
- Lin, H.F.; Ji, P.F.; Kong, X.G.; Li, S.G.; Long, H.; Xiao, T.; Li, B. Experimental study on the influence of gas pressure on CH4 adsorption-desorption-seepage and deformation characteristics of coal in the whole process under triaxial stress. Fuel 2023, 333, 126513. [Google Scholar] [CrossRef]
- Lin, H.F.; Ji, P.F.; Kong, X.G.; Li, S.G.; Dou, G.D.; Li, K. Precise hole placement pattern and engineering practice of pre-pumping coal seam gas by down-seam drilling. J. Coal 2022, 47, 1220–1234. [Google Scholar]
- Qin, L.; Li, S.G.; Zhai, C.; Lin, H.F.; Zhao, P.X.; Shi, Y.; Bing, Y. Changes in the pore structure of lignite after repeated cycles of liquid nitrogen freezing as determined by nitrogen adsorption and mercury intrusion. Fuel 2020, 267, 117214. [Google Scholar] [CrossRef]
- Ma, W.B.; Chen, Y.L.; Yi, W.; Guo, S.C. Investigation on crack evolution behaviors and mechanism on rock-like specimen with two circular-holes under compression. Theor. Appl. Fract. Mech. 2022, 118, 103222. [Google Scholar] [CrossRef]
- Zhou, D.; Ye, Y.C.; Hu, N.Y.; Wang, W.Q.; Wang, X.H. Crack evolution of soft-hard composite layered rock-like specimens with two fissures under uniaxial compression. Front. Struct. Civ. Eng. 2021, 15, 1372–1389. [Google Scholar] [CrossRef]
- Ma, W.Q.; Wang, J.T.; Li, X.X.; Wang, T.X. Crack evolution and acoustic emission characteristics of rock specimens containing random joints under uniaxial compression. Acta Geophys. 2021, 69, 2427–2441. [Google Scholar] [CrossRef]
- Munoz, H.; Taheri, A.; Chanda, E.K. Pre-peak and post-peak rock strain characteristics during uniaxial compression by 3D digital image correlation. Rock Mech. Rock Eng. 2016, 49, 2541–2554. [Google Scholar] [CrossRef]
- Ma, S.P.; Zhou, H. The evolution of strain field on specimen surface during rock failure process Characteristics study. J. Rock Mech. Eng. 2008, 27, 1667–1673. [Google Scholar]
- Hou, C.L.; Jiang, B.; Li, M.; Song, Y.; Cheng, G.X. Micro-deformation and fracture evolution of in-situ coal affected by temperature, confining pressure, and differential stress. J. Nat. Gas Sci. Eng. 2022, 100, 104455. [Google Scholar] [CrossRef]
- Lockner, D.A.; Byerlee, J.D.; Kuksenko, V.; Ponomarev, A.; Sidorin, A. Quasi-static fault growth and shear fracture energy in granite. Nature 1991, 350, 39–42. [Google Scholar] [CrossRef]
- Cox, S.J.D.; Meredith, P.G. Microcrack formation and material softening in rock measured by monitoring acoustic emissions. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1993, 30, 11–24. [Google Scholar] [CrossRef]
- He, M.C.; Miao, J.L.; Feng, J.L. Rock burst process of limestone and its acoustic emission characteristics under true-triaxial unloading conditions. Int. J. Rock Mech. Min. Sci. 2010, 47, 286–298. [Google Scholar] [CrossRef]
- Zhao, A.H.; Ma, Y.K.; Liu, J.; Chen, D.Z.; Yuan, H.Y.; Fu, M. Energy characteristics of AE signal frequency band during coal rupture in mines with gas. China Saf. Sci. J. 2020, 30, 115–121. [Google Scholar]
- Ishida, T.; Labuz, J.F.; Manthei, G.; Meredith, P.G.; Nasseri, M.H.B.; Shin, K.; Yokoyama, T.; Zang, A. ISRM suggested method for laboratory acoustic emission monitoring. Rock Mech. Rock Eng. 2017, 50, 665–674. [Google Scholar] [CrossRef]
- Zang, A.; Wagner, F.C.; Stanchits, S.; Dresen, G.; Andresen, R.; Haidekker, M.A. Source analysis of acoustic emissions in Aue granite cores under symmetric and asymmetric compressive loads. Geophys. J. Int. 1998, 135, 1113–1130. [Google Scholar] [CrossRef] [Green Version]
- Aker, E.; Kühn, D.; Vavryčuk, V.; Soldal, M.; Oye, V. Experimental investigation of acoustic emissions and their moment tensors in rock during failure. Int. J. Rock Mech. Min. Sci. 2014, 70, 286–295. [Google Scholar] [CrossRef]
- Wang, X.R.; Liu, X.F.; Wang, E.Y.; Li, X.L.; Zhang, X.; Zhang, C.; Kong, B. Experimental research of the AE responses and fracture evolution characteristics for sand-paraffin similar material. Constr. Build. Mater. 2017, 132, 446–456. [Google Scholar] [CrossRef]
- Burud, N.B.; Kishen, J.M.C. Investigation of long memory in concrete fracture through acoustic emission time series analysis under monotonic and fatigue loading. Eng. Fract. Mech. 2023, 277, 108975. [Google Scholar] [CrossRef]
- Triantis, D.; Kourkoulis, S.K. An alternative approach for representing the data provided by the acoustic emission technique. Rock Mech. Rock Eng. 2018, 51, 2433–2438. [Google Scholar] [CrossRef]
- Wang, X.R.; Wang, E.Y.; Liu, X.F. Damage characterization of concrete under multi-step loading by integrated ultrasonic and acoustic emission techniques. Constr. Build. Mater. 2019, 221, 678–690. [Google Scholar] [CrossRef]
- Lavrov, A. The Kaiser effect in rocks: Principles and stress estimation techniques. Int. J. Rock Mech. Min. Sci. 2003, 40, 151–171. [Google Scholar] [CrossRef]
- Lockner, D.A. The role of acoustic emission in the study of rock fracture. Int. J. Rock Mech. Min. Sci. Geomech. 1993, 30, 88–899. [Google Scholar] [CrossRef]
- Backers, T.; Stanchits, S.; Dresen, G. Tensile fracture propagation and acoustic emission activity in sand stone: The effect of loading rate. Int. J. Rock Mech. Mining Sci. 2005, 42, 1094–1101. [Google Scholar] [CrossRef]
- Wang, E.Y.; He, X.Q.; Liu, Z.T.; Li, Z.H. Study on frequency spectrum characteristics of acoustic emission in coal or rock de-formation and fracture. J. China Coal Soc. 2004, 29, 289–292. [Google Scholar]
- Xiao, C.X.; Jin, C.; Ding, X.; Pan, Y. Experimental study on rock burst tendency of coal with different moisture content based on acoustic emission time-frequency signals. J. China Coal Soc. 2018, 43, 931–938. [Google Scholar]
- Yang, D.; Hu, J.; Ma, S.; Zeng, P. Analysis of dynamic fracture of granite after uniaxial recompression predamaged by high confining pressure cyclic loading based on acoustic emission. Eng. Fract. Mech. 2022, 266, 108414. [Google Scholar] [CrossRef]
- Carpenter, S.R.; Brock, W.A. Rising variance: A leading indicator of ecological transition. Ecol Lett. 2006, 9, 311–318. [Google Scholar] [CrossRef]
- Yan, R.; Jiang, C.S.; Zhang, L.P. Study on critical slowing down phenomenon of radon concentrations in water before the Wenchuan Ms 8.0 earthquake. Chin. J. Geophys. 2011, 54, 1817–1826. [Google Scholar]
- Hao, W.; Wei, H.; Yan, P.C. Using the principle of critical slowing down to discuss the abrupt climate change. Acta Phys. Sin. 2013, 62, 556–565. [Google Scholar]
- Dakos, V.; Scheffer, M.; van Nes, E.H.; Brovkin, V.; Petoukhov, V.; Held, H. Slowing down as an early warning signal for abrupt climate change. Proc. Natl. Acad. Sci. USA 2008, 105, 14308–14312. [Google Scholar] [CrossRef] [PubMed]
- Hao, T.X.; Li, F.; Tang, Y.J.; Zhao, L.; Wang, Z. Infrared precursor of pre-cracked coal failure based on critical slowing down. Geomat. Nat. Hazards Risk 2022, 13, 1682–1699. [Google Scholar] [CrossRef]
- Loukidis, A.; Stavrakas, I.; Triantis, D. Non-extensive statistical mechanics in acoustic emissions: Detection of upcoming fracture in rock materials. Appl. Sci. 2023, 13, 3249. [Google Scholar] [CrossRef]
- Wei, Y.; Li, Z.H.; Kong, X.G.; Zhang, Z.B.; Wang, J.L.; Cheng, F.Q. Critical slowing characteristics of uniaxial compression damage in sandstone. J. Coal 2018, 43, 427–432. [Google Scholar]
- Zhu, X.; Liu, H.X.; Hu, J.W.; Fan, J. Experimental study on the characteristics of critical slowing precursors of sandstone damage acoustic emission. Geotechnics 2022, 43, 164–172. [Google Scholar]
- Li, D.X.; Wang, E.Y.; Li, Z.H.; Ju, Y.; Wang, D.; Wang, X. Experimental investigations of pressure stimulated currents from stressed sandstone used as precursors to rock fracture. Int. J. Rock Mech. Min. Sci. 2021, 145, 104841. [Google Scholar] [CrossRef]
- Wang, X.R.; Wang, E.Y.; Liu, X.; Zhou, X. Micromechanisms of coal fracture: Insights from quantitative AE technique. Theor. Appl. Fract. Mech. 2021, 114, 103000. [Google Scholar] [CrossRef]
- Kong, X.G.; Wang, E.Y.; Hu, S.B.; Li, Z.; Liu, X.; Fang, B.; Zhan, T. Critical slowing down on acoustic emission characteristics of coal containing methane. J. Nat. Gas Sci. Eng. 2015, 24, 156–165. [Google Scholar] [CrossRef]
- Yuan, S.X.; Jiang, T.; Lei, J.H.; Cui, C.H. Experimental study on fracture characteristics of rock-like material with prefabricated cracks under compression shear. Sci. Rep. 2022, 12, 2809. [Google Scholar] [CrossRef]
- Sun, H.; Chen, S.J.; Jin, A.B.; Zhu, D.F. Uniaxial compressive strength characteristics and crack evolution law of fractured rock samples. J. Northeast. Univ. Nat. Sci. Ed. 2022, 43, 404–413. [Google Scholar]
- Zhang, X.; Tang, J.P.; Pan, Y.S.; Yu, H. Experimental study on intensity and energy evolution of deep coal and gas outburst. Fuel 2022, 324, 124484. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, J.P.; Yu, H.H.; Pan, Y. Gas pressure evolution characteristics of deep true triaxial coal and gas outburst based on acoustic emission monitoring. Sci. Rep. 2022, 12, 21738. [Google Scholar] [CrossRef]
- Kong, X.G.; Wang, E.Y.; He, X.Q.; Li, D.; Liu, Q. Time-varying multifractal of acoustic emission about coal samples subjected to uniaxial compression. Chaos Solitons Fractals 2017, 103, 571–577. [Google Scholar] [CrossRef]
- Scheffer, M.; Bascompte, J.; Brock, W.A.; Brovkin, V.; Carpenter, S.R.; Dakos, V.; Held, H.; Van Nes, E.H.; Rietkerk, M.; Sugihara, G. Early-warning signals for critical transitions. Nature 2009, 461, 53–59. [Google Scholar] [CrossRef]
- Ramos, O. Criticality in earthquakes. Good or bad for prediction? Tectonophysics 2009, 485, 321–326. [Google Scholar] [CrossRef]
- Zhang, Z.B.; Wang, E.Y.; Zhang, H.T.; Bai, Z.M.; Zhang, Y.H.; Chen, X. Research on nonlinear variation of elastic wave velocity dispersion characteristic in limestone dynamic fracture process. Fractals 2023, 31, 2350008. [Google Scholar] [CrossRef]



| Uniaxial Compressive Resistance Intensity/MPa | Elastic Modulus/MPa | Failure Strain | |
|---|---|---|---|
| Sample 1 | 4.840 | 61.094 | 0.149 |
| Sample 2 | 10.760 | 264.151 | 0.059 |
| Sample 3 | 8.096 | 221.951 | 0.111 |
| K1 | K2 | K3 | K4 | P1 | P2 | P3 | |
|---|---|---|---|---|---|---|---|
| Sample 1 | 1.30 | 2.17 | 4.93 | 16.20 | 0.59 | 2.27 | 7.46 |
| Sample 2 | 0.03 | 0.14 | 0.64 | 9.06 | 0.21 | 4.57 | 64.71 |
| Sample 3 | 0.71 | 0.19 | 0.59 | 1.21 | 3.74 | 3.11 | 6.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, X.; Zhan, M.; Cai, Y.; Ji, P.; He, D.; Zhao, T.; Hu, J.; Lin, X. Precursor Signal Identification and Acoustic Emission Characteristics of Coal Fracture Process Subjected to Uniaxial Loading. Sustainability 2023, 15, 11581. https://doi.org/10.3390/su151511581
Kong X, Zhan M, Cai Y, Ji P, He D, Zhao T, Hu J, Lin X. Precursor Signal Identification and Acoustic Emission Characteristics of Coal Fracture Process Subjected to Uniaxial Loading. Sustainability. 2023; 15(15):11581. https://doi.org/10.3390/su151511581
Chicago/Turabian StyleKong, Xiangguo, Mengzhao Zhan, Yuchu Cai, Pengfei Ji, Di He, Tianshuo Zhao, Jie Hu, and Xi Lin. 2023. "Precursor Signal Identification and Acoustic Emission Characteristics of Coal Fracture Process Subjected to Uniaxial Loading" Sustainability 15, no. 15: 11581. https://doi.org/10.3390/su151511581
APA StyleKong, X., Zhan, M., Cai, Y., Ji, P., He, D., Zhao, T., Hu, J., & Lin, X. (2023). Precursor Signal Identification and Acoustic Emission Characteristics of Coal Fracture Process Subjected to Uniaxial Loading. Sustainability, 15(15), 11581. https://doi.org/10.3390/su151511581






