Abstract
In this paper, two flexible model tools (CO2 emissions/cost tool and CFD tool) that simulate the production process of Grecian Magnesite (GM) and extract economic and technical conclusions regarding the substitution of fossil fuels with various types of biomass are presented and analyzed. According to the analysis, the higher the substitution, the higher the profit in both CO2 emissions and cost reduction. The reduction in CO2 emissions that can be achieved through biomass fuel substitution ranges from 15% for a 30% substitution to 35% for a 70% substitution. Accordingly, production costs are also reduced with the use of biomass. The initial results of this decision-making cost tool showed that the most profitable solution is a 70% substitution, for which production costs can be reduced by up to 38.7%, while the most beneficial type of biomass proved to be the olive kernel. A proposed and feasible solution is the substitution of 50% sunflower husk pellets, which will result in a reduction of 25% in CO2 emissions and almost 10% in production cost. From CFD simulation, a reduced order model (ROM) has been developed that allows the running of scenarios in real time, instead of the usual long times required by complex simulations. Comparative studies of fuel blend and biomass type can be carried out easily and rapidly, allowing one to choose the most suitable substitution.
1. Introduction
Global energy consumption has risen by 100% in the past 40 years [1]. EIIs are one of the top energy consumers with a share of 15% through the European Union [2]. About 40 EJs are generated by coal globally annually (2019 data), of which more than 65% are used in EIIs [3]. Most of the CO2 emissions that cause global warming derive from fossil fuel combustion (over 99%). The amount of emitted CO2 jumped from 15,461 Mt in 1973 to 33,622 in 2019, of which 44% is due to the use of coal [4].
Carbon pricing is a very effective policy for promoting decarbonization. Carbon prices reduce the respective emissions making low/zero carbon energy more competitive compared to the alternative solutions with high content of carbon. It is estimated that an increase by 1 euro per ton of CO2 leads to a 0.73% reduction in CO2 emissions over time [5]. The aim of restricting the rise of the temperature of the planet to 1.5 °C, as mentioned in the Paris Agreement, requires decarbonization by 2050 [6]. According to Kaufman et al. [7] a price of 60 EUR per ton CO2 by 2030 is consistent with a slow decarbonization concept by 2060 and a cost of 120 EUR per ton CO2 by 2030 is necessary for decarbonization by mid-century under the assumption that carbon pricing plays a major role in the decarbonization effort.
The price of carbon dioxide is determined by the EU Emissions Trading System, which was established in 2005 with the aim of achieving a climate-neutral economy by 2050 [8]. Especially for the industry and EΙΙ sector the EU Emissions Trading System (ETS) aims in reducing carbon dioxide emissions by requiring companies to hold a permit for every ton of CO2 equivalent to what they emit. They are purchased through auctions while also providing incentives to drive innovation in the industry. According to the European Commission, the goal for the industry is to reduce CO2 emissions by 63% of 2005 levels by 2030 [9]. Another measure established by the European Commission aimed at reducing CO2 emissions concerns the complete abolition of the free emission rights held by industries until 2034.
Biomass, a renewable energy source, produces net zero CO2 emissions during its combustion in boilers and reactors for heat and energy production. Cofiring biomass with coal can significantly reduce greenhouse gas (GHG) emissions. The integration of carbon capture and storage in the combustion plant significantly enhances the environmental potential. However, energy consumption is a critical barrier in terms of efficiency [10]. Lopez et al. [11] reported a techno-economic analysis of coal biomass cofiring in large power plants. It was reported that the use of biomass as a raw material could reduce the oxy-plant viability. This problem could be managed by increasing the projected scale-up. A viable solution at the economic and safety level is the operation of 300 MWe power plants with a 40–50% substitution of their fuel by biomass. Such projects could also be attractive to investors. According to studies, long-term sustainable reduction in CO2 coal emissions can be achieved by converting woody biomass into fuel pellets for coal substitution [12], while biomass use for energy and heat production can increase CO2 emissions reduction potential [13]. The use of biomass also produces CO2 emissions when materials such as wood and waste are converted into energy. The substitution of fossil fuels with biomass contributes to a reduction in the net flow of CO2 emissions since CO2 emitted is recaptured as forests subsequently grow [14,15]. This is widely known as the carbon neutrality of biomass which means that the CO2 released from biomass combustion is equal to the emissions sequestered in biomass [16].
In the cement industry, which operates in a similar manner as the magnesia industry, wood-based and waste-based biomass is used. Neutral wood (such as wood chips, pellets, sawdust, etc.) tends to have a high moisture content and therefore a lower calorific value than traditional fuels. It is recognized, though, that these natural energy sources could lead to a negative carbon footprint when combined with carbon capture technologies in the kiln. A widely-used biomass waste are end of life tires. These tires are an ideal fuel due to their high calorific value and their rich biogenic carbon content, thus, contributing to a reduction in CO2 emissions related to fossil fuels. Another example of a biomass fuel that is used as an alternative fuel but also used as a raw material in clinker manufacturing is sewage sludge. This type of biomass has high calorific value and a low emissions factor compared to coal when combusted in a cement kiln [17].
Various models have been developed over the years in order to tackle the GHG emissions problem. GHG emissions calculation tool by GHG Protocol [18] uses as input data the activity type of the company using the tool, the amount of fuel consumed by adjusting the emissions factors as parameters and the output data are total GHG emissions from fossil fuels and CO2 emissions from biomass combustion. Another model [19] takes into account the fuel type and the amount consumed and calculates the total CO2 emissions. On the other hand, the computational models that have been developed and/or applied and concern the magnesite sector focus on the production process with the main objective of improving it. Akkoyun O. and Careddu N. developed a new simulation-based computer program which represents an open pit mine in detail using more than a hundred variables, providing an interactive and visual environment for the teaching and learning of mining-engineering-related subjects [19]. In addition, Jiang T. and Zhang W., developed a 3D transient multi-physical field model to capture the complex processes inside a fused magnesia furnace [20], while Ping et al. used an Aspen model in order to plan an energy-saving strategy for a transport bed flash calcination process applied to magnesite [21]. In the current work, a simplified model adapted to the needs of GM is presented which focuses on the biomass/pet coke blend optimization. The tool calculates the energy requirements for producing CCM (caustic calcined magnesia) or DBM (dead burned magnesia), CO2 emissions that emerge and the total cost expected and the critical parameters for decision making in the magnesia sector.
In addition, CFD simulation in industry already has a long history. Its main advantage is the capacity to realistically model the physical processes occurring in industrial assets, from furnaces to modern electrolyzers [22,23,24]. This approach provides rich information about the process at hand that can be used for the goal-oriented design, optimization or retrofitting of both the processes and equipment.
The main goal of CFD is to numerically solve the well-known Navier-Stokes equations that govern the behavior of fluids [25]. The direct approach consists of dividing the domain of simulation in small volumes (cells) and solve the discretized Navier–Stokes equations. This direct numerical simulation (DNS) is rarely used because it requires a huge number of cells and correspondingly huge computational resources, especially for turbulent flows. The most common strategy is to divide the velocity field into two contributions: (i) an average velocity field that is time-independent, and (ii) a fluctuating field that depends on time and space. When this ansatz is introduced in the Navier–Stokes equations, this results in a system known as Reynolds-averaged Navier–Stokes equations (RANS). The RANS system is not closed, it must be supplemented with additional equations to compute the so-called Reynolds stresses, which are products of the fluctuating part of the velocity field. For this reason, the additional equations are referred to as a turbulence model.
Turbulence models are mathematical constructions that model Reynolds stresses in terms of the mean flow, thus avoiding the need to deal with those non-linear terms. The Spalart–Allmaras model introduces one transport equation for a new quantity, the eddy turbulent viscosity, which is added to the molecular viscosity. This model was developed to perform well in the presence of relatively large pressure gradients. On an upper level of complexity, the κ-ϵ model solves two transport equations, one for the turbulent kinetic energy and another for its rate of dissipation. It has been validated in confined flows under not very large pressure gradients. Due to its balance of accuracy in the results and complexity of the implementation and calculation, this model is widely used for industrial applications. This is the model of choice for the present work.
The CFD simulation of combustion considers several processes especially for rotary kilns [26,27,28,29,30,31,32,33,34,35,36]. The chemical reactions in the gas phase comprise hundreds of species and chemical reactions. Since this complexity is unaffordable, there exist models that simplify the calculations. On the one hand, it is possible to reduce the composition of the gas to a probability density function that gives the average composition in the simulation domain. The complexity of the gas mixture is reduced to a single scalar quantity, updated by a transport equation. This model allows for fast calculations but is the least realistic. On the other hand, it is possible to use reduced models of combustion that consider few chemical reactions and species. Under this approach, the chemical kinetics are calculated explicitly, and the intervening species distribution is determined by the flow conditions. Thus, the reaction dynamics are influenced by the degree of turbulent mixing, not just the kinetics of the reactions. This method is more realistic, but also more computationally expensive since it requires one transport equation for each chemical species. This is the method chosen for this work, as explained below.
When solid fuel is used, one needs to consider the processes of devolatilization and char oxidation. The particle of fuel is characterized by its composition, proximate analysis, size, and degree of sphericity. The devolatilization can be modelled as a single-step process and characterized by a devolatilization time or as a multiple-step process. In the latter case the reaction is assumed to be of the Arrhenius type, defined by an energy of activation and a pre-exponential factor that defines a time scale. These two parameters can be determined experimentally by a thermogravimetric analysis. Currently, due to the interest in biomass as being a renewable and emissions-free solid fuel, the kinetic constants of the most usual biomasses can be found in the literature.
In this paper, the results of two flexible model tools (CO2 emissions/cost tool and CFD tool) are presented. The above tools simulate the production process of an EII such as Grecian Magnesite (GM) and extract economic and technical conclusions regarding the substitution of fossil fuels (pet coke) with various types of biomass. The novelty of this work is found in the development and application of two simulation models that thoroughly describe and analyze the production process and the operational parameters of an industry, while at the same time estimating with relative accuracy the emissions of air pollutants and the production costs. Regarding the use of the CFD, the innovation lies in the fact that it has not been used before in the simulation of a magnesite mining industry and the production of the corresponding products. The calculation model is a simplified and very easy-to-use program which, although it simulates the GM production process in high detail and can be easily modified and adopted by any EII, allowing the possibility to calculate emissions and production costs with satisfactory precision, differentiates some of the operational parameters such as the type and amount of fuel used.
2. Use of Biomass in the Case of GM
As already mentioned above, the use and effectiveness of flexible tools has been tested in practice in the production process of Grecian Magnetite.
GM was founded in 1959 and is operating in the fields of mining and industry. The main products are CCM, DBM, carbonate magnesium (MgCO3− raw magnesite) and basic monolithic refractories. The company has gained an international reputation and is a pioneer in its fields of activity, particularly in the production and exploitation of the CMM where it is considered a global leader.
The method used to extract the raw materials is the open pit method, while the production of the final product requires four stages of processing:
- Pre-beneficiation, where various impurities are removed from the raw material;
- Main-beneficiation, where the material enters the main beneficiation stage, in which it either passes through camera sorting or a combination of dense media and magnetic separation stages depending on the desired chemistry of the kiln-feed magnesite;
- Calcination and sintering, which is the main stage of the processing by firing the magnesite in kilns for the production of CCM and DBM. Calcination decomposes MgCO3 producing MgO, while with sintering the temperature increase to 2000 °C leads to firing of the material;
- Final processing, where the final product is crushed and differentiated according to its size.
The energy/thermal requirements of the processes, as they were described, are quite large and they are covered by firing mainly petroleum coke (pet coke), heavy oil and biomass. Firing processes result in the emission of large amounts of CO2 and nitrogen oxides (NOx). CO2 emissions are mainly due to two processes, the decomposition of MgCO3 and the combustion of fuels. NOx emissions are produced during DBM production, where a 2000 °C temperature is needed. Interferences in the processes of the decomposition of MgCO3 and the production of DBM are not possible, therefore the only process in which it is possible to intervene in order to reduce emissions is the combustion of fuels. Thus, GM is substituting a percentage of pet coke energy with biomass in the form of sunflower husk pellets, olive cake or sawdust according to their seasonal availability and prices. During the BAMBOO project [37], an innovative and flexible Low NOx Burner (LNB) was implemented by GM in order to mitigate the problem created with the large volumes of emissions, due to the high temperature (up to 1600 °C) and to exploit the latent energy in producing a high enough temperature for the DBM production. The flexibility of the burner lies in the fact that it is capable of burning fuel mixtures containing pulverized biomass and pet coke. In addition, another parameter that requires attention and to which the new burner must obey is the access to an adjustable swirl which is necessary for the operation of the LNB at very high temperatures (above 1600 °C).
Figure 1 presents the calcination plant of the mine installation in Yerakini.

Figure 1.
Grecian magnesite, calcination plant detail, Yerakini mine installations, Chalkidiki, Greece.
GM is one of the largest magnesite mining and production companies in Europe [38]; however, the greatest interests in as well as the reason for choosing the application of the experimental process are the peculiarities in its production process and its operational parameters. More specifically, the processes that take place presuppose very high temperatures (>1500 °C), which increases the requirements for both the quantity and the quality (high calorific value) of the fuel. At the same time, the burners used in conjunction with the type of processes result in the emission of large amounts of gaseous pollutants. It was therefore decided that such a demo site is quite demanding but also particularly challenging for the application of the computer models that have been developed.
In order to make the feeding system at the GM demo site more functional and to prevent fuel (biomass-pet coke) mixing, some changes and modifications are adopted in pre-treatment and feeding, as shown in the Figure 2. Biomass and pet coke are stored in different silos, and different mills are used to grind the two fuels. Then the ground quantities of fuel are taken to a new silo where they are homogenized and fed to the burner.
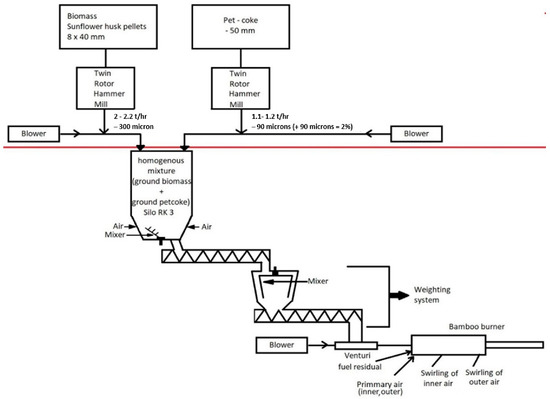
Figure 2.
The new fuel mix preparation and feed system for Rotary Kiln 3. The part under the red line is the new installation able to handle the new fuel mixture.
3. Materials and Methods
3.1. Cost and CO2 Emissions Tool
The fuel flexibility tool presented is a stand-alone model that calculates the energy requirements for CCM or DBM production, CO2 emissions that emerge and the total production cost. The tool has been adapted to the needs of GM that offered all crucial aspects for the model input parameters.
Magnesite calcination can be described by the following reaction:
from which it is derived that for 1 tn of magnesia (MgO) and 2.1 tn of magnesite is required since the molecular weight ratio is 84/40 (MgCO3/MgO).
In order to calculate CO2 emissions from magnesite decomposition, the following equation is used [39,40,41]:
where PMD stands for carbon emissions from magnesite decomposition (kg CO2), M is the quantity of magnesia (kg), G is the mass fraction of MgO in the product (%) and 44/40 is the molecular weight ratio of CO2/MgO.
The GHG emissions associated with fuel combustion derive from:
where n is the number of different fuel types, Wi is the quantity of fuel consumed (kg), NCVi is the net calorific value of fuel i (KJ/kg), Ci is the carbon content of fuel i (kg/TJ), Yi is the carbon oxidation ratio of fuel i (%), 44/12 is the molecular weight ratio of CO2/C, EFi is the CH4 emission factor of fuel i (kg/TJ) and M is the CO2 equivalent conversion factor of CH4 equal to 25 kg CO2-eq/kg.
With these values in hand, fuel cost, CO2 emissions cost by magnesite decomposition and fuel combustion are calculated automatically. The user inputs include the desired MgO product quantity, the pet coke price and lower heating value (LHV), the types of biomass, their prices and their LHVs, CO2 emission prices (EUR/tn) and the heat needed for production (GJ/tn) of CCM/DBM. The CO2 emission parameters can also be modified, if needed. Finally, the quantities of biomass that will substitute a percentage of pet coke are inserted. As a result, the fuel flexibility tool calculates CO2 quantity, production costs for CCM/DBM, CO2 emissions and energy needed for production, all of which are represented in a graph cost. Table 1 shows the main input parameters of the flexibility tool. The calcination ratio refers to the ratio of the raw ore (MgCO3) calcined/sintered to MgO which differs depending on the purity of the raw material.

Table 1.
Main input parameters of the model.
In Table 2 the simulation test program is presented. Three types of biomass were tested: (1) sunflower husk pellets (SHP), (2) olive kernel (OK), and (3) wood sawdust (WS) at a 0%, 30%, 50% and 70% substitution rate of pet coke energy while three CO2 prices were examined (80, 92.5 and 100 EUR/tn).

Table 2.
Simulation test runs.
The selection of these three types of biomass for the substitution of pet coke was made, on the one hand, for reasons of local availability as the supply of these types of biomass is easier and more economical due to lower transport costs and, on the other hand, for reasons of efficiency since they contain a relatively high calorific value. The following table (Table 3) presents the calorific value of each type of biomass, as well as its availability for use by GM as calculated from an LCA analysis developed within the framework of the BAMBOO project [37].

Table 3.
Calorific value and availability by the types of biomass used.
Table 4 presents the parameter values for the simulation runs. The type of product that was chosen for the simulations was DBM at a yearly product quantity of 43,800 tn. As a rule, to produce 1 ton of magnesia an amount of between 2.1 and 2.4 tons of magnesite is required depending on the magnesite ore, product quality and the type of kiln used. In this study, a value of 2.375 was selected as the calcination ratio. According to GM this value is more realistic since raw ore is not 100% pure. It is also mentioned that 90% of the product accounts for MgO and the other 10% accounts for CaO and other refractories. The energy demand for magnesia production ranges between 6 and 12 GJ/tn MgO and is determined by different factors such as the characteristics and moisture content (wet or dry) of raw magnesite. According to GM, 11.6 GJ/tn MgO is needed for DBM production. Data for current fuel prices were also given by GM. Representative samples of pet coke and biomass fuels (olive kernel, wood sawdust, sunflower husk pellets) were analyzed from CERTHs laboratory in order to identify the lower heating value (LHV) of the above fuels. The price of CO2 ranged from 80 to 100 EUR/tn with 92.5 EUR/tn being the average price on December 2022 [42]. A sensitivity analysis was also performed, regarding the biomass cost fluctuation for the three types of biomass (SHP, OK, WS). More specifically, the case of 45% increase in the current biomass price was examined in order to check the effect on the production cost. At this point, it should be noted that desulfurization cost which is reduced with biomass cofiring is not taken into account. The addition of desulfurization cost will lead to a more favorable production cost in the case of biomass cofiring. It should be emphasized that the results extracted from the flexibility tool for both emissions and cost were evaluated for GM and it turned out that tool estimations were really close to the reality.

Table 4.
Fixed parameter values for the simulation test runs.
3.2. CFD Tool
The methodology to develop the CFD tool comprises three main steps:
- Development a CFD model of the rotary kiln and validation with available data;
- Campaign of simulations with different substitution ratios of biomass and other operating conditions;
- Reduced order model (ROM) of the simulation using the results of the previous step.
3.2.1. CFD Model
The CFD model (geometry and mesh) is developed using ANSYS Fluent. The full set of equations is given in Appendix A. The geometric model of the rotary kiln is depicted in Figure 3 along with details of the mesh set up for calculations in Figure 4. The kiln is 90 m long and has a diameter of 3 m.
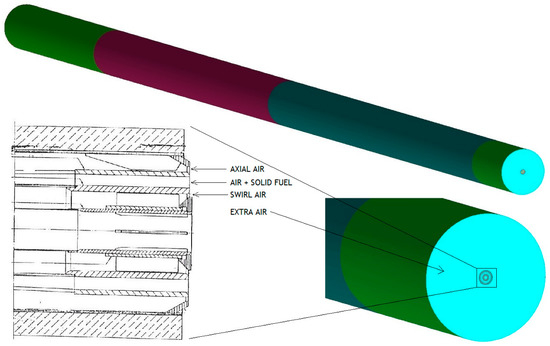
Figure 3.
Geometry of the rotary kiln used for the CFD model. The light blue areas correspond to air inlets, while the grey rings correspond to burner walls.
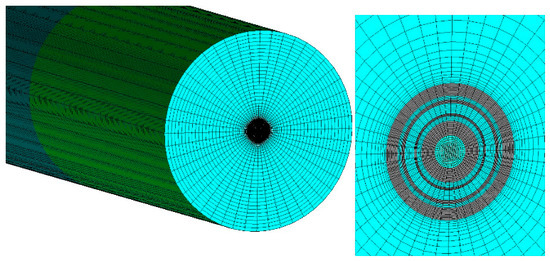
Figure 4.
Details of the mesh in the inlet area.
The burner is not simulated in detail to speed up calculations. This simplification is not expected to have a great impact on the results. We are interested in studying the trends of emissions upon changes in the fuel composition and other operating conditions, and these trends should not be affected by the details of the burner. The three ducts of the burner are included as a boundary condition (inner blue light rings) and act as air inlets. The wide outer ring corresponds to extra air introduced in the kiln. The central duct of the burner is used to burn other liquid fuels and is not used in the present configuration. Solid fuel is introduced through the middle duct. The mesh consists entirely of high-quality hexahedral cells that provide both the accuracy and speed of the calculation. A total of 6.8 million cells were used. A mesh sensitivity analysis (Figure 5) reveals that this is enough to obtain robust results and that further refinements do not lead to much more accurate results. The test uses the temperature of the gas at the exit of the kiln, averaged over the surface. The results show that mesh sizes below six million cells do not converge to the same result. Instead, above that size the results do not vary significantly. We chose the lowest possible size to speed up the calculations.
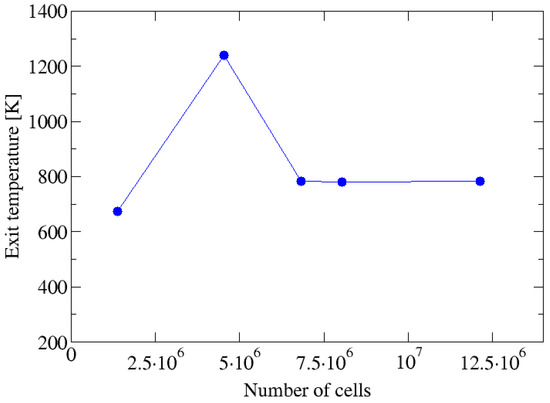
Figure 5.
Exit temperature as a function of the number of cells in the mesh.
To facilitate the understanding of the setup we summarize it in Table 5 and explain it in detail in the following paragraphs. As discussed above, the approach to solve the equations is the standard RANS which separates the average flow from the turbulent scales. The turbulence model chosen is the standard κ-ε [32,34,35,36] with non-equilibrium wall functions. Wall functions allow a faithful representation of the flow close to a wall without the need for a thin mesh, which would slow down calculations.

Table 5.
Summary of models used in the CFD simulations.
Radiation is calculated by the P1 [32,34] model. Radiation intensity is expanded into a series of spherical harmonics and this model takes the first order approximation. The model also includes the effect of particles and the properties of the wall kiln (width and internal emissivity) as well as the external convection. The exterior temperature was measured on site.
Combustion is modelled using species transport and eddy dissipation. The reaction model includes the reactions of coal, volatiles and air, solving a transport equation for each species.
Particles of coke and biomass are injected inside the kiln using the discrete phase model. Fuel particles (coke and biomass) are modelled as coal particles which experience pyrolysis at a constant rate (1/50 s) and the subsequent char combustion is modelled by the diffusion-limited approach. The composition of the generic coal particle is modified to match that of the corresponding fuel particle. The proximate and ultimate analyses of coke and biomass were used to set up the model (see Table 6 and Table 7). The kinetic parameters for the char combustion were taken from the literature [22].

Table 6.
Ultimate analysis of fuels.

Table 7.
Proximate analysis of fuels.
The main simplification applied to the model is that the load inside the kiln is not directly simulated. The reaction of the load is a very complex phenomenon and not fully understood, making its simulation very challenging. In addition, the main concerns of this work are the emissions of NOx and CO2 from combustion, hence the simulations focus on hydrodynamics and combustion reactions. A consequence of this approach is that the CO2 produced by calcination needs to be introduced in the model as a mass source. The mass flow of CO2 is estimated from production data.
Since the load is not directly simulated, it is necessary to consider the heat that it would absorb. This is done by introducing an appropriate heat transfer coefficient that varies along the wall of the kiln, see Figure 6. The same approach is followed in the literature [30,32].
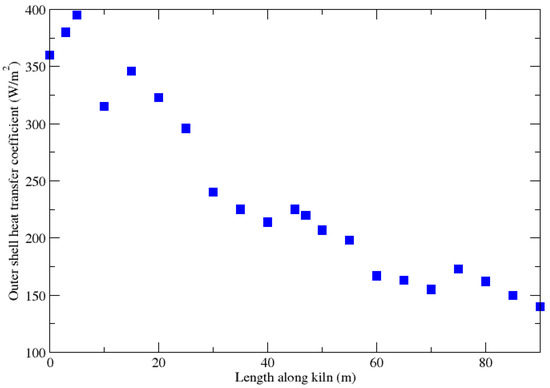
Figure 6.
Length-dependent heat transfer coefficient used as a boundary condition in the CFD model.
The calculation of NOx emissions is carried out as a post-process. This approach is generally used; its validity stems from the fact that the concentrations of NOx are too small to have an influence on hydrodynamics. In the case of solid fuels, most of the NOx comes from the combustion of particles, although thermal NOx also contributes significantly. In this work both sources were considered.
For thermal NOx, the usual Zeldovich [43] mechanism is employed. NOx production is very sensitive to temperature in the range of temperatures reached in the kiln (around 1600 °C). Thus, temperature fluctuations can give rise to large variations in the NOx concentration. To consider flame fluctuations within the steady state solution, a probability density function (PDF model) is used that superimposes fluctuations of temperature drawn from a distribution function, in this case a beta function. This approach gives more realistic values.
For the case of coke, fuel NOx is estimated considering that volatile nitrogen produces HCN while char nitrogen produces NO, both with a conversion factor of 1. This is an approach generally valid for high-range coal and similar fuels (such as coke) [44]. The distribution of nitrogen between volatiles and char is taken as 20% and 80%, respectively [45].
Finally, the porosity of the char is taken as 20,000 kg/m2 as a typical value for coal char.
The simulations are carried out in steady state and are thus representative of the long-term behavior of the kiln.
Table 5 summarizes the models used in the simulations. The numerical values to be used as inputs can be found in Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10 and in Figure 6.

Table 8.
Olive kernel composition and kinetic constants.

Table 9.
Pine saw dust composition and kinetic constants.

Table 10.
Nitrogen content and conversion route for fuel NOx in OK.
Biomasses
In a preliminary assessment, the biomasses selected to substitute part of the coke currently used as fuel are pine saw dust (PSD) and olive kernel (OK). Biomass is composed of three types of fibers: cellulose, hemicellulose and lignin. To characterize the combustion of a given biomass, a thermogravimetric analysis (TGA) is carried out for each fiber. The final values of the activation energy and the pre-exponential factor are given as weighted averages of the values measured for each fiber type [46].
The values to characterize the combustion of the PSD and OK, as given in Table 8 and Table 9, were taken from the literature [47]. The values for pine are in line with more recent results [48] although variability in biomass composition is always to be expected depending on the origin.
Both biomasses have very different composition in fibers and, therefore, differing combustion parameters.
To complete the combustion model, the ultimate and proximate analyses of the biomass must be also supplied as input for CFD calculations. The values in Table 6 and Table 7 were also taken from the relevant literature [47].
Regarding the ultimate analysis, there is some variability in the values consulted in the literature but is usually small. This is to be expected since the composition of a given biomass is dependent on its nature and should not depend greatly on the ambient conditions. The proximate analysis might be more variable, especially regarding the moisture which can be highly dependent on the origin of the biomass or storage conditions. Notwithstanding these caveats, the main aim of the CFD study is to ascertain the trends and variations with respect to the base case (burning only coke) observed under different conditions of co-firing a blend of coke and the selected biomasses. To set up the NOx emissions model for biomass particles, data from the literature were used to gather values of nitrogen content in char and volatiles, as well as the fractions of intermediate compounds. The data are summarized in Table 10 [49] and Table 11 [50,51].

Table 11.
Nitrogen content and conversion route for fuel NOx in PSD.
The fractions of NH3 and HCN represent the amount of these intermediate products, which are in turn oxidated to NO, while the fraction of NO is produced directly by oxidation of nitrogen without any other intermediate products.
Finally, the specific surface area (BET) is set at 53,000 and 1970 for the OK and PSD, respectively. It should be noted that the experimental values reported in the literature are obtained in fixed bed combustion tests.
Different combustion conditions and other factors (such as fuel granularity) may affect the conversion routes and the final NOx production [49].
3.2.2. Model Validation
A first CFD model for burning coke was used as a benchmark to set up physical models and later to check the effect of introducing an additional swirl in the outer duct air. The base case operation mode is summarized in Table 12.

Table 12.
Operation mode of benchmark case.
To validate the model, the only data available are the composition of the flue gas and its temperature. In Table 13, a comparison of measured and simulation data can be seen.

Table 13.
Comparison between measured data and simulation data.
The comparison is fairly good for the temperature and the gas, except NOx which is under predicted. Given the general difficulty in estimating NOx emissions and the possible uncertainties in the inputs of the NOx model, the value obtained is reasonable. The parameters of the NOx model were estimated using data for coal, instead of coke, which could be different. Furthermore, to test the influence of fuel composition in NOx production, the trends provide sufficient information when compared to the base case, so the exact value of emissions is not critical to carry out a comparison.
3.2.3. Campaign Simulations
The cases used to elaborate the reduced order model (ROM) were selected according to the interest of the final user. This interest determines the inputs and outputs of the ROM and the range of variation of the former. The rest of cases are added to try to complete a homogeneous sampling in the range of the inputs.
The goal of the ROM is to predict the temperature and composition of the fumes of the kiln when part of the coke used as fuel is substituted by biomass. The inputs and outputs are summarized in Table 14.

Table 14.
Summary of inputs and outputs considered to produce the ROM for the mineral sector.
The biomass share is in reference to OK. Thus, a value of 100% means that all biomass for a given energy substitution rate is OK, while a value of 0% means that all biomass is PSD. Values in between mean that a blend of both biomasses is used. Inner and outer swirl are the values of the swirl number for the respective air inlets of the burner.
3.2.4. ROM
From the set of results obtained in the previous step, a ROM correlating inputs and outputs is generated using ANSYS DesignXplorer. To realize the correlation, there are several metamodels available, including polynomial regression, kriging, support vector regression and moving least squares. Each of them has different settings and would produce a different response surface. Instead of choosing one model, there exists the possibility to make an optimization using a genetic algorithm. In this case, DesignXplorer generates a population of metamodels with different types and settings. This population corresponds to the first population of the genetic algorithm run by DesignXplorer. The next populations are obtained by the cross-over and mutation of a previous population. The details of the genetic algorithm can be checked in ANSYS documentation and in the relevant literature [52].
A file containing the ROM is exported to a functional mock-up interface (FMU) standard format and can be easily integrated within standard libraries.
In Figure 7, the goodness of fit of the ROM is shown. The horizontal axis shows the design points, i.e., the values used to produce the ROM, while the vertical axis shows the corresponding result. Both axes use normalized values. In this representation, the closer the points are to the diagonal, the better the fitness of the model. In this case, the ROM has four outputs, the temperature of the gas at the exit and its content of oxygen, carbon dioxide and nitrogen oxides. The emissions outputs are almost on top of the diagonal, implying that the response surface predicts values very close to those given by the full simulations. Instead, for oxygen level and temperature at the exit, the points show some dispersion around the diagonal.
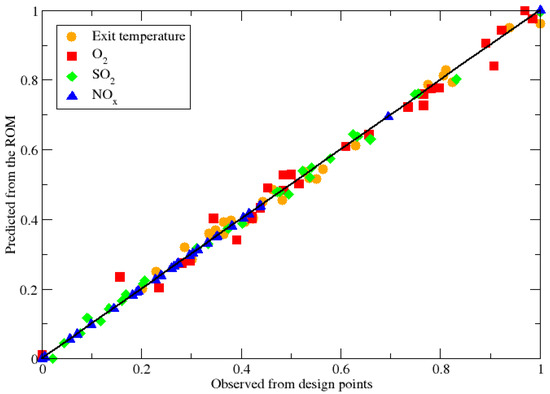
Figure 7.
Goodness of fit for the ROM. The observed (full CFD results) values are compared with those predicted by the ROM.
4. Results and Discussion
4.1. Cost and CO2 Emissions Tool
During the production process in the GM plant, carbon dioxide emissions are due to two processes. The first one is decomposition and the second one is combustion. The decomposition process does not depend on the type of fuel used, but on the raw magnesite ore quantity. The number of emissions due to decomposition equals 47,216.40 tn. Figure 8 depicts the reduction in CO2 emissions deriving from fuel combustion when biomass (SHP, OK or WS) substitutes pet coke energy by 30%, 50% or 70%. It is shown that at a 0% substitution (zero biomass), the fuel (pet coke) combustion emissions (47,103.08 tn) correspond to 50% of the total emissions (94,319.48 tn). At maximum substitution rate (70%), the CO2 emissions from fuel combustion are reduced by the same rate and reach 14,118.74 tn, since biomass is considered carbon neutral, whereas the total CO2 emissions are reduced by 35% (Table 15). It is observed that the emissions produced during the combustion process with the co-firing of pet coke and biomass can reach up to 70% in cases of a 70% substitution. This proves that the targets for reducing emissions by 63% in the industry which have been set by the European Commission could be achievable.
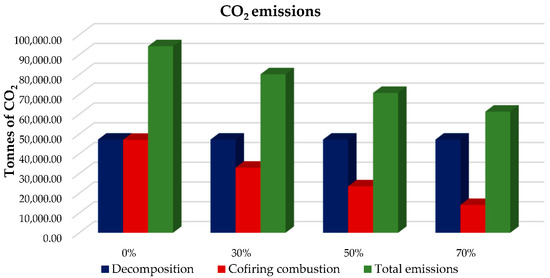
Figure 8.
CO2 emissions (tn) derived from decomposition of MgCO3, production of DBM (0% zero biomass) and different biomass co-firing cases (30%, 50% and 70%).

Table 15.
Calculation of total CO2 emissions.
The calculation of the total CO2 emissions is shown in Table 15 below, where the amount of CO2 emissions is reduced to 61,335.14 tn for the maximum (70%) substitution rate with biomass. CO2 emissions from decomposition are unchanged for each scenario examined.
Figure 9, Figure 10 and Figure 11 represent the production cost of DBM when using three different biomass types at different substitution rates and different CO2 prices.
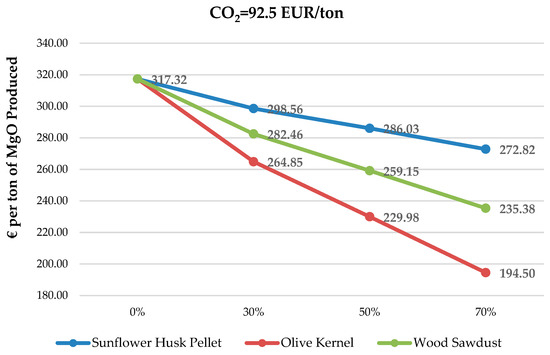
Figure 9.
Cost per ton of MgO produced at 92.5 EUR/tn CO2 for different biomass substitution rates.
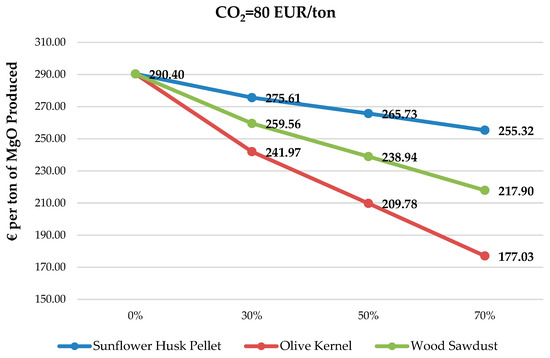
Figure 10.
Cost per ton of MgO produced at 80 EUR/tn CO2 for different biomass substitution rates.
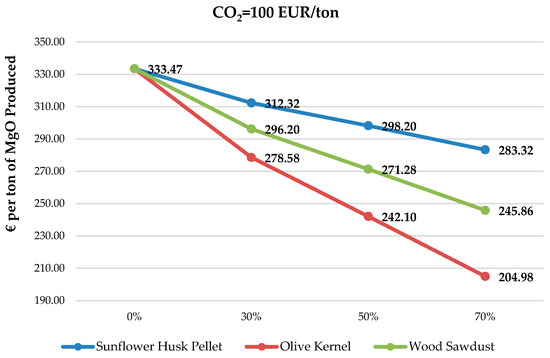
Figure 11.
Cost per ton of MgO produced at 100 EUR/tn CO2 for different biomass substitution rates.
In Figure 9, all biomass types show similar results at all three substitution rates. With the current price at 350 EUR per ton of pet coke and a price of 92.5 EUR per ton of CO2 (prices between 21 and 23 December 2022) the best-case scenario is to substitute 70% of the pet coke energy with any kind of biomass, with olive kernel being the optimum choice since it has the highest LHV (17.64 GJ/tn) and the lowest price (65.25 EUR/tn). The production cost at a 70% substitution is reduced by up to 38.71% with this type of biomass. Wood sawdust also shows a similar downward track but with a lower LHV (9.68 GJ/tn); it is obvious that in order to achieve the needed amount of energy for DBM production, a larger amount of wood sawdust is necessary. Thus, production cost is higher when compared to the olive kernel case. In the case of using sunflower husk pellets as the substitution fuel, production cost is at its lowest value (272.82 EUR/ton produced) at a 70% substitution. Based on current prices, the use of OK can reduce production costs by up to 38.7% which, if it proves feasible in practice, is particularly attractive for any company.
Figure 10 demonstrates similar results when replacing a percentage of pet coke energy with biomass but with a decreased CO2 price at 80 EUR/tn. The price of 80 EUR/tn reflects the average price of CO2 tariffs for the month of November 2022. Olive kernel and wood sawdust demonstrate a decrease in production cost by 39.04% and 24.97%, respectively, at a 70% substitution, whereas the more expensive sunflower husk, which shows the lowest production cost at a 70% substitution (255.32 EUR/ton produced), demonstrates a decreased production cost by 12.08%. Again, with the current price at 350 EUR per ton of pet coke and a price of 80 EUR per ton CO2, the best-case scenario is to substitute 70% of the pet coke energy with any kind of biomass, but with olive kernel being the optimum choice since it has the highest LHV (17.64 GJ/tn) and the lowest price (62.25 EUR/tn). Judging based on the application of the optimal proposed solution (substitution with OK by 70%), it is noticed that the reduction in production costs can be particularly high even at lower values of CO2. In fact, a slightly higher percentage of reduction (39%) is observed here compared to the values presented in Figure 8 (38.7%).
In Figure 11, where CO2 price per ton is increased at 100 EUR/tn, all types of biomasses show a profit from 15.04% when using sunflower husk pellets to 38.53% when using olive kernel at a 70% substitution rate. In the case of wood sawdust, the same trend is observed with around a 26.27% reduction in production cost. This picture can also be characterized as an illustration of future production costs for GM, as according to the European Commission and the targets it has set for the reduction of carbon emissions, the prices of CO2 allowances will continue to rise and will soon exceed 100 EUR/tn.
Figure 12 illustrates a comparison of the production costs for GM between November 2021 and November 2022. More specifically, the rise in production costs during this year is shown, which is due to both the increase in fuel prices and the increase in the prices of CO2 tariffs. Table 16 summarizes the price variation during the year.
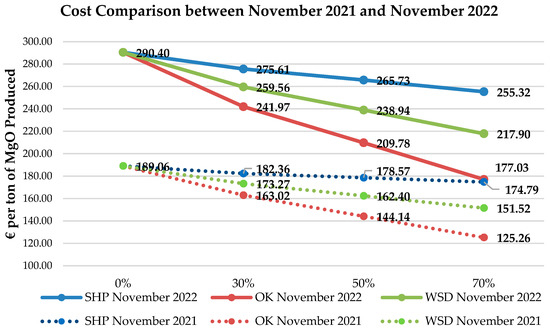
Figure 12.
Cost per ton of MgO produced for November 2021(60.37 EUR/tn CO2) and November 2022 (80 EUR/tn CO2).

Table 16.
Deviation of different fuels and the CO2 tariffs between November 2021 and November 2022.
The leap in GM production costs is clear. Comparing the costs without the use of biomass, an increase of more than 50% is observed. Corresponding increases are also observed under the optimal substitution scenario (70%) by 41%, 46% and 44% for OK, SHP and WSD, respectively. Indicative is the conclusion that no matter how much fuel prices increase, the use of olive kernels and substitution by 70% will always be the most economically optimal solution. In addition, it should be emphasized that for the scenario that has already been effectively implemented in GM (50% substitution with SHP) the increase is estimated at 49%. Examining the comparison, it is found that in just one year the production cost increased by 35%. This is mainly due to the sharp increase in the price of pet coke, but also to the continuous increase in CO2 tariffs. Obviously, biomass supply prices also increased (by about 45% for each type of biomass); however, the increase is clearly smaller, and the estimated costs are significantly lower. This diagram proves that an increase in prices is expected for the coming years, making the use of biomass to replace part of the pet coke more and more imperative.
Evaluating the conditions, the global political and economic situation, as well as the market trend, it is estimated that both fuel prices and CO2 tariffs will continue to increase. Figure 13 shows the cost of production of GM, adopting a worst-case scenario. The following table (Table 17) summarizes the values estimated to be used in the worst-case scenario as well as their increase compared to the existing ones.
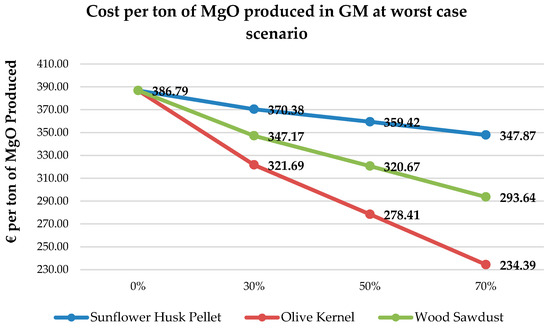
Figure 13.
Cost per ton of MgO produced in GM at worst case scenario (100 EUR/tn CO2).

Table 17.
Comparison of different fuels and the CO2 tariffs between current prices and worst-case scenario prices.
The production cost for the worst-case scenario reaches 386.79 EUR/ton of MgO produced. In this case, the substitution of fossil fuel (pet coke) is considered imperative from an economic point of view. Substituting 70% with olive kernel reduces the production cost by about 40%, estimated it to be about 234.39 EUR/ton produced. Similar, although not as impressive, reductions in costs are also observed from the use of wood sawdust (24%) and sunflower husk pellets (10%). The consecutive increases observed make the worst-case scenario a not-so-improbable case. Taking into account the results, the cost of production can rise to close to 390 EUR/ton produced which can make the production process economically unviable, essentially making the use of biomass a requisite for the sustainability of the system.
4.2. CFD Tool
The CFD tool allows many combinations of fuels, e.g., substituting a given percentage of coke (energy basis) with PSD, or with OK or with a blend of both types of biomasses. Since analyzing all the possibilities is not feasible, we present the results of the replacement using one or the other biomass as way of example.
Figure 14 shows the temperature profiles obtained in the base case (100% coke) in the longitudinal plane of the kiln. The bars shown in the plot are just visual guides to help understand the plots. They represent the distance from the burner. In Figure 14, there is a comparison of the base case with different substitution rates (SR) using PSD or OK. The maximum temperature reached with coke is above 1700 °C which is in agreement with measurements and simulations by other authors [27,28,29,30,31,32,36]. When coke is partially replaced with biomass, there is a decrease in the average temperature that is more pronounced the higher the substitution rate is. This is in agreement with the literature on alternative fuels [33]. The effect is very noticeable for PSD in which the maximum temperature decreases by 500 °C for SR = 30–40% and another 100 °C for SR = 50%. The OK behaves better as the maximum temperature decreases by 200 °C in the three cases studied. Although the substitution is carried out in an energy base, the three fuels have different carbon contents, volatiles contents and different kinetics for devolatilization and subsequent char oxidation. These differences explain the changes in the profiles of temperature and highlight the necessity to perform detailed simulations instead of relying on mass and energy balances.
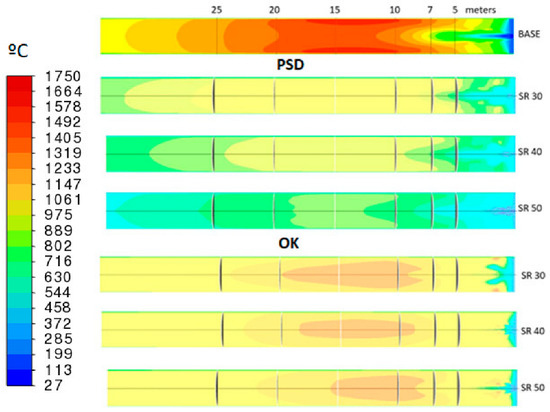
Figure 14.
Temperature profiles obtained for the base case of 100% coke and the cases with different substitution rates of pine saw dust and olive kernel.
Comparing the results in Figure 14 with the proximate analysis of the fuels (Table 7), the temperature inside the kiln is positively correlated with a fixed carbon and heating value, while it seems to be negatively correlated with the percentage of volatile matter.
An interesting observation is that in the base case the highest temperature between 10 m and 20 m is concentrated near the walls. This is common in rotary kilns, as discussed in [34]. These can be related to the fly of fuel particles (see Figure below). Instead, in the case of PSD, it is very homogeneous in the transversal direction and, in the case of OK, the maximum is in the center of the kiln.
One advantage of the lower temperatures achieved with biomass is that NOx production should be lower. In Figures below one can see reductions of up to 50% in NOx emissions using biomass. This is because thermal NOx is very sensitive at peak temperatures and increases exponentially for temperatures above 1600 °C. Of course, this is an advantage given that the minimum temperature for magnesite calcination (CCM) is reached. For example, to achieve a reduction of 50% in NOx, a decrease of 400 °C is required (see Figure below). The behavior of the particles close to the burner can be related to the velocity profiles (Figure 15)
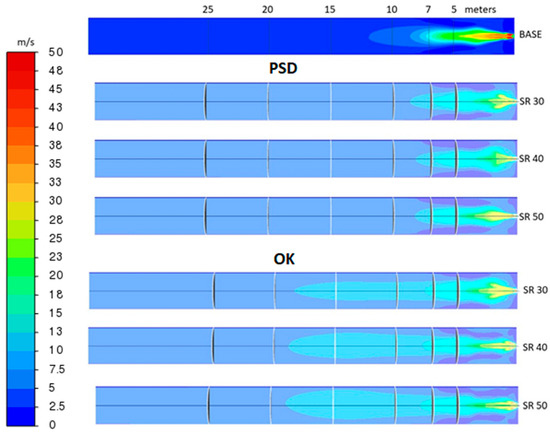
Figure 15.
Velocity profiles obtained for the base case of 100% coke and the cases with different substitution rates of pine saw dust and olive kernel.
The values of velocity (Figure 14) are similar to those reported in the literature [30] of pulverized coal. They show that the velocities of gases are lower when using biomass. The maximum velocity drops by 30%, approximately. This is because the higher size of the biomass particles, which are more difficult to grind, put an obstacle to gas propagation. On the other hand, the shape of the profile is very similar in all cases. This means that the hydrodynamics of the gases is not affected greatly by the presence of the fuel particles, despite the fact that the fuel dramatically changes the thermal picture.
The oxygen profiles for coal in Figure 16 are very similar to other CFD studies [30] which provides further validation for our work. The initial consumption of oxygen is faster in the two cases of biomass than when using only coke. Comparing the base case with PSD, the pattern is very similar between 10 m and 25 m in which a gradient of concentration is clearly visible. This is in contrast with the case of OK where the concentration is homogeneous from 7m onwards. This is in line with the homogeneity of the temperature profiles discussed above being more homogeneous for the OK. Note that the correlation between oxygen concentration and temperature is also tight in the case of PSD, since both quantities decrease fast upon increasing the substitution rate.
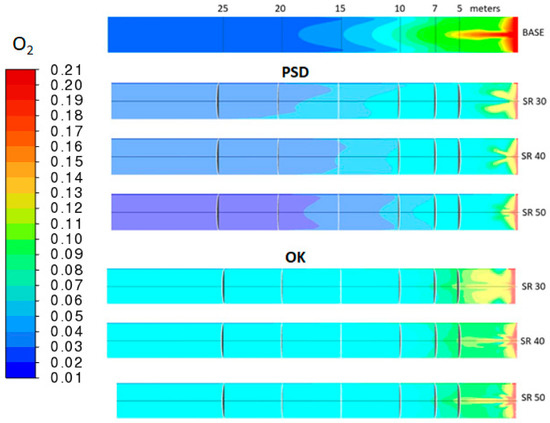
Figure 16.
Oxygen mole fraction profiles obtained for the base case of 100% coke and the cases with different substitution rates of pine saw dust and olive kernel.
The reason for the faster conversion in the two cases of biomass is most likely related to volatile matter. Devolatilization is the first process in fuel combustion, and the carbon content of the volatiles will react with the oxygen. Indeed, there is a negative correlation between the percentage of volatiles in the three fuels and the extension of the red area in Figure 14. That is to say, the more volatiles, the faster the initial oxygen depletion.
The volume where the heat of reaction is concentrated (see Figure 17) is correlated with the region where the most oxygen consumption takes place. It is also consistent with the higher reactivity of biomass due to the large number of volatiles, while its calorific value is much lower than that of coke. The higher the amount of biomass, the higher the volume where the heat of reaction reaches significant values.

Figure 17.
Heat of reaction profiles obtained for the base case of 100% coke and the cases with different substitution rates of pine saw dust and olive kernel.
The heat of reaction of the OK reaches up to 500 W while that of pine is at most 70% of that value.
The precedent results show mostly the behavior of the gas phase. It is also possible to visualize the trajectories of the fuel particles to parse their behavior. In Figure 17, the trajectories of fuel particles are shown colored according to temperature. Note that only a sample of the particles are represented, otherwise the plot would appear overcrowded and featureless. A common feature of all the results is that the trajectories are very chaotic in the first 5 m from the burner. A close inspection shows that the particles recirculate in that zone several times before starting to travel along the kiln, and finally dragged by the air. From that point onwards the particles follow more ordered trajectories. It is also noticeable that around the 5 m mark, there is a widening of the trajectories of particles that were previously close to the axis of the kiln. In some cases, the trajectories appear braided, while in others they look more or less parallel.
The behavior of the particles close to the burner can be related to the velocity profiles (see above). In all cases, a fraction of the air is ejected directly towards the wall of the kiln. The effect is more apparent in the cases with biomass but is present for coke also. Thus, a fraction of the particles travels directly towards the wall and experience rebounds which gives rise to the trajectories in Figure 18.
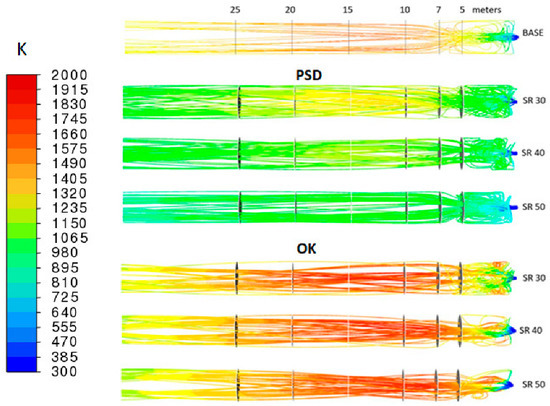
Figure 18.
Fuel particle trajectories colored according to temperature obtained for the base case of 100% coke and the cases with different substitution rates of pine saw dust and olive kernel.
Finally, there is a close correlation between the gas phase temperature (Figure 14) and the temperatures reported in Figure 19. In addition, in the latter is clear that the OK gives rise to more homogeneous temperatures than the PSD, and the average temperature is less affected by the substitution rate.
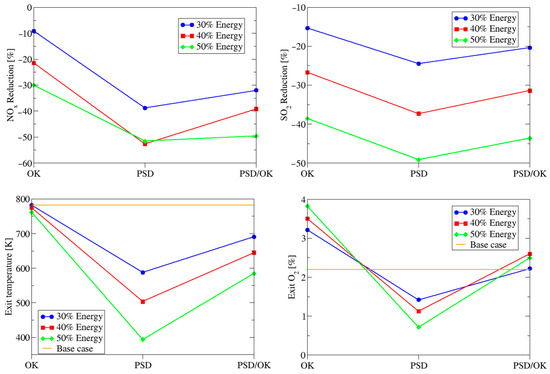
Figure 19.
Upper panel: NOx and SO2 emissions reduction at the exit of the fumes. Lower panel: temperature and oxygen level at the exit of the fumes.
The above results illustrate the use of the CFD simulation to investigate the conditions inside the kiln. Turning to the topic of emissions, the composition of the fumes can be calculated at the exit to obtain an estimation of the compounds of interest. Figure 19 shows the result of a parametric study with different substitution rates and three blends of biomass: 100% PSD, 100% OK and a blend at 50% of each type (PSD/OK). The reduction in emissions for NOx and SO2 along with data for exit temperature and oxygen level at the exit of the fumes are reported.
A reduction of up to 50% can be obtained by sacrificing 400 °C degrees of temperature using pine, which is probably too much to keep the process inside the kiln. Great reductions of NOx have been reported for similar kilns when using a biomass [23,53]. Using olive kernel, it is possible to achieve substantial reductions in NOx emissions without affecting the temperatures greatly. In fact, the drop of temperature between the base case and case SR 50 for OK is 20 K. Using a blend of both biomasses produces an intermediate result in which substantial reductions of NOx come at the cost of upsetting the temperature of the process in a substantial way.
Since the set of simulations reported have the same air conditions, the behavior of the oxygen level measured at the exit changes. It goes in different directions for pine and the olive kernel, decreasing with respect to the base case for the former and increasing for the latter. If it is desired to keep the 2% level, it is possible that this is easily achieved by slightly modifying the amount of air supplied to the burner.
The authors of [54] study the reduction in NO emissions achievable by controlling the operational parameters only. Using an analysis that considers energy balance and kinetic calculations results to a decrease of 15% in NOx. This is slightly above the minimum saving reported in Figure 19, so the use of biomass seems a very promising route to obtaining important savings in controlled emissions.
Regarding the accuracy of the results, the NOx emissions are highly dependent on the properties of the biomass nitrogen content and its distribution among volatiles and char. Since in practice is not possible to know these values, the results shown should be taken as an indication of the trends expected. On the other hand, the results concerning temperature, the main control variable, are robust. This is because they depend on the average values of carbon content in the fuel, instead of its distribution, and on the mixing inside the kiln, which is well accounted for by the hydrodynamic calculation. Indeed, comparing different simulations in the literature, the values of temperature are very similar, the differences being due to changes in the process or operating conditions.
Comparative and parametric studies of this kind can be easily and rapidly made with the ROM. Thus, it is possible to determine the most appropriate scenarios from the point of view of emissions and the process conditions.
Both tools simulate the production process and contribute to the understanding of its operational parameters. However, the flexibility tool can also contribute to the decision-making process by providing a solution to issues related to the operation, cost and environmental footprint of the unit. The application of this tool can identify with relative precision and give an initial approximation about the changes that could result from the variation or change of an operational parameter (e.g., fuel change) in costs and emissions (reduction or increase). Therefore, a company using the flexibility tool can test various scenarios at a simulation level, and based on the results decide which of them will be the most beneficial from an economic and environmental point of view so that this can be implemented in a real production process of the demo site.
5. Conclusions
In this paper, a simplified model adapted for the needs of GM was presented in order to assist the magnesia company in deciding upon the optimum blend of fossil and biomass fuel. The tool calculates the total production cost and CO2 emissions when substituting different percentages of the pet coke energy with a biomass. In the simulation test runs, the highest substitution rate was 70%, and since biomass is considered carbon neutral, CO2 emissions from fuel combustion were reduced by the same amount. At the maximum substitution rate (70%), the total CO2 emissions were reduced by 35%. Regarding the production cost, it is exhibited that biomass substitution is profitable for GM even at a 70% substitution. Both the reduction in the production cost and the reduction in CO2 emissions depend on the percentage that will be substituted by biomass and also on the type of biomass that will be used. As CO2 price increases, the use of biomass seems to be an attractive alternative for this type of company in order to remain sustainable.
In general, mineral industries, such as cement, and other energy intensive industries, such as steel and chemical, that operate in a similar way to the magnesia sector can benefit from this flexibility tool after some suitable minor adjustments such as replacing the types of fuel, the current prices, etc. This decision-making tool could encourage them to put biomass in their production process as soon as possible in order to remain sustainable and competitive against future increased CO2 prices. There are three main limitations to the effective use of the tool. The first is that it requires the very detailed and accurate input of all data and parameters into the system. The second concerns the differences/modifications that must be made so that the tool can be adopted by other production units and be effective. Finally, it should be emphasized that the flexibility tool provides an initial approximation of the results and cannot predict malfunctions in the production process.
In parallel, the CFD tool methodology presented in this work can be adapted to other rotary kilns or furnaces of a different topology for other industries. It is worth noticing that use of biomass leads to lower temperatures, lower velocities in the kiln and a lower NOx production. When using olive kernel as the biomass, it is possible to achieve substantial reductions in NOx emissions without greatly affecting the temperatures. Once obtained, the reduced order model (ROM) is easily integrated into libraries or commercial software, such as MATLAB. This ROM is not closed, it can be updated, e.g., for new biomasses just by adding the results of new simulations in the last step of the methodology presented. Its precision can be increased by adding more simulation results or even experimental measurements, a subject of further research in the future. It can be used to design the fuel blends depending upon biomass availability, the necessity to keep emissions below certain levels or the appropriate operating conditions. Likewise, new operating conditions or changes in the inputs/outputs can be readily realized, the latter without running new simulations. Thus, one can add the CO2 to the list of outputs and use the CFD tool in combination with the tool presented to calculate the cost of emissions.
Author Contributions
Conceptualization, N.M. and C.E.; methodology, C.E., H.Y. and R.A.; validation, H.Y., P.P., P.G. and R.A.; formal analysis, N.M., H.Y. and P.G.; investigation, N.M., H.Y., P.P. and R.A.; resources, P.P. and H.Y.; writing—original draft preparation, C.E., N.M. and R.A.; writing—review and editing, N.M. and R.A.; visualization, C.E. and R.A.; supervision, N.M. and P.G.; project administration, P.G.; funding acquisition, P.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by a project entitled “Boosting new Approaches for flexibility Management By Optimizing process Off-gas and waste use” (BAMBOO). This project has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No. 820771.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available on request.
Acknowledgments
The authors acknowledge Yerakini Mines and Works, Grecian Magnesite S.A. (GM) for providing the samples and giving us permission to publish this article. In addition, authors acknowledge the BAMBOO research program which, with its funding, allowed the implementation of the experimental process.
Conflicts of Interest
The authors declare that there are no conflict of interest regarding the publication of this paper.
Appendix A
The equations solved by ANSYS Fluent are the following:
Continuity equation
Momentum equation
Energy equation
Species transport equation
Turbulence closure for the k-ϵ model
Particle force balance
Particle energy equation
Radiative transfer equation
P-1 model for radiation:
Devolatilization of fuel particles
Char oxidation
Non-premixed gas combustion model
References
- Available online: https://ourworldindata.org/energy-overview (accessed on 15 May 2023).
- Available online: https://single-market-economy.ec.europa.eu/industry/strategy/energy-intensive-industries_en (accessed on 15 May 2023).
- IEA. Final Consumption—Key World Energy Statistics 2021—Analysis; IEA: Paris, France, 2021.
- IEA—International Energy Agency. Key World Energy Statistics; IEA: Paris, France, 2021.
- Sen, S.; Vollebergh, H. The effectiveness of taxing the carbon content of energy consumption. J. Environ. Econ. Manag. 2018, 92, 74–99. [Google Scholar] [CrossRef]
- Rogelj, J.; Den Elzen, M.; Höhne, N.; Fransen, T.; Fekete, H.; Winkler, H.; Schaeffer, R.; Sha, F.; Riahi, K.; Meinshausen, M. Paris Agreement climate proposals need a boost to keep warming well below 2 °C. Nature 2016, 534, 631–639. [Google Scholar] [CrossRef] [PubMed]
- Kaufman, N.; Barron, A.R.; Krawczyk, W. A near-term to net zero alternative to the social cost of carbon for setting carbon prices. Nat. Clim. Chang. 2020, 10, 1010–1014. [Google Scholar] [CrossRef]
- European Parliament Newsletter. The EU Emissions Trading Scheme (ETS) and Its Reform in Brief. 2023. Available online: https://www.europarl.europa.eu/news/en/headlines/society/20170213STO62208/the-eu-emissions-trading-scheme-ets-and-its-reform-in-brief (accessed on 15 May 2023).
- European Parliament Newsletter. Reducing Carbon Emissions: EU Targets and Policies. 2023. Available online: https://www.europarl.europa.eu/news/en/headlines/society/20180305STO99003/reducing-carbon-emissions-eu-targets-and-policies (accessed on 15 May 2023).
- Mann, M.; Spath, P. The Net CO2 Emissions and Energy Balances of Biomass and Coal-Fired Power Systems. In Proceedings of the 4th Biomass Conference, Oakland, CA, USA, 29 August–2 September 1999; pp. 2–7. [Google Scholar]
- Lopez, R.; Menendez, M.; Fernandez, C.; Bernando-Sanchez, A. The effects if scale-up and coal-biomass blending on supercritical coal oxy-combustion power plants. Energy 2018, 148, 571. [Google Scholar] [CrossRef]
- Wahlund, B.; Yan, J.; Westermark, M. Increasing biomass utilization in energy systems: A comparative study of CO2 reduction and cost for different bioenergy processing options. Biomass Bioenergy 2004, 26, 531–544. [Google Scholar] [CrossRef]
- Konig, A. Cost effective utilization of biomass in the German energy system in the context of energy and environmental policies. Energy Policy 2011, 39, 628–636. [Google Scholar] [CrossRef]
- Gustavsson, L. Energy efficiency and competitiveness of biomass—Based energy systems. Energy 1997, 22, 959–967. [Google Scholar] [CrossRef]
- Johnson, E. Goodbye to carbon neutral: Getting biomass footprints right. Environ. Impact. Assess. Rev. 2009, 29, 165–168. [Google Scholar] [CrossRef]
- Raymer, A.K.P. A comparison of avoided greenhouse gas emissions when using different kinds of wood energy. Biomass Bioenergy 2006, 30, 605–617. [Google Scholar] [CrossRef]
- The European Cement Association (CEMBUREAU). Towards Zero Carbon Fuels for Cement Manufacture; The European Cement Association: Brussels, Belgium, 2018. [Google Scholar]
- Available online: https://ghgprotocol.org/calculation-tools (accessed on 15 May 2023).
- Available online: https://tools.genless.govt.nz/businesses/wood-energy-calculators/co2-emission-calculator/ (accessed on 15 May 2023).
- Akkoyun, O.; Careddu, N. Mine Simulation for Educational Purposes: A Case Study. Comput. Appl. Eng. Educ. 2015, 23, 286–293. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, W. Numerical Simulation of Multi-Physics Fields in Fused Magnesia Furnace. Metals 2023, 13, 39. [Google Scholar] [CrossRef]
- An, P.; Han, Z.; Wang, K.; Cheng, J.; Zhao, Z.; Situmorang, Y.A.; Rizkiana, J.; Abudula, A.; Guan, G. Energy-saving strategy for a transport bed flash calcination process applied to magnesite. Carbon Resour. Convers. 2021, 4, 122–131. [Google Scholar] [CrossRef]
- Arévalo, R.; Rezeau, A.; Herce, C. CFD Analysis of Co-firing of Coke and Biomass in a Parallel Flow Regenerative Lime Kiln. Waste Biomass Valorization 2022, 13, 4925–4949. [Google Scholar] [CrossRef]
- Arroyo, J.; Pérez, L.; Cuervo-Piñera, V. CFD modelling and validation of Blast Furnace Gas/Natural Gas mixtures combustion in an experimental industrial furnace. Processes 2023, 11, 332. [Google Scholar] [CrossRef]
- Upadhyay, M.; Kim, A.; Paramanantham, S.S.; Kim, H.; Lim, D.; Lee, S.; Moon, S.; Lim, H. Three-dimensional CFD simulation of proton exchange membrane water electrolyser: Performance assessment under different condition. Appl. Energy 2022, 306, 118016. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Perić, M. Computational Methods for Fluid Dynamics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Alyaser, A.H. Fluid Flow and Combustion in Rotary Kiln. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 1998. [Google Scholar]
- Georgallis, M.; Nowak, P.; Salcudean, M.; Gartshore, I.S. Modelling the Rotary Lime Kiln. Can. J. Chem. Eng. 2005, 83, 212–223. [Google Scholar] [CrossRef]
- Mujumdar, K.S.; Ranade, V.V. Simulation of Rotary Cement Kilns Using a One-Dimensional Model. Chem. Eng. Res. Des. 2006, 84, 165–177. [Google Scholar] [CrossRef]
- Wang, S.; Lu, J.; Li, W.; Li, J.; Hu, Z. Modeling of Pulverized Coal Combustion in Cement Rotary Kiln. Energy Fuels 2006, 20, 2350–2356. [Google Scholar] [CrossRef]
- Mujumdar, K.S.; Ranade, V.V. CFD modeling of rotary cement kilns. Asia-Pac. J. Chem. Eng 2008, 3, 106–118. [Google Scholar] [CrossRef]
- Bhad, T.; Sarkar, S.; Kaushik, A. CFD Modeling of a cement kiln with multi channel burner for optimization of flame profile. In Proceedings of the 7th International Conference on CFD in the Mineral and Process Indistries, Melbourne, Australia, 9–11 December 2009. [Google Scholar]
- Ariyaratne, W.K.H.; Malagalage, A.; Melaaen, M.C.; Tokheim, L.A. CFD Modelling of Meat and Bone Meal Combustion in a Cement Rotary Kiln—Investigation of Fuel Particle Size and Fuel Feeding Position Impacts. Chem. Eng. Sci. 2015, 123, 596–608. [Google Scholar] [CrossRef]
- Elattar, H.F.; Specht, E.; Fouda, A.; Bin-Mahfouz, A.S. Study of Parameters Influencing Fluid Flow and Wall Hot Spots in Rotary Kilns using CFD. Can. J. Chem. Eng. 2016, 94, 355–367. [Google Scholar] [CrossRef]
- Agrawal, A.; Ghoshdastidar, P.S. Computer Simulation of Heat Transfer in a Rotary Lime Kiln. J. Therm. Sci. Eng. Appl. 2018, 10, 031008. [Google Scholar] [CrossRef]
- Ryan, J.; Bussmann, M.; DeMartini, N. CFD Modelling of Calcination in a Rotary Lime Kiln. Processes 2022, 10, 1516. [Google Scholar] [CrossRef]
- Available online: http://bambooproject.eu/ (accessed on 17 May 2023).
- Magnesium Investing News. 10 Top Countries for Magnesite Mining (Update 2023). 2023. Available online: https://investingnews.com/daily/resource-investing/critical-metals-investing/magnesium-investing/top-magnesite-producing-countries/ (accessed on 17 May 2023).
- An, J.; Xue, X. Life-cycle carbon footprint analysis of magnesia products. Resour. Conserv. Recycl. 2017, 119, 4–11. [Google Scholar] [CrossRef]
- An, J.; Li, Y.; Middleton, R.S. Reducing energy consumption and carbon emissions of magnesia refractory products: A life-cycle perspective. J. Clean. Prod. 2018, 182, 363–371. [Google Scholar] [CrossRef]
- TOOL03. Methodological Tool: Tool to Calculate Project or Leakage CO2 Emissions from Fossil Fuel Combustion, Version 03.0. Clean Development Mechanism, United Nations (Framework Convention on Climate Change). Available online: https://cdm.unfccc.int/methodologies/PAmethodologies/tools/am-tool-03-v3.pdf (accessed on 23 May 2023).
- Available online: https://tradingeconomics.com/commodity/carbon (accessed on 23 May 2023).
- Williams, F.A. Combustion Theory, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1985. [Google Scholar]
- Perrone, D.; Castiglione, T.; Morrone, T.P.; Barbarelli, S.; Amelio, M. NOx emissions for oxy-mild combustion of pulverized coal in high temperature pre-heated oxygen. Energy Procedia 2018, 148, 567–574. [Google Scholar] [CrossRef]
- Yuan, S.; Zhou, Z.; Li, J.; Wang, F. Nitrogen conversion during rapid pyrolysis of coal and petroleum coke in a high-frequency furnace. Appl. Energy 2012, 92, 854–859. [Google Scholar] [CrossRef]
- Caprariis, B.D.; Santarelli, M.L.; Scarsella, M.; Herce, C.; Verdone, N.; De Filipis, P. Kinetic analysis of biomass pyrolysis using a double distributed activation energy model. J. Therm. Anal. Calorim. 2015, 121, 1403–1410. [Google Scholar] [CrossRef]
- Saldarriaga, J.F.; Aguado, R.; Pablos, A.; Amutio, M.; Olazar, M.; Bilbao, J. Fast characterization of biomass fuels by thermogravimetric analysis (TGA). Fuel 2015, 140, 744–751. [Google Scholar] [CrossRef]
- George, O.S.; Dennison, M.S.; Yusuf, A.A. Characterization and energy recovery from biomass wastes. Sustain. Energy Technol. Assess. 2023, 58, 103346. [Google Scholar]
- Anca-Couce, A.; Sommersacher, P.; Evic, N.; Mehrabian, R.; Scharler, R. Experiments and modelling of NOx precursors release (NH3 and HCN) infixed-bed biomass combustion conditions. Fuel 2018, 222, 529–537. [Google Scholar] [CrossRef]
- Stubenberger, G.; Scharler, R.; Obernberger, I. Nitrogen release behaviour of different biomass fuels under lab-scale and pilot-scale conditions. In Proceedings of the 15th European Biomass Conference & Exhibition, Berlin, Germany, 7–11 May 2007. [Google Scholar]
- Widmann, E.; Scharler, R.; Stubenberger, G.; Obernberger, I. Release of NOx precursors from biomass fuel beds and application for CFD-based NOx postprocessing with detailed chemistry. In Proceedings of the 2nd World Conference and Exhibition on Biomass for Energy, Industry and Climate Protection, Rome, Italy, 10–14 May 2004. [Google Scholar]
- Ben Salem, M.; Roustant, O.; Gamboa, F.; Tomaso, L. Universal prediction distribution for surrogate models. SIAM/ASA J. Uncertain. Quantif. 2017, 5, 1086–1109. [Google Scholar] [CrossRef]
- Edland, R.; Smith, N.; Allgurén, T.; Fredriksson, C.; Normann, F.; Haycock, D.; Johnson, C.; Frandsen, J.; Fletcher, T.H.; Andersson, K. Evaluation of NOx-Reduction Measures for Iron-Ore Rotary Kilns. Energy Fuels 2020, 34, 4934–4948. [Google Scholar] [CrossRef]
- Akgun, F. Investigation of energy saving and NOx reduction possibilities in a rotary cement kiln. Int. J. Energy Res. 2003, 27, 455–465. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).