Increased Riparian Vegetation Density and Its Effect on Flow Conditions
Abstract
:1. Introduction
2. Materials and Methods
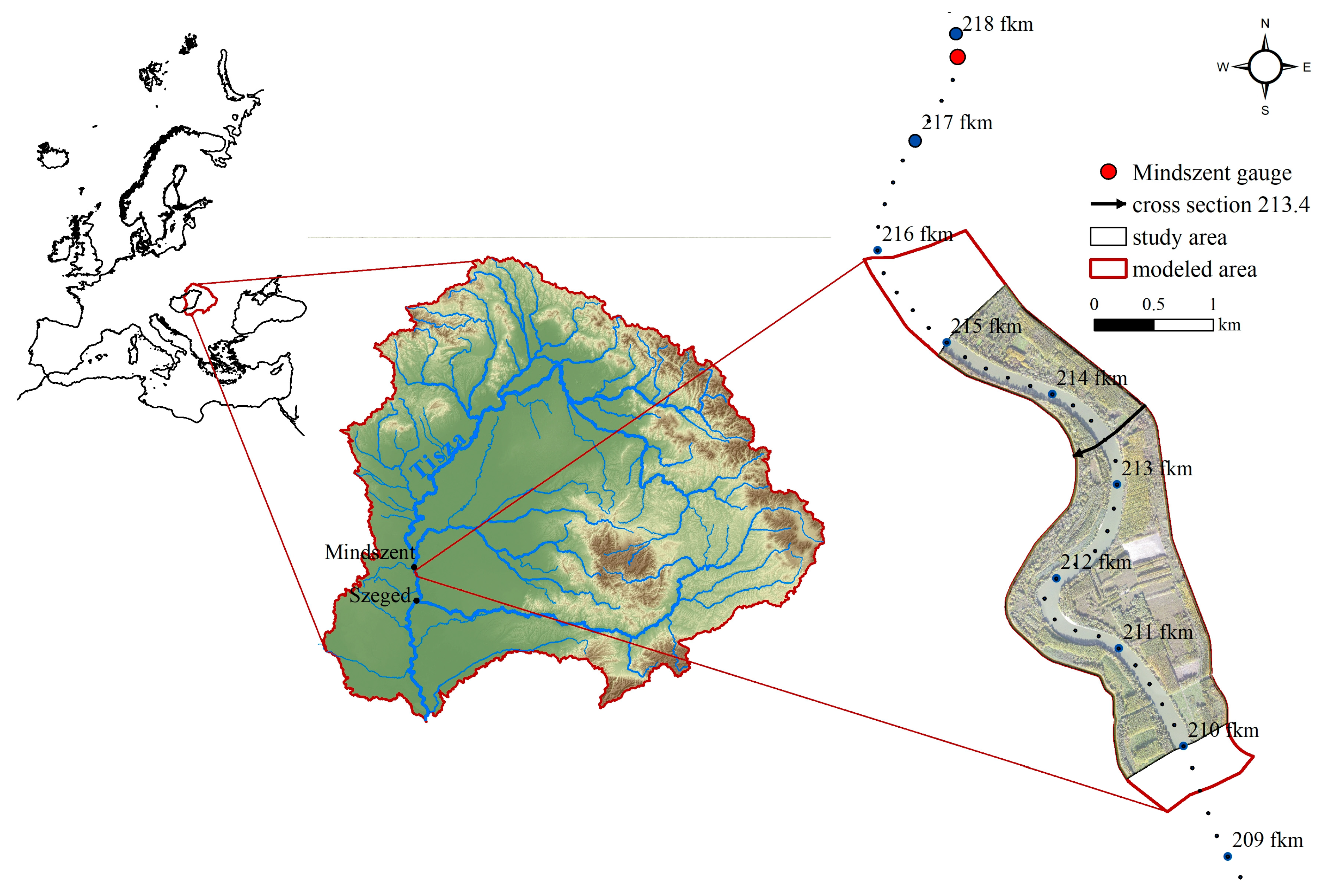
2.1. Study Area
2.2. Methods
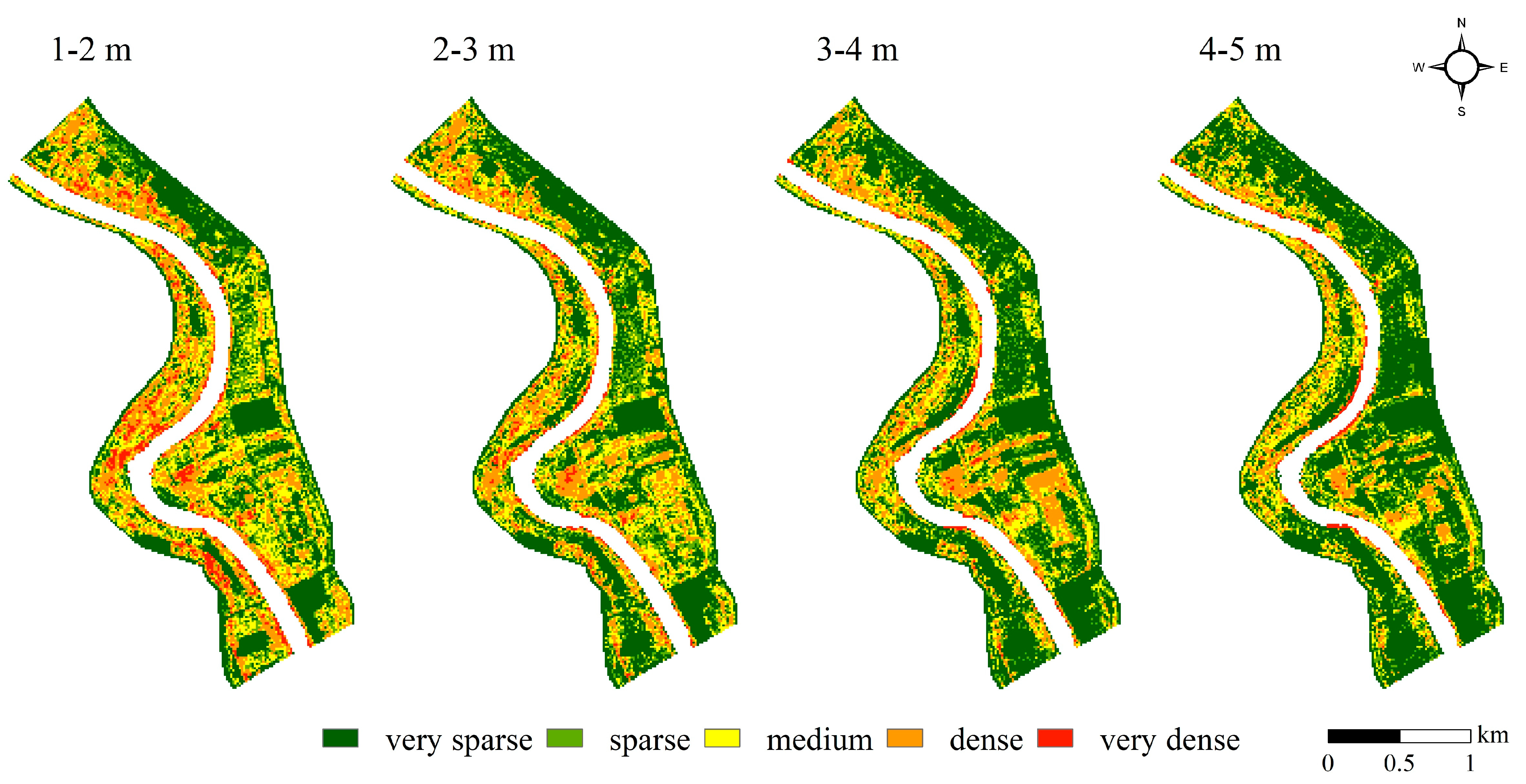
2.2.1. Vegetation Density of the Submerged Vegetation Based on the LiDAR Survey
2.2.2. Hydrodynamic Modelling in HEC–RAS 2D
Geometric Data of the Model
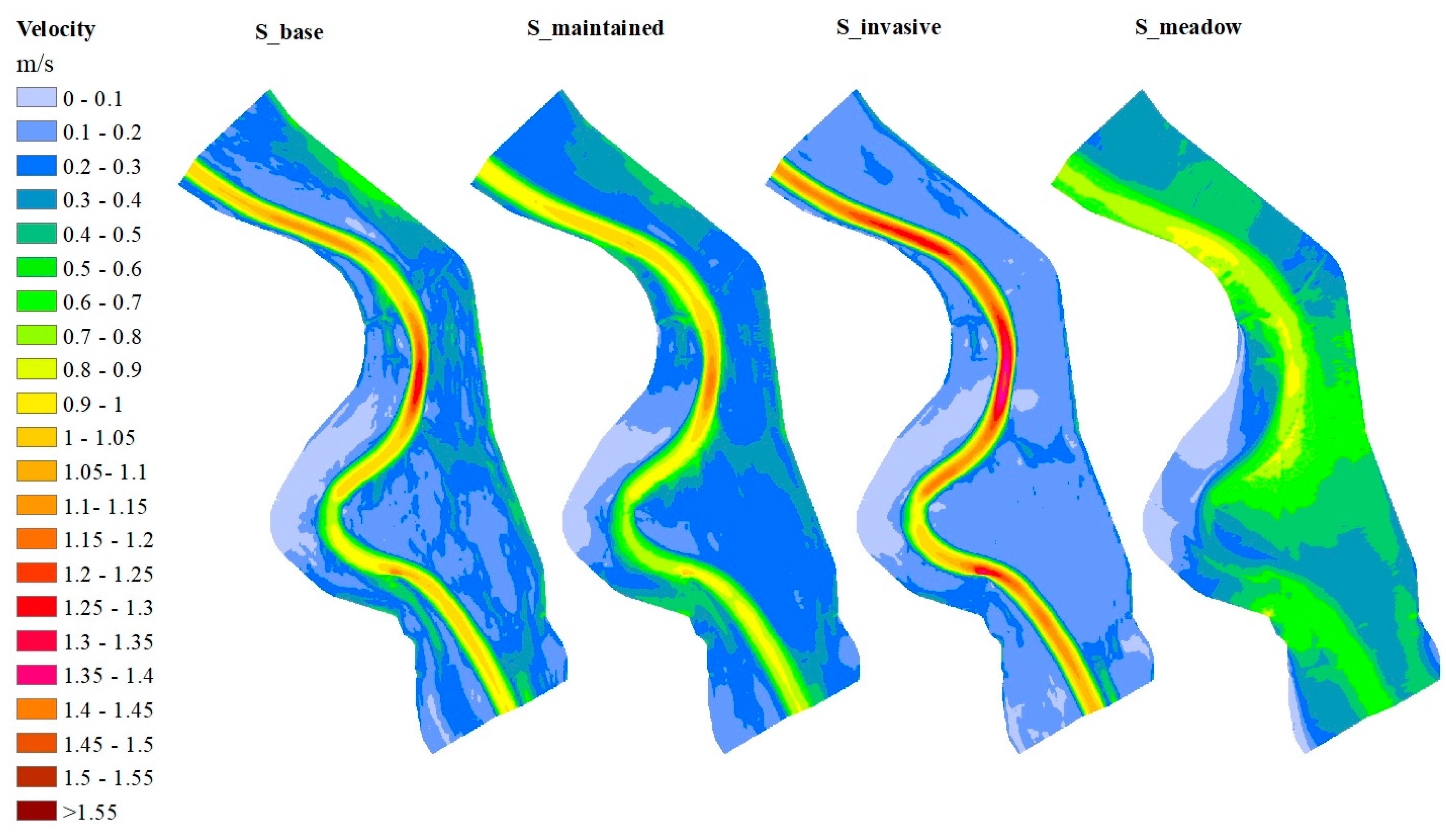
Model Scenarios
- The base scenario (S_base) corresponds to the actual state of the floodplain vegetation. It includes the spatially assigned roughness values based on the vegetation density classes calculated from the LiDAR data.
- The next scenario (S_maintained) represents a state when the actually dense (n = 0.16) and very dense (n = 0.2) understory vegetation patches dominated by invasive species are maintained by invasive plant control. Thus, the vegetation roughness in these patches is reduced to n = 0.08. This scenario represents the most reasonable compromise for the future, as it assumes that the very high areal proportion (ca. 80%) of invasive species is artificially reduced in the floodplain forests.
- In the least advantageous scenario (S_invasive), the vegetation conditions would deteriorate further, due to the further expansion of invasive species, abandonment of plough lands, and without proper management of planted forests. Thus, patches with very dense undergrowth (n = 0.2) would replace patches with dense (n = 0.16), medium (n = 0.08) and sparse (n = 0.04) undergrowth.
- The scenario with the lowest roughness (S_meadow) assumes that meadows with low grass cover the floodplain. Thus, over the entire floodplain, the roughness is 0.06. This scenario represents a significantly different state from the actual one; however, it represents 19th Century (pre-regulation) conditions, when marshes and grassy wetlands covered the study area according to the First Military Map (1763–1787).
Hydrological Boundary Conditions of the Model
Calibration of the Model
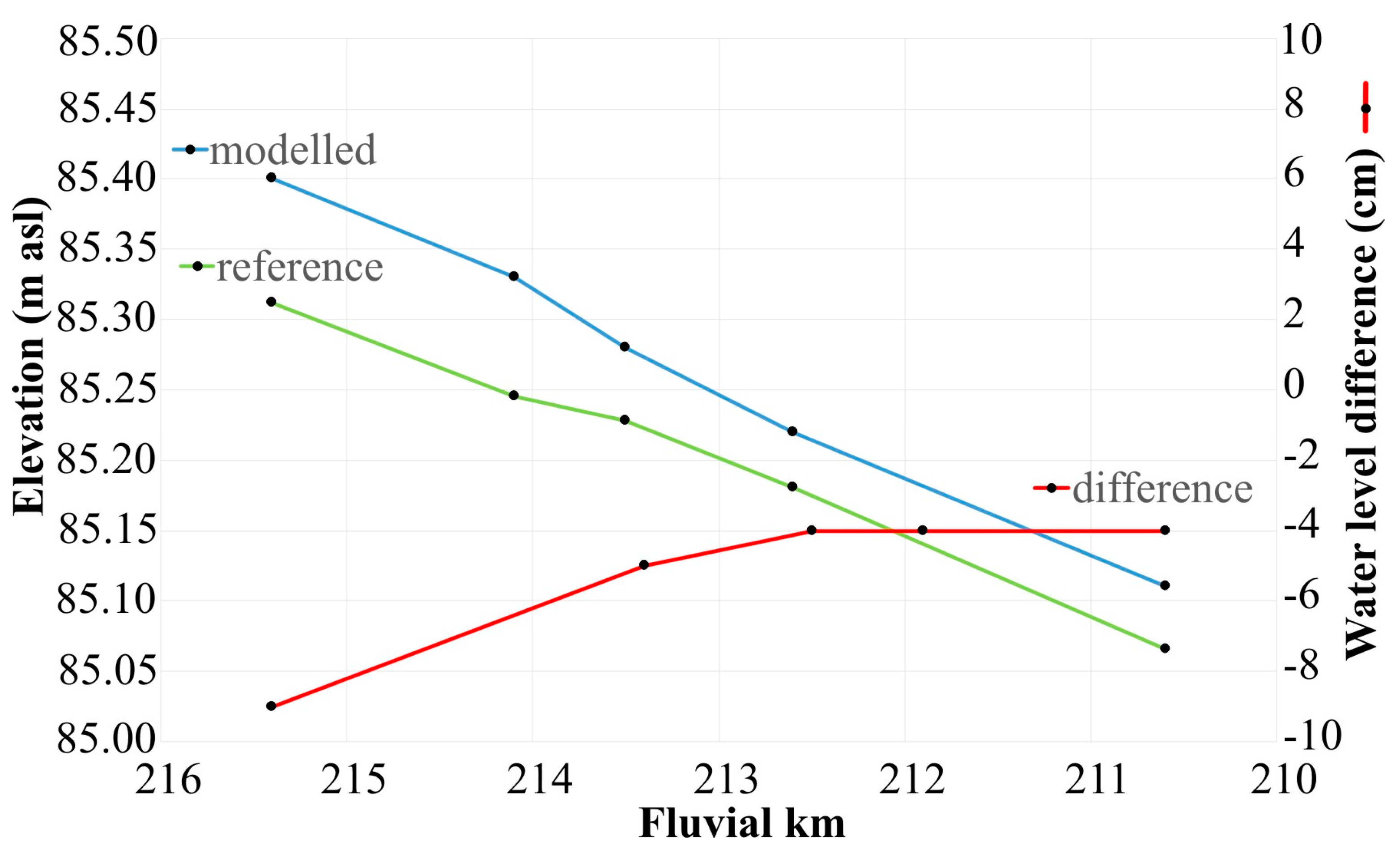
Validation of the Model for Water Level
Validation of the Model for Flow Velocity
3. Results
3.1. Vegetation Density of the Submerged Vegetation Zones
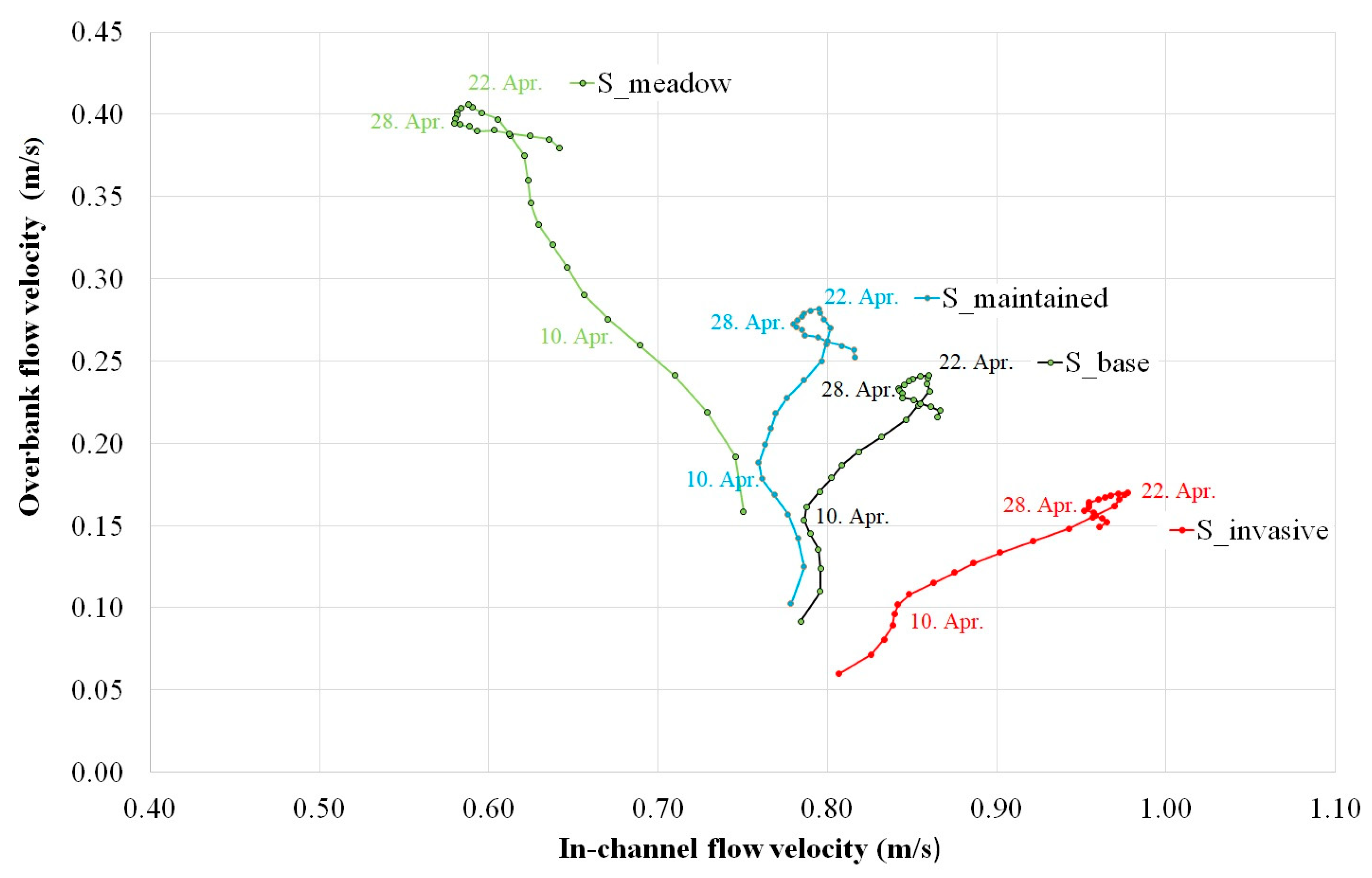
3.2. Spatial Distribution of Flow Velocity Fields in Different Scenarios
3.3. Temporal Changes in Overbank Flow Velocities in Different Scenarios
3.4. Temporal Changes in In-Channel Flow Velocities in Different Scenarios
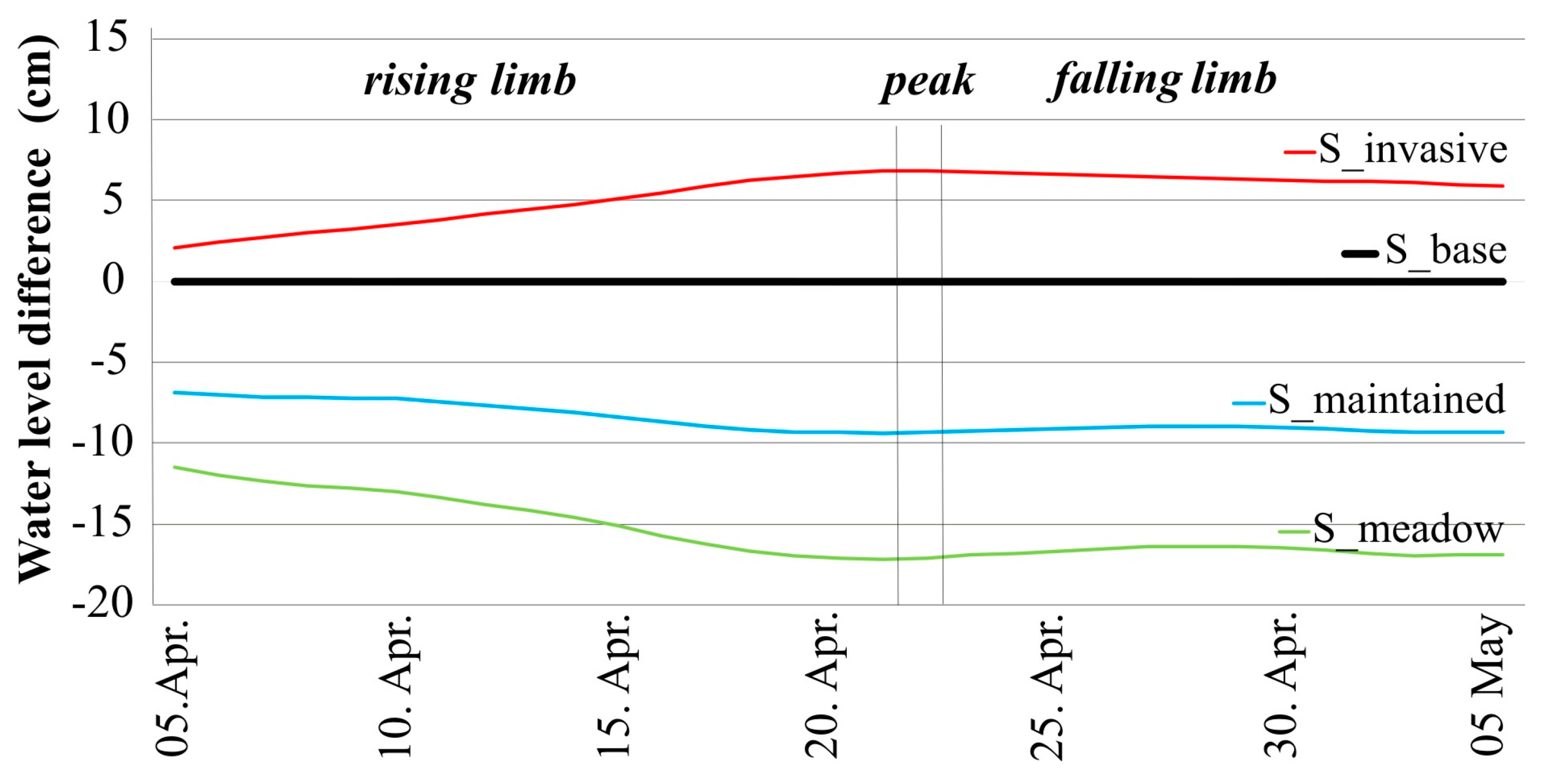
3.5. Changes in Water Levels in Different Scenarios
4. Discussion
4.1. Riparian Vegetation Density with Special Respect to the Submerged Vegetation Zones
4.2. Hydrological Consequences of Vegetation Changes
4.3. Suggestions for Sustainable Flood and Riparian Vegetation Management
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Downs, P.W.; Piegay, H. Catchment-scale cumulative impact of human activities on river channels in the late Anthropocene: Implications, limitations, prospect. Geomorphology 2019, 338, 88–104. [Google Scholar] [CrossRef]
- Galia, T. Legacy of Human Impact on Geomorphic Processes in Mountain Headwater Streams in the Perspective of European Cultural Landscapes. Geosciences 2021, 11, 253. [Google Scholar] [CrossRef]
- Timofte, F.; Onaca, A.; Urdea, P.; Právetz, T. The evolution of Mures channel in the lowland section between Lipova and Nadlac (in the last 150 years), assessed by GIS analysis. Carp. J. Earth Environ. Sci. 2016, 11, 319–330. [Google Scholar]
- Rentier, E.S.; Cammeraat, L.H. The environmental impacts of river sand mining. Sci. Total Environ. 2022, 838, 155877. [Google Scholar] [CrossRef]
- Bertalan, L.; Rodrigo-Comino, J.; Surian, N.; Šulc Michalková, M.; Kovács, Z.; Szabó, S.; Szabó, G.; Hooke, J. Detailed assessment of spatial and temporal variations in river channel changes and meander evolution as a preliminary work for effective floodplain management. The example of Sajó River, Hungary. J. Environ. Manag. 2019, 248, 109277. [Google Scholar] [CrossRef]
- Wyzga, B.; Radecki-Pawlik, A.; Galia, T.; Plesinski, K.; Skarpich, V.; Dusek, R. Use of high-water marks and effective discharge calculation to optimize the height of bank revetments in an incised river channel. Geomorphology 2020, 356, 107098. [Google Scholar] [CrossRef]
- Fan, J.; Huang, G. Evaluation of Flood Risk Management in Japan through a Recent Case. Sustainability 2020, 12, 5357. [Google Scholar] [CrossRef]
- Lóczy, D.; Kis, É.; Schweitzer, F. Local flood hazards assessed from channel morphometry along the Tisza River in Hungary. Geomorphology 2009, 113, 200–209. [Google Scholar] [CrossRef]
- Scorpio, V.; Aucelli, P.C.; Giano, S.I.; Pisano, L.; Robustelli, G.; Rosskopf, C.M.; Schiattarella, M. River channel adjustments in Southern Italy over the past 150 years and implications for channel recovery. Geomorphology 2015, 251, 77–90. [Google Scholar] [CrossRef]
- Rusnak, M.; Lehotsky, M.; Kidova, A. Channel migration inferred from aerial photographs, its timing and environmental consequences as responses to floods: A case study of the meandering Topla River, Slovak Carpathians. Morav. Geogr. Rep. 2016, 24, 32–43. [Google Scholar] [CrossRef]
- Dragićevć, S.; Pripužić, M.; Živković, N.; Novković, I.; Kostadinov, S.; Langović, M.; Milojković, B.; Čvorović, Z. Spatial and Temporal Variability of Bank Erosion during the Period 1930–2016: Case Study—Kolubara River Basin (Serbia). Water 2017, 9, 748. [Google Scholar] [CrossRef]
- Magliulo, P.; Bozzi, F.; Leone, G.; Fiorillo, F.; Leone, N.; Russo, F.; Valente, A. Channel adjustments over 140 years in response to extreme floods and land-use change, Tammaro River, southern Italy. Geomorphology 2021, 383, 107715. [Google Scholar] [CrossRef]
- Magliulo, P.; Cusano, A.; Giannini, A.; Sessa, S.; Russo, F. Channel Width Variation Phases of the Major Rivers of the Campania Region (Southern Italy) over 150 Years: Preliminary Results. Earth 2021, 2, 374–386. [Google Scholar] [CrossRef]
- Mandarino, A.; Pepe, G.; Cevasco, A.; Brandolini, P. Quantitative Assessment of Riverbed Planform Adjustments, Channelization, and Associated Land Use/Land Cover Changes: The Ingauna Alluvial-Coastal Plain Case (Liguria, Italy). Remote Sens. 2021, 13, 3775. [Google Scholar] [CrossRef]
- Liro, M. Impact of channel regulation on sedimentation on the Lower Dunajec floodplains. Prz. Geol. 2012, 60, 380–386. [Google Scholar]
- Rădoane, M.; Perșoiu, I.; Chiriloaei, F.; Cristea, I.; Robu, D. Styles of Channel Adjustments in the Last 150 Years. In Landform Dynamics and Evolution in Romania; Springer: Berlin/Heidelberg, Germany, 2017; pp. 489–518. [Google Scholar]
- Labaš, P.; Kidová, A. Anthropogenic and environmental impacts on the recent morphological degradation of the meandering Hornád River. Geogr. Casopis. 2022, 74, 159–180. [Google Scholar] [CrossRef]
- Timofte, F.; Urdea, P. Three centuries of dynamics in the lowland section, induced by human impact: A sociogeomorphic approach. Geogr. Pannonica 2022, 26, 308–318. [Google Scholar] [CrossRef]
- Nádudvari, Á.; Czajka, A.; Wyżga, B.; Zygmunt, M.; Wdowikowski, M. Patterns of Recent Changes in Channel Morphology and Flows in the Upper and Middle Odra River. Water 2023, 15, 370. [Google Scholar] [CrossRef]
- Zhou, M.; Xia, J.; Deng, S. One-dimensional modelling of channel evolution in an alluvial river with the effect of large-scale regulation engineering. J. Hydrol. 2019, 575, 965–975. [Google Scholar] [CrossRef]
- Zhou, M.; Xia, J.; Deng, S.; Li, Z. Two-dimensional modeling of channel evolution under the influence of large-scale river regulation works. Int. J. Sedi. Res. 2022, 37, 424–434. [Google Scholar] [CrossRef]
- Surian, N. Fluvial Changes in the Anthropocene: A European Perspective; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar] [CrossRef]
- Demeter, L.; Molnár, Á.P.; Bede-Fazekas, Á.; Öllerer, K.; Varga, A.; Szabados, K.; Tucakov, M.; Kiš, A.; Biró, M.; Marinkov, J.; et al. Controlling invasive alien shrub species, enhancing biodiversity and mitigating flood risk: A win–win–win situation in grazed floodplain plantations. J. Environ. Manag. 2021, 295, 113053. [Google Scholar] [CrossRef] [PubMed]
- Grabić, J.; Ljevnaić-Mašić, B.; Zhan, A.; Benka, P.; Heilmeier, H. A review on invasive false indigo bush (Amorpha fruticosa L.): Nuisance plant with multiple benefits. Ecol. Evol. 2022, 12, e9290. [Google Scholar] [CrossRef]
- Răileanu, A.B.; Rusu, L.; Rusu, E. An Evaluation of the Dynamics of Some Meteorological and Hydrological Processes along the Lower Danube. Sustainability 2023, 15, 6087. [Google Scholar] [CrossRef]
- Kucsicsa, G.; Grigorescu, I.; Dumitrascu, M.; Doroftei, M.; Nastase, M.; Herlo, G. Assessing the potential distribution of invasive alien species Amorpha fruticosa (Mill.) in the Mures Floodplain Natural Park (Romania) using GIS and logistic regression. Nat. Conserv. Bulg. 2018, 30, 41–67. [Google Scholar] [CrossRef]
- Rodriguez-Gonzalez, P.M.; Abraham, E.; Aguiar, F.; Andreoli, A.; Balezentiene, L.; Berisha, N.; Bernez, I.; Bruen, M.; Bruno, D.; Camporeale, C.; et al. Bringing the margin to the focus: 10 challenges for riparian vegetation science and management. Water 2022, 9, e1604. [Google Scholar] [CrossRef]
- Vári, Á.; Podschun, S.A.; Erős, T.; Hein, T.; Pataki, B.; Iojă, I.C.; Adamescu, C.M.; Gerhardt, A.; Gruber, T.; Dedić, A. Freshwater systems and ecosystem services: Challenges and chances for cross-fertilization of disciplines. AMBIO 2022, 51, 135–151. [Google Scholar] [CrossRef]
- Abernethy, B.; Rutherfurd, I.D. Where along a river’s length will vegetation most effectively stabilise stream banks? Geomorphology 1998, 23, 55–75. [Google Scholar] [CrossRef]
- Mao, L.; Ravazzolo, D.; Bertoldi, W. The role of vegetation and large wood on the topographic characteristics of braided river systems. Geomorphology 2020, 367, 107299. [Google Scholar] [CrossRef]
- Ciszewski, D.; Czajka, A. Human-induced sedimentation patterns of a channelized lowland river. Earth Surf. Proc. Landf. 2015, 40, 783–795. [Google Scholar] [CrossRef]
- Szabó, Z.; Buró, B.; Szabó, J.; Tóth, C.A.; Baranyai, E.; Herman, P.; Prokisch, J.; Tomor, T.; Szabó, S. Geomorphology as a driver of heavy metal accumulation patterns in a floodplain. Water 2020, 12, 563. [Google Scholar] [CrossRef]
- Chen, Y.; Overeem, I.; Kettner, A.J.; Gao, S.; Syvitski, J.P.M. Modeling flood dynamics along the superelevated channel belt of the Yellow River over the last 3000 years. J. Geophys. Res. Earth Surf. 2015, 120, 1321–1351. [Google Scholar] [CrossRef]
- Kiss, T.; Nagy, J.; Fehérváry, I.; Amissah, G.J.; Fiala, K.; Sipos, G. Increased flood height driven by local factors on a regulated river with a confined floodplain, Lower Tisza, Hungary. Geomorphology 2021, 389, 107858. [Google Scholar] [CrossRef]
- Kolaković, S.; Mandić, V.; Stojković, M.; Jeftenić, G.; Stipić, D.; Kolaković, S. Estimation of Large River Design Floods Using the Peaks-Over-Threshold (POT) Method. Sustainability 2023, 15, 5573. [Google Scholar] [CrossRef]
- González del Tánago, M.; Martínez-Fernández, V.; Aguiar, F.C.; Bertoldi, W.; Dufour, S.; García de Jalón, D.; Garófano-Gómez, V.; Mandzukovski, D.; Rodríguez-González, P.M. Improving river hydromorphological assessment through better integration of riparian vegetation: Scientific evidence and guidelines. J. Environ. Manag. 2021, 292, 112730. [Google Scholar] [CrossRef]
- Shih, S.S.; Chen, P.C. Identifying tree characteristics to determine the blocking effects of water conveyance for natural flood management in urban rivers. J. Flood Risk Manag. 2021, 14, e12742. [Google Scholar] [CrossRef]
- Peinado Guevara, H.J.; Espinoza Ortiz, M.; Peinado Guevara, V.M.; Herrera Barrientos, J.; Peinado Guevara, J.A.; Delgado Rodríguez, O.; Pellegrini Cervantes, M.J.; Sánchez Morales, M. Potential Flood Risk in the City of Guasave, Sinaloa, the Effects of Population Growth, and Modifications to the Topographic Relief. Sustainability 2022, 14, 6560. [Google Scholar] [CrossRef]
- Guida, R.J.; Remo, J.W.F.; Secchi, S. Applying geospatial tools to assess the agricultural value of Lower Illinois River floodplain levee districts. Appl. Geogr. 2016, 74, 123–135. [Google Scholar] [CrossRef]
- Perosa, F.; Gelhaus, M.; Zwirglmaier, V.; Arias-Rodriguez, L.F.; Zingraff-Hamed, A.; Cyffka, B.; Disse, M. Integrated Valuation of Nature-Based Solutions Using TESSA: Three Floodplain Restoration Studies in the Danube Catchment. Sustainability 2021, 13, 1482. [Google Scholar] [CrossRef]
- Abell, J.M.; Pingram, M.A.; Özkundakci, D.; David, B.O.; Scarsbrook, M.; Wilding, T.; Williams, A.; Noble, M.; Brasington, J.; Perrie, A. Large floodplain river restoration in New Zealand: Synthesis and critical evaluation to inform restoration planning and research. Reg. Environ. Chang. 2022, 23, 18. [Google Scholar] [CrossRef]
- Chow, V.T. Open Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959; p. 364. ISBN 978-0-12-821770-2. [Google Scholar]
- Wu, W.; He, Z. Effects of vegetation on flow conveyance and sediment transport capacity. Int. J. Sediment. Res. 2009, 24, 247–259. [Google Scholar] [CrossRef]
- Järvelä, J. Flow resistance of flexible and stiff vegetation: A flume study with natural plants. J. Hydrol. 2009, 269, 44–54. [Google Scholar] [CrossRef]
- Luhar, M.; Rominger, J.; Nepf, H. Interaction between flow, transport and vegetation spatial structure. Environ. Fluid. Mech. 2008, 8, 423. [Google Scholar] [CrossRef]
- Liu, D.; Diplas, P.; Fairbanks, J.D.; Hodges, C.C. An experimental study of flow through rigid vegetation. J. Geophys. Res. 2008, 113, F04015. [Google Scholar] [CrossRef]
- Larsen, L.G. Multiscale flow-vegetation-sediment feedbacks in low-gradient landscapes. Geomorphology 2019, 334, 165–193. [Google Scholar] [CrossRef]
- Jeffries, R.; Darby, S.E.; Sear, D.A. The influence of vegetation and organic debris on flood-plain sediment dynamics: Case study of a low-order stream in the New Forest, England. Geomorphology 2003, 51, 61–80. [Google Scholar] [CrossRef]
- Dwyer, E.; Pinnock, S.; Gregoire, J.M.; Pereira, J.M.C. Global spatial and temporal distribution of vegetation fire as determined from satellite observations. Remote Sens. 2000, 21, 1289–1302. [Google Scholar] [CrossRef]
- Naesset, E.; Gobakken, T.; Holmgren, J.; Hyyppa, J.; Maltamo, M.; Nilsson, M.; Olsson, H.; Persson, A.; Doderman, U. Laser scanning of forest resources: The Nordic experience. Scand. J. For. Res. 2004, 19, 482–499. [Google Scholar] [CrossRef]
- Heurich, M.; Thoma, F. Estimation of forestry stand parameters using laser scanning data in temperate, structurally rich natural European beech (Fagus sylvatica) and Norway spruce (Picea abies) forests. Forestry 2008, 81, 645–661. [Google Scholar] [CrossRef]
- Dufour, S.; Rodríguez-González, P.M.; Laslier, M. Tracing the scientific trajectory of riparian vegetation studies: Main topics, approaches and needs in a globally changing world. Sci. Total Environ. 2019, 653, 1168–1185. [Google Scholar] [CrossRef]
- Rusnák, M.; Goga, T.; Michaleje, L.; Šulc Michalková, M.; Máčka, Z.; Bertalan, L.; Kidová, A. Remote Sensing of Riparian Ecosystems. Remote Sens. 2022, 14, 2645. [Google Scholar] [CrossRef]
- Vetter, M.; Höfle, B.; Hollaus, M.; Gschöpf, C.; Mandlburger, G.; Pfeifer, N. Vertical vegetation structure analysis and hydraulic roughness determination using dense ALS point cloud data-A voxel based approach. Int. Arch. Photogr. Remote Sens. Spat. Inf. Sci. 2011, 38, 200–206. [Google Scholar] [CrossRef]
- Manners, R.; Schmidt, J.; Wheaton, M.J. Multiscalar model for the determination of spatially explicit riparian vegetation roughness. J. Geophys. Res. Earth Surf. 2013, 118, 65–83. [Google Scholar] [CrossRef]
- Muller, E.; Décamps, H.; Dobson, M.K. Contribution of space remote sensing to river studies. Freshw. Biol. 1993, 29, 301–312. [Google Scholar] [CrossRef]
- Goetz, S.J. Remote Sensing of Riparian Buffers: Past Progress and Future Prospects. J. Am. Water Resour. Assoc. 2007, 42, 133–143. [Google Scholar] [CrossRef]
- Ashraf, S.; Brabyn, L.; Hicks, B.J.; Collier, K. Satellite remote sensing for mapping vegetation in New Zealand freshwater environments: A review. N. Z. Geogr. 2010, 66, 33–43. [Google Scholar] [CrossRef]
- Dufour, S.; Bernez, I.; Betbeder, J.; Corgne, S.; Hubert-Moy, L.; Nabucet, J.; Rapinel, S.; Sawtschuk, J.; Trollé, C. Monitoring restored riparian vegetation: How can recent developments in remote sensing sciences help? Knowl. Manag. Aquat. Ecosyst. 2013, 410, 10. [Google Scholar] [CrossRef]
- Dufour, S.; Muller, E.; Straatsma, M.; Corgne, S. Image Utilisation for the Study and Management of Riparian Vegetation: Overview and Applications. In Fluvial Remote Sensing for Science and Management; Carbonneau, P.E., Piégay, H., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2012. [Google Scholar] [CrossRef]
- Forzieri, G.; Castelli, F.; Preti, F. Advances in remote sensing of hydraulic roughness. Int. J. Remote Sens. 2012, 33, 630–654. [Google Scholar] [CrossRef]
- Tomsett, C.; Leyland, J. Remote sensing of river corridors: A review of current trends and future directions. River Res. Appl. 2019, 35, 779–803. [Google Scholar] [CrossRef]
- Seielstad, C.A.; Queen, L.P. Using Airborne Laser Altimetry to Determine Fuel Models for estimating fire behaviour. J. For. 2003, 101, 10–15. [Google Scholar]
- Morsdorf, F.; Marell, A.; Koetz, B.; Cassagne, N.; Pimont, F.; Rigolot, E.; Allgöwer, B. Discrimination of vegetation strata in a multi-layered Mediterranean forest ecosystem using height and intensity information derived from airborne laser scanning. Remote Sens. Environ. 2010, 114, 1403–1415. [Google Scholar] [CrossRef]
- Rutherford, J.C.; Meleason, M.A.; Davies-Colley, R.J. Modelling stream shade: 2. Predicting the effects of canopy shape and changes over time. Ecol. Eng. 2018, 120, 487–496. [Google Scholar] [CrossRef]
- Richardson, J.J.; Torgersen, C.E.; Moskal, L.M. Lidar-based approaches for estimating solar insolation in heavily forested streams. Hydrol. Earth Syst. Sci. 2019, 23, 2813–2822. [Google Scholar] [CrossRef]
- Schlosser, A.D.; Szabó, G.; Bertalan, L.; Varga, Z.; Enyedi, P.; Szabó, S. Building Extraction Using Orthophotos and Dense Point Cloud Derived from Visual Band Aerial Imagery Based on Machine Learning and Segmentation. Remote Sens. 2020, 12, 2397. [Google Scholar] [CrossRef]
- Hahmraz, H.; Contreras, M.A.; Zhang, J. Forest understory trees can be segmented accurately within sufficiently dense airborne laser scanning point clouds. Sci. Rep. 2017, 7, 6770. [Google Scholar] [CrossRef] [PubMed]
- Campbell, M.J.; Dennison, P.E.; Hudak, A.T.; Parham, L.M.; Butler, B.W. Quantifying understory vegetation density using small-footprint airborne LiDAR. Remote Sens. Environ. 2018, 215, 330–342. [Google Scholar] [CrossRef]
- Riaño, D.; Valladares, F.; Condés, S.; Chuvieco, E. Estimation of leaf area index and covered ground from airborne laser scanner (Lidar) in two contrasting forests. Agric. For. Meteorol. 2004, 124, 269–275. [Google Scholar] [CrossRef]
- Jakubowksi, M.K.; Guo, Q.; Collins, B.; Stephens, S.; Kelly, M. Predicting surface fuel models and fuel metrics using lidar and CIR imagery in a dense mixed conifer forest. Photogramm. Eng. Remote Sens. 2013, 79, 37–49. [Google Scholar] [CrossRef]
- Martinuzzi, S.; Vierling, L.A.; Gould, W.A.; Falkowski, M.J.; Evans, J.S.; Hudak, A.T.; Vierling, K.T. Mapping snags and understory shrubs for a LiDAR-based assessment of wildlife habitat suitability. Remote Sens. Environ. 2009, 113, 2533–2546. [Google Scholar] [CrossRef]
- Skowronski, N.; Clark, K.; Nelson, R.; Hom, J.; Patterson, M. Remotely sensed measurements of forest structure and fuel loads in the pinelands of New Jersey. Remote Sens. Environ. 2007, 108, 123–129. [Google Scholar] [CrossRef]
- Csiszár, A.; Kézdy, P.; Korda, M.; Bartha, D. Occurrence and management of invasive alien species in Hungarian protected areas compared to Europe. Folia Oecologica 2020, 47, 178–191. [Google Scholar] [CrossRef]
- Delai, F.; Kiss, T.; Nagy, J. Field-based estimates of floodplain roughness along the Tisza River (Hungary): The role of invasive Amorpha fruticosa. Appl. Geogr. 2018, 90, 96–105. [Google Scholar] [CrossRef]
- Nagy, J.; Kiss, T.; Fehérváry, I.; Vaszkó, C. Changes in floodplain vegetation density and the impact of invasive Amorpha fruticosa on flood conveyance. J. Environ. Geogr. 2018, 11, 3–12. [Google Scholar] [CrossRef]
- Kiss, T.; Nagy, J.; Fehérváry, I.; Vaszkó, C. (Mis) management of floodplain vegetation: The effect of invasive species on vegetation roughness and flood levels. Sci. Total Environ. 2019, 686, 931–945. [Google Scholar] [CrossRef] [PubMed]
- Fehérváry, I.; Kiss, T. Riparian Vegetation Density Mapping of an Extremely Densely Vegetated Confined Floodplain. Hydrology 2021, 8, 176. [Google Scholar] [CrossRef]
- Kiss, T.; Fiala, K.; Sipos, G. Alterations of channel parameters in response to river regulation works since 1840 on the Lower Tisza River (Hungary). Geomorphology 2008, 98, 96–110. [Google Scholar] [CrossRef]
- Kiss, T.; Fiala, K.; Sipos, G.; Szatmári, G. Long-term hydrological changes after various river regulation measures: Are we responsible for flow extremes? Hydrol. Res. 2019, 50, 417–430. [Google Scholar] [CrossRef]
- Szlávik, L. A Duna és a Tisza Szorításában—A 2006. évi Árvizek és Belvizek Krónikája; KÖZDOK Kft: Budapest, Hungary, 2006; p. 304. ISBN 978-963-06-2092-5. (In Hungarian) [Google Scholar]
- Botta-Dukát, Z.; Balogh, L. (Eds.) The Most Important Invasive Plants in Hungary; Institute of Ecology and Botany, Hungarian Academy of Sciences: Vácrátót, Hungary, 2008; p. 138. ISBN 978-963-8391-42-1. [Google Scholar]
- Sándor, A. Floodplain Aggradation along the Middle and Lowland Section of the Tisza River. Ph.D. Thesis, University of Szeged, Szeged, Hungary, 2012; p. 120. (In Hungarian). [Google Scholar]
- Francisci, D.A. Python Script for Geometric Interval Classification in QGIS: A Useful Tool for Archaeologists. Environ. Sci. Proc. 2021, 10, 1. [Google Scholar] [CrossRef]
- Brunner, W.G. HEC-RAS 2D Modeling User’s Manual; Hydrologic Engineering Center, U.S. Army Corps of Engineers: Davis, CA, USA, 2021. Available online: https://www.hec.usace.army.mil/confluence/rasdocs/r2dum/latest (accessed on 15 August 2023).
- Vizi, D.B.; Právetz, T. The possibilities of improving the conveyance capacity with restoration measures along the Hungarian Middle Tisza River section, based on a pilot area. Danub. News 2020, 42, 1–7. [Google Scholar]
- Gencsi, L.; Vancsura, R. Dendrology; Mezőgazda Kiadó: Budapest, Hungary, 1997; p. 728. ISBN 9789637362989. (In Hungarian) [Google Scholar]
- Biró, M. Floodplain Hay Meadows along the River Tisza in Hungary. In Grasslands in Europe of High Nature Value; Veen, P., Jefferson, R., Smidth, J., Straaten, J., Eds.; KNNV Publishing: Zeist, The Netherlands, 2009; pp. 238–245. ISBN 978-90-04-27810-3. [Google Scholar]
- Mohsen, A.; Kovács, F.; Kiss, T. Remote sensing of sediment discharge in rivers using Sentinel-2 images and machine learning algorithms. Hydrology 2022, 9, 88. [Google Scholar] [CrossRef]
- Sándor, A.; Kiss, T. Floodplain aggradation caused by the high magnitude flood of 2006 in the Lower Tisza Region, Hungary. J. Environ. Geogr. 2008, 1, 31–39. [Google Scholar] [CrossRef]
- Amissah, G.J.; Kiss, T.; Fiala, K. Active point-bar development and river bank erosion in the incising channel of the Lower Tisza River, Hungary. ACTA Debrecina Landsc. Environ. 2019, 13, 13–28. [Google Scholar] [CrossRef]
- Várallyai, G. The effect of the 19th century engineering works on the soil conditions. In The 19th Century River Regulations and Their Geographical and Ecological Consequences in Hungary; Somogyi, S., Ed.; MTA-FKI: Budapest, Hungary, 2000; pp. 204–218. [Google Scholar]
- Wyzga, B. Impact of the channelization-induced incision of Skawa and Wisloka rivers, southern Poland, on the condition of overbank deposition. Regul. Rivers 2001, 17, 85–100. [Google Scholar] [CrossRef]
- Sheishah, D.; Sipos, G.; Barta, K.; Abdelsamei, E.; Hegyi, A.; Onaca, A.; Abbas, A.M. Comparative Evaluation of the Material of the Artificial Levees: A Case Study Along the Tisza and Maros Rivers, Hungary. J. Environ. Geogr. 2023, 16, 1–10. [Google Scholar] [CrossRef]
- Liro, M.; Mikuś, P.; Wyżga, B. First insight into the macroplastic storage in a mountain river: The role of in-river vegetation cover, wood jams and channel morphology. Sci. Total Environ. 2022, 838, 156354. [Google Scholar] [CrossRef]
- Perosa, F.; Springer, J.; Gelhaus, M.; Betz, F.; Zwirglmaier, V.; Disse, M.; Cyffka, B.; Vizi, D.; Právetz, T.; Kis, A.; et al. Results of Pilot Area Middle Tisza. Interreg Danube Transnational Project: Danube Floodplain, Munich, 2021. p. 12. Available online: http://www.geo.u-szeged.hu/images/DFGIS/MiddleTisza.pdf (accessed on 24 July 2023).

| Vegetation Density Category | Class Boundary (% of Maximum Value) |
|---|---|
| very sparse | 0–1.0 |
| sparse | 1.01–2.0 |
| medium | 2.01–4.0 |
| dense | 4.01–16.0 |
| very dense | >16.01 |
| Vegetation Density Class | Areal Distribution (%) | |||
|---|---|---|---|---|
| 1–2 m | 2–3 m | 3–4 m | 4–5 m | |
| very sparse | 38 | 45 | 53 | 58 |
| sparse | 12 | 13 | 20 | 20 |
| medium | 22 | 20 | 13 | 12 |
| dense | 23 | 20 | 14 | 10 |
| very dense | 5 | 2 | >1 | >1 |
| return period of inundation (year) | 2 | 3 | 9 | 25 |
| exceedance probability | 0.51 | 0.32 | 0.11 | 0.04 |
| Scenario | Flood Limb (Date) | Flow Velocity (m/s) | |||
|---|---|---|---|---|---|
| 0–0.3 | 0.3–0.6 | >0.6 | max. | ||
| rising (5 April) | 81 | 4 | 15 | 1.2 | |
| S_base | peak (22 April) | 62 | 23 | 15 | 1.3 |
| falling (5 May) | 69 | 16 | 15 | 1.3 | |
| rising (5 April) | 79 | 5 | 17 | 1.2 | |
| S_maintained | peak (22 April) | 56 | 28 | 16 | 1.1 |
| falling (5 May) | 65 | 18 | 18 | 1.1 | |
| rising (5 April) | 81 | 4 | 15 | 1.2 | |
| S_invasive | peak (22 April) | 79 | 5 | 16 | 1.4 |
| falling (5 May) | 80 | 4 | 16 | 1.4 | |
| rising (5 April) | 74 | 7 | 19 | 1.2 | |
| S_meadow | peak (22 April) | 15 | 69 | 16 | 0.9 |
| falling (5 May) | 19 | 64 | 17 | 0.9 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiss, T.; Fehérváry, I. Increased Riparian Vegetation Density and Its Effect on Flow Conditions. Sustainability 2023, 15, 12615. https://doi.org/10.3390/su151612615
Kiss T, Fehérváry I. Increased Riparian Vegetation Density and Its Effect on Flow Conditions. Sustainability. 2023; 15(16):12615. https://doi.org/10.3390/su151612615
Chicago/Turabian StyleKiss, Tímea, and István Fehérváry. 2023. "Increased Riparian Vegetation Density and Its Effect on Flow Conditions" Sustainability 15, no. 16: 12615. https://doi.org/10.3390/su151612615
APA StyleKiss, T., & Fehérváry, I. (2023). Increased Riparian Vegetation Density and Its Effect on Flow Conditions. Sustainability, 15(16), 12615. https://doi.org/10.3390/su151612615





