Analysis of Green Closed-Loop Supply Chain Efficiency under Generalized Stochastic Petri Nets

Abstract

In this paper, we aim to explore the operational performance of a green closed-loop supply chain under random events. A green closed-loop supply chain model based on generalized stochastic Petri nets (GSPN) is built using the Petri nets theory. According to the isomorphic relationship between GSPN and continuous-time Markov chains, the relevant Markov model is converted from GSPN, and the steady-state probability of the model is then calculated. Finally, the model is analyzed from the aspects of time performance and operation efficiency of each link. Compared to previous studies, this paper finds that: when the whole green closed-loop supply chain system reaches a dynamic equilibrium state, the product has a steady-state probability at all stages, and thus the overall operational performance of the system can be obtained; compared with the recycling of waste products, the green product takes a longer time in the production and distribution stages; since marketing, packaging processing, market feedback, and market demand formulation account for a high level of utilization throughout the life cycle of green products, decision makers need to focus on the supervision and management of these links. Managers of green closed-loop supply chain systems need to adjust their decision-making strategies in a timely manner according to the performance level of the system in the steady state to realize the efficient operation of the system. This paper not only provides theoretical support for the improvement of the operational efficiency of green closed-loop supply chain system, but also provides new ideas for the research of green closed-loop supply chain operation mode.

1. Introduction

As technology advances, people are paying more and more attention to environmental problems and sustainable development of resources. In order to address the issues of resource waste and environmental damage, many enterprises decide to produce more environmentally friendly and energy-saving green products and to recycle and remanufacture used products to realize the recycling of product resources [1]. Compared with the traditional supply chain, the green closed-loop supply chain is more powerful, not only taking into account the dual requirements of environmental protection and sustainable economic development, but also involving more operational aspects [2]. Therefore, numerous academics have studied the green closed-loop supply chain to offer advice and recommendations to enterprises and governments.

As random events occur all the time in reality, when the market is affected by random events, its internal individual operation will be implicated, the operational efficiency of the system undergoes random changes, the operation time of the supply chain system is no longer stable, and the study of its operational performance will become more complex. A Markov chain with stochastic characteristics can describe the random changes of the system and simplify the complexity of the model [3], and its isomorphism of the generalized stochastic Petri nets can intuitively and conveniently describe the dynamic characteristics of the system and test the change of business processes [4]. Many scholars will combine the two methods to analyze the dynamic characteristics of the supply chain system and the change of the business process, etc. In this paper, a green closed-loop supply chain system network with stochastic characteristics is introduced with the purpose of studying the overall operational performance of the green closed-loop supply chain system and the operational efficiency of each link under the influence of stochastic events. By constructing a generalized stochastic Petri net model and combining it with a continuous time Markov chain, we aim to answer the following research questions:

Can the operation of a green closed-loop supply chain system achieve dynamic equilibrium when there are random fluctuations in the market? How should the operation time of the system be determined?

When the system achieves dynamic equilibrium, how does the overall operational performance of the green closed-loop supply chain system and the operational efficiency of each stage change?

From the manufacture of green products to their distribution to the recycling of used products, which stages need to be focused on by decision makers, and which stages can be merged with other stages?

The structure of this paper is organized as follows: in the second section, a review of existing research is presented. The third section describes the grounded theory used in this paper. The fourth part is the assumptions and establishment of the model. The performance of the developed model is analyzed in the fifth part. Finally, in the sixth part, the conclusions of the study are given.

2. Literature Review

2.1. Optimal Decision Making in Green Closed-Loop Supply Chain

A green closed-loop supply chain not only resolves the contradiction between economic development and environmental protection, but also realizes the green sustainable development of the economy. Krikke et al. [5] initially believed that the ecological closed-loop supply chain and the green closed-loop supply chain were interchangeable, and Neto et al. [6] regarded the closed-loop supply chain with the superior benefits to the economy and environment as a green closed-loop supply chain. Nowadays, most scholars regard the green closed-loop supply chain as a combination of green supply chain and closed-loop supply chain, capable of achieving the environmental benefit target of the green supply chain as well as the economic benefit goal of the closed-loop supply chain. Currently, the primary emphasis of study on the green supply chain is the greenness of products, which also looks at the most efficient pricing strategy for green commodities. Yang et al. [7] constructed a green product supply chain model led by manufacturers and followed by retailers and investigated the effects of pre-sale size and fair concern behavior of retailers on the optimal decision-making of each member of the supply chain. Shi et al. [8] examined the green supply chain, which is made up of firms with limited resources, and discovered that sharing the cost of reducing carbon emissions can maximize the economic and environmental benefits. These studies mostly focused on coordination and decision-making for the green supply chain, and some researchers have introduced green degree into closed-loop supply chain for research. Ma [9] studied a closed-loop supply chain system comprised of one manufacturer, one retailer, and a third-party service provider, in which the manufacturer invested in green manufacturing efforts at the stages of product design and manufacturing. Zhou et al. [10] discussed carbon trading, green innovation efforts, and green customers’ preference for internal and permitted remanufacturing strategies by introducing green factors and discovered that when the price of carbon trading is low, enterprises will choose authorized remanufacturing strategies in order to obtain more benefits.

The literature listed above focused on studying the green closed-loop supply chain in a static environment. However, in reality, with the globalization of economy and the internationalization of products, the market’s internal and external environments are both dynamic, and the relationship between supply and demand of products is also changing. Many academics started researching the green closed-loop supply chain in the dynamic scenario since the standard green closed-loop supply chain in the static condition is unable to accurately reflect this impact. Zhang et al. [11] investigated joint dynamic green innovation and pricing strategies in closed-loop supply chain systems under two scenarios: loose carbon emission constraints and binding carbon emission constraints. Lu et al. [12] explored the optimal decision-making of each member of the green supply chain under different government subsidy policies and found that the optimal decision-making path of the subsidy policy over the whole period can be obtained by considering the subsidy effect and the subsidy efficiency in the steady state at the same time. Liu et al. [13] discussed a green supply chain comprised of a single supplier and two manufacturers and discussed the dynamic green competition with bounded rationality by using the gradient adjustment mechanism. Kuchesfehani et al. [14] discussed two scenarios for a closed-loop supply chain with one manufacturer and one retailer in the stochastic dynamic game: the manufacturer bears the cost of green activities alone, and the retailer shares the cost of environmental actions for the manufacturer, and the manufacturer transfers the retailer a portion of the sales proceeds. Combing through the above literature, it is obvious that most of the previous studies analyzed the optimal decision-making from the perspective of manufacturers and did not analyze the overall performance of the green closed-loop supply chain system.

2.2. Overall Supply Chain System Performance Analysis

In the aforementioned documents, the green closed-loop supply chain was primarily examined from the standpoint of the individual operations of manufacturers, but there was little attention paid to research on the functioning of the complete web of supply chains. Products need to go through a series of complicated processes from production to sales to final recycling, and the operation efficiency of supply chain is not determined by a single manufacturer. Therefore, the optimization of operating efficiency and operating costs from the viewpoint of the entire closed-loop supply chain system’s business process has been paid more and more attention. Zeballos et al. [15] studied the product and network design of multi-product, multi-level, and multi-cycle closed-loop supply chain. Yang et al. [16] studied a closed-loop supply chain network consisting of multi-manufacturing/remanufacturing plants and multi-distribution/collection centers under the background of carbon emissions, providing investment and production decision-making strategies for supply chain participants. Iryaning et al. [17] investigated the impact of carbon emission and traceability system on production and distribution of closed-loop supply chain network using a mixed integer linear programming method with an example of the canned fish food industry in Indonesia. Govindan et al. [18] created an integrated bi-objective mixed integer linear programming model that allowed for the optimization of strategic decision-making and closed-loop supply chain network operation. Yuniarti et al. [19] designed a closed-loop supply chain network model applicable to the operation of agri-food industry and analyzed the multi-period production allocation problem in the closed-loop supply chain of agricultural products. However, these studies were conducted in mature and stable market environments and did not take into account the potential impact of random events present in the market on the overall operational performance of the system.

2.3. Application of Petri Net Modeling

Real life is not set in stone; sudden natural disasters and sudden changes in market policies can have unpredictable effects on the market and further affect the participants in the market [20]. When random fluctuations occur in the market, the analysis of the overall operational performance of the system using traditional methods is no longer informative. C. A. Petri put forward the concept of the Petri net in his doctoral thesis in 1962 [21]. Since the Petri net has good characteristics such as dynamic, concurrent, and intuitive graphics, Petri nets have been used in supply chain business process simulation, supply chain management process optimization and supply chain modeling. There is a mutual isomorphism between Petri nets and Markov chains [22], so when using Petri nets to study the operational performance of supply chain systems, they are often transformed into their isomorphic Markov chain models, and further research is carried out on this basis [23]. Wang et al. [24] used generalized stochastic Petri nets to model and analyze the operational performance of remanufacturing supply chains. However, the above study was not applied to a green closed-loop supply chain system. Although Ding et al. [25] combined the performance evaluation process algebra with Petri nets to create a novel and enhanced formal modeling technique in green supply chains, the study was conducted in a green supply chain and analyzed the overall operational performance of the system as well as the operational efficiency of each link.

Throughout the above literature, most studies have investigated the optimal benefits of green closed-loop supply chains only from the perspective of manufacturers. However, in the actual operation of green closed-loop supply chains, it is equally important to study the supply chain system as a whole. Second, most of the literature has been conducted in a mature and stable market environment and has not considered the potential impact of random events in the market on the overall performance of the system. Third, few studies have combined the relevant theories of generalized stochastic Petri nets with continuous time Markov chains to analyze the green closed-loop supply chain system as a whole. In this paper, we model the green closed-loop supply chain system based on the theory of generalized stochastic Petri nets combined with its isomorphic continuous time Markov chain, study the overall operational performance of the system as well as the operational efficiency of each link, and obtain the quantitative results of the main performance indexes by combining with the arithmetic examples, and finally provide management suggestions for the managers in the system.

Table 1. Comparison between previous literature and this paper. (where ‘’√’’ indicates that the study included this element and ‘’—‘’ indicates that the study did not include this element.)

Author(s)	Green Closed Loop Supply Chain	Overall Supply Chain System Performance Analysis	Generalized Stochastic Petri Nets
Zhang et al. [11]	√	—	—
Lu et al. [12]	√	—	—
Iryaning et al. [17]	—	√	—
Yuniarti et al. [19]	—	√	—
Li et al. [23]	—	—	√
Wang and Da [24]	—	√	√
Ding et al. [25]	√	—	√
This study	√	√	√

explains the research gap that exists between this paper and the existing literature. To the best of the authors’ knowledge, this is the first study in the literature on the overall operational performance of green closed-loop supply chain systems using generalized stochastic Petri nets. Through the comparative analysis, this paper adds to the theory related to generalized stochastic Petri nets as well as the field of research on the operational performance of green closed-loop supply chain systems. The main innovations of this paper are: (1) the combination of generalized stochastic Petri nets and continuous time Markov chains, which not only realizes the intuitive description of the dynamic characteristics of the system, but also reflects the stochastic changes of the system and simplifies the complexity of the model; (2) the combination of the combined methods is applied to the green closed-loop supply chain system, which realizes the evaluation of the overall dynamic operational performance of the green closed-loop supply chain system and enriches the evaluation system of the overall operational performance of the system.

3. Basic Theory

3.1. Generalized Stochastic Petri Net (GSPN)

The Petri net model is a mathematical model of a discrete parallel system, which can accurately express parallel events through strict mathematics and intuitive graphic expression. However, traditional Petri nets are triggered as soon as the trigger conditions are met, i.e., there is no time process for the change of state to occur. Practically, since some activities take time to carry out, the absence of a time-delayed process of variation can cause the number of network elements to grow exponentially when modeling and analyzing complex system problems, resulting in an explosion of the state space. In order to solve the above problems, Molly proposed the theory of the stochastic Petri net, which links a random delay time between the implementability and implementation of each transition of a Petri net; this type of Petri net is called a stochastic Petri net (SPN) [26]. SPNs realize the combination of transitions with a random exponential implementation delay rate. SPN with instantaneous transitions and delayed transitions are called Generalized Stochastic Petri Net (GSPN). GSPN is an extension of SPN, which solves the problem that Markov chains, isomorphic to SPN, are difficult to solve as the SPN state space’s size increases exponentially with problem complexity. In this paper, GSPN is used to study the system operation performance of a green closed-loop supply chain.

Definition 1.

GSPN is composed of six tuples $(P,T,F,W,M_0,\lambda )$, in which:

$P=\left\{P_1,P_2,\dots ,P_m\right\}$ is the library’s finite non-empty set;

$T=T_t\cup T_i$ is the collection of transitions of the dynamic system, reflecting the delay required to pass from one state to another, where $T_t=\left\{t_1,t_2,\dots ,t_k\right\}$ is the set of temporal transitions, $T_i=\left\{t_{k+1},t_{k+2},\dots ,t_n\right\}$ is the set of instantaneous transitions, and $T_t\cap T_i=\varnothing$ satisfies;

$F\subseteq a^{+}\cup a^{-}$ is the collection of directed arcs, reflecting the relationship between the evolutionary directional flows of the system, where $a^{+}\subseteq T\times P$ denotes the set of all output arcs from the transformation to the depot and $a^{-}\subseteq P\times T$ denotes the set of all input arcs from the depot to the transformation;

$W:F\to N$ is a vector of arc functions, where $N=\left\{1,2,3,\dots \right\}$ reflects the capacity contained in each system variation process;

$M:P\to N$ is the state identification vector of the repository, reflecting the states that may occur in the dynamic operation of the system, $M(P)$ represents the value of the state identification vector of the repository $P$ under identification $M$, and $M_0$ is the initial identification of the system;

$\lambda =\left\{{\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n\right\}$ is the average rate of change being implemented in the system, the delay of the change occurring obeys the negative exponential distribution, and the average implementation rate of the transient change is 0.

3.2. Continuous Time Markov Chain

A stochastic process with memoryless, discrete state space and continuous in time is called a continuous time Markov chain (CTMC) [22]. Denote the state space set $S=\left\{0,1,2,\dots \right\}$, if some stochastic process set $\left\{X(t),t\ge 0\right\}$ is continuous in time and Markovian, then the stochastic process is a continuous time Markovian process and for $\forall s,t\ge 0,i,j\in S$ we have: $P\left\{X(s+t)=j\mid X(s)=i,X(u),0\le u\le s\right\}=P\left\{X(s+t)=j\mid X(s)=i\right\}$, and if the stochastic process is time flush, then:

$$P\left\{X(s+t)=j\mid X(s)=i\right\}=P\left\{X(t)=j\mid X(0)=i\right\},$$

(1)

Thus, it is possible to obtain the transfer probability matrix $P(t)$ as: $P(t)=[p_{ij}(t)]=P\left\{X(t)=j\mid X(0)=i\right\}$.

Let the sample space of a randomized experiment $E$ be $\mathsf{\Omega }$. A real number $P(A)$ is said to be the probability of an event $A$ if it is assigned to every event $A$ of $E$ and satisfies: non-negativity ($P(A)\ge 0$), normality ($P(\mathsf{\Omega })=1$), and columnar additivity, then the real number $P(A)$ is said to be the probability of event $A$ [27].

The C-K equation states [27]: let $\left\{X(n),n=0,1,2,\dots \right\}$ be a Markov chain and let the state space $E=\left\{0,\pm 1,\pm 2,\dots \right\}$ or a finite subset of it satisfy its $n$-step transfer probability: $p_{ij}^{(n)}(r)={\displaystyle {\sum }_{k\in E}{p}_{ik}^{(m)}}{p}_{kj}^{(n-m)}(r+m)$ and $i,j\in E$,$1\le m\le n$.

Thus, in a continuous time Markov chain, $p_{ij}(t)$ has nonnegativity and normality, which follows from the C-K equation: $p_{ij}(s+t)={\displaystyle {\sum }_{k\in S}{p}_{ik}(s)p_{kj}(t)}$, i.e.:

$$P(s+t)=P(s)P(t)$$

(2)

Since the continuous-time Markov chain has the property of memorylessness, and the exponential distribution can be used to reflect the probability distribution of the amount of time between two independent random events, the fact that the continuous distribution has memorylessness means that it obeys the exponential distribution. So, the dwell time of the CTMC on each state can be regarded as obeying the exponential distribution, and thus the transfer rate matrix of the CTMC can be obtained, which is noted as the Q-matrix.

Proposition 1.

The elements of the CTMC transfer rate matrix are satisfied by the properties of the continuous time Markov chain:

$$q_{ii}=\underset{△t\to 0}{lim}\frac{p_{ii}(△t)-1}{△t}\le 0$$

(3)

$$q_{ij}=\underset{△t\to 0}{lim}\frac{p_{ij}(△t)}{△t}\ge 0,$$

(4)

Corollary 1.

$${\displaystyle {\sum }_j{q}_{ij}}=q_{ii}+{\displaystyle {\sum }_{j\ne i}{q}_{ij}}=\underset{△t\to 0}{lim}(\frac{p_{ii}(△t)-1}{△t}+\frac{p_{ij}(△t)}{△t})=\underset{△t\to 0}{lim}\frac{{\displaystyle {\sum }_j{p}_{ij}(△t)}-1}{△t}=0$$

i.e., the row sum is 0.

If the continuous-time Markov chain has constant return, i.e., the probability of starting from a state and returning to it is 1; it is known that the smooth distribution exists according to the sufficient condition for the Markov chain to have a smooth distribution is that it has a constant return state. For the probability distribution $\mathsf{\Pi }=({\pi }_i,i\in S)$, the probability of CTMC in the steady state is: $\mathsf{\Pi }=\mathsf{\Pi }P(t),\forall t\ge 0$. Combining the Q-matrices, the solution of the steady-state probability of CTMC can be obtained as:

$$\{\begin{array}{l}\mathsf{\Pi }Q=0\\ {\displaystyle {\sum }_{i\in S}{\pi }_i=1}\end{array}$$

(5)

Since the occurrence of potential stochastic processes (variational) of GSPN obeys the Poisson process, which in turn can be regarded as a kind of the most basic continuous-time Markov chain, the GSPN and the continuous-time Markov chain are considered to be isomorphic to each other. The related Markov chain can be created by analyzing the set of GSPNs that are reachable, and from there, the likelihood of the system being in steady state can be calculated. The following three steps can be used to roughly categorize the modelling work in this paper:

Step 1: The GSPN model is constructed by analyzing the dynamical system under current study.

Step 2: Construct a synchronized continuous-time Markov chain based on the existing GSPN model.

Step 3: The relevant performance analysis of the system is carried out using simulation, and each performance is evaluated.

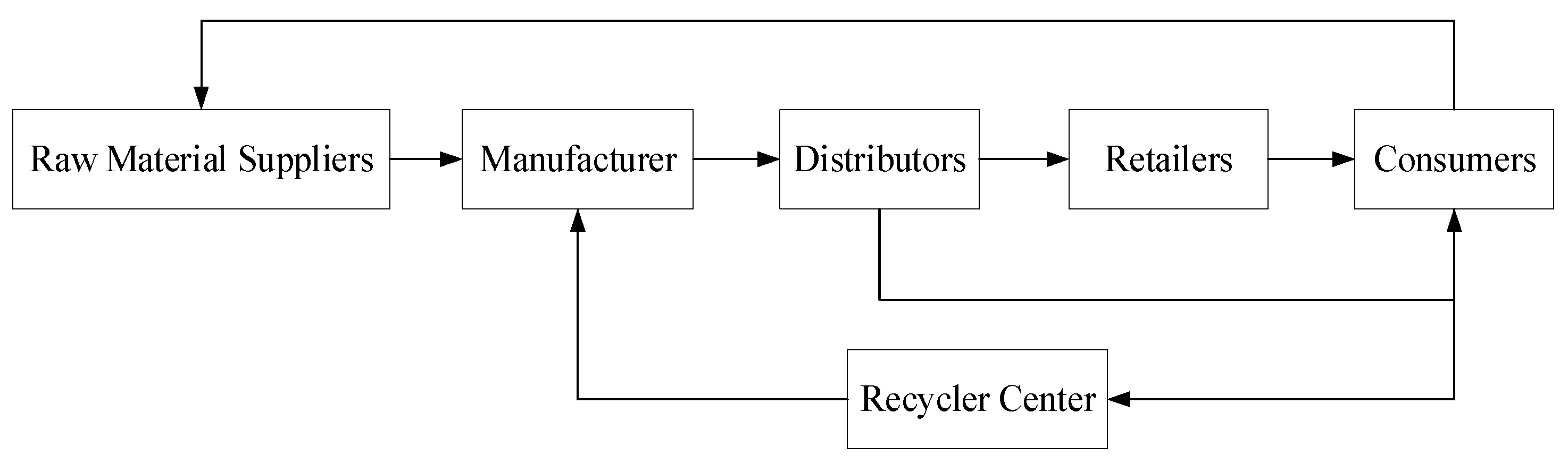
4. GSPN Model of Green Closed-Loop Supply Chain (GSPN of Green CLSC)

Green products are a class of products that are energy-efficient, water-saving, low-polluting, low-toxic, renewable, and recyclable, and are fundamentally different from traditional products because of their function of improving the environment and the quality of life of the society [6]. For example, compared with traditional fuel vehicles, new energy vehicles drive efficiency of the actual use of more than 85%, and can achieve 0 emissions or less emissions. The development of new energy vehicles cannot be separated from new energy batteries; compared to traditional batteries, new energy batteries have a higher energy density, longer service life, and will not produce harmful gases and waste in the process of use, which can effectively reduce the pollution of the environment. In this paper, we call the closed-loop supply chain of producing, selling, buying back, and remanufacturing green products a green closed-loop supply chain.

Consider the green CLSC network in Figure 1, which includes manufacturers of green products, suppliers of raw materials, distributors, retailers, and third-party recycling facilities. Suppliers deliver raw materials to manufacturers, who then create green products before giving them to distributors, all in accordance with the upstream and downstream principles, which begin with raw material distribution and end with waste product recycling. The distributor can choose to directly put the products into the market for sale or hand them over to the retailer, who will put them into the market for sale. The supplier adjusts the delivery of raw materials according to the feedback from the market on the products, and the third-party recycling center is responsible for recycling and processing the waste products and handing over the processed products to the manufacturer as raw materials for secondary production.

The circle in the GSPN model denotes the “location”, and the box represents the “transition”. Based on the green closed-loop supply chain network in Figure 1, the corresponding green closed-loop supply chain GSPN model is established by combining the relevant theory of generalized stochastic Petri nets [25], as shown in Figure 2.

In the GSPN of green CLSC, Figure 2 depicts the entire process of making green products, from the procurement of raw materials to the manufacturing process and, finally, the recycling of waste goods. The whole process contains 12 depots and 11 changes, and the specific meanings of each depot and change are shown in

Table 2. Meaning of location and transition in green closed-loop supply chain.

Location	Meaning	Transition	Meaning	$\mathbf{Time-Delay}\mathbf{Coefficient}{\mathit{\lambda }}_{\mathit{i}}$
$p_1$	Configure raw materials according to market demand	$t_1$	Raw material transportation process	2
$p_2$	Arrival of raw materials to manufacturers	$t_2$	Green product manufacturing process	3
$p_3$	Green product production is complete	$t_3$	Retailer contact and product marketing process	2
$p_4$	Green products arrive at distributors	$t_4$	Distribution process of distributors	2
$p_5$	Green products arrive at retailers	$t_5$	Retailers’ packaging processes	1
$p_6$	Green products are sold by distributors to consumers	$t_6$	Market sales process of green products	4
$p_7$	Green products sold by retailers to consumers	$t_7$	Marketing feedback process	1
$p_8$	Green product sales complete	$t_8$	The recycling process in the recycling center	4
$p_9$	Waste products to recycling centers for recycling	$t_9$	Develop demand plans for the market	1
$p_{10}$	Market attitude	$t_{10}$	Contact manufacturer for secondary process	2
$p_{11}$	Processing complete	$t_{11}$	Manufacturer secondary processing into raw material process	3
$p_{12}$	Treated product arrives at manufacturer

. The variables $t_1,t_2,\dots ,t_{11}$ are all time-delayed variables with negative exponential distribution, and the corresponding time-delay coefficients are ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_{11}$.

Proposition 2.

According to the generalized stochastic Petri diagram, there is a reachable graph of GSPN, and the average implementation rate is labeled on each arc in the reachable graph to obtain a Markov chain schematic with its isomorphism as Figure 3:

Based on the Markov chain schematic shown in Figure 3, the initial identifier of the system is one token (i.e., the number of resources in the network system, the number of tokens, i.e., the number of resources.) in the library, no token in the other libraries, and the initial state $M=(1,0,0,0,0,0,0,0,0,0,0,0)$, which enables to obtain the set of reachable identifiers of this GSPN of green CLSC.

Proposition 3.

The set of reachable identifiers for the green closed-loop supply chain GSPN model as

Table 3. Reachable markings of the green closed-loop supply chain GSPN.

State	$p_1$	$p_2$	$p_3$	$p_4$	$p_5$	$p_6$	$p_7$	$p_8$	$p_9$	$p_{10}$	$p_{11}$	$p_{12}$
$M_1$	1	0	0	0	0	0	0	0	0	0	0	0
$M_2$	0	1	0	0	0	0	0	0	0	0	0	0
$M_3$	0	0	1	0	0	0	0	0	0	0	0	0
$M_4$	0	0	0	1	0	0	0	0	0	0	0	0
$M_5$	0	0	0	0	1	0	0	0	0	0	0	0
$M_6$	0	0	0	0	0	1	0	0	0	0	0	0
$M_7$	0	0	0	0	0	1	1	0	0	0	0	0
$M_8$	0	0	0	0	0	0	0	1	0	0	0	0
$M_9$	0	0	0	0	0	0	0	0	1	0	0	0
$M_{10}$	0	0	0	0	0	0	0	0	0	1	0	0
$M_{11}$	0	0	0	0	0	0	0	0	0	1	1	0
$M_{12}$	0	0	0	0	0	0	0	0	0	0	0	1

:

Proposition 4.

The corresponding transfer rate matrix can be obtained from Propositions 1, 2, and 3 as:

$$Q=\left[\begin{array}{cccccccccccc}-2& 2& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& -3& 3& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& -2& 2& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& -4& 2& 2& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& -1& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& -4& 0& 4& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& -4& 4& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& -2& 1& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& -4& 0& 4& 0\\ 1& 0& 0& 0& 0& 0& 0& 0& 0& -1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& -2& 2\\ 0& 3& 0& 0& 0& 0& 0& 0& 0& 0& 0& -3\end{array}\right]$$

Proposition 5.

According to Equation (5) and Proposition 4, the set of smooth probability equations for the Markov chain in the smooth state among the variable states is obtained as:

$$\{\begin{array}{l}-2{\pi }_1+{\pi }_{10}=0\hfill \\ 2{\pi }_1-3{\pi }_2+3{\pi }_{12}=0\hfill \\ 3{\pi }_2-2{\pi }_3=0\hfill \\ 2{\pi }_3-4{\pi }_4=0\hfill \\ 2{\pi }_4-{\pi }_5=0\hfill \\ 2{\pi }_4-4{\pi }_6=0\hfill \\ {\pi }_5-4{\pi }_7=0\hfill \\ 4{\pi }_6+4{\pi }_7-2{\pi }_8=0\hfill \\ {\pi }_8-4{\pi }_9=0\hfill \\ {\pi }_8-{\pi }_{10}=0\hfill \\ 4{\pi }_9-2{\pi }_{11}=0\hfill \\ 2{\pi }_{11}-3{\pi }_{12}=0\hfill \\ {\displaystyle {\sum }_{i=1}^{12}{\pi }_i=1}\hfill \end{array}$$

(6)

Corollary 2.

Since this system of equations is a super definite linear system of equations, the most reliable results are obtained by using the left division method for the solution. Equation (6) is solved programmatically using Matlab software, and the solution obtained for this system of equations is the stability probability of the Markov chain in each state: $P(M_i)={\pi }_i(i=1,2,\dots ,12)$. The steady-state probabilities for each variational state are:

$$\begin{array}{l}P(M_1)=0.06897\hspace{1em}P(M_2)=0.09195\hspace{1em}P(M_3)=0.1379\hspace{1em}P(M_4)=0.06897\\ P(M_5)=0.1379\hspace{1em}P(M_6)=0.03448\hspace{1em}P(M_7)=0.03448\hspace{1em}P(M_8)=0.1379\\ P(M_9)=0.03448\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}P(M_{10})=0.1379\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}P(M_{11})=0.06897\\ P(M_{12})=0.04598\end{array}$$

Based on the calculated steady-state probabilities for each variation state, the system performance of the green closed-loop supply chain is examined.

5. Performance Analysis of Green Closed-Loop Supply Chain

5.1. Time Performance Analysis

One of the key indicators used to assess the performance of the green closed-loop supply chain system is how quickly it operates. The average delay time of its operation process refers to the total amount of time needed for the products to go from manufacturing to final recycling in a stable state. This time includes the transportation of raw materials, production of green products, sales of environmentally friendly products, recycling, and waste product disposal, as well as market feedback on the products.

Proposition 6.

Little’s law and the equilibrium principle state that when a system is stable, its inflow and outflow rates are equal, or that the inflow rate equals the outflow rate. Therefore, the following information can be used to determine the green closed-loop supply chain system’s average delay time:

$$\overline{T}=\frac{\overline{N}}{R(t,s)},$$

(7)

$\overline{N}$ is a subsystem’s average token number in a stable Petri net system, $R(t,s)$, is the token number of transitions per unit time into a subsystem, i.e., the token rate of transitions.

Corollary 3.

$\overline{T}$ directly reflects the operational efficiency of the whole system. The smaller the $\overline{T}$ value, the less time the system needs in the whole operation process.

Corollary 4.

In the Petri net model, the ratio of the time required for each business process to the total time required for the whole business process is the probability of the number of tokens owned by each library, that is, the probability of the busy period of each library, and its value reflects the operational efficiency of each business, which helps to further optimize the operation of the closed-loop supply chain system and strengthen the control of running time.

Let $P(M(s)=i)$ denote the probability that the token number contained in a bank is $i$, $\forall s\in S$, $\forall i\in N$. The token rate of change, $R(t,s)$, is the average token number per unit time into the posterior position $s$ of $t$.

Proposition 7.

According to the definition of the token rate of variation, the average token number is calculated as:

$$R(t,s)=W(t,s)\times U(t)\times \lambda$$

(8)

Define a subsystem of the GSPN: $P{N}^{\prime }=(P^{\prime },T^{\prime },F^{\prime },M_0,{\lambda }^{\prime })$, where $P^{\prime }=\left\{P-P_1\right\}$, $F^{\prime }$ are the sets of directed arcs remaining after $F$ removes the directed arcs connected to the library $P_1$. $T^{\prime }$ and ${\lambda }^{\prime }$ remain unchanged and are the same as $T$ and $\lambda$ in the original network. The quantity of tokens per unit time entering this subsystem is considered to be equal to the quantity of tokens per unit time leaving the library $P_1$, and the occurrence of all transitions is contained in this subsystem. Therefore, by computing the average delay time of this subsystem, it is possible to determine the average delay time of the closed-loop supply chain system as a whole.

In the defined subsystem $P{N}^{\prime }$, the quantity of entering tokens $P{N}^{\prime }$ per unit time is the number of tokens passing through the variation $t_1$ per unit time, and the transfer rate ${\lambda }_1=2$ during the occurrence of the variation $t_1$. Thus, the number of tokens entering the green closed-loop supply chain subsystem $P{N}^{\prime }$ per unit time is obtained as:

$$R(t,s)=R(t_1,P_2)=2\times 0.09195=0.1839$$

The green closed-loop supply chain subsystem token’s average value is:

$$\overline{N}={\displaystyle {\sum }_{i=2}^{12}P(M(P_i=1))=0.9309}$$

According to Equations (7) and (8), we obtain: $\overline{T}=\frac{\overline{N}}{R(t,s)}=5.062$ (unit time).

Corollary 5.

From the above calculation results, the average execution time of this green closed-loop supply chain is 5.062 units of time. The size of the average execution time  $\overline{T}$ can reflect the operation efficiency of the whole system organization structure, when the more token numbers enter the subsystem in unit time, the shorter the average execution time of the system as a whole, the higher the efficiency; the more average token numbers exist in the subsystem, the longer the average execution time of the system as a whole, and the lower the efficiency.

Corollary 6.

When managing the green closed-loop supply chain system, the overall operation efficiency of the system can be adjusted by adjusting the number of tokens in the subsystem. The more reasonable the overall design of the green closed-loop supply chain system is, the smoother the green action of the green products from production to sales to the recycling of waste products will be, so that enterprises can obtain more benefits at the cost of minimizing the loss of resources, the environment, and time, etc., and the higher the operational efficiency of the green closed-loop supply chain system is.

5.2. Utilization Analysis of Changes

The variation of the GSPN model corresponds to a workflow in a green closed-loop supply chain, and the analysis of variation utilization can guide management decisions in the management process. The outcome is equal to the total of the probability that all state identifiers that can be implemented are in the steady state. The utilization rate of variation $t_i$ is denoted by $U(t_i)$.

Proposition 8.

Based on the definition of variation utilization, the variation utilization of each workflow can be obtained:

$$U(t_1)=P(M(P_1=1))=0.06897,U(t_2)=P(M(P_2=1))=0.09195,$$

$$U(t_3)=P(M(P_3=1))=0.1379,U(t_4)=P(M(P_4=1))=0.06897$$

$$U(t_5)=P(M(P_5=1))=0.1379$$

$$U(t_6)=P(M(P_6=1))+P(M(P_7=1))=0.06896$$

$$U(t_7)=P(M(P_8=1))=0.1379,U(t_8)=P(M(P_9=1))=0.03448$$

$$U(t_9)=P(M(P_{10}=1))=0.1379,U(t_{10})=P(M(P_{11}=1))=0.06897$$

$$U(t_{11})=P(M(P_{12}=1))=0.04598$$

In the green closed-loop supply chain, the decision-makers should concentrate on controlling and overseeing the high-utilization processes before deciding whether to combine the low-utilization processes with other processes in light of the real scenario.

Corollary 7.

From the calculation results, it can be seen that: the system utilization rate of the processes of sales promotion process of distributors, packaging processing of retailers, market feedback, and market demand plan development are all 13.79%, which is significantly higher than the variation utilization rate of other links. This indicates that these links use the system significantly more than the other links in the whole operation process, so the decision makers need to focus on supervision and management of these links, while some of the links with lower utilization rates, such as recycling processing and conversion of waste products into raw materials, can be considered to be merged in order to improve the utilization rate.

5.3. Operational Efficiency Analysis

The green closed-loop supply chain covers the business process of how quickly green products can be produced, how rapidly green products can be sold in the consumer market, and how used products are recyclable and re-manufacturable. Its operational efficiency reflects the speed of process synergy of the green closed-loop supply chain, and also includes the close connection between the members of the green closed-loop supply chain. Operational efficiency is the key to the sale of green products and is one of the key indicators to evaluate the performance of the green closed-loop supply chain.

In the GSPN of green CLSC shown in Figure 2, the busyness of each link can be reflected by the number of tokens in the depot. If there are tokens in the depot, then the corresponding link in the green closed-loop supply chain process is busy, and vice versa; the more tokens in the depot, the busier it is. In this paper, we analyze the production efficiency ($A_1$), sales efficiency ($A_2$), and recycling efficiency ($A_3$) of green products by calculating the operational efficiency of green closed-loop supply chain business process.

Proposition 9.

According to Proposition 2 and Corollary 2, the production, marketing and recycling efficiencies of green products are obtained:

$$A_1=\left\{M(P_2=1),M(P_3=1)\right\}$$

$$A_2=\left\{M(P_5=1),M(P_6=1),M(P_7=1)\right\}$$

$$A_3=\left\{M(P_9=1),M(P_{11}=1)\right\}$$

Proposition 10.

According to Proposition 9, the operational efficiencies of production, distribution and recycling of green products can be obtained respectively:

$$P(A_1)=P(M(P_2=1))+P(M(P_3=1))=0.2299$$

$$P(A_2)=P(M(P_5=1))+P(M(P_6=1))+P(M(P_7=1))=0.2069$$

$$P(A_3)=P(M(P_9=1))+P(M(P_{11}=1))=0.1035$$

Corollary 8.

From the aforementioned calculation results, it can be seen that in the business process of the green closed-loop supply chain, the operational efficiency of the product production, and sales process is higher compared to the operational efficiency of the product recycling process of 0.1035. This indicates that the average execution time required for the production and sales stages of green products is longer than the time spent on recycling of used products. For the less efficient recycling segment, consideration could be given to reducing the number of staff in the segment or arranging additional other work when it is idle, etc., while for the more efficiently operated production and distribution segments, constant supervision and maintenance is required to achieve efficient and continuous operation of the segment.

6. Discussion and Conclusions

6.1. Discussion

Most scholars study green closed-loop supply chains from the perspective of optimal decision-making, for example, literature [12] studied the optimal decision-making problem of green supply chains under different government subsidy policies, but the study did not analyze the overall operational performance of green closed-loop supply chain systems. Although some scholars have utilized the mixed-integer linear programming method to study the closed-loop supply chain network [17,19], the subject of these studies is not the green closed-loop supply chain and at the same time did not take into account the impact of stochastic perturbations caused by the occurrence of stochastic events on the system as a whole. Compared with the same research on the green supply chain system as a whole [23], this paper starts from the perspective of the green supply chain system as a whole and analyzes the operational performance of the system as a whole as well as the operational efficiency of each link by using the relevant theories of the generalized stochastic Petri nets, which expands the scope of the application of the generalized stochastic Petri nets, enriches the relevant theories on the green closed-loop supply chain and generalized stochastic Petri nets, and at the same time provides a theoretical basis for the subsequent research on the green closed-loop supply chain system as a whole.

6.2. Research Conclusions

Due to the random events occurring in real life, it will affect the product market and cause the system operation to change from fixed time to random time. This paper takes the green closed-loop supply chain as the research object and utilizes the generalized stochastic Petri nets to study the operational performance of the green closed-loop supply chain system as a whole and the operational efficiency problem of each link.

It is found that:

(1)

When the green closed-loop supply chain system as a whole is affected by the market random events, the required transfer rate between the links will constantly change, and at this time, the steady state probability of the system as a whole will also change.

(2)

When the green closed-loop supply chain system as a whole reaches a steady state, the time performance of the system as a whole can be obtained based on the steady state probability of each link, and the greater the number of tokens passing through the subsystems per unit of time, the shorter the average operation time required for the system as a whole.

(3)

From a manufacturer’s perspective, in a constant market environment, decision makers need to focus on monitoring the following segments: marketing, packaging and processing, market feedback, and market demand planning, which require a higher percentage of time. Since the third-party recycling center only begin operations when used goods are collected for disposal, the time required to run this segment is much less significant.

(4)

From the perspective of green products, the average execution time of the production and sales process of products is longer than the average execution time of the re-cycling and treatment process.

Our findings have the following managerial implications:

(1)

For each manufacturer in the green closed-loop supply chain, it is necessary to maintain the stability of the system as a whole, and each manufacturer pays attention to the market risk and takes the initiative to reduce the impact of non-systematic risks that may exist during the operation of green products, so as to ensure that the system as a whole can operate smoothly and efficiently.

(2)

From the perspective of the system as a whole, decision makers need to focus on the overall operational performance, as well as the utilization level of each member and each link, and make constant adjustments to the green closed-loop supply chain system, so as to make it run smoothly and shorten the time period required for the system operation as much as possible, so as to realize a good and high-yield cycle.

6.3. Limitations and Challenges

In this section, we focus on some limitations of this paper. There are the following shortcomings in this paper: firstly, this paper uses the relevant theory of generalized stochastic Petri nets to model and analyze the green closed-loop supply chain system. Although this method can simplify the overall state space of the system to a certain extent, with the exponential increase of the number of markers, it will be more and more difficult to analyze the performance of the system. Secondly, this paper only considers a simple green closed-loop supply chain system operation model, but in the actual operation of the market, the overall structure of the green closed-loop supply chain system is much more complex.

6.4. Future Research

In this section, we focus on providing new ideas for future research. In future re-search, we can further explore derivative models that are isomorphic to the GSPN and capable of solving for more complex supply chain system structures for the convenience of solving. In addition, future research can cover more complex green closed-loop supply chain networks, where the greenness level of green products often affects the decision makers in each link, so the impact of the greenness level of products on the decision makers in the supply chain can be investigated in the future.