Comparing Darcy’s Law and the Brinkman Equation for Numerical Simulations of Saltwater Intrusion
Abstract
:1. Introduction
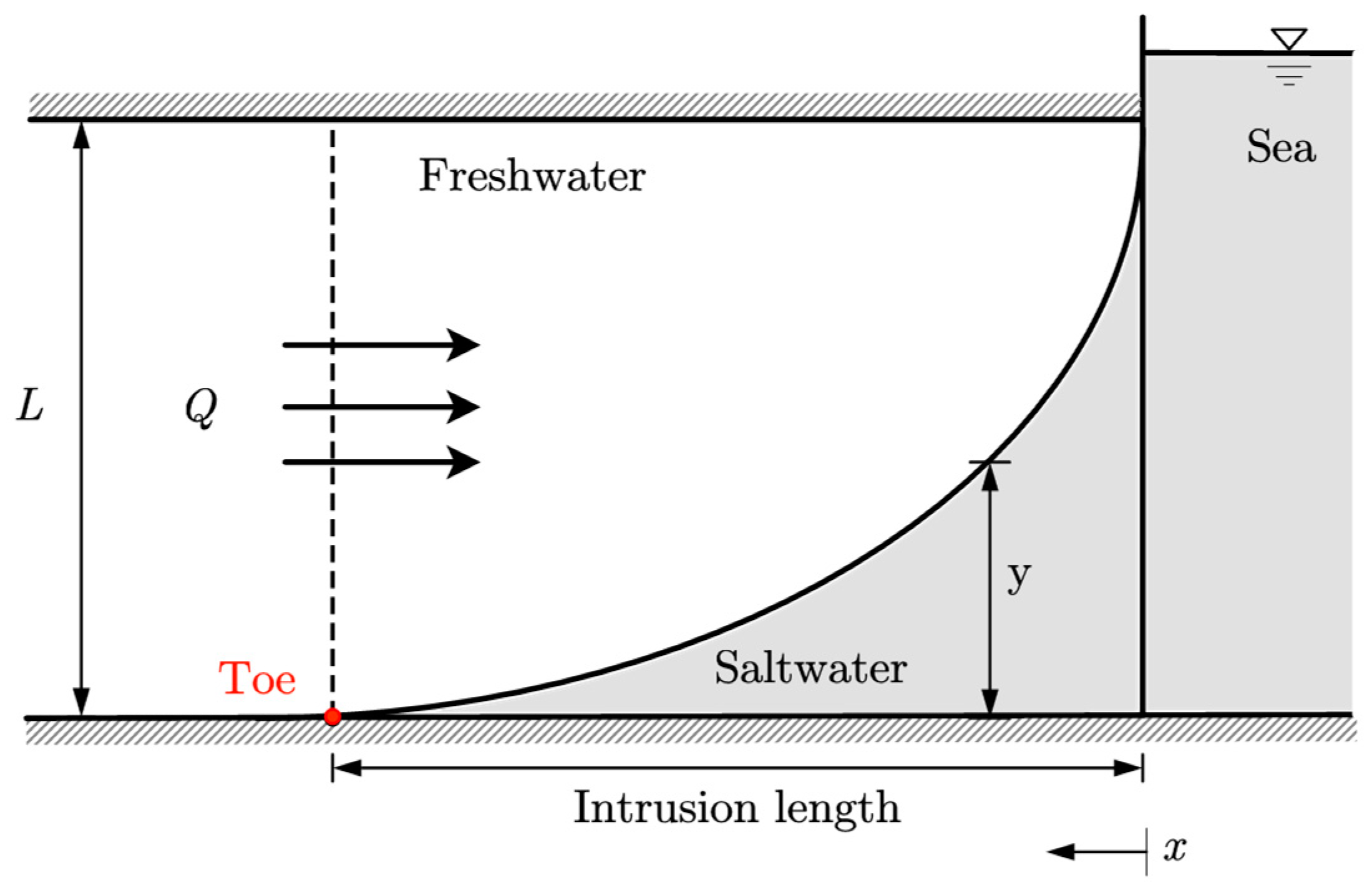
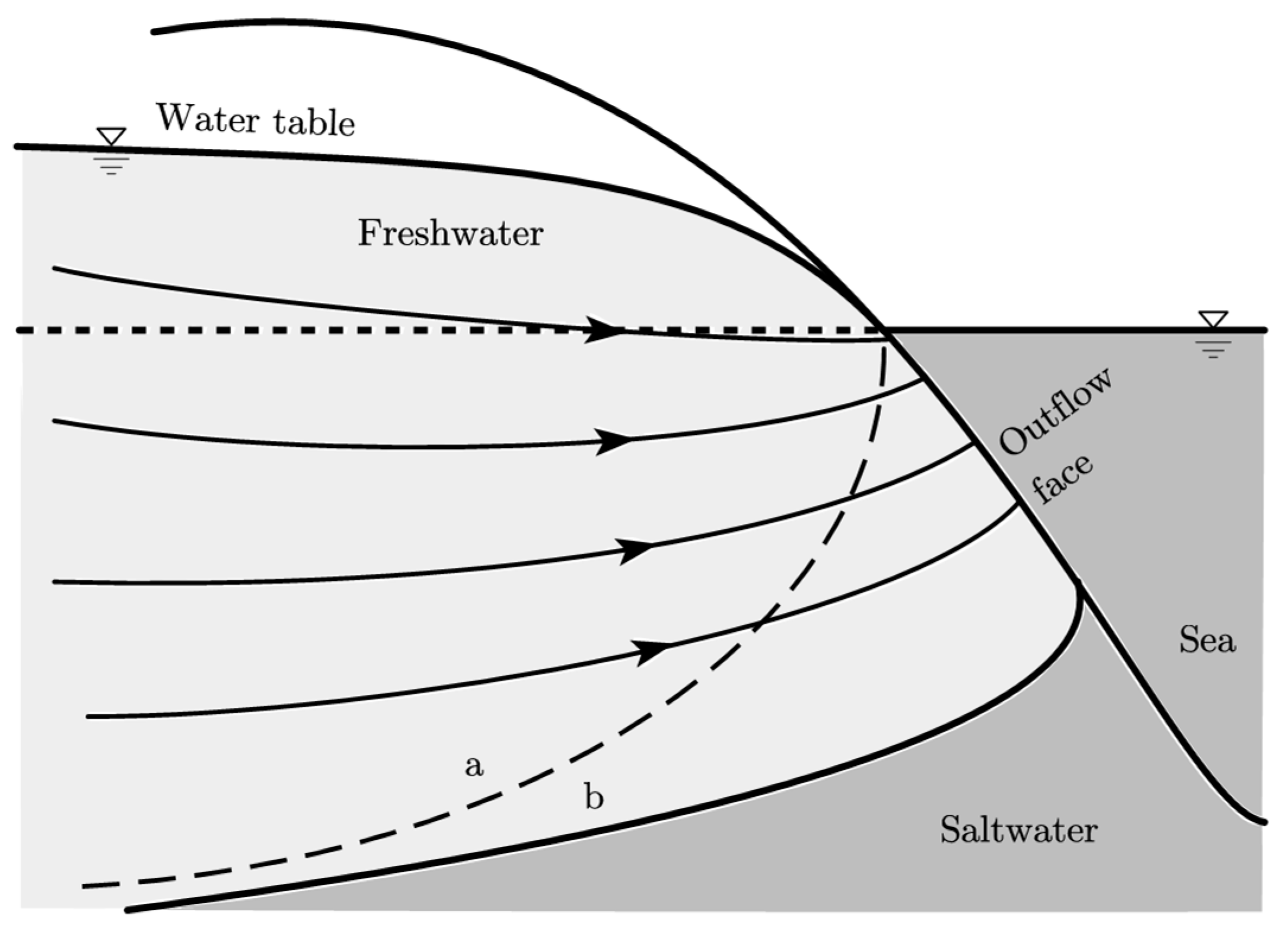
2. Materials and Methods
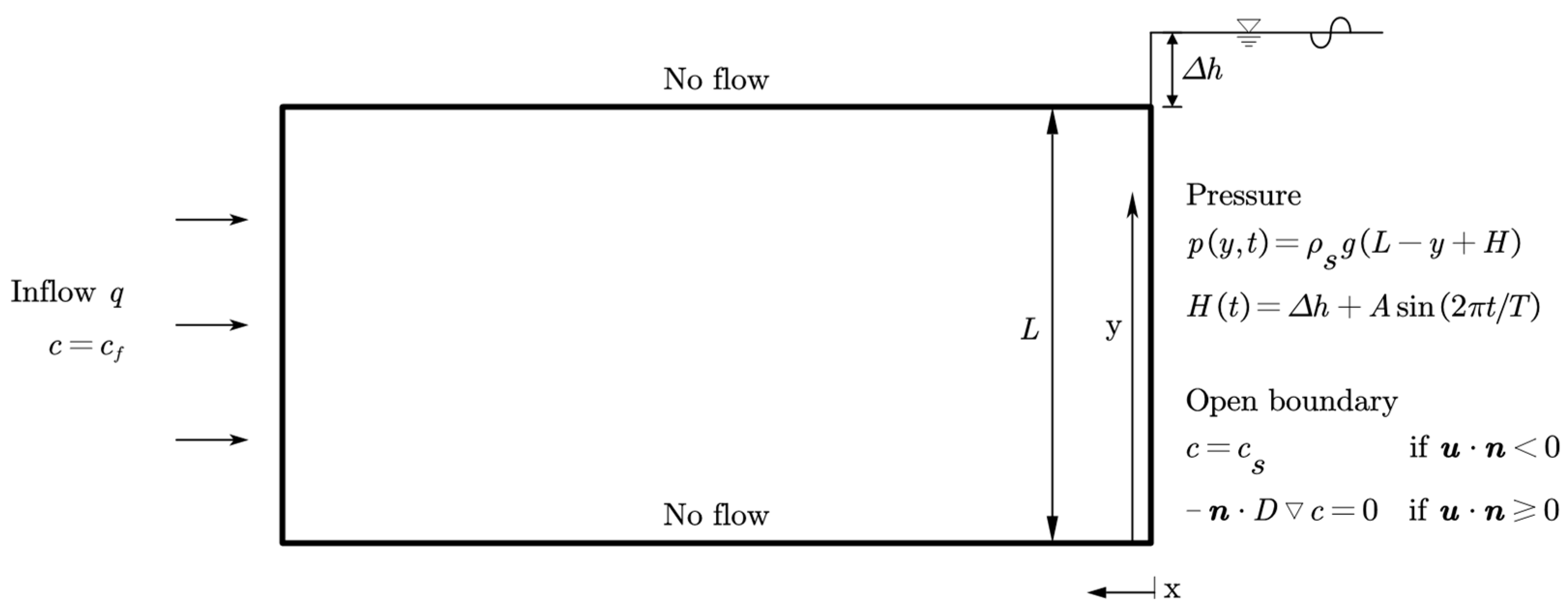
2.1. Numerical Models
2.2. Analytical Solutions
3. Results
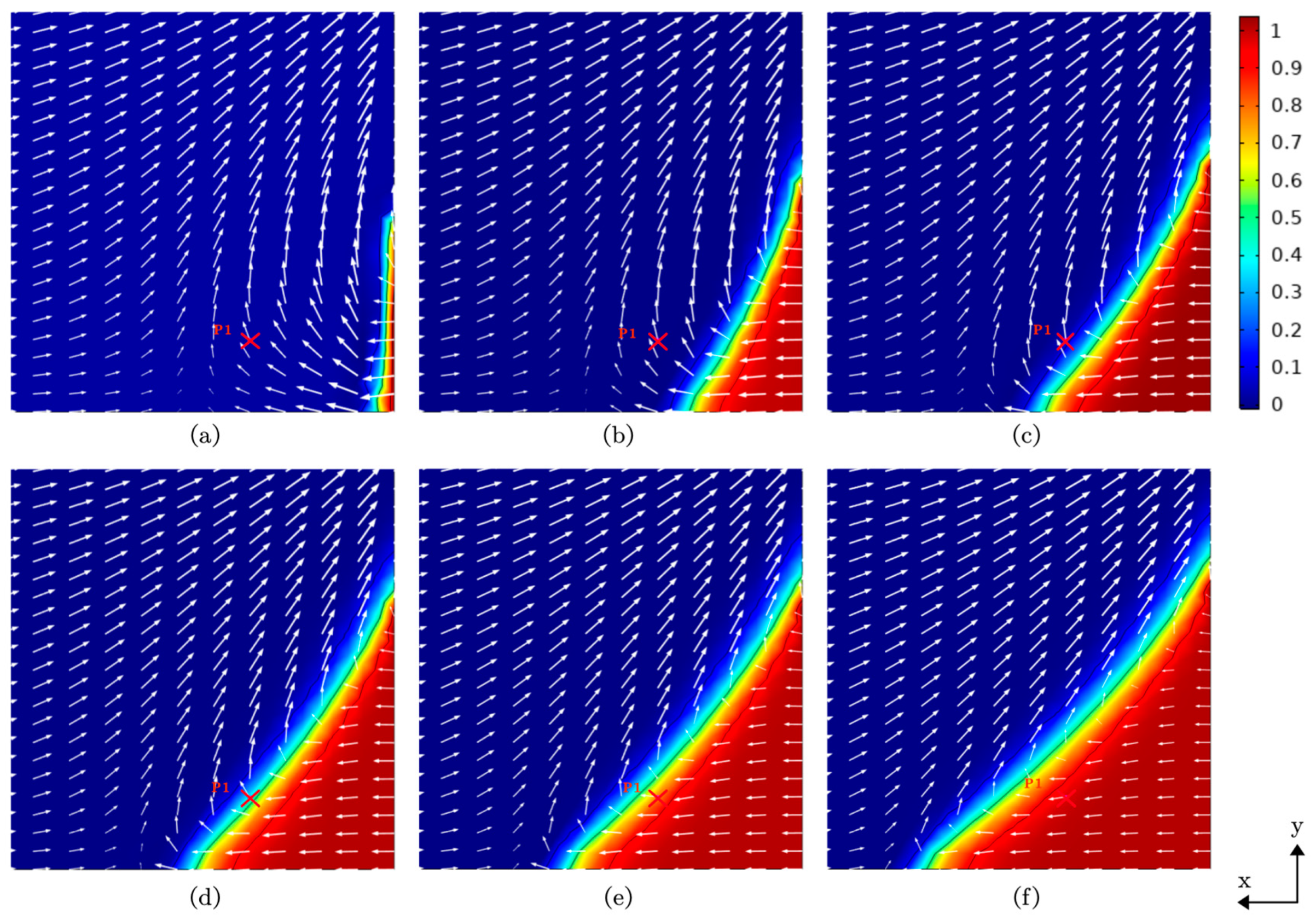
3.1. Numerical Model Validation
3.2. Comparisons of the Two Models
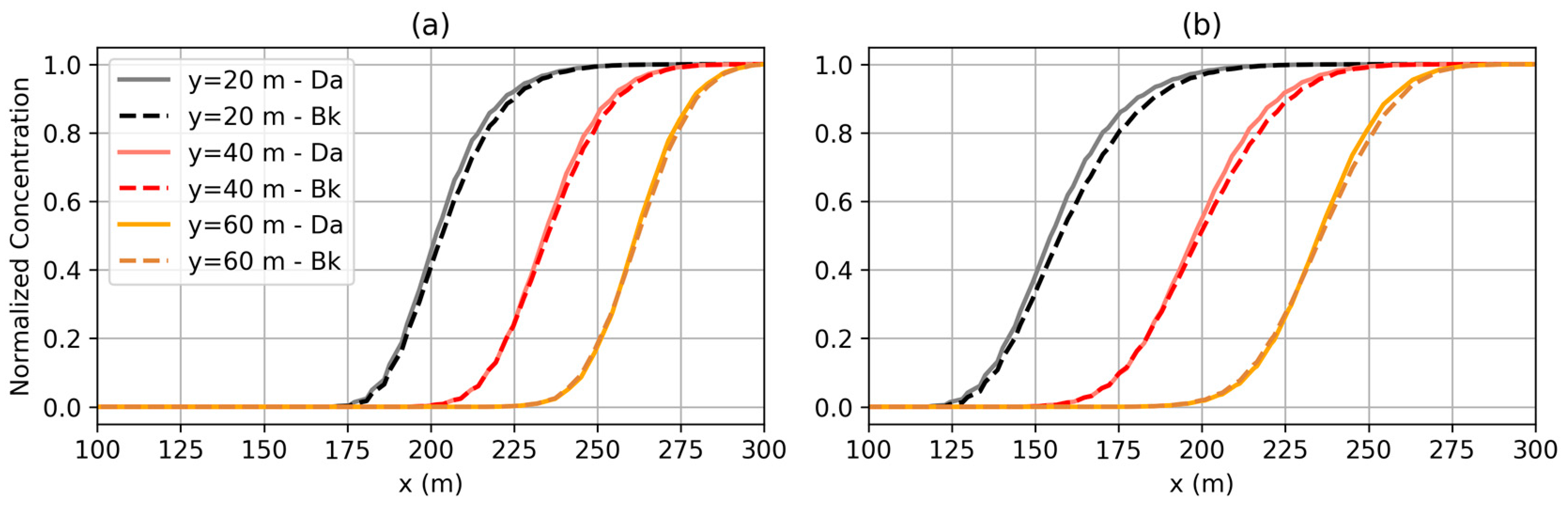
3.2.1. Aquifer Properties
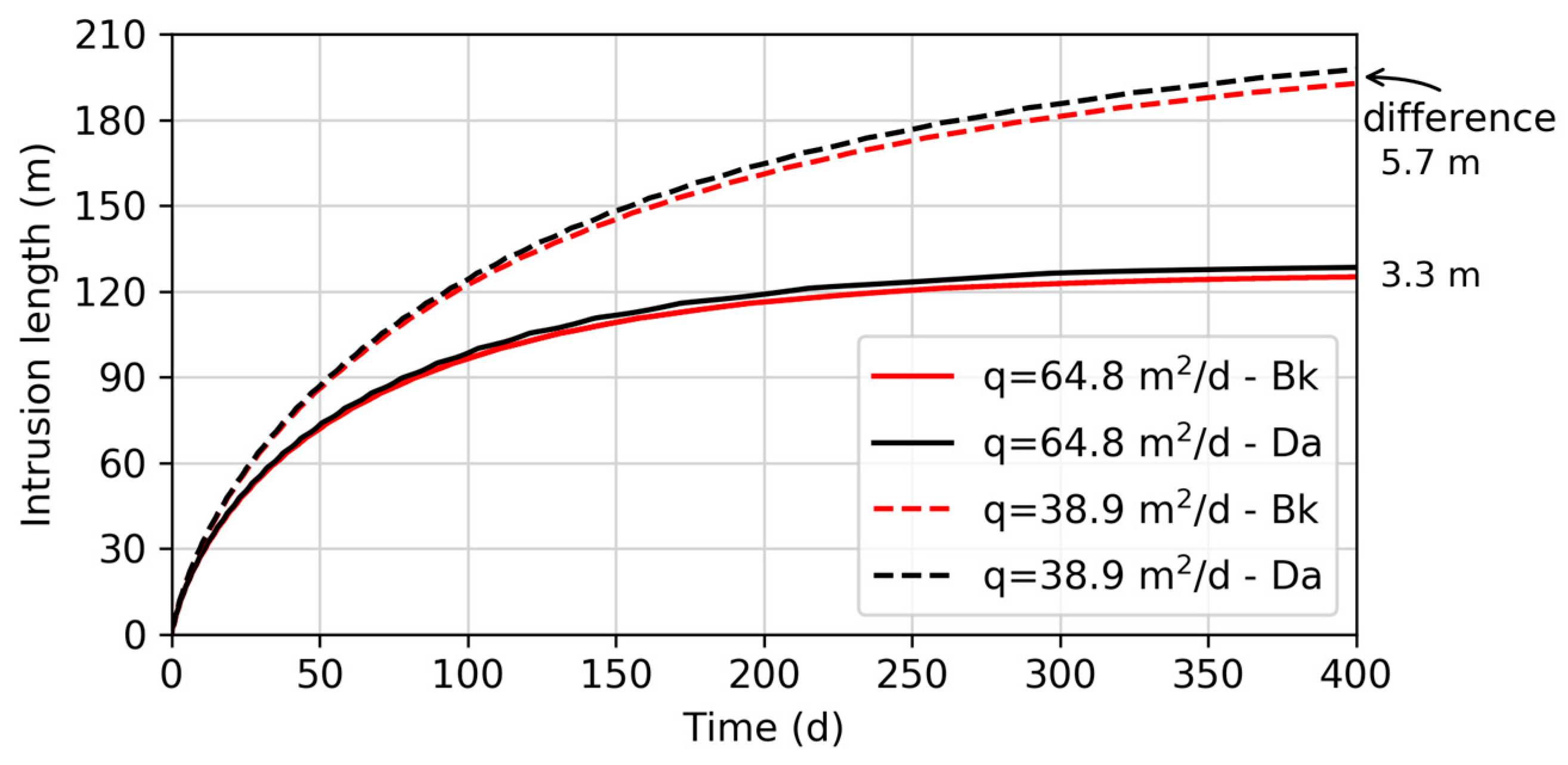
3.2.2. Inflow Rate
3.2.3. Tidal Effects
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maul, G.A.; Duedall, I.W. Demography of Coastal Populations. In Encyclopedia of Coastal Science; Finkl, C.W., Ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2019; pp. 692–700. ISBN 978-3-319-93805-9. [Google Scholar]
- Werner, A.D.; Bakker, M.; Post, V.E.A.; Vandenbohede, A.; Lu, C.; Ataie-Ashtiani, B.; Simmons, C.T.; Barry, D.A. Seawater intrusion processes, investigation and management: Recent advances and future challenges. Adv. Water Resour. 2013, 51, 3–26. [Google Scholar] [CrossRef]
- Michael, H.A.; Russoniello, C.J.; Byron, L.A. Global assessment of vulnerability to sea-level rise in topography-limited and recharge-limited coastal groundwater systems. Water Resour. Res. 2013, 49, 2228–2240. [Google Scholar] [CrossRef]
- Hussain, M.S.; Abd-Elhamid, H.F.; Javadi, A.A.; Sherif, M.M. Management of Seawater Intrusion in Coastal Aquifers: A Review. Water 2019, 11, 2467. [Google Scholar] [CrossRef]
- Zhang, H.; Hocking, G.C.; Barry, D.A. An analytical solution for critical withdrawal of layered fluid through a line sink in a porous medium. J. Aust. Math. Soc. Ser. B Appl. Math. 1997, 39, 271–279. [Google Scholar] [CrossRef]
- Lu, C.; Xin, P.; Li, L.; Luo, J. Seawater intrusion in response to sea-level rise in a coastal aquifer with a general-head inland boundary. J. Hydrol. 2015, 522, 135–140. [Google Scholar] [CrossRef]
- Cartwright, N.; Li, L.; Nielsen, P. Response of the salt–freshwater interface in a coastal aquifer to a wave-induced groundwater pulse: Field observations and modelling. Adv. Water Resour. 2004, 27, 297–303. [Google Scholar] [CrossRef]
- Post, V.E.A.; Houben, G.J.; van Engelen, J. What is the Ghijben-Herzberg principle and who formulated it? Hydrogeol. J. 2018, 26, 1801–1807. [Google Scholar] [CrossRef]
- Bear, J.; Cheng, A.H.-D. Modeling Groundwater Flow and Contaminant Transport; Springer: Dordrecht, The Netherlands; London, UK, 2010; ISBN 9781402066825. [Google Scholar]
- Fahs, M.; Ataie-Ashtiani, B.; Younes, A.; Simmons, C.T.; Ackerer, P. The Henry problem: New semianalytical solution for velocity-dependent dispersion. Water Resour. Res. 2016, 52, 7382–7407. [Google Scholar] [CrossRef]
- Zhang, H.; Hocking, G.C. Withdrawal of layered fluid through a line sink in a porous medium. J. Aust. Math. Soc. Ser. B Appl. Math. 1996, 38, 240–254. [Google Scholar] [CrossRef]
- Lu, C.; Chen, Y.; Zhang, C.; Luo, J. Steady-state freshwater–seawater mixing zone in stratified coastal aquifers. J. Hydrol. 2013, 505, 24–34. [Google Scholar] [CrossRef]
- Yu, X.; Xin, P.; Lu, C. Seawater intrusion and retreat in tidally-affected unconfined aquifers: Laboratory experiments and numerical simulations. Adv. Water Resour. 2019, 132, 103393. [Google Scholar] [CrossRef]
- Felder, C.; Oltean, C.; Buès, M.A. Density-driven flow and transport in saturated porous media. Salt solute infiltration into Hele-Shaw cells—A comparison between numerical and experimental results. In Computational Methods in Water Resources, Proceedings of the XIVth International Conference on Computational Methods in Water Resources (CMWR XIV), Delft, The Netherlands, 23–28 June 2002; Hassanizadeh, S.M., Schotting, R.J., Gray, W.G., Pinder, G.F., Eds.; Elsevier: Amsterdam, The Netherlands, 2002; pp. 515–522. ISBN 0167-5648. [Google Scholar]
- Zhang, Q.; Volker, R.E.; Lockington, D.A. Influence of seaward boundary condition on contaminant transport in unconfined coastal aquifers. J. Contam. Hydrol. 2001, 49, 201–215. [Google Scholar] [CrossRef]
- Zhang, Q.; Volker, R.E.; Lockington, D.A. Numerical investigation of seawater intrusion at Gooburrum, Bundaberg, Queensland, Australia. Hydrogeol. J. 2004, 12, 674–687. [Google Scholar] [CrossRef]
- Henry, H.R. Effects of Dispersion on Salt Water Encroachment in Coastal Aquifers. U.S. Geol. Surv. Water Supply Pap. 1964, 1613-C, C70–C84. [Google Scholar]
- Kuan, W.K.; Xin, P.; Jin, G.; Robinson, C.E.; Gibbes, B.; Li, L. Combined Effect of Tides and Varying Inland Groundwater Input on Flow and Salinity Distribution in Unconfined Coastal Aquifers. Water Resour. Res. 2019, 55, 8864–8880. [Google Scholar] [CrossRef]
- Mastrocicco, M.; Busico, G.; Colombani, N.; Vigliotti, M.; Ruberti, D. Modelling Actual and Future Seawater Intrusion in the Variconi Coastal Wetland (Italy) Due to Climate and Landscape Changes. Water 2019, 11, 1502. [Google Scholar] [CrossRef]
- Abdoulhalik, A.; Ahmed, A.A. Transience of seawater intrusion and retreat in response to incremental water-level variations. Hydrol. Process. 2018, 32, 2721–2733. [Google Scholar] [CrossRef]
- AL-ALI, S.; Hocking, G.C.; Farrow, D.E.; Zhang, H. A spectral modelling approach for fluid flow into a line sink in a confined aquifer. Eur. J. Appl. Math. 2022, 33, 960–981. [Google Scholar] [CrossRef]
- Vu, T.-D.; Ni, C.-F.; Li, W.-C.; Truong, M.-H.; Hsu, S.M. Predictions of groundwater vulnerability and sustainability by an integrated index-overlay method and physical-based numerical model. J. Hydrol. 2021, 596, 126082. [Google Scholar] [CrossRef]
- Barzehkar, M.; Parnell, K.E.; Soomere, T.; Dragovich, D.; Engström, J. Decision support tools, systems and indices for sustainable coastal planning and management: A review. Ocean. Coast. Manag. 2021, 212, 105813. [Google Scholar] [CrossRef]
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon: Exposition et application des principes à suivre et des formules à employer dans les questions de distribution d’eau ouvrage terminé, par un appendice relatif aux fournitures d’eau de plusieurs villes au filtrage des eaux; Dalmont, V., Ed.; Libraire des Corps imperiaux des ponts et chaussées et des mines: Paris, France, 1856. [Google Scholar]
- Brinkman, H.C. A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. 1949, 1, 27–34. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media, 4th ed.; Springer Science + Business Media: New York, NY, USA, 2013; ISBN 9781461455400. [Google Scholar]
- Ehlers, W. Darcy, Forchheimer, Brinkman and Richards: Classical hydromechanical equations and their significance in the light of the TPM. Arch. Appl. Mech. 2022, 92, 619–639. [Google Scholar] [CrossRef]
- Chabanon, M.; Valdés-Parada, F.J.; Ochoa-Tapia, J.A.; Goyeau, B. Large-scale model of flow in heterogeneous and hierarchical porous media. Adv. Water Resour. 2017, 109, 41–57. [Google Scholar] [CrossRef]
- Tam, C.K.W. The drag on a cloud of spherical particles in low Reynolds number flow. J. Fluid Mech. 1969, 38, 537–546. [Google Scholar] [CrossRef]
- Auriault, J.-L.; Geindreau, C.; Boutin, C. Filtration Law in Porous Media with Poor Separation of Scales. Transp. Porous Med. 2005, 60, 89–108. [Google Scholar] [CrossRef]
- Rubinstein, J. Effective equations for flow in random porous media with a large number of scales. J. Fluid Mech. 1986, 170, 379–383. [Google Scholar] [CrossRef]
- Durlofsky, L.; Brady, J.F. Analysis of the Brinkman equation as a model for flow in porous media. Phys. Fluids 1987, 30, 3329. [Google Scholar] [CrossRef]
- Liang, M.; Fu, C.; Xiao, B.; Luo, L.; Wang, Z. A fractal study for the effective electrolyte diffusion through charged porous media. Int. J. Heat Mass Transf. 2019, 137, 365–371. [Google Scholar] [CrossRef]
- Liang, M.; Liu, Y.; Xiao, B.; Yang, S.; Wang, Z.; Han, H. An analytical model for the transverse permeability of gas diffusion layer with electrical double layer effects in proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2018, 43, 17880–17888. [Google Scholar] [CrossRef]
- Long, G.; Liu, Y.; Xu, W.; Zhou, P.; Zhou, J.; Xu, G.; Xiao, B. Analysis of Crack Problems in Multilayered Elastic Medium by a Consecutive Stiffness Method. Mathematics 2022, 10, 4403. [Google Scholar] [CrossRef]
- Sheibani, S.; Ataie-Ashtiani, B.; Safaie, A.; Simmons, C.T. Influence of lakebed sediment deposit on the interaction of hypersaline lake and groundwater: A simplified case of lake Urmia, Iran. J. Hydrol. 2020, 588, 125110. [Google Scholar] [CrossRef]
- Sayyah Alborzi, Z.; Amini, Y.; Amirabedi, P.; Raveshiyan, S.; Hassanvand, A. Computational Fluid Dynamics Simulation of a Membrane Contactor for CO2 Separation: Two Types of Membrane Evaluation. Chem. Eng. Technol. 2023, 46. [Google Scholar] [CrossRef]
- COMSOL Multiphysics, Version 5.6; Introduction to COMSOL Multiphysics. Available online: https://cdn.comsol.com/doc/5.6/IntroductionToCOMSOLMultiphysics.pdf (accessed on 21 April 2021).
- Bear, J.; Bachmat, Y. Introduction to Modeling of Transport Phenomena in Porous Media; Kluwer Academic: Dordrecht, The Netherlands; London, UK, 1990; ISBN 9789400919266. [Google Scholar]
- Chen, L.; Hu, B.X.; Dai, H.; Zhang, X.; Xia, C.-A.; Zhang, J. Characterizing microbial diversity and community composition of groundwater in a salt-freshwater transition zone. Sci. Total Environ. 2019, 678, 574–584. [Google Scholar] [CrossRef]
- Muhsun, S.S.; Saleh, M.S.; Qassim, A.R. Physical and CFD Simulated Models to Analyze the Contaminant Transport through Porous Media under Hydraulic Structures. KSCE J. Civ. Eng. 2020, 24, 3674–3691. [Google Scholar] [CrossRef]
- Pažanin, I.; Radulović, M. Effects of the viscous dissipation on the Darcy-Brinkman flow: Rigorous derivation of the higher-order asymptotic model. Appl. Math. Comput. 2020, 386, 125479. [Google Scholar] [CrossRef]
- Hung, Y.-M.; Tso, C.P. Effects of viscous dissipation on fully developed forced convection in porous media. Int. Commun. Heat Mass Transf. 2009, 36, 597–603. [Google Scholar] [CrossRef]
- Werner, A.D.; Simmons, C.T. Impact of sea-level rise on sea water intrusion in coastal aquifers. Ground Water 2009, 47, 197–204. [Google Scholar] [CrossRef]
- Teng, B.; Luo, W.; Chen, Z.; Kang, B.; Chen, L.; Wang, T. A comprehensive study of the effect of Brinkman flow on the performance of hydraulically fractured wells. J. Pet. Sci. Eng. 2022, 213, 110355. [Google Scholar] [CrossRef]
- Marušić-Paloka, E.; Pažanin, I.; Marušić, S. Comparison between Darcy and Brinkman laws in a fracture. Appl. Math. Comput. 2012, 218, 7538–7545. [Google Scholar] [CrossRef]
- Salinger, A.G.; Aris, R.; Derby, J.J. Finite element formulations for large-scale, coupled flows in adjacent porous and open fluid domains. Int. J. Numer. Meth. Fluids 1994, 18, 1185–1209. [Google Scholar] [CrossRef]





| Parameters | Values |
|---|---|
| Seawater density | 1024 kg/m3 |
| Freshwater density | 1000 kg/m3 |
| Dynamic viscosity μ | 0.001 Pa·s |
| Normalized seawater concentration | 1 mol/m3 |
| Normalized freshwater concentration | 0 mol/m3 |
| Fluid diffusion coefficient | 3.56 × 10−6 m2/s |
| Porosity ε | 0.4 |
| Tortuosity τ | 1 |
| Hydraulic conductivity | 43.2 m/d |
| Longitudinal dispersivity | 0.005 m |
| Transverse dispersivity | 0.0005 m |
| Inflow rate | 64.8 m2/d |
| Raised sea level | 3 m |
| Parameters | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| Tidal amplitude A (m)/period T (h) | 0 | 0 | 0 | 2/12 |
| Hydraulic conductivity K (m/d) | 43.2 | 60.5 | 43.2 | 43.2 |
| Inflow rate q (m2/d) | 64.8 | 64.8 | 38.9 | 64.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, J.; Zhang, H. Comparing Darcy’s Law and the Brinkman Equation for Numerical Simulations of Saltwater Intrusion. Sustainability 2023, 15, 13287. https://doi.org/10.3390/su151813287
Yao J, Zhang H. Comparing Darcy’s Law and the Brinkman Equation for Numerical Simulations of Saltwater Intrusion. Sustainability. 2023; 15(18):13287. https://doi.org/10.3390/su151813287
Chicago/Turabian StyleYao, Jingwei, and Hong Zhang. 2023. "Comparing Darcy’s Law and the Brinkman Equation for Numerical Simulations of Saltwater Intrusion" Sustainability 15, no. 18: 13287. https://doi.org/10.3390/su151813287





