Research on Design and Control Strategy of Novel Independent Metering System
Abstract
:1. Introduction
1.1. System Design
1.2. Control Strategy
- (1)
- The disadvantages of the independent metering composed of the traditional cartridge proportional valve were investigated. Moreover, a scheme of the independent metering valve was proposed based on pilot hydraulic control, and its working principle was explained. Combined with the design requirements of pressure and flow, the two-valve spool structure and valve body size were designed, the main valve spool simulation model was built, and the parameters affecting the dynamic response characteristics of the main spool were investigated and then optimized.
- (2)
- The simulation model of the independent metering system based on pilot hydraulic control and the traditional valve control system was built, and the two-chamber pressure of the hydraulic actuator and pump source power variation characteristics under constant load conditions were investigated to prove the feasibility and energy-saving of the proposed scheme. A control strategy was proposed following the load force direction prediction and two-chamber pressure switching, which was applied to the independent metering system following pilot hydraulic control. The effectiveness and reliability of the proposed control strategy were verified through simulation.
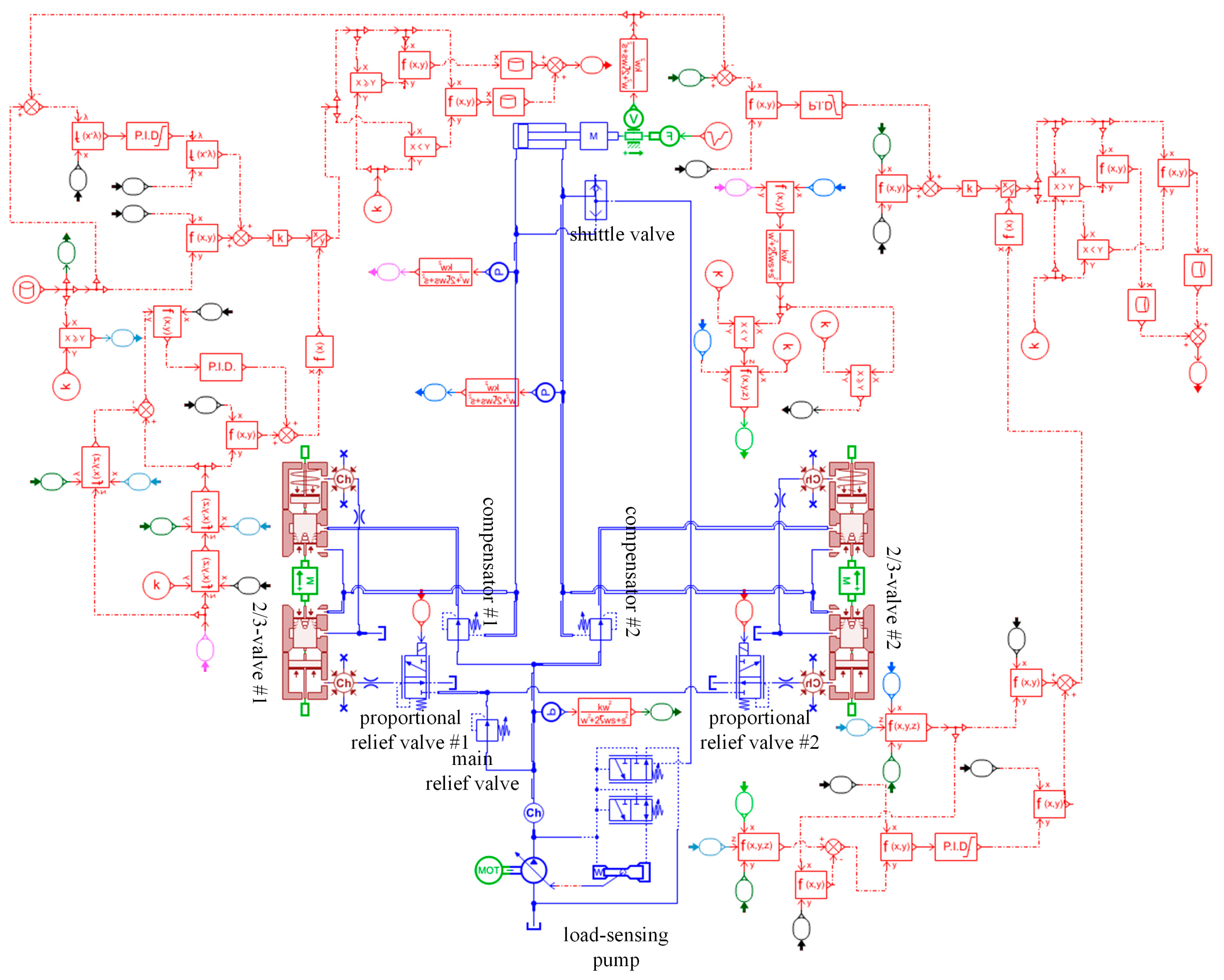
2. Introduction of New Independent Metering System
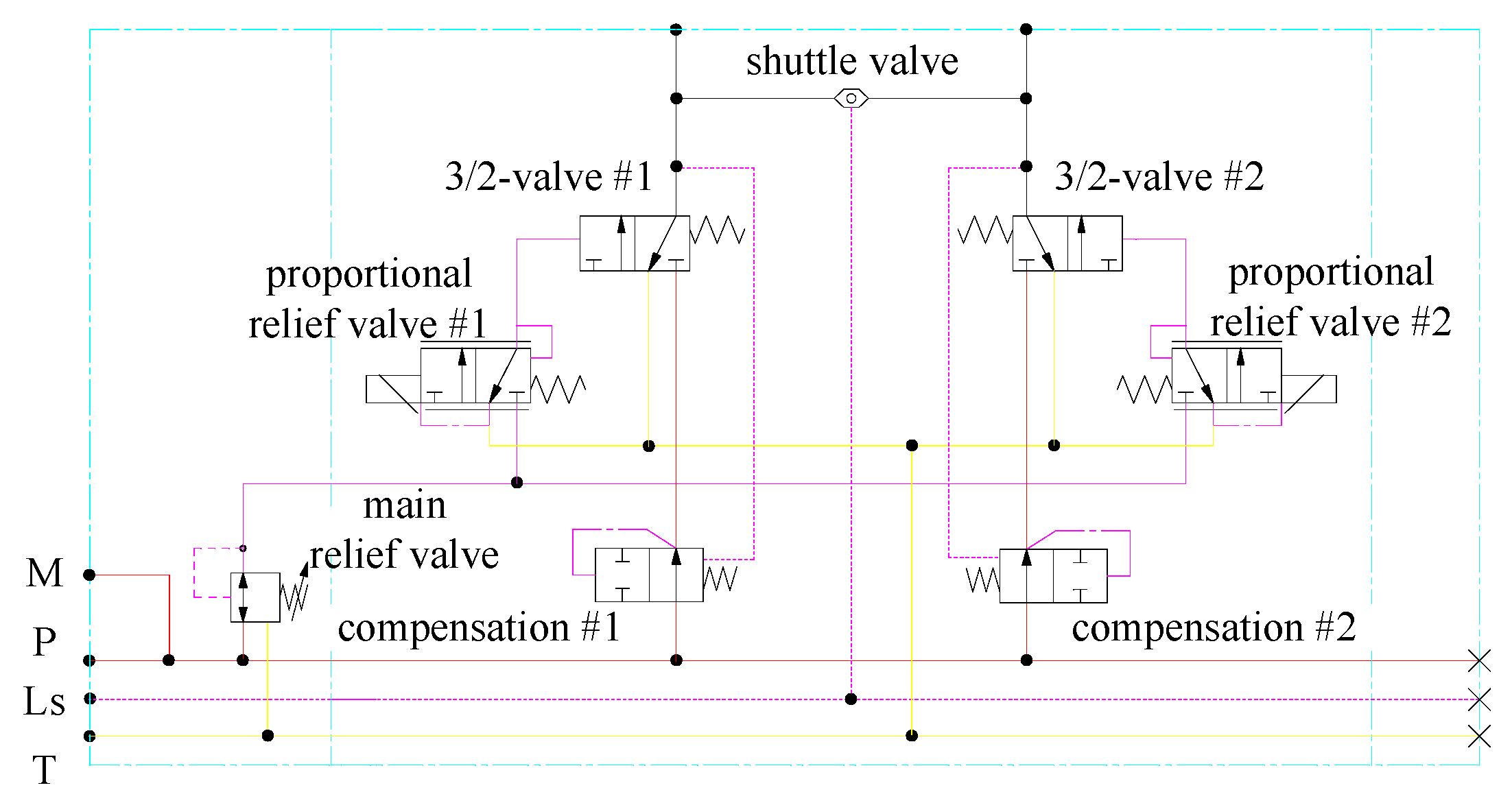
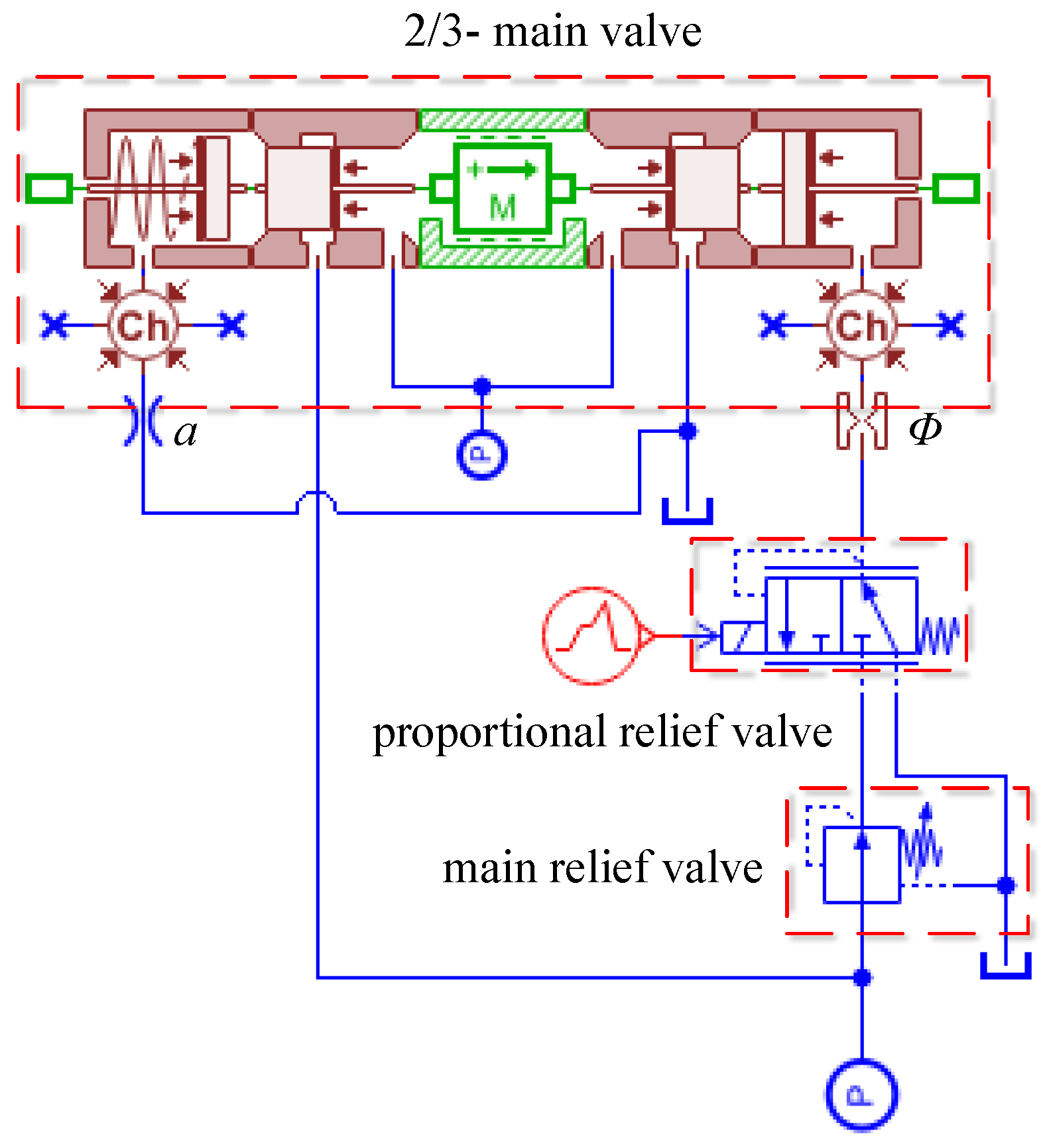
2.1. The Principle of New Control Valve
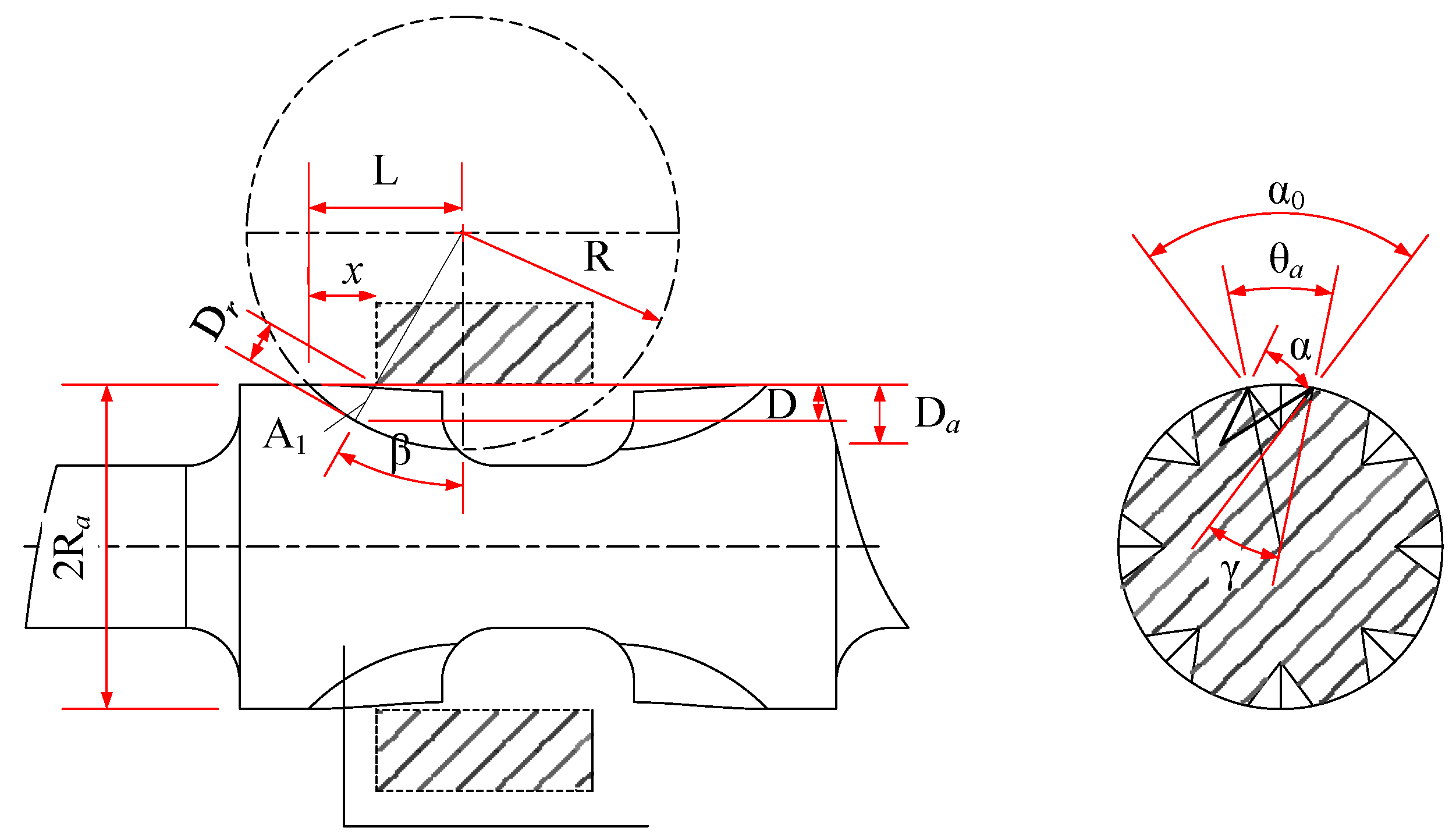
2.2. Design of Control Valve
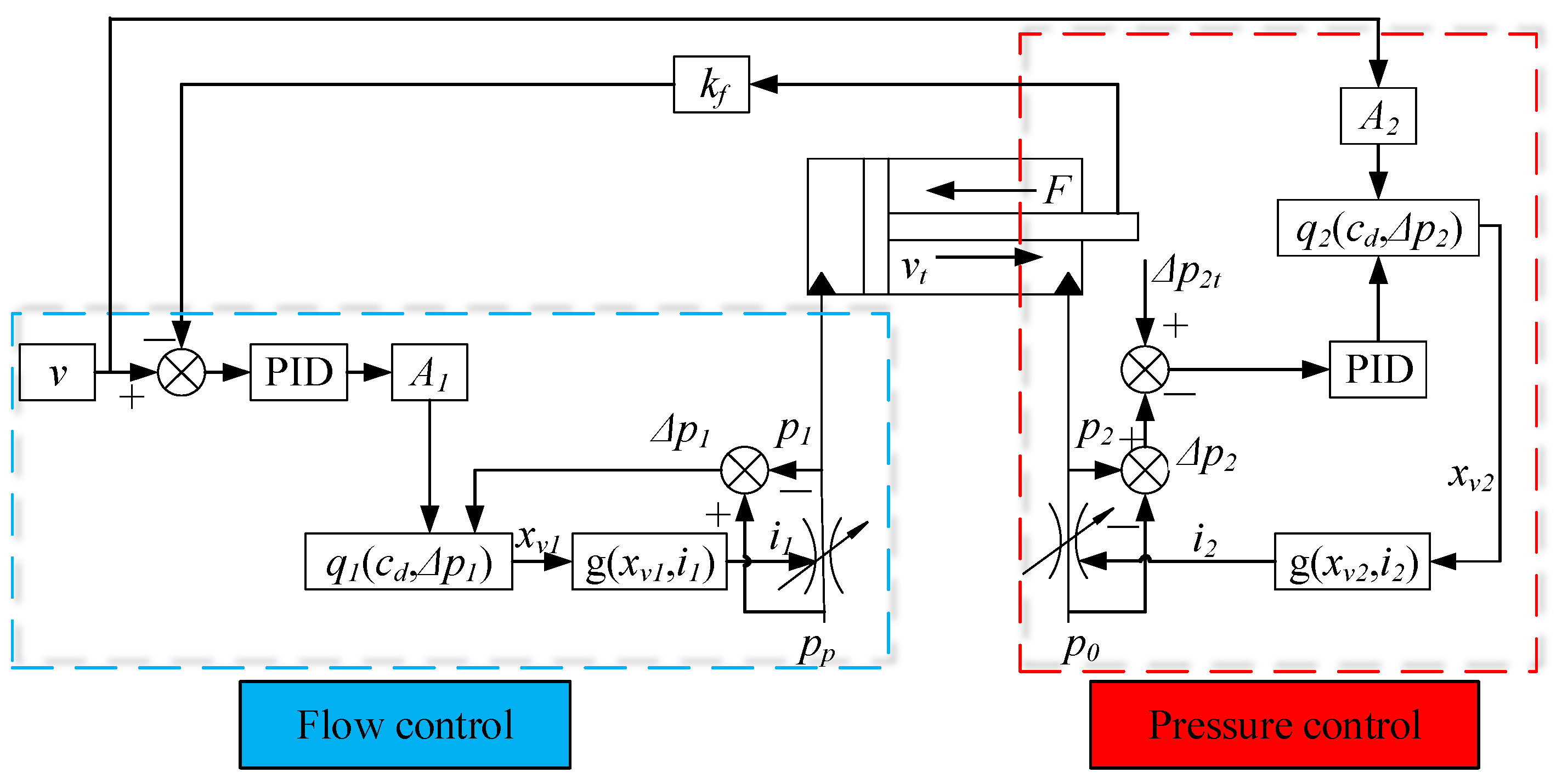
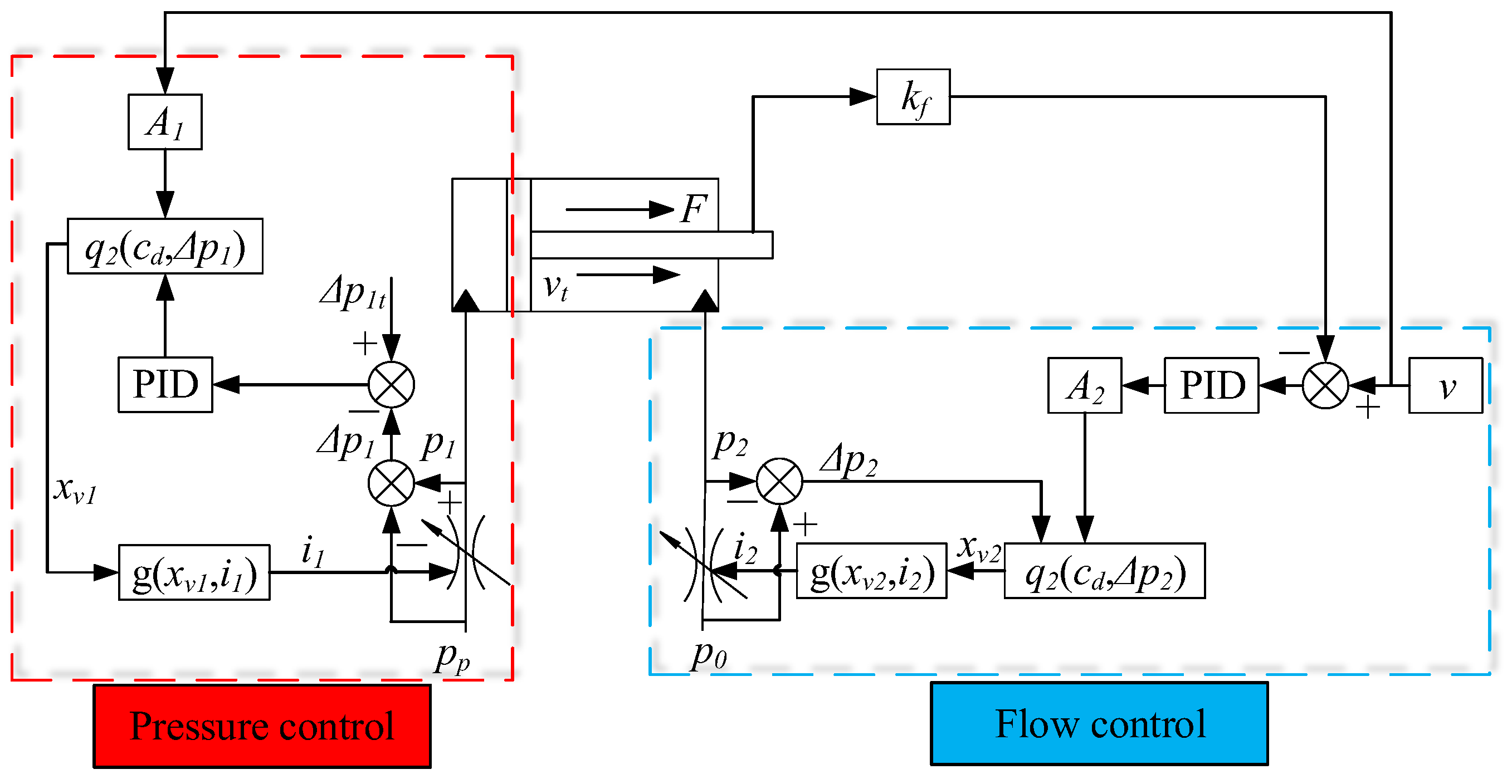
2.3. New Control Strategy
3. Simulation Research
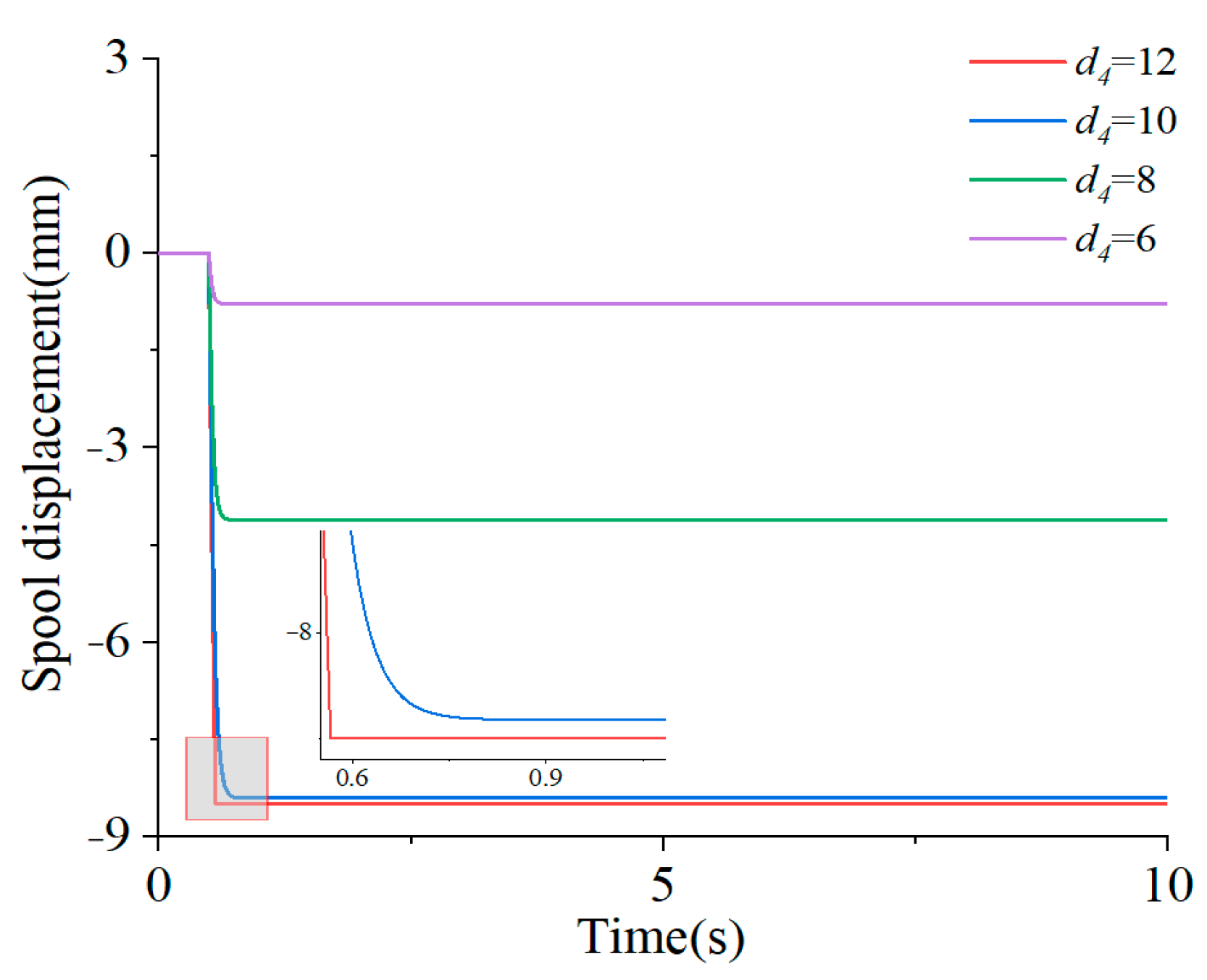
3.1. The Influence of Key Parameters on the Dynamic Characteristics of the Main Valve
- (1)
- Damping of main spool pressure chamber
- (2)
- Pilot pressure chamber diameter
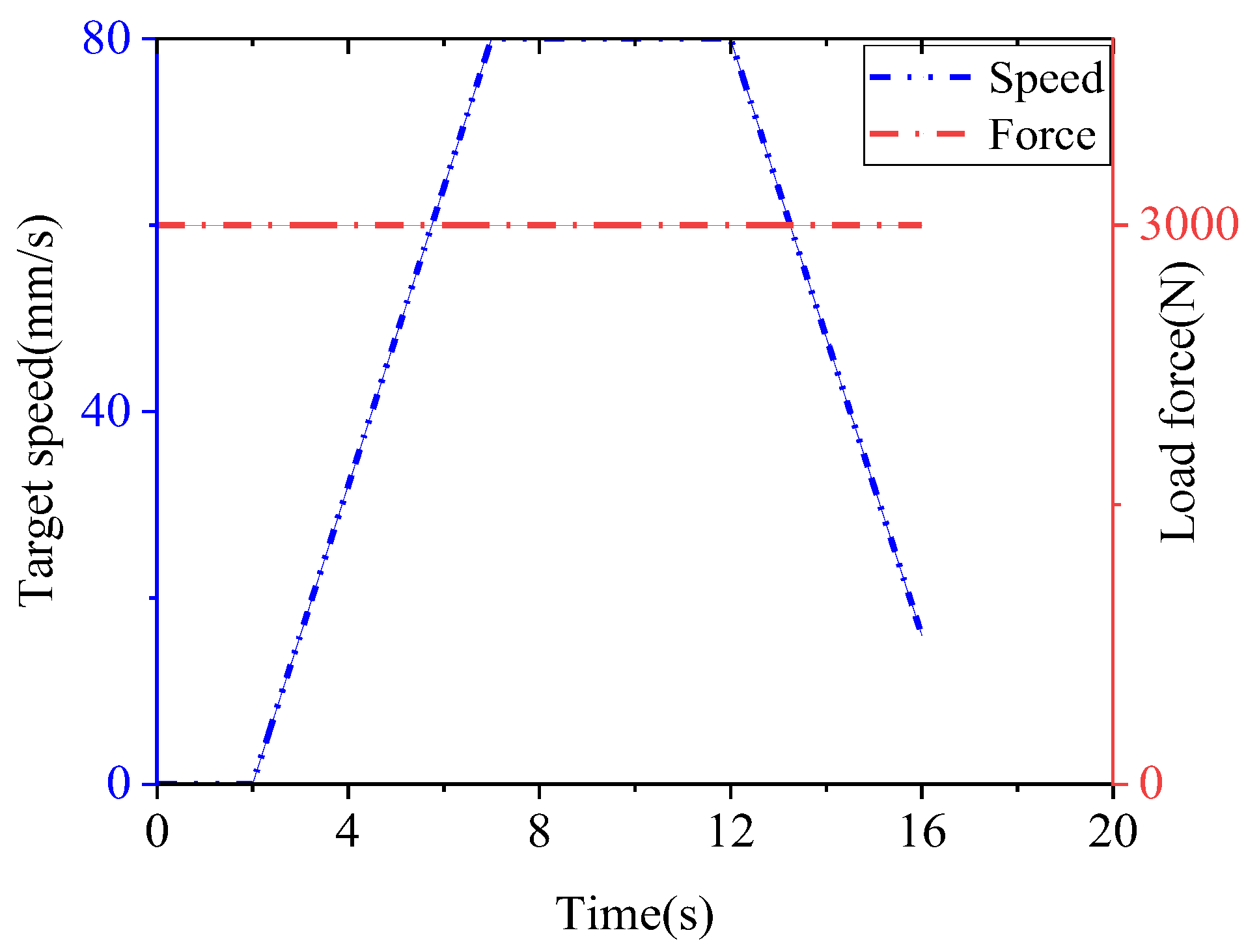
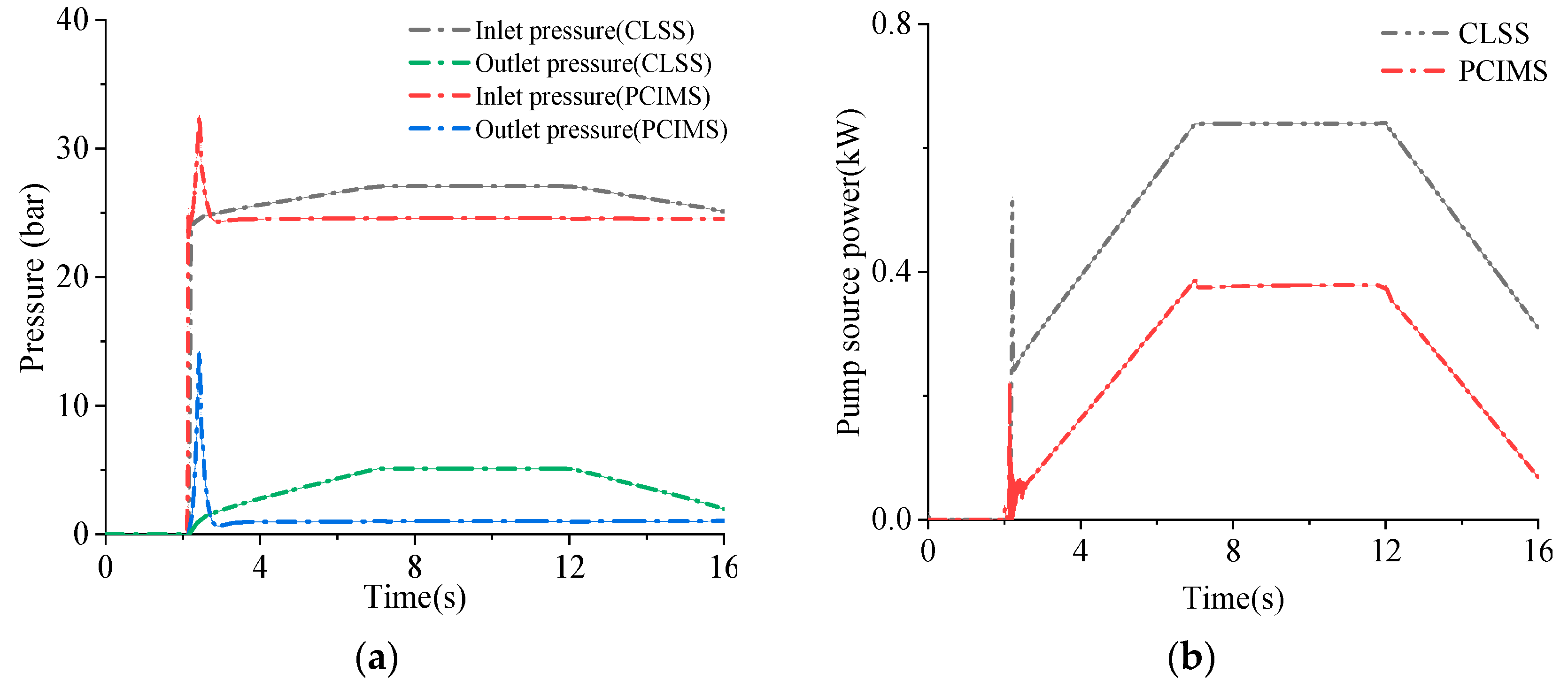
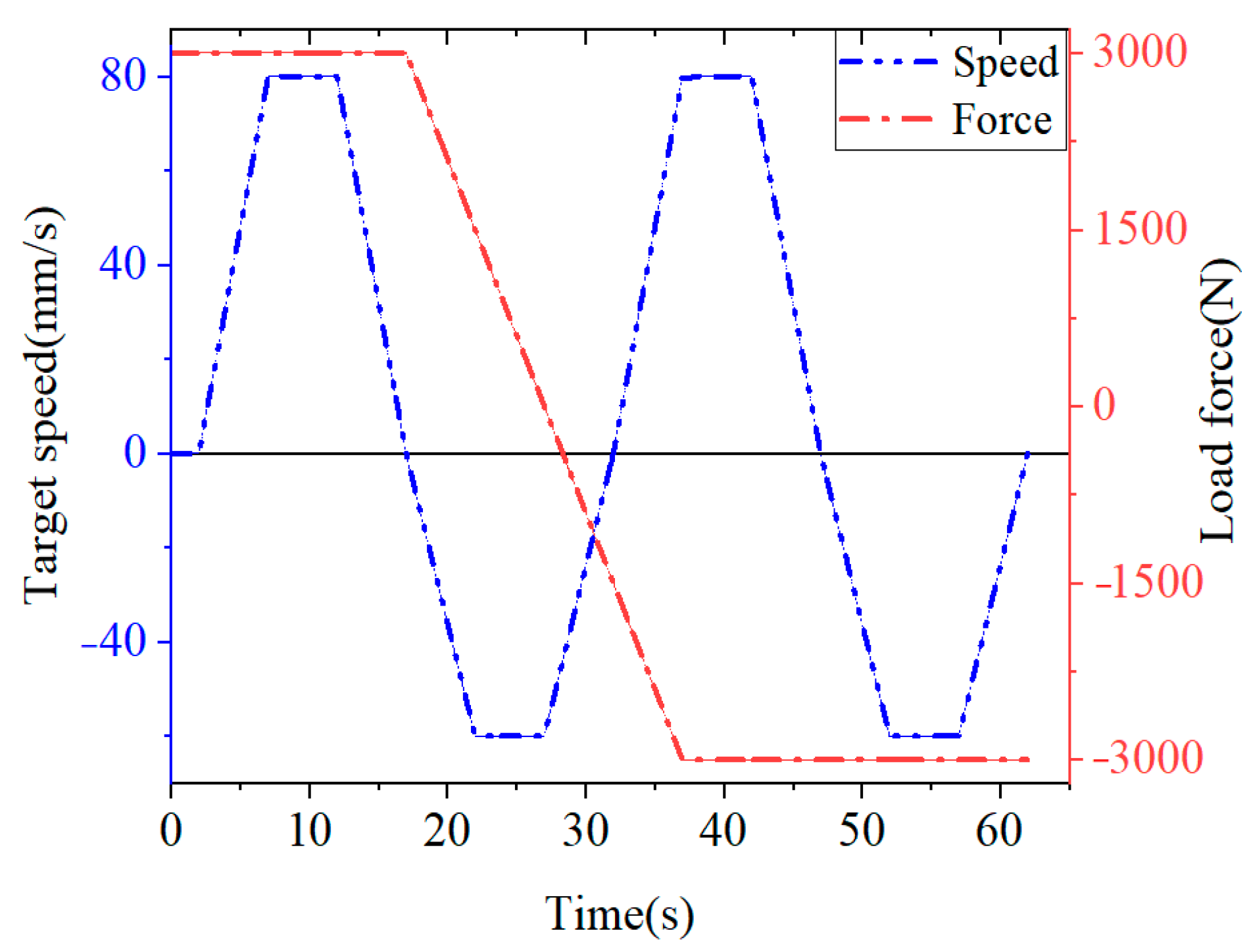
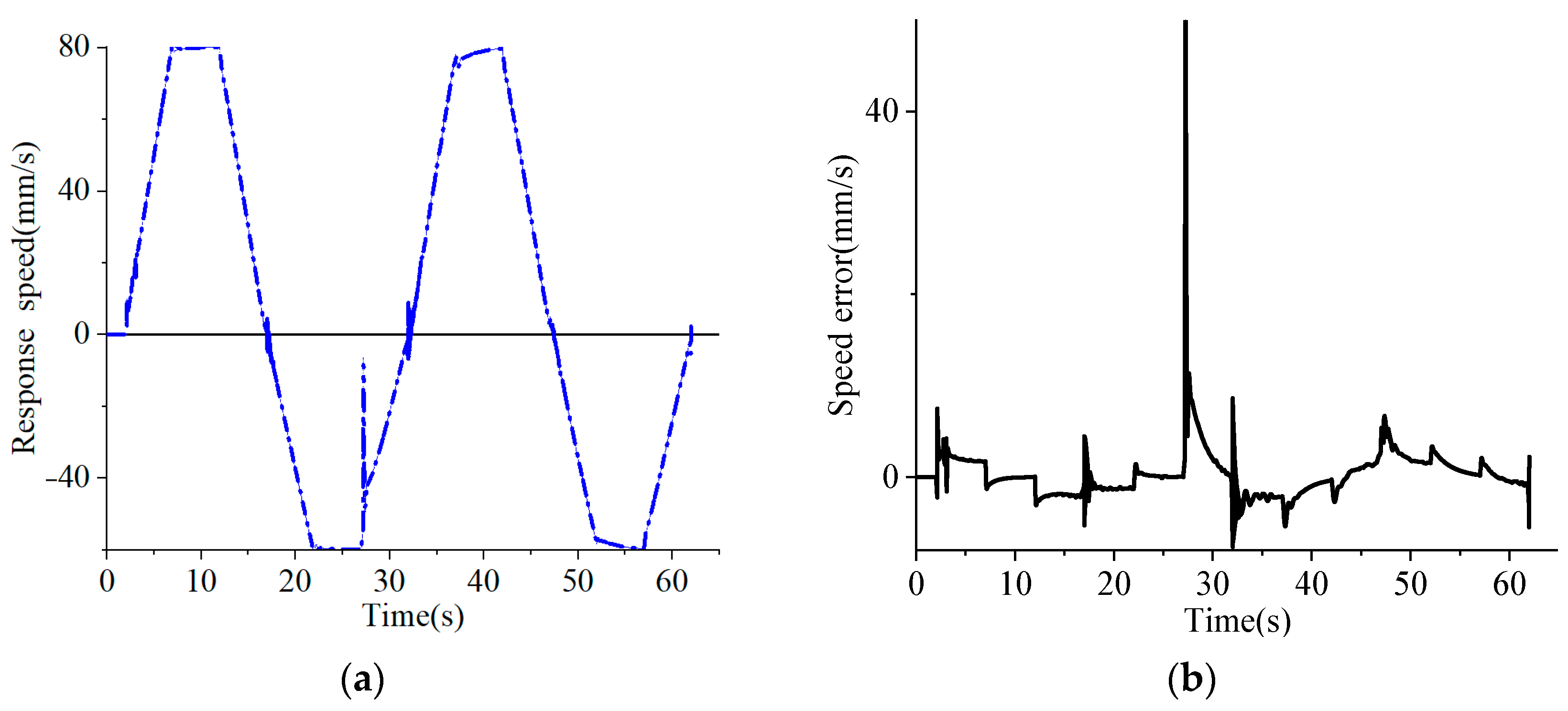
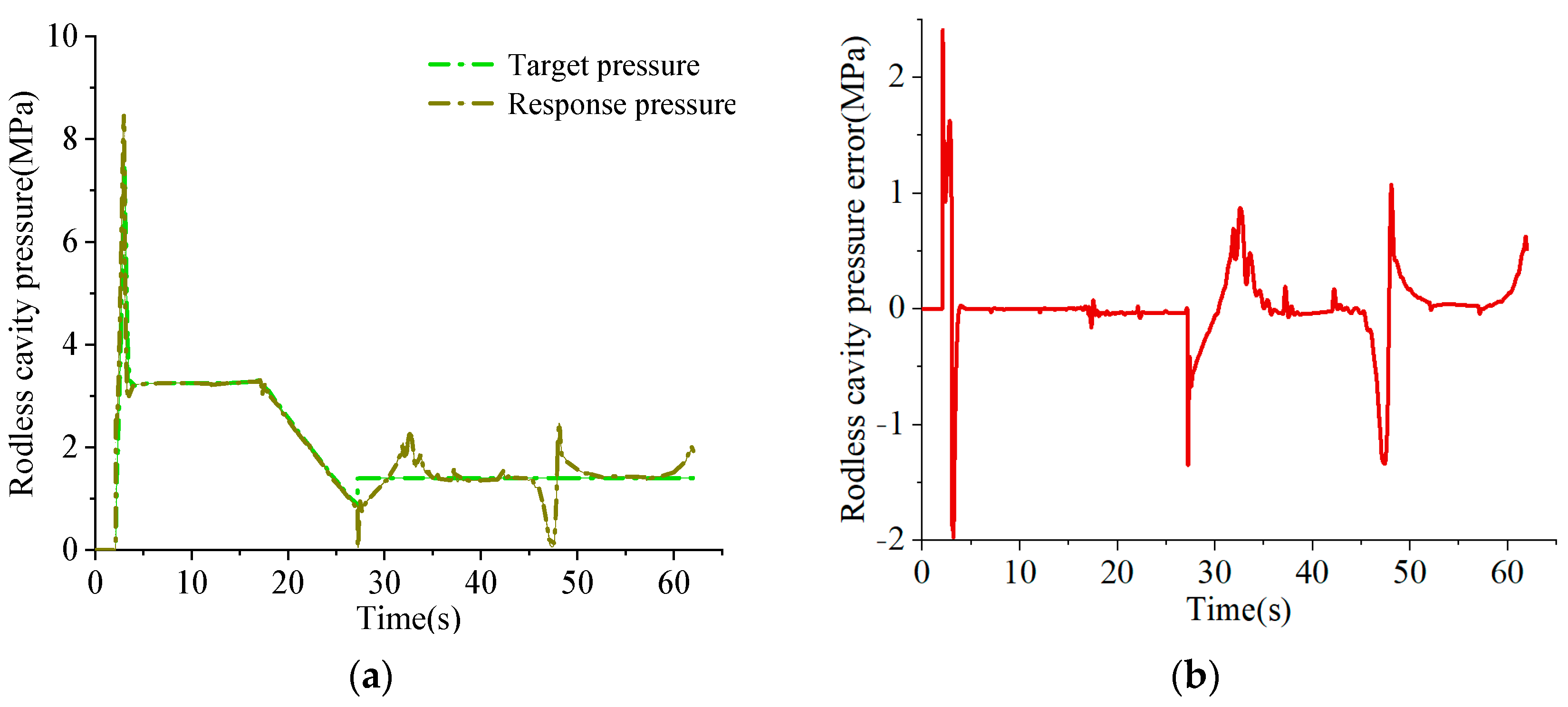
3.2. Analysis of Independent Metering System Based on Pilot Hydraulic Control
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, W.; Quan, L.; Ge, L.; Xia, L. Combined velocity and position control of large inertial hydraulic swing mechanism considering energy balance of supply and demand. Autom. Constr. 2019, 106, 102899. [Google Scholar] [CrossRef]
- Liu, K.; Gao, Y.; Tu, Z.; Lin, P. Energy-saving analysis of the independent metering system with pressure compensation for excavator’s manipulator. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2016, 230, 905–920. [Google Scholar] [CrossRef]
- Abuowda, K.; Noroozi, S.; Dupac, M.; Godfry, P. A dynamic model and performance analysis of a stepped rotary flow control valve. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2019, 233, 1195–1208. [Google Scholar] [CrossRef]
- Liu, Q.; Du, H.; Cai, Z.; Guo, K.; Fang, J. Application research of electro-hydraulic servo steering system based on independent metering system. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 09544070221139553. [Google Scholar] [CrossRef]
- Nguyen, T.; Do, T.; Ahn, K. A Study on a New Independent Metering Valve for Hydraulic Boom Excavator. Appl. Sci. 2022, 12, 605. [Google Scholar] [CrossRef]
- Chen, G.; Wang, J.; Wang, S.; Ma, L. Separate meter in and separate meter out energy saving control system using dual servo valves under complex load conditions. Trans. Beijing Inst. Technol. 2016, 36, 1053–1058. [Google Scholar]
- Ahamad, M.; Dinh, Q.; Nahian, S.; Ahn, K. Development of a New Generation of Independent Metering Valve Circuit for Hydraulic Boom Cylinder Control. Int. J. Autom. Technol. 2015, 9, 143–152. [Google Scholar] [CrossRef]
- Zhong, Q.; Bao, H.; Li, Y.; Hong, H.; Zhang, B.; Yang, H. Investigation into the independent metering control performance of a twin spools valve with switching technology-controlled pilot stage. Chin. J. Mech. Eng. 2021, 34, 91. [Google Scholar] [CrossRef]
- Zhong, Q.; Zhang, B.; Bao, H.; Hong, H.; Ma, J.; Ren, Y.; Yang, H.; Fung, R. Analysis of pressure and flow compound control characteristics of an independent metering hydraulic system based on a two-level fuzzy controller. J. Zhejiang Univ.-Sci. A 2019, 20, 184–200. [Google Scholar] [CrossRef]
- Liu, K.; Kang, S.; Qiang, H.; Yu, C. Cavitation Prevention Potential of Hydromechanical Pressure Compensation Independent Metering System with External Active Load. Processes 2021, 9, 255. [Google Scholar] [CrossRef]
- Choi, K.; Seo, J.; Nam, Y.; Kim, K. Energy-saving in excavators with application of independent metering valve. J. Mech. Sci. Technol. 2015, 29, 387–395. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, Q. Realization of programmable control using a set of individually controlled electrohydraulic valves. Int. J. Fluid Power 2002, 3, 29–34. [Google Scholar] [CrossRef]
- Shi, J.; Quan, L.; Zhang, X.; Xiong, X. Electro-hydraulic velocity and position control based on independent metering valve control in mobile construction equipment. Autom. Constr. 2018, 94, 73–84. [Google Scholar] [CrossRef]
- Ding, R.; Zhang, J.; Xu, B.; Cheng, M.; Pan, M. Energy efficiency improvement of heavy-load mobile hydraulic manipulator with electronically tunable operating modes. Energy Convers. Manag. 2019, 188, 447–461. [Google Scholar] [CrossRef]
- Koivumäki, J.; Zhu, W.; Mattila, J. Energy-efficient and high-precision control of hydraulic robots. Control Eng. Pract. 2019, 85, 176–193. [Google Scholar] [CrossRef]
- Liu, B.; Quan, L.; Ge, L. Research on the performance of hydraulic excavator boom based pressure and flow accordance control with independent metering circuit. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2017, 231, 901–913. [Google Scholar] [CrossRef]
- Bao, H.; He, D.; Zhang, B.; Zhong, Q.; Hong, H.; Yang, H. Research on Dynamic Performance of Independent Metering Valves Controlling Concrete-Placing Booms Based on Fuzzy-LADRC Controller. Actuators 2023, 12, 139. [Google Scholar] [CrossRef]
- Lyu, L.; Chen, Z.; Yao, B. Advanced valves and pump coordinated hydraulic control design to simultaneously achieve high accuracy and high efficiency. IEEE Trans. Control Syst. Technol. 2020, 29, 236–248. [Google Scholar] [CrossRef]
- Abuowda, K.; Noroozi, S.; Dupac, M.; Godfrey, P. Algorithm design for the novel mechatronics electro-hydraulic driving system: Micro-independent metering. IEEE Int. Conf. Mechatron. (ICM) 2019, 1, 7–12. [Google Scholar]
- Nguyen, T.; Do, T.; Nguyen, V.; Ahn, K. High Tracking Control for a New Independent Metering Valve System Using Velocity-Load Feedforward and Position Feedback Methods. Appl. Sci. 2022, 12, 9827. [Google Scholar] [CrossRef]
- Su, W.; Ren, W.; Sun, H.; Liu, C.; Lu, X.; Hua, Y.; Wei, H.; Jia, H. Data-Based Flow Rate Prediction Models for Independent Metering Hydraulic Valve. Energies 2022, 15, 7699. [Google Scholar] [CrossRef]
- Lyu, L.; Chen, Z.; Yao, B. Energy saving motion control of independent metering valves and pump combined hydraulic system. IEEE/ASME Trans. Mechatron. 2019, 24, 1909–1920. [Google Scholar] [CrossRef]
- Li, C.; Lyu, L.; Helian, B.; Chen, Z.; Yao, B. Precision motion control of an independent metering hydraulic system with nonlinear flow modeling and compensation. IEEE Trans. Ind. Electron. 2021, 69, 7088–7098. [Google Scholar] [CrossRef]
- Hu, S.; Wang, L.; Li, Y.; Zhang, L. Variable Universe Fuzzy Controller for an Independent Metering System of Construction Machinery. Processes 2023, 11, 901. [Google Scholar] [CrossRef]
- Ding, R.; Cheng, M.; Zheng, S.; Xu, B. Sensor-fault-tolerant operation for the independent metering control system. IEEE/ASME Trans. Mechatron. 2020, 26, 2558–2569. [Google Scholar] [CrossRef]
- Ji, H.; Wang, D.; Liu, X.; Fu, X. Flow control characteristic of the orifice in spool valve with notches. Trans. Chin. Soc. Agric. Mach. 2009, 40, 199–202. [Google Scholar]
- Wang, A.; Kuang, L.; Zhang, X. A study on flow coefficient of combined throttling groove in spool valves. J. Xian Jiaotong Univ. 2018, 52, 110–117. [Google Scholar]
- Wang, R.; Xu, B.; Wang, D.; Zhang, C. Research on Intelligent Flow Control Method Based on Proportional Directional Valve. Trans. Beijing Inst. Technol. 2020, 40, 486–490. [Google Scholar]









| Number | Variable | Value | Number | Variable | Value |
|---|---|---|---|---|---|
| 1 | total length of valve spool | 71.5 mm | 6 | stem diameter | 9 mm |
| 2 | spool displacement | 3.5 mm | 7 | pressure-equalizing groove | 0.2 mm × 0.5 mm |
| 3 | throttling groove shape | V | 8 | sinking slot diameter | 18 mm |
| 4 | negative coverage | 0.5 mm | 9 | width of sinking slot | 10 mm |
| 5 | valve spool outer diameter | 12 mm | 10 | oil channel diameter | 8 mm |
| Variable | Parameter | Variable | Parameter |
|---|---|---|---|
| cylinder piston diameter D (mm) | 40 | leakage flow (L/min/MPa) | 0.02 |
| cylinder piston rod diameter d (mm) | 25 | damping coefficient (N/m/s) | 120 |
| hydraulic cylinder stroke L (mm) | 1200 | cylinder dead zone (cm3) | 50 |
| Ls pump displacement (mL/r) | 100 | Ls valve setting pressure (MPa) | 2 |
| cut-off valve pressure (MPa) | 28 | motor speed (r/min) | 1500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Li, J.; Zhong, Y.; Gao, Y.; Guo, R.; Zhao, J. Research on Design and Control Strategy of Novel Independent Metering System. Sustainability 2023, 15, 13359. https://doi.org/10.3390/su151813359
Yang J, Li J, Zhong Y, Gao Y, Guo R, Zhao J. Research on Design and Control Strategy of Novel Independent Metering System. Sustainability. 2023; 15(18):13359. https://doi.org/10.3390/su151813359
Chicago/Turabian StyleYang, Jing, Jiadong Li, Yuhang Zhong, Yingjie Gao, Rui Guo, and Jingyi Zhao. 2023. "Research on Design and Control Strategy of Novel Independent Metering System" Sustainability 15, no. 18: 13359. https://doi.org/10.3390/su151813359










