Bayesian-Optimization-Based Long Short-Term Memory (LSTM) Super Learner Approach for Modeling Long-Term Electricity Consumption
Abstract
:1. Introduction
- (1)
- Investigate the details of the yearly electricity consumption in Saudi Arabia;
- (2)
- Determine the exogenous variables that have a significant impact on REC and TEC;
- (3)
- Apply the long short-term memory algorithm to forecast long-term REC and TEC;
- (4)
- Find the optimum super learner BOA-LSTM model via the Bayesian optimization approach to automatically tune the model’s hyperparameters;
- (5)
- Compare the proposed model to the traditional statistical approaches, namely multiple linear regression and exponential smoothing;
- (6)
- Estimate the performance of the developed models through numerous estimation measures, viz. MAPE, RMSE, MAE, and ;
- (7)
- Forecast and validate forthcoming yearly residential and total electricity consumption.
2. Materials and Methods
2.1. Data Description
2.2. Computational Techniques
2.2.1. Multiple Linear Regression (MLR)
2.2.2. Exponential Smoothing (EXPS)
2.2.3. Long Short-Term Memory (LSTM)
2.2.4. Hyperparameters Optimization for LSTM
2.2.5. Performance Evaluation Metrics
3. Results
3.1. Development of Forecasting Models
3.1.1. Development of MLR Model for TEC and REC
3.1.2. Development of EXPS Model for TEC and REC
3.1.3. Development of LSTM Model for REC and TEC
3.2. Performance Evaluation and Model Comparison
3.2.1. Prediction Accuracy of the Developed Models
3.2.2. Generalizability of the Developed Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Description | Abbreviation | Description |
| ACF | Autocorrelation Function | KWh | Kilowatt hour |
| ADF | Augmented Dickey Fuller | LEAP | Long-range Energy Alternative Planning |
| AIM | Abductory Induction Mechanism | LSTM | long short-term memory |
| ANN | Artificial Neural Network | MA | Moving Average |
| AR | Auto-Regressive | MAE | Mean Absolute Error |
| ARDL | Autoregressive Distributed Lag | MAPD | Mean Absolute Percentage Deviation |
| ARIMA | Autoregressive Integrated Moving Average | MAPE | Mean Absolute Percentage Error |
| ARIMAX | Autoregressive Integrated Moving Average with Exogenous Inputs | MARAFIQ | Power and Water Utility Company for Jubail and Yanbu |
| BOA | Bayesian Optimization Algorithm | ML | Machine Learning |
| CGE | Computable General Equilibrium | MLR | Multiple Linear Regression |
| CNN | Convolutional Neural Network | MSPE | Mean Square Percentage Error |
| CVRMSE | Coefficient of the Variation in the Root Mean Square Error | MW | Megawatt |
| DE | Differential Evolution | PACF | Partial Autocorrelation Function |
| DL | Deep-Learning | PJ | Petajoule |
| EC | Electricity Consumption | PSO | Practical Swarm Optimization |
| ECON | Economic Factor | RE | Relative Error |
| EGDi | Electricity Generation Demand for i | REC | Residential Electricity Consumption |
| EL | Electric Load | REEM | Residential Energy Model |
| ENVI | Environmental Factor | RF | Random Forest |
| EP | Electric Price | RMSE | Root Mean Square Error |
| EXPS | Exponential Smoothing | RNN | Recurrent Neural Network |
| EXT | Empirical Wavelet Transform | SA | Simulated Annealing |
| GA | Genetic Algorithm | SEC | Saudi Electricity Company |
| GDP | Gross Domestic Product | SEM-VARIMAX | Structural Equation Modelling-Vector Autoregressive with Exogeneous Variables |
| GP | The Gaussian process | SOCI | Social Component |
| GRU | Gated Recurrent Unit | STSM | Structural Time Series Model |
| GW | Gigawatt | SVR | Support Vector Regression |
| ICA | Independent Component Analysis | TCN | Temporal Convolutional Networks |
| IPPs | Independent Power Producers | TEC | Total Electricity Consumption |
| IQR | Inter Quartile Range | TMY | Typical Meteorological Year |
| IWPPs | Independent Water and Power Producers | TWh | Terawatt hour |
| JLSTM | Jaya Long Short-Term Memory | UAE | United Arab Emirates |
| KPX | Korea Power Exchange | VAR | Vector Auto-Regression |
| KSA | Kingdom of Saudi Arabia | The Coefficient of Determination |
References
- Khan, A.; Chiroma, H.; Imran, M.; Khan, A.; Bangash, J.I.; Asim, M.; Hamza, M.F.; Aljuaid, H. Forecasting Electricity Consumption Based on Machine Learning to Improve Performance: A Case Study for the Organization of Petroleum Exporting Countries (OPEC). Comput. Electr. Eng. 2020, 86, 106737. [Google Scholar] [CrossRef]
- Kaboli, S.H.A.; Selvaraj, J.; Rahim, N.A. Long-Term Electric Energy Consumption Forecasting via Artificial Cooperative Search Algorithm. Energy 2016, 115, 857–871. [Google Scholar] [CrossRef]
- Ur Rehman, S.A.; Cai, Y.; Fazal, R.; Das Walasai, G.; Mirjat, N.H. An Integrated Modeling Approach for Forecasting Long-Term Energy Demand in Pakistan. Energies 2017, 10, 1868. [Google Scholar] [CrossRef]
- Kankal, M.; Uzlu, E. Neural Network Approach with Teaching–Learning-Based Optimization for Modeling and Forecasting Long-Term Electric Energy Demand in Turkey. Neural Comput. Appl. 2017, 28, 737–747. [Google Scholar] [CrossRef]
- Yukseltan, E.; Yucekaya, A.; Bilge, A.H. Hourly Electricity Demand Forecasting Using Fourier Analysis with Feedback. Energy Strategy Rev. 2020, 31, 100524. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. Adv. Neural Inf. Process. Syst. 2012, 25, 2960–2968. [Google Scholar]
- Lee, J.; Cho, Y. National-Scale Electricity Peak Load Forecasting: Traditional, Machine Learning, or Hybrid Model? Energy 2022, 239, 122366. [Google Scholar] [CrossRef]
- Sutthichaimethee, P.; Naluang, S. The Efficiency of the Sustainable Development Policy for Energy Consumption under Environmental Law in Thailand: Adapting the SEM-Varimax Model. Energies 2019, 12, 3092. [Google Scholar] [CrossRef]
- Aurangzeb, K.; Alhussein, M.; Javaid, K.; Haider, S.I. A Pyramid-CNN Based Deep Learning Model for Power Load Forecasting of Similar-Profile Energy Customers Based on Clustering. IEEE Access 2021, 9, 14992–15003. [Google Scholar] [CrossRef]
- Khalid, R.; Javaid, N.; Al-zahrani, F.A.; Aurangzeb, K.; Qazi, E.U.H.; Ashfaq, T. Electricity Load and Price Forecasting Using Jaya-Long Short Term Memory (JLSTM) in Smart Grids. Entropy 2020, 22, 10. [Google Scholar] [CrossRef]
- Aasim; Singh, S.N.; Mohapatra, A. Data Driven Day-Ahead Electrical Load Forecasting through Repeated Wavelet Transform Assisted SVM Model. Appl. Soft Comput. 2021, 111, 107730. [Google Scholar] [CrossRef]
- Haq, M.R.; Ni, Z. A New Hybrid Model for Short-Term Electricity Load Forecasting. IEEE Access 2019, 7, 125413–125423. [Google Scholar] [CrossRef]
- Alharbi, F.R.; Csala, D. A Seasonal Autoregressive Integrated Moving Average with Exogenous Factors (SARIMAX) Forecasting Model-Based Time Series Approach. Inventions 2022, 7, 94. [Google Scholar] [CrossRef]
- Yearly Statistics. Available online: https://www.sama.gov.sa/en-us/EconomicReports/pages/YearlyStatistics.aspx (accessed on 3 May 2022).
- Krarti, M.; Aldubyan, M.; Williams, E. Residential Building Stock Model for Evaluating Energy Retrofit Programs in Saudi Arabia. Energy 2020, 195, 116980. [Google Scholar] [CrossRef]
- Alrashed, F.; Asif, M. Trends in Residential Energy Consumption in Saudi Arabia with Particular Reference to the Eastern Province. J. Sustain. Dev. Energy Water Environ. Syst. 2014, 2, 376–387. [Google Scholar] [CrossRef]
- Alyousef, Y.; Abu-ebi, M. Energy Efficiency Initiatives for Saudi Arabia on Supply and Demand Sides. In Energy Efficiency—A Bridge to Low Carbon Economy; InTech: Rijeka, Croatia, 2012. [Google Scholar] [CrossRef]
- Mattas, C.; Dimitraki, L.; Georgiou, P.; Venetsanou, P. Use of Factor Analysis (Fa), Artificial Neural Networks (Anns) and Multiple Linear Regression (Mlr) for Electrical Conductivity Prediction in Aquifers in the Gallikos River Basin, Northern Greece. Hydrology 2021, 8, 127. [Google Scholar] [CrossRef]
- Civelekoglu, G.; Yigit, N.O.; Diamadopoulos, E.; Kitis, M. Prediction of Bromate Formation Using Multi-Linear Regression and Artificial Neural Networks. Ozone Sci. Eng. 2007, 29, 353–362. [Google Scholar] [CrossRef]
- Obaid, R.R.; Mufti, A.H. Present State, Challenges, and Future of Power Generation in Saudi Arabia. In Proceedings of the 2008 IEEE Energy 2030 Conference, Atlanta, GA, USA, 17–18 November 2008; pp. 1–6. [Google Scholar]
- Ouda, M.; El-Nakla, S.; Yahya, C.B.; Omar Ouda, K.M. Electricity Demand Forecast in Saudi Arabia. In Proceedings of the IEEE 7th Palestinian International Conference on Electrical and Computer Engineering, Gaza, Palestine, 26–27 March 2019; pp. 1–5. [Google Scholar]
- Alsaedi, Y.H.; Tularam, G.A. The Relationship between Electricity Consumption, Peak Load and GDP in Saudi Arabia: A VAR Analysis. Math. Comput. Simul. 2020, 175, 164–178. [Google Scholar] [CrossRef]
- Senan, N.A.M.; Mahmood, H.; Liaquat, S. Financial Markets and Electricity Consumption Nexus in Saudi Arabia. Int. J. Energy Econ. Policy 2018, 8, 12–16. [Google Scholar]
- Alkhraijah, M.; Alowaifeer, M.; Alsaleh, M.; Alfaris, A.; Molzahn, D.K. The Effects of Social Distancing on Electricity Demand Considering Temperature Dependency. Energies 2021, 14, 473. [Google Scholar] [CrossRef]
- Mikayilov, J.I.; Darandary, A.; Alyamani, R.; Hasanov, F.J.; Alatawi, H. Regional Heterogeneous Drivers of Electricity Demand in Saudi Arabia: Modeling Regional Residential Electricity Demand. Energy Policy 2020, 146, 111796. [Google Scholar] [CrossRef]
- Alarenan, S.; Gasim, A.A.; Hunt, L.C. Modelling Industrial Energy Demand in Saudi Arabia. Energy Econ. 2020, 85, 104554. [Google Scholar] [CrossRef]
- Al-Zayer, J.; Al-Ibrahim, A.A. Modelling the Impact of Temperature on Electricity Consumption in the Eastern Province of Saudi Arabia. J. Forecast. 1996, 15, 97–106. [Google Scholar] [CrossRef]
- Guleryuz, D. Determination of Industrial Energy Demand in Turkey Using MLR, ANFIS and PSO-ANFIS. J. Artif. Intell. Syst. 2021, 3, 16–34. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Alden, R.E.; Gong, H.; Ababei, C.; Ionel, D.M. LSTM Forecasts for Smart Home Electricity Usage. In Proceedings of the 9th International Conference on Renewable Energy Research and Applications, ICRERA 2020, Glasgow, UK, 27–30 September 2020; pp. 434–438. [Google Scholar] [CrossRef]
- Wang, F.; Xuan, Z.; Zhen, Z.; Li, K.; Wang, T.; Shi, M. A Day-Ahead PV Power Forecasting Method Based on LSTM-RNN Model and Time Correlation Modification under Partial Daily Pattern Prediction Framework. Energy Convers. Manag. 2020, 212, 112766. [Google Scholar] [CrossRef]
- Zheng, Z.; Chen, H.; Luo, X. Spatial Granularity Analysis on Electricity Consumption Prediction Using LSTM Recurrent Neural Network. Energy Procedia 2019, 158, 2713–2718. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) Network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Kim, T.Y.; Cho, S.B. Predicting Residential Energy Consumption Using CNN-LSTM Neural Networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Metaheuristics for Electric Load Forecasting. Energies 2020, 3, 1–21. [Google Scholar]
- Almazrouee, A.I.; Almeshal, A.M.; Almutairi, A.S.; Alenezi, M.R.; Alhajeri, S.N. Long-Term Forecasting of Electrical Loads in Kuwait Using Prophet and Holt–Winters Models. Appl. Sci. 2020, 10, 5627. [Google Scholar] [CrossRef]
- Alam, M.S.; Sultana, N.; Hossain, S.M.Z. Bayesian Optimization Algorithm Based Support Vector Regression Analysis for Estimation of Shear Capacity of FRP Reinforced Concrete Members. Appl. Soft Comput. 2021, 105, 107281. [Google Scholar] [CrossRef]
- Chang, D.T. Bayesian Hyperparameter Optimization with BoTorch, GPyTorch and Ax. arXiv 2019, arXiv:1912.05686. [Google Scholar]
- Statistical Report. Available online: https://www.sama.gov.sa/en-US/EconomicReports/Pages/report.aspx?cid=126 (accessed on 11 December 2022).
- Shadkam, A. Using Sarimax to Forecast Electricity Demand and Consumption in University Buildings; University of British Columbia: Vancouver, BC, Canada, 2020. [Google Scholar]
- Alraddadi, G.H.; Othman, M.T. Ben Development of an Efficient Electricity Consumption Prediction Model Using Machine Learning Techniques. Int. J. Adv. Comput. Sci. Appl. 2022, 13, 376–384. [Google Scholar] [CrossRef]
- Al-Garni, A.Z.; Zubair, S.M.; Nizami, J.S. A Regression Model for Electric-Energy-Consumption Forecasting in Eastern Saudi Arabia. Energy 1994, 19, 1043–1049. [Google Scholar] [CrossRef]
- Soummane, S.; Ghersi, F. Projecting Saudi Sectoral Electricity Demand in 2030 Using a Computable General Equilibrium Model. Energy Strategy Rev. 2022, 39, 100787. [Google Scholar] [CrossRef]
- Aldubyan, M.; Krarti, M. Impact of Stay Home Living on Energy Demand of Residential Buildings: Saudi Arabian Case Study. Energy 2022, 238, 121637. [Google Scholar] [CrossRef]
- Sharma, M.; Mittal, N.; Mishra, A.; Gupta, A. Machine Learning-Based Electricity Load Forecast for the Agriculture Sector. Int. J. Softw. Innov. 2022, 11, 1–21. [Google Scholar] [CrossRef]
- Abdel-Aal, R.E.; Al-Garni, A.Z. Forecasting Monthly Electric Energy Consumption in Eastern Saudi Arabia Using Univariate Time-Series Analysis. Energy 1997, 22, 1059–1069. [Google Scholar] [CrossRef]
- Fahmy, M.S.E.; Ahmed, F.; Durani, F.; Bojnec, Š.; Ghareeb, M.M. Predicting Electricity Consumption in the Kingdom of Saudi Arabia. Energies 2023, 16, 506. [Google Scholar] [CrossRef]
- Saoud, A.; Recioui, A. Load Energy Forecasting Based on a Hybrid PSO LSTM-AE Model. Alger. J. Environ. Sci. Technol. 2021, 9, 2886–2894. [Google Scholar]
- Peng, L.; Wang, L.; Xia, D.; Gao, Q. Effective Energy Consumption Forecasting Using Empirical Wavelet Transform and Long Short-Term Memory. Energy 2022, 238, 121756. [Google Scholar] [CrossRef]
- Hadjout, D.; Torres, J.F.; Troncoso, A.; Sebaa, A.; Martínez-Álvarez, F. Electricity Consumption Forecasting Based on Ensemble Deep Learning with Application to the Algerian Market. Energy 2022, 243, 123060. [Google Scholar] [CrossRef]
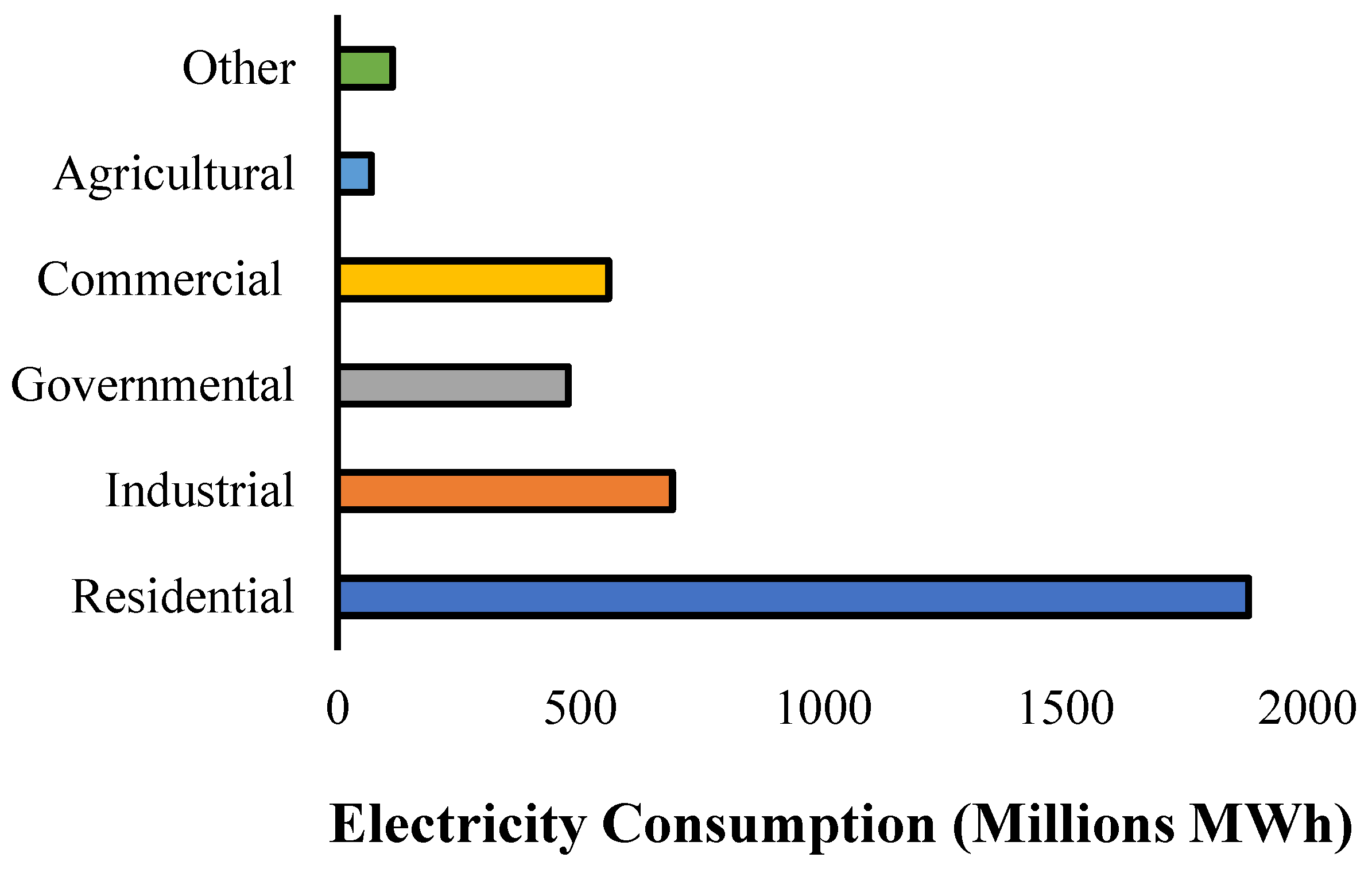









| Variable | Significant or Not | p-Value | Pearson Test |
|---|---|---|---|
| Population | Significant | <0.001 | 0.900 |
| GDP | Significant | <0.001 | 0.833 |
| Total refined products | Significant | 0.003 | 0.697 |
| Exports | Not significant | 0.801 | 0.069 |
| Imports | Significant | <0.001 | 0.861 |
| Variable | Significant or Not | p-Value | Pearson Test |
|---|---|---|---|
| Population | Significant | <0.001 | 0.952 |
| GDP | Significant | <0.001 | 0.886 |
| Total refined products | Significant | 0.001 | 0.728 |
| Exports | Not significant | 0.754 | 0.085 |
| Imports | Significant | <0.001 | 0.843 |
| Parameter | Value | Standard Error | t Statistic | p-Value | |
|---|---|---|---|---|---|
| TEC | Intercept | −458.366700 | 89.733900 | −5.108100 | 0.000340 |
| Beta{GDP} | −0.000042 | 0.000045 | −0.916530 | 0.379050 | |
| Beta{imports} | 0.000635 | 0.000149 | 4.269700 | 0.001321 | |
| Beta{population} | 0.000030 | 0.000006 | 4.930900 | 0.000449 | |
| Beta{refndProducts} | 0.000286 | 0.000092 | 3.109100 | 0.009942 | |
| AIC: 108.554 | |||||
| REC | Intercept | −134.103900 | 50.786700 | −2.640500 | 0.022971 |
| Beta{GDP} | 0.000069 | 0.000026 | −2.692100 | 0.020949 | |
| Beta{imports} | 0.000479 | 0.000084 | 5.692700 | 0.000140 | |
| Beta{population} | 0.000013 | 0.000003 | 3.777300 | 0.003061 | |
| Beta{refndProducts} | 0.000135 | 0.000052 | 2.597100 | 0.024820 | |
| AIC: 103.704 | |||||
| Model | Dataset | MAE | RMSE | MAPE | |
|---|---|---|---|---|---|
| TEC | MLR | Training | 19.06701 | 25.23917 | 2.584842 |
| Testing | 26.50708 | 35.54441 | 2.610455 | ||
| Exp smoothing | Training | 19.00243 | 22.51706 | 2.366063 | |
| Testing | 33.95365 | 39.60389 | 3.306198 | ||
| BOA-LSTM | Training | 10.52504 | 13.1502955 | 1.349303 | |
| Testing | 8.379883 | 8.51760718 | 0.812599 | ||
| REC | MLR | Training | 11.91499 | 13.30789 | 2.958642 |
| Testing | 15.38693 | 22.83597 | 3.315328 | ||
| Exp smoothing | Training | 11.79371 | 13.90347 | 2.768225 | |
| Testing | 34.36913 | 39.54887 | 7.28927 | ||
| BOA-LSTM | Training | 10.50998 | 11.9220839 | 2.510966 | |
| Testing | 7.330428 | 8.78461017 | 1.528486 |
| Hyperparameters | TEC | REC |
|---|---|---|
| (Level factor) | 0.708000 | 1.000000 |
| (Trend factor) | 0.999000 | 0.000005 |
| (Trend damping factor) | 0.901000 | 0.999000 |
| AIC: | 108.554 | 103.704 |
| Hyperparameters | No. of Layer | No. of Units | Initial Learning Rate | L2 Regularization | Max Epochs | Minibatch Siz | Training Function | Training Error | |
|---|---|---|---|---|---|---|---|---|---|
| LSTM (REC) | Range for BOA | - | [12, 500] | [1 × 10−2, 1] | [1 × 10−10, 1 × 10−2] | - | - | - | - |
| Optimized Value | 1 | 198 | 0.012716 | 0.0090583 | 3000 | 16 | adam | RMSE | |
| Elapsed time: 742.38 s | |||||||||
| LSTM (TEC) | Range for BOA | - | [12, 500] | [1 × 10−2, 1] | [1 × 10−10, 1 × 10−2] | - | - | - | - |
| Optimized Value | 1 | 169 | 0.025567 | 2.57 × 10−8 | 3000 | 16 | adam | RMSE | |
| Elapsed time: 392.46 s | |||||||||
| TEC | REC | |||
|---|---|---|---|---|
| Relative Improvement of BOA-LSTM wrt MLR (%) | Relative Improvement of BOA-LSTM wrt EXPS (%) | Relative Improvement of BOA-LSTM wrt MLR (%) | Relative Improvement of BOA-LSTM wrt EXPS (%) | |
| MAE | 58.6% | 58.1% | 64.0% | 71.9% |
| RMSE | 64.2% | 60.1% | 60.8% | 71.2% |
| MAPE | 59.6% | 54.8% | 62.7% | 68.9% |
| 2.1% | 1.4% | 4.1% | 6.5% | |
| TEC (PJ) in 2021 | Residual | RE (%) | |
| Historical | 1085.6290 | - | - |
| MLR | 1021.5092 | 64.1198 | 5.9062 |
| EXPS | 1036.843 | 48.786 | 4.4938 |
| BOA-LSTM | 1064.3199 | 21.3091 | 1.9628 |
| REC (PJ) in 2021 | Residual | RE (%) | |
| Historical | 512.9241 | - | - |
| MLR | 485.7546 | 27.1695 | 5.2970 |
| EXPS | 510.186 | 2.7381 | 0.5338 |
| BOA-LSTM | 501.8886 | 11.0356 | 2.1515 |
| Ref | Region | Data Description | Method | Major Findings and Performance |
|---|---|---|---|---|
| [22] | Saudi Arabia | Yearly data from 1990 to 2015 GDP, PL | VAR | The growth rate for electricity consumption, pick load, and GDP of 7.21%, 6.87%, and 14.14%, respectively, higher in the last ten years |
| [21] | Saudi Arabia, UAE, and Australia | Yearly data from 2006 to 2014 | Electricity Generation Demand () for the | Saudi Arabia consumed the lowest amount of power compared to UAE and Australia |
| [23] | Saudi Arabia | Dataset from 1970 to 2015 Economic growth and Urbanization | (ADF) test and (ARDL) cointegration technique. | Economic growth and urbanization have a positive relationship with electricity consumption |
| [24] | Saudi Arabia | January 2020–July 2020, Effect of social distancing and temperature | Linear correlation coefficients | A strong correlation was observed between temperature and electricity consumption during the curfew |
| [25] | Saudi Arabia | Time series data from1990 to 2018 Energy price, weather conditions, and income | STSM | All regions showed a significant relationship between hot weather and electricity consumption |
| [26] | Saudi Arabia | EC data from 1986 to 2016 | STSM, decomposition analysis | Incomes and energy prices influence the total demand for industrial energy |
| [42] | Eastern region in Saudi Arabia | Monthly dataset for five years, August 1987–July 1992. POP, weather condition: air temperature, humidity, solar radiation | Regression model | Weather temperatures significantly affected the demand stability in high and low temperatures |
| [43] | Saudi Arabia | Electricity demand and price data | Computable general equilibrium (CGE) | Price reforms and efficiency measures may reduce total demand by 11–32% in 2030, with higher savings realized under energy efficiency measures |
| [44] | Saudi Arabia | Hourly EC and weather data from 15 March to 15 June 2020 | Residential Energy Model | Increasing by 13.5% in long-term stay-at-home living |
| [46] | Saudi Arabia | Monthly data for six years August 1987–July 1993. Weather parameters, demographic, and economic variables. | ARIMA AIM and multivariate regression models. | ARIMA: APE = 3.8%, AIM: APE = 8.1% Multivariate regression model: APE = 5.6% |
| [47] | Saudi Arabia | Yearly dataset from 1990 to 2019 | Polynomial models, ARIMA | Polynomial models are performed better than ARIMA |
| [13] | Saudi Arabia | Electricity consumption, generation, peak load, and installed capacity | SARIMAX | = 0.99 and MAPE ≤ 0.40 |
| [36] | Kuwait | Peak Load, dataset obtained powerplants from 2010 to 2020. | The Prophet model, EXPS | Prophet model performed the best with MAPE = 1.75%, MAE = 147.89, RMSE = 205.64, CVRMSE = 7.61%, and = 0.9942 |
| [45] | India | The monthly dataset containing sector-specific power consumption. Statistics from January 2015 to November 2020 | SARIMA, LSTM, RF, and EXPS | RMSPE (%): 8.69 (SARIMA), 7.98 (EXPS), 13.50 (LSTM), and 11.03 (RF) |
| [7] | Korea | The power peak load data from KPX and the weather data were obtained from the National Climate Data Center (From 2014 to 2019) | SARIMAX, ANN, SVR, LSTM | SARIMAX- LSTM hybrid model achieved the best results: MAPE = 3.4737, AND = 0.918 |
| [10] | Big data sources | Electric load and price. | JLSTM | RMSE was 0.02 and 0.04, while MEA was 0.1 and 0.47 for demand and price, respectively |
| [48] | USA | Hourly dataset from 2004 to 2018 | LSTM-AE LSTM, CNN, ANN, and random forest | LSTM-AE with RMSE = 680.89 and MAE = 486.28 |
| [49] | China | Monthly industrial electricity consumption data from 2010 to 2015, China’s monthly total power consumption from 2010 to 2019 | LSTM | MAPE of 4.01%, 5.37%, and 1.60% for the three real-life scenarios |
| [50] | Algeria | Monthly power use data from 2006 to 2019 | LSTM, GRU, TCN | TCN achieved the minimum RMSE |
| [41] | London, UK | Daily and monthly power consumption values from 5567 London households from November 2011 to February 2014 | LSTM | RMSE of 0.362 and an MAE of 17.8% |
| Proposed models | Saudi Arabia | Dataset: yearly electricity consumption, GDP, population, import, refined oil products from 2005 to 2020 | MLR, EXPS, BOA-LSTM | MAPE and of BOA-LSTM(TEC) is 1.05%, and 0.998, respectively; MAPE and of BOA-LSTM(REC) are 1.13%, 0.988, respectively |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almuhaini, S.H.; Sultana, N. Bayesian-Optimization-Based Long Short-Term Memory (LSTM) Super Learner Approach for Modeling Long-Term Electricity Consumption. Sustainability 2023, 15, 13409. https://doi.org/10.3390/su151813409
Almuhaini SH, Sultana N. Bayesian-Optimization-Based Long Short-Term Memory (LSTM) Super Learner Approach for Modeling Long-Term Electricity Consumption. Sustainability. 2023; 15(18):13409. https://doi.org/10.3390/su151813409
Chicago/Turabian StyleAlmuhaini, Salma Hamad, and Nahid Sultana. 2023. "Bayesian-Optimization-Based Long Short-Term Memory (LSTM) Super Learner Approach for Modeling Long-Term Electricity Consumption" Sustainability 15, no. 18: 13409. https://doi.org/10.3390/su151813409
APA StyleAlmuhaini, S. H., & Sultana, N. (2023). Bayesian-Optimization-Based Long Short-Term Memory (LSTM) Super Learner Approach for Modeling Long-Term Electricity Consumption. Sustainability, 15(18), 13409. https://doi.org/10.3390/su151813409






