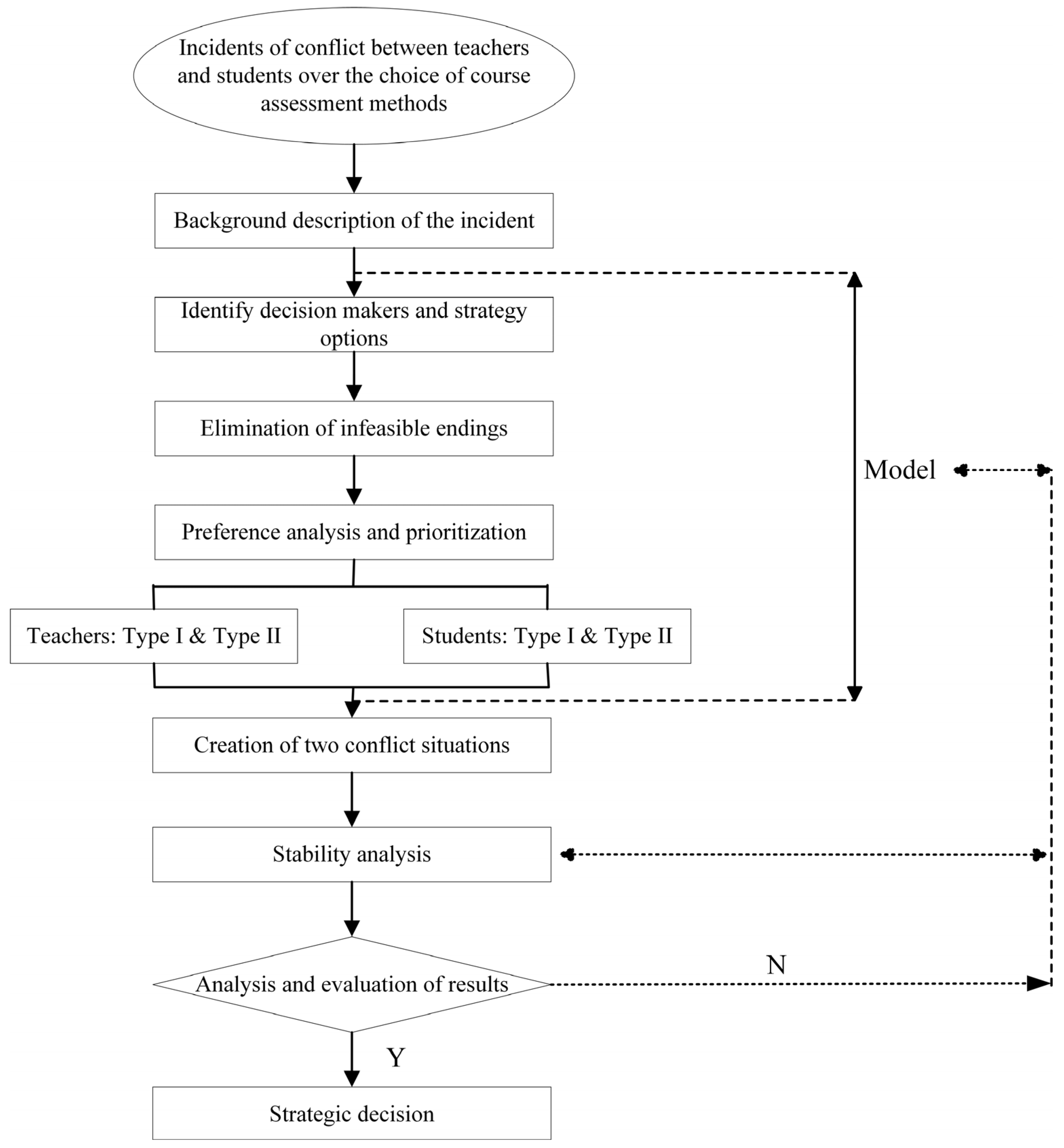
3.2.1. Build a Model
Determination of point in time (T): T = (t1, t2, t3, …, tn) refers to when a disagreement arises between a student and faculty member concerning the selection of a course. It includes the first course t1, second course t2, third course t3 and so on. The study examines “T” as a whole, meaning there is no differentiation between courses, and the final month or final week of the college term is used to define the time period.
Identification of the players in the game (N): Teacher “r” and student “b” are the two sides of the game.
Identification of action programs (O): curriculum assessment methods are selected by teachers, while students hold varying attitudes toward test-taking.
(1) Teachers Or = {Or1, Or2, …, Orn}: There are three possible courses of action, denoted by n = 3. (1) Closed-book examination (No. 1). In the context of online teaching, exams are conducted digitally with the support of platforms like Study Pass, Voov Meeting, and U Campus, featuring the electronic distribution of examination papers echoing the traditional approach of paper distribution in previous years. In offline mode, exams are administered directly and responded to uniformly within a designated time-frame. Or1 = {Closed-book examination}; (2) Open-book examination (No. 2). At the end of the course, examination papers, unlike in the closed-book examination format, are distributed. The testing timeline is predetermined, and the exam is conducted in unison, with students providing their answers autonomously by referring to their textbooks, lecture notes, and other resources. Or2 = {Open-book examination}; (3) Innovative examinations (No. 3–No. 7). Various methods such as papers, reports, group presentations, and others are implemented to conclude the course, depending on its features. Or3 = {Innovative examinations}.
(2) Students Ob = {Ob1, Ob2, …, Obm}: There are two courses of action. At once m = 2. (1) Strive to improve your performance to achieve high grades and approach exams with a constructive mindset. Ob1 = {Positive}. (2) Passive test-taking with the only objective of passing the exam. Ob2 = {Negative}.
- 4.
Determination of teacher-student gaming rules (A):
(1) Every teacher selects at least one assessment method. However, there could be cases in which students cannot take the exam because of illness, personal reasons, emergencies, or other reasons; hence, no action will be taken.
(2) As there is a combined form of assessment for the final exam, each course can be presented in only one of two ways, and it is not possible to choose both “Or1” and “Or2”.
(3) Both the teacher and the student can perceive information about the opponent’s posture. They are aware of all possible strategic options of the opponent, but they cannot determine the final course of action.
(4) Both teachers and students are rational individuals with their respective goals; teachers aim to motivate students to take the test, and students hope to be graded fairly while achieving higher grades in the course.
Finalize the expression: Assign the value “0” to indicate that the player in the game does not take action and “1” to indicate that they take action. Denote the conclusion of the event with a decimal number (“A” represents a decimal number).
Formula (2), where x
i = 0, 1; I = 1, 2, 3, …, r; “r” is the number of courses of action for all players [
37]. There are 2
5 outcomes to this conflict event, or 32 outcomes. The “2” in “2
5” refers to the two choices of action and inaction, and the “5” is “r = 5 “, i.e., 3 actions for teachers and 2 actions for students.
Table 4 shows all possible outcomes for the initial.
3.2.3. Preference Vector of Different Categories of Teachers and Students (P)
A questionnaire was utilized to explore the perceptions of curriculum assessment among teachers and students. Both groups were classified into two categories based on survey results and real-life experiences.
Teachers: The issue of how college courses are assessed can be classified into two groups, based on the differences in teachers’ teaching approach and their personal values. Type Ⅰ teachers are rigorous and conscientious, setting high standards and emphasizing teaching quality. They are strict with students and can make fair evaluations of grades. Type Ⅱ teachers are known as the permissive and casual type. They tend to be lenient with students and prioritize accomplishing the task of teaching and examining. Their work also targets other areas.
Students: All students aim to pass course exams, but they can be classified into two groups based on their attitudes towards exams and desired outcomes. The first category refers to students who aim only to pass the exam and approach it perfunctorily without regard to its format. The second category consists of students who are disciplined and aim to achieve high scores. They exhibit a great initiative towards learning and intend to enhance their knowledge and expertise by taking the exam.
The questionnaire survey was conducted in an offline mode where we questioned and recorded data from teachers and students in the school. The total number of valid respondents was 68 (16 teachers and 52 students). The dimension and content of the question and answer was their hesitancy scoring (1–10) about the assessment methods, positive/negative, and absenteeism. They have been made to cognize their self attitude towards learning and teaching before questioning. The test style in the strategy options is graded by designing categories such as “very satisfied”, “satisfied”, “fair”, “dissatisfied”, and “very dissatisfied”. The data are collected through the questionnaire. After assigning scores, the average score is calculated, and the concept of “hesitancy” is introduced. Here, hesitancy is defined as an integer between 1 to 10. For a player in a department, the impact of other players’ conduct in the department is indicated by the degree of hesitation (H). In the end, we calculate the total rejection degree “H” for each possible outcome of the game for every player, then rank the preference vectors of the players based on the magnitude of “H”. This ranking allows us to obtain the preference vectors of the players in the game. The degree of hesitation of a person in the bureau towards this behavior is higher as “H”, the degree of hesitation, increases, and conversely lower as “H” decreases. Formula (3) represents the summation of these “h”s:
From the teachers’ perspective, student engagement during exams is desirable. Additionally, teachers aim to prevent absenteeism and truancy during any type of exam, which could increase their workload and negatively impact students’ academic progress. Therefore, the value of teacher hesitancy is presented in
Table 6.
From the students’ perspective, one group prefers higher grades while the other prefers a greater differentiation of questions and stricter and fairer grading from teachers. The first group desires to pass the test with minimal effort.
Table 7 displays the values of the students’ hesitancy.
We calculated the total hesitancy “Hj” for each possible conclusion, and
Table 8,
Table 9,
Table 10 and
Table 11 show, in order, type Ⅰ teachers, type Ⅱ teachers, type Ⅰ students, type Ⅱ students.
The teachers aim to select rigorous and innovative assessment methods to identify students with high academic potential and positive learning attitudes. They prioritize Or3, Or1, and Or2 decision-making approaches while keeping efficiency in mind. To achieve this, adopting a scientific examination format is considered the best option. Therefore, among the suggested strategies, S9, S10, and S15 are better choices than S5, S6, S13, S3, S4, S12, S1, S2, S11, S7, S8, and S14. The least desirable ones are S7, S8, and S14. The priorities of the suggested strategies are as follows: S9, S10, S15, S5, S6, S13, S3, S4, S12, S1, S2, S11, S7, S8, and S14. The least desirable strategies are S7, S8, and S14. Strategies related to avoiding taking the test are ranked according to their degree of hesitancy and placed at the end of the prioritized order. Then, the overall degree of hesitancy is combined and the final prioritized order is determined by arranging the strategies in ascending order as follows: S9 > S5 > S3 > S1 > S7 > S10 > S6 > S4 > S2 > S8 > S15 > S13 > S12 > S11 > S14.
They are more willing to adopt innovative exam formats, such as essays and reports, that simplify task administration and reduce assessment time. Open-book examination is the next preferred format, with decision-making preferences of Or3, Or2, and Or1. When compared, strategies S9, S10, and S15 are preferred over S7, S8, and S14 and even better than S1, S2, and S11. S3, S4, and S12 are less preferred, while S5, S6, and S13 are the least preferred. Teachers are more forgiving with students, but still want students to complete the assessment. Therefore, the final prioritization order is S9 > S10 > S7 > S8 > S1 > S2 > S3 > S4 > S5 > S6 > S15 > S14 > S11 > S12 > S13.
Their decision preferences are Or5 and Or4, and it is in their best interest to pass the exams with ease and achieve high scores. Therefore, strategies S2, S4, S6, S8, and S10 are preferred over S1, S3, S5, S7, and S9, and even more so over S11, S12, S13, S14, and S15. Open-book examination is the easiest to pass, followed by innovative forms of exams, and lastly, traditional exams. When facing a situation with a missing exam, students regret taking the form of examination they expected to adopt the most. Therefore, the strategies with the highest degree of hesitation should be given a higher priority. The final priority order is as follows: S8 > S7 > S10 > S9 > S4 > S3 > S2 > S1 > S6 > S5 > S13 > S11 > S12 > S15 > S14.
Type II students has a positive attitude towards all types of exams. Therefore, strategies S1, S3, S5, S7, and S9 are preferable to S2, S4, S6, S8, and S10. They are also more suitable than S11, S12, S13, S14, and S15, especially if the exam is in the form of final essays, reports, etc. This type of exam is more likely to allow the second group of students to perform at their level. However, they are also concerned about perfunctory exams, which may lead to unfair score differentiation. They would prefer traditional exams in this scenario as they are interested in widening the score gap and obtaining more knowledge. Therefore, they are not willing to adopt open-book examination. The same rules for ranking apply for the type II students in case of missing exams, as described above for the first category of students. Therefore, the prioritization order of the final strategy for the Type II students is as follows: S5 > S1 > S9 > S3 > S7 > S6 > S2 > S10 > S4 > S8 > S14 > S12 > S15 > S11 > S13.